Security or severity? A research of COVID-19 pandemic control policy based on nonlinear programming approach

Abstract

The COVID-19 pandemic has caused huge impacts to human health and world's econ-omy. Finding out the balance between social productions and pandemic control becomes crucial. In this paper, we first extend the SIR model by introducing two new status. We calibrate the model by 2022 Shanghai COVID-19 outbreak. The results shows compared to zero-constraint policy, under our control policy, 50 % more life can be saved at the cost of 2.13 % loss of consumptions. Our results also emphasize the importance of the dynamic nature and the timing of control policy, either a static pandemic control or a lagged pandemic control damages badly to people's livelihood and social productions. Counter factual experiments show that compared to the baseline, when a persistent high-strength control is applied, aggregate productions decreases by 57 %; when pandemic control ends too early, the death would rise by 15 %, when pandemic control starts too late, the death rises by 23 % and aggregate productions decreases by 13 %.

1. Introduction

Over the last 2 years, COVID-19 has caused huge damage to the world, so far, WHO reports 570 million global accumulated COVID-19 cases and 6.4 million deaths, in the United States, life expectancy has dropped to 76.6 years old from 78.78 years old in only 2 years. Consecutive waves of COVID-19 outbreaks have also caused huge damage to economic production activities, in 2020, only two countries of G20 had positive GDP growth, in 2021 there has been a shortage of global labors and the inflation rate started to rise. The first half of 2022 is also tough, the United States has contracted a negative annualized quarter-on-quarter GDP growth rate in the first two seasons, China only reports a 2.5 % GDP growth for the first half of 2022, which is the second lowest GDP growth in almost 40 years. As COVID-19 continues to spread throughout the world, governments find themselves struggling dealing with the pandemic, various policies have been proposed but it is difficult to tell which one is the most appropriate in order to maintain social production activities while simultaneously contain the spread of the pandemic.

2. Literature review

Epidemiologists have put efforts in order to contain the COVID-19 pandemic, Wu and McGoogan [43] investigate early development of COVID-19 outbreak in Wuhan and summaries characteristics of this disease, Kucharski et al. [26] combine a stochastic transmission model and data from Wuhan to study early dynamics of COVID-19 transmission, Cai et al. [8] construct a modified SIR model and predicts 1.55 million deaths caused by unabated Omicron pandemic in China. In summary, the COVID-19 causing virus is highly contagious and is able to spread even at incubation stage. 2 approaches are widely accepted as being effective against the COVID-19 pandemic, the first one is mass vaccination [4,24,37], the other one is isolation of patients [11,40,41]. Unfortunately, there hasn't been a COVID-19 vaccine that can provide strong enough immunity against COVID-19 causing virus and all its variants [6,22,42], in addition, the problem of immunity escape becomes more and more severe [3,16,19], making it harder to only rely on vaccines to contain the COVID-19 pandemic. In comparison, isolation of patients is a more direct policy since it aims at cutting virus transmissions, nevertheless, a partial or a full lock down often plays as the practical form of this isolation policy, which by consequence interrupts or even suspends social production activities and worsens the economy.

Today's world is almost divided in half in terms of COVID-19 pandemic control, on the one hand, all developed countries choose to start loosening or completely abandon pandemic control since 2022 [13]. The COVID-19 disease does have a relative low rate of death and a high chance of recovery, which gives space to the herd immunity policy whose core is to spread the disease as fast as possible [36]. However, the problem of immunity escape mentioned above and the “long covid” effect that affects working abilities of recovered people [10,17,32,35] have significantly reduced the feasibility of this policy. On the other hand, some countries are still applying pandemic control at a relatively more restrictive level, China, as one of the exemplary countries, still insist on applying “dynamic zero-COVID policy”. However, when it is applied at local level, being free of any possible infection often becomes the only goal of this policy, all associated economic damage due to interruptions or suspension of productions activities are considered as acceptable costs. We consider these two pandemic control policies both extreme measures, it's therefore necessary to look for a policy that is capable of controlling the pandemic scale while simultaneously maintaining aggregate production activities.

Lack of effective vaccines makes the isolation policy a substantial measure in order to control the pandemic. Canuto [9] studies the COVID-19 pandemic and finds out that the pandemic could have been contained through necessary government's interventions, overload of medical system could also have been avoided. Hellewell et al. [20] builds a stochastic COVID-19 transmission model and the model shows that at least 70 % contacts with infected patients need to be reduced in order to contain the outbreak. Ali et al. [2] builds a deterministic model and finds out that the isolation policy is effective to contain a pandemic by significantly reducing the basic reproduction number (R₀). Nevertheless, application of isolation policy requires expensive costs. Meltzer et al. [33] studies the effect of flu season on American's economy and the results show that influenza vaccination coverage needs to be at 60 % in order for the vaccination policy to generate economical benefits. Sander et al. [39] compares plural combinations of pandemic control strategies and finds out that they all generate enormous financial pressure for the government. In a nutshell, government's choice of control policy has an important effect on pandemic containment. However, since the ultimate goal of pandemic control is to get people's daily life back to normal as soon as possible, the economic costs of control strategy is thus necessary to be taken into account, i.e. cost and return of control policy need to be carefully discussed when making the decision.

Plentiful discussions have already been made on this cost and return issue, most of them focus on finding the optimum strategy that minimizes direct monetary cost of intervention policy [7,31]. But as Beutels et al. [5] argues, this definition remains narrow since pandemic control generates a serial of consequences that produces derived effects such as interruptions of aggregate production activities. These effects should also be considered as costs of pandemic control. Eichenbaum et al. [14] simulates the diffusion process of COVID-19 in the United States based on SIR transmission model, the results show that at maximum 70 % more consumption tax needs to be imposed in order to contain the pandemic, by consequence, aggregate consumptions would decrease by 30 % than before the pandemic.

In this paper we focus on how the isolation policy should be pursued in order to balance pandemic containment and social production activities. Following most prior literatures [1,14,38], we also simulate COVID-19 transmissions using the SIR model, we assume that the virus can be transmitted through consumption, work and other contacts. We extend the original model by introducing two new status, the exposed (E) and the quarantined(Q), the former is referred to people who have already been infected but not yet shown symptoms, the latter is referred to people who are isolated by government's intervention policy. By this extension, our model is able to replicate a dynamic transmission process involving government's interventions. We then design the optimal policy that maximizes social welfare, while holding the equilibrium between aggregate consumptions (Demand) and aggregate productions (Supply) everywhere in the model. We further assume that an individual always needs to consume no matter his status, but only those who are not isolated can produce, from this perspective, the policy maker faces the tradeoff between present production activities and future production activities, a weaker pandemic control increases present aggregate productions but decreases future productions as the virus spreads, contrarily, a stronger pandemic control decreases present aggregate productions but restores productivities more quickly as the pandemic is well contained. Similar to Eichenbaum et al. [14], we also conclude that an economy recession caused by the pandemic is inevitable. The aggregate supply goes down because of decrease of number of workers as the virus begins to spread, the aggregate demand also drops because people would like to decrease their consumptions for being afraid of getting infected and losing incomes. Nevertheless, our model is able of providing an isolation policy that helps reduce the effect of economy recession as much as possible. We calibrate our model with 2022 outbreak in Shanghai, this outbreak of Omicron variant has been the most severe COVID-19 outbreak since Wuhan, it has the biggest pandemic scale and also cause most damage to Chinese economy. It's therefore necessary to carefully examine this outbreak and learn lessons from it. We find out that a dynamic control policy with well timing is the most suitable choice. However, mass COVID-19 nucleic acid tests combined with 0 mobility restriction does generate the highest aggregate productions yet at the cost of 50 % more deaths than in the benchmark model, nevertheless, if “long covid” effect is taken into account, aggregate productions in this scenario decline and eventually falls below the scenario where optimal isolation policy from the benchmark model is applied. Compared to a static high-strength mobility restriction, the dynamic isolation policy can save up to 56.9 % more aggregate productions while not causing too many “excess” deaths. Using the benchmark model, we also test the effect of ending the pandemic control too early and the effect of starting the pandemic control too late, results show that in either scenario the costs would be highly expensive, when end the control too early, there will be 15.4 % more deaths, when start the control too late, not only there would be 23.3 % more deaths and 23.55 % more accumulated infected cases, but also the total social productions would decrease by 12.9 % since the control needs to be strengthened from the start.

The remainder of this paper is organized as follows. In section 2, we first introduce the original SIR model, then we discuss how we build our extension, afterwards, we discuss how to solve the related optimal problem. In section 3 we discuss how we calibrate our model then we present the benchmark results and robustness examinations. In section 4 we conduct 2 series of counter factual experiments, then we compare their results with the benchmark model and perform analysis. In section 5, we conclude the paper and offer some concluding remarks.

3. The extended SIR model

3.1. Dynamics of virus transmission

Our model is build based on the SIR virus transmission model [25], the original model contains three status, S (Suspected) is referred to people who have not yet been infected by the virus; I (Infected) is referred to people who are already infected; R (Recovered) denotes those who have recovered from the disease. Furthermore, D denotes the death and T denotes the newly infected case. Total population is normalized to 1, the initial fraction of infected people is denoted as I₁, thus the dynamics of virus transmission process can be described by equation system (1):

$$\begin{array}{l}{S}_t=S_{t-1}-T_{t-1}\\ I_t=I_{t-1}+T_{t-1}-\left({\pi }_r+{\pi }_d\right)I_{t-1}\\ R_t=R_{t-1}+{\pi }_r{I}_{t-1}\\ D_t=D_{t-1}+{\pi }_d{I}_{t-1}\end{array}$$ (1)

where π_r is the rate of recovery and π_d is the rate of death.

We extend the SIR model by introducing two new status, E (Exposed) and Q (Quarantined), the former is referred to people who are infected but not yet show symptoms, i.e. an exposed person and an infected person are distinguished by whether he shows symptoms or not. The quarantined is referred to people who are isolated by government's intervention, it includes the infected cases as well as people who have been exposed to virus and detected by the government through mass COVID-19 nucleic acid tests. After a certain period of time, an exposed person will begin to show symptoms and become an infected case, we use n_inc to denote the average duration of this period. Hence, the probability for an exposed person to become an infected person at t is given by ${\pi }_{EI}=\frac{1}{n_{inc}}$.A quarantined person shares the same probability of becoming an infected case as an exposed person.

For reason of simplicity, we use the SEQIR model as the name of our extension hereafter. Total population is normalized to 1, the initial fraction of exposed people is denoted as E₁, thus we have $I_1={\pi }_{EI}{E}_1$ and $S_1=1-E_1$. The dynamics of virus transmission process can be described by equations system (2)

$$\begin{array}{r}{S}_t=S_{t-1}-N{E}_{t-1}\\ E_t=E_{t-1}\left(1-{\pi }_{EI}\right)\left(1-\phi \right)+N{E}_{t-1}\\ Q_t=\left(1-{\pi }_{EI}\right)\left(E_{t-1}\phi +Q_{t-1}\right)\\ I_t=\left(1-{\pi }_r-{\pi }_d\right)I_{t-1}+{\pi }_{EI}\left(Q_{t-1}+E_{t-1}\right)\\ R_t=R_{t-1}+{\pi }_r{I}_{t-1}\\ D_t=D_{t-1}+{\pi }_d{I}_{t-1}\end{array}$$ (2)

where φ denotes the mean coverage rate of COVID-19 tests and NEt denotes the number of newly exposed case at t. We follow Eichenbaum et al. [14] assuming that the COVID-19 virus is only transmitted through three ways, consumption, work and other contacts. The probability of transmission of these three ways are denoted by π₁, π₂ and π₃, respectively. Besides, we define $r_t^m$ as the level of restriction on mobility by government's isolation policy at t, thus the number of newly increased exposed case can be described as equation (3)

$$N{E}_t=\left[S_t{E}_t{c}_t^s{c}_t^e{\pi }_1+S_t{E}_t{n}^2{\pi }_1+S_t{E}_t{\pi }_3\right]\times \left(1-r_t^m\right)$$ (3)

where $c_t^s$ and $c_t^e$ are consumptions of suspected people at t, n is number of working hours and is assumed to be constant.

3.2. Optimal pandemic control policy

In this paper we aim at looking for isolation policy that is able to contain the pandemic and simultaneously maintains social productions. We assume that the government can only adjust its mobility restriction level while holding a constant COVID-19 test coverage rate. Following Eichenbaum et al. [14], the amount of aggregate productions is defined as the product of productivity parameter A and the number of available workers at t, in addition, productions are also affected by government's mobility restriction level. The amount of aggregate productions V at t can be written as equation (4)

$$V_t=A\left[S_t+E_{t-1}\left(1-{\pi }_{EI}\right)\left(1-\phi \right)+R_{t-1}\right]\left(1-r_t^m\right)$$ (4)

At equilibrium, aggregate consumptions equal to aggregate productions, as shown by equation (5)

$$A\left[S_t+E_{t-1}\left(1-{\pi }_{EI}\right)\left(1-\phi \right)+R_{t-1}\right]\left(1-r_t^m\right)=c_t^s{S}_t+c_t^e{E}_t+c_t^q{Q}_t+c_t^i{I}_t+c_t^r{R}_t$$ (5)

At each moment, an individual consumes all his income after paying his tax, as shown

by equation below

$$c_t^s=\left(1-{\tau }_t\right)w_t;c_t^e=\left(1-{\tau }_t\right)w_t;c_t^q=w_1-b_2;c_t^i=k_i{w}_1;c_t^r=\left(1-{\tau }_t\right)w_t$$

we further define the utility function as

$$u\left(c_t^j\right)=\mathit{ln}\left(c_t^j\right)j=S,E,Q,I,R$$

where w1 is the income before outbreak, k_i denotes the ratio between lump-sum transfers given to the infected people and w1, τt represents the rate of tax collected from available workers. During the pandemic control, the government provides financial aids to the exposed and the infected, it also pays all COVID-19 treatment fees and COVID-19 nucleic acid tests fees. Quarantine fees needs to be paid by a quarantined person himself. The cost of one single COVID-19 test is denoted as b₁, quarantine fees at t is denoted as b₂, treatment fees at t is denoted as m, the aforementioned relationship can be written by equation (6)

$${\tau }_t{w}_t\left[S_t+E_{t-1}\left(1-{\pi }_{EI}\right)\left(1-\phi \right)+R_{t-1}\right]=b_1\left(S_t+E_t\left(1-{\pi }_{EI}\right)\right)\phi +\left(m+k_i{w}_1\right)I_t+w_1{Q}_t$$ (6)

The government aims at maximizing social welfare, which means maximizing aggregate consumption, since aggregate consumptions equals to aggregate productions at any moment, this optimal problem can be easily translated as equation (7)

$${\max }_{r_t^m}{\mathrm{\Sigma }}_{t=1}^T{\beta }^{t-1}{V}_t$$ (7)

where T is the assumed length of pandemic control period.

We assume that w₁ = A, before the outbreak, profits Π of the representative firm can be written as

$$\mathrm{\Pi }=AN-w_{1}N$$

Clearly when w₁ = A, the representative firm's profit is maximized.

The government's constraint is given by the following 2 equations

$$\begin{array}{c}A\left[S_t+E_{t-1}\left(1-{\pi }_{EI}\right)\left(1-\phi \right)+R_{t-1}\right]\left(1-r_t^m\right)=c_t^s{S}_t+c_t^e{E}_t+c_t^q{Q}_t+c_t^i{I}_t+c_t^r{R}_t\\ {\tau }_t{w}_t\left[S_t+E_{t-1}\left(1-{\pi }_{EI}\right)\left(1-\phi \right)+R_{t-1}\right]=b_1\left(S_t+E_t\left(1-{\pi }_{EI}\right)\right)\phi +\left(m+k_i{w}_1\right)I_t+w_1{Q}_t\end{array}$$

Assuming that S₁ and E₁ are known, R₁ = Q₁ = D₁ = 0, the optimal pandemic control problem can be therefore written in the form of a Lagrangian function as follows,

$$\mathcal{L}={\mathrm{\Sigma }}_{t=2}^T{\beta }^{t-1}A{S}_t\left(1-r_t^m\right)+{\mathrm{\Sigma }}_{t=1}^{T-1}{\beta }^{t}A{E}_t\left(1-{\pi }_{EI}\right)\left(1-\phi \right)\left(1-r_{t+1}^m\right)+{\mathrm{\Sigma }}_{t=1}^{T-1}{\beta }^{t}A\left(R_t+{\pi }_r{I}_t\right)\left(1-r_{t+1}^m\right)+A\left(S_1+E_1\left(1-{\pi }_{EI}\right)\right)\left(1-r_1^m\right)n+{\mathrm{\Sigma }}_{t=2}^T{\beta }^{t-1}{\lambda }_t^e{E}_t-{\mathrm{\Sigma }}_{t=1}^{T-1}{\beta }^t{\lambda }_{t+1}^e{E}_t\left(1-{\pi }_{EI}\right)\left(1-\phi \right)-{\mathrm{\Sigma }}_{t=1}^{T-1}{\beta }^t{\lambda }_{t+1}^{e}N{E}_{t}n+{\mathrm{\Sigma }}_{t=2}^T{\beta }^{t-1}{\lambda }_t^s{S}_t-{\mathrm{\Sigma }}_{t=1}^{T-1}{\beta }^t{\lambda }_{t+1}^s{S}_t+{\mathrm{\Sigma }}_{t=1}^{T-1}{\beta }^t{\lambda }_{t+1}^{s}N{E}_t+{\mathrm{\Sigma }}_{t=1}^T{\beta }^{t-1}{\lambda }_t^{ne}\left[N{E}_t-\left(S_t{E}_t{c}_t^s{c}_t^e{\pi }_1+S_t{E}_t{n}^2{\pi }_2+S_t{E}_t{\pi }_3\right)\left(1-r_t^m\right)\right]+{\mathrm{\Sigma }}_{t=2}^T{\beta }^{t-1}{\lambda }_t^i{I}_t-{\mathrm{\Sigma }}_{t=1}^{T-1}{\beta }^t{\lambda }_{t+1}^i\left(1-{\pi }_r-{\pi }_d\right)I_t-{\mathrm{\Sigma }}_{t=1}^{T-1}{\beta }^t{\lambda }_{t+1}^i{\pi }_{EI}\left(Q_t+E_t\right)+{\mathrm{\Sigma }}_{t=2}^T{\beta }^{t-1}{\lambda }_t^q{Q}_t-{\mathrm{\Sigma }}_{t=1}^{T-1}{\beta }^t{\lambda }_{t+1}^q\left(1-{\pi }_{E}I\right)\left(E_t\phi +Q_t\right)+{\mathrm{\Sigma }}_{t=1}^T{\beta }^{t-1}{\lambda }_t^{cs}\left[c_t^s-w_t\left(1-{\tau }_t\right)\right]+{\mathrm{\Sigma }}_{t=1}^T{\beta }^{t-1}{\lambda }_t^{ce}\left[c_t^e-w_t\left(1-{\tau }_t\right)\right]+{\mathrm{\Sigma }}_{t=2}^T{\beta }^{t-1}{\lambda }_t^b\left(A{S}_t\left(1-r_t^m\right)-c_t^s{S}_t-c_t^e{E}_t-c_t^q{Q}_t-c_t^i{I}_t-c_t^r{R}_t\right)+{\mathrm{\Sigma }}_{t=1}^{T-1}{\beta }^t{\lambda }_{t+1}^{b}A\left[E_t\left(1-{\pi }_{EI}\right)\left(1-\phi \right)+R_t+{\pi }_r{I}_t\right]\left(1-r_{t+1}^m\right)n+{\lambda }_1^{b}A\left[\left(S_1+E_1\left(1-{\pi }_{EI}\right)\right)\left(1-r_1^m\right)-c_1^s{S}_1-c_1^e{E}_1-c_1^i{I}_1\right]+{\mathrm{\Sigma }}_{t=2}^T{\beta }^{t-1}{\lambda }_t^{\tau }{\tau }_t{w}_t{S}_t-b1\left(S_t+E_t\left(1-{\pi }_{EI}\right)\right)\phi -\left(m+k_i{w}_t\right)I_t-w_1{Q}_t]+{\mathrm{\Sigma }}_{t=1}^{T-1}{\beta }^t{\lambda }_{t+1}^{\tau }\left[{\tau }_{t+1}{w}_t\left(E_t\left(1-{\pi }_{EI}\right)\left(1-\phi \right)\right)+R_t+{\pi }_r{I}_t\right]+{\lambda }_1^{\tau }\left[{\tau }_1{w}_1\left(S_1+E_1\left(1-{\pi }_{EI}\right)\right)-b_1\left(S_1+E_1\left(1-{\pi }_{EI}\right)\right)\phi -\left(m+k_i\right)I_1\right]$$

The First order conditions are given by

$$\begin{array}{l}\frac{\partial \mathcal{L}}{\partial S_t}=A\left(1-r_t^m\right)+{\lambda }_t^s-\beta {\lambda }_{t+1}^s-{\lambda }_t^{ne}\left(E_t{c}_t^s{c}_t^e{\pi }_1+E_t{n}^2{\pi }_2+E_t{\pi }_3\right)\left(1-r_t^m\right)\\ +{\lambda }_t^b\left(A\left(1-r_t^m\right)-c_t^s\right)+{\lambda }_t^{\tau }\left({\tau }_t{w}_t-b_1\phi \right)t=2\dots T-1\\ \frac{\partial \mathcal{L}}{\partial E_t}=\beta A\left(1-{\pi }_{EI}\right)\left(1-\phi \right)\left(1-r_{t+1}^m\right)+{\lambda }_t^e-\beta {\lambda }_{t+1}^e\left(1-{\pi }_{EI}\right)\left(1-\phi \right)\\ -{\lambda }_t^{ne}\left(S_T{c}_T^s{c}_T^e{\pi }_1+S_T{n}^2{\pi }_2+S_T{\pi }_3\right)\\ -\beta {\lambda }_{t+1}^i{\pi }_{EI}-\beta {\lambda }_{t+1}^q\phi \left(1-{\pi }_{EI}\right)-{\lambda }_t^b\left(c_t^e\right)+\beta {\lambda }_{t+1}^{b}A\left(1-{\pi }_{EI}\right)\left(1-\phi \right)\left(1-r_{t+1}^m\right)-{\lambda }_t^{\tau }{b}_1\phi \left(1-{\pi }_{EI}\right)\\ +\beta {\lambda }_{t+1}^{\tau }{\tau }_{t+1}{w}_t\left(1-{\pi }_{EI}\right)\left(1-\phi \right)t=2\dots T-1\\ \frac{\partial \mathcal{L}}{\partial E_T}={\lambda }_T^e-{\lambda }_T^{ne}\left(S_T{c}_T^s{c}_T^e{\pi }_1+S_T{n}^2{\pi }_2+S_T{\pi }_3\right)\left(1-r_T^m\right)-b_1\left(1-{\pi }_{EI}\right)\phi {\lambda }_T^{\tau }\\ \frac{\partial \mathcal{L}}{\partial I_t}=\beta A{\pi }_r\left(1-r_{t+1}^m\right)+{\lambda }_t^i-\beta {\lambda }_{t+1}^i\left(1-{\pi }_r-{\pi }_d\right)-{\lambda }_t^b{c}_t^i+\beta {\lambda }_{t+1}^{b}A{\pi }_r\left(1-r_{t+1}^m\right)\\ -{\lambda }_t^{\tau }\left(m+k_i{w}_1\right)+\beta {\lambda }_{t+1}^{\tau }{\pi }_r{w}_{t}t=2\dots T-1\\ \frac{\partial \mathcal{L}}{\partial I_T}=-c_T^i-\left(m+k_i{w}_1\right){\lambda }_T^{\tau }\\ \frac{\partial \mathcal{L}}{\partial r_1^m}={\lambda }_1^{ne}\left(S_1{E}_1{c}_1^s{c}_1^e{\pi }_1+S_1{E}_1{n}^2{\pi }_2+S_1{E}_1{\pi }_3\right)\\ -A\left[S_t+E_{t-1}\left(1-{\pi }_{EI}\right)\right]-A{\lambda }_1^b\left[S_t+E_{t-1}\left(1-{\pi }_{EI}\right)\right]\\ \frac{\partial \mathcal{L}}{\partial r_t^m}={\lambda }_t^{ne}\left(S_t{E}_t{c}_t^s{c}_t^e{\pi }_1+S_t{E}_t{n}^2{\pi }_2+S_t{E}_t{\pi }_3\right)\\ -A\left[S_t+E_{t-1}\left(1-{\pi }_{EI}\right)\left(1-\phi \right)+R_{t-1}+{\pi }_{EI}{I}_{t-1}\right]\\ -A{\lambda }_t^b\left[S_t+E_{t-1}\left(1-{\pi }_{EI}\right)\left(1-\phi \right)+R_{t-1}+{\pi }_{EI}{I}_{t-1}\right]t=2\dots T\\ \frac{\partial \mathcal{L}}{\partial N{E}_t}=-\beta {\lambda }_{t+1}^e+\beta {\lambda }_{t+1}^s+{\lambda }_t^{ne}t=1\dots T-1\\ \frac{\partial \mathcal{L}}{\partial N{E}_T}={\lambda }_T^{ne}\\ \frac{\partial \mathcal{L}}{\partial Q_t}=-\beta {\lambda }_{t+1}^i{\pi }_{EI}-\beta {\lambda }_{t+1}^q\left(1-{\pi }_{E}I\right){\lambda }_t^b{c}_t^q+{\lambda }_t^q-{\lambda }_t^{\tau }{w}_{1}t=2\dots T-1\\ \frac{\partial \mathcal{L}}{\partial Q_T}=-{\lambda }_T^b{c}_T^q-{\lambda }_T^{\tau }{w}_1\\ \frac{\partial \mathcal{L}}{\partial c_t^s}={\lambda }_t^{cs}-{\lambda }_t^b{S}_t-{\lambda }_t^{ne}{S}_t{E}_t{\pi }_1\left(1-r_t^m\right)c_t^{e}t=1\dots T\\ \frac{\partial \mathcal{L}}{\partial c_t^e}={\lambda }_t^{ce}-{\lambda }_t^b{E}_t-{\lambda }_t^{ne}{S}_t{E}_t{\pi }_1\left(1-r_t^m\right)c_t^{s}t=1\dots T\end{array}$$

In this system, unknown variables are ${\left\{S_t\right\}}_{t=2}^T,{\left\{E_t\right\}}_{t=2}^T,{\left\{N{E}_t\right\}}_{t=1}^T,{\left\{Q_t\right\}}_{t=2}^T,{\left\{I_t\right\}}_{t=1}^T,{\left\{R_t\right\}}_{t=2}^T,{\left\{c_t^s\right\}}_{t=1}^T\text{,}$.

${\left\{{\mathrm{c}}_{\mathrm{t}}^{\mathrm{e}}\right\}}_{\mathrm{t}=1}^{\mathrm{T}},{\left\{{\mathrm{c}}_{\mathrm{t}}^{\mathrm{q}}\right\}}_{\mathrm{t}=1}^{\mathrm{T}},{\left\{{\mathrm{c}}_{\mathrm{t}}^{\mathrm{i}}\right\}}_{\mathrm{t}=1}^{\mathrm{T}},{\left\{{\mathrm{c}}_{\mathrm{t}}^{\mathrm{r}}\right\}}_{\mathrm{t}=1}^{\mathrm{T}},{\left\{{\mathrm{\tau }}_{\mathrm{t}}\right\}}_{\mathrm{t}=1}^{\mathrm{T}},{\left\{{\mathrm{\lambda }}_{\mathrm{t}}^{\mathrm{e}}\right\}}_{\mathrm{t}=2}^{\mathrm{T}},{\left\{{\mathrm{\lambda }}_{\mathrm{t}}^{\mathrm{s}}\right\}}_{\mathrm{t}=2}^{\mathrm{T}},{\left\{{\mathrm{\lambda }}_{\mathrm{t}}^{\text{ne}}\right\}}_{\mathrm{t}=1}^{\mathrm{T}},{\left\{{\mathrm{\lambda }}_{\mathrm{t}}^{\mathrm{i}}\right\}}_{\mathrm{t}=2}^{\mathrm{T}},{\left\{{\mathrm{\lambda }}_{\mathrm{t}}^{\mathrm{q}}\right\}}_{\mathrm{t}=2}^{\mathrm{T}},{\left\{{\mathrm{\lambda }}_{\mathrm{t}}^{\text{cs}}\right\}}_{\mathrm{t}=1}^{\mathrm{T}},{\left\{{\mathrm{\lambda }}_{\mathrm{t}}^{\text{ce}}\right\}}_{\mathrm{t}=1}^{\mathrm{T}},{\left\{{\mathrm{\lambda }}_{\mathrm{t}}^{\mathrm{b}}\right\}}_{\mathrm{t}=1}^{\mathrm{T}}$ and ${\left\{{\mathrm{\lambda }}_{\mathrm{t}}^{\mathrm{\tau }}\right\}}_{\mathrm{t}=1}^{\mathrm{T}}$.in total there are 21 × T – 8 variables. Correspondingly, we also have 21 × T − 8 function. The algorithm applied is described as follows, the command fsolve in Matlab is applied to solve such a non-linear programming problem

• ●With calibrated values of parameters and assuming that for now no external intervention is made, given initial guess of S₁, E₁, Q₁, I₁ and R₁, we first compute sequences of ${\left\{S_t,E_t,Q_t,I_t,R_t,N{E}_t\right\}}_{t=1}^T$, we take S_T, E_T, Q_T, I_T, R_T as fraction of people of different groups in steady status, besides, we also take NE_T and τ_T as the steady value of NE and τ;
• ●We update the ${\left\{S_t,E_t,Q_t,I_t,R_t,N{E}_t\right\}}_{t=1}^T$ by their respective steady status value and solve the steady status version of our model with Matlab command fsolve in order to get initial guess of Lagrangian multipliers ${\left\{{\lambda }_t^e\right\}}_{t=2}^T,{\left\{{\lambda }_t^s\right\}}_{t=2}^T,{\left\{{\lambda }_t^{ne}\right\}}_{t=1}^T，{\left\{{\lambda }_t^i\right\}}_{t=2}^T,{\left\{{\lambda }_t^q\right\}}_{t=2}^T,{\left\{{\lambda }_t^{cs}\right\}}_{t=1}^T,{\left\{{\lambda }_t^{ce}\right\}}_{t=1}^T,{\left\{{\lambda }_t^b\right\}}_{t=1}^T$ and ${\left\{{\lambda }_t^{\tau }\right\}}_{t=1}^T$, the steady status version of our model is in appendix A;
• ●Updating the value of Lagrangian multipliers, with given initial value of all other variables, we apply fsolve to solve the model and compute the sequence optimal mobility restriction level ${\left\{r_t^m\right\}}_{t=1}^T$, the actual process is described in appendix B.

3.3. Parameter calibration

Data collected from the COVID-19 outbreak in Shanghai in March 2022 is taken as reference to calibrate the model. We made this decision for two main reasons: first, this outbreak is the largest COVID-19 outbreak in China since Wuhan, it therefore offers relatively rich data to calibrate parameter values in our model; second, not only it causes severe damage to local economy as well as nation's, but also it is the most controversial issue in China during the first half of 2022 and raises huge concerns about how to choose an appropriate pandemic control policy. It is therefore necessary to take this outbreak as an example, examine it, study it and learn lessons from it. In latter sections, we shall use other outbreaks as examples to test the robustness of our model. Data we use are collected from Shanghai statistical yearbook published by Shanghai Municipal Bureau of Statistics and press conferences hold by Shanghai CDC on a daily base during the outbreak. We consider 20 accumulated exposed people as the starting point, the corresponding date is 7th March 2022, 24th June is considered as the end, the duration of this outbreak cycle is 112 days, thus we set T = 112. According to Shanghai CDC, up to 24th June, the number of total accumulated infected case is 649,651 and the total death toll is 595, hence we set the rate of death as πd = 0.000916. Cai et al. [8] predicts on average, a person infected by Omicron can recover in 6.8 days, which is almost the same as the median of recovery cycle obtained from ex-post analysis by Shanghai CDC, therefore we set rate of recovery as ${\pi }_r=\frac{1}{6.8}-{\pi }_d$. We follow Cai et al. [8] assuming that the time needed for an exposed case to become an infected case is about 1.2 days, i.e. n_inc = 1.2, hence the transformation probability for an exposed case to become an infected case equals to ${\pi }_{EI}=\frac{1}{n_{inc}}=0.833$.

We calculate the average COVID-19 test coverage rate in Shanghai from March to July by following the press conference hold by Shanghai CDC on a daily base, we set φ = 0.37. The cost of one single COVID-19 test is set to b₁ = 8 yuan, quarantined fees per day are set to b₂ = 300 yuan, treatment fees per day are set to m = 400 yuan. Number of working hours is fixed to 8 h per day. According to Shanghai statistical yearbook of 2021, daily income in Shanghai equals to w₁ = 135485/360 = 376.35 yuan. A quarantined person's disposable income is therefore set to w₁ −b₂ = 76.35 yuan. For an infected case, his income equals to kiw1 and Shanghai government fixes k_i = 0.6. At last, we follow Eichenbaum et al. [14] to set β equals to β = 0.961/360. The initial total population has been set to 1, thus the initial fraction of exposed cases is set to E₁ = 0.00000078.

To calibrate the parameter values of π₁, π₂ and π₃, we follow the same method applied by Eichenbaum et al. [14]. Ferguson et al. [15] has calculated that during the flu season, 33 % of infected case are related to consumptions, 37 % of infected cases are related to workplace and school, the rest 30 % infected cases are related to other activities. According to 2018 Chinese time utilization report, urban citizens spend on average 105 min per day on eating activities. HU [21] calculated that the share of out door eating activities in all eating activities for urban citizens is 17.34 %, thus we can compute that the average time spent on out door eating activities for Chinese urban citizens is 18.207 min per day. According to 2018 Chinese time utilization report, urban citizens spend on average 25 min per day on out door purchasing merchandises and services, 24 min per day on social interaction events, 29 min per day on learning and training activities, 3 min per day on public events and 44 min per day on traffics. In total, we compute that urban citizens spend on average 87.207 min per day on consumption activities of all types, 143.207 min per day on out door activities, the share of out door consumption activities of all types is around 61 %, since 33 % of infected cases are related to consumptions, we assume that 20 % (0.61 × 0.33) of transmissions are associated with consumptions. As for transmissions occurred in workplace and school, the Shanghai statistical yearbook of 2021 reports 1,603,590,000 residents between age 25 and 65, 380,320,000 residents between age 5 and 24, we consider the former group as the worker group and the latter group as the student group, following Lee et al. [28], we assume that a student meets on average 10 people and a worker meets on average 4 people on a daily base, we therefore obtain that 62 % of transmissions occur in workplaces ((1602.59 × 4)/(1602.59 × 4 + 382.32 × 10)), since 37 % of all infected cases are related to workplace and school, we set 23 % as the share of transmissions occur in workplaces (0.62 × 0.37).

The rest infected cases are assumed to be related to other activities. In summary, values of π₁, π₂ and π₃ must satisfy the following two equations

$$\begin{array}{c}\frac{{\pi }_1{C}^2}{{\pi }_1{C}^2+{\pi }_2{N}^2+{\pi }_3}=0.2\\ \frac{{\pi }_2{N}^2}{{\pi }_1{C}^2+{\pi }_2{N}^2+{\pi }_3}=0.23\end{array}$$

where C and N are consumptions and working hours before the outbreak, i.e. C = A = w₁ and N = n. Finally, we adjust values of transmission parameters by calibrating basic reproduction number R₀ of Omicron, the transmissibility of Omicron is estimated to be about 3 times greater than that of Delta variant [12,23,34], whose R0 is estimated to be between 3 and 5. We therefore set R₀ of Omicron as 10, we use the same method as Eichenbaum et al. [14] to calculate R₀, which is written as follows

$$R_0=\frac{N{E}_1/E_1}{{\pi }_r+{\pi }_d}$$

The calibrated values of π₁, π₂ and π₃ are 2.0766 × 10⁻6, 0.005 and 0.8382, respectively.

4. Numerical results

4.1. Optimal solution in the benchmark model

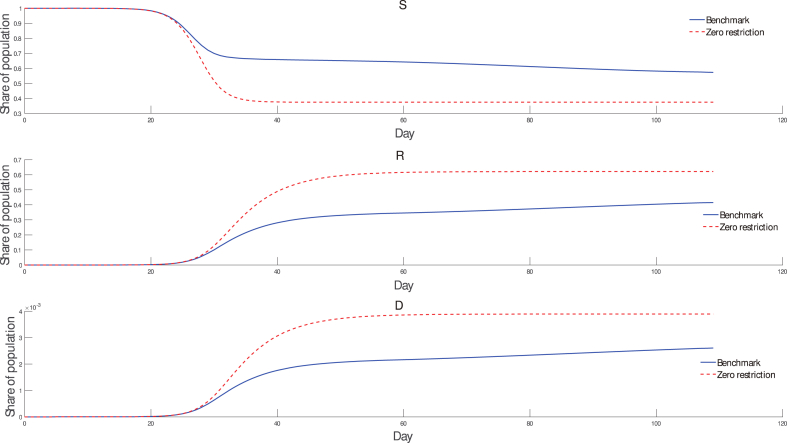
Fig. 1 shows the dynamics of the suspected, the recovered and the death throughout the outbreak cycle. It's clear to see that this outbreak tends to end after 90 days. The simulation starts with 20 exposed cases, the corresponding date is at 7th March, it is 14th June after 90 days, this date is quite close to the actual date (10th June) when the Shanghai government started loosening its pandemic control. In addition, Fig. 1 shows that this outbreak includes 2 stages, the first stage is from the start to day 31, during which we observe a quick increase of deaths and also a quick decrease of the number of suspected people; the second stage is from day 32 to the end, during which we observe an obvious slowed down increase of death toll. This pattern can be more clearly seen in Fig. 2, the number of newly increased exposed cases rises sharply from day 17 and reaches its peak on day 27, on day 31, the number of newly increased exposed cases as well as the number of accumulated exposed cases have already dropped to a relatively low level. By comparison, the number of infected cases starts to rise quickly from day 22 and reaches the peak around day 31. This asynchronism can be explained by the existence of the incubation period that an exposed person will experience to become an infected, besides, government's intervention policy also plays an important role. The government can intervene through mass COVID-19 tests and isolates in advance those who have been exposed to the virus, we assume that there always exists a fraction of exposed people who are not detected by the government. In our model, the government can choose freely the size of COVID-19 tests and the level of mobility restriction, therefore the trade-off it faces is a substitution between present production activities and future production activities. A smaller COVID-19 test size and a weaker control strength reduce the economic impact of pandemic control, but surely will accelerate the transmission speed and by consequence worsens future production activities, on the contrary, a larger COVID-19 test coverage rate and a stronger control strength bring more severe economic impacts on present productions, but help contain the pandemic more quickly and by consequence restore quicker future production activities.

Fig. 1.

Dynamics of people in different status (1).

Fig. 2.

Dynamics of people in different status (2).

Fig. 3 shows how consumptions and productions evolve during the outbreak. Aggregate consumptions and productions keeps decreasing for 31 days and then increase, it matches Fig. 1, Fig. 2 where the peak of the outbreak comes on day 31. Fig. 4 shows the optimal policy during the outbreak, the mobility restriction level rises as the virus spreads, the maximum level of 39.22 % mobility restriction is reached on day 32. It's interesting to see that the trajectory of optimal policy first synchronizes with the evolution of newly increased exposed case but then continues to rise even after the peak of newly increased exposed cases has passed. The government should strength its control not when the number of infected people starts to rise, but as soon as the number of exposed people starts to rise, therefore conducting regular COVID-19 tests is essential since it's the only way to detected exposed cases in advance. The government should not loosen its control once the number of newly increased exposed people starts to fall, a relatively strengthened pandemic control should be hold for a certain amount of time, in section 5.2 we will discuss the consequences of either ending the control too early or starting the control too late.

Fig. 3.

Dynamics of consumptions and production.

Fig. 4.

Mobility restriction policy.

4.2. Robustness

In this section, we first test the robustness of our model using 3 different sets of parameter values following 3 different COVID-19 outbreaks. We choose these 3 outbreaks as examples because they took place in different places, have different durations of pandemic cycles, and are caused by different variants. Each of the chosen outbreak has a relative big scale in order to calibrate the model. Table 1 summaries key elements of all 3 chosen outbreaks, the dominant variant in France outbreak is Alpha variant, the virus that causes Wuhan outbreak is the original COVID-19 virus, the dominant variant in Shanghai outbreak is Omicron.

Table 1.

Characteristics of 3 chosen outbreak.

	Duration (days)	R0	Death rate/day	Recovery rate/day	Incubation (Days)	Initial infection share	Average income/day
France	210	4.19	0.01738	0.081	5	0.109 %	105.4
Wuhan	91	2.79	0.057	0.005	5	0.0149 %	288.92 RMB
Shanghai (benchmark)	112	10	0.000916	0.146	1.2	0.000078 %	376.35 RMB

Data source: OECD stat, Kumar et al. [27], Lei et al. [29], Hart et al. [18], Liu and Rocklöv [30].

Table 2 reports the results of our robustness examination. It is clear that the conclusions we draw from our benchmark model are consistent under different set of parameter values. Depends on the scale of the outbreak, the economy will experience a recession to a certain extent, the larger the initial infection share and the greater the reproduction number (R₀), the larger the outbreak scale and by consequence the more severe the economy recession.

Table 2.

Robustness of the benchmark model.

	Consumption variationa	Maximum infection scale	Death scale
France	−15.5 %	17.19 %	11.56 %
Wuhan	−6.81 %	0.0254 %	0.0787 %
Shanghai (benchmark)	−7.16 %	17 %	0.26 %

^aThe mean variation of aggregate consumptions compared to the scene with no outbreak.

We continue examining the robustness of our model by analyzing sensitivity of key parameters. We divide these parameters into 2 categories, the first category includes parameters that affect the pecuniary side of pandemic control, such as the mean coverage rate of COVID test, φ, the replacement rate, k_i, income before outbreak, w₁. The second category includes parameters that affect health consequences of pandemic control, such as values of transmission parameters, π₁, π₂ and π₃, the mortality rate, π_d, the basic reproduction number, R₀. Table 3 reports the results, a strategy that is more costly generates a more severe economy recession, however, a greater finance aid for the infected leads to a lower peak of infection scale but greater death toll. Since finance aids of the infected are financed by taxes collected from workers, the greater these aids, the smaller the disposable part of income for available workers, therefore less aggregate consumptions but simultaneously less virus transmissions through consumptions, by consequence, the outbreak cycle is smoother but also longer, causing more accumulated infection cases and more deaths. Besides, a higher income before the outbreak seems to have little impact, either in terms of economy or in terms of health consequences.

Table 3.

Sensitivity of parameters.

	Consumption	Maximum infection	Accumulated	Death scale
	variation	scale	infection scale
The mean coverage rate of COVID test, φ
0.37 (benchmark)	−7.16 %	17 %	42.82 %	0.26 %
0.5	−6.88 %	16.25 %	40.94 %	0.25 %
The replacement rate, ki
0.6 (benchmark)	−7.16 %	17 %	42.82 %	0.26 %
0.8	−8.18 %	15.58 %	45.94 %	0.28 %
Income before outbreak, w1
376.35 (benchmark)	−7.16 %	17 %	42.82 %	0.26 %
800	−7.19 %	16.9 %	42.82 %	0.26 %
Weight of transmission parameters, π1, π2and π3
0.2/0.23/0.57 (benchmark)	−7.16 %	17 %	42.82 %	0.26 %
0.8/0.1/0.1	−6.42 %	10 %	45.8 %	0.29 %
0.1/0.8/0.1	−7.29 %	18.8 %	40.72 %	0.25 %
Mortality rate, πd
0.000916 (benchmark)	−7.16 %	17 %	42.82 %	0.26 %
0.0018	−7.3 %	17 %	45.93 %	0.51 %
The basic reproduction number, R0
10 (benchmark)	−7.16 %	17 %	42.82 %	0.26 %
12	−9.5 %	24.27 %	58.02 %	0.35 %

Either a more lethal or a faster spread outbreak leads to a more severe economy recession as well as worse health consequences. When work activities weight the most in virus transmissions, the government is forced to apply a stricter mobility restriction policy, resulting in a more severe recession but less infection cases and less deaths; when consumption activities weight the most in virus transmissions, the government loosens its pandemic control, therefore the economy recession is lesser but health consequences of the outbreak are worsened.

To summarize, we prove confidence of the robustness of our model, conclusions draw from various tests are consistent. The policy maker always faces the trade-off between economy recession and health consequences, greater present production activities causes worse health consequences and therefore worse future production activities, on the contrary, greater future production activities requires better health consequences, which is the result of a stricter pandemic control that harms present production activities. In next section we shall discuss how our optimal solution of pandemic control policy help contain the outbreak as well as maintaining present production activities.

5. Counter factual experiments on isolation policy

The 2022 Omicron outbreak in Shanghai has raised huge concerns about how the “Dynamic zero-COVID policy” should be carried out in actual practice. There are people who declare that the “Dynamic zero-COVID policy” has failed, they demand the Chinese government to abandon it and loosen its control like west countries. Other people argue that it is thanks to the “Dynamic zero-COVID policy” and the full lock down over 3 months that the Omicron outbreak in Shanghai can be contained, despite at the cost of a huge economy step back. In response to these concerns, we carry 2 series of counter factual experiments. In the first series we simulate 2 scenarios where either a 0 mobility restriction policy or a strict mobility restriction is applied throughout the outbreak, then we compare them with the benchmark model to see how a static control policy changes the dynamics of virus transmission. We proceed to analyse the effect of a static control policy on aggregate consumptions and productions, by comparing them with the benchmark model, we show why a dynamic control policy is a better choice.

In the second series of counter factual experiments, we simulate 2 scenarios where the control policy is either lifted too early or applied too late. We also compare these 2 scenarios with the benchmark model to see how the dynamics of virus transmission is affected and to analyse the effects of these changes on aggregate consumptions and productions.

5.1. The effect of the static pandemic control

We begin with the static pandemic control. We first assume that $r_t^m=0\text{,}\forall t\in T$, note that in this scenario the government is still assumed to conduct regular COVID-19 tests as in the benchmark model, only all mobility restrictions are lifted. Fig. 5, Fig. 6 show the dynamics of virus transmission in this scenario.

Fig. 5.

Dynamics of virus: Zero mobility restriction vs. benchmark model (1).

Fig. 6.

Dynamics of virus: Zero mobility restriction vs. benchmark model (2).

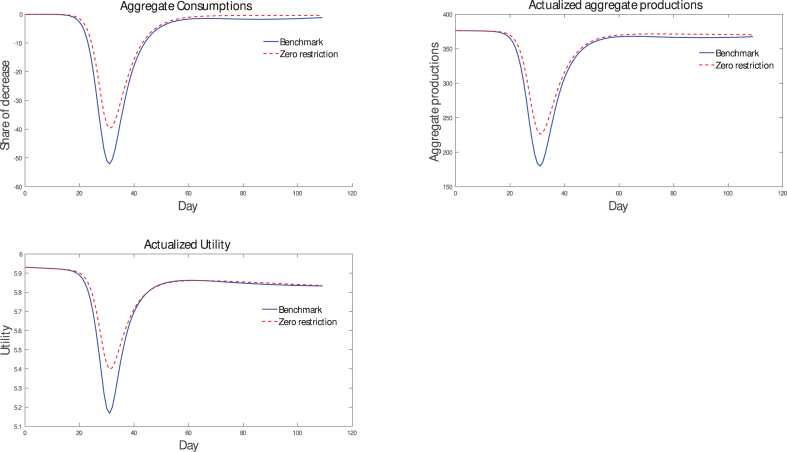
With no mobility restriction, the pandemic is much more violent than in the benchmark model, by consequence, it causes 81.47 % more infected cases and 50 % more deaths. In Fig. 6, we also observe a slightly longer outbreak cycle, showing that not only the 0 mobility restriction causes a more violent outbreak, but also it takes more time to recover. Fig. 7 shows the evolution of aggregate consumptions and productions, we observe that comparing to the 0 mobility restriction policy, our optimal control policy in the benchmark model actually leads to a slightly more severe economy recession, Table 4 emphasizes this point by summarizing the accumulated social welfare and accumulated aggregate productions. From this perspective, “there is indeed an inevitable trade-off between the severity of the recession and health consequences of the epidemic.”, just as Eichenbaum et al. [14] declares. Nevertheless, we argue that the optimal pandemic control policy should not only take care of the economy issue, but also pay attention to health outcomes of the pandemic, if an economy step-back is inevitable, then the optimal control policy should be a policy that minimize the economy loss, while saving as many lives as possible.

Fig. 7.

Dynamics of consumption and productions: Zero mobility restriction vs. benchmark model.

Table 4.

Aggregate productions and social welfare.

	Accumulated social welfarea	Accumulated productions	Maximum infection scale	Death scale
The benchmark model	643.81	3.8505e+04	17 %	0.26 %
Zero mobility	646.78	3.9324e+04	30.85 %	0.39 %
restriction	(+0.46 %)	(+2.13 %)	(+81.47 %)	(+50 %)
Strong mobility	552.44	1.6606e+04	1.0370e-04 %	1.4758e-06 %
restriction	(-14.2 %)	(-56.9 %)	(-99.94 %)	(-99.94 %)

^aAccumulated social welfare is computed by$U={\mathrm{\Sigma }}_{t=1}^T{\beta }^{t-1}\mathit{ln}\left(c_t^s{S}_t+c_t^e{E}_t+c_t^q{Q}_t+c_t^i{I}_t+c_t^r{R}_t\right)$.

Next we would simulate the scenario where a relative stricter restriction is applied throughout the outbreak. We assume that $r_t^m=0.6\text{,}\forall t\in T$. Fig. 8, Fig. 9 show the dynamics of virus transmission in this scenario.

Fig. 8.

Dynamics of virus: Strong mobility restriction vs. benchmark model (1).

Fig. 9.

Dynamics of virus: Strong mobility restriction vs. benchmark model (2).

With a persistent strong mobility restriction, the outbreak is quickly contained, the number of newly increased exposed cases, newly increased infected cases and the number of deaths almost immediately cease to increase, however, this is all at costs of a huge economy recession, as what Fig. 10 shows, the aggregate consumptions as well as the aggregate productions are far below the lowest point of their counterparts in the benchmark model. The bottom line of Table 4 emphasizes this point by showing that the accumulated social welfare decreases by 14.2 % and the accumulated productions decreases by 56.9 % than in the benchmark model. A persistent mobility restriction is effective in terms of controlling the outbreak, but in turn it generates derived damages to aggregate productions, by consequence, causing a much more severe economy recession.

Fig. 10.

Dynamics of consumption and productions: Strong mobility restriction vs. benchmark model.

5.2. The effect of ending the pandemic control too early or starting it too late

A dynamic isolation policy helps better balance the pandemic containment and aggre-gate production activities, nevertheless, how long should the control policy be maintained is another question that worth discussing. Similar to Eichenbaum et al. [14], we examine the effects of 2 options: either lift the control earlier than in the benchmark model, or start the control later than in the benchmark model.

We have shown that the mobility restriction policy generates 2 contradictory effects on the diffusion of the epidemic and on aggregate productions, in this section, we examine the effect of different control durations can have on the pandemic and also on the aggregate productions.

According to the benchmark model, the peak of infected cases is reached on day 32. In order to highlight the effect, we assume that the control is either lifted on this day or applied from this day. The red dashed line in panel A of Fig. 11 shows the changes of the epidemic diffusion and the economy when the control is lifted earlier. Once the control ends, the number of infected people and deaths rise up immediately, aggregate consumptions and productions also sharply increase immediately following the end of the mobility control, but they both later on slows down in response to the re-emerged epidemic. The second line of Table 5 shows that compared to the benchmark model, an early end of pandemic control gains a slightly greater economy benefits with 1.3 % more aggregate productions and 0.33 % more social welfare, at the cost of 11.16 % more accumulated infected cases and 15.4 % more deaths.

Fig. 11.

Early exit and late start of pandemic control.

Table 5.

Aggregate productions and social welfare: early exit and late start.

	Accumulated social welfare	Accumulated productions	Accumulated infection scale	Death scale
The benchmark	643.81	3.8505e+04	42.82 %	0.26 %
Early exit	645.97	3.9123e+04	47.6 %	0.3 %
	(+0.33 %)	(+1.6 %)	(+11.16 %)	(+15.4 %)
Late start	604.95	3.3485e+04	58.81 %	0.37 %
	(-6.03 %)	(-13.03 %)	(+23.55 %)	(+23.3 %)

In this scenario we assume that the government only starts to control the pandemic from day 33.

The black dashed line in panel B of Fig. 11 represents the changes of the epidemic diffusion and the economy when the control is applied too late. The outbreak is much more violent than in the benchmark model, the number of the infected people only stops increasing several days after the control is applied. After reaching its peak, the infected cases drops quicker than in the benchmark model, which shows the effect of the highly strengthened mobility restriction. As the government prohibits most mobilities, aggregate consumptions and productions fall dramatically than in the benchmark model. The bottom line of Table 5 shows that in this scenario, both people's lives and people's livelihoods suffer huge loss, the accumulated infection scale and the death scale increase by 23.55 % and 23.3 % respectively, the accumulated social welfare and accumulated productions decrease by 6 % and 12.9 % respectively.

6. Conclusion

In this paper we research the COVID-19 pandemic control policy, our goal is to find out a solution that is capable of balancing the outbreak control as well as aggregate production activities. We first extend the SIR transmission model to SEQIR transmission model by introducing 2 new status quarantined(Q) and exposed(E), this extension allows us to replicate a dynamic transmission process involving government's interventions. We then process to look for the optimal pandemic control policy. We calibrate parameter values using the 2022 Shanghai outbreak as reference, results of our model suggests that there is an inevitable trade-off between present production activities and future production activities, the policy maker either chooses to have a lesser economy recession at present with worse health consequences, either the exact opposite.

Then we run various robustness tests to examine the consistency of conclusions draw from our model, the results show that whichever the set of parameter values, the policy maker always faces the trade-off between a severe economy recession and health consequences. This conclusion is similar to Eichenbaum et al. [14], but, by running 2 series of counter factual experiments, we prove that the optimal control policy obtained by our model is able to contain the outbreak as well as maintaining production activities as much as possible. Our optimal control policy is able to save 50 % more lives compared to static 0 mobility restriction policy at the cost of 0.46 % of social welfares, and increase aggregate productions by 56.9 % compared to static strong mobility restriction. Furthermore, our optimal control policy is also able to save 15.4 % more lives compared to the early exit policy and is able increase aggregate productions by 13.03 % compared to the late start policy.

In a nut shell, an optimal pandemic control policy should take care of both economy as well as health issue, if an economy step-back during the pandemic is inevitable, then the optimal control policy should be a policy that aiming at minimizing the economy loss, while saving as many lives as possible. Results of our model suggest that a dynamic mobility restriction policy combining with organization of regular COVID-19 tests at mass scale is essential to achieve this goal. In addition, the government should start the isolation policy as soon as the number of exposed and not the infected people begins rising, the government should not loosen its control once the number of newly increased exposed people starts to fall, a relatively strengthened pandemic control should be hold for a certain amount of time.

This version of our research still presents absence of factors such as the problem of reinfection by different variants, post-effects of COVID pandemic or a dynamic COVID test policy. In addition, an outbreak of unknown virus or a latent outbreak can also be considered. These are of course explorable approaches for future studies. Be that as it may, we believe that introduction of new elements to our model will not fundamentally change our conclusions, a pandemic control policy that balances between the containment of epidemic outbreak and production activities is actually feasible and needed to be pursued.

Data availability statement

No data associated with this study been deposited into a publicly available repository and data will be made available on request.Q6Please confirm that given names and surnames have been identified correctly and are presented in the desired order and please carefully verify the spelling of all authors' names.ResolvedFootnoteView Edit Log2

CRediT authorship contribution statement

Ze Zhong Shang: Writing – review & editing, Writing – original draft, Visualization, Validation, Supervision, Software, Resources, Project administration, Methodology, Investigation, Formal analysis, Data curation, Conceptualization.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A.

With initial guess of S₁, E₁, R₁, D₁ and $Q_1=E_1\left(1-{\pi }_{EI}\right)\phi$ and $I_1=E_1{\pi }_{EI}$, following the below equations, we compute sequences of ${\left\{S_t,E_t,Q_t,I_t,R_t,N{E}_t,{\tau }_t\right\}}_{t=1}^T$ under the assumption that no external interventions is made

$$\begin{array}{l}N{E}_t=S_t{E}_t{c}_t^s{c}_t^e{\pi }_1+S_t{E}_t{n}^2{\pi }_1+S_t{E}_t{\pi }_3\\ S_t=S_{t-1}-N{E}_{t-1}\\ E_t=E_{t-1}\left(1-{\pi }_{EI}\right)\left(1-\phi \right)+N{E}_{t-1}\\ Q_t=\left(1-{\pi }_{EI}\right)\left(E_{t-1}\phi +Q_{t-1}\right)\\ I_t=\left(1-{\pi }_r-{\pi }_d\right)I_{t-1}+{\pi }_{EI}\left(Q_{t-1}+E_{t-1}\right)\\ R_t=R_{t-1}+{\pi }_r{I}_{t-1}\\ D_t=D_{t-1}+{\pi }_d{I}_{t-1}\\ {\tau }_t{w}_t\left[S_t+E_{t-1}\left(1-{\pi }_{EI}\right)\left(1-\phi \right)+R_{t-1}\right]=b_1\left(S_t+E_t\left(1-{\pi }_{EI}\right)\right)\phi +\left(m+k_i{w}_1\right)I_t+w_1{Q}_t\end{array}$$

The steady status is addressed to the ex post period of pandemic control, therefore we assume that consumptions and income of all people restore to the level in the ex-ante period of pandemic control, we also take S_T, E_T, R_T, D_T, Q_T, I_T and NE_T as the steady distribution of population, τ_T as the steady tax rate. Then we rewrite our model in steady status, the corresponding Lagrangian function is written as

$$\mathcal{L}=A\left(S_T+E_T\left(1-{\pi }_{EI}\right)\left(1-\phi \right)+R_T+{\pi }_r{I}_T\right)n+{\lambda }_{ss}^e\left[E_T-E_T\left(1-{\pi }_{EI}\right)\left(1-\phi \right)-N{E}_T\right]n+{\lambda }_{ss}^s\left[S_T-S_T+N{E}_T\right]n+{\lambda }_{ss}^{ne}\left[N{E}_T-\left(S_T{E}_T{c}_T^s{c}_T^e{\pi }_1+S_T{E}_T{n}^2{\pi }_2+S_T{E}_T{\pi }_3\right)\right]n+{\lambda }_{ss}^i\left[\left(1-{\pi }_r-{\pi }_d\right)I_T+{\pi }_{EI}\left(Q_T+E_T\right)\right]n+{\lambda }_{ss}^q[Q_T-\left(1-{\pi }_{E}I\right)\left(E_T\phi +Q_T\right)n+{\lambda }_{ss}^{cs}\left[c_T^s-w_1\left(1-{\tau }_T\right)\right]+{\lambda }_{ss}^{ce}\left[c_T^e-w1\left(1-{\tau }_T\right)\right]n+{\lambda }_{ss}^{b}A\left(S_T+E_T\left(1-{\pi }_{EI}\right)\left(1-\phi \right)+R_T+{\pi }_r{I}_T\right)-c_{ss}^s{S}_T-c_{ss}^e{E}_T-c_{ss}^q{Q}_T-c_{ss}^i{I}_T-c_{ss}^r{R}_T)n+{\lambda }_{ss}^{\tau }\left[{\tau }_T{w}_1\left(S_T+E_T\left(1-{\pi }_{EI}\right)\left(1-\phi \right)+R_T+{\pi }_r{I}_T\right)\right]-b_1\left(S_T+E_T\left(1-{\pi }_{EI}\right)\right)\phi n-\left(m+k_i{w}_1\right)I_T-w_1{Q}_T]$$

where ${\left\{c_{ss}^j\right\}}_j=s,e,q,i,r$ refers to steady status consumption choice of different group of people.

Appendix B.

Retrieving values of all Lagrangian multipliers from the steady status version of our model and set them as initial guess of these variables, with the initial guess of other variables and calibrated parameters, solving the following equations

$$\begin{array}{l}A\left(1-r_t^m\right)+{\lambda }_t^s-\beta {\lambda }_{t+1}^s-{\lambda }_t^{ne}\left(E_t{c}_t^s{c}_t^e{\pi }_1+E_t{n}^2{\pi }_2+E_t{\pi }_3\right)\left(1-r_t^m\right)\\ +{\lambda }_t^b\left(A\left(1-r_t^m\right)-c_t^s\right)+{\lambda }_t^{\tau }\left({\tau }_t{w}_t-b_1\phi \right)=0t=2\dots T-1\\ A\left(1-r_T^m\right)+S_T-{\lambda }_T^{ne}\left(E_T{c}_T^s{c}_T^e{\pi }_1+E_T{n}^2{\pi }_2+E_T{\pi }_3\right)\left(1-r_T^m\right)\\ +{\lambda }_T^b\left(A\left(1-r_T^m\right)-c_T^s\right)+{\lambda }_T^{\tau }\left({\tau }_T{w}_T-b_1\phi \right)=0\\ \beta A\left(1-{\pi }_{EI}\right)\left(1-\phi \right)\left(1-r_{t+1}^m\right)+{\lambda }_t^e-\beta {\lambda }_{t+1}^e\left(1-{\pi }_{EI}\right)\left(1-\phi \right)\\ -{\lambda }_t^{ne}\left(S_T{c}_T^s{c}_T^e{\pi }_1+S_T{n}^2{\pi }_2+S_T{\pi }_3\right)\\ -\beta {\lambda }_{t+1}^i{\pi }_{EI}-\beta {\lambda }_{t+1}^q\phi \left(1-{\pi }_{EI}\right)-{\lambda }_t^b\left(c_t^e\right)+\beta {\lambda }_{t+1}^{b}A\left(1-{\pi }_{EI}\right)\left(1-\phi \right)\left(1-r_{t+1}^m\right)-{\lambda }_t^{\tau }{b}_1\phi \left(1-{\pi }_{EI}\right)\\ +\beta {\lambda }_{t+1}^{\tau }{\tau }_{t+1}{w}_t\left(1-{\pi }_{EI}\right)\left(1-\phi \right)=0t=2\dots T-1\\ {\lambda }_T^e-{\lambda }_T^{ne}\left(S_T{c}_T^s{c}_T^e{\pi }_1+S_T{n}^2{\pi }_2+S_T{\pi }_3\right)\left(1-r_T^m\right)-b_1\left(1-{\pi }_{EI}\right)\phi {\lambda }_T^{\tau }=0\\ \beta A{\pi }_r\left(1-r_{t+1}^m\right)+{\lambda }_t^i-\beta {\lambda }_{t+1}^i\left(1-{\pi }_r-{\pi }_d\right)-{\lambda }_t^b{c}_t^i+\beta {\lambda }_{t+1}^{b}A{\pi }_r\left(1-r_{t+1}^m\right)\\ -{\lambda }_t^{\tau }\left(m+k_i{w}_1\right)+\beta {\lambda }_{t+1}^{\tau }{\pi }_r{w}_t=0t=2\dots T-1\\ -c_T^i-\left(m+k_i{w}_1\right){\lambda }_T^{\tau }=0\\ {\lambda }_1^{ne}\left(S_1{E}_1{c}_1^s{c}_1^e{\pi }_1+S_1{E}_1{n}^2{\pi }_2+S_1{E}_1{\pi }_3\right)\\ -A\left[S_t+E_{t-1}\left(1-{\pi }_{EI}\right)\right]-A{\lambda }_1^b\left[S_t+E_{t-1}\left(1-{\pi }_{EI}\right)\right]=0\\ {\lambda }_t^{ne}\left(S_t{E}_t{c}_t^s{c}_t^e{\pi }_1+S_t{E}_t{n}^2{\pi }_2+S_t{E}_t{\pi }_3\right)\\ -A\left[S_t+E_{t-1}\left(1-{\pi }_{EI}\right)\left(1-\phi \right)+R_{t-1}+{\pi }_{EI}{I}_{t-1}\right]\\ -A{\lambda }_t^b\left[S_t+E_{t-1}\left(1-{\pi }_{EI}\right)\left(1-\phi \right)+R_{t-1}+{\pi }_{EI}{I}_{t-1}\right]=0t=2\dots T\end{array}$$

$$\begin{array}{l}-\beta {\lambda }_{t+1}^e+\beta {\lambda }_{t+1}^s+{\lambda }_t^{ne}=0t=1\dots T-1\\ {\lambda }_T^{ne}=0\\ -\beta {\lambda }_{t+1}^i{\pi }_{EI}-\beta {\lambda }_{t+1}^q\left(1-{\pi }_{E}I\right){\lambda }_t^b{c}_t^q+{\lambda }_t^q-{\lambda }_t^{\tau }{w}_1=0t=2\dots T-1\\ -{\lambda }_T^b{c}_T^q-{\lambda }_T^{\tau }{w}_1=0\\ {\lambda }_t^{cs}-{\lambda }_t^b{S}_t-{\lambda }_t^{ne}{S}_t{E}_t{\pi }_1\left(1-r_t^m\right)c_t^e=0t=1\dots T\\ {\lambda }_t^{ce}-{\lambda }_t^b{E}_t-{\lambda }_t^{ne}{S}_t{E}_t{\pi }_1\left(1-r_t^m\right)c_t^s=0t=1\dots T\end{array}$$

Adjust values of ${\left\{{\lambda }_t^e\right\}}_{t=2}^T,{\left\{{\lambda }_t^s\right\}}_{t=2}^T,{\left\{{\lambda }_t^{ne}\right\}}_{t=1}^T,{\left\{{\lambda }_t^i\right\}}_{t=2}^T,{\left\{{\lambda }_t^q\right\}}_{t=2}^T,{\left\{{\lambda }_t^{cs}\right\}}_{t=1}^T,{\left\{{\lambda }_t^{ce}\right\}}_{t=1}^T,{\left\{{\lambda }_t^b\right\}}_{t=1}^T,{\left\{{\lambda }_t^{\tau }\right\}}_{t=1}^T$ so that the following 2 equations are hold everywhere

$$\begin{array}{l}A\left[S_t+E_{t-1}\left(1-{\pi }_{EI}\right)\left(1-\phi \right)+R_{t-1}\right]\left(1-r_t^m\right)=c_t^s{S}_t+c_t^e{E}_t+c_t^q{Q}_t+c_t^i{I}_t+c_t^r{R}_t\\ {\tau }_t{w}_t\left[S_t+E_{t-1}\left(1-{\pi }_{EI}\right)\left(1-\phi \right)+R_{t-1}\right]=b_1\left(S_t+E_t\left(1-{\pi }_{EI}\right)\right)\phi +\left(m+k_i{w}_1\right)I_t+w_1{Q}_t\end{array}$$

Finally, compute the sequence of optimal mobility restriction level by the following equation

$$r_t^m=\frac{1-({\lambda }_t^s-\beta {\lambda }_{t+1}^s-{\lambda }_t^b{c}_t^s+{\lambda }_t^{\tau }{\tau }_t{w}_t-b_1\phi }{-A-A{\lambda }_t^b+{\lambda }_t^{ne}\left(E_t{c}_t^s{c}_t^e{\pi }_1+E_t{n}^2{\pi }_2+E_t{\pi }_3\right)}t=2\dots T-1$$

Assuming that $r_1^m=r_T^m=0$, we obtain the full sequence of optimal mobility restriction level. Substituting ${\left\{r_t^m\right\}}_{t=1}^T$ into the model, we can compute the sequence ${\left\{S_t,E_t,Q_t,I_t,R_t,D_t,N{E}_t,c_t^s,c_t^e,c_t^q,c_t^i,c_t^r\right\}}_{t=1}^T$.