Skip to main content
. 2023 Oct 21;145(46):25033–25042. doi: 10.1021/jacs.3c04142

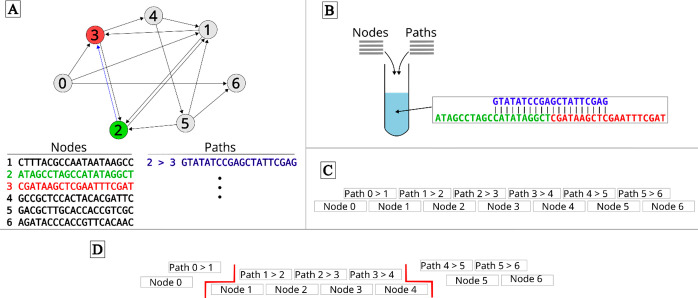
Figure 1.

Figure 1

Hamiltonian problem solution with the DNA reaction. (A) This Hamiltonian problem has multiple nodes (1–7) and defined directed paths (arrows). The solution is to find a path that starts at node 0 and ends at node 6, while visiting each node only once. Unique DNA sequences of 20 bases are assigned to nodes and defined paths. (B) A sequence of paths must be the unique reverse complement of the two nodes it connects in the Hamiltonian problem. All node and path sequences are added to a polymerase chain reaction mixture for hybridization of path and node DNA molecules. (C) The solution to the path problem is contained in a DNA strand of length 140 bases (seven nodes of 20 bases each). (D) Restriction enzymes can be used to cleave DNA strands at specific sequences to define the start and end points (boundaries) of a path. If the desired path starts at node 1 and ends at node 4, the restriction enzymes can be used to cleave at the sequence of [path 0 > 1 and node 1] and [node 4 and path 4 > 5].