Efficiently Differentiating Agonists and Competitive Antagonists for Weak Allosteric Protein–Ligand Interactions with Linear Response Theory

Abstract

What makes an agonist and a competitive antagonist? In this work, we aim to answer this question by performing parallel tempering Monte Carlo simulations on the serotonin type 3A (5-HT_3A) receptor. We use linear response theory to predict conformational changes in the 5-HT_3A receptor active site after weak perturbations are applied to its allosteric binding sites. A covariance tensor is built from conformational sampling of its apo state, and a harmonic approximation allows us to substitute the calculation of ligand-induced forces with the binding site’s displacement vector. Remarkably, our study demonstrates the feasibility of effectively discerning between agonists and competitive antagonists for multiple ligands, requiring computationally expensive calculations only once per protein.

1. Introduction

The serotonin type 3, or 5-hydroxytryptamine type 3, or 5-HT₃, receptor is a member of the Cys-loop ligand-gated ion channel family, which also includes the nicotinic acetylcholine (nACh), glycine, and γ-aminobutyric acid (GABA_A) receptors. These proteins are responsible for fast synaptic transmission and are the targets of many neuroactive drugs. The 5-HT₃ receptor consists of five subunits arranged around a central ion channel. There are five subunit types, named A to E, though only the A and B subunits have been characterized in detail. The A subunit can be expressed as a homomer, resulting in a 5-HT_3A receptor. These receptors are involved in nausea and vomiting caused by radiotherapy and chemotherapy, and competitive 5-HT₃ antagonists have been used to reduce such vomiting for decades.¹

The first electron microscopy structure of this receptor appeared in 1995.² Recently, a number of experimental structures of higher resolution have become available with a variety of ligands bound.³⁻⁶ In 2018, Basak et al.⁷ solved the structure of the apo-form of the 5-HT_3A receptor to 4.3 Å resolution using cryo-electron microscopy (cryo-EM); no antibodies were bound to the receptor (PDB code: 6BE1). These researchers followed up with a study of the open-channel states of the 5-HT_3A receptor by administering 5-HT to the protein (PDB codes: 6DG7 and 6DG8).⁸ Then, in 2020, Basak et al.⁹ solved the structure of this receptor bound to the antagonists alosetron (PDB code: 6W1J), granisetron (PDB code: 6NP0), ondansetron (PDB code: 6W1M), and palonosetron (PDB code: 6W1Y). These structures provide a reference for both the binding site displacement, which serves as an input to our method, as well as the active site changes to compare against after generating our computational predictions.

The dynamics and allostery of the 5-HT_3A receptor have been studied in silico.¹⁰⁻¹⁴ Trajectories from Yuan et al.¹¹ identified how 5-HT bound to the receptor site and changed the site conformation and demonstrated that those changes lead to ion channel opening. Guros et al.¹² found that 5 mM 5-HT was adequate to activate the receptor. While these studies are invaluable, they are computationally expensive and would need to be rerun for each ligand to determine its biological effect. In this work, we aim to define the mechanical linkage between binding site perturbation and ion channel opening (gating) using methods that are less computationally demanding. To this end, we have performed a parallel tempering Monte Carlo simulation of the structure 6BE1 using the CRANKITE^15,16 method and analyzed its trajectory to attempt to define agonists and competitive antagonists and their associated direction of conformational change.

2. Methods

2.1. Structure

The starting structure of the simulation is the cryo-EM structure of the apo-form of the 5-HT_3A receptor, PDB code 6BE1.⁷ We chose this structure because it has been solved without any extra proteins attached to it. Furthermore, the same method was used to solve the structure of this receptor in the open-channel state as when it was bound to four different kinds of competitive antagonists. This structure is shown in Figure 1.

Figure 1.

Diagram showing the 5-HT_3A receptor with a coordinate system aligned along the receptor’s long axis. The extracellular domain is in the region z > 25 Å, the transmembrane domain is in the region −25 Å ≤ z ≤ 25 Å, and the intracellular domain is in the region z < – 25 Å. The agonist and competitive antagonist binding site is situated between individual subunits and is in the region of z = 50 Å. These z-values will be referred to later in the paper when describing different parts of the receptor.

For comparison with open-channel states, we use the structures of the 5-HT_3A receptor bound to 5-HT.⁸ For structures bound to antagonists, we use the structures of the 5-HT_3A receptor bound to alosetron (PDB code: 6W1J), granisetron (PDB code: 6NP0), ondansetron (PDB code: 6W1M), and palonosetron (PDB code: 6W1M).⁹

2.2. Simulations

For the molecular simulations, we used CRANKITE,¹⁵ a Monte Carlo simulation program that employs a Go-like coarse-grained force field. We chose CRANKITE because its Monte Carlo move set consists of local moves of crankshaft rotations of the protein backbone and changes of the side chain dihedral angles, the former of which allows a fast conformational sampling of proteins. CRANKITE uses a full atom representation of the protein backbone, together with explicit side chain β atoms and γ atoms, to include entropic contributions arising from the torsional flexibility of the side chains. Each amino acid is treated as hydrophobic or amphipathic. The γ atoms represent the rest of the side chain, with an elongated distance between β and γ atoms to place them near the center-of-mass of the side chain. In the energy function, the volume exclusion of beads, hydrogen bonds between backbone amide H atoms and carbonyl O atoms, and hydrophobic interactions between γ atoms are modeled explicitly. The secondary structure of the protein is held together by an additional energy term, which keeps the backbone of α-helices and β-strands at the correct backbone twist, and a Go-like contact potential term keeps β-sheets intact. The secondary structure of the protein is predetermined and did not change within the simulation.

We used the force field parameters optimized previously using a set of non-transmembrane proteins, with the addition of a conical external potential on the transmembrane and intracellular regions to mimic the membrane. The energy contribution of this external potential on an amino acid in the transmembrane and intracellular regions is

1

if z/z_tip ∈[0,1] and x² + y² > r²₀, otherwise E = 0, where x, y, and z are the coordinates of the center-of-mass of the amide N, C_α, and carbonyl C of the amino acid, k = 100 RT, r₀ = 45 Å, z_tip = −120 Å, z_com is the z-coordinate of the center-of-mass of the whole protein, where the pore of the protein was aligned to the z-axis with the intracellular domain pointing in the positive direction as illustrated in Figure 1. The shape of the potential was chosen such that it helps maintain the initial structure of the 5-HT_3A receptor but does not squeeze the pore closed (there is a minimal energy penalty with the receptor in the initial state).

To explore the possible conformations of the protein while keeping its secondary structure intact, we used parallel tempering simulations with 32 temperature levels ranging from 310 to 1023 K, sampling conformations at the lowest temperature level. The simulation was performed in 10⁶ steps. After the simulation finished, we carried out an analysis to confirm that the system was equilibrated after 220 000 steps. To allow us a safety margin, useful data were collected from step 240 000. We then performed data analysis of the trajectory using the following methods.

2.3. Correlation Tensor

To evaluate how the movements of one amino acid correlate with the movements of another, we construct a correlation tensor, as in Várnai et al.¹⁷ We coarse-grain the CRANKITE trajectory to individual amino acids, the position of which becomes its center-of-mass. We assume that each amino acid has a set of principal directions, which can be defined by an ellipsoidal cloud of coordinates x_at = [x_a1t, x_a2t, x_a3t] for the a’th amino acid, t’th snapshot, and first, second, or third dimension. These orthonormalized principal axes of motion vectors are equivalent to the eigenvectors of the self-correlation matrix for amino acid a in Cartesian [x, y, z] coordinates. Note that these are spatial correlations rather than temporal correlations. We construct a 3 × 3 correlation matrix for each pair of amino acids a and b, denoted as R⁽²⁾_ab, whose elements are given by

2

with i and j as the i^th and j^th principle axes of motion of amino acids a and b, respectively, and μ as the average position across all N_t snapshots.

2.4. Impulse Response

2.4.1. Time-Independent Linear Response Theory

Since our simulation is not consecutive in time, with all computed expectation values corresponding to ensemble averages, we use time-independent linear response theory developed by Ikeguchi et al.¹⁸ to predict the protein’s response to ligand binding. Physically, time averages of the protein structural configuration should coincide with corresponding ensemble averages as a result of ergodicity, which we expect to hold in classical systems such as proteins. For weak protein–ligand interactions, we can approximate our response to first order in the forces

3

where Δ⟨X_bj⟩ is the expected displacement of amino acid b in direction j induced on binding the ligand, β = 1/k_BT, ⟨δX_bjδX_ai⟩₀ is the covariance between X_bj and X_ai at equilibrium (mean position) with no ligand, which multiplied by β is a mechanical susceptibility for the response in amino acid positions due to the external ligand forces acting on a protein, consistent with the fluctuation–dissipation relations. F_ai represents the ligand-induced force on amino acid a in the direction i. In the case of strong interactions, we expect an analogous response, captured by a proportionality relation, to hold

4

The relation follows from expanding the displacements to higher order in the forces, obtained from a Taylor expansion of the generating functional 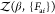in terms of forces around zero force limit F_ai = 0.

5

The generating functional is obtained by adding a coupling term V_coupling = −∑_a,iF_aiΔX_ai to the protein Hamiltonian 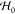, which is quadratic in the amino acid displacements within harmonic approximation, exponentiated in a partition function of the ligand-free protein 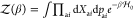, where p_ai denote components of amino acid momentum in units of the Planck constant. The quadraticity of 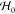allows us to apply Wick’s probability (Isserlis’) theorem, which holds for Gaussian variables, by which all terms odd in fluctuations (e.g., ⟨δX_bjδX_aiδX_a′i′⟩₀) vanish. At the same time, any even term can be expanded in products of all possible permutations of two-amino-acid displacement correlators. In the case of the fourth moment (cokurtosis), for example,

6

Having applied Wick’s theorem, the higher moments can be collected into a proportionality factor

, as suggested by Punia and Goel.¹⁹ Hence, explicitly, strong interaction amounts to

7

where in the limit of small forces F_ai → 0, by inspection S ≈ 1, restoring the weak interaction limit.

2.4.2. Linear Force Approximation

The potential V_int which describes the amino acid interactions in the ligand-free protein can be Taylor expanded around the equilibrium positions to give

8

where {x_ai}_eq corresponds to the average equilibrium positions of amino acids in the protein without a ligand, {x_ai}_eq ≡ {x_ai}₀, and Δx_ai denotes a displacement of amino acid a in direction i. The first term is a trivial constant, and the second one vanishes by the equilibrium condition, i.e., derivatives of the potential vanishing at its minimum. In the harmonic approximation, we disregard the terms of higher than quadratic order, as these represent anharmonicity. We define spring constants

9

as well as interaction forces on amino acids due to the collective effects of all other amino acids,

10

component-wise yielding F_int,ai = −∂_xaiV_int ≈ −k_aiΔx_ai.

We assume that upon inserting the ligand, the new configuration satisfies F_ai = −F_int,ai within the binding site, where F_ai represents a ligand-induced force due to the interaction of amino acid a with the ligand. Hence, utilizing the harmonic approximation, we obtain F_ai = k_aiΔx_ai for amino acids a ∈ the binding site. In this context, {Δx_ai} denotes displacements of these amino acids from their apo-state equilibrium positions.

Thus, the ligand-induced forces can be approximated as long as we know the spring constants k_ai and the displacement Δx_ai of the amino acids in the binding site (from either experiment or docking). CRANKITE simulations provide us with the variance ⟨δX_aiδX_ai⟩₀ = σ_ai², and we can apply the equipartition theorem to the protein described with the Gaussian model, given V_int consists only of quadratic degrees of freedom to give

11

for each component of amino acid displacement X_a giving 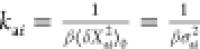. Having deduced spring constants from the ensemble of protein structures, as well as displacements around the binding site Δx_ai, we can infer approximate ligand-induced forces F_ai, and therefore other amino acid displacements not in the binding site using the linear response theory introduced in the section above. However, we emphasize that in this harmonic approximation, we neglect entropic contributions to the force, which is close to the positionally constrained binding center we assume to be negligible.

We can further justify the validity of the harmonic potential and linear force approximations. The statistical relationship between the covariance and the correlation coefficient of X_bj and X_ai is given by

12

where σ_ai represents the standard deviation of the position of amino acid a in the direction i.

Using the above harmonic approximation F_ai = k_aiΔx_ai gives

13

where the set of {X_ai} represents the positions of amino acids across the entire protein and {x_ai} represents the positions of amino acids in the binding site, taken to be any amino acid within 6 Å of the ligand. Let us explore a small induced movement of only a single amino acid a along only one of its principal axes of motion i, represented as Δx_ai, and we wish to find Δ⟨X_bj⟩ in the special case, where b = a and j = i. Since self-correlation coefficients are equal to one and we can remove the summation because no other amino acids are externally perturbed under the assumption, we arrive at

14

The predicted reactive displacement would be equal to the actual displacement caused by ligand-induced forces in this case: Δ⟨X_ai⟩ = Δx_ai. Solving for k_ai, we obtain

15

which is equivalent to the previous equipartition theorem result within the harmonic approximation. Finally, reinserting the previous equation into the time-independent linear response relation gives

16

The result is highly intuitive in that one can normalize the input Δx_ai by its standard deviation σ_ai, apply its correlation coefficient with X_bj, and then analogously normalize the output by its standard deviation σ_bj to obtain an induced response Δ⟨X_bj⟩. Overall, this framework allows us to reconstruct the displacements of amino acids not in the binding sites from the displacements of amino acids in the binding site. To perform the approximations required by the linear response theory, we have to assume that the ligand induces only a weak perturbation. Therefore, we do not account for major structural rearrangements. However, these are not present between the apo- (PDB code: 6BE1) and holo- (PDB code: 6DG8) form of the 5-HT_3A receptor.

2.4.3. Response Measurement

We estimated the pore radius of the receptor at a set of sampling points along the z-axis (the pore axis) to which the protein ion channel was aligned, as illustrated in Figure 1. Samples were taken at 1 Å intervals from −80 Å < z < +100 Å; this range covered the main parts of interest of the protein. At each sampling point, the ten nearest-neighbor residues were considered and the approximate exponentially smoothed radius was reported as

17

where d_k is the distance from the pore axis to the kth nearest neighbor.

18

The movements of these amino acids are nonlinear and it is quite possible that the M2 helices rotate upon activation with respect to an axis not coaxial with the protein’s pore axis. We note that our choice of a Cartesian coordinate system results in any magnitude of forces causing some amino acids to move in toward the channel and some to move out. Thus, we must keep the selection of amino acids k, and their respective weights e^–k, consistent between the apo- and holo-form of the protein, else we risk improperly favoring the amino acids that move inward in our radius calculations.

3. Results

Analysis using autocorrelation functions showed that the CRANKITE equilibration period finished at 220 000 steps of the 10⁶ step simulation. We used the last 760 000 configurations to construct a covariance tensor for the displacement of every amino acid along its principal axes of motion. We used the displacement from the experimental apo-binding site (PDB code: 6BE1) to the experimental holo-binding site to approximate ligand-induced forces and predict the protein’s response to ligand binding for the agonist serotonin (PDB code: 6DG8), and four antagonists—alosetron (PDB code: 6W1J), granisetron (PDB code: 6NP0), ondansetron (PDB code: 6W1M), and palonosetron (PDB code: 6W1Y).

An ensemble-averaged simulation structure should theoretically be indicative of the ensemble-averaged cryo-EM, which determined the protein’s structure experimentally. We should note that 58 amino acids in the intracellular domain of each subunit could not be resolved by the experiment. Thus, our simulations have been carried out with 290 amino acids missing (there are a total of 2285 amino acids in the protein, but only 1995 of them are resolved), but the experimental structure is stabilized by the presence of those 290 amino acids. The structures of the intracellular domain from the experiment and simulation are thus quite different. A comparison between the channel profiles of the experimental and simulated apo-structures is shown in Supporting Figures. Though the structures differ, it is important to look at the differences between the pairs of structures being compared in each figure.

3.1. Agonist Binding

For comparison purposes, we calculated the channel radius profile for the experimental apo-structure 6BE1 and compared it with the experimental holo-structure 6DG8; this is considered the experimental baseline. Figure 2 shows that binding of five 5-HT molecules to the 5-HT_3A receptor caused the ion channel to increase in radius, especially in the transmembrane domain and the extracellular domain. The increase in the transmembrane region radius was about 1.5 Å. We notice a large increase in channel radius around z = −20 Å. There are reductions in the channel radius around z = −40 Å, z = −25 Å, z = 35 Å, and z = 65 Å.

Figure 2.

Diagram showing the radius of the ion channel along the length of the 5-HT_3A receptor. The solid line represents the data for the experimental apo-structure 6BE1. The broken line represents the profile for the receptor bound to five 5-HT molecules 6DG8. The transmembrane domain, in the region −25 Å < z < 25 Å, is denoted by the broken vertical lines. BS denotes the position of the binding site. The spaces between the solid and broken lines are filled with red (reduction of ion channel radius) or green (increase of ion channel radius).

We then evaluated the channel radii of the predicted structures along the long axis. We used the equilibrium apo-structure, μ, averaged from the 760 000 configurations from the data-collection period as the baseline structure. We then used our method to predict the protein structure for one 5-HT to five 5-HT molecules bound (Supporting Figures).

We observe that applying 5-HT forward vectors to different numbers of binding sites caused the ion channel to open, especially in the transmembrane domain. We observe that two serotonins provide more activation than one serotonin and that applying forward vectors to two adjacent binding sites triggers a stronger response than when applied to nonadjacent binding sites. Since the experimental structure 6DG8 has five serotonins bound, we should compare the experimental results with five 5-HT bound (Figure 2) and simulation results with five 5-HT bound (Figure 3a). The only common point is that the ligands caused an increase of the pore width in the transmembrane domain, but in other domains, the simulation results are different from the experimental results. Interestingly, the experimental holo-structure (Figure 2) is most similar to the simulation results for three 5-HT bound in adjacent sites (Figure 3); both showed a general increase in the ion channel radius of the transmembrane domain up to z = 30 Å, an increase in the extracellular domain except where z = 35 Å, and a decrease in the region −40 Å < z < −25 Å. We also note that previous electrophysiology experiments showed that three 5-HT molecules were required to achieve maximal gating efficacy.²⁰⁻²²

Figure 3.

Diagram showing the predicted ion channel radius along the length of the 5-HT_3A receptor with (a) five and (b) three adjacent serotonin molecules bound. The solid line represents the data for the simulated equilibrium apo-structure, denoted by μ, the average position across all N_t snapshots. The broken line represents the profile of the receptor bound to three 5-HT molecules in adjacent binding sites. The figure legends are as in Figure 2. The five identical subunits of the 5-HT_3A receptor are denoted A to E in a clockwise direction when viewed from the extracellular space toward the cytoplasm. The ligands bind to the space between the subunits, and the binding site is denoted by the subunits adjacent to the binding site.

Lastly, we note that there are larger differences between the intracellular domains of the experimental structure and the simulated structure. This is mainly due to the 290 amino acids that have not been resolved experimentally. Even if we performed a simulation with an explicit solvent and membrane, the absence of these 290 amino acids would cause the intracellular domain to exhibit conformations that would not be observed in experiments.

3.2. Antagonist Binding

We applied our method for the competitive antagonists alosetron (PDB code: 6W1J), granisetron (PDB code: 6NP0), ondansetron (PDB code: 6W1M), and palonosetron (PDB code: 6W1Y). These four antagonists produced similar responses in the channel radius profile both experimentally and computationally. Varying the number of antagonists bound also produced similar results (see Supporting Figures).

Figure 4 shows the experimental results for the 5-HT_3A structure with five granisetrons bound (PDB code: 6NP0) in comparison to the experimental apo-structure (PDB code: 6BE1). The bottleneck radius in the transmembrane domain decreases from 2.63 to 2.55 Å, the rest of the transmembrane domain opens slightly but the binding of the competitive antagonists negligibly affects the ion channel. We evaluated the simulated structures in the same manner as we did the agonists. With five granisetron molecules bound, as shown in Figure 5, the channel bottleneck radius decreases from 1.81 to 1.67 Å. There is an increase in channel radius at −10 Å < z < 10 Å as well as at 30 Å < z < 40 Å in the extracellular domain. We note again that there are larger differences between the intracellular domains of the experimental structure and of the simulated structure. This is mainly due to the 290 amino acids that cannot be resolved experimentally. There are quantitative differences between the profiles of the extracellular domain of the experimental structure and simulated structure, but the qualitative fit pertaining to the difference in channel radii between the respective pairs is good: as one goes in the extracellular direction, the ion channel narrows, then it widens and stays wide for about 20 Å and then it narrows. The agreement is very good, given that the experiments were performed with an intact protein in a hydrated membrane but the simulations were carried out in vacuo on a protein with 15% of the amino acids missing.

Figure 4.

Diagram showing the radius of the ion channel along the length of the 5-HT_3A receptor. The solid line represents the data for the experimental apo-structure 6BE1. The broken line represents the profile for the receptor bound to five granisetron molecules 6NP0. The figure legends are as in Figure 2.

Figure 5.

Diagram showing the radius of the predicted ion channel along the length of the 5-HT_3A receptor with five granisetron molecules bound. The solid line represents the data for the simulated equilibrium apo-structure μ. The broken line represents the profile for the receptor bound to five granisetron molecules. The figure legends are as in Figure 2.

4. Discussion

What is an agonist, and what is a competitive antagonist? How do they act on the receptor to exert their effects? These are questions that have occupied the minds of pharmacologists for a long time. In this work, we built upon a method to predict the gating effects (if any) of a ligand on its receptor. By gating, we mean the action of an agonist on a receptor that leads to its activation. In this case, it is the binding of agonists that leads to the opening of the central ion channel.

Previously, structure determination experiments showed the effects of different ligands on the 5-HT_3A receptor and how different domains of the receptor were moved to either open the central ion channel, keep it closed, or even close it down further.^5,9 Further studies showed that this opening is probably asymmetric in the homopentamer.⁶

Maio et al.¹⁰ used 4PIR as the starting structure, placed it in a hydrated membrane, and performed molecular dynamics simulations and free energy calculations. They showed that ion permeation was through the five lateral channels in the intracellular domain, the same region in which we see a sharp peak in the channel radius at z = −20 Å in the experimental structures. The experimental structure of the intracellular domain is not well resolved in the 5-HT_3A receptor; this combined with the lack of membrane in our simulations may explain the limitations of our method not detecting the enlargement of channel radius at z = −20 Å.

Várnai et al.¹⁷ used a model of the GABA_A receptor, carried out a CRANKITE simulation on the protein, and developed a correlation tensor to relate agonist binding to gating; their implementation of the method resulted in an estimation of F_i = kΔx_i, with some generic spring constant, which was never defined. Our current work extends previous results¹⁷ by providing a more accurate method to study the effects of agonists and competitive antagonists on a receptor. We have applied the harmonic approximation to quickly estimate ligand-induced forces while staying within the bounds of the assumptions made in the derivation of the linear response theory. We have shown that spring constants should be inversely proportional to the variance of a given amino acid. Previous work¹⁷ failed to correctly implement a spring constant, resulting in an improperly normalized result, where the most flexible amino acids would be heavily favored in calculations. Furthermore, they used correlation instead of covariance without any proper derivation.

As opposed to molecular dynamics studies, the use of CRANKITE does not require a large amount of computer time. The application of linear response theory is a general method: once we have calculated the covariance tensor, we can evaluate the perturbation caused by a ligand to the binding site and thus predict the effect of the ligand; to study another ligand, we can use the same covariance tensor but re-evaluate the binding site perturbation. This makes it possible to rapidly define the effect of a large number of ligands on the same receptor. Moreover, we use the perturbed structure of the binding site rather than ligand-induced forces as our input, which provides better intuition for what novel drug candidates should look like. Lastly, our methods are able to accurately differentiate the behavior of agonists and competitive antagonists: when agonists bind, there is widening of the ion channel in the transmembrane domain; and when competitive antagonists bind, there is no opening in the ion channel bottleneck.

The assumptions of our model only hold for weak perturbations in allosteric interactions. The perturbation must be weak enough that the higher-order terms of the Taylor expanded potential are indeed negligible. The interaction must also take place sufficiently far away from the active site so that there are no direct ligand-induced forces acting on the site of interest. Some enzymes and most ligand-gated and voltage-gated ion channels would meet this condition, as their functional movements are small.

In the future, it would be interesting to develop a method to reverse the following question: if one would like to open an ion channel, in what ways should one perturb the binding site? If one were to develop a competitive antagonist, what freedoms does one have to perturb the binding site without causing activation? Our method would be useful in drug design, in combination with drug discovery methods that tend to be good at designing binders but still have difficulty designing agonists or competitive antagonists.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.3c03503.

• Predicted channel radius profiles of the 5-HT_3A receptor after applying our method to a variety of ligands, along with experimental profiles (Supporting Figures) (PDF)

The authors declare no competing financial interest.