Coevolution combined with molecular dynamics simulations provides structural and mechanistic insights into the interactions between the integrator complex subunits

Abstract

Finding the 3D structure of large, multi-subunit complexes is difficult, despite recent advances in cryo-EM technology, due to remaining challenges to expressing and purifying subunits. Computational approaches that predict protein-protein interactions, including Direct Coupling Analysis (DCA), represent an attractive alternative for dissecting interactions within protein complexes. However, they are readily applicable only to small proteins due to high computational complexity and a high number of false positives. To solve this problem, we proposed a modified DCA approach, a powerful tool to predict the most likely interfaces of protein complexes. Since our modified approach cannot provide structural and mechanistic details of interacting peptides, we combine it with Molecular Dynamics (MD) simulations. To illustrate this novel approach, we predict interacting domains and structural details of interactions of two Integrator complex subunits, INTS9 and INTS11. Our predictions of interacting residues of INTS9/INTS11 are highly consistent with crystallographic structure. We then expand our procedure to two complexes whose structures are not well-studied: 1) The heterodimer formed by the Cleavage and Polyadenylation Specificity Factor 100-kD (CPSF100) and 73-kD (CPSF73); 2) The heterotrimer formed by INTS4/INTS9/INTS11. Experimental data supports our predictions of interactions within these two complexes, demonstrating that combining DCA and MD simulations is a powerful approach to revealing structural insights of large protein complexes.

Graphical Abstract

Figure: (A) The principle of coevolution analysis. Coevolution between residues of interacting proteins can be used to predict the binding interfaces. (B) DCA map. For large proteins, the predictions are hindered by false positives resulting from statistical background noise. (C) Optimized DCA map. Local convolution of evolutionary scores and structural properties can reduce the noise and filter out the false positives, thus allowing to correctly identify the interacting regions. Because this optimized DCA still cannot provide structural and mechanistic details of interacting peptides, we further combine it with Molecular Dynamics simulation. (D) Structural details of interacting peptides. The most likely interacting peptides of both proteins are used as input for MD simulations. So, we demonstrated that combining our optimized DCA and MD simulations is a powerful approach to revealing structural insights of large protein complexes.

1. Introduction

Traditional methods of studying protein association, including the yeast two-hybrid and co-immunoprecipitation analyses, are reliable in characterizing protein complexes, but they remain laborious and time-consuming. Therefore, computational methods to predict protein-protein interactions are an attractive alternative to experimental methods. One such method is evolutionary coupling analysis. The underlying idea of evolutionary coupling is that to preserve function, a mutation in one of the interacting residues is likely to be compensated by a complementary mutation in the other. The key advantage of this approach is that interactions between residues are detected not only based on their physical proximity (as in co-crystallization studies) but on evolutionary pressure and, therefore, are more likely functional. For decades, the coevolution of residues in protein sequences has been used to predict residue-residue interactions (contacts) in small bacterial proteins [1], [2], [3]. As observed by us and others [4], [5], [6], [7], [8], with the rapid increase in sequenced animal genomes, these methods also became feasible for protein interactions in metazoans, including humans, and larger proteins and even protein complexes [4], [5], [8], [9], [10], [11], [12], [13], [14], [15], [16], [17], [18], [19].

Specific interactions between proteins impose evolutionary constraints on the interacting partners. For instance, mutation of a contact residue in one partner generally impairs binding but may be compensated by a complementary mutation in the other partner. Such coevolution of interaction partners results in correlations between their amino acid sequences that can be observed by analyzing Multiple Sequence Alignment (MSA) of the interacting proteins across multiple species and can be used to predict residue–residue contacts [2], [20], [21], [22]. Recently, statistical physics methods were used to disentangle signals related to actual residue interactions (direct coupling) from non-meaningful correlations between MSA columns. This has resulted in a new class of methods, including the Direct Coupling Analysis (DCA), that can reliably predict protein structures using only sequence information provided enough homologous sequences are available. The threshold of 0.7 for the ratio of homologous sequences divided by combined protein length expressed in amino acids has been proposed for reliable DCA application [23]. However, this condition is usually unmet for large proteins (like >500 aa proteins discussed in this paper). Therefore, the applications of DCA methods to large proteins are limited by the high number of false positives generated. To reduce the number of false positives, we recently proposed using a local convolution of evolutionary coupling (EC) scores with a Gaussian kernel [6], [7], [24]. Although the modified DCA method can accurately predict the binding interfaces, it cannot provide structural details of interacting residues. As previously shown, such information could be obtained using biased Molecular Dynamics (MD) simulations [7], [8]. Here, we will adapt the two-step procedure (unbiased prediction of binding interface and biased MD) to study interactions within two cellular complexes critical to transcription termination: the Integrator complex (INT) and the Cleavage and polyadenylation machinery (CPA). Both complexes have been investigated structurally in various capacities [25], [26], [27], [28], [29], [30], [31], [32], [33], but not all aspects have been elucidated due to dynamic or disordered regions. Thus, DCA is a potential alternative to generating new insight into protein interactions that can bridge the gap of cryo-EM or AlphaFold predictions.

The Integrator complex (INT) is a critical transcriptional component in regulating the 3′-end processing of non-coding RNA (reviewed in [34]). INT has been shown to broadly participate in transcription processes at protein-coding genes by associating with paused RNA polymerase II [35], [36], [37]. Several INT subunits have been found to play essential roles in human brain development [38], cancer [39], lung function [40], embryogenesis [41], and adipose differentiation [42]. Among at least the 17 subunits of Integrator, subunits 9 and 11 (INTS9-INTS11) constitute a catalytic core of INT and are paralogs of two 100 kDa and 73 kDa subunits of the Cleavage and Polyadenylation Specificity Factor (CPSF) [25], [26]. INTS11 forms a stable complex with INTS9 through their C-terminal domains (CTDs) that also exist in CPSF73 and CPSF100 but with poor sequence conservation. [26], [43] The crystal structure of the INTS9/INTS11 CTD complex has been reported at 2.1 Å resolution, which explains the high binding affinity for the two proteins [25]. Moreover, the binding of INTS9/INTS11 is a prerequisite to recruiting INTS4, which forms the INTS4/INTS9/INTS11 Integrator Cleavage Module (ICM) [26], [29], [33]. Like their INT counterparts, CPSF73 and CPSF100 are in a stable complex and are also required for 3′-end processing of all metazoan pre-mRNAs [44]. Although the crystal structures of human CPSF73 and yeast CPSF100 individually [45] have been reported, not all aspects of their interaction have been elucidated using cryo-EM [27].

Here, we use the modified DCA approach to accurately predict the binding residues of the INTS9/INTS11 heterodimer and MD simulations to determine the mechanistic and structural details of the interactions. We also study the interaction between INTS9 and INTS11 paralogs, CPSF73 and CPSF100, and identify their most likely binding interfaces as the C-terminal domains of both proteins. Although multiple structures of the Integrator Cleavage Module have been solved [26], [29], [33], not all regions of the subunit interfaces have been defined. Thus, we used our two-step procedure to show that such heterotrimerization involves the N- and C-terminal domains of INTS4. As a utility, the DCA approach will aid in de novo protein-protein interface predictions and help guide experimental validations, thus speeding up the complete structure description.

2. Results

To reduce running time, we built our method around a variant of DCA, the pseudo-likelihood maximization Direct-Coupling Analysis (plmDCA) [46], which has a lower computational cost than traditional DCA. Therefore, the plmDCA was used to compute the evolutionary coupling score (ECs) and to build the corresponding coupling matrix between proteins.

2.1. Modified Direct Coupling Analysis (DCA) approach

DCA algorithms have been shown to produce a large number of false positives, but we recently suggested [6] that post-processing of DCA map data, based on the local convolution with Gaussian kernel, may lead to reducing noise in the prediction of most likely interacting residues [6]. A schematic description of the method is presented in Fig. 1.

Fig. 1.

Prediction of protein-protein interactions based on coevolutionary analysis. (a) The principle of coevolution analysis. Coevolution between residues of interacting proteins can be used to predict the binding interfaces as described by Hopf et al. [23]. (b) Optimizing the coevolution maps. For large proteins, the predictions are hindered by false positives resulting from statistical background noise. Genuine interactions between proteins generally involve stretches of residues rather than individual amino acids. Therefore, local convolution of evolutionary scores and structural properties can reduce the noise and filter out the false positives, thus allowing the correct identification of the interacting regions, as described by Fongang et al. [6].

The strength of this approach is that to improve our prediction and avoid false positives in DCA analysis, we use local convolution of ECs. Gaussian convolution is applied to local structural elements (here defined by secondary structure, such as α helix, β sheet, and coil, as predicted by PSIPRED [47]) to count the contribution of neighboring residues with an assumption that contacts between proteins occur locally and drive residues evolving within the same structural elements. In our experience, an isolated strong EC peak surrounded by low EC values for residues belonging to different secondary structure elements is more likely to be a false positive than a cluster of less high EC values for residues in the same secondary structure element. Therefore, a convolution of EC scores with a kernel based on secondary structure information can predict the more likely interacting residues.

The convolution algorithm depends on several parameters, including the number of interacting residues on each side, l, the variances of the Gaussian, and the predicted structures. The convolved EC score for a pair of residues (i,j) is $Q_{i,j}^l$,

$$Q_{i,j}^l=\sum _{\propto =i-l}^{i+l}\sum _{\beta -j-l}^{j+l}{P}_{i,j}{K}_{a,b}(\propto ,\beta )$$

where $P_{i,j}$ are the EC scores computed using the evolutionary coupling algorithm and.

$K_{a,b}\left(\propto ,\beta \right)=\exp \left(-\left\{{a\propto }^2+b{\beta }^2\right\}\right)$is the Gaussian kernel function with parameters a and b related to the variances. The critical innovation over the previous variant of the DCA method we proposed in Fongang et al. [6] is to derive the optimal values of the parameters a b, based on the interaction details as characterized by a previous crystallographic study. Second, based on previous experience and the argument that an interaction interface is expected to affect both proteins in a statistically similar manner, we decided only to consider convolution models assuming a = b. The parameters were optimized using the INTS9/INTS11 complex for which structural information of their interacting C-terminal domains was available. We started the optimization from Evolutionary Coupling (EC) scores of INTS9/INTS11, which were generated based on multiple sequence alignments of both proteins over 204 species. Next, we converted EC scores into DCA maps representing interactions between residues of the two proteins (Fig. 2a). Finally, the optimal values of a, b, and l were selected to maximize the overlap between the prediction and the experimental distances for INTS9/INTS11 interaction and also used for other cases for which crystal structures are unknown. The optimized parameters for the Gaussian convolution are shown in Table 1.

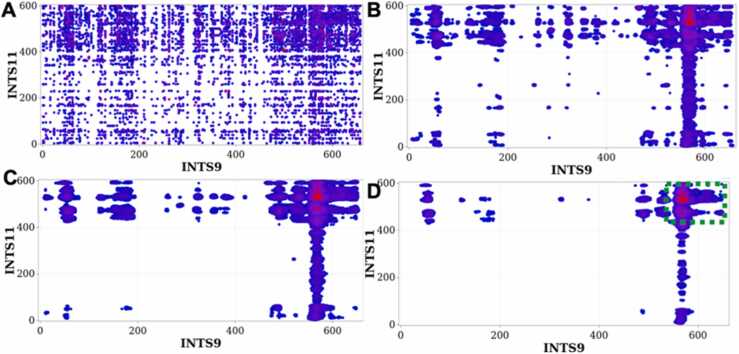
Fig. 2.

Convolved ECs of INTS9/INTS11 reveal most likely interacting residues. The local convolution method was applied to the top 1% of raw ECs (A) using different parameters representing the length of the interacting residues l, and the variances of the Gaussian kernels a and b. (B): l = 18 AA, a = b = 0.1; (C): l = 21AA, a = b = 0.05; (D): l = 21AA, a = b = 0.01. The green rectangle on (D) delimits the most likely interacting region.

Table 1.

Optimized values of the Gaussian convolution. Parameters a and b are the optimized variances of the Gaussian Kernel, l is the average length of the interval with interacting residues and γ = 1 if the residues belong to the same secondary structure, if not γ = 2.

	a	b	l(AA)
γ = 1	0.01 – 0.05	0.01 – 0.05	17–24
γ = 2	0.001–0.008	0.001 – 0.008	17–24

2.2. Modified DCA correctly predicts the interacting residues of INTS9/INTS11 heterodimer

To validate our method, we used it to predict interactions of the INTS9 and INTS11 heterodimer, whose interface has been solved by crystallography. However, the raw DCA method applied to predicting INTS9/INTS11 interactions generated a very high level of statistical background noise in the EC map, leading to false positives, thereby making the identification of binding residues very challenging (Fig. 2a). Therefore, we applied our local convolution algorithm to the EC map of INTS9/INTS11 with variable parameters describing the variances of the Gaussian kernel and the lengths of stretches of interacting residues (Figs. 2b-2d). Indeed, as we changed the convolution parameters, stretches of residues starting at residue 553 of INTS9 and 422 of INTS11 yielded highly optimized coevolutionary scores compared to the entire DCA map. The optimized parameters corresponding to the final convolved DCA map (Fig. 2d) are l = 21 AA, a = b = 0.01, where l corresponds to the number of interacting residues, and a and b are parameters of the Gaussian kernel function with equal variances. Applying this algorithm indicated that the C-terminal domains of INTS9 and INTS11 contain the most likely interacting residues of the INTS9/INTS11 heterodimer.

Experimental evidence demonstrates that INTS9 and INTS11 interact through their C-terminal domains (CTD). Indeed, the report by Wu et al. [25] explains the molecular basis and the functionality of the INTS9/INTS11 heterodimer as well as the crystal structure of the CTD at 2.1 Å. To assess the accuracy of our predictions, we compared the pairs of residues (one from INTS9, one from INTS11) at distances less than 6.0 Å to the pairs of interacting residues we predicted. Using this criterion for comparison, we observed excellent agreement between our modified DCA predictions and the INTS9/INTS11 CTD crystal structure. We found that 73% of the pairs with the top 5% highest convolved signals are within the CTD of both proteins, and 81% of the experimentally determined contacts were predicted by our method. Also, convolved ECs are correlated with structural information, including solvent accessibility, secondary structure, and physical-chemical properties. This test shows that our method has the potential to accurately predict residues involved in protein-protein interactions. It also confirms that the previously observed contact between the CTDs of INTS9 and INTS11 is a physiologically significant interaction subject to positive evolutionary pressure (see Fig. 3a). Finally, we need to note that we used the INTS9/INTS11 structure to validate the method, while we also used the same interaction to optimize the convolution procedure parameters. Nonetheless, the amount of information recycled here is minimal. The INTS9/INTS11 structure was only used to optimize the values of the three parameters (a, b, and l), while the validation is based on a very large number (>10⁵) of EC scores.

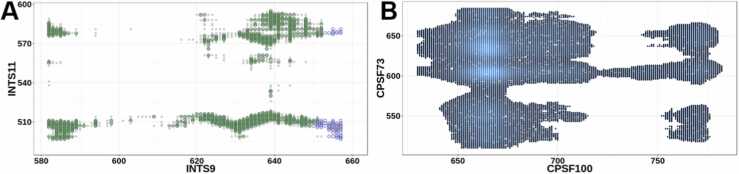
Fig. 3.

(A) Example of quality of contact inference. After EC averaging and secondary structure information refinement, our contact predictions are highly consistent with crystallographic contacts from the INTS9/INTS11 dimer structure. Green: predicted contacts that were confirmed experimentally, gray: experimental contacts that were not predicted, empty blue circles: predicted contacts that were not experimentally verified. X- and Y-axes: positions in INTS9 and INTS11 (only the interacting C-terminal region is shown). (B) Optimized coevolution map of the C-Terminal Domains from the CPSF100/CPSF73 heterodimer. The figure shows the predicted and optimized EC scores (l = 21AA, a = b 0.01, top 1%). Grey indicates the predicted interactions and blue- most likely interactions.

2.3. Predicting Interacting interfaces of the CPSF100/CPSF73 heterodimer

The validation of the predicted INTS9/INST11 interfaces allowed us to expand our study to the Cleavage and Polyadenylation Specificity Factor (CPSF) complex, which is involved in the 3′-end cleavage of pre-mRNA prior to polyadenylation. Within the CPSF complex, CPSF73 has been shown to form a stable and functional heterodimer with CPSF100. Moreover, CPSF100 and CPSF73 are structurally very similar to INTS9 and INTS11 and are annotated as their paralogs. INTS11 contains its highest degree of conservation with CPSF73 over much of the N-terminal MBL domains, and the β-CASP domains are highly divergent at the C-terminal regions [43]. CPSF100 and INTS9 are inactivated through changes in key catalytic residues, but INTS9, with a molecular mass of 74 kDa, is much smaller than CPSF100. Studies have shown that, like the INTS9/INTS11 heterodimer, CPSF100 and CPSF73 rely on their C-terminal domains to form a dimer, crucial to their function in UsnRNA biogenesis. [48], [49] However, not all information is available on the structural basis of the CPSF100/CPSF73 heterodimer, and computational methods can provide further insights.

As with INTS9/INTS11, we used 138 pairs of CPSF100 and CPSF73 orthologous sequences from metazoans to compute DCA maps of both proteins (Fig. 4a). Then, we applied the local convolution of ECs scores with optimized parameters obtained from the previous case to highlight the most likely interacting residues (Fig. 4b-d). This analysis predicts that the most likely interacting residues of CPSF100/CPSF73 involve their respective C-terminal domains (Fig. 4d and Fig. 3b). Indeed, 88% of the top 5% highest convolved EC scores are within the region comprising the last 115 and 164 amino acids of CPSF100 and CPSF73, respectively. The second most likely interacting residues comprised the region from 367 to 533 on CPSF100 and the CTD of CPSF73 (Fig. 4d). These predicted interactions are similar to those of INTS9/INTS11, highlighting the striking similarity between these complexes. Moreover, the findings obtained using our modified DCA method are consistent with those obtained biochemically by Michalski et al. [50] in that both the C-terminal domains of CPSF100 and CPSF73 are required for the core cleavage complex formation and structurally with the cryo-EM based models of the histone pre-mRNA processing complex [27].

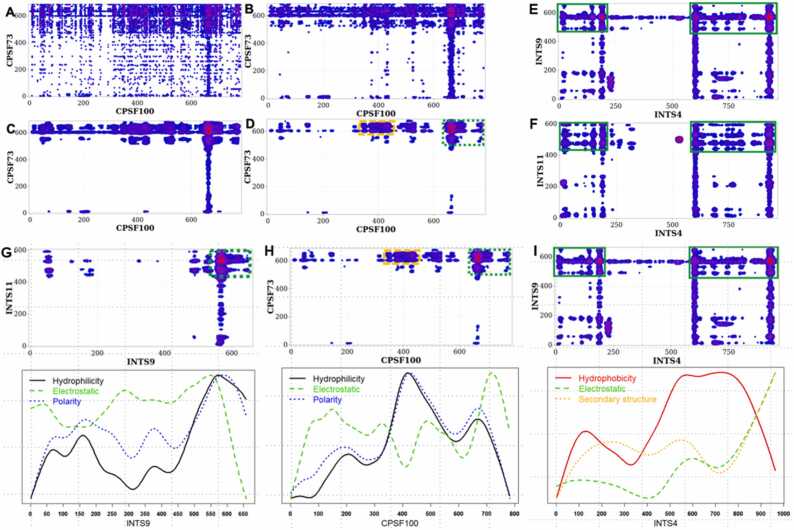
Fig. 4.

(A) - (D) Convolved ECs of CPSF100/CPSF73 reveal most likely interacting residues. The local convolution method was applied to the top 1% of raw ECs (A) using different parameters representing the length of the interacting residues l, and the variances of the Gaussian kernels a and b. (B): l = 18 AA, a = b = 0.1; (C): l = 21AA, a = b = 0.05; (D): l = 21AA, a = b = 0.01. The green and orange rectangles on (D) delimit the most likely (green rectangle) and the second likely (orange rectangle) interacting regions of the CPSF100/CPSF73 heterodimer, respectively. (E) and (F) The predicted contacts between INTS4/INTS9 and INTS4/INTS11 involve the C- and N-terminal domains of INTS4. The figure shows the convolved ECs (l = 21AA, a = b = 0.01, top 1%) of the INTS4/INTS9 (E) and INTS4/INTS11 (F). (G) - (I) INTS9/INTS11, INTS9/INTS4, and CPSF73/CPSF100 interactions are driven by the physicochemical properties at the interfaces. (G) INTS9/INTS11 dimerization is driven on average by the hydrophilicity (solid black line in the bottom plot) and polarity (dotted blue line) of the INTS9 amino acids and their electrostatic charges (dashed green line), which are higher at the predicted hot spots. (H) Similarly, the CPSF100/CPSF73 dimerization is driven by hydrophilicity (solid black line), polarity (dotted blue line), and electrostatic (dashed green line). (I) INTS4/INTS9 dimerization is favored by hydrophobicity (solid red line), electrostatic (dashed green line), and secondary structure similarity (dotted orange line) of INTS4.

2.4. Predicting interacting residues of the INTS4/INTS9/INTS11 heterotrimer

Encouraged by the results of our modified DCA approach for the above two heterodimers, we applied our method to a heterotrimeric complex. Predicting the structure of heterotrimers presents an additional challenge to current DCA analyses because, in heterotrimers, indirect interactions may be viewed as couplings between residues, thus significantly increasing the number of possible indirect links between the residues. For example, the interaction between residue A_i in subunit A with any of the hundreds of residues in subunit B, combined with the interaction between the residues in B and residue C_j in subunit C, may be interpreted as an interaction between A_i and C_j. This effect may increase the number of false positives and decrease the sensitivity and specificity of our results. Therefore, reducing the number of artifacts through post-processing the EC maps is even more critical in the case of heterotrimeric complexes. INTS4 has been reported to associate with INTS9 and INTS11 to form the INTS4/INTS9/INTS11 heterotrimer. Notably, at the time we ran our analysis, there had been no reported structures. Using the plmDCA algorithm coupled to the convolution of resulting ECs as previously described, we predicted that the N- and C-terminal domains of INTS4 interact with INTS9/INTS11 (see Fig. 4e-f). Our results also suggest that INTS4 can bind both INTS9 and INTS11 at the same time. This prediction ended up being validated by recently released structures of the ICM as INTS4 indeed contacts INTS9 and INTS11 while they are associated with each other [29], [33]. However, our coevolutionary analysis could not distinguish which N- or C-terminal was associated with INTS9 (or INTS11), as shown in Fig. 4e-f. The recent structures of the ICM demonstrate that the N-terminus of INTS4 indeed contacts INTS9/11, but the C-terminus of INTS4 was able to be resolved [33], [37]. Thus, the meaning of these other predicted interactions remains to be seen. Interestingly, our model is strikingly similar to the heterotrimerization of CPSF100/CPSF73/Symplekin proposed by Michalski et al. [50] and is consistent with independently published biochemical experiments analyzing binding domains involved in the INTS4/INTS9/INTS11 heterotrimer.

2.5. INTS9/INTS11, INTS9/INTS4, and CPSF73/CPSF100 interactions are driven by the physicochemical properties at the interfaces

We sought to determine the physicochemical properties of the Integrator subunits driving the formation of the complex. We computed the properties of INTS9 driving the formation of the INTS9/INTS11 complex by averaging known physicochemical properties' metrics on the sequence length. [51], [52] As shown in Fig. 4g, the heterodimerization of INTS9 and INTS11 is driven by higher hydrophilicity, higher polarity, and a higher electrostatic charge of INTS9 residues at the predicted host-spots. Similarly, the physicochemical properties of CPSF100 drive its association with CPSF73 (Fig. 4h), including high hydrophilicity and polarity. Finally, the binding of INTS4 to INTS9 (Fig. 4i) is mainly driven by high hydrophobicity, electrostatic charges, and secondary structure similarity scores of INTS4 amino acids.

2.6. Molecular dynamics simulations highlight the structural details of interacting peptides

The modified DCA is a powerful tool to predict the most likely interfaces of protein complexes. However, this approach cannot provide structural and mechanistic details of interacting peptides. On the other hand, all-atom MD simulations, a technique generally used to compute such information, remain a challenge for large proteins. [53], [54], [55] Therefore, to estimate the structural and mechanistic details of the Integrator complex's interfaces, we used a biased MD approach with simulation boxes limited to the most likely interacting peptides as predicted by the DCA (Table 2). [8] We performed MD simulations of the most likely interacting peptides of INTS9/INTS11, CPSF100/CPSF73, INTS4/INTS9, and INTS4/INTS11, as described in the Methods section. Despite fluctuations observed along the MD process, the dynamic evolution of the average of the total energy in the different interacting regions of each complex recorded along the simulation over three replicates shows that these regions have reached thermal equilibrium after around 400,000-time steps (Fig. 5 and Fig. SF2), suggesting the stability of the hotspots. The mean radius of gyration, which is generally used to detect the compactness of the binding regions of the complex, displayed stable contact formed for INTS9/INTS11, INTS4/INTS9, and INTS4/INTS11 starting at around 1000,000-time steps. However, for the interacting regions of CPSF100/CPSF73, we also observed stable contact formed after around 1000,000-time steps. Additionally, the slight deviations in the first hotspot of CPSF100/CPSF73 at around 3000,000-time steps might indicate that transient contacts are broken, allowing the most stable contact to be formed. The distribution of the radius of gyration along the simulations for each binding interface is depicted in Fig. SF3. It is often used to define a collapsed or extended conformation. These results indicate the compactness and stability of binding domains predicted by the modified DCA approach. Then, we used the Critical Assessment of Prediction of Interactions (CAPRI) criterion [56] to decide if contacts exist between residues.

Table 2.

Peptides selected for molecular dynamic simulations. MD simulations assess the stable conformations of interacting residues.

Protein A	Protein B	Main observation
INTS9 I490 – P556	INTS11 S500 – L601	β-sheet conformation
INTS4 Q125 – I200 P885 – P936	INTS9 M486 – P556 M486 – P556	β-sheet conformation
INTS4 Q125 – I200 P885 – P936	INTS11 K425 – H524 K425 – H524	Helical conformation and β-sheet conformation
CPSF100 V325 – K386 W630 - P702	CPSF73 R480 – K512 R480 – K512	β-sheet conformation

Fig. 5.

MD simulations convergence. Variations of the average total (in kcal/mol) energy and the average radius of gyration (in $\mathrm{\AA }$) over three trajectories as a function of time steps for the different hotspots inform on the convergence of the simulation. The average radius of gyration (${\stackrel{\circledR }{R}}_g\pm \mathit{sd}$) of each binding interface along the simulations are, black: ($19.29\pm 3.04$) $\mathrm{\AA }$; blue: ($15.58\pm 2.33$) $\mathrm{\AA }$; red: ($14.36\pm 0.71$) $\mathrm{\AA }$; green: ($17.51\pm 0.77$) $\mathrm{\AA }$; purple: ($21.34\pm 1.37$) $\mathrm{\AA }$; orange: ($17.36\pm 2.61$) $\mathrm{\AA }$; pink: ($23.24\pm 2.04$) $\mathrm{\AA }$.

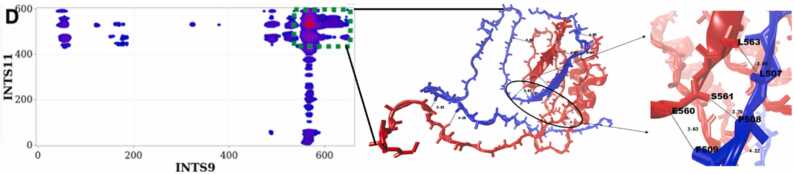
We found that INTS9 and INTS11 interact mainly through their β-sheet conformations at the interface, with Y499/L523, I535/E507, and F509/E560 as the closest residues on both proteins (Fig. 6).

Fig. 6.

Structural details of INTS9/INTS11 interacting peptides. The most likely interacting peptides of INTS9 (blue) and INTS11 (red) are used as input for MD simulations. [57] After MD convergence, a snapshot of the stable configuration shows the details of interactions. INTS9 and INTS11 interact mainly through their β-sheet conformations at the interface, with Y499/L523, I535/E507, and F509/E560 as the closest residues on both proteins. The average radius of gyration (${\stackrel{\circledR }{R}}_g\pm \mathit{sd}$) of INTS9/INTS11 along the simulations, is ($19.29\pm 3.04$) $\mathrm{\AA }$.

Similarly, MD simulations using the most likely and the second most likely interacting peptides of the CPSF100/CPSF73 heterodimer showed that the interactions involve β-sheet conformations for both interfaces, as shown in Fig. 7. Although we were limited by the lack of a crystal structure of the C-terminal domain of CPSF73, we found the closest residues for the CPSF100/CPSF73 complex are I631/P497, P698/V481, and S352/F490.

Fig. 7.

Structural details of CPSF100/CPSF73 interacting peptides. The most (green rectangle) and the second most (orange rectangle) likely interacting peptides of CPSF100 (blue) and CPSF73 (red) are used as input for MD simulations. Due to the lack of 3D structure of the whole C-terminal domain of CPSF73, our MD simulations did not include the full predicted interacting sites. We found the closest residues for the CPSF100/CPSF73 complex are I631/P497, P698/V481, and S352/F490. The average radius of gyration (${\stackrel{\circledR }{R}}_g\pm \mathit{sd}$) of the first binding region of CPSF100/CPSF73 along the simulations is ($15.58\pm 2.33$) $\mathrm{\AA }$, and is ($14.36\pm 0.71$) $\mathrm{\AA }$ for the second one.

Finally, we used MD simulations to investigate the structural conformations of INTS9 and INTS11 when they bind to INTS4 to form the INTS4/INTS9/INTS11 heterotrimer (Fig. 8). Like previous complexes, INTS4 and INTS11/INTS9 interaction involves the proteins' β-sheet conformations and helical conformation. After MD convergence, we observed that the closest residues at the interface of INTS4/INTS9 are W903/E517, A906/G534, V126/H545, L130/A542, L171/D524, and D153/V504. For the INTS4/INTS11 heterodimer, the closest residues were found to be H164/K425, R520/R912, V896/S463, E905/L515, L151/P453, and M149/C441.Fig. 9.

Fig. 8.

Structural details of INTS4/INTS9/INTS11 heterotrimer based on interacting peptides predicted by the DCA. The most likely interacting peptides of INTS4 (green), INTS9 (blue), and INTS11 (red) are used as input for MD simulations. (A) N-terminal of INTS4 and C-terminal of INTS9; (B) C-terminal of INTS4 and C-terminal of INTS9; (D) N-terminal of INTS4 and C-terminal of INTS11; and (D) C-terminal of INTS4 and C-terminal of INTS11. After MD convergence, the closest residues for each sub-complex are reported (see text).

Fig. 9.

Schematic view of the predicted structure of INTS4/9/11 trimer. The N- and C-terminal domains of INTS4 interact with the C-terminal domains of INTS9 and INTS11.

3. Discussion

In this study, we applied coevolutionary methods and molecular dynamics simulations to identify the most likely binding residues of the INTS9/INTS11, CPSF100/CPSF73, and INTS4/INTS9/INTS11 complexes. We used the Direct Coupling Analysis (DCA) algorithm with several changes we introduced to allow more accurate inference of interactions. Specifically, we used local Gaussian convolution and predicted secondary structure to reduce the number of false positives and thus increase the accuracy of predicted interactions. As discussed above, coevolution between residues of interacting proteins can be used to predict the binding interfaces. However, for large proteins, the predictions are hindered by statistical background noise and the many false positives generated. Because interactions between proteins generally involve stretches of residues rather than individual amino acids, in our experience, local convolution of evolutionary scores and structural properties tend to predict more accurately the most likely interacting residues [6].

We inferred the binding interface of INTS9/INST11 heterodimer as a proof-of-concept using our local convolution algorithm [6]. Our results show that the most likely interacting residues of the INTS9/INTS11 heterodimer are located on the C-terminal domains of both INTS9 and INTS11. This prediction aligns with the results from Wu et al. [25], who used a U7-GFP reporter to show that mutations at the C-terminal domain specifically disrupt the formation of the INTS9/INTS11 heterodimer. Encouraged by the fact that our method accurately predicted large protein binding residues, we then applied it to another two important proteins in pre-mRNA cleavage: CPSF100 and CPSF73, paralogs of INTS9 and INTS11, respectively, whose interactions are not as well-defined. Our prediction confirmed that both the C-terminal domains of CPSF100 and CPSF73 are required for the core cleavage complex formation in vivo and the binding with Symplekin, as reported by Michalski et al. [50]. Further, we found that the N- and C-terminal domains of INTS4 could interact with INTS9 and INTS11, as shown in Fig. 5, suggesting INTS4 can bind both INTS9 and INTS11. This finding is consistent with previous biochemical studies [49] and recent structural studies [29], [33].

Using the coevolution of residues, we have characterized several interactions between proteins related to the Integrator complex. The results are shown in Table 3. Our analysis confirms the physiological nature of several interactions indicated by previous studies and predicts new interactions that can help to explain the nature of the Integrator, a complex molecular machine. Finally, the predicted characteristics of the interactions between pairs of proteins and identified domains and residues potentially crucial for the respective dimerization and trimerization can inform future experimental studies, such as targeted mutations that may disrupt complex formation.

Table 3.

Properties of the protein heterodimers studied. The significant length (number of sequences in cMSA / Size of both proteins) is indicated for each protein complex. As they are all lower than the required 0.7 for most DCA analysis in single proteins [23], we used our method, based on the local convolution of ECs, to reduce the number of false positives generated and highlight the most likely interacting partners [6].

	Protein size (AA)	Number of individual sequences	Number of sequences in cMSA	Sig. length	Sequence coverage
INTS9	658	223	204	0.16	55 – 90%
INTS11	600	239
INTS4	963	202	171	0.11	55 – 90%
INTS9	658	223
INTS4	963	202	171	0.11	55 – 90%
INTS11	600	239
CPSF100	782	179	138	0.1	55 – 90%
CPSF73	684	161

The modified DCA algorithm is an efficient strategy for predicting the binding interfaces of protein complexes. Still, additional efforts are needed to estimate the interfaces' local conformation and structural details. Thus, we conducted MD simulations using the most likely interacting peptides of the predicted hot spots highlighted in the modified DCA contact map for the INTS9/INTS11, CPSF100/CPSF73, and INTS4/INTS9/INTS11 complexes. We found that in each of these complexes, the interactions at the interfaces involved the β-sheet conformations of the proteins. Although several contacts were observed using VMD [57], we just listed the closest residues suggesting the strong interactions for each studied complex. Our findings align with experimental results reporting interactions between CPSF100 and CPSF73 as well as the trimerization of INTS4, INTS9, and INTS11. [26], [33], [37], [44], [45].

4. Materials and methods

4.1. Protein sequence collection and alignment

We first constructed a concatenated Multiple Sequences Alignment (cMSA) by aligning the orthologs of studied proteins and joining the alignments from different proteins by species. INTS4, INTS9, INTS11, CPSF73, and CPSF100 have all been well conserved across metazoans, with sequences comprising the β-Lactamase, β-CASP, and C-terminal domains. Their sequences were extracted by querying GENBANK [58] and running genome-wide tblastn [59] against genomes absent in GENBANK. The sequences were aligned to the human reference sequence, and those with 60–90% similarity were used. 223, 239, 202, 179, and 161 orthologs of INTS9, INTS11, INTS4, CPSF100, and CPSF73 were obtained. Common orthologs for a pair of proteins were aligned using Clustal-Ω [60] (see Table 3).

4.2. Prediction of protein heterodimers and heterotrimers

Evolutionary couplings between INTS9/INTS11, INTS4/INTS9, INTS4/INTS11, and CPSF100/CPSF73 were analyzed using Direct Coupling Analysis (DCA) algorithm [2], which can distinguish direct functional residue interactions from correlations resulting from indirect interactions and assign higher scores to direct correlations rather than to indirect ones. To reduce running time, we used a variant of DCA, the pseudo-likelihood maximization Direct-Coupling Analysis (plmDCA) [46], which has a lower computational cost than traditional DCA. Evolutionary coupling scores (ECs) were calculated and used to build the corresponding coupling matrix. To improve our prediction and avoid false positives in DCA analysis, we used local convolution of ECs, as described above. Briefly, Gaussian convolution is applied to local structural elements (in this study, defined by protein secondary structure, such as α-helix and β-sheet, predicted by PSIPRED [47]) to count the contribution of neighboring residues with an assumption that contacts between proteins occur locally and drive residues evolving within the same structural elements. In our experience, an isolated strong EC peak surrounded with weak ECs for residues belonging to different secondary structure elements is more likely to be a false positive than a cluster of less strong ECs for residues in the same secondary structure element. Therefore, a convolution of ECs with a kernel based on the secondary structure can predict the more likely interacting residues. The convolution algorithm depends on several parameters: the number of interacting residues and the variances of the Gaussian and the predicted secondary structures. The convolved ECs for a pair of residues (i,j) is $Q_{i,j}^l=\sum _{\propto =i-l}^{i+l}\sum _{\beta =j-l}^{j+l}{P}_{i,j}{K}_{a,b}(\propto ,\beta )$ where $K_{a,b}(\propto ,\beta )=\exp (-\left\{{a\propto }^2+b{\beta }^2\right\})$.

is the kernel function fitted on the structural elements and $P_{i,j}$ the ECs computed using any evolutionary coupling algorithm. The optimized values of the Gaussian convolution are provided in Table 1. These parameters were optimized using the INTS9/INTS11 complex for which structural information of the CTDs were available. Briefly, we picked the values of a,b, and l for which there is a maximum overlap between the prediction and the experimental distances.

4.3. Molecular dynamic simulations

Molecular dynamics simulations were restricted to the most likely interacting peptides (see Table 4) of INTS9/INTS11, CPSF100/CPSF73, and INTS4/INTS9/INTS11. The following 3D structures, which were retrieved from the protein data bank, were used to perform the simulations: INTS4 (ID: 7CUN, Chain D) [61] INTS9 (7CUN, Chain I) [61], INTS11 (7CUN, Chain K) [61], CPSF100 (6V4X, Chain I) [62], and CPSF73 (6V4X, Chain H) [62]. The forces in the simulations were calculated using AWSEM (Associative Memory, Water-mediated, Structure, and Energy Model), a coarse-grained protein force field in which only the positions of $C_{\alpha }$, $C_{\beta }$, and O atoms of each residue are explicitly represented. The coordinates of these and other heavy atoms are calculated following the total Hamiltonian of AWSEM as previously described. [24] Briefly, the Hamiltonian is a summation of the 1) physics-based term, involving bonds and angles through the terms such as backbone, contact, burial, and hydrogen bond, and 2) bioinformatics term which represents the fragment memory potential used to aid local-in-sequence structure formation [24], [54], [63], [64].

Table 4.

Characterization of the different complexes studied. The global p-value was computed using the simulated phylogeny described by Fongang et al. [6]. Briefly, we randomized the sequence distribution of one protein while keeping the other unchanged and computed the ECs of the interaction. The p-value was then estimated by counting the ECs higher than a predefined cutoff for the 100 randomizations. (*** denotes the most likely and * second most likely binding region, N-C means protein A's N-terminal domain and protein B's C-terminal domain. When necessary, the specific amino acids are indicated).

Protein A	Protein B	Sequences in cMSA	Global p-value for interaction	Most likely interacting domains
INTS9	INTS11	204	< 0.01	C-C (***), N-C (*)
INTS4	INTS9	171	0.01	N-N, N-C, C-N, or C-C
INTS4	INTS11	171	0.01	N-N, N-C, C-N, or C-C
CPSF100	CPSF73	138	0.04	C-C (***), C-R344–525(*)

We performed all MD simulations using the open-source software LAMMPS [53], in which AWSEM codes were implemented [63]. For each complex, we built a LAMMPS-AWSEM simulation box. We ran three simulations at $T=300\mathit{K}$ with an integration time step of$2\mathit{fs}$ after setting the parameters, such as the initial conditions, the periodic boundary conditions, and the ensemble. The initial conditions consisted of placing the two monomers (interacting peptides) in a simulation box at a distance of $30\mathrm{\AA }$ apart from each other and choosing initial velocities randomly from the Boltzmann distribution with the average squared velocity equal to $3K_{B}T/m$. Next, we used the periodic boundary conditions on the cubic box of $400\mathrm{\AA }$ on each side, the canonical ensemble, and the Nose-Hoover thermostat. The coordinates were recorded every 1000-time steps over a set of 5000000-time steps simulations were carried out for each binding domain. Finally, we used the Visual Molecular Dynamics (VMD) software [57] to visualize the structures and identify contacts based on the CAPRI criterion [56], which suggests that a contact exists between each pair of residues if at least two heavy atoms are separated by a distance $<5\mathrm{\AA }$.

5. Conclusion

Computational approaches have become an excellent complement to experimental techniques in investigating the interactions between protein complexes. In this study, as proof-of-the-concept, we applied our modified DCA approach to predict the binding domains of the INTS9/INTS11, CPSF100/CPSF73, and INTS4/INTS9/INTS11 complexes. Since binding interfaces predicted by DCA align with experimental results, we built upon this success using Molecular Dynamics simulations to compute local conformations and closest residues to generate precise hypotheses for follow-up studies. Using this two-step strategy, which combines unbiased identification of binding interfaces and biased MD simulations, we have characterized several interactions between proteins related to the Integrator complex. Our analysis confirms the physiological nature of several interactions indicated by previous studies and predicts new interactions that can help to explain the nature of the Integrator, a complex molecular machine. Finally, the predicted characteristics of the interactions between pairs of proteins and identified domains and residues potentially crucial for the respective dimerization and trimerization can inform future experimental studies, such as targeted mutations that may disrupt complex formation. The same method can be used for multi-scale prediction of interactions, as described above, in other difficult-to-characterize complexes such as G-protein coupled receptors. Therefore, we expect our method to become part of a toolbox for characterizing interactions within complex molecular machines and to advance our understanding of how such machines function.

Author statement

We confirm that all authors have read and approved the manuscript.

CRediT authorship contribution statement

M.R. conceived and supervised the project, A.K., and M.R. and B.F. conceived the local convolution method, M.R. and B.F. proposed convolution dependent on secondary structure elements A.K. developed a simulated phylogeny approach and contributed to statistical analysis, B.F. implemented the methods and developed software, B.F. performed multiple sequence alignments, DCA computations and data post-processing, Y.W., E.J.W., and Y.Z. contributed to data interpretation, E.J.W. proposed some target proteins. Y.W. performed MD simulations and protein visualization. Finally, B.F., Y.W., Y.Z., E.J.W., A.K., and M.R. discussed the results and wrote the manuscript; all authors read and approved the manuscript.

Declaration of Competing Interest

The authors declare no competing interests.

Appendix A. Supplementary material

Supplementary material

.