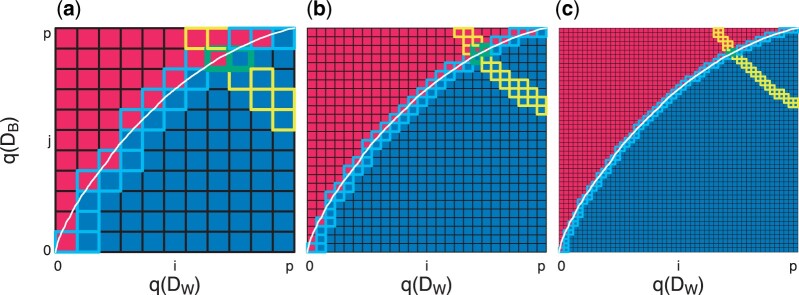
Fig. 4.
Graphical representation of two HPE algorithms to estimate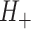 
. We simulate observations from two Gaussian distributions, namely 
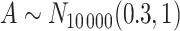and 
and 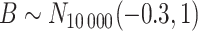calculate the quantiles 
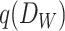and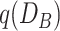 
for each of the sets with (a) 
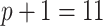, (b)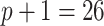 
, and (c) 
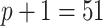. The white curve represents the percent of elements in 
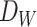that are strictly less than each element in 
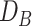. The goal is to estimate the true 
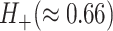(area under the white curve) using one of two HPE algorithms. The brute force approach (HPE algorithm 1) uses Riemann integration to approximate the white curve by summing the area of the blue squares below the curve. The grid search approach (HPE algorithm 2) starts at the minimum of 
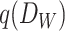and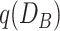 
and moves along the red–blue border to approximate the white curve (path followed represents the squares with the light blue borders). The HPE contour 
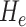(or estimate of 
) 
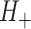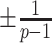is given by yellow-bordered squares. In other words, every pair 
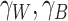such that 
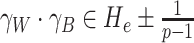, the interval guaranteed to contain 
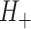. The intersection of this yellow contour (
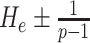) and blue contour (grids visited by HPE algorithm 2) are the green-bordered squares, which represents the numerical estimate for 
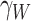and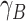 
.