A comparative study on the rheological properties of upper convected Maxwell fluid along a permeable stretched sheet

Abstract

The objective of this paper is to examine the flow of a non-Newtonian Maxwell fluid induced by a permeable stretching sheet in motion within a porous medium. The research incorporates the Cattaneo-Christov heat flux model to study the heat transfer process. The utilization of the Cattaneo-Christov heat flux approach becomes relevant in scenarios involving materials with high thermal conductivity or during short time intervals. Consequently, the current investigation holds significant importance. It is assumed that the viscosity of the Maxwell fluid changes exponentially as the temperature changes. The modeling of the physical phenomena being investigated takes into account the effects of a magnetic field, thermal radiation, velocity, and thermal slip conditions. In this study, the viscous dissipation phenomenon is taken into account because it can have notable impacts on the temperature and viscosity of the fluid, and is known to play a crucial role in fluid flow phenomena. The equations developed to model fluid flow are transformed into nonlinear ordinary differential equations through the use of appropriate similarity transformations. The focus of the research revolves around investigating the numerical solution of ordinary differential equations accompanied by boundary conditions using the shooting technique. The findings are then showcased via tables and graphs and scrutinized in order to arrive at conclusions. Furthermore, the precision of the present findings was evaluated by contrasting the heat transfer rate with outcomes that were previously published. Based on the obtained outcomes, it can be concluded that both the Eckert number and thermal radiation have a comparable enhancing influence, whereas the thermal relaxation parameter and thermal slip parameter exhibit opposing effects.

1. Introduction

The significance of Non-Newtonian fluids is noteworthy across a broad range of industries, including chemical, polymer, and biomedical. These fluids possess intricate and varied rheological properties, which allow them to fulfill specific demands in diverse applications. The significant implications of the non-linear correlation between stress and deformation rate in Non-Newtonian fluids are in the design and optimization of processes and products. They can be found in a wide range of applications, such as blood, mayonnaise, starch suspension, fruit juices, among others. Notably, in biological and industrial settings, the relationship between stress and the rate of deformation is typically non-linear for most fluids. Comprehending the behavior of Non-Newtonian fluids is critical to enhance productivity, precision, and safety in these industrial settings ([1]). The Non-Newtonian Maxwell model is a significant model among non-Newtonian models, extensively employed to characterize the viscoelastic nature of intricate fluids, including biological materials and polymers ([2]). The application of the Non-Newtonian Maxwell model has enabled comprehending the viscoelastic behavior of materials under diverse conditions. This model has found numerous uses in industrial and biomedical contexts, including the development of medical implants, drug delivery systems, and food processing ([3]). Many researchers have extensively discussed the flow and heat transport characteristics of Non-Newtonian Maxwell fluids and their significance. These discussions have been documented in several references ([4], [5], [6], [7], [8], [9]), which have highlighted the diverse manufacturing applications of this fluid type. The investigation of fluid flow in a non-Newtonian Maxwell fluid boundary layer with regards to the impact of magnetic fields on various flow phenomena is documented in references ([10], [11], [12]).

Maxwell fluid flow through a porous medium pertains to the motion of a viscoelastic complex fluid. The rheological properties of this type of fluid, which includes both elastic and viscous features, are influenced by the porous structure of the medium as it flows through. This phenomenon results in non-Newtonian behavior and can be described by factors such as the medium's permeability and porosity, the flow rate, and the rheological properties of the fluid. Applications of this type of fluid flow are found in several fields, including oil and gas production, groundwater hydrology, and biomedical engineering ([13], [14], [15]).

Thermal radiation refers to a mechanism of heat transfer where heat energy is transmitted through the emission of electromagnetic waves. This process is crucial in various applications, including the development of propulsion systems for spacecraft, gas turbines and nuclear power plants. In such scenarios, controlling the heat transfer in the flow of Maxwell fluid through thermal radiation is essential, and estimating its effects on processes with high temperatures is unavoidable. In space applications, where devices must operate at elevated temperatures to achieve optimal thermal efficiency, the impact of thermal radiation is particularly significant [16]. Given the significance of thermal radiation on both non-Newtonian fluid flow and heat transfer, several researchers ([17], [18], [19]) have explored real-world problems associated with this phenomenon under diverse conditions.

This research aims to investigate a novel study area by examining the characteristics of a magnetohydrodynamic non-Newtonian Maxwell fluid as it flows through a porous medium, while also examining the associated heat transfer processes. The study incorporates the concept of slip velocity into the momentum field and incorporates the Cattaneo-Christov heat flux theory into the energy equation for the purpose of analyzing heat transfer phenomena. The model encompasses a range of factors, such as thermal radiation, viscous dissipation, conditions involving thermal and momentum slip, and the presence of a magnetic field. Additionally, Darcy's law is introduced into the model to address the impact of a porous medium.

2. Formulation of the problem

The problem being examined pertains to the analysis of the flow of a non-Newtonian Maxwell fluid caused by a stretching surface in the presence of a porous medium. The equations that govern this particular problem consist of the continuity equation, momentum equation, energy equation, and constitutive equation for a Maxwell fluid, which are interconnected with the Darcy model of a porous medium with permeability k. The flow is assumed to be steady, incompressible, laminar, and viscous. The slip velocity phenomenon, which accounts for the non-zero relative motion between a Maxwell fluid and a solid boundary at the interface, is also considered in this study. The analysis involves a stretched sheet with a velocity u along the x-axis, and a magnetic field strength $B_0$ oriented perpendicular to it in accordance with the information outlined in Fig. 1.

Figure 1.

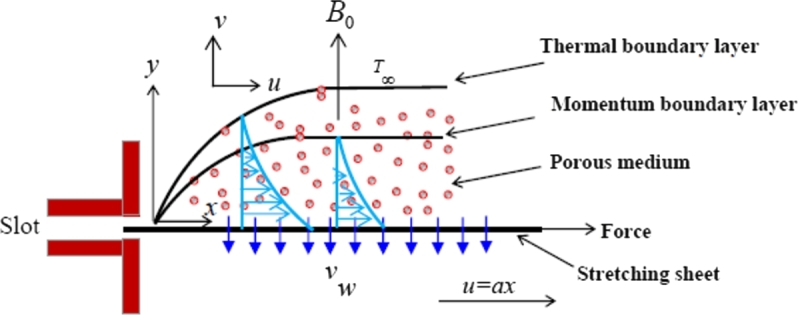
Geometry of the physical model.

Boundary conditions are defined for the velocity and temperature at both the stretching sheet and the far-field. The Cattaneo-Christov heat flux model is employed to describe heat transfer mechanism. In our investigation, the relaxation time of the heat flux is considered and denoted by the symbol ${\lambda }_2$. The appropriate set of partial differential equations that govern the proposed MHD non-Newtonian Maxwell flow model are expressed in terms of the mass, momentum, and energy equations, which are as follows ([20]-[21]):

$$\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0,$$ (1)

$$u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}=\frac{1}{{\rho }_{\infty }}\frac{\partial }{\partial y}(\mu (T)\frac{\partial u}{\partial y})-(\frac{\sigma B_0^2}{{\rho }_{\infty }}+\frac{\mu (T)}{k{\rho }_{\infty }})u-{\lambda }_1(u^2\frac{{\partial }^{2}u}{\partial x^2}+v^2\frac{{\partial }^{2}u}{\partial y^2}+2uv\frac{{\partial }^{2}u}{\partial x\partial y}),$$ (2)

$$u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}=\frac{1}{{\rho }_{\infty }{c}_p}(\mu (T){(\frac{\partial u}{\partial y})}^2-{\rho }_{\infty }{\lambda }_1[v^2{(\frac{\partial u}{\partial y})}^2+2uv\frac{\partial u}{\partial x}\frac{\partial u}{\partial y}])+\frac{\kappa }{{\rho }_{\infty }{c}_p}\frac{{\partial }^{2}T}{\partial y^2}-\frac{1}{{\rho }_{\infty }{c}_p}\frac{\partial q_r}{\partial y}-{\lambda }_2(u^2\frac{{\partial }^{2}T}{\partial x^2}+v^2\frac{{\partial }^{2}T}{\partial y^2}+u\frac{\partial u}{\partial x}\frac{\partial T}{\partial x}+v\frac{\partial v}{\partial y}\frac{\partial T}{\partial y}+2uv\frac{{\partial }^{2}T}{\partial x\partial y}+u\frac{\partial v}{\partial x}\frac{\partial T}{\partial y}+v\frac{\partial u}{\partial y}\frac{\partial T}{\partial x}).$$ (3)

The structure involves several parameters, including a specific heat $c_p$, the relaxation time of the fluid denoted by ${\lambda }_1$, the constant density of the fluid represented by ${\rho }_{\infty }$, and the velocity vector components u and v. Additionally, the electrical conductivity is denoted by σ, the dynamic viscosity by μ, and the Maxwell thermal conductivity by κ. Likewise, $q_r$ refers to the radiative heat flux. Radiative heat flux is the transfer of heat energy between two surfaces or objects by means of electromagnetic radiation, specifically infrared radiation, that happens due to the difference in temperature between the two surfaces or objects, resulting in the flow of energy from the warmer object to the cooler one through radiation. Therefore, the radiative heat flux is basically dependent on temperature according to the following relation [22]:

$$q_r=-\frac{4{\sigma }^{⁎}}{3k^{⁎}}\frac{\partial T^4}{\partial y},$$ (4)

where ${\sigma }^{⁎}$ is the Stefan-Boltzmann constant, $k^{⁎}$ is the absorption coefficient. The variable $T^4$ in the final equation represents a small fluctuation in temperature within the fluid. To expand this variable as a linear function, the Taylor series is applied with $T_{\infty }$ as the reference point. By neglecting the terms of higher order, the resulting equation is obtained [23]:

$$T^4\cong 4T_{\infty }^{3}T-3T_{\infty }^4.$$ (5)

The following boundary conditions are used to govern the coupled partial differential equations ([20]):

$$u-U={\alpha }_0[\frac{\mu (T)}{{\mu }_{\infty }}\frac{\partial u}{\partial y}-\left(\frac{{\rho }_{\infty }{\lambda }_1}{{\mu }_{\infty }}\right)(v^2\frac{\partial u}{\partial y}+2uv\frac{\partial u}{\partial x})],v=-v_w,T=T_w+\mathrm{\Gamma }\frac{\partial T}{\partial y},aty=0,$$ (6)

$$u\to 0,T\to T_{\infty },\text{ as }y\to \infty ,$$ (7)

where ${\alpha }_0$ is the coefficient of slip velocity, $U=ax$ is the stretching velocity, $T_{\infty }$ is the ambient temperature, $v_w$ is the suction velocity, $T_w$ is the sheet temperature, a is a positive constant, and Γ is the thermal slip coefficient. Furthermore, it's crucial to highlight that the incorporation of both slip velocity and thermal slip considerations, as outlined in equation (6), offers a more intricate and all-encompassing insight into intricate behaviors occurring in close proximity to boundaries. This amplifies the practical importance of the research outcomes in engineering and scientific contexts. Moreover, the integration of thermal slip conditions brings forth numerous benefits. Specifically, it accurately delineates temperature distribution and the conveyance of heat in close proximity to surfaces, which is indispensable for tasks like optimizing heat exchanger designs and overseeing processes sensitive to temperature changes. Applying the following transformations ([20]) is more useful in converting the dimensional governing partial differential equations into a set of dimensionless ordinary differential equations:

$$\eta =y\sqrt{\frac{a{\rho }_{\infty }}{{\mu }_{\infty }}},\theta (\eta )=\frac{T-T_{\infty }}{T_w-T_{\infty }},u=ax{f}^{\prime }(\eta ),v=-\sqrt{\frac{a{\mu }_{\infty }}{{\rho }_{\infty }}}f(\eta ).$$ (8)

To ensure accurate predictions of fluid behavior in such systems, accounting for the effects of variable viscosity is frequently deemed necessary. Therefore, in this proposed model, we assume that the viscosity is described by an exponential function of temperature, as given below:

$$\mu ={\mu }_{\infty }{e}^{-\gamma \theta },$$ (9)

where γ is the viscosity parameter. The implications of variable viscosity can be significant in various scientific and engineering applications, including but not limited to the design of heat exchangers and the modeling of fluid dynamics in geophysical systems. Mathematically, the following structure of ordinary differential equations and boundary conditions is obtained as a result of employing Eqs. (8) and (9) in the controlling system (1)-(3) together with the boundary conditions (6)-(7):

$$e^{-\gamma \theta }(f^{‴}-\gamma f^{″}{\theta }^{\prime })+\mathrm{\Lambda }(2f{f}^{\prime }{f}^{″}-f^2{f}^{‴})-f^{\prime 2}-(\mathrm{\Omega }{e}^{-\gamma \theta }+M)f^{\prime }+f{f}^{″}=0,$$ (10)

$$\left(\frac{1+R}{\mathrm{Pr}}\right){\theta }^{″}+f{\theta }^{\prime }-\beta [f{f}^{\prime }{\theta }^{\prime }+f^2{\theta }^{″}]+Ec{f}^{″}[\mathrm{\Lambda }(2f{f}^{\prime 2}-f^2{f}^{″})+e^{-\gamma \theta }{f}^{″}]=0,$$ (11)

$$\theta (0)=1+\delta {\theta }^{\prime }(0),f(0)=f_w,f^{\prime }(0)=1+\alpha [e^{-\gamma \theta }{f}^{″}+\mathrm{\Lambda }(2f{f}^{\prime 2}-f^2{f}^{″})],$$ (12)

$$f^{\prime }(\infty )=0,\theta (\infty )=0,$$ (13)

where $\mathrm{\Lambda }=a{\lambda }_1$ is the Maxwell parameter, $\mathrm{\Omega }=\frac{{\mu }_{\infty }}{a{\rho }_{\infty }k}$ is the porous parameter, $M=\frac{\sigma B_0^2}{a{\rho }_{\infty }}$ is the magnetic number, $\beta =a{\lambda }_2$ is the thermal relaxation parameter, $\mathrm{Pr}=\frac{{\mu }_{\infty }{c}_p}{\kappa }$ is the Prandtl number, $R=\frac{16{\sigma }^{⁎}{T}_{\infty }^3}{3k^{⁎}\kappa }$ is the radiation parameter, $\delta =\mathrm{\Gamma }{\left(\frac{a{\rho }_{\infty }}{{\mu }_{\infty }}\right)}^{\frac{1}{2}}$ is the thermal slip parameter, $f_w=\frac{v_w\sqrt{{\rho }_{\infty }}}{\sqrt{a{\mu }_{\infty }}}$ is the suction (or injection) velocity parameter, $Ec=\frac{U^2}{c_p(T_w-T_{\infty })}$ is the Eckert number and $\alpha ={\alpha }_0{\left(\frac{a{\rho }_{\infty }}{{\mu }_{\infty }}\right)}^{\frac{1}{2}}$ is the slip velocity parameter.

3. Engineering interest

Many engineering applications, especially those related to fluid mechanics, rely heavily on skin friction coefficient $\frac{1}{2}C{f}_{x}R{e}_x^{\frac{1}{2}}$, which is a dimensionless measure that indicates the level of drag force that a fluid exerts on a surface when in contact. When a solid object moves through a fluid and has contact with its surface, it experiences a resistance or frictional force known as the drag force. The drag force acts parallel to the surface and in the opposite direction to the object's motion. The Nusselt number $R{e}_x^{\frac{-1}{2}}N{u}_x$ is another crucial parameter that describes the heat transfer properties of a fluid and is dimensionless. Engineers often rely on it to assess the efficiency of various thermal processes, cooling systems, and heat exchangers in diverse engineering applications. The following are definitions of the surface drag force or skin friction coefficient and the heat transfer rate or Nusselt number:

$$\frac{1}{2}C{f}_{x}R{e}_x^{\frac{1}{2}}=-(e^{-\gamma \theta (0)}{f}^{″}(0)-\mathrm{\Lambda }(f^{″}(0)f_w^2-2f_w{f}^{\prime 2}(0))),R{e}_x^{\frac{-1}{2}}N{u}_x=-(1+R){\theta }^{\prime }(0),$$ (14)

where $R{e}_x=\frac{{\rho }_{\infty }Ux}{{\mu }_{\infty }}$ is the local Reynolds number.

4. Numerical methodology

Equations (10)-(11), along with the boundary conditions (12)-(13), constitute a set of extremely nonlinear ordinary differential equations that are interrelated. As a result, we employ a combination of the numerical shooting technique and the Runge-Kutta integration method. This simplifies the governing boundary value problem into a system of five simultaneously interconnected first-order ordinary differential equations. Hence, our initial assumption is introduced as follows:

$$F_1=f,F_2=f^{\prime },F_3=f^{″},F_4=\theta ,F_5={\theta }^{\prime }.$$ (15)

Equations (10) to (11) were subsequently transformed into a system of first-order ordinary differential equations, denoted as follows:

$$F_1^{\prime }=F_2,F_1(0)=f_w,$$ (16)

$$F_2^{\prime }=F_3,F_2(0)=1+\alpha [e^{-\gamma F_4(0)}{F}_3(0)+\mathrm{\Lambda }(2F_1(0)F_2^2(0)-F_1^2(0)F_3(0))],$$ (17)

$$F_3^{\prime }=\left(\frac{\gamma e^{-\gamma F_4}{F}_3{F}_5-2\mathrm{\Lambda }{F}_1{F}_2{F}_3+F_2^2+(\mathrm{\Omega }{e}^{-\gamma F_4}+M)F_2-F_1{F}_3}{e^{-\gamma F_4}-\mathrm{\Lambda }{F}_1^2}\right),F_3(0)={\epsilon }_1,$$ (18)

$$F_4^{\prime }=F_5,F_4(0)=1+\delta F_5(0),$$ (19)

$$F_5^{\prime }=\frac{\beta F_1{F}_2{F}_5-Ec[\mathrm{\Lambda }(2F_1{F}_2^2-F_1^2{F}_3)+e^{-\gamma F_4}{F}_3]-F_1{F}_5}{(\frac{1+R}{Pr}-\beta F_1^2)},F_5(0)={\epsilon }_2.$$ (20)

The selection of ${\epsilon }_1$ and ${\epsilon }_2$ is made to satisfy the boundary conditions at infinity $F_2(\infty )$ and $F_4(\infty )$. The decision regarding the appropriate value at infinity ($\eta ={\eta }_{\infty }$) constitutes a pivotal aspect of this approach. The shooting method is employed iteratively to propose values for ${\epsilon }_1$ and ${\epsilon }_2$ until the outer boundary conditions are satisfied. Afterward, the Runge-Kutta fourth-order integration method is employed for integrating the derived differential equations. The described process is reiterated until the attained results achieve the required precision of ${10}^{-6}$.

5. Validating the code

Testing the code to ensure that it meets the intended specifications and performs as expected is a vital stage in the software development process, known as code validation. By validating the code, developers can ascertain that the software is trustworthy, resilient, and satisfies the demands of its intended users. To ensure the precision of our findings, we conducted a comparison of the Nusselt number $-{\theta }^{\prime }(0)$ presented in Table 1 with the results in Shateyi ([24]) and Zeb et al. ([21]), using different values of the porous parameter Ω. This comparison revealed a significant degree of consistency between the two sets of results.

Table 1.

Comparison of −θ′(0) with findings of Shateyi ([24]) and Zeb et al. ([21]) for various values of Ω when M = 1.0,Pr = 0.7,Λ = 0.2,R = 0.4 and γ = α = f_w = δ = β = Ec = 0.

Ω	Shateyi ([24])	Zeb et al. ([21])	Present work
0.0	0.50658616	0.50658617	0.5065861989
0.5	0.47655131	0.47655134	0.4765513359
1.0	0.44621677	0.44621668	0.4462166774
2.0	0.38737709	0.38737709	0.3873770885

6. Graphical and tabular findings with discussion

The section presents the outcomes and discusses the implications of a study focused on the flow features of a Maxwell fluid. The flow was induced by a permeable stretching sheet with Cattaneo-Christov heat flux within a porous medium, while considering the presence of a magnetic field. To accomplish this, the governing equations were solved, which incorporated several coupled effects, including the non-Newtonian behavior of the fluid, variable viscosity, viscous dissipation, slip effects, and magnetic field. The analysis enabled the authors to gain insights into various aspects of the flow, such as velocity profiles, shear stress distributions, and the impact of critical parameters like the porous medium permeability, magnetic field strength, and viscoelastic properties of the Maxwell fluid. The discussion comprehensively explores the significance of these findings concerning heat transfer, energy dissipation, and transport phenomena associated with this complex fluid flow. Fig. 2 depicts how the velocity plot, represented by $f^{\prime }(\eta )$, and temperature plot, represented by $\theta (\eta )$, change as the magnetic parameter M is altered, with respect to variations in the similarity variable η. The magnetic parameter exhibits contrasting effects on the flow behavior of Maxwell fluids. Firstly, it induces a decrease in velocity as a result of the resistive impact of Lorentz forces. Conversely, it also triggers an increase in temperature by enhancing heat transfer mechanisms. These dual effects play a vital role in understanding the influence of magnetic fields on flow dynamics and the consequential thermal phenomena in systems containing Maxwell fluids. It is crucial to consider these factors when analyzing such systems. Moreover, the influence of a magnetic field on the flow characteristics has been corroborated by significant and relevant research studies ([25], [26], [27], [28], [29], [30], [31], [32]).

Figure 2.

(a) f′(η) for various M, (b) θ(η) for various M.

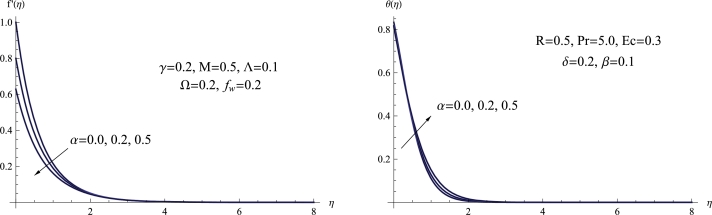
Fig. 3 illustrates the changes in the slip velocity parameter α, and how it affects both the velocity distribution, $f^{\prime }(\eta )$, and the temperature distribution, $\theta (\eta )$. The impact of the slip velocity parameter on fluid flow is twofold and opposite in nature. Firstly, it impedes the fluid's motion by increasing the resistance to flow, which results in a decrease in velocity. Secondly, it generates more internal friction due to higher viscosity, leading to an increase in temperature by dissipating extra energy. Physically, a rise in the viscosity parameter leads to increased internal resistance and elevated temperature as the fluid moves, resulting in the generation of greater heat within the system.

Figure 3.

(a) f′(η) for various α, (b) θ(η) for various α.

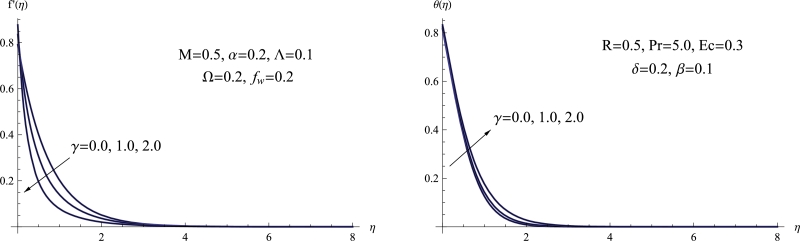
Fig. 4 depicts how the viscosity parameter γ affects the velocity $f^{\prime }(\eta )$ and temperature $\theta (\eta )$ profiles' changes. According to the findings, when the viscosity parameter increases, the velocity of the non-Newtonian Maxwell fluid decreases, while the temperature profile in the boundary layer region increases. Physically, a rise in the viscosity parameter indicates an enhanced opposition of the fluid to flow. This greater resistance causes a boost in internal friction within the fluid, resulting in the release of additional energy as heat. As a result, the fluid's velocity decreases since a larger proportion of energy is transformed into heat rather than being converted into kinetic energy responsible for the fluid's motion.

Figure 4.

(a) f′(η) for various γ, (b) θ(η) for various γ.

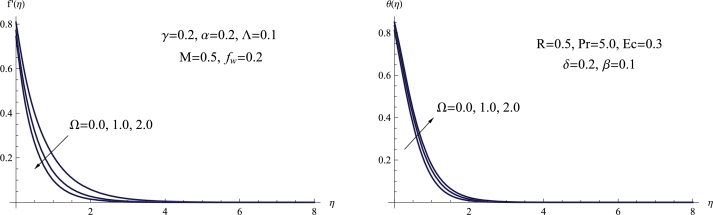
Fig. 5 illustrates the influence of the porous factor Ω on the temperature $\theta (\eta )$ and velocity $f^{\prime }(\eta )$ distributions. The velocity plot reveals that as the porous parameter values increase, the velocity distributions decrease. This decrease is more pronounced for higher values of the porous parameter, and gradually diminishes for lower values of the porous parameter. Additionally, the same figure demonstrates that increasing the porous parameter values amplifies both the magnitude of the temperature distribution and the thickness of the thermal boundary layer. Physically, increasing the porous parameter reduces velocity because the porous medium creates resistance to fluid flow, resulting in obstacles and increased friction that decrease the fluid's speed.

Figure 5.

(a) f′(η) for various Ω, (b) θ(η) for various Ω.

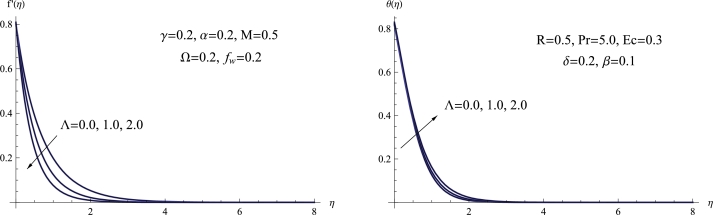
Fig. 6 depicts the relationship between the Maxwell parameter, denoted as Λ, and variations in temperature $\theta (\eta )$ and velocity $f^{\prime }(\eta )$ distributions. It is worth noting that higher values of the Maxwell parameter lead to a decrease in fluid velocity and the thickness of the velocity boundary layer. Conversely, the temperature distribution shows an opposite trend, where higher values of the Maxwell parameter result in an increase in temperature distribution. Physically, raising the Maxwell parameter prompts the emergence of viscoelastic consequences in the fluid motion, resulting in added internal friction and hindrance. As a result, the fluid velocity decreases due to the development of molecular formations caused by its viscoelastic characteristics, impeding its unrestricted movement.

Figure 6.

(a) f′(η) for various Λ, (b) θ(η) for various Λ.

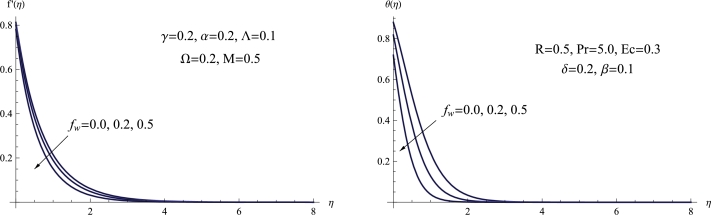
Fig. 7 illustrates the impact of the suction parameter, denoted as $f_w$, on the velocity field $f^{\prime }(\eta )$ and temperature field $\theta (\eta )$. At higher values of the suction parameter, both the temperature and velocity profiles, along with their respective boundary layer thickness, exhibit a decrease throughout the entire boundary layer region. Physically, an elevated suction parameter leads to a heightened removal of fluid, which diminishes the fluid's momentum close to the surface and lowers the overall speed. The suction creates a pulling force that reduces the flow rate and thins out the boundary layer, resulting in decreased variations in velocity.

Figure 7.

(a) f′(η) for various f_w, (b) θ(η) for various f_w.

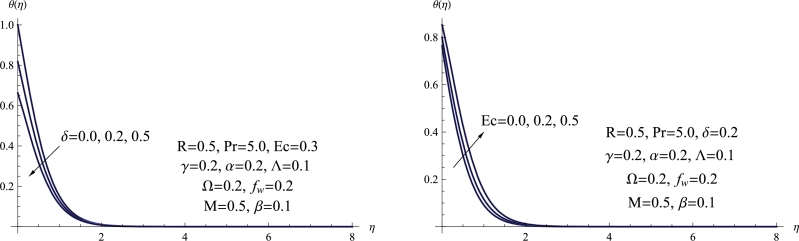
Fig. 8 depicts the effect of the thermal slip parameter δ and the Eckert number Ec on the temperature characteristics $\theta (\eta )$ of the Maxwell fluid. When the thermal slip parameter increases, both the wall temperature $\theta (0)$ and the temperature profile decrease. Conversely, higher values of the Eckert number result in an increase in both the wall temperature $\theta (0)$ and the temperature of the fluid, attributed to enhanced fluid motion. Physically, this phenomenon arises because higher Eckert numbers result in the fluid having greater kinetic energy. As a consequence, there is an augmented rate of heat transfer from the wall to the fluid particles.

Figure 8.

(a) θ(η) for various δ, (b) θ(η) for various Ec.

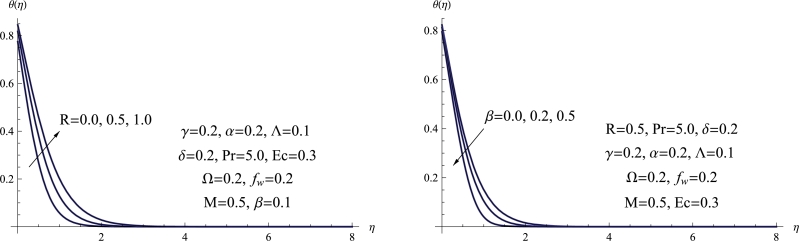
In Fig. 9, the temperature profile $\theta (\eta )$ of the Maxwell fluid is depicted, highlighting the impacts of both the thermal relaxation parameter β and the radiation parameter R. This visualization demonstrates how variations in these parameters influence the distribution of temperature within the fluid. According to this figure, the Maxwell fluid temperature decreases with an increasing the thermal relaxation parameter. Physically, a higher thermal relaxation parameter leads to a narrower temperature distribution in the fluid. This occurs because the fluid requires more time to reach thermal equilibrium after a temperature change, limiting its ability to respond to temperature variations and distribute heat evenly. Consequently, the temperature profile becomes more constrained. Furthermore, an opposite trend is observed for the temperature distribution when the radiation factor is increased. In this case, an enhancement in the radiation factor leads to improvements in both the temperature distribution $\theta (\eta )$ and the thickness of the thermal boundary layer. Additionally, extensive and pertinent research studies have confirmed the impact of thermal radiation on heat transfer properties ([33]-[34]).

Figure 9.

(a) θ(η) for various R, (b) θ(η) for various β.

Calculating the local Nusselt number $N{u}_{x}R{e}_x^{\frac{-1}{2}}$ and the local skin friction coefficient $\frac{1}{2}C{f}_{x}R{e}_x^{\frac{1}{2}}$ has become indispensable due to their significant role in examining and forecasting the characteristics of heat transfer and fluid flow in diverse engineering and practical scenarios. As stated in the definition of the skin friction coefficient, it is evident that it is consistently negative for all governing parameters. From a physical standpoint, a negative value of the skin friction coefficient signifies that the fluid experiences a drag force from the surface, while a positive value indicates the opposite. This observation is expected because we are examining the scenario of a stretching sheet, which induces the flow. The data presented in Table 2 clearly demonstrates that the skin-friction coefficient undergoes a significant rise when there are high values of the magnetic parameter, porous parameter, suction parameter, thermal slip parameter, and thermal relaxation parameter. Conversely, the opposite pattern is observed for the remaining governing parameters. Moreover, the local Nusselt number exhibits an increase with higher values of the suction parameter, thermal relaxation parameter, and slip velocity parameter. Conversely, an increase in the radiation parameter, Maxwell parameter, Eckert number, thermal slip parameter, magnetic factor, porous parameter, and viscosity parameter leads to a decrease in the local Nusselt number.

Table 2.

Values of $\frac{1}{2}C{f}_{x}R{e}_x^{\frac{1}{2}}$ and $N{u}_{x}R{e}_x^{\frac{-1}{2}}$ for various values of M,α,f_w,γ, Ω,Λ,Ec,R,β and δ with Pr = 5.0.

M	α	γ	Ω	Λ	fw	δ	Ec	R	β	$\frac{1}{2}C{f}_{x}R{e}_x^{\frac{1}{2}}$	$N{u}_{x}R{e}_x^{\frac{-1}{2}}$
0.0	0.2	0.2	0.2	0.1	0.2	0.2	0.3	0.5	0.1	0.873961	0.986643
0.5	0.2	0.2	0.2	0.1	0.2	0.2	0.3	0.5	0.1	1.000910	0.912241
1.0	0.2	0.2	0.2	0.1	0.2	0.2	0.3	0.5	0.1	1.103731	0.852266
0.5	0.0	0.2	0.2	0.1	0.2	0.2	0.3	0.5	0.1	1.325221	0.833405
0.5	0.2	0.2	0.2	0.1	0.2	0.2	0.3	0.5	0.1	1.000910	0.912241
0.5	0.5	0.2	0.2	0.1	0.2	0.2	0.3	0.5	0.1	0.743445	0.938376
0.5	0.2	0.0	0.2	0.1	0.2	0.2	0.3	0.5	0.1	1.045452	0.919881
0.5	0.2	1.0	0.2	0.1	0.2	0.2	0.3	0.5	0.1	0.823746	0.881338
0.5	0.2	2.0	0.2	0.1	0.2	0.2	0.3	0.5	0.1	0.615689	0.838156
0.5	0.2	0.2	0.0	0.1	0.2	0.2	0.3	0.5	0.1	0.958192	0.938352
0.5	0.2	0.2	1.0	0.1	0.2	0.2	0.3	0.5	0.1	1.142440	0.826799
0.5	0.2	0.2	2.0	0.1	0.2	0.2	0.3	0.5	0.1	1.278571	0.746931
0.5	0.2	0.2	0.2	0.0	0.2	0.2	0.3	0.5	0.1	1.003581	0.914826
0.5	0.2	0.2	0.2	1.0	0.2	0.2	0.3	0.5	0.1	0.979025	0.884952
0.5	0.2	0.2	0.2	2.0	0.2	0.2	0.3	0.5	0.1	0.956441	0.850026
0.5	0.2	0.2	0.2	0.1	0.0	0.2	0.3	0.5	0.1	0.938329	0.603753
0.5	0.2	0.2	0.2	0.1	0.2	0.2	0.3	0.5	0.1	1.000910	0.912241
0.5	0.2	0.2	0.2	0.1	0.5	0.2	0.3	0.5	0.1	1.096952	1.406073
0.5	0.2	0.2	0.2	0.1	0.2	0.0	0.3	0.5	0.1	0.991605	1.190031
0.5	0.2	0.2	0.2	0.1	0.2	0.2	0.3	0.5	0.1	1.000910	0.912241
0.5	0.2	0.2	0.2	0.1	0.2	0.5	0.3	0.5	0.1	1.008856	0.675174
0.5	0.2	0.2	0.2	0.1	0.2	0.2	0.0	0.5	0.1	1.006472	1.177073
0.5	0.2	0.2	0.2	0.1	0.2	0.2	0.2	0.5	0.1	1.002752	1.000412
0.5	0.2	0.2	0.2	0.1	0.2	0.2	0.5	0.5	0.1	0.997227	0.736225
0.5	0.2	0.2	0.2	0.1	0.2	0.2	0.3	0.0	0.1	1.007161	1.126741
0.5	0.2	0.2	0.2	0.1	0.2	0.2	0.3	0.5	0.1	1.000910	0.912241
0.5	0.2	0.2	0.2	0.1	0.2	0.2	0.3	1.0	0.1	0.996473	0.775383
0.5	0.2	0.2	0.2	0.1	0.2	0.2	0.3	0.5	0.0	0.999882	0.886568
0.5	0.2	0.2	0.2	0.1	0.2	0.2	0.3	0.5	0.2	1.001982	0.939229
0.5	0.2	0.2	0.2	0.1	0.2	0.2	0.3	0.5	0.5	1.005463	1.028423

7. Concluding remarks

The article examines the flow of a non-Newtonian Maxwell fluid through a porous medium along a stretched sheet, employing the Cattaneo-Christov heat flux model. The mathematical model utilized for this study incorporates various factors, such as thermal radiation, the presence of a magnetic field, the effects of slip conditions, viscous dissipation, all these factors through a porous medium. An appropriate set of similarity transformations is applied to convert the equations governing the model into non-linear ordinary differential equations. Subsequently, the shooting approach is utilized to examine the numerical solutions. To evaluate the accuracy of our results, we compare the Nusselt number values against the porous parameter with those from prior research in the literature. We also tabulate the effects of significant parameters on the Nusselt number. Some of the key discoveries from this research are as follows:

• 1.The temperature profile shows that the Eckert number and thermal radiation have a similar enhancing effect, while the thermal relaxation parameter and thermal slip parameter have an opposite impact.
• 2.As the slip velocity parameter, magnetic parameter, viscosity parameter, porous factor, and Maxwell parameter increased, the thermal boundary layer thickness expanded, while the momentum boundary layer thickness diminished.
• 3.The temperature, velocity, and boundary layer thickness decrease with an increase in the suction parameter.
• 4.With an increase in the magnetic number, porous parameter, and Eckert number, the Nusselt number experienced a decrease. Conversely, the Nusselt number exhibited an increase with an increase in the slip velocity parameter, suction parameter, and thermal relaxation parameter.
• 5.As the viscosity parameter and slip velocity parameter increased, the skin friction coefficient exhibited a decrease. Conversely, an increase in the porous parameter and suction parameter resulted in an increase in the skin friction coefficient.
• 6.Future investigations will build upon this research by exploring the effects of Joule heating and chemical reactions on the flow of Maxwell nanofluids, while also considering the influence of nonlinear thermal radiation.

CRediT authorship contribution statement

Sara I. Abdelsalam: Conceptualization, Formal analysis, Funding acquisition, Investigation, Methodology, Supervision, Validation, Writing – review & editing. W. Abbas: Conceptualization, Formal analysis, Investigation, Methodology, Resources, Software, Validation, Writing – original draft. Ahmed M. Megahed: Conceptualization, Formal analysis, Investigation, Methodology, Resources, Software, Supervision, Writing – review & editing. Ahmed A.M. Said: Conceptualization, Formal analysis, Investigation, Methodology, Resources, Software, Validation, Writing – original draft.

Declaration of Competing Interest

The authors declare the following financial interests/personal relationships which may be considered as potential competing interests: Sara I. Abdelsalam reports travel was provided by Fundación Mujeres Por África.

Data availability

No data was used for the research described in the article.