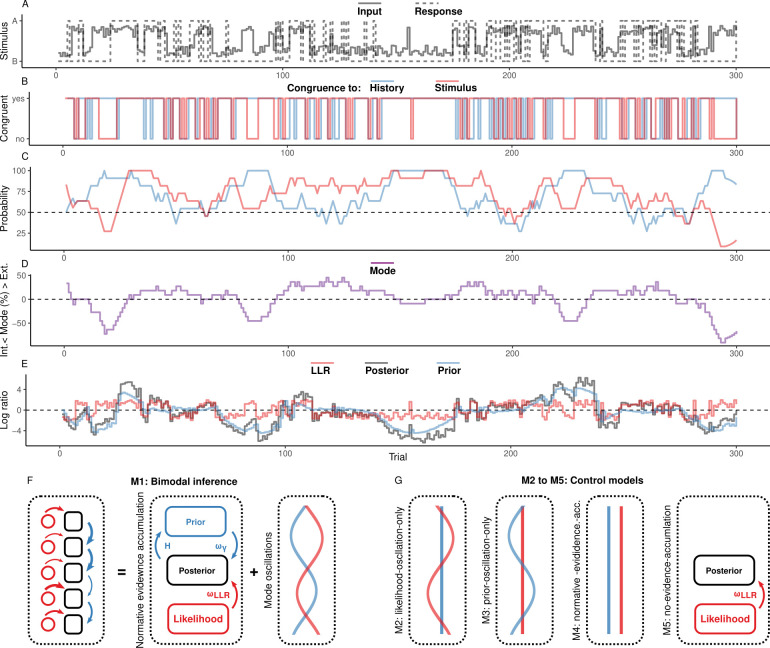
Fig 1. Concept.

(A) In binary perceptual decision-making, a participant is presented with stimuli from 2 categories (A vs. B; solid line) and reports consecutive perceptual choices via button presses (solid line). All panels below refer to these stimulated example data. (B) When the response matches the external stimulus information (i.e., overlap between the dotted and solid lines in panel (A)), perceptual choices are stimulus-congruent (red line). When the response matches the response at the preceding trial, perceptual choices are history-congruent (blue line). (C) The dynamic probabilities of stimulus- and history-congruence (i.e., computed in sliding windows of ±5 trials) fluctuate over time. (D) The mode of perceptual processing is derived by computing the difference between the dynamic probabilities of stimulus- and history-congruence. Values above 0% indicate a bias toward external information, whereas values below 0% indicate a bias toward internal information. (E) In computational modeling, internal mode is caused by an enhanced impact of perceptual history. This causes the posterior (black line) to be close to the prior (blue line). Conversely, during external mode, the posterior is close to the sensory information (log likelihood ratio, red line). (F) The bimodal inference model (M1) explains fluctuations between externally and internally biased modes (left panel) by 2 interacting factors: a normative accumulation of evidence according to parameter H (middle panel), and antiphase oscillations in the precision terms ω_LLR and ω_ψ (right panel). (G) The control models M2-M5 were constructed by successively removing the antiphase oscillations and the integration of information from the bimodal inference model. Please note that the normative-evidence-accumulation model (M4) corresponds to the model proposed by Glaze and colleagues [51]. In the no-evidence-accumulation model (M5), perceptual decisions depend only on likelihood information (flat priors).