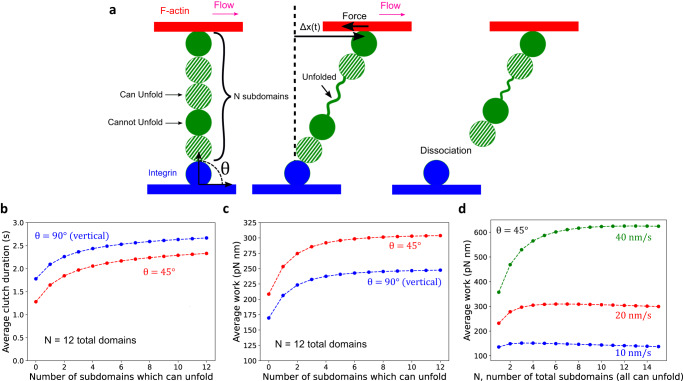
Fig. 4. Mathematical model of a single Talin chain.
a Talin is represented as a string of rod subdomains (green), the ends of which associate with stationary integrin (blue) and permanently with F-actin (red) moving at constant retrograde flow speed. The model is studied as a function of the total number of rod subdomains that can unfold (dashed green) or not (solid green). We varied the initial angle θ between the axis of Talin, assumed that it started linearly in the plane of the figure. The master equation of the system evolves over time, satisfying the force balance along Talin, up to the point of dissociation from integrin. The work on F-actin is calculated as the sum of the product of the force on actin along the flow direction times the displacement. b Average clutch duration as a function of the number of subdomains that can unfold, with the total subdomain number fixed at 12 and retrograde flow speed 20 nm/s. The clutch duration is longer for chains that are at θ = 90° compared to 45° since Talin tension increases faster at lower values of θ. c Average work as function of the number of subdomains that can unfold, with the total subdomain number fixed at 12. The work is less at θ = 90° compared to 45°, since at a starting angle of θ = 90°, it takes longer for Talin to be fully stretched, and integrin dissociation may meanwhile occur. d Average work as a function of the total number of rod subdomains, all assumed to be able to unfold, and retrograde flow speed. (In this calculation we assume a fixed retrograde speed and do not consider the feedback between retrograde flow and clutch strength in the whole lamellipodium, which would associate lower retrograde flow speeds with higher work done by Talin).