Figure 2.

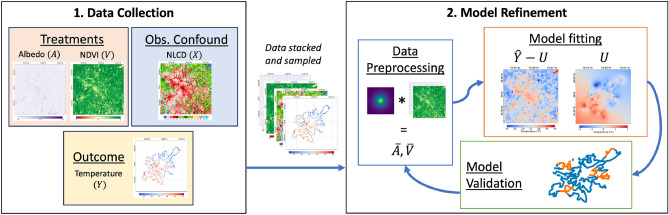
Summary of approach. We first collect data on the treatments of interest (A and V) and outcome (Y), as well as confounding variables that also impact the outcome (X). We stack and sample this data to create the dataset used for model fitting. Since the temperature data was collected via vehicular traversal through the study area, this process entails sampling each point along the traversal, then selecting the 51 $\times$ 51 pixel window from the treatments and confound that are centered on this point. We start refining the model by preprocessing the data. The 51 $\times$ 51 pixel windows corresponding to treatments are multiplied by a weight matrix that weights pixels closer to the center higher than points further away, as dictated by a length scale parameter on the weight matrix definition. This product provides a spatially-averaged value that estimates the effect of neighboring pixels on the temperature at the center of the sample, denoted by $\overline{A}$ and $\overline{V}$. We select the center pixels from the treatments to capture the direct effect of treatments on the outcomes. The preprocessed dataset used for model fitting is then a set of tuples comprised of spatially weighted albedo, center pixel albedo, spatially weighted vegetation, center pixel vegetation, average land cover class, and temperature. Our model fits the data with a regression, then adjusts the regression with a Gaussian process that models unobserved confounding (denoted U). This provides us with an estimate of temperature ($\widehat{Y}$) with and without the effect of unobserved confounding. The model is then validated using a cross-validation strategy that segments out samples from the traversal into blocks, with a subset of blocks held-out from model fitting to evaluate model performance. We update the weight matrix and model parameters to maximize the performance of the model on this held-out set. The best model is used to estimate effects of interventions on temperature.