Figure - PMC

Skip to main content

An official website of the United States government

Here's how you know

Here's how you know

Official websites use .gov
A .gov website belongs to an official government organization in the United States.

Secure .gov websites use HTTPS
A lock ( ) or https:// means you've safely connected to the .gov website. Share sensitive information only on official, secure websites.

View full-text article in PMC

. 2023 Dec 7;27(1):108654. doi: 10.1016/j.isci.2023.108654

Search in PMC
Search in PubMed
View in NLM Catalog
Add to search

© 2023 The Authors.

This is an open access article under the CC BY license (http://creativecommons.org/licenses/by/4.0/).

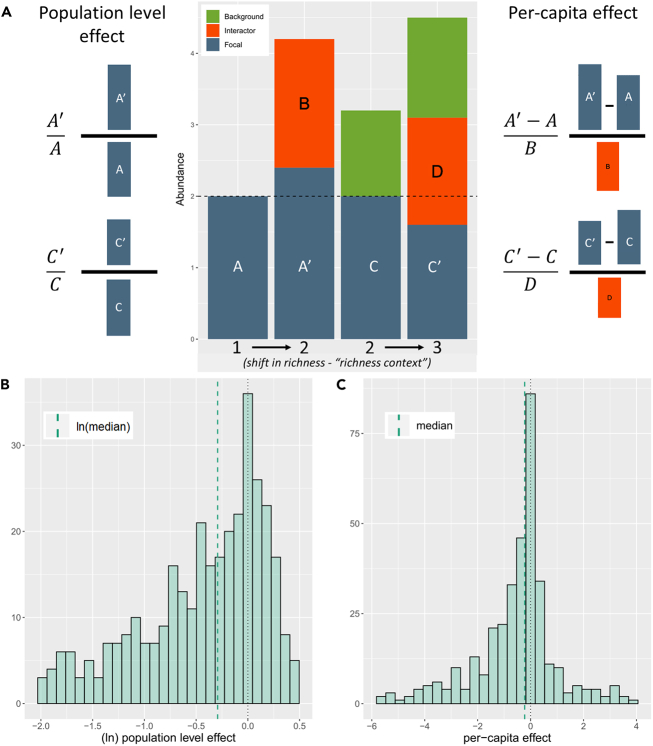
PMC Copyright notice

Distributions of observed interactions

(A) Interactions between a “focal” isolate and “interactor” isolate were calculated as two measures, 1) a population effect, calculated as the ratio of the focal isolate’s density with and without the interactor present, and 2) a per-capita effect, calculated as the change in density of the focal isolate between contexts with and without the interactor, scaled by the abundance of the interactor. Interactions were always calculated between communities, varying by a single isolate – the interactor. However, additional isolates (“background” isolates) could also be present in the compared communities. The “richness context” of an interaction refers to the richness of the pairs of community contexts from which an interaction is observed (e.g., 1=>2 for the first example interaction, 2=>3 for the second example interaction including a “background” isolate).

(B) The distribution of all observed interactions, as population level effects, (natural-log transformed to symmetrize ratios).

(C) The distribution of all observed interactions, as per-capita effects. In B and C, the dotted black line marks 0, and the dashed green line marks the median respective interaction (natural-log transformed for the population level effects).