Figure - PMC

Skip to main content

An official website of the United States government

Here's how you know

Here's how you know

Official websites use .gov
A .gov website belongs to an official government organization in the United States.

Secure .gov websites use HTTPS
A lock ( ) or https:// means you've safely connected to the .gov website. Share sensitive information only on official, secure websites.

View full-text article in PMC

. 2023 Dec 21;21(1):132–141. doi: 10.1038/s41592-023-02098-1

Search in PMC
Search in PubMed
View in NLM Catalog
Add to search

© The Author(s) 2023

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.

PMC Copyright notice

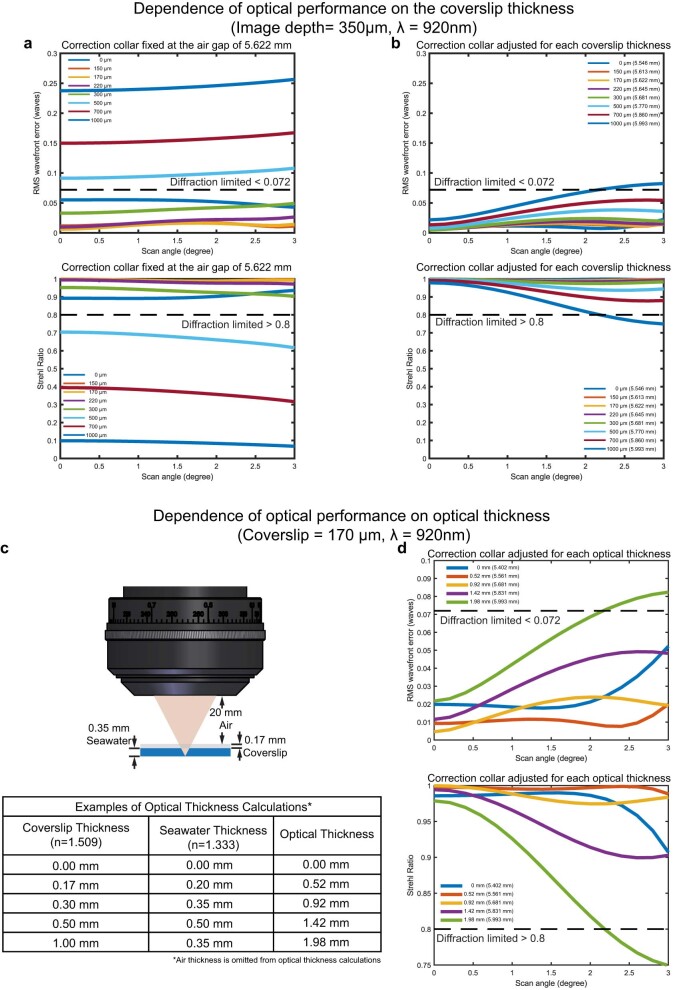
Extended Data Fig. 7 — The root-mean-squared (RMS) wavefront error (top) and the Strehl ratio (bottom) as a function of the scan angle at the back aperture and coverslips of different thickness are shown with the correction collar fixed at an air gap of 5.622 mm in (a), and with the correction collar optimized for coverslips of different thickness in (b). The thickness of coverslips ranging from 0-1000 µm are color coded. (c) The schematic shows the Cousa objective focuses light through a 0.17 mm thick coverslip and 0.35 mm of seawater. The optical thickness of the non-air elements between the objective and the focal plane can be calculated: multiply the thickness of a material (ignoring air) in millimeters by its refractive index, and sum over all of these products. For example, the optical thickness shown in the schematic is 0.723 (0.17 mm × 1.509 + 0.35 mm × 1.333). The table below shows combinations of the coverslip thickness and the seawater thickness, and the resultant optical thickness for each combination. The correction collar can be adjusted to compensate for the optical thickness over the range of 0 - 2 mm, and maintain the diffraction-limited performance. (d) The root-mean-squared (RMS) wavefront error (top) and the Strehl ratio (bottom) as a function of the scan angle at the back aperture are shown when the correction collar is optimized for different optical thickness of non-air materials. Each curve is color coded for different optical thickness shown as the number before the parenthesis. The number in the parenthesis is the optimal thickness of air gap to achieve the best optical performance.