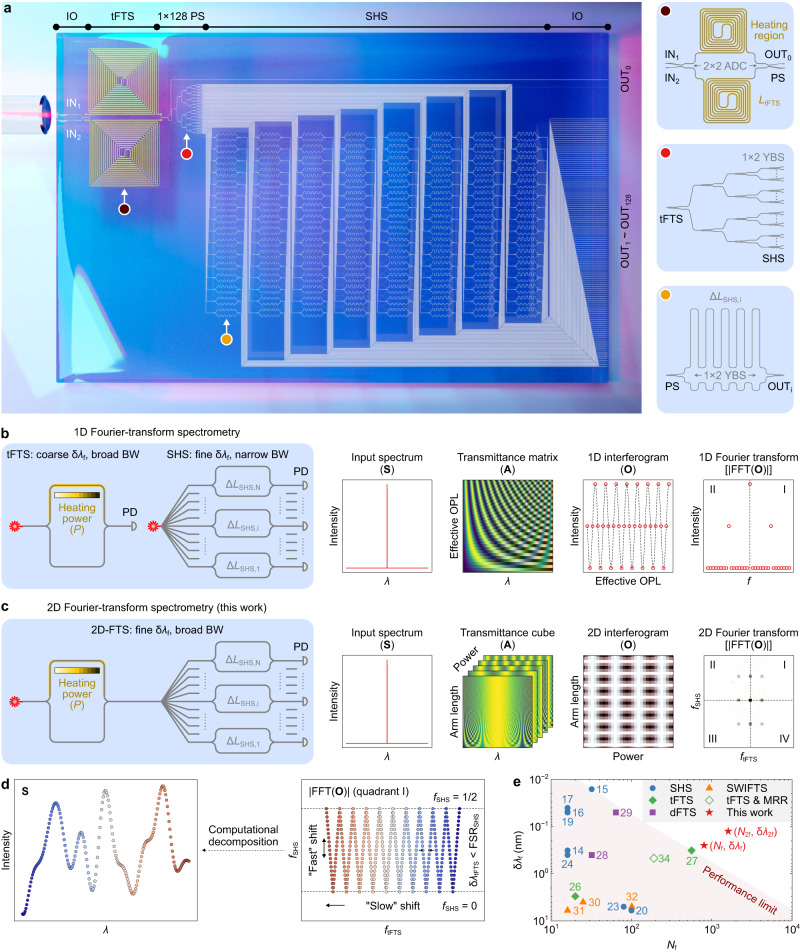
Fig. 1. Principle of the two-dimensional Fourier-transform spectrometer (2D-FTS).

a Schematic layout of the 2D-FTS. The insets show the enlarged views of key components. The 2D-FTS comprises of a tunable Fourier-transform spectrometer (tFTS) and a spatial heterodyne spectrometer (SHS) that are connected via a 1×128 power splitter (PS). The edge couplers are utilized as input and output (IO) ports, i.e., IN_i and OUT_i. Conceptual illustrations of the b 1D and c 2D Fourier-transform spectrometry. For a stand-alone tFTS/SHS, the period of the sinusoidal response is tuned by changing the heating power (P) or arm-length difference (ΔL_SHS). At a single wavelength (λ), the interferogram (O) is a 1D sequence sliced from a 2D transmittance matrix (A). The 1D fast Fourier transform (FFT) of the interferogram contains a peak in each quadrant. For the 2D-FTS, A is a 3D cube with variations of both P and ΔL_SHS. Hence, the interferogram is a 2D diagram that is modulated along two axes. By applying 2D FTT, each wavelength is mapped to a single spot in the Fourier domain. d Reconstruction principle. The intensity information of a continuous spectrum (S) is encoded by a cluster of spots in FFT(O). At varying wavelengths, the spot location shifts “slowly” along f_tFTS and “fast” along f_SHS. Here, f_tFTS and f_SHS denote the Fourier frequencies. The shift direction relies on the phases of sinusoidal responses. Any spectrum can be retrieved via decomposition, as long as the resolution (δλ_tFTS) of the tFTS is finer than the free spectral range (FSR_SHS) of the SHS, thereby breaking the inherent limit between the resolution (δλ_f) and bandwidth (BW). e Comparison of integrated FTSs in terms of the channel capacity (N_f) and δλ_f at the Rayleigh criterion. δλ_f and N_f can be improved to δλ_2f and N_2f using computational methods. OPL, optical path length. ADC, adiabatic directional coupler. YBS, Y-branch splitter. PD, photodetector. MRR, microring resonator. dFTS, digital FTS. SWIFTS, stationary-wave integrated FTS.