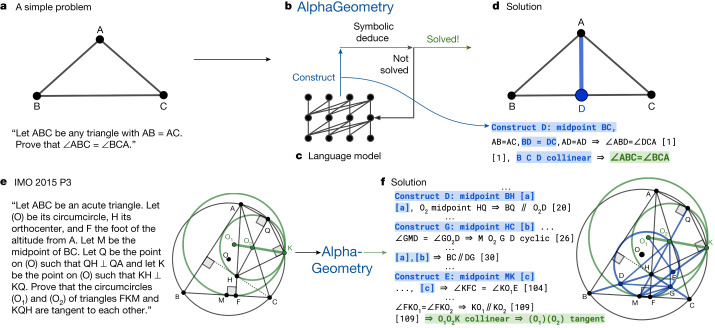
Fig. 1. Overview of our neuro-symbolic AlphaGeometry and how it solves both a simple problem and the IMO 2015 Problem 3.

The top row shows how AlphaGeometry solves a simple problem. a, The simple example and its diagram. b, AlphaGeometry initiates the proof search by running the symbolic deduction engine. The engine exhaustively deduces new statements from the theorem premises until the theorem is proven or new statements are exhausted. c, Because the symbolic engine fails to find a proof, the language model constructs one auxiliary point, growing the proof state before the symbolic engine retries. The loop continues until a solution is found. d, For the simple example, the loop terminates after the first auxiliary construction “D as the midpoint of BC”. The proof consists of two other steps, both of which make use of the midpoint properties: “BD = DC” and “B, D, C are collinear”, highlighted in blue. The bottom row shows how AlphaGeometry solves the IMO 2015 Problem 3 (IMO 2015 P3). e, The IMO 2015 P3 problem statement and diagram. f, The solution of IMO 2015 P3 has three auxiliary points. In both solutions, we arrange language model outputs (blue) interleaved with symbolic engine outputs to reflect their execution order. Note that the proof for IMO 2015 P3 in f is greatly shortened and edited for illustration purposes. Its full version is in the Supplementary Information.