Fig. 3.

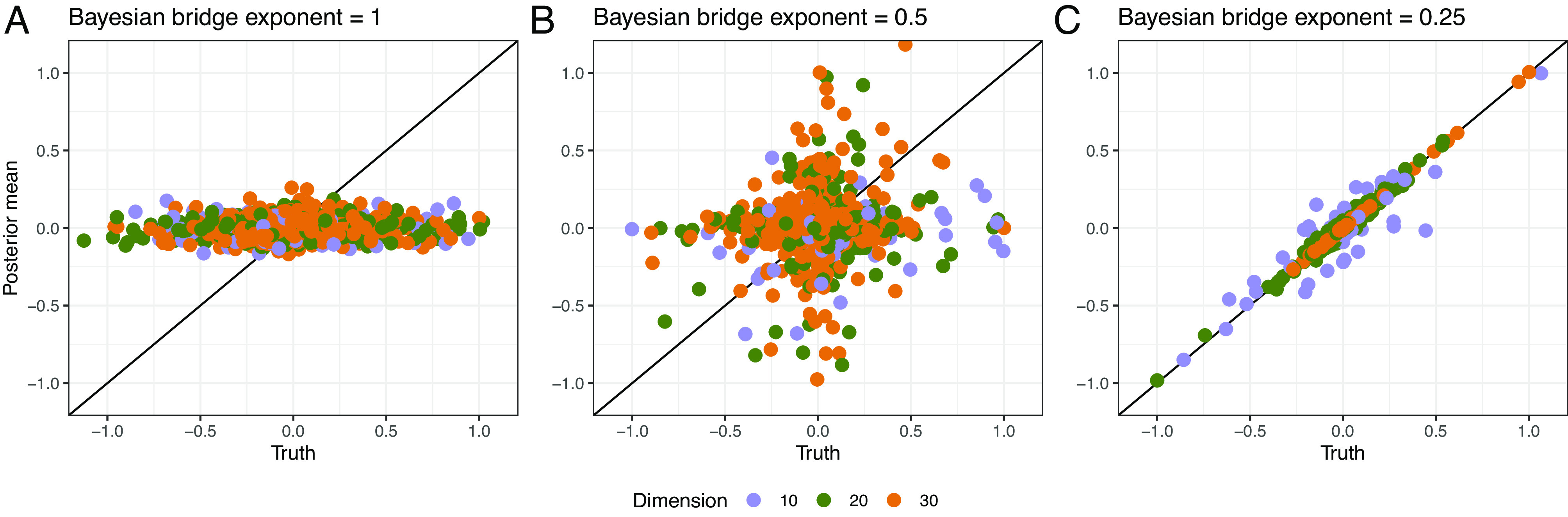
Posterior means versus truth for CTMC generator matrix elements within differing sparsity regimes and with different dimensionalities $d$, holding observation count fixed at 300. We generate posteriors using surrogate-trajectory HMC with the naive matrix exponential derivative. To affect sparsity levels, we generate generator matrix entries according to the Bayesian bridge distribution (34) with different exponents ($\alpha \in \{1,1/2,1/4\}$ for plots A, B and C, respectively), normalizing by the largest absolute values to ease comparison. Smaller $\alpha$ values encode more peaked distributions with heavier tails and thus enforce greater sparsity. Plot C reflects the fact that the Bayesian bridge prior with exponent $\alpha =1/4$ helps identify non-null parameters in small sample contexts (18). With this intuition in mind, we specify such a prior on generator random effects in Section 3.