Computational Modeling of the Subject-Specific Effects of Annuloplasty Ring Sizing on the Mitral Valve to Repair Functional Mitral Regurgitation

Abstract

Surgical repair of functional mitral regurgitation (FMR) that occurs in nearly 60% of heart failure patients is currently performed with undersizing mitral annuloplasty (UMA), which lacks short and long-term durability. Heterogeneity in each patient’s valve geometry makes tailoring this repair to each patient challenging, and predictive models that can help with planning this surgery are lacking. In this study, we present a 3D echo derived computational model, to enable subject-specific, pre-surgical planning of the repair. Three computational models of the mitral valve were created from 3D echo data obtained in three pigs with heart failure and FMR. An annuloplasty ring model of seven sizes was created, each ring was deployed, and post-repair valve closure was simulated. The results indicate that large annuloplasty rings (> 32 mm) were not effective in eliminating regurgitant gaps, nor in restoring leaflet coaptation or reducing leaflet stresses and chordal tensions forces. Smaller rings (≤ 32 mm) restored better systolic valve closure in all investigated cases, but excessive valve tethering and restricted motion of the leaflets were still present. This computational study demonstrates that for effective correction of FMR, the extent of annular reduction differs between subjects, and overly reducing the annulus has deleterious effects on the valve.

1. Introduction

Functional mitral regurgitation (FMR) is the leakage of blood through the mitral valve (MV), the left sided atrioventricular valve, that occurs in nearly 60% of the patients with heart failure (HF) after surviving a myocardial infarction [31, 32]. Akinesis of the infarcted left ventricular wall, along with dilatation of the left ventricular chamber volume, distorts the MV geometry and restricts its proper closure during systole, causing FMR [1, 26, 54]. Though FMR is the end result diagnosed in these patients, the geometric distortions of the MV that lead to FMR differ between individual patients [3, 24, 43, 51]. Some patients present with clinically significant FMR, with regional akinesia but minimal left ventricular dilatation, whereas others present with significant left ventricular dilatation but not visible dyssynchrony of the myocardial segments. The mitral annulus is also dilated in most patients, with uniform dilatation along its entire circumference in some patients, whereas in others the dilatation is more regional along the posterior annulus [18]. Such heterogeneity in the MV geometric distortions that cause FMR have made effective surgical or transcatheter repair of the MV very challenging and lacking durability. Such heterogeneity in MV geometries is also compounded by heterogeneity in surgical techniques innovated to repair this valve [39], and the lack of any standardization in the repair strategy. Thus, the outcomes of some surgical centers are promising [52], while those of a majority are poor [10, 13, 38], which continues to be a significant challenge impacting this clinical problem.

Of the many techniques available today, surgical undersizing mitral annuloplasty (UMA) is a technique that has gained most clinical adoption and has been in use to repair FMR for the past two decades [41]. In this surgery, the dilated MV annulus is reduced to a smaller size by placing sutures into the native annulus and tying them onto a prosthetic ring that is smaller in size. Downsizing the annulus in this manner is hypothesized to draw the native leaflets into the mitral orifice and enable easier and better systolic coaptation and correction of regurgitation. Though effective in some patients, clear guidance is lacking on which MV geometries may benefit from this repair, and which may not. Furthermore, the prosthetic annuloplasty rings are available in several sizes, and optimal sizing of the ring to the patient remains a challenge during surgery [17]. Though the smallest size ring could be chosen in all patients, the risk of increasing the transmitral diastolic pressure gradient and creating MV stenosis after the repair is high [27, 28]. The lack of standardization with this technique is reflected in the 29% persistent FMR rates at 30 days after annuloplasty procedure, and 58.8% reported recurrence rate of moderate or greater degree of FMR within 24 months after UMA [13]. While resizing the MV annulus helps to restore some degree of leaflet coaptation, tethering forces might not be reduced, as demonstrated in a recent ex vivo study from our group [59]. Such excessive valve tethering can increase the risk of pathological remodeling such as thickening, fibrosis, and calcification of the leaflets, and eventually lead to FMR repair failure [48]. Therefore, a better understanding of the individualized, patient-specific impact of UMA on MV mechanics and function is warranted, and computational platforms to achieve such surgical planning could have a significant impact [7, 53].

Computational models simulating mitral annuloplasty were developed and reported previously. Early computational studies, published by Maisano et al. [29] and Votta et al. [55], used a simplified model of the MV and investigated the impact of different ring shapes on the outcomes of UMA. In both studies the simplified MV model represented an average human MV, but not the variability in geometries leading to FMR. Stevanella et al. [49] and Wong et al. [57] reported MRI-derived patient-specific models, used for UMA simulations. However, both studies adopted the assumption of strain-free diastolic configuration of the MV, thus a good morphological congruence between computational results and truth datasets was not achieved. Choi et al. [8, 9] simulated the outcomes of mitral annuloplasty using a pair of ultrasound-derived computational models, but no annular downsizing was introduced as only true-sized annuloplasty rings were simulated. In addition, the models lacked patient-specific motion of the papillary muscles (PMs), which are crucial to investigate any sub-valvular effects of annuloplasty. Kong et al. [21] presented detailed MV model, created from CT data, and used it to compare UMA with PM relocation technique. The authors sought to create a realistic chordal network but were not able to detect all the chordae, thus a complete patient-specific chordal distribution was not achieved. In addition, ring annuloplasty procedure was simplified by prescribing boundary conditions on the annulus rather than implanting a virtual ring.

Building upon this prior work, in this study, we developed a subject-specific, clinically relevant, computational modeling framework to investigate the impact of different annuloplasty ring sizes on the outcomes of UMA for FMR repair. Our modeling approach addressed several previous limitations: (1) subject-specific MV model was created using the data from diseased animal models with heart failure and FMR, using 3D echocardiography, which is a clinical standard for MV imaging; (2) subject-specific motion of the PMs was measured from the animal imaging data and prescribed to obtain a realistic sub-valvular behavior of the model; (3) to achieve leaflet concavity toward the left atrium, which is characteristic to FMR [33], we imposed pre-strain on the chordae in diastole; (4) annular downsizing was performed using actual models of different size annuloplasty rings and deforming the native annulus to conform to each ring size, thus simulating realistic post-repair effects. A total of three subject-specific FMR computational models, created and validated in our previous study [11], were used for UMA simulations.

2. Materials and Methods

A. Subject-specific MV model with FMR

Three subject-specific computational disease models of the MV were created from 3D epicardial echocardiography data obtained in three pigs that were induced with a myocardial infarction via percutaneous occlusion of the left circumflex artery, and as a result developed FMR after 3 months of follow up. The modeling workflow used in this study was based on the approach developed and validated previously [11]. Briefly, for each case, geometry of the MV annulus, leaflets, and PM tips in diastole was semi-automatically reconstructed from echo images using proprietary software Siemens AutoValve (Siemens Healthineers, Issaquah, WA) and in-house written MATLAB (MathWorks, Natick, MA) code. Each PM was subdivided into three regions, representing individual PM heads, as seen in ex vivo MV specimens. MV model was completed by adding a branched network of chordae, connecting the MV leaflets to the PMs. Since chordae are not visible on echo, their insertion points on the leaflets were determined according to the pattern reported in the literature [49], while chordal insertion sites on the PMs were identified according to published reports [4, 42] and our observations in ex vivo MV specimens.

The reconstructed geometry of the MV was meshed and material properties were prescribed. The MV leaflets were meshed using 3-node general-purpose conventional shell elements (type S3R in Abaqus (Simulia, Providence, RI)), and a total of 18,600 elements were created to define the surface of the leaflets. As the lengths of the leaflets significantly exceed their corresponding leaflet thickness, thin shell element formulation with the reduced numerical integration for the prediction of the element behavior was used. Since in the present study only the closure of the MV was considered, the chordae were discretized with tension-only truss elements (type T3D2 in Abaqus). A total of 944 elements were created to define the branched network of the chordae, with the branching pattern defined based on anatomical data from humans. To describe nonlinear, incompressible, and anisotropic mechanical behavior of the leaflets, Fung-based anisotropic hyperelastic model [25] was implemented. For nonlinear, incompressible, and isotropic mechanical behavior of the chordae, 3rd order Ogden hyperelastic model was used [34]. Regionally varying leaflet thickness with mean values of 1.32±0.11 mm for the anterior leaflet (AL) and 1.22±0.03 mm for the posterior leaflet (PL) was assigned according to the measurements reported earlier [23]. Constant chordal cross-sectional area values of 0.40 mm² for marginal, 1.15 mm² for strut, and 0.79 mm² for basal were set [50]. The simulated leaflet and chordal mass density was assumed to be ten times higher than the real density, as suggested by Hamid et al. [15] The assumption is that this “effective” mass accounts for the inertial effects of the blood volume spanned and moved by the mitral valve during its closure. Such volume is about ten times larger than the volume of the valve leaflets. This approach was used by other groups as well to simulate the effects of blood volume on the mitral valve, without performing fluid-structure interaction modeling [22, 40, 50]. To define coaptation between MV leaflets, general contact algorithm with penalty method and friction coefficient of 0.05 was set. Such interaction was justified previously [55] as a good approximation to characterize the contact between soft and wet surfaces.

FMR state of the MV was created by displacing the PMs apically, thus stretching the chordae and imposing a pre-strain on both chordae and MV leaflets. In such way, chordal tethering forces inherent to functional mitral regurgitation were taken into the account. Such pre-tension was optimized iteratively until the deformed model could closely match the valve configuration seen in echo images. In each case, the largest pre-strain was imposed on the strut chordae, with maximum value of 0.088±0.016, as struts experienced the highest pre-tension which was necessary to achieve leaflet concavity toward the left atrium, characteristic to functional mitral regurgitation. To simulate MV closure before the repair (Fig 1A), physiologic transvalvular pressure gradient with a peak value of 120 mmHg was applied to the leaflets (Fig 1B), and subject-specific annular contraction and movement of the PMs were prescribed as kinematic boundary conditions (Fig 1C). Dynamic simulation of the valve closure was performed in Abaqus using explicit solver, which contains a global estimation algorithm to automatically determine the smallest stable time increment for the explicit integration scheme used in this simulation. After the simulation, pre-repair peak systolic configuration of the MV was obtained (Fig 1D).

Figure 1.

Simulation of pre-repair mitral valve closure: (A) Subject-specific computational model in diastole; (B) Transvalvular pressure gradient applied on the leaflets to simulate valve closure; (C) Annular contraction and motion or the papillary muscles set as kinematic boundary conditions; (D) Systolic configuration of pre-repair mitral valve model.

B. Simulation of MV function after UMA

The outcomes of undersizing mitral annuloplasty (UMA) were examined by simulating the effects of differently sized annuloplasty rings on three distinct MV computational models. An annuloplasty ring model of seven different sizes (40, 38, 36, 34, 32, 30, 28 mm) were created based on the shape and measurements (Fig 2D) of Carpentier-Edwards Physio I ring (Edwards Lifesciences, Irvine, CA) [5]. Each ring model was meshed using quadratic tetrahedron elements.

Figure 2.

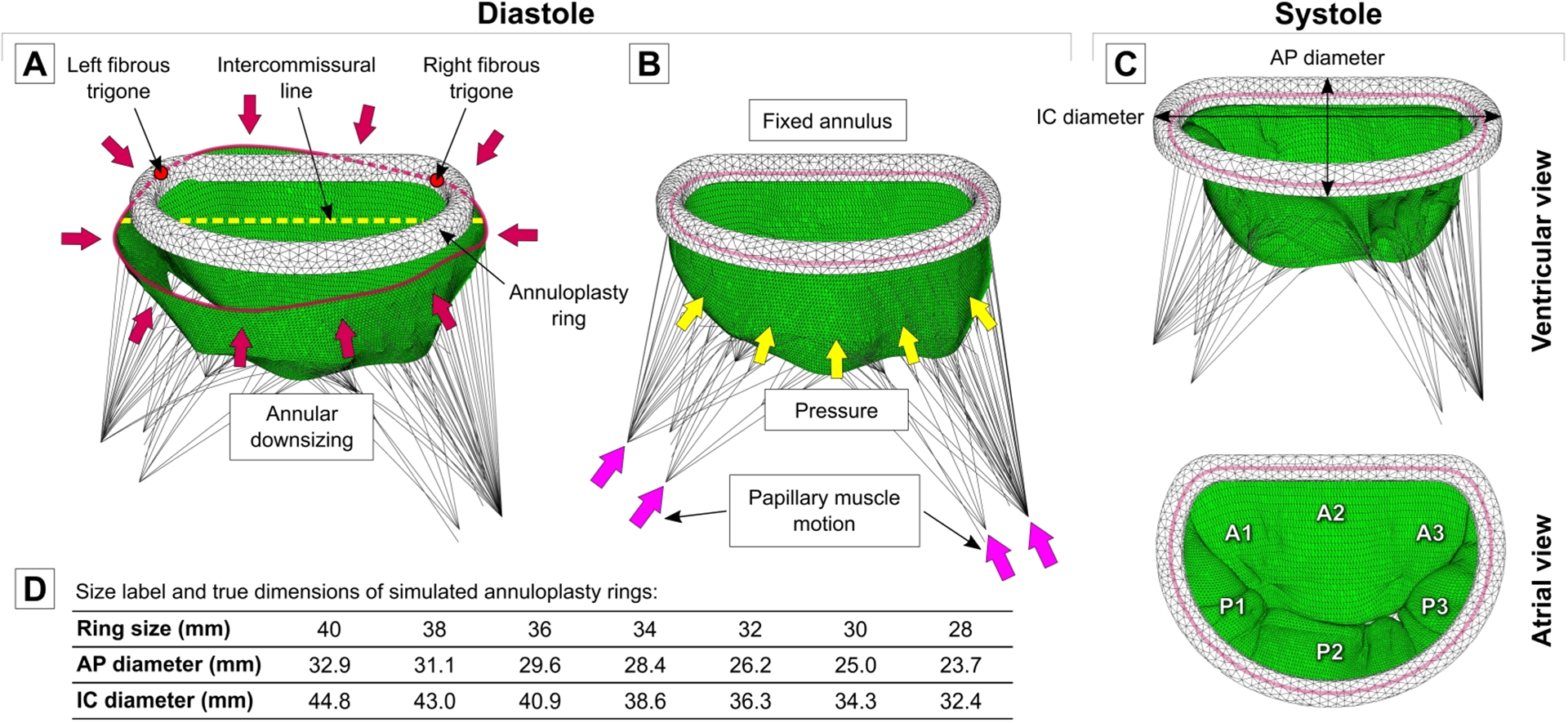
(A) Positioning of annuloplasty ring in diastole and deformation of mitral annulus to ring dimensions. (B) Simulation of mitral valve closure after annuloplasty.

(C) Systolic configuration of post-UMA mitral valve. (D) Size label and dimensions of seven annuloplasty rings used in this study.

For each investigated case, all seven rings were used to downsize the mitral annulus in diastole, mimicking implantation of the ring on an arrested heart during surgery. Each annuloplasty ring was placed on the implied regions of left and right fibrous trigones. Ring height was adjusted according to the positions of the MV commissures, such that the intercommissural line of the mitral annulus and the XY plane of the ring coincided. After the ring was positioned, the mitral annulus was deformed to the ring configuration by prescribing appropriate displacements to the annular nodes (Fig 2A). Lastly, dynamic simulations were run for each model with different size rings. The contact between annuloplasty ring and MV annulus and leaflets was defined using general contact algorithm with penalty method and friction coefficient of 0.2, as suggested in the literature for interactions between rigid devices and MV tissue [30]. Physiologic transvalvular pressure gradient was applied to the leaflets, and movement of the PMs was prescribed as a boundary condition. For the mitral annulus, fixed boundary condition was applied to avoid deformation of the annulus or the ring during MV closure (Fig 2B). Peak systolic configuration of the post-UMA valve was obtained after each simulation (Fig 2C).

C. Data analysis

After each simulation, i.e., pre-repair (or FMR) and UMA (7 ring sizes), the following parameters were calculated for each investigated case: stress distribution on the leaflets, tension forces in the chordae, reaction forces acting on the PMs, and coaptation length of the leaflets. As suggested by Auricchio et al. [2], to prevent local stress concentration areas from biasing the results, 1% of the highest stress values were excluded from the data analysis. In addition, to investigate the mobility of the leaflets and measure clinically relevant indices of MV function, tenting height, tenting area, and excursion angles of both MV leaflets were computed. Finally, post-repair systolic results were compared with pre-repair values.

3. Results

To emphasize the subject-specific effects of UMA and its sizing on valve closure, the average results for the three valves are presented alongside the individual results of each valve geometry here and in Tables 1–5 and Fig 3–6.

Table 1.

Impact of annular downsizing on MV geometry in diastole.

	Annular area (mm2)	Reduction (%)	AP diameter (mm)	Reduction (%)	IC diameter (mm)	Reduction (%)
	Case 1
FMR	1192.5	-	33.5	-	43.2	-
UMA 40	1049.8	12.0	29.9	10.8	41.8	3.2
UMA 38	944.0	20.8	28.1	16.1	40.0	7.4
UMA 36	846.7	29.0	26.6	20.6	37.9	12.3
UMA 34	758.4	36.4	25.4	24.2	35.6	17.6
UMA 32	649.7	45.5	23.2	30.8	33.3	22.9
UMA 30	578.8	51.5	22.0	34.3	31.3	27.6
UMA 28	510.8	57.2	20.7	38.2	29.4	31.9
	Case 2
FMR	1103.6	-	34.0	-	39.9	-
UMA 40	1049.8	4.9	29.9	12.1	41.8	−4.8
UMA 38	944.0	14.5	28.1	17.4	40.0	−0.3
UMA 36	846.7	23.3	26.6	21.8	37.9	5.0
UMA 34	758.4	31.3	25.4	25.3	35.6	10.8
UMA 32	649.7	41.1	23.2	31.8	33.3	16.5
UMA 30	578.8	47.6	22.0	35.3	31.3	21.6
UMA 28	510.8	53.7	20.7	39.1	29.4	26.3
	Case 3
FMR	1063.9	-	32.1	-	41.3	-
UMA 40	1049.8	1.3	29.9	6.9	41.8	−1.2
UMA 38	944.0	11.3	28.1	12.5	40.0	3.2
UMA 36	846.7	20.4	26.6	17.1	37.9	8.2
UMA 34	758.4	28.7	25.4	20.9	35.6	13.8
UMA 32	649.7	38.9	23.2	27.7	33.3	19.4
UMA 30	578.8	45.6	22.0	31.5	31.3	24.2
UMA 28	510.8	52.0	20.7	35.5	29.4	28.8
	Mean±SD
FMR	1120.0±65.9	-	33.2±1.0	-	41.5±1.7	-
UMA 40	1049.8	6.1±5.4	29.9	9.9±2.7	41.8	−0.9±4.0
UMA 38	944.0	15.5±4.9	28.1	15.3±2.5	40.0	3.4±3.8
UMA 36	846.7	24.2±4.4	26.6	19.8±2.4	37.9	8.5±3.6
UMA 34	758.4	32.1±3.9	25.4	23.4±2.3	35.6	14.1±3.4
UMA 32	649.7	41.9±3.4	23.2	30.1±2.1	33.3	19.6±3.2
UMA 30	578.8	48.2±3.0	22.0	33.7±2.0	31.3	24.4±3.0
UMA 28	510.8	54.3±2.6	20.7	37.6±1.9	29.4	29.0±2.8

Table 5.

Stresses and forces for every investigated case before and after FMR repair.

	Peak AL stress (MPa)	Peak PL stress (MPa)	Peak anterior marginal force (N)	Peak posterior marginal force (N)	Peak anterior strut force (N)	Peak posterior strut force (N)	PMs reaction force (N)
	Case 1
FMR	0.53	0.762	0.528	0.369	2.343	2.593	23.883
UMA 40	0.478	2.671	0.50	0.359	1.997	7.344	30.184
UMA 38	0.436	1.945	0.435	0.273	1.902	5.363	24.561
UMA 36	0.419	1.478	0.383	0.233	1.78	4.004	20.624
UMA 34	0.38	1.192	0.339	0.323	1.581	3.212	18.28
UMA 32	0.346	0.851	0.286	0.279	1.404	2.049	14.735
UMA 30	0.342	0.736	0.269	0.24	1.31	1.769	13.639
UMA 28	0.349	0.684	0.268	0.184	1.222	1.36	12.386
	Case 2
FMR	0.697	0.695	0.468	0.65	4.308	2.912	24.717
UMA 40	0.977	0.481	0.425	0.548	2.255	1.418	15.994
UMA 38	0.902	0.422	0.32	0.529	2.127	1.213	14.45
UMA 36	0.929	0.364	0.219	0.466	1.994	1.146	13.225
UMA 34	0.691	0.298	0.182	0.415	1.896	0.88	12.386
UMA 32	0.748	0.26	0.158	0.339	1.72	0.76	11.692
UMA 30	0.786	0.239	0.114	0.289	1.58	0.677	11.783
UMA 28	0.662	0.233	0.11	0.249	1.372	0.599	11.402
	Case 3
FMR	1.053	0.52	0.788	0.177	4.275	1.411	25.856
UMA 40	0.556	0.572	0.685	0.154	2.83	1.251	15.098
UMA 38	0.515	0.49	0.634	0.127	2.687	1.17	13.406
UMA 36	0.434	0.412	0.553	0.118	2.525	1.147	12.248
UMA 34	0.432	0.397	0.487	0.113	2.397	0.91	11.214
UMA 32	0.413	0.332	0.374	0.105	2.169	0.772	10.114
UMA 30	0.371	0.30	0.329	0.105	2.016	0.686	9.86
UMA 28	0.392	0.294	0.317	0.106	1.763	0.622	9.419
	Mean±SD
FMR	0.76±0.27	0.659±0.12	0.595±0.17	0.399±0.24	3.642±1.13	2.305±0.79	24.819±0.99
UMA 40	0.67±0.27	1.241±1.24	0.537±0.13	0.354±0.20	2.361±0.43	3.338±3.47	20.425±8.46
UMA 38	0.618±0.25	0.952±0.86	0.463±0.16	0.31±0.20	2.239±0.40	2.582±2.41	17.472±6.16
UMA 36	0.594±0.29	0.751±0.63	0.385±0.17	0.272±0.18	2.10±0.38	2.099±1.65	15.366±4.58
UMA 34	0.501±0.17	0.629±0.49	0.336±0.15	0.284±0.15	1.958±0.41	1.667±1.34	13.96±3.79
UMA 32	0.502±0.22	0.481±0.32	0.273±0.11	0.241±0.12	1.764±0.38	1.194±0.74	12.18±2.35
UMA 30	0.50±0.25	0.425±0.27	0.237±0.11	0.211±0.10	1.635±0.36	1.044±0.63	11.761±1.89
UMA 28	0.468±0.17	0.404±0.24	0.232±0.11	0.18±0.07	1.452±0.28	0.86±0.43	11.069±1.51

Figure 3.

(A) Measurement of leaflet coaptation length (CoL) at A1-P1, A2-P2, and A3-P3 regions in pre- and post-repair models. (B) Comparison of coaptation length values before and after annuloplasty in each investigated case.

Figure 6.

(A) Pre- and post-repair stresses in marginal and strut chordae.

(B) Comparison of peak chordal tension forces before and after UMA.

A. Mitral valve function in FMR model

In all pre-repair models, the echo derived MV geometry had a dilated mitral annulus and enlarged interpapillary distance in diastole, compared to healthy controls. Compared to in vivo echo measurements on healthy porcine valves made in our lab [37] and data from the literature [19], the average pre-repair mitral annulus was dilated (annular area: 1120.0±65.9 mm²; anteroposterior (AP) diameter: 33.2±1.0 mm; inter-commissural (IC) diameter: 41.5±1.7 mm), and enlarged interpapillary distance of 41.3±4.4 mm was present. The average diastolic orifice area, defined as the area bounded by the free margin of the leaflets, in pre-repair models was 394.3±19.6 mm². Geometric parameters of mitral annulus and orifice area for every case are presented in Tables 1–2.

Table 2.

Orifice area and area of regurgitant gaps before and after undersizing annuloplasty.

	Diastolic orifice area (mm2)	Reduction (%)	Regurgitant gap area in systole (mm2)
	Case 1
FMR	415.6	-	14.2
UMA 40	403.7	2.9	16.3
UMA 38	384.4	7.5	6.4
UMA 36	370.5	10.9	1.3
UMA 34	355.7	14.4	0
UMA 32	334.6	19.5	0
UMA 30	318.8	23.3	0
UMA 28	311.8	25.0	0
	Case 2
FMR	390.3	-	7.2
UMA 40	356.5	8.7	12.1
UMA 38	350.4	10.2	3.1
UMA 36	348.3	10.8	0
UMA 34	344.8	11.7	0
UMA 32	334.6	14.3	0
UMA 30	331.7	15.0	0
UMA 28	330.6	15.3	0
	Case 3
FMR	377.1	-	19.1
UMA 40	378.5	−0.4	19.7
UMA 38	367.3	2.6	9.5
UMA 36	359.5	4.7	4.3
UMA 34	356.6	5.4	2.6
UMA 32	352.9	6.4	0
UMA 30	349.2	7.4	0
UMA 28	347.1	8.0	0
	Mean±SD
FMR	394.3±19.6	-	13.5±6.0
UMA 40	379.6±23.6	3.7±4.6	16.0±3.8
UMA 38	367.3±17.0	6.8±3.9	6.3±3.2
UMA 36	359.4±11.1	8.8±3.6	1.9±2.2
UMA 34	352.4±6.5	10.5±4.6	0.9±1.5
UMA 32	340.7±10.6	13.4±6.6	0
UMA 30	333.2±15.3	15.2±8.0	0
UMA 28	329.8±17.6	16.1±8.5	0

In systole, the imposed boundary conditions resulted in tethered valve geometry, lack of coaptation, and formation of regurgitant gaps. The systolic annular area was 988.5±63.8 mm², AP diameter was 30.5±1.4 mm, IC diameter was 38.9±1.2 mm, and interpapillary distance was 38.1±2.7 mm. Two regurgitant gaps near A1-P1 and A3-P3 segments of the leaflets were present. In cases 1 and 3, echocardiographic images showed a larger regurgitant jet in A3-P3 region and a small jet in A1-P1 region. In case 2, a small jet was observed in A3-P3 region, while a larger jet was present in A1-P1 region. Similar regurgitant gap formation was observed in pre-repair computational models, with an average regurgitant gap area of 13.5±6.0 mm². Individual results of every case are shown in Table 2.

Leaflet coaptation length at A2-P2 region was 2.3±0.5 mm, which is lower than 5 mm, a value considered clinically adequate for long term repair durability [16, 45]. Due to the presence of regurgitant gaps, no coaptation was observed at A1-P1 and A3-P3 regions. On average, coaptation area of 168.2±14.2 mm² was measured in systole. Pre-repair leaflet coaptation parameters are presented in Table 3 and Fig 3. Compared to in vivo measurements [37], increased tenting height of 10.9±0.4 mm and tenting area of 165.8±2.0 mm², as well as reduced leaflet excursion angles (anterior: 24.7±1.5°; posterior: 22.5±2.8°) were observed (for individual results of every case see Table 4 and Fig 4). Areas of high leaflet stresses, exceeding threshold value of 0.5 MPa inherent to healthy valve [44, 46, 49], were found on both AL and PL, near the insertion sites of the strut chordae (peak AL: 0.76±0.27 MPa; peak PL: 0.659±0.12 MPa; see Table 5 and Fig 5). Elevated peak chordal tension forces, higher than the ones measured ex vivo [59], were calculated in marginal and strut chordae (anterior marginal: 0.595±0.17 N; posterior marginal: 0.399±0.24 N; anterior strut: 3.642±1.13 N; posterior strut: 2.305±0.79 N; see Table 5 and Fig 6), thus demonstrating the presence of valve tethering.

Table 3.

Leaflet coaptation length and area before FMR repair and with different size annuloplasty rings.

	A1-P1 coaptation length (mm)	A2-P2 coaptation length (mm)	A3-P3 coaptation length (mm)	Coaptation area (mm2)
	Case 1
FMR	0	1.8	0	153.2
UMA 40	0.7	1.6	0	257.9
UMA 38	1.4	3.1	0	351.0
UMA 36	1.4	4.2	0	442.2
UMA 34	2.5	5.2	0.7	513.7
UMA 32	3.2	6.3	1.9	625.9
UMA 30	3.7	6.8	2.2	698.6
UMA 28	5.0	7.5	3.4	763.1
	Case 2
FMR	0	2.8	0	181.3
UMA 40	0	3.8	0	260.8
UMA 38	0	4.6	4.4	358.4
UMA 36	3.6	5.4	5.4	470.0
UMA 34	4.5	6.0	5.9	549.1
UMA 32	5.2	6.9	6.4	627.7
UMA 30	5.2	7.4	6.5	654.2
UMA 28	7.3	8.5	8.1	740.8
	Case 3
FMR	0	2.3	0	170.2
UMA 40	0	2.8	0	296.6
UMA 38	0	3.8	3.1	397.1
UMA 36	0	4.9	3.8	488.3
UMA 34	0	5.2	4.4	558.8
UMA 32	4.0	6.3	4.7	650.8
UMA 30	4.4	6.9	5.1	723.8
UMA 28	4.7	7.4	6.8	788.8
	Mean±SD
FMR	0	2.3±0.5	0	168.2±14.2
UMA 40	0.2±0.4	2.7±1.1	0	271.7±21.6
UMA 38	0.5±0.8	3.9±0.7	2.5±2.3	368.9±24.8
UMA 36	1.7±1.8	4.8±0.6	3.1±2.8	466.8±23.2
UMA 34	2.3±2.3	5.5±0.5	3.7±2.7	540.5±23.7
UMA 32	4.1±1.0	6.5±0.3	4.3±2.3	634.8±13.9
UMA 30	4.4±0.7	7.1±0.3	4.6±2.2	692.2±35.3
UMA 28	5.7±1.4	7.8±0.6	6.1±2.5	764.3±24.0

Table 4.

Tenting parameters in pre- and post-repair models.

	Tenting height (mm)	Tenting area (mm2)	AL diastolic angle (deg)	AL systolic angle (deg)	AL excursion angle (deg)	PL diastolic angle (deg)	PL systolic angle (deg)	PL excursion angle (deg)
	Case 1
FMR	10.5	167.2	50.7	24.8	25.9	73.1	48.8	24.3
UMA 40	9.7	144.6	58.3	25.7	32.6	71.7	44.6	27.1
UMA 38	8.3	116.1	59.1	23.2	35.9	75.0	43.2	31.8
UMA 36	7.6	101.5	59.6	22.2	37.4	78.0	43.9	34.1
UMA 34	7.0	88.9	59.8	21.0	38.8	80.3	44.4	35.9
UMA 32	6.5	75.4	59.9	20.7	39.2	85.0	47.2	37.8
UMA 30	6.1	67.2	59.8	20.5	39.3	87.5	47.0	40.5
UMA 28	5.8	60.1	59.9	20.4	39.5	91.0	49.0	42.0
	Case 2
FMR	11.2	163.5	55.1	30.0	25.1	68.2	48.9	19.3
UMA 40	6.6	98.8	58.8	19.8	39.0	61.4	29.7	31.7
UMA 38	6.3	88.9	60.0	19.1	40.9	66.2	32.9	33.3
UMA 36	5.9	77.8	60.6	18.5	42.1	70.7	32.6	38.1
UMA 34	5.6	70.7	61.0	18.1	42.9	74.2	33.8	40.4
UMA 32	5.5	63.3	61.3	19.1	42.2	81.1	36.5	44.6
UMA 30	4.8	52.4	59.8	17.5	42.3	84.2	34.6	49.6
UMA 28	4.1	41.9	60.9	15.7	45.2	90.3	32.8	57.5
	Case 3
FMR	11.0	166.6	50.3	27.3	23.0	73.8	50.0	23.8
UMA 40	8.2	122.7	62.0	23.7	38.3	67.3	36.3	31.0
UMA 38	7.5	105.0	63.8	22.6	41.2	70.0	36.4	33.6
UMA 36	6.8	91.0	65.0	21.7	43.3	72.5	36.0	36.5
UMA 34	6.7	85.1	66.0	21.6	44.4	75.4	38.3	37.1
UMA 32	6.1	70.6	66.7	20.4	46.3	81.7	41.9	39.8
UMA 30	5.8	63.9	67.5	20.3	47.2	84.5	42.6	41.9
UMA 28	5.4	55.9	67.3	19.8	47.5	89.8	43.5	46.3
	Mean±SD
FMR	10.9±0.4	165.8±2.0	52.0±2.7	27.4±2.6	24.7±1.5	71.7±3.1	49.2±0.7	22.5±2.8
UMA 40	8.2±1.5	122.0±22.9	59.7±2.0	23.1±3.0	36.6±3.5	66.8±5.2	36.9±7.4	29.9±2.4
UMA 38	7.4±1.0	103.3±13.6	61.0±2.5	21.6±2.2	39.4±3.0	70.4±4.4	37.5±5.2	32.9±1.0
UMA 36	6.7±0.9	90.1±11.9	61.8±2.9	20.8±2.0	40.9±3.1	73.8±3.8	37.5±5.8	36.2±2.0
UMA 34	6.4±0.8	81.6±9.6	62.3±3.3	20.2±1.9	42.0±2.9	76.6±3.3	38.8±5.3	37.8±2.3
UMA 32	6.0±0.5	69.8±6.1	62.6±3.6	20.1±0.9	42.6±3.6	82.6±2.1	41.9±5.3	40.8±3.5
UMA 30	5.6±0.7	61.2±7.8	62.4±4.4	19.4±1.7	42.9±4.0	85.4±1.8	41.4±6.3	44.0±4.9
UMA 28	5.1±0.9	52.6±9.5	62.7±4.0	18.6±2.5	44.1±4.2	90.4±0.6	41.8±8.2	48.6±8.0

Figure 4.

(A) Measurement of tenting parameters in diastole and systole. (B) Pre- and post-repair tenting height and tenting area. (C) Comparison of leaflet excursion angles before and after undersizing annuloplasty.

Figure 5.

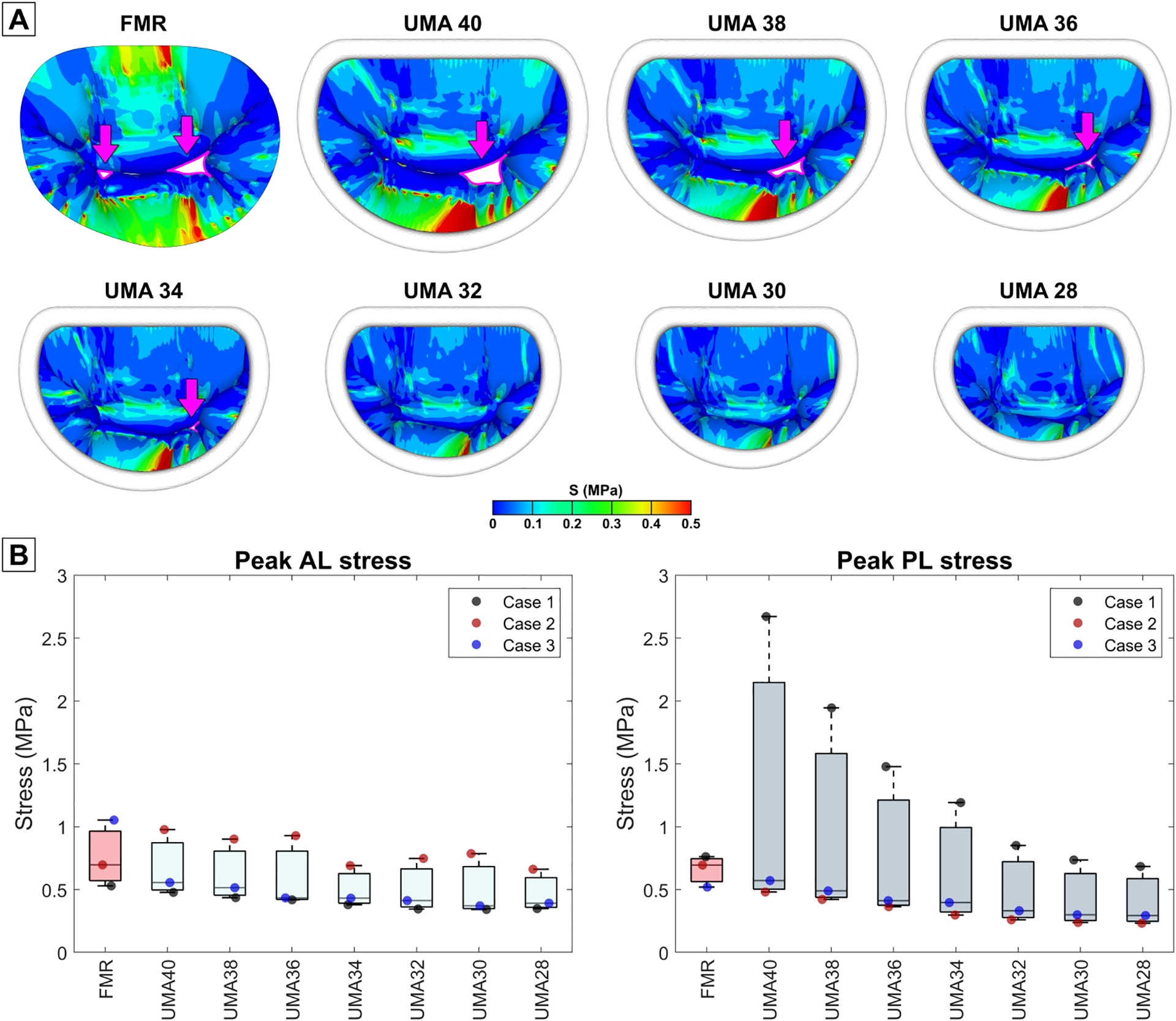
(A) Stress distribution on the mitral valve leaflets in pre- and post-repair models. Regurgitant gaps are indicated with arrows. (B) Comparison of peak stresses on anterior and posterior leaflets before and after UMA with different size rings.

B. Post-repair simulation results

Annular geometry:

On average, the largest annuloplasty ring of 40 mm reduced native mitral annular area by 6.1±5.4%, while the smallest ring of 28 mm decreased annular area by 54.3±2.6%. The extent of annular reduction varied between the three simulated cases and is summarized in Table 1. Since the same rings were used for every simulated case, the reduction in annular geometric parameters depended upon the initial shape and size of the mitral annulus in each model with FMR. For example, in case 1, the smallest ring reduced AP diameter by 38.2% and IC diameter by 31.9%. In case 2, the same ring reduced AP diameter by 39.1% but IC diameter was reduced only by 26.3%. While in case 3, AP diameter was reduced by 35.5% and IC diameter by 28.8%.

Orifice area:

After UMA with the largest annuloplasty ring, mean diastolic orifice area was reduced by 3.7±4.6%, while the smallest ring reduced it by 16.1±8.5%. The reduction of orifice area was observed in cases 1 and 2 with all annuloplasty ring sizes. In case 3, a slight increase of orifice area by 0.37% was noticed after deployment of 40 mm ring, while area reduction was observed with other smaller rings. Detailed values of pre- and post-repair diastolic orifice area are presented in Table 2.

Valve closure:

Regurgitant gaps in all simulated cases were eliminated with annuloplasty, but at different ring sizes. In case 1, regurgitant gaps were eliminated after downsizing the annulus by 36.4% with 34 mm ring. In case 2, smaller annular reduction of 23.3% with 36 mm ring was needed for FMR correction. In case 3, mitral annulus had to be downsized by 38.9% with 32 mm ring to restore a sufficient valve closure (see Table 2).

Leaflet coaptation:

On average, clinically adequate leaflet coaptation length at A2-P2 region, larger than 5 mm, was restored using rings of 34 mm or smaller. The highest mean coaptation length value of 7.8±0.6 mm was obtained after UMA with 28 mm ring. In case 1, UMA increased A2-P2 coaptation length with rings of 38 mm or smaller. However, an adequate leaflet coaptation was restored only with rings of 34 mm or smaller. In case 2, UMA increased leaflet coaptation with all ring sizes, but an adequate A2-P2 coaptation was restored after UMA with rings of 36 mm or smaller. Similarly, in case 3, all rings increased leaflet coaptation, whereas larger than 5 mm coaptation length was observed only after UMA with rings of 34 mm or smaller. The rings used to restore A2-P2 coaptation length to an adequate level coincided well with the ones used to eliminate regurgitant gaps. In cases 1 and 2, the same ring sizes (34 mm and 36 mm, respectively) eliminated FMR and restored a decent A2-P2 coaptation length. In case 3, coaptation length larger than 5 mm was restored with 34 mm ring, while regurgitation was eliminated with one size smaller ring of 32 mm.

After UMA, leaflet coaptation length at A1-P1 and A3-P3 increased as well. On average, leaflet contact at A1-P1 was restored with 36 mm or smaller rings. At A3-P3, leaflet contact was restored with 38 mm or smaller rings. In both regions, coaptation length larger than 5 mm was restored only with 28 mm ring: 5.7±1.4 mm at A1-P1, and 6.1±2.5 mm at A3-P3.

Leaflet coaptation area increased incrementally with all ring sizes. After UMA with the largest annuloplasty ring, coaptation area increased to 271.7±21.6 mm² (62.1±16.1% increase from pre-repair), while the smallest ring increased it to 764.3±24.0 mm² (356.7±45.1% increase). The comparison of leaflet coaptation before and after FMR repair is summarized in Table 3 and presented in Fig 3.

Leaflet tethering and mobility:

Tenting parameters measured in pre- and post-repair MV models are explained in Fig 4, with detailed values presented in Table 4. All UMA ring sizes used in this study reduced tenting height and tenting area. However, a clinically acceptable tenting height (less than 5 mm [47]) was observed only in case 2 with rings of 30 and 28 mm. In cases 1 and 3, tenting height was not reduced to less than 5 mm with any size ring. The largest annuloplasty ring reduced tenting height to 8.2±1.5 mm (24.6±16.6% reduction from pre-repair) and tenting area to 122.0±22.9 mm² (26.5±13.0% reduction). The smallest ring reduced tenting height to 5.1±0.9 mm (53.0±9.9% reduction) and tenting area to 52.6±9.5 mm² (68.3±5.4% reduction).

While tenting height was not restored in most simulations, the reduction of leaflet tethering was achieved, leading to the increased MV leaflet mobility, which was quantified by calculating the excursion angles of AL and PL. In all cases, excursion angles increased after UMA with any size ring. For the anterior leaflet, the largest ring increased excursion angle to 36.6±3.5° (49.1±21.2% increase from pre-repair), while with the smallest ring excursion angle increased to 44.1±4.2° (79.7±27.4% increase). For the posterior leaflet, 40 mm ring increased excursion angle to 29.9±2.4° (35.3±26.7% increase), while 28 mm ring to 48.6±8.0° (121.7±67.0% increase). The ring size impact on the leaflet mobility is summarized in Table 4.

Leaflet stresses:

On average, stresses in the AL were reduced with all ring sizes, with a reduction that paralleled ring size. The largest annuloplasty ring reduced mean peak stress to 0.67±0.27 MPa (5.6±43.8% reduction from pre-repair), while the smallest ring to 0.468±0.17 MPa (34.0±28.9% reduction). In the PL, however, peak stresses increased after UMA with 40, 38, and 36 mm rings. Annuloplasty rings of 34 mm or smaller were necessary to reduce PL stresses. On average, using 40 mm ring, mean peak stress in the PL was 1.241±1.24 MPa (76.6±152.0% increase from pre-repair), while with 28 mm ring mean peak stress was 0.404±0.24 MPa (40.1±28.3% reduction).

In case 1, all ring sizes reduced peak leaflet stresses in the AL, while in the PL the increase of stresses was observed with annuloplasty rings larger than 30 mm. On the contrary, in case 2, PL stresses were reduced with all ring sizes, while in the AL peak stresses were reduced only with 34 and 28 mm rings. In case 3, stresses increased in the PL after UMA with 40 mm ring. All other ring sizes allowed to reduce AL and PL peak stresses. Peak systolic configurations of pre- and post-repair MV leaflets and leaflet stress distributions are shown in Fig 5. Detailed values of peak leaflet stresses for every case are presented in Table 5.

Chordal tension forces:

Marginal chordal tension was reduced with all ring sizes. With the largest ring size (size 40), peak marginal chordal tension forces were 0.537±0.13 N in the anterior marginal chordae (9.2±3.9% reduction from pre-repair) and 0.354±0.2 N in the posterior (10.5±6.9% reduction). At the smallest ring size, 28 mm, peak forces reduced further to 0.232±0.11 N in the anterior marginal chordae (61.8±13.8% reduction compared to pre-repair and 58.1±14.4% compared to the largest ring size), and 0.18±0.07 N in the posterior (50.6±10.8% reduction compared to pre-repair and 44.8±12.2% compared to the largest ring size).

In the anterior strut chordae, all ring sizes reduced tension forces. In the posterior strut chordae, tension forces increased after UMA with 40 and 38 mm rings. All smaller rings reduced chordal forces. Using 40 mm ring, peak forces were reduced to 2.361±0.43 N in the anterior strut chordae (32.1±16.5% reduction) and increased to 3.338±3.47 N in the posterior (40.2±125.5% increase). With 28 mm ring, peak forces were reduced to 1.452±0.28 N in the anterior strut chordae (58.3±10.2% reduction compared to pre-repair and 38.6±0.8% compared to the largest ring size) and to 0.86±0.43 N in the posterior (61.0±16.5% reduction compared to pre-repair and 63.2±16.3% compared to the largest ring size).

In case 1, UMA with rings larger than 32 mm greatly increased tension forces in the posterior strut chordae. All other rings, as well as all ring sizes for cases 2 and 3, helped to decrease forces in both strut and marginal chordae. Comparison of pre- and post-repair chordal tension forces are presented in Fig 6. Computed force values are summarized in Table 5.

PMs reaction forces:

The reaction forces acting on the PMs showed the overall tension forces in the chordae. On average, UMA with 40 mm ring reduced reaction force to 20.425±8.46 N (16.8±37.6% reduction from pre-repair). The lowest mean PMs reaction force of 11.07±1.51 N was obtained with 28 mm ring (55.2±7.8% reduction). In case 1, reaction forces were reduced after UMA with rings of 36 mm or smaller. In cases 2 and 3, all ring sizes reduced reaction forces on the PMs. The obtained results are summarized in Table 5.

4. Discussion

Mitral valve systolic closure, simulated from the diastolic 3D echo derived geometries, was in agreement with the systolic geometries seen on ultrasound. Comprehensive validation of these three cases used for surgical planning was reported earlier [11]. The results of this subject-specific computational model were in general agreement with experimental data we measured earlier in the ex vivo model of FMR [59]. Our experimental work demonstrated that FMR was associated with higher MV tethering forces, tenting height, and tenting area. In addition, excursion angles for both MV leaflets were reduced from the ventricular tethering. After UMA with 26 mm ring, chordal forces, tenting height, and tenting area were reduced, while excursion angles for both leaflets increased. In the computational model, similar trends were observed: elevated chordal tension forces, tenting height, tenting area, and reduced excursion angles for both MV leaflets were present in all three models with FMR. After UMA with the smallest 28 mm ring, chordal forces, tenting height, and tenting area were reduced in a similar manner as in the ex vivo model, but the magnitude of reduction of measured parameters was higher. Leaflet mobility was improved, as seen by the increase of both excursion angles, but again the post-repair values were higher than in the experimental study. Such discrepancies between computational and experimental results can be explained by the differences in annular reduction size and restrictions of the PMs kinematics induced in both studies. Firstly, the pre-repair mitral annulus was reduced more in computational models (AP diameter: 33.2±1.0 mm reduced to 23.7 mm in computational model vs. 30 mm reduced to 21.9 mm in ex vivo model), thus greater alterations of the computed parameters were seen in simulation data. Also, in ex vivo models, FMR was induced by displacing the PMs in apical, lateral, and posterior directions, while in computational models the PMs were displaced only apically. The lateral and posterior displacement of the PMs restricted the systolic leaflet motion in a different manner, which affected the leaflet kinematics. Finally, there were no systolic motion of the PMs in the ex vivo models, thus additionally affecting valve kinematics and therefore the experimental results.

For each simulated case, the best results defined in terms of valve coaptation were achieved after annuloplasty with the smallest 28 mm ring. Such ring eliminated regurgitant gaps in all investigated cases and increased A2-P2 coaptation length, restoring an adequate (> 5 mm) coaptation level. Still, even with the smallest ring, post-repair valve biomechanics remained unphysiological. Firstly, while such annuloplasty ring greatly reduced leaflet tenting, an adequate (< 5 mm) tenting height was restored only in case 2. Also, after UMA with 28 mm ring, peak leaflet stresses were still high, exceeding threshold value of 0.5 MPa for healthy valve in cases 1 and 2. Finally, while the smallest annuloplasty ring reduced chordal tension and rebalanced force distribution across the whole chordal network (see Fig 6), peak marginal and strut chordal forces in all three investigated cases were higher than those we measured earlier in the ex vivo model of FMR [59]. Therefore, even with the smallest 28 mm ring, the excessive valve tethering was not eliminated. Such tethering is mainly defined by the kinematics of the PMs, and in the presence of FMR, the motion of the PMs is restricted [20]. Since the reduction of the mitral annulus has no impact on the kinematics of the PMs, valve tethering after annular downsizing is not improved much. During UMA, the annulus is reshaped to match the size and shape of the annuloplasty ring, thus the leaflets are moved closer to each other, and decent leaflet coaptation can be restored. Still, if no subannular repair is performed, the valve tethering is not eliminated, increasing the risk of FMR recurrence [12]. Moreover, the larger the annuloplasty ring is used, the less annular reshaping is done. The leaflets are not moved as close to each other, thus decent leaflet coaptation cannot be restored and FMR remains present.

Though the data from our simulations indicates that the smallest ring can effectively eliminate FMR and aid in better systolic valve closure, the risk of creating MV stenosis after such excessive annular downsizing should be considered. Clinically, the problem of elevated transmitral gradients and functional mitral stenosis with use of small annuloplasty rings is known [6]. In our computational models, the smallest ring reduced diastolic orifice area to 329.8±17.6 mm², which is higher than the threshold value of 200 mm² that is associated with mitral stenosis [36]. However, the 28 mm ring also reduced annular area by 54.3±2.7%. From the Gorlin formula [14], 50% reduction of the annular area increases transmitral gradient by four times, worsening intracardiac hemodynamics, patient’s functional capacity, and affecting repair durability [28]. For this reason, UMA with small rings might appear as an effectiverepair at first, but it may lead to greatly increased transmitral gradients later after the surgery, and that could limit the benefit of this repair technique [56]. On the other hand, while larger annuloplasty rings allow to avoid the problem of elevated transmitral gradients and functional mitral stenosis, the valve biomechanics after such repair is poor. In our computational models, the rings larger than 32 mm, were not able to eliminate FMR. After the deployment of the rings larger than 34 mm, decent coaptation length and tenting height was not restored, and leaflet stresses were not reduced. Finally, the rings larger than 36 mm were not able to reduce chordal tension forces. Such unphysiological valve biomechanics might induce fibrotic remodeling and stiffening of the MV leaflets [48], and therefore lead to additional reduction of leaflet mobility and further worsening of the MV biomechanics.

Therefore, the procedure of annuloplasty ring sizing for FMR repair is a challenging task, as too large a ring size may fail to repair FMR, and too small a size may increase transmitral gradients or cause functional mitral stenosis. At present, there is a wide variety of different ring types and sizes but no actual scientific approach to the sizing procedure, as sizing methods vary greatly among products [5, 35]. The subject-specific computational model presented in this study allows to evaluate the possible effects of various ring types and sizes for FMR repair, and thus can be useful in clinical decision making. As the modeling approach itself is not limited to annular repair but can be used to simulate the outcomes of sub-annular repair techniques as well, integration of such tool into a clinical environment might help with procedure planning and eventually ensure better durability after MV repair.

This study has some limitations, which are noted here. As highlighted in our previous work [11], MV leaflet thickness was assigned according to the measurements reported earlier from actual mitral valves [23], and chordal distribution scheme was adopted from the literature as well from actual mitral valves [49]. These limitations cannot be avoided if geometry reconstruction is done from ultrasound data due to insufficient image resolution and inability to see chordae in echocardiographic images. However, since the published data that we relied upon was validated, we have considered the expected range of leaflet thickness and chordal distribution, minimizing the uncertainty in this model. However, use of generalized leaflet thickness and chordal distribution makes our model non-subject specific in this regard, which is a limitation. Another limitation of this study is the use of isolated MV model without any ventricular geometry, enabling the investigation of the UMA impact on the MV itself but not on the ventricle. A recent animal study from our group [58] suggests that UMA can unphysiologically impair ventricular mechanics and torsion, especially if smaller annuloplasty ring sizes are used. Development of integrated valvular and ventricular computational models is warranted and is part of our future work.

We conclude that conservative annular downsizing with large annuloplasty rings (> 32 mm) is not effective in repairing FMR. The use of smaller rings (≤ 32 mm) provides better systolic valve closure but increases the risk of elevated transmitral gradients, that could limit the repair benefits. The addition of subannular repair techniques should be considered to ensure effective and durable FMR repair.