Abstract
Cryo-electron microscopy (cryo-EM), the subject of the 2017 Nobel Prize in Chemistry, is a technology for obtaining 3-D reconstructions of macromolecules from many noisy 2-D projections of instances of these macromolecules, whose orientations and positions are unknown. These molecules are not rigid objects, but flexible objects involved in dynamical processes. The different conformations are exhibited by different instances of the macromolecule observed in a cryo-EM experiment, each of which is recorded as a particle image. The range of conformations and the conformation of each particle are not known a priori; one of the great promises of cryo-EM is to map this conformation space. Remarkable progress has been made in reconstructing rigid molecules based on homogeneous samples of molecules in spite of the unknown orientation of each particle image and significant progress has been made in recovering a few distinct states from mixtures of rather distinct conformations, but more complex heterogeneous samples remain a major challenge.
We introduce the “hyper-molecule” theoretical framework for modeling structures across different states of heterogeneous molecules, including continuums of states. The key idea behind this framework is representing heterogeneous macromolecules as high-dimensional objects, with the additional dimensions representing the conformation space. This idea is then refined to model properties such as localized heterogeneity. In addition, we introduce an algorithmic framework for reconstructing such heterogeneous objects from experimental data using a Bayesian formulation of the problem and Markov chain Monte Carlo (MCMC) algorithms to address the computational challenges in recovering these high dimensional hyper-molecules. We demonstrate these ideas in a preliminary prototype implementation, applied to synthetic data.
Keywords: cryo-EM, continuous heterogeneity, hyper-molecules, hyper-objects, dynamical systems, non-rigid deformations, MCMC
1. Introduction
Cryo-electron microscopy (cryo-EM) is joining X-ray crystallography and nuclear magnetic resonance (NMR) as a technology for recovering high-resolution reconstructions of biological molecules [1, 2, 3, 4, 5]. A typical study produces hundreds of thousands of extremely noisy images of individual particles where the orientation of each individual particle is unknown, giving rise to a massive computational and statistical challenge. Current algorithms (e.g., [6, 7, 8, 9, 10, 11]) have been successful in recovering remarkably high-resolution reconstructions of static macromolecules in homogeneous samples with little variability, and have also been rather successful in recovering molecules from heterogeneous samples consisting of a small number of distinct different molecular conformations (referred to as discrete heterogeneity). Even in homogeneous cases, there is ongoing work on improving resolution, and there are several open questions about validating the results and estimating the uncertainty in the solutions.
Structural variations are intrinsic to the function of many macromolecules. Molecular motors, ion pumps, receptors, ion channels, polymerases, ribosomes, and spliceosomes are some of the molecular machines for which conformational fluctuations are essential to their function. As just one example, the reaction cycle of the molecular motor kinesin is seen to involve a combination of discrete states (i.e., bound kinesin monomers in different stages of ATP hydrolysis) and also a continuous motion in which one monomer “strides” ahead while it is tethered by a linker to its microtubule-bound companion [12]. As another example, fluctuations in the conformation of ligand-binding domains drive the response of neuronal glutamate receptors [13]. While technologies like X-ray crystallography and NMR measure ensembles of particles, cryo-EM produces images of individual particles, and one of the great promises of cryo-EM is that these noisy images, depicting individual particles at unknown states viewed from unknown directions, could potentially be compiled into maps of the dynamical processes in which these macromolecules participate [14, 15]. This, in turn, would help uncover the functionality of these molecular machines.
Due to the difficulties in the analysis of heterogeneous samples, researchers attempt to purify homogeneous samples; in doing so they lose information about other states/conformations. Alternatively, they model the macromolecules observed in heterogeneous samples as a small number of distinct macromolecules (e.g., [16]); this approach overlooks relationships between states (e.g., similarity between different conformations of the molecule) and leads to an impractical number of distinct objects when the variability is complex or when there is a continuum of states rather than distinct independent states. Currently, the analysis of heterogeneous macromolecules often misses states, achieves limited resolution, or yields remarkably high-resolution reconstructions of static regions, from which hang “blurry” heterogeneous pieces that cannot be accurately recovered. The study of heterogeneity is considered an open problem without a well-established solution (see the recent survey [17]); existing approaches often rely on assumptions such as small modes of perturbation or piece-wise rigidity. In other cases, they require a reliable alignment of images before the heterogeneity can be addressed.
In some ways, the heterogeneity problem in cryo-EM is an extreme case of related problems that appear in the analysis of other systems that exhibit some intrinsic variability, such as the imaging of the body of a patient in computed tomography (CT) while the patient breathes [18] (in this case, the viewing directions are known, and there are some indications for the state in the breathing cycle).
We introduce a new mathematical framework with a Bayesian formulation for describing and mapping continuous heterogeneity in macromolecules and an algorithmic approach for computing these heterogeneous reconstructions which addresses some of the computational and statistical challenges. We present a preliminary implementation and experimental results. Ultimately, the goal of this line of work is to produce scalable computational tools for analyzing complex heterogeneity in macromolecules. One of the goals in this design is to allow the use of a wide range of models and solvers that would enable the user to encode prior knowledge about the specific macromolecule being studied. For the implementation of these ideas, we envision software for modeling of complex heterogeneous molecules in computer code (or simpler interfaces for common templates) as differentiable components, analogous to deep neural network models. The prototype presented in this paper to demonstrate these ideas is more modest in its capabilities and scalability.
We start with the question: What does it mean to recover a heterogeneous macromolecule compared to a homogeneous/rigid macromolecule? We propose that this boils down to the question of representing a heterogeneous macromolecule in all its states; in other words, a “solution” would allow us to view the macromolecule at any state in a user interface that would provide us with “knobs” that we could turn to observe the molecule transition between states through a continuum of states. Often, it is useful to have statistics of how populated the states are, along with the map of states. We recall the representation of molecules as 3-D functions using a linear combination of 3-D basis functions:
| (1) |
with spatial coordinates . We generalize this representation to describe a heterogeneous macromolecule in all its states. This generalization, which we refer to as a “hypermolecule,” is described as follows. In Section 3.2, we propose a generic generalization of (1). We represent hyper-molecules as linear combinations of higher-dimensional basis functions :
| (2) |
where the new dimensions capture heterogeneity, so that identifies a conformation, or a location in the map of states, and the macromolecule at state/conformation is the 3-D density function obtained by fixing in . In other words, we generalize the classic problem of “estimating a homogeneous macromolecule” to the problem of “estimating a heterogeneous hyper-molecule,” a single high-dimensional object that encodes all the conformations of the macromolecule together. The (possibly high-dimensional) variable represents the map of states, or the “knobs” which a user would turn in order to transition between states. Furthermore, we argue that hyper-molecules are not merely a way to express the solution of some computation: the representation through a finite set of basis functions serves as a regularizer in the computational problem, much like band-limit assumptions in many inverse problems, including the homogeneous case of cryo-EM. In particular, the high-dimensional basis functions, each supported on multiple states, impose relations between states and define a continuum of states. This property distinguishes between hyper-molecules and a small set of independent macromolecules. This mathematical model of heterogeneous macromolecules is accompanied by a Bayesian formulation for recovering hyper-molecules from data, which is a generalization of the Bayesian formulation of cryo-EM that allows a continuum of states and addresses the relationships between states.
Increasingly complex heterogeneity is formulated using increasingly higher-dimensional hyper-molecules. However, in Section 3.4 we find that these hyper-molecules can be “too generic”: the natural generalization of traditional algorithms to recover very high-dimensional hyper-molecules requires impractically large datasets and computational resources. We address these problems in the remaining subsections of Section 3 and in Section 4.
First, in Section 3.5, we introduce “composite hyper-molecules,” a generalization of hyper-molecules that capture additional properties of macromolecules often known to scientists or readily identifiable. Specifically, a macromolecule can often be modeled as a sum of rigid and heterogeneous components , each with its own state . The state determines not only the shape of the component but also its position with respect to the other components through a function denoted by :
| (3) |
In this case, “recovering the heterogeneous macromolecule” means recovering the coefficients that describe each individual component of and recovering the coefficients that describe the trajectory of each component.
Next, in Section 3.6, we note that the Bayesian formulation of hyper-molecule does not rely on a specific representation of the hyper-molecule and it interacts with the model of the hyper-molecule mainly through the comparison of particle images with the hyper-molecule at certain viewing directions and states, and through priors on the hyper-molecule structure. Therefore, we may replace our proposed hyper-molecules and composite hyper-molecules with other models, having coefficients . We would then have an algorithm which accesses a black-box function and a prior , and updates the coefficients , the viewing directions, state variables and so on without explicit knowledge of the detailed model of . This formulation, which separates the model and prior of the hyper-molecule from the algorithm allows users to define more elaborate models as needed in their application.
The high-dimensional nature of hyper-molecules leads to a computational challenge. Specifically, the main computational challenge in current software packages, such as RELION [6, 19, 20] and cryoSPARC [7], is that each iteration of the algorithms involves a comparison of each particle image to the current estimate of the molecule as viewed from any possible direction (despite modifications that significantly reduce the number of comparisons required in practice). In hyper-molecules, we add the high-dimensional state variable , so that the natural generalization of current algorithms would require comparison of each particle image to each possible molecule (i.e., the hyper-molecule at any possible state) at each possible viewing direction, increasing the computational complexity exponentially with the increase in dimensionality. The variability in the nature of the heterogeneity and models makes it more challenging to develop generic solutions for reducing the number of comparisons. In Section 4 we propose a framework based on Markov chain Monte Carlo (MCMC) algorithms to address some of the computational complexity. This framework would allow complex, flexible, programmable black-box models and bypasses the need for exhaustive searches in each iteration.
In Section 5, we present a Matlab prototype which implements a subset of the proposed hyper-molecules and MCMC frameworks. This prototype demonstrates the applicability of hyper-molecules, composite hyper-molecules and MCMC to the mapping of continuous heterogeneity. We note that the current prototype is slow, requires manual configuration and it does not scale well to high resolution and large datasets. Therefore, in this paper, we present experiments with synthetic data and defer the discussion of preliminary results with experimental data to future work. We are currently developing the next version, which will be scalable, faster and more accessible, this version will also allow more general models of hyper-molecules. The implementation of generalized prolate spheroidal functions, a new numerical tool used in this work that had not been publicly available previously, but which is not the main topic of this paper, has been rewritten and made publicly available in [21] and https://github.com/lederman/Prol; the remaining functionality will be made available when the new Python version is ready.
Some of the preliminary work leading to this paper is available in an earlier technical report [22].
2. Preliminaries
The purpose of this section is to briefly review some of the technical tools used in this paper. In addition, we present the cryo-EM problem and related work on the problem, and we formulate the mathematical and statistical models which we will generalize in the remainder of the paper.
2.1. Representation of Functions
A function such as can be represented in many ways. In this discussion, we assume a default representation which is a linear combination of a finite set of basis functions :
| (4) |
Such representations (often accompanied by some penalties on large coefficients ) imply regularity of the objects; the specific type of regularity is determined by the choice of basis functions. Typical examples of such functions would be low-frequency (band-limited) sine and cosine functions, and low-order polynomials. The key properties of these representations are that once the model is formulated (i.e., once the basis functions are chosen), the function is completely determined by the coefficients , and that the choice of basis functions imposes constraints or regularizes the function (a sum of low-frequency sines cannot yield a higher-frequency sine).
In cryo-EM, the functions are sometimes described, loosely speaking, as “band-limited” and “compactly supported.” Often, these functions are defined through samples on a 3-D grid, with different interpolations in different implementations. We represent functions with these properties in this work using generalized prolate spheroidal functions (see [21] and Section 5), however, the particular choice of basis functions is not the main topic of this paper, and the discussion applies to various representations of functions.
A linear combination of basis functions is not the only way to represent functions. In particular, a Gaussian mixture model (GMM) has been proposed in [23] for low-resolution representation of molecules in cryo-EM; in this representation, the function is a sum of Gaussian masses. In this case, the coefficients determine the amplitude, centers, and covariances of the masses. The discussion in this paper also applies to representations like these, with some modifications. In Sections 3.5 and 3.6 we extend the discussion to more general forms.
Remark 1 (Terminology: “representation”) Our use of the term “representation” in the context of this paper is different from the context in which we use the term in [24]. However, we have not found a better term that would avoid this confusion. In this paper “representation” is a way of expressing a function or a problem, typically an expansion of a function in some basis, whereas in [24] it is a technical representation theory term. These two works are independent; the conceptual relation between the two is the motivation to treat heterogeneity as “just another variable,” analogous to the viewing direction variable.
2.2. Cryo-EM and the Forward Model
The purpose of this section is to formulate the standard cryo-EM problem in the homogeneous case. We review the main characteristics of the cryo-EM imaging process and the forward model briefly, and discuss the Bayesian formulation of the problem of mapping a macromolecule. One of the goals of this paper is to introduce an idea of a flexible framework where components can be exchanged for others to reflect slightly different models, therefore, we restrict the discussion in this section to the general formulation and highlight the key difficulties. While it is certainly tempting to delve into the mathematical and numerical properties of the forward operator and the different parameters associated with it, the finer details are beyond the scope of this section. A broader discussion of the imaging model and challenges can be found in many surveys such as [25, 26, 27, 28, 29], and further discussions of a Bayesian framework for cryo-EM — in the context of a maximum a posteriori (MAP) formulation — can be found in [16, 6]. We diverge slightly from the standard numerical representation of the homogeneous case in our use of generalized prolate spheroidal functions as natural basis functions for the problem (see Section 5), but otherwise make use of a standard imaging model.
Electron microscopy is an important tool for 3-D reconstruction of molecules. Of particular interest in the context of this paper is single particle reconstruction (SPR), and, more specifically, cryo-EM, where multiple 2-D projections, ideally of identical particles viewed from different directions, are used in order to reconstruct a 3-D object representing the molecule. Compared to other imaging problems, the cryo-EM inverse problem is characterized by low SNR and the unknown orientation of each particle image.
The following formula is a simplified noiseless imaging model of SPR for obtaining the noiseless particle image from a function (representing the molecule’s density or a potential):
| (5) |
where , is a 2-D contrast transfer function (CTF) convolved with each 2-D projection of a particle, is the rotation that determines the direction from which the molecule is viewed, is the in-plane shift, and is a positive real valued contrast (amplitude). The viewing direction and the in-plane shift are typically unknown. The parameters of the CTF are not all known; for simplicity, we will assume in this simplified model that they are known or estimated by other means.
A Fourier transform of both sides of Equation (5) reveals that, in the Fourier domain, the Fourier transform of the image is related to the 3-D Fourier transform of the density by the formula
| (6) |
where , is the shift operator in the Fourier domain (which is a pointwise multiplication in the Fourier domain), and is the Fourier transform of the CTF. In other words, in the Fourier domain, this imaging model reduces to an evaluation of the Fourier transform in the plane perpendicular to the viewing direction, and to pointwise multiplications to compute the effects of CTF, shift and contrast.
In practice, the particle image obtained in experiments is discrete (composed of pixels) and noisy. We will study through its discrete Fourier transform (as implemented by the FFT) of , evaluated at regular grid points in the Fourier domain. First, with a minor abuse of notation, we define the discrete noiseless particle image by sampling at the points in the Fourier domain:
| (7) |
We note that and is real-valued, because is real-valued by definition.
For brevity and generality, we absorb the various imaging parameters such as the in-plane shift and contrast (as well as noise and CTF variables where applicable) of each particle image into an imaging variable which we denote by . For the purposes of this discussion, we denote the forward model operator by . The noiseless imaging model is then summarized by the formula
| (8) |
The map is typically linear.
Next, we model the noise in a simplified imaging model for :
| (9) |
where and are i.i.d, except for if since the noisy image is real valued in the spatial domain. The sample at has no imaginary component for the same reason. The noise variance depends on the frequency; in this simplified model, we assume that the noise variance is known and is similar for all particle images; in practice it can be one of the model variables.
These simplified models neglect several aspects of the physical model, numerical computation, and experimental setup. For example, in practice, the images of individual particles must first be extracted from a larger image (micrograph). As we noted above, the parameters determining the CTF and noise profile are sometimes added to the model. To allow a more general formulation, we add the variable which encodes latent variables of the experiment that are not particle-specific (e.g., the noise standard deviation ).
Given this model, the likelihood of a particle image given the object and particle-specific variables and is given by
| (10) |
This leads to a Bayesian description of the problem, with a probability density for an object, image parameters and observed images given by:
| (11) |
where is a prior for the molecule and the particle-specific variables such as the viewing direction. The posterior distribution of the variables given the data is therefore proportional to the right-hand side of this equation:
| (12) |
The variables are particle image specific latent variables, while the object itself, represented by , is the variable of interest. In other words, the distribution that we are interested in is
| (13) |
This model is often simplified by setting a uniform prior for the viewing directions and adding the assumption that the viewing directions and particle-specific variables and of each particle are sampled independently from those of other particles. In this case, we obtain the posterior
| (14) |
where is a prior for molecules (e.g., weighted norms of coefficients representing the molecule), and is a prior for the random variables controlling each individual image, such as in-plane shifts.
While this general framework is sufficient for the purpose of this paper, we note that in the very influential work of [16, 6], a Bayesian framework was used to formulate the problem of recovering a molecule as a MAP estimation problem, implemented using an expectation-maximization algorithm. We choose a slightly different formulation and different algorithms for our purpose due to several technical and computational considerations discussed below. Different algorithms use slightly different models and may absorb different components of the model into different latent variables.
2.3. Heterogeneity in Cryo-EM
The description of the cryo-EM problem in Section 2.2 assumes that all the particles in all the projection images are identical (but viewed from different directions). However, the particles in a sample are often not identical. In some cases, several different types of macromolecules or different conformations of the same macromolecule are mixed together, and sometimes the macromolecule itself is flexible, a property which is manifested as a continuum of slightly different versions of the molecule. The first case of distinct classes of macromolecules is called discrete heterogeneity and the second case is called continuous heterogeneity. In this paper we focus on continuous heterogeneity, although much of the discussion applies to discrete heterogeneity with small modifications.
A primary goal of this paper is to generalize the mathematical formulation in Section 2.2 to the continuously heterogeneous case.
2.4. Existing Methods in Cryo-EM and Related Work
Many of the existing algorithms for cryo-EM try to estimate the maximum-likelihood or the MAP molecule from models formulated roughly like the model in Section 2.2 (see, for example, [30, 31, 16]). One of the popular methods for this is a family of expectation-maximization algorithms, implemented in software such as RELION [6, 19, 20]. Another is based in part on stochastic gradient descent (SGD), implemented in cryoSPARC [7]. These algorithms alternate between estimating the viewing direction (or conditional distribution of viewing directions) for each particle image given the current estimate of the macromolecule and updating the estimate of the macromolecule given the estimated viewing direction for each particle image (or its distribution). In these updates, the algorithm must compare each particle image to the estimated macromolecule as viewed from each (discretized) viewing direction, at each value of the other variables (most notably, the in-plane shifts). Naturally, this comparison is expensive. In recent years, several algorithms have been very successful in solving the homogeneous case (no heterogeneity). Clever algorithms and heuristics which reduce the number of comparisons significantly, and efficient use of hardware components such as GPUs have made the recent implementation of these algorithms rather fast [6, 19, 32, 7]. In addition to the expectation-maximization algorithms, an MCMC algorithm which models rigid molecules as a sum of Gaussians has been proposed in [33]. Other approaches to the cryo-EM problem rely on similarity between images to align the images before reconstructing the molecule [34, 35, 36, 37].
In addition to homogeneous reconstruction, many of the methods mentioned above also accommodate discrete heterogeneity through a 3-D classification framework, where each particle image is assigned to a separate 3-D reconstruction by maximizing a similarity measure. Expectation-maximization algorithms, such as those implemented in RELION [6], generalize to discrete heterogeneity by estimating conditional joint distributions of orientations and discrete class assignment. While this approach has led to impressive results, it requires significant human intervention in a process of successive refinement of the datasets to achieve a more homogeneous sample, and components and conformations that are not well represented in the data tend to be lost [26].
A few approaches have emerged to treat the continuous heterogeneity problem. The remainder of this section briefly surveys some of the main approaches that are guided directly by cryo-EM images; a broader discussion is available in the recent survey [17]. The method proposed in [38, 39, 40] first groups images by viewing direction then attempts to learn the manifold formed by the set of images for each of those directions. Following this, the various direction-specific manifolds are registered with one another, and a global manifold is obtained. A 3-D model may then be constructed for each point on that manifold, providing the user with a description of the continuous varying reconstruction. This method requires a consistent assignment of viewing directions across all states, and relies on a delicate metric for comparing noisy images to which different filters have been applied. The method assumes that certain properties of the manifold are conserved across the different viewing directions and requires a successful and globally consistent registration of the manifolds observed in different directions, which is not always possible. Furthermore, complex heterogeneity with more degrees of freedom results in manifolds that are intrinsically high-dimensional; such high-dimensional manifolds are difficult to estimate without exponential increase in the number of samples, and become more difficult to align. This method has been demonstrated in the mapping of the continuous heterogeneity of the ribosome.
More recently, the RELION framework has been extended to include multi-body refinement [41] (also see [4, 42, 43, 43, 44, 45]). In this approach, the user selects different rigid 3-D models that are to be refined separately from the main, or consensus, model. Each separate sub-model is then refined separately, with its own viewing direction and translation, allowing it to move with respect to the consensus model in a rigid-body fashion. This method is limited to rigid-body variability in a few sub-volumes, and cannot handle non-rigid deformations or other types of variability. In particular, the region at the interface between the sub-models is likely to vary as their relative positions vary, and it is therefore lost in this method.
The covariance estimation approach proposed in [46] does not rely on a particular model for heterogeneity, be it discrete or continuous. Indeed, the authors present a method for characterizing continuous variability in synthetic data. However, the covariance approach is adapted to a linear model of variability and is therefore not well-suited for continuous and non-linear variability. Furthermore, the limited resolution of the reconstruction precludes the study of heterogeneity at higher level of detail. Another approach has been to study the normal modes of perturbation of a macromolecule [47, 48]. Some of the recent work on these directions has been used to study separate domains in the molecule [49].
2.5. Markov Chain Monte Carlo (MCMC)
MCMC is a collection of methods which have been used in statistical computing for decades. The full extent of these methods is beyond the scope of this paper. The purpose of this section is to briefly mention a few properties of some MCMC methods that will be useful in our discussion, while inevitably omitting some technical details. A review of MCMC can be found in many textbooks, such as [50].
MCMC algorithms are designed to sample from a probability distribution by constructing a Markov chain (i.e., a model of transitions between states at certain probabilities), such that the desired distribution is the equilibrium distribution of the Markov chain. Often, like in this paper, the desired probability from which we wish to sample is the posterior distribution of a variable , given a statistical model and data . Very often, we have access only to an unnormalized density , so that we can compute the ratio between densities at two states and , but not and directly.
The Metropolis-Hastings (MH) algorithm, which is the basis for many MCMC algorithms, is based on the following Metropolis-Hastings Update:
Given the state at step , propose a new state with conditional probability given the current state . The probability of proposing given the current state is denoted by . MH can be implemented in different ways, with different methods for proposing a new state, each method has a different function associated with it.
Compute the Hastings ratio:
| (15) |
Approve the transition to the new state (i.e., ) with probability
| (16) |
If the proposed state is rejected, the previous state is retained with .
Over time, under some conditions, MCMC samples states from the equilibrium distribution, which is designed in MH to be .
Remark 2 The Metropolis algorithm is a special case of the Metropolis-Hastings algorithm, with the transition probability chosen such that .
Remark 3 MCMC allows a composition of update rules in different steps. For example, at each step, a subset of variables can be updated separately given the other variables.
Remark 4 Gibbs sampling is a version of MCMC where at each step the algorithm samples some of the variables conditioned on other variables. It is used when the joint distribution of all the variables is difficult to compute, but it is computationally feasible to sample some of the variables at each step while holding other variables fixed. Formally, this is a special case of MH. We mention this important variant here for completeness, but the algorithms described in this paper do not rely on this version of MCMC, which is often not trivial to compute for all variables.
We reiterate that this brief discussion of MCMC is not a comprehensive overview. The purpose of this discussion is to emphasize that MCMC can, in principle, be used to sample from a complicated posterior distribution even when the normalization of this distribution is unknown, and that various update strategies can be mixed together in MCMC algorithms. Samples from the posterior produced by MCMC can be used to approximate an expected value of a variable, but also to study the uncertainty.
2.6. Metropolis-Adjusted Langevin Algorithm (MALA)
MALA is a MH algorithm where the update proposal is given by the formula
| (17) |
where
| (18) |
Here, is the gradient of the log-likelihood with respect to the variables. Note that the unnormalized is sufficient for computing the MALA steps. The parameter is set by the user.
A positive definite preconditioner matrix can be added without changing the equilibrium distribution:
| (19) |
MALA is just an update rule for which the Hastings ratio can be computed as usual, making it a standard Metropolis Hastings update. The MALA algorithm is motivated by the Langevin stochastic differential equation. Loosely speaking, the Langevin stochastic differential equation describes a stochastic process which is analogous to Equation (17), with infinitesimally small updates (small ); the equilibrium distribution of this stochastic process is .
Works such as [51] find relations between the Langevin equation and SGD, a key algorithm in the area of deep learning, which has also been applied to cryo-EM by cryoSPARC [7].
2.7. Hamiltonian Monte Carlo (HMC)
Hamiltonian Monte Carlo (HMC) is a another MCMC algorithm, which does not use the MH propose-accept-reject algorithm. HMC does not require sampling from a conditional distribution (required in Gibbs updates), but rather uses the gradient of the log-likelihood (like MALA) for a combination of deterministic steps (unlike MALA) and randomized steps. Due to the limited scope of this paper, and the complexity of ideas behind HMC, we refer the reader to one of the many resources about MCMC and HMC, such as [50], for additional information. In the context of this discussion, the key property of HMC is its use of the gradient, which we discuss in the context of MALA; however, HMC often has more advantageous mixing properties compared to MALA.
3. Hyper-Molecules
3.1. Toy Examples
The purpose of this section is to introduce synthetic examples which we will use to illustrate some of the ideas and in numerical experiments.
3.1.1. The “Cat”:
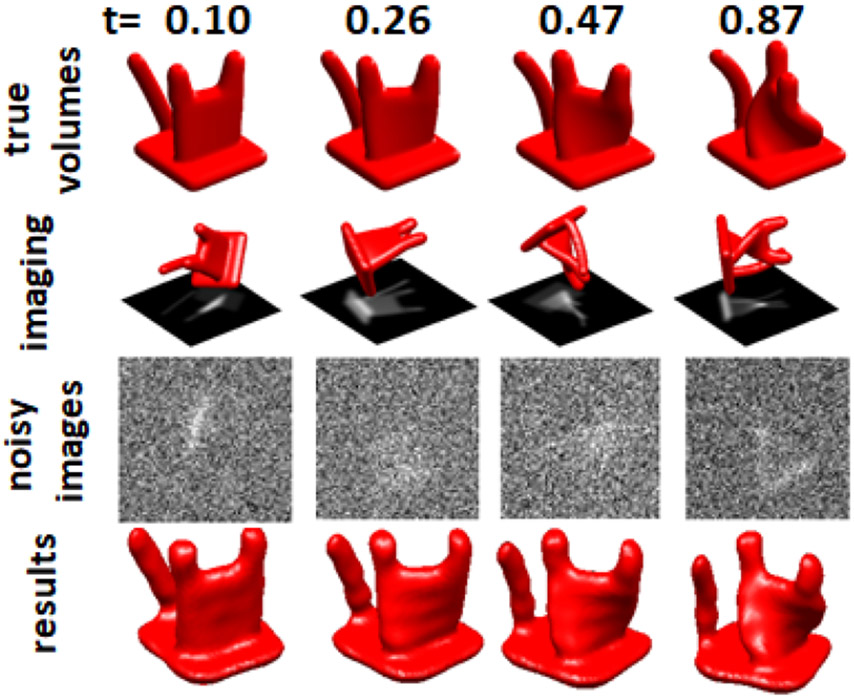
To illustrate the problem, we constructed the “cat,” an object composed of Gaussian elements in real space, where each Gaussian follows a continuous trajectory as a function of the parameter , so that we have a continuous space of objects corresponding to an object with extensive large-scale heterogeneity. The heterogeneity is one-dimensional, where the state corresponds to the direction in which the cat’s “head” is turned. Examples of synthetic 3-D object instances and the 2-D projections are presented in Figure 1 (rows 1-3).
Figure 1.
Sample cats: true 3-D instances (top row), rotated instance and noiseless projection images (second row), images with noise as used in the simulation (third row), and the reconstructed cat (bottom row, discussed in more detail in an earlier technical report [22])
3.1.2. The “Pretzel”:
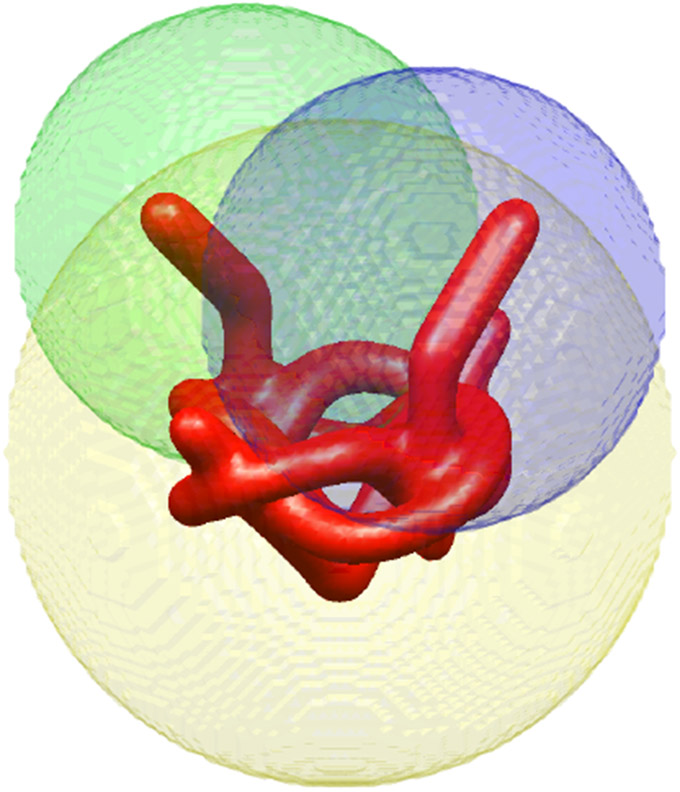
To illustrate continuous heterogeneity with more structure, we constructed the “pretzel,” which is composed of three parts: a rigid “base” and two independent “arms.” The two heterogeneous regions are highlighted in the green and blue balls in Figure 2. In Figure 3(top) we present different conformations of the pretzel. In our simulations, each arm can take any state independently of the other, but for the purpose of illustration in Figure 3, we hold one of the arms in a fixed state and sample different states of the other arm.
Figure 2.
The anatomy of the pretzel: the green and blue regions identify the heterogeneous “arms.” In the analysis in Section 5, the yellow region marked the boundary of the rigid component, and the green and blue balls marked the boundaries of the two heterogeneous components. The components are allowed to overlap.
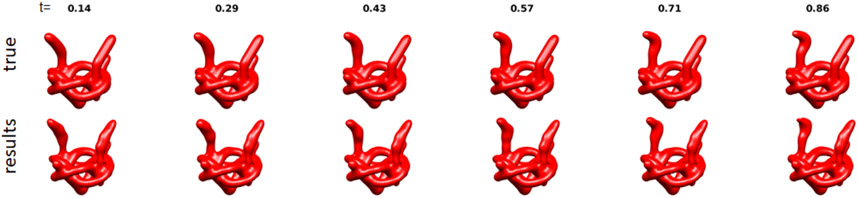
Figure 3.
The pretzel: samples of true pretzels (top row) and reconstructed pretzels (bottom row, see Section 5). The two arms have the same shape and range of motion, but for each instance of the synthetic molecule the conformation of each arm is chosen independently from the state of the other arm. For the purpose of this illustration, we present various states of one of the arms (the arm in the green ball in Figure 2), while holding the other arm (the arm in the blue ball in Figure 2) at a fixed state. In the simulation and the recovered object, the arms move independently.
The resulting hyper-molecule has two state variables: one state variable encodes the state of the “arm” in the green ball (see Figure 2) and the other state variable encodes the state of the arm in the blue ball (see Figure 2). The third state variable for the rigid center in the yellow ball is ignored in this figure. Again, for illustration purposes, we present one of the arms at various states, while holding the other arm fixed. The reconstruction captures the conformation found in the synthetic molecule. The reconstruction at a given value of is similar to the true object at that state, but they do not correspond to the exact same state (see discussion in Section 5), since the choice of parameterization of states is not unique (see discussion in Section 6.2).
This is a simplified illustrative mock-up of a typical experiment where one part of the macromolecule is rigid and others are heterogeneous and deforming. A dataset and a simulation using this model are described in Section 5.
3.2. Generalizing Molecules: Hyper-Molecules
Hyper-molecules generalize 3-D density functions to higher-dimensional functions with the new state variable . For a fixed conformation or state , the 3-D density function represents the molecule at that given conformation.
To illustrate the idea, we consider the cat example in Section 3.1.1. A natural way to view this cat is to produce a 3-D movie of the cat, where we would see a different conformation of the cat in each frame of the movie. In other words, each frame would present for a different value of . Since the deformation of the cat is continuous, we could sample it at any arbitrary value of ; a viewer may expect the movie to show a continuous transformation, with the cat not changing considerably as we move from one frame to the next. In other words, the movie would be expected to be relatively smooth (with several possible definitions of smoothness). This property of the movie reflects relations between different conformations. Hyper-molecules enforce such relations in the modeling of .
We recall that density functions in cryo-EM are often assumed to be band-limited, effectively making them smooth in the spatial domain. This regularity is enforced by the representation defined in (1) where the basis functions are approximately band-limited. Hyper-molecules enforce regularity in the state space through the definition in (2) by choosing that have a similar regularity property in the state variable. For example, in the case of 1-D state space in the cat example, with the state variable representing the direction in which the cat is looking, a natural generalization of the representation in (1) generates 4-D basis functions from products of 3-D functions and low-degree orthogonal polynomials (e.g., Chebyshev polynomials) such that
| (20) |
More generally, when there are degrees of freedom of flexible motion, the manifold of conformations is of dimension and the time variable in Equation (20) is replaced by manifold coordinates . The polynomials are replaced by a truncated set of basis functions over the manifold, denoted , with a minor abuse of notation:
| (21) |
For example, the basis function can be the product of polynomials in multiple variables.
The model in Section 2.2 then generalizes naturally, such that Equation (5) is generalized to
| (22) |
the corresponding operator to , and the posterior (12) to
| (23) |
In other words, we use the formulation of the continuously heterogeneous molecules as hyper-molecules to generalize the Bayesian formulation of the cryo-EM problem from a problem of recovering a 3-D molecule from 2-D projections in unknown viewing directions to a problem of recovering a higher dimensional hyper-molecule from 2-D projections. The key to this formulation, compared to a formulation as a collection of independent molecules (e.g., [9, 6]), is that hyper-molecules encode relations between states, with the related property that they encode a smoothly varying continuum of states.
3.3. Enforcing Structure
We note that there exists an equivalent scheme using appropriate samples in the state space, which would be numerically equivalent to our use of polynomials in the state variable. However, hyper-molecules are different from independent molecules because they provide relations between states. This regularity in the relation between states can be further reinforced by generalizing other ideas implemented for 3-D molecules such as priors that favor smaller coefficients for basis functions with high-frequency components in the state variable. Furthermore, the interpolation allows us to assign to each particle image any state in the continuum, rather than only the sampled states.
The basis functions presented above are not the only way to define such relations between states; for example, one can use a discretized state space and use linear interpolation between sorted discretized states (equivalent to a basis of triangles in the state space) to obtain a continuum of states. In order to enforce further smoothness, one can also penalize for large differences between adjacent states using a term of the form
| (24) |
In fact, smoothness and continuity are crude proxies for properties that we would expect to find in the state space of molecules. For example, often, we would expect to observe a flow of mass as we move between states. This would be captured better through a Wasserstein distance between states; additional physical properties are discussed in the remainder of the paper and in a technical report [22]. In the Bayesian formulation, it is natural to add explicit priors for hyper-molecules.
3.4. A Curse of Dimensionality
Building upon the success of the maximum likelihood and MAP frameworks in cryo-EM (see discussion in Section 2.4), it is natural to consider their application to the hyper-volume reconstruction problem. The expectation-maximization algorithms are iterative refinement algorithms which attempt to recover the maximum-likelihood or MAP solution by alternating between updating the distributions of variables such as the viewing direction and updating the estimate of the molecule (i.e., coefficients in the representation of the object as defined in Equation (1)). Generating the projections for all viewing directions and comparing them to all particle images are computationally intensive operations in the implementation.
In the case of hyper-molecules, expectation-maximization would be generalized to alternating between updating the joint distribution over viewing directions and (possibly high-dimensional) state variables (compared to a small number of discrete conformations in current algorithms) and updating the hyper-molecule (21). In other words, one would have to project the hyper-molecule in every possible state in every possible viewing direction and compare each particle image with each of these projections, rapidly increasing the number of comparisons in this already expensive procedure. More complex models of hyper-molecules, introduced later in this paper, would make it more difficult to design specialized algorithms and heuristics to optimize this procedure.
In addition, we note that the number of coefficients required to represent a molecule as a linear combination of basis functions in Equation (1), at a resolution corresponding to about voxels, is . Similarly, adding -dimensional heterogeneity at “state space resolution” corresponding to state coefficients requires coefficients. High-dimensional heterogeneity, arising, for example, in molecules that have several independent heterogeneous regions, results in a large number coefficients which could exceed the total number of pixels in all particle images of an experiment. Indeed, since hyper-molecules have the capacity to represent very generic molecules, it is natural to expect that a lot of data would be required to estimate them; in particular, if the number of possible states (in some discretization) grows exponentially fast with the dimension , it is natural to expect the required number of particle images to grow as fast, if not faster. Given infinite data and infinite computational resources, it is tempting to model very little and allow the data and algorithm to map and reconstruct a heterogeneous macromolecule. Unfortunately, despite the rapid growth in cryo-EM throughput and computational resources, they are far from “infinite.” The natural question to ask is if we can use prior knowledge and assumptions to reduce the amount of data that we need, even in the case of high-dimensional heterogeneity.
In the remainder of this paper, we address some of these challenges.
3.5. Finer Structures I: Composite Hyper-Molecules
In the previous section, we found that recovering a hyper-molecule which describes very generic, and potentially complicated, dynamics of a macromolecule requires massive amounts of data. Often, researchers have prior knowledge about the structure and dynamics of the macromolecule that they study. For example, many macromolecules are composed of a static component to which smaller flexible heterogeneous components are attached (for an illustrative toy example, see the pretzel example in Section 3.1.2). Often, practitioners are able to use traditional cryo-EM algorithms to recover the static component at high resolution, but the regions of the flexible components are blurry. In these cases, researchers are often able to hypothesize where each component is located, which components are static, and which components are heterogeneous. Tools for estimation of local variance and resolution help researchers in identifying these regions (see, for example, [52, 53, 54, 55, 56, 57, 46]).
We introduce composite hyper-molecules, a model which is the sum of components , each of which is a hyper-molecule. The following formula describes a simple version of a composite hyper-molecule:
| (25) |
Each component is constrained to a certain region of space where it is assumed to be supported (the regions may overlap). Each component has its own set of state variables and coefficients that describe it. In our pretzel example, the yellow region in Figure 2 is modeled as a rigid static “body,” and the green and blue regions represent regions of space where two one-dimensional heterogeneous components are supported. As can be seen in this example, the regions may overlap and do not have to be tight around the actual component.
In some cases, the different components could be roughly described as moving one with respect to the other, in addition to more subtle deformations (for example, at the interface between the components). Indeed, heterogeneous macromolecule have been modeled as a superposition of several rigid objects in somewhat arbitrary relative positions in work such as [41, 4, 42, 43, 43, 44, 45]. We observe that hyper-molecules and the composite hyper-molecules in Equation (25) are generic enough to describe the relative motion of these components, but if such dynamics can be assumed, capturing them in the model is advantageous for computational and statistical reasons. Therefore, a more complete version of composite hyper-objects allows both motion and heterogeneity in each component
| (26) |
where is a function that describes the trajectory of the th component, so that the component is in heterogeneity state and its location along the “trajectory” is determined by the position variable . For example, a simple affine can take the form
| (27) |
where . The variables , which determine the trajectory, are part of the variables describing the hyper-molecule, much like the coefficients in Equation (25). Actual trajectory functions would presumably be more complex and could involve rotations and deformations.
The variables for the position and state can be closely related (the position can be related to the heterogeneity state variable for that component); for brevity, we use as a state variable that encapsulates both and .
Compared to previous work like [41, 4, 42, 43, 43, 44, 45], the composite hyper-molecule formulation models components that are inherently non-rigid, and, in particular, models the flexible interface between components. Furthermore, composite hyper-molecules model the set of possible relative positions (trajectories) of the different components with respect to each other (as opposed to more arbitrary possible relative positions), which are parametrized and fitted using data.
Remark 5 In some cases, there are relations between the different regions that can be captured in the description of the composite hyper-molecule. For example, our pretzel has two identical arms (shifted and rotated with respect to each other). While each arm can appear in a different state independently from the other arm, they have the same fundamental structure (i.e., they are the same hyperobject, at a different state and position). A similar phenomenon is observed in some macromolecules that have certain symmetries. We capture this fact in our model in the particular example in Section 5 by defining the hyper-objects representing the two arms so that they share coefficients in their representation. This is analogous to “weight sharing” in deep neural networks.
3.6. Finer Structures II: Priors and “Black-Box Hyper-Molecules”
The purpose of this section is to add a layer of abstraction to the modeling of hyper-molecules, where the model can be implemented as a “black box” provided to an algorithm designed to recover hyper-molecules; the algorithms themselves are discussed in later sections, while this section focuses on the formal modeling of these components. These black-box models will allow users with different levels of technical expertise to define more elaborate models and priors which reflect assumptions and prior knowledge about the experiment, to the extent that such assumptions are necessary given the amount of data, model complexity and available computational resources. While the implementation presented in this paper treats simpler models, this section provides context for goals of this line of work, and additional motivation for algorithms guided by gradients (MALA and HMC) and for the work on MCMC algorithms. We envision a set of different “black boxes” that scientists can choose from, reflecting their prior knowledge and constraints imposed by the amount of data and computational resources available to them.
We revisit the formulation of the hyper-molecule as a sum of basis functions in Equation (21). We denote the coefficients of these basis functions by . Similarly, in the formulation in Equation (26), the coefficients of the basis functions in all components and the coefficients of the trajectories are denoted collectively by . We write this fact explicitly using the notation . We revisit Equation (23), and add this explicit notation:
| (28) |
In particular, it is compelling to factorize (28) into simpler components and formulate a more specific structure:
| (29) |
where is a black-box prior for the hyper-molecule, is a black-box prior for imaging variables and latent variables (e.g., noise parameters and CTF parameters for micrographs), is a prior for the variables of each particle image (e.g., shift from center, contrast parameters), and is the relation to the measurements.
In this formulation, can be replaced by an arbitrary black-box function that produces a consistent notion of a hyper-molecule; this black-box formulation decouples the specifics of the model from the algorithm, giving the scientist more flexibility in defining their model. The key components in this formulation are the model which defines the density (or its Fourier transform) at any position and state as a function of the coefficients , and a prior . These two components encode the scientist’s assumptions, prior knowledge and physical constraints. Another key component is , which encapsulates the imaging model. The components and give some additional flexibility in modeling.
Having defined the models, we turn to the discussion of the algorithms. The general black-box form of the models presented in Section 3.6 above provides some of the motivation for algorithms that are compatible with such generic model.
4. Algorithms
In this section we discuss the role of MCMC algorithms in a framework for recovering hyper-molecules.
4.1. MCMC, MALA and HMC
We consider the Bayesian formulation of hyper-molecules in Equation (29). The difficulty with expectation-maximization algorithms is that they compute as a function of all possible combinations of viewing directions , states , and some of the other particle-image specific variable (e.g., in-plane shift) at every iteration (the update of involves another computationally expensive operation for similar reasons). This involves some discretization of these variables and a large number of comparisons which are computationally expensive at every iteration. This is a computational challenge in the homogeneous case and in the case of discrete heterogeneity when there is a small number of conformations; the natural generalization to high-dimensional continuous heterogeneity increases the computational complexity exponentially in the dimensionality of the heterogeneity. Indeed, algorithms and heuristics have been developed for reducing the number of comparisons in existing software, but it is a challenge to generalize them to apply to high-dimensional hyper-molecules and generic black-box models whose specific form is defined by a user and is not available when the software is written.
We propose an MCMC framework for sampling from the posterior in Equation (29); some of the main features of MCMC are reviewed briefly in Section 2.5. We note that MCMC is not a single algorithm, but a collection of algorithms that can be used together.
Equation (29) and the analogy to expectation-maximization suggests that different variables in the MCMC formulation can be treated separately, mixing strategies for updating a subset of variables while holding the others constant. In particular, the particle-image variables , and can be evaluated separately and in parallel because they are independent conditioned on and . MCMC algorithms such as a simple MH (with a simple update strategy) do not require the computation of the distribution for every value of , and , but rather require only the ratio between the likelihoods of different values of the variables. In other words, at every iteration, this version of MCMC requires the computation of only at two sample points (two sets of values of , and ). Furthermore, since we are computing a ratio, does not need to be normalized such that the probability would integrate to 1; computing this normalization factor would have typically involved evaluating at many points. Other strategies, such as MALA and HMC, require the gradient of the log-likelihood with respect to the different variables (again, implying that the probability does not need to be normalized to integrate to 1). Similar considerations apply to the update of other variables. We note that MCMC is not a “magic solution” to the computational challenge, because it may require more steps than expectation-maximization, but each step is computationally tractable and different strategies and tools can easily be combined to improve performance; where expectation-maximization is feasible, analogous MCMC steps can be applied.
MCMC yields a sample of the variables and latent variable; we can restrict our attention to variables such as which are sampled hyper-molecules, and we can consider the statistics of if we wish to study the statistics of states’ occupancy. Most often, in practice, or can be averaged over all the samples to produce an “expected” hyper-molecule, although this averaging can introduce some technical difficulties due to ambiguities which we will discuss briefly later; these technical issues are not uncommon in this type of problems, and in practice they are rarely a problem since the mixing over symmetries, such as global rotation of the entire molecule, is slow. A similar problem happens the maximum-likelihood and MAP approaches, since there are several equivalent solutions. There too, this is not a problem in practice. The advantage of having multiple samples from the posterior, however, is that they allow us to study the uncertainty in the solution by studying the variability of .
4.2. A Remark about Black-Box Hyper-Molecules
In this section, we revisit the Bayesian formulation of Equation (29) and discuss some aspects of the formulation of generalized hyper-molecules that are related to the algorithms and implementation. In principle, it is sufficient to define black-box functions which would evaluate the prior and the density at any spatial (or frequency) location , and any state (and possibly provide the interface for computing gradients over the difference variables); the algorithm would use these functions to compute using its imaging model.
We note that the explicit evaluation of is not required in Equation (29). Instead, is considered implicitly in the prior and in the comparisons to images in . The way that is used in implies that the algorithm would use the black-box to evaluate the hyper-molecule at some points in order to produce an image using the algorithm’s own imaging models. In fact, this can be numerically inaccurate and computationally expensive without certain assumptions on the structure of . It is therefore useful to implement efficient functions that produce projections of the hyper-molecule that are consistent with the model implemented internally in the black box . In addition, algorithms such as MALA and HMC benefit from models that can be differentiated, such that the gradients of the log-likelihood with respect to and other variables such as and are available to the algorithm. In our implementation, such a module computes (i.e., the comparison to the particle image is done internally in the module). Our current implementation computes gradients only with respect to .
These considerations highlight the fact that complete decoupling of the hyper-molecule model from other components may present a trade-off between generality and efficient implementation considerations.
5. Implementation and Numerical Results
In this section we discuss a prototype constructed for the recovery of hyper-molecules based on the ideas presented in this paper, and present the results of experiments with synthetic data. This implementation extends an early simplified prototype and a simpler model that did not take shifts and CTF into account and allowed only 1-D non-localized heterogeneity; that prototype was not based on MCMC. The earlier prototype is discussed in more detail in an earlier technical report [22]. Examples of objects reconstructed with the earlier prototype are presented in Figure 1 (bottom).
The current prototype implements simple composite hyper-molecules (see Section 3.5); the user can define the number and positions of heterogeneous components of the hyper-molecule. Each component can be defined to be rigid, or heterogeneous with a 1-D or 2-D state space. Finally, the user can define components that share the same parameters, but not the same state; in the pretzel example, the two arms are modeled using the same coefficients , but in each image each arm can be in a different state. Each object is represented using 3-D generalized prolate spheroidal functions, which are the optimal basis for representing objects that are as concentrated as possible in the spatial domain and in the frequency domain (as close as possible to “compactly supported and band-limited”); for more details see [21]. These 3-D basis functions are multiplied by 1-D or 2-D cosines and sines to produce higher-dimensional components.
The MCMC algorithm implements MALA steps for updating the coefficients of the hyper-molecule, and simpler MH steps (random perturbation of the variables to propose new values) for updating the viewing direction, state, in-plane shift, and contrast of each particle image. We are working on implementing MALA and HMC for additional variables. The algorithm has a second mode, provided as a crude approximation of MCMC, where in each iteration, only a subset of the particle image variables (viewing direction, state, etc.) are updated (using a MH step for each particle image); the hyper-molecule is updated using a gradient step, based only on the subset of particle images considered in that iteration. The prototype was implemented in Matlab.
We generated a dataset of 20,000 synthetic pretzel images (synthetic model described in Section 3.1.2), 151 × 151 pixels each, at an SNR of 1/30, and included simulated in-plane shifts and CTF. The synthetic pretzel is generated as a sum of Gaussians, each of which has a center following a “trajectory” which is a continuous function of the state. The projections are computed analytically in the Fourier domain.
The algorithm was provided with the CTF parameters of each particle image, but not with the viewing directions, shifts, amplitudes or heterogeneity states. Moreover, the algorithm was not provided with an initial molecular structure or a tight “mask.” The algorithm was provided with a relatively “loose” prior which penalizes for large norm of the coefficients in the representation of the hyper-molecule.
We assigned initial viewing directions for each particle image uniformly at random, initial shift from a normal distribution with standard deviation of about 7 pixels on each axis, and constant initial amplitudes. The state variable of each particle image was chosen uniformly at random from the interval [0, 1]. First, we set up a homogeneous model in the algorithm (although the dataset is heterogeneous) and set the initial model to zero everywhere (at this point, the state variables are still ignored). This run produced a low-resolution initial model, presented in Figure 4, which we rotated to fit the axes of the molecule (in this example, we recovered an approximate axis of symmetry automatically, which we aligned with the the axis).
Figure 4.
The first step recovers a very low resolution object. Since the object has approximate C2 symmetry, we rotated the crude low resolution result so that it was roughly symmetric around the z-axis.
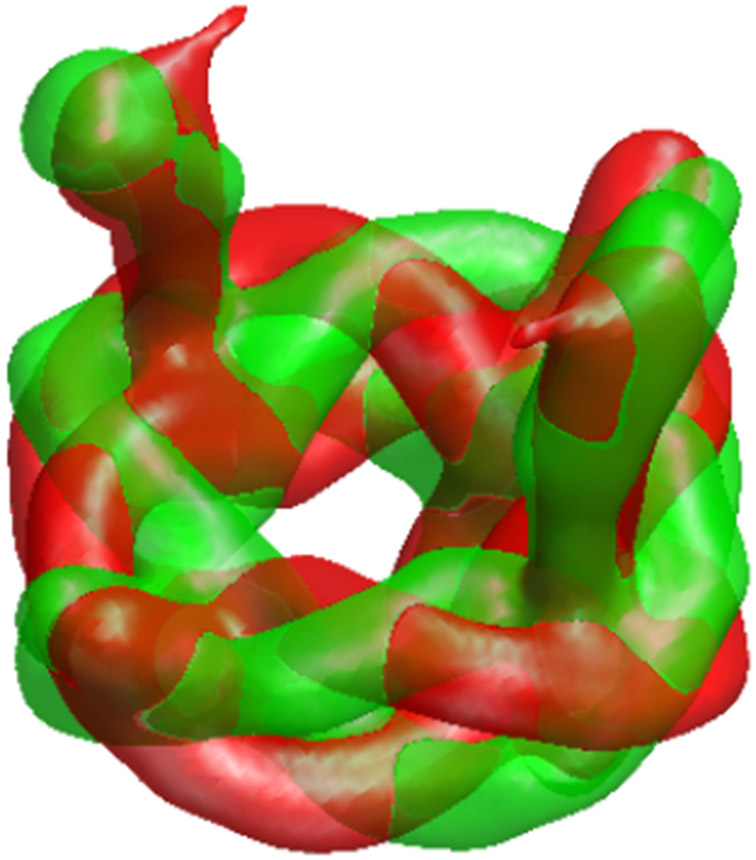
We proceeded to run the algorithm using a simple hyper-molecule model that allows heterogeneity anywhere in the molecule. The algorithm starts with a low-frequency representation of hyper-molecule (initialized again to zero), then gradually increases the frequencies allowed in the representation; the gradual increase in frequency of the representation of 3-D density functions is a common practice in cryo-EM [6, 58, 59], which is generalized here to gradual increase in the frequencies allowed in the state variable. Two representing states produced by the algorithm are presented in Figure 5. We observed that the different “heterogeneity” states are in fact the molecule and its reflection. It is well known that 2D projections cannot be used to distinguish between a molecule and its reflection, so the two versions are indeed valid molecules. However, it is desirable for algorithms to quotient out this symmetry (“choose one of the two versions arbitrarily”). In practice, algorithms are often initialized using some low-resolution model that effectively chooses the version they would use. In this case, the artifact is a result of the many approximate symmetries in this synthetic model at low resolution. We use this example to demonstrate a simple method for resolving such artifacts: we reinitialized the hyper-molecule to a representative state, and reran the algorithm, allowing most of the particle images to be aligned with one version of the molecule.
Figure 5.
Running the heterogeneity algorithm reveals a technical artifact: the algorithm recovered the pretzel and its reflection as two heterogeneity state (green and red, superimposed).
At this point we set up the model depicted in Figure 2, with a rigid object supported in the yellow ball, and two heterogeneous regions, each supported in one of the other balls. In many cases, the molecules studied have a known form of symmetry. In this example, we model a molecule with symmetry. The two heterogeneous regions are identical components but each of them can appear in a different state in each particle image. These two components can be modeled independently, but since we know that these two components are identical “hyper-molecules” at different states, the two models share coefficients (shifted and rotated with respect to one another).
In implementations of MCMC algorithms and some optimization algorithms it is common to implement procedures that can be broadly interpreted as occasional increase of the “temperature.” Such procedures improve the mixing properties of the algorithm and mitigate the effects of deep local minima. In the current implementation, we restart the algorithm at a lower resolution a few times to achieve an analogous effect; unlike a traditional change of temperature, the change in resolution also accelerates the iterations, because the numerical implementation of projections is much faster at lower resolution.
The processing requires 14 days, using a server equipped with a E5-2680 CPU and one NVIDIA Tesla P100 GPU with 16 GB of RAM (the GPU was used for most of the numerical computation). Most of the time was spent on the preliminary assignment of viewing directions, shifts and amplitudes, before the heterogeneity analysis was activated, due to limitations in this version. The viewing directions, shifts and amplitude continue to be refined together with the state variables during the heterogeneity analysis.
The results presented in Figure 3(bottom) illustrate qualitatively the recovery of the different conformations of the synthetic molecule. In addition, we present in Figure 6 the distribution of errors in assignment of viewing directions, and in Figure 7 the distribution of the assignment of the state variables. Some of the particle images are assigned a wrong viewing direction (and subsequently a wrong state variable) – this is attributed to the noise and approximate symmetries in the model, as well as inefficiencies in the current implementation.
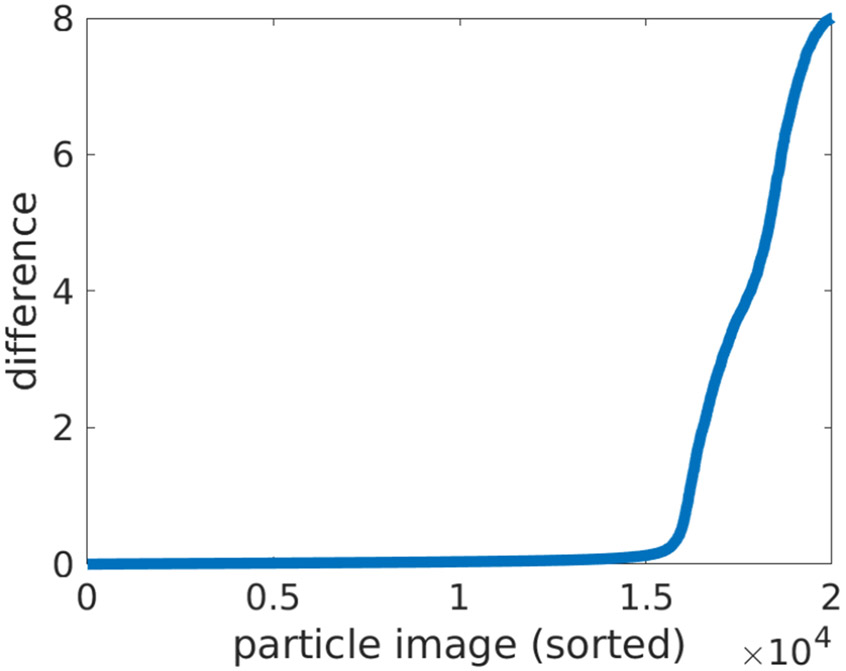
Figure 6.
The errors in viewing directions, sorted by error size. The error is defined as the Frobenius norm of the difference between the true rotation matrix and the recovered rotation matrix. Due to the symmetry, there are two valid “true” rotation matrices, therefore the distance is measured to the nearest matrix. About a quarter of the particle images are poorly aligned (partly due to noise and approximate symmetries and partly due to technical limitations of the current prototype).
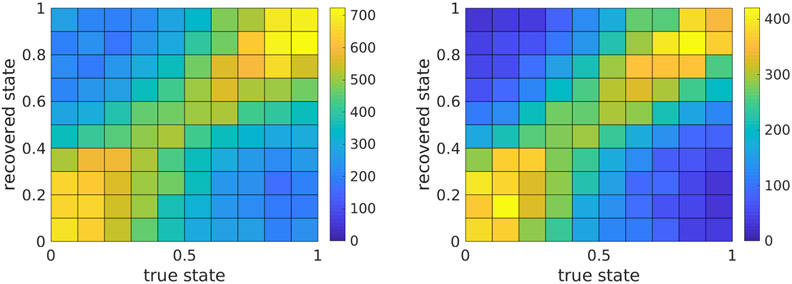
Figure 7.
The distribution of recovered state parameters vs. true state, aggregated over both arms (left). Since some of the particle images are not aligned properly, their state variables are meaningless. Therefore, we also present the distribution of recovered states for the 10,000 particle images with the smallest alignment error (right). The alignment quality was determined using the true orientations. Additional experiments with lower noise and otherwise similar conditions yield a sharper distribution (not presented here).
The current Matlab implementation was developed as a proof of concept, but it is very inefficient and thus difficult to scale to a larger number of images or high resolution. A new implementation in Python is currently in development with the goal of making it more accessible and scalable. We plan to release the future version of the new implementation when the core functionality and simple user-friendly models are ready.
6. Discussion and Future Work
The main goal of this paper is to introduce the idea of hyper-molecules as high-dimensional representations of 3-D molecules at all their conformations; this idea is applicable to other inverse problem such as CT. In addition to the generalization of 3-D molecules to hyper-molecules, we generalize the Bayesian formulation of cryo-EM to a Bayesian formulation of continuous heterogeneity in cryo-EM. Compared to existing work on representing molecules in a small number of discrete conformations, hyper-molecules provide a way of describing a continuum of conformations and the relations between states.
These higher dimensional objects can be represented as generic high-dimensional functions, but we discuss statistical and computational motivations to introduce additional models of hyper-molecules, that describe more specific objects, when prior knowledge is available. We also discuss an MCMC framework which overcomes some of the technical computational difficulties in each iteration of current algorithms in the more general settings that we propose, and we note additional benefits of this framework in characterizing the uncertainty in solutions. Furthermore, we note that the MCMC framework provides a natural connection to atomic models and other experimental modalities, demonstrated for example in [60], which uses a density map produced from a cryo-EM experiment together with physical models and other modalities.
Ultimately, the goal of this line of work is to provide a highly customizable framework for encoding prior knowledge about complex molecules and to find a practical trade-off between the bias that can be introduced by assumptions and the realistic constraints on the amount of data that can be collected. We envision this framework as a combination of imaging modules for modeling hyper-molecules adapted to fast computation of projection images and to computing gradients with respect to variables such as the viewing direction and model coefficients. Such modules will be used in a framework inspired by TensorFlow [61], PyTorch [62] (both designed primarily for deep learning) and Edward [63, 64], which allow to construct modules analogous to the black-box modules discussed in this paper, with more focus on imaging as in ODL [65]. Ideally, a wide array of general purpose tools and algorithms constructed for optimization, Bayesian inference, deep learning and imaging could be used together with this framework. However, the large scale of the cryo-EM problem and various properties of the problem require a more specialized framework and flexibility in solver strategies; for example, the memory management in software designed for deep learning is often optimized for small batches, whereas in some implementations of imaging algorithms there are computational advantages in working with very large batches. Another example is the update of in-plane shift variables, which can be performed without recomputing the entire image. Among other things, a speedup may be obtained by simultaneously computing cross-correlations for multiple in-plane rotations using the recently proposed method of [66]. We demonstrated some of the ideas in this paper in a prototype implementation; we are currently building the next prototype, which will be more customizable and scalable.
Our reference to tools such as TensorFlow, PyTorch and Edward demonstrates that the lines between optimization, stochastic optimization, MCMC and other algorithms are not entirely rigid, in the sense that modules used in one framework can be used in some other frameworks. We expect to experiment with other algorithms for initialization of MCMC and approximation of steps, and to examine additional Bayesian inference algorithms. Indeed, we have already experimented with expectation-maximization algorithms to initialize crude viewing directions in cryo-EM data and with SGD hybrids for approximating MCMC steps.
In the following sections we briefly comment on some additional aspects of the problem.
6.1. The Homogeneous Case, Discrete Heterogeneity, and Continuous Heterogeneity
In many cases, molecules appear mainly in a discrete set of conformations that are very similar to one another. While we mainly discuss continuous heterogeneity in the paper, the framework proposed here applies to the discrete case (or mixtures of discrete and continuous heterogeneity in different regions) with few changes (for example, the basis functions used to capture the variability as a function of the heterogeneity parameter can be replaced by the Haar basis). Hyper-molecules, composite hyper-molecules and the algorithms discussed here are advantageous in the discrete case as well: they allow to use the similarity between different conformations, and they allow to decompose the heterogeneity to local heterogeneity in different regions.
More generally, we hope that a generic Bayesian framework could also be used to study more elaborate models for imaging and experiment latent variables even in the homogeneous case.
6.2. Ambiguity
We note that even in the classic cryo-EM problem, certain ambiguities emerge in the macro-molecules that are recovered: any result has “equivalent” results that are identical up to global rotation, shifts and reflection. Naturally, hyper-molecules have similar ambiguities. Since hyper-objects generalize the spatial coordinates and in many ways treat the state parameters in the same way as they treat the spatial coordinate, one may expect a generalized form of ambiguity to appear. Indeed, there is ambiguity in how the molecules in different states are aligned with respect to each other and ambiguity in the parameterization of the state space. These ambiguities are reduced by regularization or priors, or when the model contains rigid components that align other components.
One such effect can be observed in the cat example in Figure 1, where the recovered cats are aligned slightly differently with respect to each other compared to the original cats (the change in alignment is continuous, so the “movie of cat” is still continuous). Of course, our original alignment was arbitrary, so the algorithm’s choice is no better or worse than ours, but it is better suited to the limited degree polynomials we allowed the algorithm to use to represent these recovered cats.
6.3. Additional Practical Considerations
The discussion of priors and models in this paper is partly abstract and the priors and models implemented in our examples are relatively simple. Indeed, there is room for extensive future work on improved priors and models that can be efficiently implemented within this framework and on automation of tests.
We note that we do not advocate the use of “strong” priors indiscriminately because they can bias the results. We believe that the most useful use cases in the near future would involve a gradual process of testing alternative priors, starting with the simplest “loose” priors, and verifying the stability of solutions with respect to priors and parameters (even if at a lower resolution). Once patterns are identified reliably, they can be encoded into more elaborate models and priors (e.g. “there is a rigid component in the middle, and with two identifiable regions where something is moving”) and then to finer models (e.g. specific space of deformations in the flexible regions) and finer models (e.g. atomic structures). These models formulate explicit and implicit models used in other tools. For example, multi-body models [41] are a subset of the models proposed in this paper. The specialized implementation of this model of multiple rigid components in RELION has been successful but does not fully resolve the challenge of continuous heterogeneity.
The Bayesian approach and the sampling of solutions from the posterior in MCMC algorithms provide means for evaluating uncertainty in solutions given a model and a prior. The ability to choose different models and priors can be used to identify modelling artifacts which could either bias the posterior or slow the mixing of states. One of the tools for studying possible artifacts is the use of extra degrees of freedom, as demonstrated in our experiment where we modeled the rigid molecule as a heterogeneous molecule and discovered that our intermediate solution was a superposition of the molecule and its reflection.
We reiterate that the MCMC formulation is not a magic solution that resolves all the computational problems. Furthermore, our current implementation is limited and slow. Specialized algorithms for particular types of heterogeneity may be faster than than a general purpose implementation of MCMC. Where there exist efficient methods like multi-body [41] models or study of covariances (e.g. [46, 67]), they be used in the construction of models, initialization of the MCMC algorithm, or can be reformulated as hyper-molecules. MCMC enjoys theoretical properties and offers tools for quantifying the uncertainty in solutions, and a rigorous framework for combining different models, priors and update strategies. We believe that a flexible implementation of an MCMC (or variational) framework which offers an accessible selection of priors, models and update strategies, and which incorporates successful ideas implemented in other tools, will be a tool in careful studies of molecular structures which consider different hypotheses. Further work on models and automated hypothesis testing would simplify the process and make it more robust and reproducible.
7. Conclusions
A mathematical formulation and a Bayesian formulation has been presented for the modeling of continuously heterogeneous molecular conformations. This formulation “hyper-molecules” and its generalizations allow to model generic heterogeneous molecules or to encode structural constraints and priors where these are available or required for practical reasons.
In addition, we proposed an approach based on MCMC for the recovery of hyper-molecules from cryo-EM data. This approach addresses some of the challenges associated with generalizing existing popular algorithms to this formulation of the cryo-EM problem. In particular, it bypasses the estimation of the conditional distribution of variables such as the viewing direction of each particle image at each iteration of expectation-maximization, which becomes infeasible if additional state variables are introduced in the case of continuous heterogeneity. This approach also offers a natural way to incorporate elaborate black-box models that researchers can customize for their needs and a tool for studying the uncertainty in solutions.
The ideas presented in this paper have been demonstrated in a preliminary, prototype implementation applied to synthetic data. Work on experimental datasets will be discussed separately. More scalable implementations are being constructed for more generic models, larger datasets, and more efficient computation.
Table 1.
Table of Notation
| three- or higher-dimensional function | |
| the Fourier transform of in spatial coordinates | |
| the vector rotated by | |
| the function rotated by , so that | |
| bold fonts are used to emphasize that a certain variable may be a vector, not just a scalar, when this is not obvious from the context. |
Acknowledgments
The authors would like to thank Fred Sigworth for his help, and the anonymous referees for their valuable comments.
A. Singer was partially supported by NIGMS Award Number R01GM090200, AFOSR FA955017-1-0291, Simons Investigator Award, the Moore Foundation Data-Driven Discovery Investigator Award, and NSF BIGDATA Award IIS-1837992. These awards also partially supported R. R. Lederman at Princeton University. The Flatiron Institute is a division of the Simons Foundation.
References
- [1].Kühlbrandt W. The resolution revolution. Science, 343(6178):1443–1444, 2014. [DOI] [PubMed] [Google Scholar]
- [2].Smith Martin TJ and Rubinstein John L. Beyond blob-ology. Science, 345(6197):617–619, 2014. [DOI] [PubMed] [Google Scholar]
- [3].Liao Maofu, Cao Erhu, Julius David, and Cheng Yifan. Structure of the TRPV1 ion channel determined by electron cryo-microscopy. Nature, 504(7478):107–112, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Amunts Alexey, Brown Alan, Bai Xiao-Chen, Llácer Jose L., Hussain Tanweer, Emsley Paul, Long Fei, Murshudov Garib, Scheres Sjors H. W., and Ramakrishnan V. Structure of the yeast mitochondrial large ribosomal subunit. Science, 343(6178):1485–1489, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Bartesaghi Alberto, Merk Alan, Banerjee Soojay, Matthies Doreen, Wu Xiongwu, Milne Jacqueline LS, and Subramaniam Sriram. 2.2 Å resolution cryo-EM structure of -galactosidase in complex with a cell-permeant inhibitor. Science, 348(6239):1147–1151, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Scheres S. RELION: Implementation of a Bayesian approach to cryo-EM structure determination. J. Struct. Biol, 180(3):519–530, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Punjani Ali, Rubinstein John L, Fleet David J, and Brubaker Marcus A. cryoSPARC: algorithms for rapid unsupervised cryo-EM structure determination. Nat. Methods, 14(3):290–296, 2017. [DOI] [PubMed] [Google Scholar]
- [8].Tang Guang, Peng Liwei, Baldwin Philip R, Mann Deepinder S, Jiang Wen, Rees Ian, and Ludtke Steven J. EMAN2: an extensible image processing suite for electron microscopy. J. Struct. Biol, 157(1):38–46, 2007. [DOI] [PubMed] [Google Scholar]
- [9].van Heel Marin, Portugal Rodrigo, Rohou A, Linnemayr C, Bebeacua C, Schmidt R, Grant T, and Schatz M. Four-dimensional cryo-electron microscopy at quasi-atomic resolution: IMAGIC 4D. International Tables for Crystallography, pages 624–628, 2006. [Google Scholar]
- [10].De la Rosa-Trevín JM, Otón J, Marabini R, Zaldivar A, Vargas J, Carazo JM, and Sorzano COS. Xmipp 3.0: an improved software suite for image processing in electron microscopy. J. Struct. Biol, 184(2):321–328, 2013. [DOI] [PubMed] [Google Scholar]
- [11].Grigorieff Nikolaus. FREALIGN: High-resolution refinement of single particle structures. J. Struct. Biol, 157(1):117 – 125, 2007. [DOI] [PubMed] [Google Scholar]
- [12].Liu Daifei, Liu Xueqi, Shang Zhiguo, and Sindelar Charles V. Structural basis of cooperativity in kinesin revealed by 3D reconstruction of a two-head-bound state on microtubules. eLife, 6:e24490, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Dolino Drew M, Rezaei Adariani Soheila, Shaikh Sana A, Jayaraman Vasanthi, and Sanabria Hugo. Conformational selection and submillisecond dynamics of the ligand-binding domain of the n-methyl-d-aspartate receptor. Journal of Biological Chemistry, 291(31):16175–16185, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Nogales Eva. The development of cryo-EM into a mainstream structural biology technique. Nat. Methods, 13(1):24–27, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Glaeser Robert M. How good can cryo-EM become? Nat. Methods, 13(1):28–32, 2016. [DOI] [PubMed] [Google Scholar]
- [16].Scheres Sjors HW. A Bayesian view on cryo-EM structure determination. J. Mol. Biol, 415(2):406–418, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Sorzano COS, Jiménez A, Mota J, Vilas JL, Maluenda D, Martínez M, Ramírez-Aportela E, Majtner T, Segura J, Sánchez-García R, et al. Survey of the analysis of continuous conformational variability of biological macromolecules by electron microscopy. Acta Crystallographica Section F: Structural Biology Communications, 75(1):19–32, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Low Daniel A, Nystrom Michelle, Kalinin Eugene, Parikh Parag, Dempsey James F, Bradley Jeffrey D, Mutic Sasa, Wahab Sasha H, Islam Tareque, Christensen Gary, et al. A method for the reconstruction of four-dimensional synchronized CT scans acquired during free breathing. Medical Physics, 30(6):1254–1263, 2003. [DOI] [PubMed] [Google Scholar]
- [19].Kimanius Dari, Forsberg Björn O, Scheres Sjors HW, and Lindahl Erik. Accelerated cryo-EM structure determination with parallelisation using GPUs in RELION-2. eLife, 5, nov 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Zivanov Jasenko, Nakane Takanori, Forsberg Björn O, Kimanius Dari, Hagen Wim JH, Lindahl Erik, and Scheres Sjors HW. New tools for automated high-resolution cryo-EM structure determination in RELION-3. eLife, 7:e42166, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].Lederman Roy R.. Numerical algorithms for the computation of generalized prolate spheroidal functions. arXiv preprint arXiv:1710.02874, 2017. [Google Scholar]
- [22].Lederman Roy R. and Singer Amit. Continuously heterogeneous hyper-objects in cryo-EM and 3-D movies of many temporal dimensions. arXiv preprint arXiv:1704.02899, 2017. [Google Scholar]
- [23].Kawabata Takeshi. Multiple subunit fitting into a low-resolution density map of a macromolecular complex using a Gaussian mixture model. Biophysical Journal, 95(10):4643–4658, 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24].Lederman Roy R and Singer Amit. A representation theory perspective on simultaneous alignment and classification. Applied and Computational Harmonic Analysis, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Frank J. Three-dimensional electron microscopy of macromolecular assemblies. Academic Press, 2006. [Google Scholar]
- [26].Sigworth Fred J.. Principles of cryo-EM single-particle image processing. Microscopy, 65(1):57–67, December 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27].Cheng Yifan, Grigorieff Nikolaus, Penczek Pawel A., and Walz Thomas. A primer to single-particle cryo-electron microscopy. Cell, 161(3):438–449, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28].Milne Jacqueline LS, Borgnia Mario J, Bartesaghi Alberto, Tran Erin EH, Earl Lesley A, Schauder David M, Lengyel Jeffrey, Pierson Jason, Patwardhan Ardan, and Subramaniam Sriram. Cryo-electron microscopy–A primer for the non-microscopist. FEBS Journal, 280(1):28–45, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [29].Vinothkumar Kutti R and Henderson Richard. Single particle electron cryomicroscopy: Trends, issues and future perspective. Q. Rev. Biophys, 49, 2016. [DOI] [PubMed] [Google Scholar]
- [30].Sigworth Fred J.. A maximum-likelihood approach to single-particle image refinement. J. Struct. Biol, 122(3):328–339, 1998. [DOI] [PubMed] [Google Scholar]
- [31].Sigworth Fred J, Doerschuk Peter C, Carazo Jose-Maria, and Scheres Sjors HW. Chapter ten—an introduction to maximum-likelihood methods in cryo-EM. Methods Enzymol., 482:263–294, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32].Punjani Ali, Brubaker Marcus, and Fleet David. Building proteins in a day: Efficient 3D molecular structure estimation with electron cryomicroscopy. IEEE Trans. Pattern Anal. Mach. Intell, 2016. [DOI] [PubMed] [Google Scholar]
- [33].Joubert Paul and Habeck Michael. Bayesian inference of initial models in cryo-electron microscopy using pseudo-atoms. Biophysical Journal, 108(5):1165–1175, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34].Shatsky M, Hall R, Nogales E, Malik J, and Brenner S. Automated multi-model reconstruction from single-particle electron microscopy data. J. Struct. Biol, 170(1):98–108, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [35].Singer Amit, Coifman Ronald R, Sigworth Fred J, Chester David W, and Shkolnisky Yoel. Detecting consistent common lines in cryo-EM by voting. J. Struct. Biol, 169(3):312–322, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [36].Shkolnisky Yoel and Singer Amit. Viewing direction estimation in cryo-EM using synchronization. SIAM J. Imaging Sci, 5(3):1088–1110, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [37].Bandeira Afonso S, Chen Yutong, and Singer Amit. Non-unique games over compact groups and orientation estimation in cryo-EM. arXiv preprint arXiv:1505.03840, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [38].Dashti Ali, Schwander Peter, Langlois Robert, Fung Russell, Li Wen, Hosseinizadeh Ahmad, Liao Hstau Y., Pallesen Jesper, Sharma Gyanesh, Stupina Vera A., Simon Anne E., Dinman Jonathan D., Frank Joachim, and Ourmazd Abbas. Trajectories of the ribosome as a Brownian nanomachine. Proc. Natl. Acad. Sci. U.S.A, 111(49):17492–17497, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [39].Schwander P, Fung R, and Ourmazd A. Conformations of macromolecules and their complexes from heterogeneous datasets. Phil. Trans. R. Soc. B, 369(1647):20130567, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [40].Frank Joachim and Ourmazd Abbas. Continuous changes in structure mapped by manifold embedding of single-particle data in cryo-EM. Methods, 100:61–67, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [41].Nakane Takanori, Kimanius Dari, Lindahl Erik, and Scheres Sjors HW. Characterisation of molecular motions in cryo-EM single-particle data by multi-body refinement in RELION. eLife, 7:e36861, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [42].Wong Wilson, Bai Xiao-Chen, Brown Alan, Fernandez Israel S, Hanssen Eric, Condron Melanie, Tan Yan Hong, Baum Jake, and Scheres Sjors HW. Cryo-EM structure of the Plasmodium falciparum 80S ribosome bound to the anti-protozoan drug emetine. eLife, 3:e03080, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [43].Zhou Qiang, Huang Xuan, Sun Shan, Li Xueming, Wang Hong-Wei, and Sui Sen-Fang. Cryo-EM structure of SNAP-SNARE assembly in 20S particle. Cell Research, 25(5):551, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [44].Bai Xiao-Chen, Rajendra Eeson, Yang Guanghui, Shi Yigong, and Scheres Sjors HW. Sampling the conformational space of the catalytic subunit of human -secretase. eLife, 4:e11182, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [45].Ilca Serban L, Kotecha Abhay, Sun Xiaoyu, Poranen Minna M, Stuart David I, and Huiskonen Juha T. Localized reconstruction of subunits from electron cryomicroscopy images of macromolecular complexes. Nat. Commun, 6:8843, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [46].Andén Joakim and Singer Amit. Structural Variability from Noisy Tomographic Projections. SIAM J. Imaging Sci, 11(2):1441–1492, jan 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [47].Tama Florence, Wriggers Willy, and Brooks Charles L III. Exploring global distortions of biological macromolecules and assemblies from low-resolution structural information and elastic network theory. J. Mol. Biol, 321(2):297–305, 2002. [DOI] [PubMed] [Google Scholar]
- [48].Jin Qiyu, Sorzano Carlos Oscar S., de la Rosa-Trevín José Miguel, Bilbao-Castro José Román, Núñez-Ramírez Rafael, Llorca Oscar, Tama Florence, and Jonić Slavica. Iterative elastic 3D-to-2D alignment method using normal modes for studying structural dynamics of large macromolecular complexes. Structure, 22(3):496–506, 2014. [DOI] [PubMed] [Google Scholar]
- [49].Schilbach Sandra, Hantsche Merle, Tegunov Dmitry, Dienemann Christian, Wigge Cristoph, Urlaub Henning, and Cramer Patrick. Structures of transcription pre-initiation complex with tfiih and mediator. Nature, 551(7679):204, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [50].Brooks Steve, Gelman Andrew, Jones Galin, and Meng Xiao-Li. Handbook of Markov chain Monte Carlo. CRC press, 2011. [Google Scholar]
- [51].Welling Max and Teh Yee W.. Bayesian learning via stochastic gradient Langevin dynamics. In Proc. ICML, pages 681–688, 2011. [Google Scholar]
- [52].Liu Weiping and Frank Joachim. Estimation of variance distribution in three-dimensional reconstruction. I. Theory. J. Opt. Soc. Am. A, 12(12):2615–2627, Dec 1995. [DOI] [PubMed] [Google Scholar]
- [53].Penczek PA. Variance in three-dimensional reconstructions from projections. In Proc. ISBI, pages 749–752, 2002. [Google Scholar]
- [54].Penczek Pawel A., Yang Chao, Frank Joachim, and Spahn Christian M.T.. Estimation of variance in single-particle reconstruction using the bootstrap technique. J. Struct. Biol, 154(2):168–183, 2006. [DOI] [PubMed] [Google Scholar]
- [55].Liao H and Frank J. Classification by bootstrapping in single particle methods. In Proc. ISBI, pages 169–172. IEEE, April 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [56].Penczek P, Kimmel M, and Spahn C. Identifying conformational states of macromolecules by eigen-analysis of resampled cryo-EM images. Structure, 19(11):1582–1590, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [57].Andén J, Katsevich E, and Singer A. Covariance estimation using conjugate gradient for 3D classification in cryo-EM. In Proc. ISBI, pages 200–204, April 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [58].Barnett Alex, Greengard Leslie, Pataki Andras, and Spivak Marina. Rapid solution of the cryo-EM reconstruction problem by frequency marching. SIAM J. Imaging Sci, 10(3):1170–1195, 2017. [Google Scholar]
- [59].Sorzano COS, Vargas J, de la Rosa-Trevín JM, Jiménez A, Maluenda D, Melero R, Martínez M, Ramírez-Aportela E, Conesa P, Vilas JL, et al. A new algorithm for high-resolution reconstruction of single particles by electron microscopy. Journal of structural biology, 204(2):329–337, 2018. [DOI] [PubMed] [Google Scholar]
- [60].Habeck Michael. Bayesian modeling of biomolecular assemblies with cryo-EM maps. Frontiers in Molecular Biosciences, 4:15, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [61].Abadi Martín, Agarwal Ashish, Barham Paul, Brevdo Eugene, Chen Zhifeng, Citro Craig, Corrado Greg S., Davis Andy, Dean Jeffrey, Devin Matthieu, Ghemawat Sanjay, Goodfellow Ian, Harp Andrew, Irving Geoffrey, Isard Michael, Jia Yangqing, Jozefowicz Rafal, Kaiser Lukasz, Kudlur Manjunath, Levenberg Josh, Mané Dandelion, Monga Rajat, Moore Sherry, Murray Derek, Olah Chris, Schuster Mike, Shlens Jonathon, Steiner Benoit, Sutskever Ilya, Talwar Kunal, Tucker Paul, Vanhoucke Vincent, Vasudevan Vijay, Viégas Fernanda, Vinyals Oriol, Warden Pete, Wattenberg Martin, Wicke Martin, Yu Yuan, and Zheng Xiaoqiang. TensorFlow: Large-scale machine learning on heterogeneous systems, 2015. Software available from tensorflow.org. [Google Scholar]
- [62].Paszke Adam, Gross Sam, Chintala Soumith, Chanan Gregory, Yang Edward, DeVito Zachary, Lin Zeming, Desmaison Alban, Antiga Luca, and Lerer Adam. Automatic differentiation in PyTorch. 2017. [Google Scholar]
- [63].Tran Dustin, Kucukelbir Alp, Dieng Adji B., Rudolph Maja, Liang Dawen, and Blei David M.. Edward: A library for probabilistic modeling, inference, and criticism. arXiv preprint arXiv:1610.09787, 2016. [Google Scholar]
- [64].Tran Dustin, Hoffman Matthew D., Saurous Rif A., Brevdo Eugene, Murphy Kevin, and Blei David M.. Deep probabilistic programming. In Proc. ICLR, 2017. [Google Scholar]
- [65].Adler Jonas, Kohr Holger, and Öktem Ozan. ODL—a Python framework for rapid prototyping in inverse problems. Technical report, Royal Institute of Technology, 2017. [Google Scholar]
- [66].Rangan Aaditya, Spivak Marina, Andén Joakim, and Barnett Alex. Factorization of the translation kernel for fast rigid image alignment. Inverse Problems, 2019. [Google Scholar]
- [67].Moscovich Amit, Halevi Amit, Andén Joakim, and Singer Amit. Cryo-EM reconstruction of continuous heterogeneity by laplacian spectral volumes. Inverse Problems, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]