Electromagnetic fields effects on microbial growth in cocoa fermentation: A controlled experimental approach using established growth models

Abstract

Understanding the effects of electromagnetic fields is crucial in the fermentation of cocoa beans, since through precise control of fermentation conditions the sensory and nutritional properties of cocoa beans could be improved. This study aimed to evaluate the effect of oscillating magnetic fields (OMF) on the kinetic growth of the core microbial communities of the Collections Castro Naranjal (CCN 51) cocoa bean. The data was obtained by three different models: Gompertz, Baranyi, and Logistic. The cocoa beans were subjected to different OMF strengths ranging from 0 mT to 80 mT for 1 h using the Helmholtz coil electromagnetic device. The viable microbial populations of lactic acid bacteria (LAB), acetic acid bacteria (AAB), and yeast (Y) were quantified using the colony-forming unit (CFU) counting method. The logistic model appropriately described the growth of LAB and Y under magnetic field exposure. Whereas the Baranyi model was suitable for describing AAB growth. The microbial populations in cocoa beans exposed to magnetic fields showed lower (maximum specific growth rate (μmax), values than untreated controls, with AAB exhibiting the highest average growth rate value at 5 mT and Y having the lowest average maximum growth rate value at 80 mT. The lower maximum specific growth rates and longer lag phases when exposed to magnetic fields compared to controls demonstrate the influence of magnetic fields on microbial growth kinetics.

1. Introduction

Kinetic growth studies of microorganisms are crucial for understanding and optimizing fermentations and other biological processes. These studies provide insights into growth patterns, metabolic activities, population dynamics, nutrient utilization, and product formation [[1], [2], [3], [4]]. They are especially important for applications in the fermentation process, i.e., bioremediation [1], biodegradation of pollutants [2,3], and biogas production [4].

Kinetic information on specific growth rates, lag phases, biomass yields, and substrate consumption rates under different environmental conditions helps construct mathematical models that optimize and predict bioprocess outcomes [5]. In the food industry, selection of appropriate models depends on the characteristics of the microorganism and the food matrix, and their accuracy should be validated with experimental data [6,7]. Comparative analysis of different mathematical models has shown that specific models are suitable for different types of microorganisms and food matrices [6,8].

Logistic, Baranyi, and Gompertz models are widely used in the analysis of microbial kinetics. The logistic model characterizes the growth of the microbial population considering the initial density, time, growth rate and final density. In contrast, the Baranyi model takes dynamic conditions into account and incorporates lag, exponential, and stationary phases of microbial growth [9,10]. The Gompertz model is suitable for microorganisms with longer lag phases and slower growth rates, since it assumes an exponential decline in growth rate over time [9]. Recent investigations have proposed modifications to these models and have carried out significant tests on their parameters to improve their understanding and application in studies of microbial growth [11].

Cocoa fermentation is a complex process driven by the metabolic activity of diverse microorganisms, including yeasts, lactic acid bacteria, and acetic acid bacteria. These microorganisms break down sugars and other compounds in the cocoa pulp, resulting in the formation of flavor and aroma compounds that significantly influence the quality of the final cocoa product [[12], [13], [14], [15]]. However, the growth kinetics of cocoa bean fermentation microorganisms do not conform to conventional models, mainly due to the need for improved process control and the complexity of the microbial communities involved [16,17].

In cocoa fermentation systems, the microbial community may exhibit dominance of a limited number of several major taxa within a complex network. Fitting kinetic models in fermentation involves determining an optimal time frame and sampling frequency to consider each group of microorganisms as an individual population [17]. Various strategies have been employed, including models incorporating substrate utilization, microbial growth, metabolite production, and transport processes [16]. However, the choice of the model also depends on the specific fermentation system and the microorganisms being studied. These approaches have proven effective in fitting kinetic models and advancing fermentation research.

Recent studies have explored various techniques to speed up fermentation, improve the quality and intensity of flavor, and aroma of cocoa beans. These techniques such as: pulp preconditioning [18], aeration [19], started culture [20], acetic and lactic reagents [21], enzymes [22], ohmic heating [23] and extremely low frequency electromagnetic fields (EMF) [24] have improved the overall quality of the beans, offering new development opportunities in the chocolate industry.

The potential influence of extremely low-frequency electromagnetic fields (EMF) on microbial fermentation processes is remarkable. The findings indicate that electromagnetic fields can affect microbial growth and metabolic activity, which could affect the production of fermentation products [25,26]. Understanding the effects of electromagnetic fields is particularly crucial in cocoa bean fermentation, as it improves the sensory and nutritional properties of cocoa beans by precisely controlling fermentation conditions [24,27]. This knowledge also presents opportunities to optimize the production of flavor precursors, antioxidants, and other bioactive compounds from cocoa beans.

This study aims to provide empirical evidence on the influence of electromagnetic fields on microbial growth through controlled investigations using established models. The research seeks to advance scientific understanding of the relationship between electromagnetic fields and microbial activity in cocoa bean fermentation context. The findings will offer insights to optimize the cocoa bean fermentation process by implementing strategies based on electromagnetic fields to improve process conditions. Achieving these aims will ultimately enhance cocoa bean quality, flavor development and product characteristics, while also contributing to knowledge advancement in this area.

2. Materials and methods

2.1. The cocoa beans processing

The methodology used in this study involved selecting and preparing cocoa pods, followed by two different fermentation conditions: controlled conditions with specific control of temperature and humidity and uncontrolled conditions without environmental control. Controlled conditions included sanitization, inoculation with a starter culture, and monitoring of fermentation parameters, while uncontrolled conditions omitted these steps. These experimental setups allowed us to investigate and compare the effects of controlled and uncontrolled fermentation conditions on growth kinetics.

2.1.1. Selection and preparation of cocoa pods

The CCN 51 variety cocoa pods were carefully chosen based on consistent coloration, level of maturity, and the absence of pest-related damage or defects. The selected pods were packed in polyethylene bags and refrigerated at temperatures between 7 and 12 °C. The maximum storage time before the experiment was limited to 32 h [24].

2.1.2. Controlled fermentation conditions (CFC)

Under controlled fermentation conditions, each cocoa pod was sanitized by immersing it in a 200 ppm sodium hypochlorite solution for 5 min. After this, the cocoa beans were aseptically extracted and placed in plastic containers with lateral and ventral openings, in an amount of 3 kg per experimental unit. The beans were inoculated with a previously obtained natural starter culture (section 2.2). The containers were placed in a fermentation chamber with controlled temperature (37 °C ± 0.5) and humidity (85 % ± 0.8) for 84 h, with periodic shifts every 24 h. Experimental conditions were regularly monitored following established protocols [24,28].

2.1.3. Uncontrolled fermentation conditions (UFC)

Cocoa beans were obtained from the pods without any prior chemical treatment for uncontrolled fermentation conditions. Similar to the controlled conditions, the beans were placed in plastic containers at a rate of 3 kg per unit. No inoculation with a starter culture was performed. The containers were placed in an isolated, cool place, free of pests and insects, but without environmental control [24].

2.2. Preparation of natural starter culture

To acquire a natural inoculum of CCN 51 cocoa pulp, the beans were initially manually de-pulped, resulting in a semi-liquid mucilage subjected to controlled fermentation for 8 h at 37 °C [28]. This suspension was subjected to different electromagnetic field density treatments for 1 h, followed by inoculation via spraying, according to the experimental design detailed in section 2.5.

2.3. Electromagnetic field (EMF) system

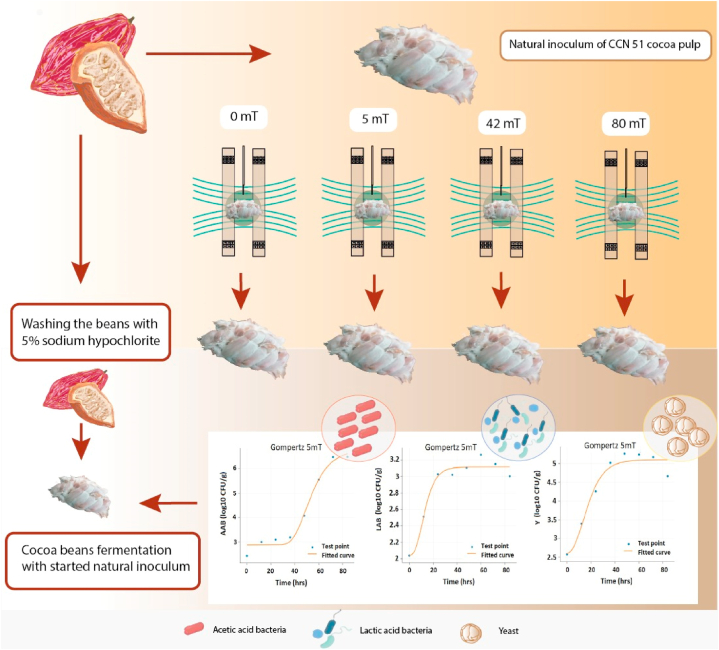
Helmholtz coils were employed to produce an electromagnetic field according to the method described by Hu [29]. The system comprised two circular coils with a radius of 0.205 m, connected in series and powered by a variable voltage source operating at 60 Hz, generating a magnetic field density ranging from 1 to 120 mT. During the magnetic field treatment, the samples were positioned between the coils. A Hall effect Tesla meter (SS49E) measured the magnetic fields, regulated through a specialized electronic board (Arduino nano) to obtain a digital signal transmitted to a computer [30]. The v9.0 interface of the Laboratory Virtual Instrument Engineering Workbench (LabVIEW) software was used for data output Software, and the Comsol Multiphysics Software v12 to model the magnetic field lines between the coils (see Fig. 1).

Fig. 1.

Influence of oscillating magnetic fields (OMF) by Helmholtz coil electromagnetic device, on the microbial growth kinetics of cocoa beans CCN 51. OMF intensities ranging from 0 mT to 80 mT for 1 h. Viable populations of lactic acid bacteria (LAB), acetic acid bacteria (AAB), and yeasts (Y) determined quantitatively as a function of time.

2.4. Electromagnetic treatment

Each natural inoculum was placed at the center of the Helmholtz coils and exposed to varying intensities of OMF, as per the experimental design (section 2.5). The OMF densities used in the experiment were 0 mT, 5 mT, 42 mT, and 80 mT [24] (Table 1). In the fermentation conditions, two types of exposure were distinguished and carried out according to the experimental design: exposure to the beans (EB) and exposure to the culture (EC). The samples were placed as close as possible to the center of both rings while maintaining an appropriate distance between them. All treatments were monitored and randomized.

Table 1.

Factors and levels of experimental design.

Type	Factor Name	Units	Type	Levels	L [1]	L [2]	L [3]	L [4]
A [Categoric]	OMF density	mT	Ordinal	4	0	5	42	80
B [Categoric]	Exposure time	min	Ordinal	2	30	60	–	–
C [Categoric]	Exposure type	–	Nominal	2	EB	EC	–	–
D [Categoric]	Operating conditions	–	Nominal	2	CFC	UFC	–	–

2.5. Evaluation procedure

2.5.1. Microbial concentrations

The viable bacteria and yeast in cocoa bean samples and their growth were monitored every 12 h using the colony-forming unit (CFU) method [31]. The samples of fermented cocoa beans were diluted in peptone water, homogenized, and then subjected to serial dilution, aiming for a maximum of 150–200 colonies per plate. Subsequently, aliquots of the diluted samples were plated onto selective agar media, including malt extract agar (MEA, Oxoid) for yeast, De Man, Rogosa, and Sharpe (MRS) agar for lactic acid bacteria and mannitol yeast extract agar (MYP, Oxoid) for acetic acid bacteria [19,28]. The plates were incubated at optimal temperatures for yeast growth (24 °C) and lactic and acetic acid bacteria growth (30 °C) [32]. A digital colony counter (Isolab brand) was used to determine the number of colonies on each plate. The N values for each sample were calculated using equation (1) [31].

$$N=\mathit{Log}\left(\frac{\sum _{n=i}^{j}Ci}{Vi\times p\times d}\right)$$ (1)

Where n: replicas, i: the subset of n; j: a total of replicas, Ci, the total number of colonies in each replicate; V: Inoculum volume, p: number of plates counted and d: minor dilution obtaining the microbial group's colony-forming units (CFU) from cocoa beans.

2.5.2. Kinetics models

Three mathematical models, namely Gompertz [33], Baranyi [34], and Logistic Models [35], were employed to analyze the microbial growth curves during fermentations. The model parameters were estimated through non-linear regression analysis, and the experimental data were fitted to the model equations (2), (3), (4), (5).

2.5.2.1. Gompertz kinetic model

The Gompertz model's parameters have significant biological implications. The maximum growth rate (k) is the slope of the curve at the inflection point, while the maximum population density represents the upper asymptote of the curve. The initial population density (No) is the curve's lower asymptote [9]. The Gompertz model assumes that the growth rate decreases exponentially as the population approaches the environment's carrying capacity. This model is commonly utilized to describe bacterial population growth [33].

$$N_{\left(t\right)}=N_0*\mathit{exp}\left[-\mathit{exp}\left(\mu e^{\left(\frac{1}{N_0}\right)}\left(t-t_{lag}\right)\right)\right]$$ (2)

where N(t) is the population size at time t, No is the initial population size, μ is the maximum specific growth rate, t_lag is the lag time, and e is the base of the natural logarithm (2)

2.5.2.2. Baranyi kinetic model

The Baranyi model assumes that bacterial growth occurs in two stages: a lag phase and an exponential phase, with the latter characterized by constant growth. The Baranyi kinetic model's parameters include the lag phase duration (λ) when bacteria adapt to a new environment and initiate growth. The maximum growth rate (μmax) is the maximum bacterial growth rate during the exponential phase. The shoulder duration (δ) is when bacteria reach their full growth rate after the lag phase. The final cell concentration (Nf) is the maximum cell concentration achieved at the end of the exponential phase [34]. The model also accounts for a stationary phase in which growth slows due to nutrient depletion or waste accumulation [9,34].

$$N_{\left(t\right)}=N_0+\frac{\lambda }{\alpha }*\mathit{ln}\left[\frac{\left(e^{\left(\alpha \left({\mu }_{\mathit{max}}-\lambda \right)t\right)}\right)+\left(e^{\left(-\alpha *\lambda *t\right)}\right)}{2}\right]$$ (3)

Where: N(t) is the bacterial population at time t, No is the initial bacterial population, λ is the lag phase duration, μmax is the maximum specific growth rate, α is the mean growth rate during the exponential phase, given by α = (μmax - λ)/Nmax, where Nmax is the carrying capacity of the system [35,36].

2.5.2.3. Logistic kinetic model

The intrinsic growth rate (r) and carrying capacity (N) are the parameters resulting from the Logistic model and are used to describe population growth dynamics. The intrinsic growth rate represents the maximum growth rate in an unlimited environment, while the carrying capacity represents the maximum population size the environment can sustain [37]. The logistic model assumes that the population growth rate is proportional to the current population size and is limited by the environment's carrying capacity. This model is frequently used in population biology and ecology to describe the growth of populations over time [9,37].

$$N_{\left(t\right)}=N_0*{\left(1+e^{\left(-rt\right)}\right)}^N$$ (4)

Where: N(t) is the population size at time t, No is the initial population size, N is the growth rate constant, r is the maximum population size, also known as the carrying capacity.

The kinetic Lag Logistic model is a modification that incorporates a lag phase, during which the microorganisms adapt to the environment, followed by an exponential growth phase that slows down as the available resources are depleted [9,36,37]. This model has been applied in various fields, including food microbiology and environmental science, to study the growth of microorganisms under different conditions [37].

$$N_{\left(t\right)}=N_0+\frac{\left(N_{\mathit{max}}-N_0\right)}{\left(1+\exp \left(\frac{\left(lag-t\right)}{\lambda }\right)\right)}$$ (5)

where N(t) is the number of microorganisms at time t, N_0 is the initial number of microorganisms, Nmax is the maximum number of microorganisms that the environment can support, lag is the lag time, and λ is a parameter that determines the steepness of the growth curve.

2.6. Statistic procedure

2.6.1. Experimental design

The adjustment of growth models, Gompertz, Baranyi, and Logistic, was analyzed using logistic regression design in the Design Expert v 13 software from historical data (Table S1 in supplementary material). The analysis considered four factors: OMF Density (0, 5, 42, and 80 mT), exposure type (exposure to beans and exposure to culture), exposure time (30 and 60 min), and operating conditions (uncontrolled and controlled fermentation conditions) [38]. The response variable used was a binary variable: level 1 represented Model Fit Success (MFS), while level 0 indicated Model Fit Failure (MFF) (Tables S2a and b) in supplementary material).

The growth parameters and metrics, including μmax (maximum specific growth rate), N (maximum population density), lag (lag phase duration), RMSE (Root Mean Square Error), AIC (Akaike Information Criterion), and BIC (Bayesian Information Criterion), were evaluated using factorial design with historical data analysis in the same software [39]. The factors considered in the analysis were OMS density, with levels set at 0 mT, 5 mT, 42 mT, and 80 mT, and model type, with levels set as Gompertz, Baranyi, and Logistic (Tables S3a and b in supplementary material).

2.6.2. Models fit

The fermentation process was mathematically modeled using online Micro Risk Lab predictive microbiology statistical software [40]. Various metrics were used in the same software to assess the fit and accuracy of the model predictions. Gompertz, Baranyi, and logistic equations were used to model microbial growth under different experimental conditions [9]. It was assumed that these models were competent in describing the growth of mixed microbial species that belong to different microbial groups under identical conditions [9,17]. For the fit of the kinetic models, the first 84 h of fermentation microbial growth were considered, taking samples every 12 h and considering each group's growth as a single population [16,17].

The model equations were fitted to the experimental data to estimate the equations' kinetic parameters of the equations. The goodness of fit was assessed by calculating AIC and BIC. The AIC was calculated as AIC = −2 log(L) + 2p, where L represents the likelihood function, and p represents the number of parameters utilized in the model. The BIC was calculated as BIC = −2 log(L) + p log(n), where n represents the sample size [39]. Furthermore, the RMSE measured accuracy by the differences between the predicted and actual values. This statistic expresses the effect size as the two distributions' standardized mean difference [39].

3. Results and discussion

To assess the influence of oscillating magnetic fields (OMF) on the growth kinetics of the core microbial communities in cocoa beans derived from the CCN 51 variety, this study employed three distinct mathematical models: Gompertz, Baranyi, and Logistic. The cocoa beans were subjected to various OMF intensities ranging from 0 mT to 80 mT for 1 h, utilizing a Helmholtz coil electromagnetic device. The viable populations of lactic acid bacteria (LAB), acetic acid bacteria (AAB), and yeasts (Y) were quantitatively determined using the colony-forming unit (CFU) enumeration method. The results are described in the coming sections.

3.1. The logistic model exhibited the best fit for LAB and Y and Baranyi model to AAC

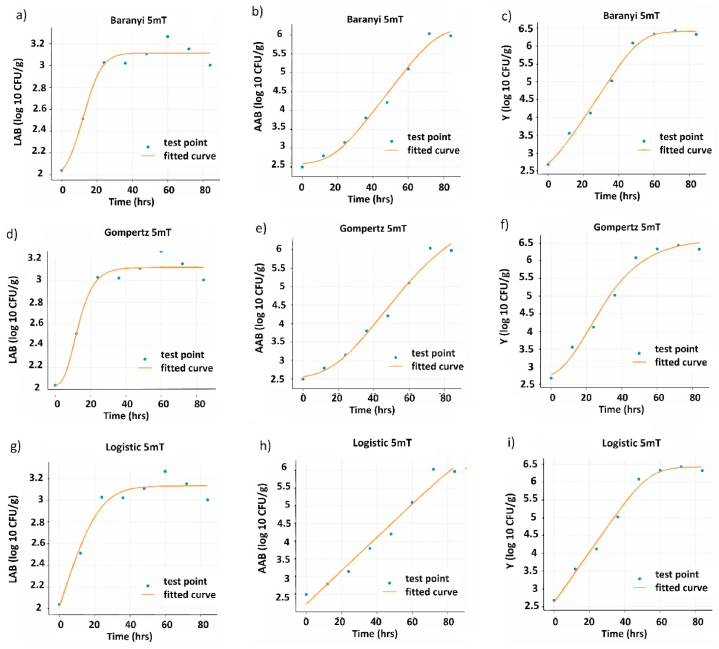
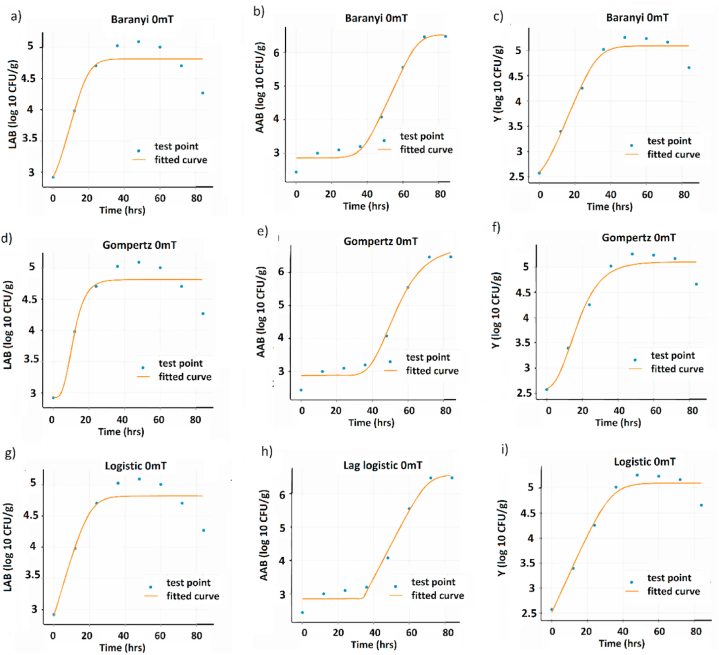
The logistic model demonstrated its suitability in describing the growth of lactic acid bacteria (LAB) and yeasts (Y) more effectively than the Gompertz and Baranyi models, under controlled fermentation conditions (CFC) as shown in Fig. 2a, b, c, g, h, and i. On the other hand, the Baranyi model better represented the growth of acetic acid bacteria (AAB) (Fig. 2e) compared to the Gompertz and Logistic models (2d and f), ANOVA analysis of LAB, AAC and Y metrics also reveals statistically significant differences between treatments and controls of the different microbial groups (Table S4). The evaluation of the model was based on three metrics: RMSE, AIC, BIC. In all cases, the logistic model exhibited the lowest values for these metrics, indicating a better fit. Specifically, at a magnetic field strength of 5 mT, the logistic model showed the best fit for LAB growth (Fig. 2, Fig. 3g), as evidenced by the lowest values of the RMSE, AIC, and BIC metrics, while the logistic model's worst fit was observed in the non-magnetic control group under the same CFC (Fig. 2, Fig. 4g) [40]. For yeast growth under the same CFC, the best fit results for all models were obtained at 80 mT, while the highest fit values were obtained at 42 mT (Fig. 2g, h, i; 5i and 6i).

Fig. 2.

ANOVA Interaction plots. responses of LAB (a) Gomperzt model, (b) Baranyi model, and (c) Logistic model; AAB (d) Gomperzt model, (e) Baranyi model, and (f) Logistic model; and Y (g) Gomperzt model, (h) Baranyi model, and (i) Logistic model. The nominal factor, Metrics (RMSE, AIC, and BIC), was presented continuously, while the nominal OMF density factor (A) was displayed discretely as separate lines: A1 (0 mT) represented by a red line, A2 (5 mT) represented by a green line, A3 (42 mT) represented by a blue line, and A4 (80 mT) represented by a gray line. The “I-Beam” symbols depict the 95 % least significant difference (LSD) interval for the plotted points. The dots on the plots indicated the values of the response variable around the mean, while the midpoint of the bar represented the mean value. Overlapping bar lines between levels indicated p > 0.05, while the absence of overlap indicated p < 0.05. (For interpretation of the references to color in this figure legend, the reader is referred to the Web version of this article.)

Fig. 3.

Growth curves of the model for the different microbial groups at 5 mT. Baranyi model: (a) AAB, (b) LAB, and (c) Y. Gomperzt model: (d) AAB, (e) LAB, and (f) Y. Logistics model: (g) AAB, (h) LAB, and (i) Y.

Fig. 4.

Growth curves of the model for the different microbial groups at 0 mT. Baranyi model: (a) AAB, (b) LAB, and (c) Y. Gomperzt model: (d) AAB, (e) LAB, and (f) Y. Logistics model: (g) AAB, (h) LAB, and (i) Y.

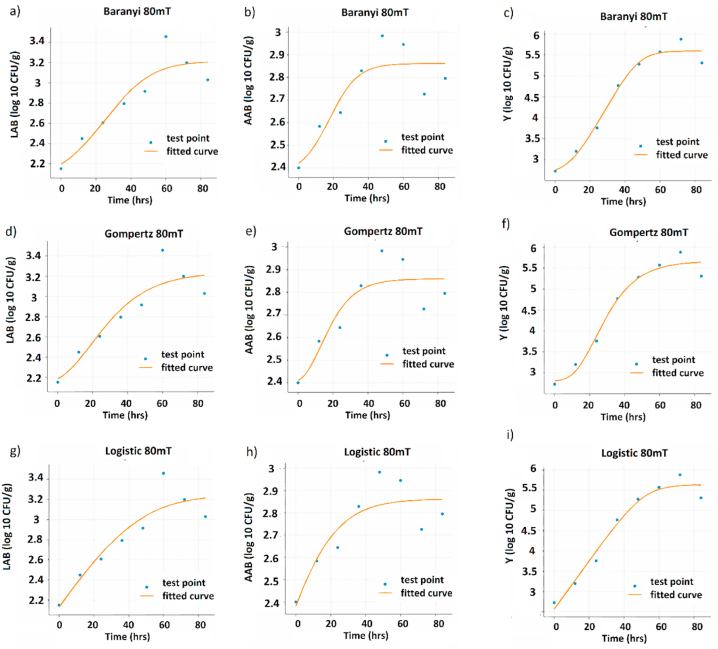
Regarding AAB, the Baranyi model provided the best fit for its growth in CFC (Fig. 2e) at 0 mT (Fig. 4b), 5 mT (Fig. 3b), and 42 mT (Fig. 6b). However, at 80 mT, the logistic model displayed the best fit (Fig. 2, Fig. 5h). The highest growth adjustment for AAB was observed at 80 mT, while the lowest was observed in the control group. In all cases, there were significant differences (p < 0.05) between the treatments and controls based on AIC and BIC metrics. The RMSE metric showed significant differences only between the control group and the treatment group in yeast growth in CFC (Fig. 2b).

Fig. 6.

Growth curves of the model for the different microbial groups at 42 mT. Baranyi model: (a) AAB, (b) LAB, and (c) Y. Gomperzt model: (d) AAB, (e) LAB, and (f) Y. Logistics model: (g) AAB, (h) LAB, and (i) Y.

Fig. 5.

Growth curves of the model for the different microbial groups at 80 mT. Baranyi model: (a) AAB, (b) LAB, and (c) Y. Gomperzt model: (d) AAB, (e) LAB, and (f) Y. Logistics model: (g) AAB, (h) LAB, and (i) Y.

Interestingly, the logistic model effectively captured the growth dynamics of most microbial groups in CFCs, indicating that this model effectively captured the CFC growth dynamics. Similarly, Noboa et al. (2021) [41] provide valuable information on the optimization of bioethanol production from cocoa mucilaginous residues. The application of the integrated logistic model allowed determining the maximum specific growth rate (μmax) of Saccharomyces cerevisiae, which was estimated at 0.39 h. This logistic model proved to be a suitable option to describe the growth dynamics of the microorganism under the given fermentation conditions. Consistently, at a magnetic field strength of 80 mT, the logistic model also showed the best fit for AAB growth. This indicates a change in AAB growth behavior at higher magnetic field strengths, which requires a different model for a more accurate representation.

Regarding AAB growth, the Baranyi model provided the best fit with magnetic field strengths of 0 mT, 5 mT, and 42 mT. This is consistent with rapid growth of this microbial group in the exponential phase and suggests that Baranyi's model was able to capture these growth dynamics well in CFCs and EMFs.

Fujikawa et al. (2005) (2006) [42,43], compared the newly developed logistic model and the Baranyi model to predict the microbial growth in foods. The first study revealed that the logistic model provides more accurate predictions of the constant growth rate of E. coli and Salmonella and lag time compared to the Baranyi model [42]. The second finding of the Baranyi model exhibited the smallest error in cell number estimation. In contrast, the logistic model demonstrated the smallest error in estimating the constant rate and lag period. In the case of dynamic temperature conditions, the logistic model successfully predicted bacterial growth, whereas the Baranyi model tended to overestimate it significantly. These results suggest that the logistic model accurately describes bacterial growth curves in bagged mashed potatoes [42]. These investigations support that each model has its own strengths and weaknesses, and selecting an appropriate model depends on the specific application and the microbial growth pattern under investigation.

Supporting the results of this study, the works of Mitchell et al. (2004) [44] and Mazaheri and Shojaosadati, (2013) [45] provide further support for the importance of accurate modeling in understanding microbial growth dynamics. The authors also emphasized the importance of modeling microbial growth and substrate utilization in wastewater treatment processes. Taken together, several investigations have highlighted the need to select appropriate models that are adapted to the specific fermentative system in order to obtain reliable predictions. Consistently the variability in growth patterns between different microbial species and the need to consider specific models adapted to their characteristics is evidenced in this study.

However, it should be noted that the worst fit of the logistic model was observed in the control group without magnetic treatment. This further emphasizes the influence of magnetic treatment on microbial growth dynamics and highlights the potential of magnetic fields to modulate microbial behavior. It also suggests that the increase of magnetic treatment could have influenced the microbial growth behavior of AABs resulting in a deviation from the Baranyi model predictions. These findings highlight the importance of considering external factors, such as magnetic treatment, which can potentially impact microbial growth and affect model performance.

The results obtained in this study also corroborate the findings of different authors that indicate that variations in the densities of magnetic fields can significantly affect the rates and patterns of microbial growth [25,26]. The interaction between magnetic fields and charged particles, such as ions and charged molecules, has been shown to influence key cellular processes [25,[46], [47], [48], [49]]. Magnetic fields can modulate enzyme activity, ion transport, and signal transduction, which are essential for microbial growth and metabolism [25,47]. Furthermore, changes in membrane permeability and potential induced by magnetic fields can affect nutrient uptake and energy production in microorganisms [46,48]. Also, alterations in the orientation and movement of cellular components [25,47], such as proteins and organelles [48], due to magnetic fields can affect their functionality and cellular processes in general [46,49].

Overall, comparisons with other studies support the notion that different models have their strengths and weaknesses, and the selection of an appropriate model depends on the specific application and microbial growth pattern under investigation. In addition, it is important to highlight that the influence of external factors, such as magnetic treatment, and process control, influence the dynamics of microbial growth and the fit of the model.

3.2. CEC influence on model's fit

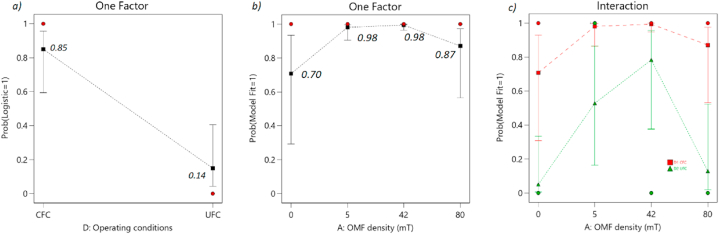
The analysis of the experimental data showed that the fit of the kinetic models was not affected by the time and type of exposure examined. This observation was supported by the results presented in Table S5. However, it was found that when the Controlled Fermentation Conditions (CEC) were applied, there was a probability exceeding 95 % of successfully adjusting the growth models (MFS) (Fig. 7a, b, and c). These findings suggest that the probability of achieving a successful model fit increases under different combinations of operating conditions. Thus implementation of CEC had a significant (p < 0.05) impact on improving the fit of the growth models to the experimental data, as illustrated in Fig. 7 and Table S6.

Fig. 7.

Logistic probability plots. binary variable with level 1 denoting Model Fit Success (MFS) and level 0 representing Model Fit Failure (MFF). Two factors were considered in the analysis: a) Operating conditions, with levels of UFC and CFC, b) OMF density, with levels of 0 mT, 5 mT, 42 mT, and 80 mT, c) Interactions.

The above findings highlight the importance of kinetic models for understanding fermentation processes under controlled conditions. Studies have shown that specific environmental factors, such as temperature, humidity, and starter cultures, significantly influence the dynamics of solid state (SSF) fermentations. Particularly in cocoa bean fermentation these factors play a crucial role affecting microbial growth and fermentation performance [16,45,50].

Findings from previous studies by Hamidi-Esfahani et al. (2019) [50], He et al. (2019) [51], Calvo et al. (2021) [52] and Rahardjo et al. (2022) [53] collectively highlight the importance of environmental factors in microbial growth and fermentation processes. In the current study, the implementation of CEC had a significant impact in improving the fit of the growth models to the experimental data.

The study by Rahardjo et al. (2022) [53] showed that controlled fermentation emerged as the most effective method to achieve shorter fermentation times and improve grain quality. This technique not only influenced microbial succession, but also had a significant impact on growth patterns. The probability of successfully fitting the growth models increased to more than 80 % when CEC was applied, indicating that the implementation of controlled fermentation conditions improved the fit of the growth models to the experimental data.

Similarly, the study by Hamidi-Esfahani et al. (2019) [50] demonstrated that temperature and humidity were influential factors in microbial growth. On the other hand, Calvo et al. (2021) [52] highlighted the role of pH and temperature regulation in the control of microbial succession during cocoa fermentation. In the current study, regulated temperature and humidity improved the fit of the growth models. This suggests that the controlled environmental conditions provided by CEC contributed to a more accurate representation of microbial growth dynamics. These factors probably influenced the growth models contributing to a better fit to the experimental data.

Additionally, moisture content is known to influence microbial growth and fermentation processes, and maintaining optimal moisture conditions is crucial to achieving desired results. He et al. (2019) [51] emphasized the importance of moisture content regulation in solid state fermentation (SSF). The implementation of CEC involved careful control of moisture content, which has played an important role in improving the fit of growth models.

Furthermore, our findings are also consistent with the significant impact of starter cultures on microbial growth in fermentation processes. Rahardjo et al. (2022) [53] also found that the inoculation of starter cultures in cocoa fermentation reduced fermentation time and maintained bean quality. This indicates that the presence of specific microbial strains in the form of starter cultures may influence the growth dynamics of cocoa fermentation.

The use of starter cultures can potentially alter the microbial composition and succession patterns, thus influencing the growth behavior of the different microbial species involved in cocoa fermentation [[12], [13], [14], [15]]. In addition, the presence of starter cultures can introduce specific metabolic pathways and interactions between microbial populations, which can determine changes in the fit of mathematical models that accurately represent growth dynamics.

The dynamics of microbial communities in cocoa fermentation are closely linked to process parameters and the initial microorganisms responsible for initiating the transformation of cocoa beans. The interplay of these fermentations can positively impact the quality of cocoa beans. These observations highlight the intricate influence of multiple parameters on microbial growth kinetics during cocoa fermentation, underscoring the complex nature of microbial physiology and its interactions with the surrounding environment.

3.3. OMF density increases MFS probability and induces changes in growth parameters

Table S4 revealed a significant (p < 0.05) influence of OMF density on the fit of the kinetic models. Furthermore, Fig. 7b displayed the variation in the probability of attaining a successful model fit across different OMF density levels, exhibiting a progressive pattern until reaching 80 mT. However, at 80 mT, a decline in the probability of SMF was observed, while continuing to outperform the control group (Fig. 7b).

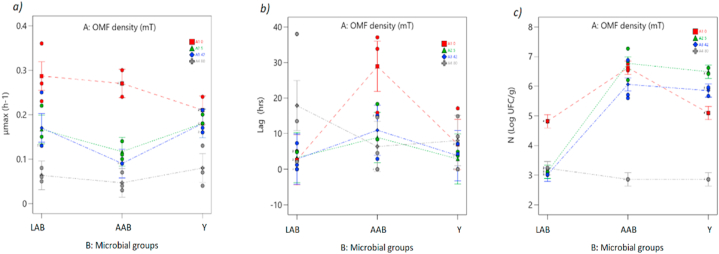
The maximum specific growth rate (μmax) of lactic acid bacteria (LAB) in the untreated control ranged from 0.23 to 0.35 h-1, which was significantly higher (p < 0.05) than the other treatments (Fig. 4, Fig. 8a). The μmax values for the treatments were as follows: 5 mT ranged from 0.15 to 0.22 h-1 42 mT ranged from 0.13 to 0.25 h-1, and 80 mT ranged from 0.23 to 0.35 h-1(Fig. 3, Fig. 5, Fig. 6; sub a, d, g). Among these treatments, the lowest range of μmax values was observed in the 80 mT treatment (Fig. 8a).

Fig. 8.

ANOVA interaction plots. responses (a) max, (b) lag, and (c) N. The nominal factor, Microbial group, was displayed continuously, while the nominal OMF density factor (A) was presented discretely as separate lines: A1 (0 mT) represented by a red line, A2 (5 mT) represented by a green line, A3 (40 mT) represented by a blue line, and A4 (80 mT) represented by a gray line. The “I-Beam” symbols depict the 95 % least significant difference (LSD) interval for the plotted points. The dots on the plots indicated the values that the response variable takes around the mean, while the midpoint of the bar represented the mean value. Overlapping bar lines between levels indicated p > 0.05, while the absence of overlap indicated p < 0.05. (For interpretation of the references to color in this figure legend, the reader is referred to the Web version of this article.)

Similar statistically significant differences (p < 0.05) between the controls and treatments were found for AAB and Y. As shown in Fig. 8a, AAB exhibited μmax values ranging from 0.24 to 0.30 h-1 in the untreated control, 0.09 to 0.14 h-1 in the 5 mT treatment, 0.10 to 0.14 h-1 in the 42 mT treatment, and 0.04 to 0.13 h-1 in the 80 mT treatment (Fig. 3, Fig. 4, Fig. 5, Fig. 6 sub b, e, h). For Y, the μmax values ranged from 0.18 to 0.24 h-1 in the untreated control, 0.13 to 0.20 h-1 in the 5 mT treatment, 0.16 to 0.21 h-1 in the 42 mT treatment, and 0.23 to 0.35 h-1 in the 80 mT treatment (Fig. 3, Fig. 4, Fig. 5, Fig. 6 sub c, f, i and 8a).

Significant differences between the control and treatment groups were observed primarily in the lag phase for LAB and AAB (Fig. 3, Fig. 4, Fig. 5, Fig. 6 sub a, b, d, e, g, h and 8a). In the case of LAB, the longest lag phase was observed in the 80 mT treatment, ranging from 13 to 38 h, with statistically significant differences compared to the control and other treatments (0 mT: lag phase 1.24–2.59 h, 5 mT: lag phase 3.25–5.08 h, 42 mT: lag phase 1.24–7.31 h (Fig. 8b).

For AAB, the longest lag phase was observed in the control group, ranging from 15 to 37.8 h, and showed statistically significant differences compared to the other treatments (Fig. 8b). On the other hand, the shortest lag phase was observed in the 80 mT treatment, ranging from 4.53 to 14.59 h, with significant differences compared to the control and other treatments (5 mT: lag phase 2.31–18.33 h, 42 mT: lag phase 2.91–10.95 h) (Fig. 8b).

Among all treatments and microbial groups, AABs exhibited the highest average growth rate value at 5 mT (N = 7.25 Log CFU/g), as shown in Fig. 3, Fig. 8 b, e, h. Under the same conditions, yeast (Y) levels remained lower than the control, while lactic acid bacteria (LAB) did not surpass the control, (Fig. 3, Fig. 8 a, c, d, f, i). Conversely, AAB and Y at 80 mT had the lowest mean value of maximum growth rate, with AAB at 80 mT (N = 2.80 Log CFU/g) and Y at 80 mT (N = 2.86 Log CFU/g), showing a significant difference (p < 0.05) compared to the control and other treatments (Fig. 5, Fig. 8 b, c, e, f, h, i). The control group of LAB displayed the highest growth rate within its group (N = 4.87 Log CFU/g) compared to the other treatments, including 5 mT (N = 3.2 Log CFU/g), 42 mT (N = 3.01 Log CFU/g), and 80 mT (N = 3.23 Log CFU/g), as illustrated in Fig. 3, Fig. 4, Fig. 5, Fig. 6, Fig. 8 sub a-i.

Previous studies have reported a range of μmax values for yeast between 0.07 and 0.53 h-1, LAB between 0.06 and 0.36 h-1, and AAB between 0.414 and 0.49 h-1. The reported results align more closely with the findings observed in the control groups of the current study and stand in contrast to the outcomes observed in the magnetic treatment group [24,36,47,[54], [55], [56]]. Consistent with previous studies, cocoa bean fermentations are characterized by initial microbial counts ranging from approximately 3 to 7 log CFU g-1 for yeast, 4 to 5 and 8 to 9 log CFU g-1 for lactic acid bacteria (LAB), and 3 to 4 and 6 to 7 log CFU g-1 for acetic acid bacteria (AAB). These counts gradually decline throughout the fermentation process, ultimately reaching final levels of approximately 2–3 log CFU g-1 for yeast, 1.5 log CFU g-1 for LAB, and 0 log CFU g-1 for AAB [47,55,56].

In the present study, the final counts attained by different microbial groups were not considered for the model fitting; however, the growth profiles exhibited a notable initial population and rapid growth of both yeast and LAB, while AAB proliferation occurred concurrently but at a slower pace. These observations align with the counts reported in previous studies on heap fermentations of cocoa beans from Ghana as well [55,56].

The observed distinctions between the treatment groups and control groups were notable, and upon analyzing the kinetic parameters, it became evident that electromagnetic fields had a discernible influence on the fermentation process. Consequently, these findings align with prior studies that emphasize the effects of magnetic fields on the growth of bacteria and yeasts.

While some studies have reported stimulating effects of magnetic fields on certain microbial species, the presence of magnetic fields has also been shown to have inhibitory effects on cell growth. These studies suggest that exposure to magnetic fields can modulate the growth and metabolic activity of various microorganisms. Masod et al. (2018) (2020) [47,57]conducted an investigation to assess the impact of various types of exposure to weak magnetic fields on bacterial growth. The studies focused on comparing the relative changes in bacterial growth subsequent to the removal of magnetic fields. Bacteria were cultivated on a single glass surface in both liquid and solid media, under different weak magnetic field conditions. The findings revealed that the growth pattern of bacteria was influenced differently by distinct magnetic fields, depending on the specific bacterial strain. Notably, the weak magnetic field was observed to impede the growth rate even after the removal of the magnetic field. The study suggests that magnetic fields can affect the growth rate, mutation frequency, and other mechanisms within bacteria.

The findings from the present study are consistent with previous research examining the effects of magnetic fields on microbial growth and metabolic processes. Konopacka et al. (2019) [58] investigated the impact of a rotating magnetic field (RMF) on bioethanol production and observed that it stimulated the growth and metabolic activity of S. cerevisiae, resulting in increased ethanol production and overall process productivity. This aligns with the current study's results, which showed that exposure to magnetic fields had a significant influence on the specific growth rate (μmax) of lactic acid bacteria (LAB) and acetic acid bacteria (AAB). The μmax values for LAB and AAB were lower in the treatment groups compared to the control, with the lowest values observed in the 80 mT treatment.

Konopacki et al. (2019) [59] also studied the effects of RMF on different bacterial strains and found strain-specific responses. The present study observed similar strain-specific effects, with increased cell growth in Gram-positive bacteria and inhibition in E. coli and K. oxytoca strains. Kohno et al. (2000) [60] explored the effects of static magnetic fields on bacterial growth and found that the strength of the magnetic field influenced the growth rate and maximum growth number of specific bacterial species. This is consistent with the current study's findings, which showed that the lag phase and μmax values varied depending on the magnetic field strength and microbial group.

Furthermore, Sudarti (2020) [27] demonstrated the impact of extremely low-frequency (ELF) magnetic fields on lactobacillus growth, similar to the current study's findings on LAB. Zhao et al. (2020) [61] investigated the effects of static magnetic fields on biogas production and observed significant increases in gas and methane volumes, as well as changes in microbial community composition. These findings align with the current study's observations on the growth rates of LAB and AAB and indicate that magnetic fields can influence microbial growth and metabolic processes. Additionally, Ciecholewska et al. (2022) [62] found that exposure to a rotating magnetic field reduced the number of viable bacterial cells within biofilms, which is consistent with the current study's results on the lag phase and growth rates of LAB and AAB.

In a broader context, the findings also align with previous studies by Novák et al. (2007) [63] who observed a similar inhibitory effect on the growth of Saccharomyces cerevisiae when manipulating the magnetic field parameters with Bm = 10 mT, f = 50 Hz, and 24 min exposure. Similarly, Potenza et al. (2004) [64], indicated a detrimental impact of 300 mT static magnetic fields (SMF) on E.coli cell growth. These findings emphasize that exposure to magnetic fields can affect microbial growth characteristics.

In summary, an increase in magnetic field strength was associated with a decrease in the maximum growth rate, a longer delay phase, and lower μmax (maximum specific growth rate) values for these microbial groups. The mechanism behind the change in the growth rate of microorganisms under weak magnetic fields is not fully understood, but research suggests that it may involve perturbation of ion transport in the nutrient broth and bacterial cell dynamics, thus affecting the mobility and absorption of nutrients in the cells and therefore their duplication rate [25,48,49,57].

The observed disparities in kinetic parameters between experimental treatments and control groups suggest that factors beyond nutrient depletion and toxic metabolite accumulation, which are commonly known to affect batch fermentations, may be influencing microbial growth during the fermentation of the cocoa bean. Consequently, the impact of EMF on the fermentation process is becoming evident based on the analysis of kinetic parameters.

The impact of magnetic fields on microbial growth is a complex phenomenon that delves into the intricate dynamics of cellular processes. While the precise mechanisms remain somewhat difficult to elucidate, emerging research is shedding light on several fascinating aspects of this interaction.

In essence, the influence of magnetic fields on microbial growth is believed to revolve around their ability to disrupt ion transport within the nutrient medium and the internal dynamics of bacterial cells. This alteration can have important repercussions and affect fundamental cellular activities, such as nutrient absorption and doubling rates. The cited studies [25,48,49,57] indicate that the interaction between magnetic fields and charged particles plays a fundamental role in the modulation of crucial processes such as enzymatic activity, ion transport and signal transduction, all of which are integral for the growth of microorganisms and their metabolic functions.

Furthermore, the effect extends to the properties of the membrane. Magnetic fields have been shown to induce changes in membrane permeability and potential, directly influencing nutrient absorption and cellular energy production. This alteration in membrane characteristics, supported by research [46,48], signifies a fundamental change in the way microbial cells interact with their environment, ultimately affecting their growth dynamics.

Another intriguing aspect lies in the alterations in the orientation and movement of cellular components under the influence of magnetic fields. This alteration not only affects physical positioning but also extends to functionality. As noted [25,47], changes in orientation and movement can alter the usual functionality of cellular components, which could affect several cellular processes vital for growth and metabolism.

This multifaceted impact of magnetic fields on microbial growth highlights a complex interplay between external stimuli and internal cellular mechanisms. While the precise mechanisms remain an area of active research, evidence suggests a significant influence on the fundamental biological processes that govern microbial growth. Exploring these intricate dynamics promises to reveal deeper insights into the relationship between magnetic fields and microbial behavior, which could open new avenues for understanding and manipulating microbial processes in diverse domains.

3.4. Magnetic fields can affect the cocoa beans' fermentative processes

The present study builds upon prior research conducted by the authors [24], in which they aimed to optimize the fermentation process of CCN 51 cocoa beans by utilizing indigenous species and electromagnetic fields (CEM) in order to enhance both yield and quality. The investigation employed response surface methodology to optimize the magnetic field density (D), exposure time (T), and inoculum concentration (IC) as variables, resulting in the development of 2 s-order models. These models accounted for 88.39 % and 92.51 % of the variability in yield and grain quality, respectively. The findings demonstrated that exposure to CEM exerted a significant impact on both the yield and quality of CCN 51 cocoa beans. The optimal combination of 5 mT (D), 22.5 min (T), and 1.6 % (CI) led to a remarkable improvement, with a 110 % increase in yield and a 120 % enhancement in grain quality compared to the control group. Metagenomic analysis further revealed that alterations in microbial communities at lower and moderate field densities (5–42 mT) positively influenced the aroma profile, resulting in higher yields and the presence of floral, fruity, and nutty flavors. Conversely, field densities of 80 mT resulted in lower yields and undesirable notes of acidity and bitterness.

Similarly, Sudarti et al. (2022) [25] conducted a study to investigate the impact of exposure to extremely low frequency (ELF) magnetic fields on the fermentation process of dried cocoa beans. Various parameters such as moisture content, alcohol content, and pH were analyzed. The findings revealed that the fermentation process of dried cocoa beans can be influenced by exposure to ELF magnetic fields. Notably, the samples exposed to a magnetic field density (MFD) of 0.2 mT for 5 min exhibited the highest bacterial growth. These results indicate that exposure to ELF magnetic fields could serve as an alternative approach to enhance the fermentation process of dried cocoa beans.

Both studies deliver evidence suggesting that exposure to extremely low frequency (ELF) magnetic fields impact the fermentation process of dried cocoa beans. These findings highlight the need for further research to validate and expand upon these observations, and to identify the optimal conditions for utilizing ELF magnetic fields in cocoa bean fermentation. Furthermore, these studies offer valuable insights into the potential advantages of magnetic field exposure during the fermentation process of cocoa beans. Continued investigation in this field has the potential to contribute to the development of innovative techniques aimed at optimizing cocoa bean fermentation, thereby enhancing product quality and yield in the cocoa industry.

4. Conclusions

The study used modeling to analyze the growth kinetics of key microbial groups during cocoa bean fermentation when exposed to magnetic fields. The results indicated that magnetic fields influenced parameters such as maximum specific growth rates and lag phases, and that accurate model adjustments are more possible under controlled fermentation conditions. The logistic model effectively described the growth of most microbial groups, while the Baranyi model was more suitable for AAB. In general, magnetic field treatments showed lower maximum specific growth rates and longer lag phases compared to controls, highlighting the impact of electromagnetic fields on microbial growth in cocoa fermentation. The study suggests the need for more research, particularly in the real context of cocoa bean fermentation.

Data availability statement

The data associated with the study appear in the supplementary material of this article.

CRediT authorship contribution statement

Tania María Guzmán-Armenteros: Writing – original draft, Methodology, Investigation, Formal analysis, Data curation, Conceptualization. José Villacís-Chiriboga: Writing – review & editing, Writing – original draft, Validation, Supervision. Luis Santiago Guerra: Writing – review & editing, Writing – original draft, Visualization, Validation, Supervision. Jenny Ruales: Writing – review & editing, Writing – original draft, Visualization, Validation, Supervision.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Supplementary data

The following is the Supplementary data to this article.