Figure 2.

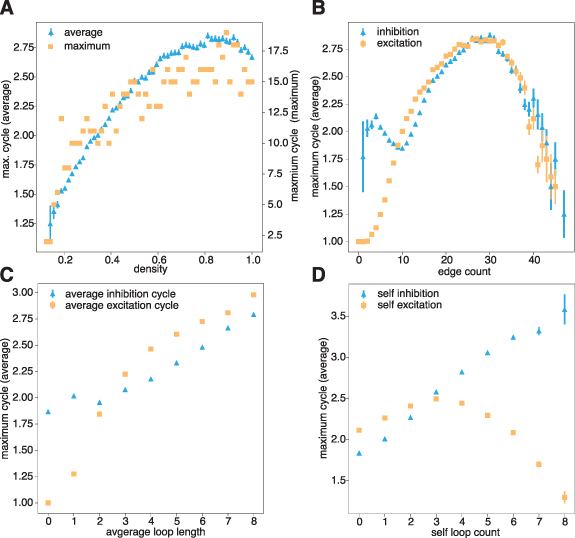
Topological properties of random networks. (A) The average and largest maximal cycle length as a function of density for an eight-node network. (B) The average maximal cycle length as a function of the number of edges of each type: excitatory and inhibitory. (C) The average maximal cycle length as a function of the average size of physical cycles within the interaction network. Note that the former is a dynamical property and the latter is an interaction property. (D) The average maximal cycle length as a function of the number of self-loops, as given by the diagonal entries in the adjacency matrix. All plots use a sample of 400 000 random networks.