FIG. Extended Data Fig. 1. Global parameterization of tube-like surfaces with material coordinates proceeds by a sequence of mapping steps.

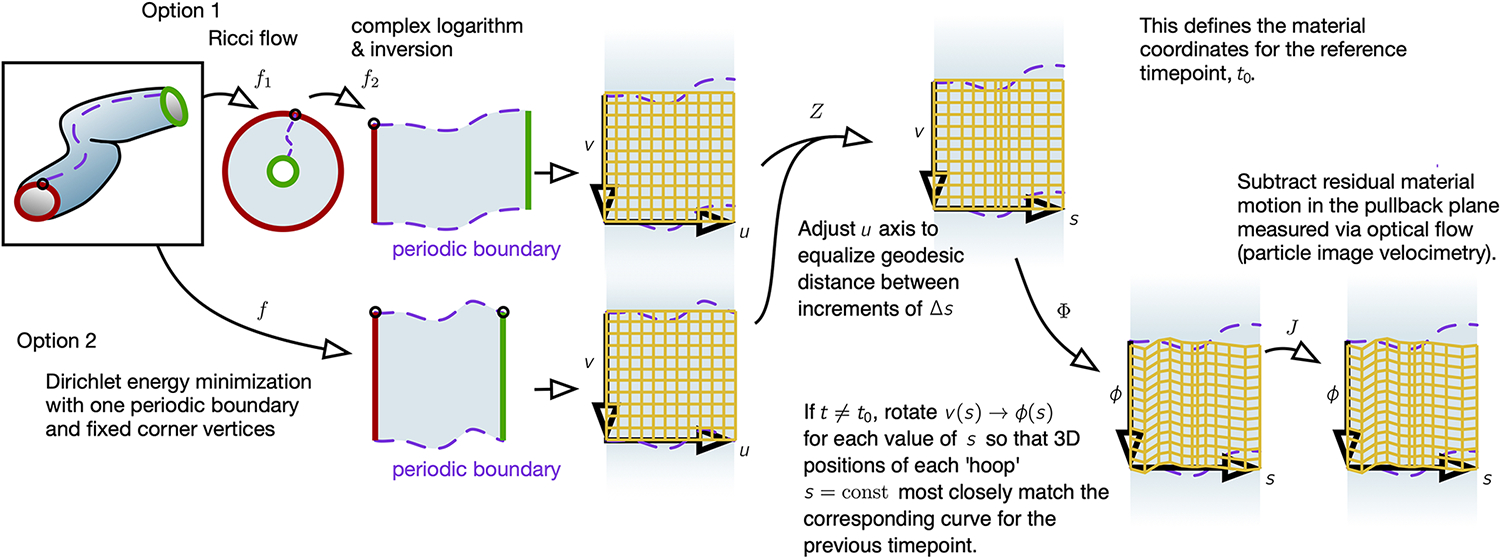
The 3D surface is first mapped via $f$ to the plane, either through Ricci flow (which is slower but results in a more exactly conformal map) or through minimization of a Dirichlet energy (faster but less precisely conformal, see Supplementary Information Section VIIa). In either case, the material is periodic in the $v$ dimension and finite in extent along the longitudinal direction $u$. The resulting coordinate system is then adjusted. First we apply $Z:u\to s$, where $s$ is a distance along the longitude of the tissue defined by Eq. (1), which we find aids in parameterization for tubes with varying radii (Supplementary Information Section VIIb). If the timepoint under question is the reference timepoint $t_0$, this defines the material coordinates. Otherwise, if $t>t_0$, we then apply $\mathrm{\Phi }:v\to \varphi$, where $\varphi$ is given by Eq. (2), and then apply $J$ to stabilize the resulting coordinates based on material motion measured through particle image velocimetry (phase correlation analysis) relative to the previous timepoint.