Abstract
The prediction of the thermodynamic properties of lactones is an important challenge in the flavor, fragrance, and pharmaceutical industries. Here, we develop a predictive model of the phase behavior of binary mixtures of lactones with hydrocarbons, alcohols, ketones, esters, aromatic compounds, water, and carbon dioxide. We extend the group-parameter matrix of the statistical associating fluid theory SAFT-γ Mie group-contribution method by defining a new cyclic ester group, denoted cCOO. The group is composed of two spherical Mie segments and two association electron-donating sites of type e1 that can interact with association electron-accepting sites of type H in other molecules. The model parameters of the new cCOO group interactions (1 like interaction and 17 unlike interactions) are characterized to represent target experimental data of physical properties of pure fluids (vapor pressure, single-phase density, and vaporization enthalpy) and mixtures (vapor–liquid equilibria, liquid–liquid equilibria, solid–liquid equilibria, density, and excess enthalpy). The robustness of the model is assessed by comparing theoretical predictions with experimental data, mainly for oxolan-2-one, 5-methyloxolan-2-one, and oxepan-2-one (also referred to as γ-butyrolactone, γ-valerolactone, and ε-caprolactone, respectively). The calculations are found to be in very good quantitative agreement with experiments. The proposed model allows for accurate predictions of the thermodynamic properties and highly nonideal phase behavior of the systems of interest, such as azeotrope compositions. It can be used to support the development of novel molecules and manufacturing processes.
1. Introduction
A lactone is an ester in which the functional group −C(=O)–O– is a part of a cycle. The most common approach for the synthesis of lactones involves the intramolecular esterification of hydroxy acids. Numerous other approaches have been developed to obtain specific lactone structures.1
Lactones are widely present in fruits, milk, fermentation products, and in many drinks and foods (from plant or animal origin); as such, they are of major interest for the flavor and fragrance industries1−5 and are relevant to chemical, biological,6 and pharmaceutical processes.1 For example, oxolan-2-one is present in a large range of food products2 (dehydrated orange powder, tomato, bread, liquid smoke, popcorn, cocoa, coffee, black tea, wines, beef, etc.) but is also used as an organic solvent and as an intermediate in many syntheses7 (e.g., for pyrrolidone and derivate compounds).
Knowledge of the thermodynamic properties of lactones can be helpful to synthesize and characterize these molecules and their mixtures and to develop chemical and industrial processes. Oxolan-2-one is, for example, known to be miscible with alcohols, ketones, esters, aromatic compounds, and water, but is not miscible with linear and cyclic aliphatic hydrocarbons.7 One of the aims of our work is to study the thermodynamic properties and phase behavior of pure lactones and their binary mixtures with a range of solvents using the SAFT-γ Mie group-contribution approach.8−11 Predictive group-contribution approaches can be used in molecular and process design12−14 to reduce the number of experiments and material use and to study systems over a large range of thermodynamic conditions.
The statistical associating fluid theory (SAFT)15,16 is a molecular equation of state based on statistical physics at the microscopic scale, providing an accurate description of complex fluids over a large range of thermodynamic conditions. In the original approach, molecules were treated as homonuclear chains of tangentially bonded spherical segments with embedded associating sites to mediate directional interactions that mimic hydrogen bonds.17,18 More-recent versions have been developed to consider spherical segments interacting through various pair potentials,19,20 e.g., the SAFT-VR version for the square-well potential,21 soft-SAFT for the Lennard-Jones potential,22−26 and SAFT-VR Mie,27 which incorporates the Mie potential (a generalized Lennard-Jones potential) and a third-order high-temperature expansion of the attractive contributions to the free energy. A reference chain fluid is used in PC-SAFT,28 ePC-SAFT,29 and PCP-SAFT.30 The PC-SAFT and PCP-SAFT approaches have been used to model 5-methyloxolan-2-one,31,32 and the polymerization of oxepan-2-one33 and of ω-pentadecalactone34 in a mixture of carbon dioxide and dichloromethane have also been studied with PC-SAFT. These approaches, however, are not group-contribution methods, and as a result the molecular parameters presented are not transferable to other lactones or their mixtures.
The SAFT-VR Mie equation was recast as a group-contribution approach in the SAFT-γ Mie equation of state8−11 in which molecules are modeled in terms of their constituent chemical moieties (groups) such that once a group is characterized the thermodynamic properties of molecules and mixtures containing the group can be predicted. The method has been shown to deliver an accurate prediction of a broad range of equilibrium thermodynamic properties, including vapor–liquid equilibria (VLE), liquid–liquid equilibria (LLE), and solid–liquid equilibria (SLE), as well as single-phase and derivative properties.11 Furthermore, the approach can be used to develop SAFT-γ transferable force-field parameters for use in molecular simulation.35 An update of the current capabilities of the SAFT-γ Mie method and the available group interactions can be found in Haslam et al.11
Recently, the SAFT-γ Mie approach has also been applied to systems of pharmaceutical interest: octanol–water partition coefficients for a range of active pharmaceutical ingredients were predicted by Hutacharoen et al.,36,37 aqueous mixtures of choline and geranate were modeled by Di Lecce et al.,38 solubility predictions were obtained for mefenamic acid in a range of solvents by Febra et al.,39 and pH solubility profiles of aqueous buffered solutions of ibuprofen and ketoprofen were predicted by Wehbe et al.40 It has also been used to develop accurate models of amines and alkanolamines of interest in the field of carbon capture.41,42 In addition, the predictive capability of SAFT-γ Mie has been tested with the Clapeyron.jl toolkit by Walker et al.,43 and the transferability of the SAFT-γ Mie parameters has been examined by Crespo and Coutinho.44 An alternative treatment, referred to as (structural) s-SAFT-γ Mie,45−47 has also been proposed to take into account functional group interactions.
Here, we extend the SAFT-γ Mie group-contribution method to represent the family of saturated lactones. The transferability of the new parameters is assessed for a large set of compounds of the lactone family. The parameter estimations and the predictive calculations are carried out by considering vapor-pressure, density, and vaporization-enthalpy data of pure compounds and VLE (including bubble and dew temperature, bubble and dew pressure, and azeotrope composition and temperature), LLE, SLE, density, and molar excess-enthalpy data of binary mixtures.
The different lactones are characterized by their ring size, the presence or absence of side chains, the saturation or unsaturation of the cycle, and the chirality of the atoms of the cycle.1,3 Distinct families of lactones can be defined from their structures; for example, phthalides and coumarins contain an aromatic cycle fused to the lactone cycle. The smallest saturated lactone found in nature is oxolan-2-one, which is a five-membered cycle composed of three cyclic methylene (cCH2) groups and one lactone (cCOO) group (Figure 1a). The heterocycle results in dipole moments that are larger for lactones than those of free ester chains; for example, the dipole moment of oxolan-2-one is reported as 3.8 D by Longster and Walker48 and as 4.27 ± 0.03 D in the CRC Handbook of Chemistry and Physics49 compared with 1.9 D for open-chain esters.48 In addition, the electron pairs of the oxygen atoms in the lactone group can form hydrogen bonds with hydrogen atoms from other molecules.50
Figure 1.
SAFT-γ Mie molecular models of: (a) oxolan-2-one; (b) 5-methyloxolan-2-one; (c) 6-propyloxan-2-one; and (d) oxepan-2-one. The rings of these saturated lactones are modeled with one cCOO group and the corresponding number of cCH2 groups (in blue and gray, respectively). The linear side chains are modeled with CH2 (in brown) and CH3 groups (in green). The carbon participating in the ring and side chain is modeled with a cCH group (in yellow). Association sites are denoted by the smaller red circles, labeled e for electronegative (acceptor) sites.
In our model, different ring sizes and side chains are accounted for. Chirality, however, cannot be considered with a first-order group-contribution proposition because proximity effects are not taken into account.11 As chiral molecules present near identical thermodynamic properties, there is no need to differentiate between these types of isomers.
In Section 2, we present the SAFT-γ Mie approach and parameter-estimation methods. We detail the models and results for saturated lactones in Section 3 by considering pure fluids (Section 3.1.1) and binary mixtures in a range of solvents: saturated hydrocarbons (Section 3.1.2), primary and secondary alcohols (Section 3.2), 2-ketones (Section 3.3), esters (Section 3.4), aromatic compounds (Section 3.5), water (Section 3.6), and carbon dioxide (Section 3.7). We conclude and summarize our main findings in Section 4.
2. Methods
2.1. SAFT-γ Mie Model and Theory
In the SAFT-γ Mie approach,8,51 molecules are modeled as associating heteronuclear chains of fused spherical segments that interact through Mie potentials of variable range, while attractive short-range directional interactions are added by embedding square-well association sites on a given segment. The total Helmholtz free energy A of a fluid of nonionic species is expressed as the sum of four contributions:8−10,51
| 1 |
where Aideal is the ideal free energy of the mixture, Amonomer is the contribution accounting for the Mie segment interactions, Achain is the free energy associated with the formation of chains, and Aassociation is the contribution to the free energy due to association. (Note that the Born and ionic contributions, which appear in the full SAFT-γ Mie free-energy expression,11 are not included in eq 1 since we do not consider any ionic species in our current work.) Detailed expressions for each contribution can be found in previous work.8−10,51
Following the group-contribution premise, molecules are modeled in terms of functional groups, and it is assumed that the properties of a given molecule (or mixture) can be obtained by accounting for the appropriate contributions of the groups. The parameters characterizing any given group are treated as transferable to other molecules and mixtures containing the same group. The SAFT-γ Mie representation of four saturated lactones (oxolan-2-one, 5-methyloxolan-2-one, 6-propyloxan-2-one, and oxepan-2-one) can be seen in Figure 1. A given group k incorporates a number ν*k of identical spherical segments and a shape factor Sk (0 ≤ Sk ≤ 1), which is introduced to characterize the contribution of the segment to the overall molecular properties of the molecule. In the simplest case, the interaction between two segments of groups k and l is described through a Mie potential:8
| 2 |
where rkl is the distance between
the centers of the two segments, σkl is the segment diameter, εkl is
the depth of the potential well, and λrkl and λakl are the repulsive and attractive exponents
of the Mie potential, respectively. The prefactor 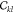 is a function
of the exponents that ensures
that the minimum of potential is −εkl, and can be expressed as
is a function
of the exponents that ensures
that the minimum of potential is −εkl, and can be expressed as
| 3 |
When relevant, hydrogen bonding and strong polar interactions are represented by short-ranged square-well association sites placed on the segments.52 The parameter NST,k corresponds to the number of association site types in a group k, and nk,a corresponds to the number of sites of a given type a = 1, ..., NST,k. The interaction between a site of type a placed on a segment of type k and a site of type b placed on a segment of type l is given by
| 4 |
where rkl,ab is the distance between the centers of the two sites, εHBkl,ab is the association energy, and rckl,ab is the cutoff range of the interaction. Site a is positioned at distance rdkk,aa from the center of segment k, and site b is positioned at distance rdll,bb from the center of segment l. The range of the association can equivalently be described by the cutoff rckl,ab or by the bonding volume KHBkl,ab for given values of rdkk,aa and rdll,bb. The interactions between groups k and l involve unlike parameters, which can be obtained through combining rules8 (CR) in the first instance. In our current work, however, εkl, KHBkl,ab, and εHBkl,ab are systematically estimated by comparing target calculated and experimental thermophysical properties of pure fluids or mixtures in which the functional group is present, and λrkl is occasionally estimated for better agreement.
The equilibrium thermodynamic properties of the fluid with c components can be determined from the total Helmholtz
free energy A at a temperature T, volume V, and vector number N of molecules, composed of elements Ni of compounds i, such that 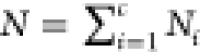 is the total number of molecules in the
system. The pressure is obtained from
is the total number of molecules in the
system. The pressure is obtained from
| 5 |
and the chemical potential of a compound i is obtained from
| 6 |
These standard relations can be used to determine the fluid-phase equilibrium conditions.
The solid–liquid solubility of compound i in a given solvent at a given temperature T and pressure P is obtained by solving the equality between the chemical potential of i in the solid phase, assumed pure here, and in the liquid phase: μSi(T,P,xSi=1) = μsati(T,P,xsat), where xsat is the mole fraction of the saturated solution. The solute mole fraction xsati(T,P,xsat) can be calculated as39
 |
7 |
where Tfusi is the melting temperature, Δhfusi(Tfusi,P) is the molar enthalpy of fusion, Δcp,i(Tfusi,P) = cLp,i(Tfusi,P) – cSp,i(Tfusi,P) is the difference at Tfusi between the molar heat capacity of the liquid phase cLp,i(Tfusi,P) and the molar heat capacity of the solid phase cSp,i(Tfusi,P), and γi(T, P, xsat) is the activity coefficient calculated with SAFT-γ Mie.
Although neglecting Δcp,i(Tfusi,P) can significantly affect the solubility prediction,53−55 depending on the mixture and the temperature, experimental values for Δcp,i(Tfusi,P) are unknown for most of the molecules considered in our work. Hence, we do not take this contribution into account in our current calculations. Thus, eq 7 is approximated as
| 8 |
The molar enthalpies of fusion Δhfusi(Tfusi,P) and melting temperatures Tfusi of the lactones and solvents studied in the current work are reported in Table 1, together with their corresponding sources.56−63
Table 1. Molar Enthalpy of Fusion Δhfusi and Melting Temperature Tfusi of Lactones and Solvents Used in All of the SAFT-γ Mie Calculations and Predictions (cf. eq 8) in Our Current Work.
| compound i | Δhfusi(Tfusi, P = 1 bar)/(kJ/mol) | Tfusi/K | ref |
|---|---|---|---|
| oxolan-2-one | 9.57 | 229.78 | (56) |
| oxepan-2-one | 13.82 | 272.13 | (57) |
| 5-methyloxolan-2-one | 7.1 | 238.34 | (58) |
| cyclohexane | 2.63 | 279.75 | (56) |
| methanol | 3.21 | 175.49 | (59) |
| ethanol | 5.02 | 158.65 | (56) |
| propan-1-ol | 5.20 | 147.05 | (56) |
| butan-1-ol | 9.28 | 183.35 | (56) |
| pentan-1-ol | 9.83 | 194.25 | (56) |
| acetone | 5.69 | 178.35 | (56) |
| butan-2-one | 8.44 | 186.48 | (56) |
| pentan-2-one | 10.63 | 196.31 | (60) |
| hexan-2-one | 14.9 | 216.25 | (56) |
| methyl acetate | 7.97 | 175 | (56) |
| ethyl acetate | 10.48 | 189.55 | (56) |
| propyl acetate | 11.2 | 178 | (56) |
| butyl acetate | 14.4 | 199.7 | (56) |
| diethylbutanedioate | − | 252.55 | (61) |
| benzene | 9.82 | 278.33 | (62) |
| toluene | 6.6 | 178.2 | (63) |
| ethylbenzene | 9.2 | 178.2 | (63) |
| water | 6.0 | 273.15 | (63) |
| carbon dioxide | 7.9 | 216.6 | (63) |
2.2. Parameter Estimation
The parameters characterizing the groups are determined by minimizing the objective function fobj:
| 9 |
where Θ is the vector of model parameters, Nexp is the total number of experimental points considered in the parameter estimation, NS is the number of systems (pure compounds/mixtures) used in the estimation, NPs is the number of property types for system s, NDs,p is the number of experimental data points for system s and property p, and ws,p,i is a weight that is used to control the relative importance of data point i for property p of system s. We consider here the same weight for each point (i.e., ws,p,i = 1, for all points). Xexps,p,i is the ith measured value of property p of system s, and Xcalcs,p,i(Θ) is the corresponding value calculated with SAFT-γ Mie and the parameters Θ.
The percentage absolute average deviation (%AAD) of a property p for a system s,
| 10 |
and the absolute average deviation,
| 11 |
are used as measures of the accuracy of the theoretical approach.
We use the gPROMS64 tools to perform the parameter estimation and calculations. The open-source toolkits SGTPy65 and Clapeyron.jl43 can also be used to reproduce the calculations.
3. Results and Discussion
3.1. SAFT-γ Mie Modeling of Lactones: cCOO–cCOO, cCOO–cCH2, cCOO–cCH, cCOO–CH3, and cCOO–CH2 Interactions
3.1.1. Pure Lactones
The lactones considered in our current work are shown in Table 2 together with the details of the groups used in the SAFT-γ Mie modeling.
Table 2. List of the Saturated Lactones and Solvents Considered in Our Work, Together with the SAFT-γ Mie Group Representation.
| compound name | CAS number | molecular formula | SAFT-γ Mie modeling |
|---|---|---|---|
| oxolan-2-one/γ-butyrolactone | 96-48-0 | C4H6O2 | cCOO, cCH2 (×3) |
| oxan-2-one/δ-valerolactone | 542-28-9 | C5H8O2 | cCOO, cCH2 (×4) |
| oxepan-2-one/ε-caprolactone | 502-44-3 | C6H10O2 | cCOO, cCH2 (×5) |
| oxocan-2-one | 539-87-7 | C7H12O2 | cCOO, cCH2 (×6) |
| oxonan-2-one | 5698-29-3 | C8H14O2 | cCOO, cCH2 (×7) |
| oxecan-2-one | 6008-27-1 | C9H16O2 | cCOO, cCH2 (×8) |
| 5-methyloxolan-2-one/γ-valerolactone | 108-29-2 | C5H8O2 | cCOO, cCH2 (×2), cCH, CH3 |
| 5-ethyloxolan-2-one/γ-caprolactone | 695-06-7 | C6H10O2 | cCOO, cCH2 (×2), cCH, CH2, CH3 |
| 5-propyloxolan-2-one/γ-heptalactone | 105-21-5 | C7H12O2 | cCOO, cCH2 (×2), cCH, CH2 (×2), CH3 |
| 5-butyloxolan-2-one/γ-octalactone | 104-50-7 | C8H14O2 | cCOO, cCH2 (×2), cCH, CH2 (×3), CH3 |
| 5-pentyloxolan-2-one/γ-nonalactone | 104-61-0 | C9H16O2 | cCOO, cCH2 (×2), cCH, CH2 (×4), CH3 |
| 5-hexyloxolan-2-one/γ-decalactone | 706-14-9 | C10H18O2 | cCOO, cCH2 (×2), cCH, CH2 (×5), CH3 |
| 6-methyloxan-2-one/δ-caprolactone | 823-22-3 | C6H10O2 | cCOO, cCH2 (×3), cCH, CH3 |
| 6-ethyloxan-2-one/δ-heptalactone | 3301-90-4 | C7H12O2 | cCOO, cCH2 (×3), cCH, CH2, CH3 |
| 6-propyloxan-2-one/δ-octalactone | 698-76-0 | C8H14O2 | cCOO, cCH2 (×3), cCH, CH2 (×2), CH3 |
| 6-butyloxan-2-one/δ-nonalactone | 3301-94-8 | C9H16O2 | cCOO, cCH2 (×3), cCH, CH2 (×3), CH3 |
| 6-pentyloxan-2-one/δ-decalactone | 705-86-2 | C10H18O2 | cCOO, cCH2 (×3), cCH, CH2 (×4), CH3 |
| cyclohexane | 110-82-7 | C6H12 | cCH2 (×6) |
| n-alkanes (ethane, propane, n-butane, etc.) | − | CnH2n+2 | CH3 (×2), CH2 [×(n – 2)], for n ≥ 2 |
| methanol | 67-56-1 | CH4O | CH3OH |
| 1-alcohols (ethanol, propan-1-ol, butan-1-ol, etc.) | − | CnH2n+2O | CH3, CH2 [×(n – 2)], CH2OH, for n ≥ 2 |
| 1,4-butanediol | 110-63-4 | C4H10O2 | CH2 (×2), CH2OH (×2) |
| 2-methy-1-propanol | 78-83-1 | C4H10O | CH3 (×2), CH, CH2OH |
| 3-methyl-1-butanol | 123-51-3 | C5H12O | CH3 (×2), CH2, CH, CH2OH |
| 2-alcohols (propan-2-ol, butan-2-ol, pentan-2-ol, etc.) | − | CnH2n+2O | CH3 (×2), CH2 [×(n – 3)], CHOH, for n ≥ 3 |
| acetone | 67-64-1 | C3H6O | CH3COCH3 |
| 2-ketones (butanone, pentan-2-one, hexan-2-one, etc.) | − | CnH2nO | CH3CO, CH2 [×(n – 3)], CH3, for n ≥ 4 |
| methyl acetate | 79-20-9 | C3H6O2 | COO, CH3 (×2) |
| ethyl acetate | 141-78-6 | C4H8O2 | COO, CH2, CH3 (×2) |
| diethyl butanedioate | 123-25-1 | C8H14O4 | COO (×2), CH2 (×4), CH3 (×2) |
| benzene | 71-43-2 | C6H6 | aCH (×6) |
| toluene | 108-88-3 | C7H8 | aCH (×5), aCCH3 |
| ethylbenzene | 100-41-4 | C8H10 | aCH (×5), aCCH2, CH3 |
| water | 7732-18-5 | H2O | H2O |
| carbon dioxide | 124-38-9 | CO2 | CO2 |
We introduce here a new cyclic ester group, denoted as cCOO. Ester groups in linear chains can already be modeled with SAFT-γ Mie using the COO group developed in previous work.8 The influence of the heterocycle means, however, that a new cCOO group needs to be characterized for an accurate description of the lactone family. It is worth noting that a cyclic ester group66 (labeled cy-COO-C) has been introduced in the Modified UNIFAC67 approach. As in the case of the linear COO group, two association sites of type e are included in our new cCOO group; no like association occurs between cCOO groups, as no e–e bonding is allowed, but these electronegative sites can bond to H sites in other molecules.
We refer to molecules composed only of one cCOO group and a number of cCH2 groups51 as ring lactones: three cCH2 groups for oxolan-2-one (Figure 1a), four cCH2 groups for oxan-2-one, and five cCH2 groups for oxepan-2-one (Figure 1d). In addition, we also consider lactones that incorporate an alkyl side chain next to the cCOO group; the intramolecular esterification of hydroxy acids favors the formation of these branches when the OH group of the hydroxy acid is not terminal. Two examples of lactones with side chains can be seen in Figure 1b,c: 5-methyloxolan-2-one and 6-propyloxan-2-one, respectively. In order to treat these molecules, the junction between the ring and the side chain is modeled with a cCH group.41 A methyl side chain is composed of a CH3 group8 only, and longer linear alkyl chains are modeled by one or several CH2 groups,8 with a terminal CH3 group.
We consider experimental data for 5-alkyloxolan-2-ones (from methyl to hexyl chains) and for 6-alkyloxan-2-ones (from methyl to pentyl chains) to characterize the relevant group interactions. The matrix of group interactions used in current and previous work is shown in Table 3, and the like and unlike group parameter values can be found in Tables 4, 5, and 6 with the corresponding references as appropriate. In order to characterize the group interactions, we use pure-component58,69−82 and mixture31,66,83−89 data of relevant systems. The new group interactions required to model pure lactones and mixtures of lactones and linear alkanes are cCOO–cCOO, cCOO–cCH2, cCOO–cCH, cCOO–CH3, and cCOO–CH2. The results for pure lactones are detailed in the current section; the results for mixtures of lactones and linear alkanes are detailed in the next section. The experimental and calculated vapor pressures (Pvap), single-phase densities (ρ), and vaporization enthalpies (Δhvap) for oxolan-2-one, oxan-2-one, and oxepan-2-one are compared in Figure 2. As expected, lower vapor pressures and higher vaporization enthalpies are reported for larger ring sizes. For a given temperature, the vapor pressure and liquid-phase density decrease with increasing ring size of the lactone, while the vaporization enthalpy increases with increasing ring size. Good agreement between the calculations and experiments can be seen, although we note that limited data are available for these molecules.
Table 3. Group Interactions Used to Model Saturated Lactones in a Range of Solvents With the SAFT-γ Mie Approacha.
Blue shading denotes that group interaction parameters have been optimized in previous work. The new (N) optimized parameters developed in our current work are denoted by yellow shading. Dark blue shading denotes unlike interaction parameters developed in a separate recent work (R) to be published.68 Gray shading denotes that unlike interaction parameters are predicted using combining rules (CR).8
Table 4. SAFT-γ Mie Group Like Parameters of the Groups Considered in Our Current Work (Excluding Association)a.
| k | group | ν*k | Sk | σkk/Å | λrkk | λakk | (εkk/kB)/K | NST,k | nk,H | nk, e1 | nk, e2 | ref |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | cCOO | 2 | 0.5787 | 3.2787 | 11.855 | 6.0000 | 763.67 | 1 | − | 2 | − | * |
| 2 | cCH2 | 1 | 0.2475 | 4.7852 | 20.386 | 6.0000 | 477.36 | − | − | − | − | (51) |
| 3 | cCH | 1 | 0.0961 | 5.4116 | 8.0000 | 6.0000 | 699.92 | − | − | − | − | (41) |
| 4 | CH3 | 1 | 0.5726 | 4.0772 | 15.050 | 6.0000 | 256.77 | − | − | − | − | (8) |
| 5 | CH2 | 1 | 0.2293 | 4.8801 | 19.871 | 6.0000 | 473.39 | − | − | − | − | (8) |
| 6 | CH | 1 | 0.0721 | 5.2950 | 8.0000 | 6.0000 | 95.621 | − | − | − | − | (51) |
| 7 | CH3OH | 2 | 0.8352 | 3.2462 | 19.235 | 6.0000 | 307.69 | 2 | 1 | 2 | − | (51) |
| 8 | CH2OH | 2 | 0.5854 | 3.4054 | 22.699 | 6.0000 | 407.22 | 2 | 1 | 2 | − | (36) |
| 9 | CHOH | 2 | 0.1896 | 4.5381 | 18.185 | 6.0000 | 599.66 | 2 | 1 | 2 | − | (11) |
| 10 | CH3COCH3 | 3 | 0.7214 | 3.5981 | 17.433 | 6.0000 | 286.02 | 3 | 1 | 1 | 1 | (51) |
| 11 | CH3CO | 2 | 0.5469 | 3.9112 | 19.050 | 6.0000 | 525.22 | 1 | − | 2 | − | (39) |
| 12 | COO | 1 | 0.6526 | 3.9939 | 31.189 | 6.0000 | 868.92 | 1 | − | 2 | − | (8) |
| 13 | aCH | 1 | 0.3218 | 4.0578 | 14.756 | 6.0000 | 371.53 | 1 | − | 1 | − | (51) |
| 14 | aCCH3 | 1 | 0.3166 | 5.4874 | 23.627 | 6.0000 | 651.41 | 1 | − | 1 | − | (37,90) |
| 15 | aCCH2 | 1 | 0.2086 | 5.2648 | 8.5433 | 6.0000 | 591.56 | 1 | − | 1 | − | (51) |
| 16 | H2O | 1 | 1.0000 | 3.0063 | 17.020 | 6.0000 | 266.68 | 2 | 2 | 2 | − | (9,10) |
| 17 | CO2 | 2 | 0.8468 | 3.0500 | 26.408 | 5.0550 | 207.89 | 2 | − | 1 | 1 | (90) |
The asterisk * in the ref column indicates that the cCOO group is characterized in the current work.
Table 5. Unlike Group Parameters (Excluding Association) for Use with the SAFT-γ Mie Approacha.
| k | l | group k | group l | (εkl/kB)/K | λrkl | ref |
|---|---|---|---|---|---|---|
| 1 | 1 | cCOO | cCOO | 763.67 | 11.855 | * |
| 1 | 2 | cCOO | cCH2 | 414.07 | 11.043 | * |
| 1 | 3 | cCOO | cCH | 519.28 | 8.2819 | * |
| 1 | 4 | cCOO | CH3 | 411.61 | 33.394 | * |
| 1 | 5 | cCOO | CH2 | 618.67 | 31.395 | * |
| 1 | 6 | cCOO | CH | 0.0000 | CR | * |
| 1 | 7 | cCOO | CH3OH | 434.59 | CR | * |
| 1 | 8 | cCOO | CH2OH | 500.14 | CR | * |
| 1 | 9 | cCOO | CHOH | 373.30 | CR | * |
| 1 | 10 | cCOO | CH3COCH3 | 482.68 | CR | * |
| 1 | 11 | cCOO | CH3CO | 625.98 | CR | * |
| 1 | 12 | cCOO | COO | 756.57 | 9.9399 | * |
| 1 | 13 | cCOO | aCH | 543.64 | 17.749 | * |
| 1 | 14 | cCOO | aCCH3 | 460.79 | 9.2834 | * |
| 1 | 15 | cCOO | aCCH2 | 464.16 | 8.0000 | * |
| 1 | 16 | cCOO | H2O | 419.86 | CR | * |
| 1 | 17 | cCOO | CO2 | 261.21 | 8.0000 | * |
| 2 | 2 | cCH2 | cCH2 | 477.36 | 20.386 | (51) |
| 2 | 3 | cCH2 | cCH | 321.71 | CR | (41) |
| 2 | 4 | cCH2 | CH3 | 355.95 | CR | (51) |
| 2 | 5 | cCH2 | CH2 | 469.67 | CR | (51) |
| 2 | 6 | cCH2 | CH | 570.45 | CR | (51) |
| 2 | 7 | cCH2 | CH3OH | 361.42 | CR | (68) |
| 2 | 8 | cCH2 | CH2OH | 424.64 | CR | (68) |
| 2 | 9 | cCH2 | CHOH | 554.50 | CR | (11) |
| 2 | 10 | cCH2 | CH3COCH3 | 352.19 | CR | (11) |
| 2 | 11 | cCH2 | CH3CO | 435.86 | CR | (68) |
| 2 | 12 | cCH2 | COO | 498.60 | CR | (36) |
| 2 | 13 | cCH2 | aCH | 393.05 | 15.377 | (39) |
| 2 | 14 | cCH2 | aCCH3 | 540.63 | 21.082 | (39) |
| 2 | 15 | cCH2 | aCCH2 | 439.78 | 9.9058 | (39) |
| 2 | 16 | cCH2 | H2O | 350.99 | 28.000 | (41) |
| 2 | 17 | cCH2 | CO2 | 269.68 | CR | (42) |
| 3 | 3 | cCH | cCH | 699.92 | 8.0000 | (41) |
| 3 | 4 | cCH | CH3 | 690.17 | CR | (41) |
| 3 | 5 | cCH | CH2 | 522.57 | CR | (41) |
| 3 | 6 | cCH | CH | 0.0000 | CR | (68) |
| 3 | 7 | cCH | CH3OH | 345.00 | CR | (68) |
| 3 | 8 | cCH | CH2OH | 242.45 | CR | (68) |
| 3 | 9 | cCH | CHOH | 640.38 | CR | * |
| 3 | 10 | cCH | CH3COCH3 | 409.28 | CR | (68) |
| 3 | 11 | cCH | CH3CO | 265.24 | CR | (68) |
| 3 | 12 | cCH | COO | 0.0000 | CR | (68) |
| 3 | 13 | cCH | aCH | 377.21 | CR | (39) |
| 3 | 14 | cCH | aCCH3 | 792.29 | CR | (39) |
| 3 | 15 | cCH | aCCH2 | 162.65 | CR | (39) |
| 3 | 16 | cCH | H2O | 377.16 | 22.265 | (41) |
| 3 | 17 | cCH | CO2 | 294.99 | CR | (42) |
| 4 | 4 | CH3 | CH3 | 256.77 | 15.050 | (8) |
| 4 | 5 | CH3 | CH2 | 350.77 | CR | (8) |
| 4 | 6 | CH3 | CH | 387.48 | CR | (51) |
| 4 | 7 | CH3 | CH3OH | 275.76 | 15.537 | (51) |
| 4 | 8 | CH3 | CH2OH | 333.20 | CR | (36) |
| 4 | 9 | CH3 | CHOH | 479.38 | CR | (11) |
| 4 | 10 | CH3 | CH3COCH3 | 233.48 | 14.449 | (51) |
| 4 | 11 | CH3 | CH3CO | 344.57 | CR | (39) |
| 4 | 12 | CH3 | COO | 402.75 | CR | (8) |
| 4 | 13 | CH3 | aCH | 305.81 | CR | (51) |
| 4 | 14 | CH3 | aCCH3 | 358.58 | CR | (36) |
| 4 | 15 | CH3 | aCCH2 | 396.91 | CR | (51) |
| 4 | 16 | CH3 | H2O | 358.18 | 100.00 | (36) |
| 4 | 17 | CH3 | CO2 | 205.70 | CR | (90) |
| 5 | 5 | CH2 | CH2 | 473.39 | 19.871 | (8) |
| 5 | 6 | CH2 | CH | 506.21 | CR | (51) |
| 5 | 7 | CH2 | CH3OH | 341.41 | 17.050 | (51) |
| 5 | 8 | CH2 | CH2OH | 423.17 | CR | (36) |
| 5 | 9 | CH2 | CHOH | 517.64 | CR | (11) |
| 5 | 10 | CH2 | CH3COCH3 | 299.48 | 11.594 | (51) |
| 5 | 11 | CH2 | CH3CO | 431.49 | CR | (39) |
| 5 | 12 | CH2 | COO | 498.86 | CR | (8) |
| 5 | 13 | CH2 | aCH | 415.64 | CR | (51) |
| 5 | 14 | CH2 | aCCH3 | 569.18 | CR | (36) |
| 5 | 15 | CH2 | aCCH2 | 454.16 | CR | (51) |
| 5 | 16 | CH2 | H2O | 423.63 | 100.00 | (36) |
| 5 | 17 | CH2 | CO2 | 276.45 | CR | (90) |
| 6 | 6 | CH | CH | 95.621 | 8.0000 | (51) |
| 6 | 7 | CH | CH3OH | CR | CR | − |
| 6 | 8 | CH | CH2OH | 329.22 | CR | (37) |
| 6 | 9 | CH | CHOH | 0.0000 | CR | (11) |
| 6 | 10 | CH | CH3COCH3 | 637.29 | CR | (51) |
| 6 | 11 | CH | CH3CO | 321.91 | CR | (39) |
| 6 | 12 | CH | COO | 353.65 | CR | (37) |
| 6 | 13 | CH | aCH | 441.43 | CR | (51) |
| 6 | 14 | CH | aCCH3 | 769.36 | 8.0000 | (39) |
| 6 | 15 | CH | aCCH2 | 65.410 | CR | (51) |
| 6 | 16 | CH | H2O | 275.75 | CR | (37) |
| 6 | 17 | CH | CO2 | CR | CR | − |
| 7 | 7 | CH3OH | CH3OH | 307.69 | 19.235 | (51) |
| 7 | 8 | CH3OH | CH2OH | CR | CR | − |
| 7 | 9 | CH3OH | CHOH | CR | CR | − |
| 7 | 10 | CH3OH | CH3COCH3 | CR | CR | − |
| 7 | 11 | CH3OH | CH3CO | CR | CR | − |
| 7 | 12 | CH3OH | COO | CR | CR | − |
| 7 | 13 | CH3OH | aCH | 330.19 | CR | (39) |
| 7 | 14 | CH3OH | aCCH3 | 405.45 | CR | (39) |
| 7 | 15 | CH3OH | aCCH2 | CR | CR | − |
| 7 | 16 | CH3OH | H2O | 278.45 | CR | (51) |
| 7 | 17 | CH3OH | CO2 | 157.83 | 8.3462 | (90) |
| 8 | 8 | CH2OH | CH2OH | 407.22 | 22.699 | (36) |
| 8 | 9 | CH2OH | CHOH | 389.23 | CR | (11) |
| 8 | 10 | CH2OH | CH3COCH3 | 338.47 | CR | (11) |
| 8 | 11 | CH2OH | CH3CO | CR | CR | − |
| 8 | 12 | CH2OH | COO | CR | CR | − |
| 8 | 13 | CH2OH | aCH | 386.05 | CR | (37) |
| 8 | 14 | CH2OH | aCCH3 | 486.62 | CR | (37) |
| 8 | 15 | CH2OH | aCCH2 | 434.37 | CR | (37) |
| 8 | 16 | CH2OH | H2O | 353.37 | CR | (36) |
| 8 | 17 | CH2OH | CO2 | 312.30 | CR | (42) |
| 9 | 9 | CHOH | CHOH | 599.66 | 18.185 | (11) |
| 9 | 10 | CHOH | CH3COCH3 | 340.81 | CR | (11) |
| 9 | 11 | CHOH | CH3CO | CR | CR | − |
| 9 | 12 | CHOH | COO | CR | CR | − |
| 9 | 13 | CHOH | aCH | 512.16 | CR | (11) |
| 9 | 14 | CHOH | aCCH3 | 762.86 | CR | (11) |
| 9 | 15 | CHOH | aCCH2 | 357.91 | CR | (11) |
| 9 | 16 | CHOH | H2O | 479.16 | CR | (11) |
| 9 | 17 | CHOH | CO2 | CR | CR | − |
| 10 | 10 | CH3COCH3 | CH3COCH3 | 286.02 | 17.433 | (51) |
| 10 | 11 | CH3COCH3 | CH3CO | CR | CR | − |
| 10 | 12 | CH3COCH3 | COO | 547.44 | CR | (11) |
| 10 | 13 | CH3COCH3 | aCH | 333.11 | CR | (51) |
| 10 | 14 | CH3COCH3 | aCCH3 | 479.55 | 35.957 | (39) |
| 10 | 15 | CH3COCH3 | aCCH2 | 394.83 | CR | (51) |
| 10 | 16 | CH3COCH3 | H2O | 287.26 | CR | (51) |
| 10 | 17 | CH3COCH3 | CO2 | CR | CR | − |
| 11 | 11 | CH3CO | CH3CO | 525.22 | 19.050 | (39) |
| 11 | 12 | CH3CO | COO | CR | CR | |
| 11 | 13 | CH3CO | aCH | 426.72 | 18.030 | (39) |
| 11 | 14 | CH3CO | aCCH3 | 552.62 | 36.429 | (39) |
| 11 | 15 | CH3CO | aCCH2 | 663.71 | 30.712 | (39) |
| 11 | 16 | CH3CO | H2O | CR | CR | − |
| 11 | 17 | CH3CO | CO2 | CR | CR | − |
| 12 | 12 | COO | COO | 868.92 | 31.189 | (8) |
| 12 | 13 | COO | aCH | 534.18 | 22.088 | (39) |
| 12 | 14 | COO | aCCH3 | 595.48 | 15.874 | (39) |
| 12 | 15 | COO | aCCH2 | 265.62 | 9.3393 | (39) |
| 12 | 16 | COO | H2O | 396.81 | 15.140 | (91) |
| 12 | 17 | COO | CO2 | CR | CR | − |
| 13 | 13 | aCH | aCH | 371.53 | 14.756 | (51) |
| 13 | 14 | aCH | aCCH3 | 471.23 | CR | (90) |
| 13 | 15 | aCH | aCCH2 | 416.69 | CR | (51) |
| 13 | 16 | aCH | H2O | 357.78 | 38.640 | (51) |
| 13 | 17 | aCH | CO2 | CR | CR | − |
| 14 | 14 | aCCH3 | aCCH3 | 651.41 | 23.627 | (37,90) |
| 14 | 15 | aCCH3 | aCCH2 | CR | CR | − |
| 14 | 16 | aCCH3 | H2O | 360.70 | CR | (37) |
| 14 | 17 | aCCH3 | CO2 | CR | CR | − |
| 15 | 15 | aCCH2 | aCCH2 | 591.56 | 8.5433 | (51) |
| 15 | 16 | aCCH2 | H2O | 329.03 | CR | (37) |
| 15 | 17 | aCCH2 | CO2 | CR | CR | − |
| 16 | 16 | H2O | H2O | 266.68 | 17.020 | (9,10) |
| 16 | 17 | H2O | CO2 | 226.38 | CR | (90) |
| 17 | 17 | CO2 | CO2 | 207.89 | 26.408 | (90) |
The asterisk * indicates that the parameters are characterized in the current work.
Table 6. Group Association Parameters for Use with the SAFT-γ Mie Approacha.
| k | l | group k | site a of group k | group l | site b of group l | (εHBkl,ab/kB)/K | KHBkl,ab/Å3 | ref |
|---|---|---|---|---|---|---|---|---|
| 1 | 7 | cCOO | e1 | CH3OH | H | 1267.6 | 1095.9 | * |
| 1 | 8 | cCOO | e1 | CH2OH | H | 1496.8 | 626.15 | * |
| 1 | 9 | cCOO | e1 | CHOH | H | 1674.2 | 635.00 | * |
| 1 | 16 | cCOO | e1 | H2O | H | 1385.6 | 576.40 | * |
| 7 | 7 | CH3OH | H | CH3OH | e1 | 2062.1 | 106.57 | (51) |
| 7 | 16 | CH3OH | e1 | H2O | H | 1993.5 | 104.11 | (51) |
| 7 | 16 | CH3OH | H | H2O | e1 | 1993.5 | 104.11 | (51) |
| 8 | 8 | CH2OH | H | CH2OH | e1 | 2097.9 | 62.309 | (36) |
| 8 | 9 | CH2OH | H | CHOH | e1 | 2500.0 | 10.444 | (11) |
| 8 | 9 | CH2OH | e1 | CHOH | H | 1464.1 | 591.55 | (11) |
| 8 | 10 | CH2OH | e1 | CH3COCH3 | H | 686.93 | 585.99 | (11) |
| 8 | 10 | CH2OH | H | CH3COCH3 | e1 | 1844.8 | 991.95 | (11) |
| 8 | 16 | CH2OH | e1 | H2O | H | 2153.2 | 147.40 | (36) |
| 8 | 16 | CH2OH | H | H2O | e1 | 621.68 | 425.00 | (36) |
| 9 | 9 | CHOH | H | CHOH | e1 | 2480.6 | 8.4740 | (11) |
| 9 | 10 | CHOH | e1 | CH3COCH3 | H | 1186.9 | 731.08 | (11) |
| 9 | 10 | CHOH | H | CH3COCH3 | e1 | 1323.1 | 635.37 | (11) |
| 9 | 16 | CHOH | e1 | H2O | H | 2140.9 | 19.478 | (11) |
| 9 | 16 | CHOH | H | H2O | e1 | 2289.1 | 63.813 | (11) |
| 10 | 10 | CH3COCH3 | H | CH3COCH3 | e1 | 980.20 | 2865.2 | (51) |
| 10 | 16 | CH3COCH3 | H | H2O | e1 | 1386.8 | 188.83 | (51) |
| 10 | 16 | CH3COCH3 | e1 | H2O | H | 1588.7 | 772.77 | (51) |
| 10 | 16 | CH3COCH3 | e2 | H2O | H | 417.24 | 1304.3 | (51) |
| 12 | 16 | COO | e1 | H2O | H | 1245.8 | 454.98 | (91) |
| 13 | 16 | aCH | e1 | H2O | H | 563.56 | 339.61 | (51) |
| 14 | 16 | aCCH3 | e1 | H2O | H | 563.56 | 339.61 | (37) |
| 15 | 16 | aCCH2 | e1 | H2O | H | 563.56 | 339.61 | (37) |
| 16 | 16 | H2O | H | H2O | e1 | 1985.4 | 101.69 | (9,10) |
| 16 | 17 | H2O | e1 | CO2 | e1 | 1398.1 | 91.419 | (90) |
The asterisk * indicates that the parameters are characterized in the current work.
Figure 2.

Selected thermodynamic properties of ring lactones: oxolan-2-one (light blue), oxan-2-one (red), and oxepan-2-one (dark red). The curves represent the calculations with SAFT-γ Mie. Experimental data used in the estimation of the group-interaction parameters are represented with filled symbols, and those not used are represented with open symbols. (a) Vapor pressure, with experimental data for oxolan-2-one (triangles69 and diamonds70), oxan-2-one,71 and oxepan-2-one.72 (b) Temperature–density diagram, with experimental data for oxolan-2-one,76 oxan-2-one,79 and oxepan-2-one.80 Saturation densities are represented by the continuous curves, and densities at 1 bar are represented by the dashed curves and lines. (c) Vaporization enthalpy, with experimental data for oxolan-2-one,69 oxan-2-one,71 and oxepan-2-one.72 Thermodynamic conditions and the accuracy of the calculations are detailed in Table 7 and in the Zenodo datafile.
The family of 5-alkyloxolan-2-ones corresponds to lactones with five atoms in the lactone ring and an alkyl side chain (in position 5) next to the oxygen of the ring (position 1). Similarly, the family of 6-alkyloxan-2-ones corresponds to lactones with six atoms in the lactone ring and an alkyl side chain (in position 6). The calculated vapor pressures, single-phase densities, and vaporization enthalpies are compared with the corresponding experimental data for pure 5-alkyloxolan-2-ones and 6-alkyloxan-2-ones with several side-chain lengths in Figure 3 and Figure 4, respectively. The vapor pressure and liquid-phase density decrease with increasing length of the side chain, while the vaporization enthalpy increases with increasing length of the side chain. Very good quantitative agreement can be seen for alkyllactones although the comparison with experimental data is possible only for a small temperature range, far from the critical temperature.
Figure 3.

Selected thermodynamic properties of oxolan-2-one (light blue) and alkyloxolan-2-ones: 5-methyloxolan-2-one, 5-ethyloxolan-2-one, 5-propyloxolan-2-one, 5-butyloxolan-2-one, 5-pentyloxolan-2-one, and 5-hexyloxolan-2-one (from dark blue to pale blue). The curves represent the calculations with SAFT-γ Mie. Experimental data used in the estimation of group-interaction parameters are represented with filled symbols, and those not used are represented with open symbols. (a) Vapor pressure, with experimental data of oxolan-2-one (triangles69 and diamonds70), 5-methyloxolan-2-one (triangles58 and diamonds73), 5-ethyloxolan-2-one,74 5-propyloxolan-2-one,74 5-butyloxolan-2-one,75 5-pentyloxolan-2-one,74 and 5-hexyloxolan-2-one.74 (b) Temperature–density diagram, with experimental data of oxolan-2-one,76 5-methyloxolan-2-one,73 5-butyloxolan-2-one,81 5-pentyloxolan-2-one,81 and 5-hexyloxolan-2-one.81 Saturation densities are represented by the continuous curves, and densities at 1 bar are represented by the dashed curves and lines. (c) Vaporization enthalpy, with experimental data of oxolan-2-one,69 5-methyloxolan-2-one,74 5-ethyloxolan-2-one,74 5-propyloxolan-2-one,74 5-butyloxolan-2-one,75 5-pentyloxolan-2-one,74 and 5-hexyloxolan-2-one.74 Thermodynamic conditions and the accuracy of the calculations are detailed in Table 7 and in the Zenodo datafile.
Figure 4.

Selected thermodynamic properties of oxan-2-one (red) and alkyloxan-2-ones: 6-methyloxan-2-one, 6-ethyloxan-2-one, 6-propyloxan-2-one, 6-butyloxan-2-one, and 6-pentyloxan-2-one (from dark orange to pale orange). The curves represent the calculations with SAFT-γ Mie. Experimental data used in the estimation of group-interaction parameters are represented with filled symbols, and those not used are represented with open symbols. (a) Vapor pressure, with experimental data of oxan-2-one,71 6-methyloxan-2-one,71 6-propyloxan-2-one,71 6-butyloxan-2-one,71 and 6-pentyloxan-2-one.71 (b) Temperature–density diagram, with experimental data of oxan-2-one,71 and 6-methyloxan-2-one.82 Saturation densities are represented by the solid curves, and densities at 1 bar are represented by the dashed curves and line. (c) Vaporization enthalpy, with experimental data of oxan-2-one,71 6-methyloxan-2-one,71 6-propyloxan-2-one,71 6-butyloxan-2-one,71 and 6-pentyloxan-2-one.71 Thermodynamic conditions and accuracy are detailed in Table 7 and in the Zenodo datafile.
We report %AAD and AAD in order to assess the performance of our model. It is especially relevant to consider both measures, given the limited data available for comparison and the low-temperature and pressure nature of the data. The accuracy of the results for pure lactones is summarized in Table 7, where %AADs and AADs can be found for each system and property. The %AADs for the vapor pressure of oxolan-2-one and oxepan-2-one are both smaller than 10% (5.063%, and 7.853%, respectively). The AAD obtained for the vapor pressure of oxolan-2-one (1796 Pa) is, however, much larger than the AAD obtained for oxepan-2-one (5.722 Pa) because of the difference in the temperature ranges (289–478 and 283–353 K, respectively). The largest %AAD shown in Table 7 is for the vapor pressure of oxan-2-one (44.58%) but corresponds to a small AAD (46.23 Pa). The largest AAD is obtained for the vapor pressure of 5-methyloxolan-2-one (1929 Pa) because of the large temperature range (308–470 K). All %AADs for the liquid-phase densities and the vaporization enthalpy of the pure lactones considered are smaller than 5%. In absolute terms, this corresponds to a maximum AAD in liquid-phase densities for oxepan-2-one (51.40 kg/m3) and a maximum AAD in vaporization enthalpy for 6-pentyloxan-2-one (2441 J/mol).
Table 7. Overview of the Accuracy of SAFT-γ Mie in the Calculation of Vapor Pressures Pvap(T), Densities ρ(T,P), and Vaporization Enthalpies Δhvap(T) for Pure Lactones, Where NDs,p Is the Number of Experimental Data Points Used in the Parameter Estimation, and ND,totals,p Is the Number of Experimental Data Used to Calculate %AADsp and AADsp for System s and Property p.
| compound s | T/K range | NDs,p | ND,totals,p | %AADsPvap(T) | AADsPvap (T)/Pa | figure | ref |
|---|---|---|---|---|---|---|---|
| oxolan-2-one | 289–478 | 11 | 26 | 5.063 | 1796 | 2(a,b), 3(a,b) | (69,70) |
| oxan-2-one | 278–353 | 9 | 51 | 44.58 | 46.23 | 2(a,b) | (71) |
| oxepan-2-one | 283–353 | 9 | 16 | 7.853 | 5.722 | 2(a,b) | (72) |
| 5-methyloxolan-2-one | 308–470 | 9 | 33 | 25.17 | 1929 | 3(a,b) | (58,73) |
| 5-ethyloxolan-2-one | 283–353 | 9 | 24 | 32.58 | 41.39 | 3(a,b) | (74) |
| 5-propyloxolan-2-one | 298–363 | 7 | 14 | 22.26 | 31.59 | 3(a,b) | (74) |
| 5-butyloxolan-2-one | 293–298 | 1 | 2 | 28.76 | 0.6564 | 3(a,b) | (75) |
| 5-pentyloxolan-2-one | 296–363 | 7 | 14 | 21.01 | 6.107 | 3(a,b) | (74) |
| 5-hexyloxolan-2-one | 298–365 | 10 | 23 | 17.58 | 2.262 | 3(a,b) | (74) |
| 6-methyloxan-2-one | 283–353 | 10 | 29 | 10.09 | 4.150 | 4(a,b) | (71) |
| 6-propyloxan-2-one | 288–353 | 10 | 18 | 1.663 | 0.3405 | 4(a,b) | (71) |
| 6-butyloxan-2-one | 293–348 | 7 | 12 | 8.045 | 0.6939 | 4(a,b) | (71) |
| 6-pentyloxan-2-one | 309–358 | 10 | 23 | 30.63 | 3.206 | 4(a,b) | (71) |
| compound s | T/K range | P/MPa range | NDs,p | ND,totals,p | %AADs ρ(T, P) | AADs ρ(T,P)/(kg/m3) | figure | ref |
|---|---|---|---|---|---|---|---|---|
| oxolan-2-one | 253–473 | 0.101–35.0 | 13 | 363 | 1.021 | 10.90 | 2(c), 3(c) | (76,77) |
| oxan-2-one | 293–318 | 0.101–10.0 | 4 | 10 | 3.416 | 37.62 | 2(c) | (78),79 |
| oxepan-2-one | 293–323 | 0.100 | 3 | 7 | 4.834 | 51.40 | 2(c) | (80) |
| 5-methyloxolan-2-one | 293–453 | 0.186–0.983 | 14 | 72 | 1.257 | 11.92 | 3(c) | (73) |
| 5-butyloxolan-2-one | 273–293 | 0.101 | 0 | 2 | 1.838 | 18.09 | 3(c) | (81) |
| 5-pentyloxolan-2-one | 273–290 | 0.101 | 0 | 2 | 1.870 | 18.18 | 3(c) | (81) |
| 5-hexyloxolan-2-one | 273–294 | 0.101 | 0 | 2 | 2.109 | 20.22 | 3(c) | (81) |
| 6-methyloxan-2-one | 294 | 0.101 | 0 | 1 | 2.399 | 24.87 | 4(c) | (82) |
| compound s | T/K range | ΝDs,p | ND,totals,p | %AADs Δhvap(T) | AADs Δhvap (T)/(J/mol) | figure | ref |
|---|---|---|---|---|---|---|---|
| oxolan-2-one | 289–329 | 10 | 14 | 2.462 | 1329 | 2(d), 3(d) | (69) |
| oxan-2-one | 278–353 | 9 | 51 | 3.659 | 2095 | 2(d) | (71) |
| oxepan-2-one | 283–353 | 9 | 16 | 0.7581 | 454.7 | 2(d) | (72) |
| 5-methyloxolan-2-one | 276–350 | 10 | 22 | 2.751 | 1453 | 3(d) | (74) |
| 5-ethyloxolan-2-one | 283–353 | 9 | 24 | 4.048 | 2273 | 3(d) | (74) |
| 5-propyloxolan-2-one | 298–363 | 7 | 14 | 2.349 | 1407 | 3(d) | (74) |
| 5-butyloxolan-2-one | 298–324 | 2 | 2 | 3.159 | 2054 | 3(d) | (75) |
| 5-pentyloxolan-2-one | 296–363 | 7 | 14 | 3.400 | 2291 | 3(d) | (74) |
| 5-hexyloxolan-2-one | 298–365 | 10 | 23 | 2.141 | 1546 | 3(d) | (74) |
| 6-methyloxan-2-one | 283–353 | 10 | 29 | 3.988 | 2388 | 4(d) | (71) |
| 6-propyloxan-2-one | 288–353 | 10 | 18 | 0.6015 | 392.0 | 4(d) | (71) |
| 6-butyloxan-2-one | 293–348 | 7 | 12 | 1.865 | 1281 | 4(d) | (71) |
| 6-pentyloxan-2-one | 309–358 | 10 | 23 | 3.458 | 2441 | 4(d) | (71) |
3.1.2. Binary Mixtures of Lactones + Linear/Cyclic Alkanes
We now consider binary mixtures of lactones with cyclohexane or n-alkanes; the groups involved in these mixtures are the same as the groups involved in pure lactones. Specifically, we consider mixtures containing linear n-alkanes from n-hexane to n-octane and from n-undecane to n-nonadecane. Cyclohexane is modeled using six cCH2 groups; linear alkanes comprise CH2 and CH3 groups. As mentioned in the previous section, the experimental data related to these mixtures (summarized in Table 8) are used together with the experimental data for pure lactones (cf. Table 7) to estimate the parameters of the cCOO group and the unlike interactions (specifically for cCOO–CH2 and cCOO–CH3).
Table 8. Overview of the Accuracy of SAFT-γ Mie in the Calculation of the Azeotrope Composition xazoxolan-2-one and Temperature Taz, Liquid–Liquid Equilibrium Compositions xLLE1, Solubilities xsat1, and Excess Molar Enthalpies Δhmix for Binary Mixtures of Lactones and Hydrocarbons, Where NDs,p Is the Number of Experimental Data Used in the Parameter Estimation, and ND,totals,p Is the Number of Experimental Data Used to Calculate %AADsp and AADsp for System s and Property p.
| system s (1 + 2) | T/K range | P/MPa range | x1 range | NDs,p | Ntotals,p | %AADsxazoxolan-2-one | AADsxazoxolan-2-one | figure | ref |
|---|---|---|---|---|---|---|---|---|---|
| oxolan-2-one + n-octane | − | 0.101 | − | 0 | 1 | 10.34 | 0.007960 | 5(e), 6(a) | (83) |
| oxolan-2-one + n-undecane | − | 0.00267 | − | 0 | 1 | 1.883 | 0.008285 | 6(a) | (83) |
| oxolan-2-one + n-dodecane | − | 0.00267 | − | 0 | 1 | 1.241 | 0.008252 | 6(a) | (83) |
| oxolan-2-one + n-tridecane | − | 0.00267 | − | 0 | 1 | 1.635 | 0.01329 | 6(a) | (83) |
| oxolan-2-one + n-tetradecane | − | 0.00267 | − | 0 | 1 | 0.9825 | 0.008941 | 6(a) | (83) |
| oxolan-2-one + n-pentadecane | − | 0.00267 | − | 0 | 1 | 1.470 | 0.01417 | 6(a) | (83) |
| oxolan-2-one + n-hexadecane | − | 0.00267 | − | 0 | 1 | 1.075 | 0.01062 | 6(a) | (83) |
| oxolan-2-one + n-heptadecane | − | 0.00267 | − | 0 | 1 | 0.3060 | 0.003036 | 6(a) | (83) |
| oxolan-2-one + n-octadecane | − | 0.00267 | − | 0 | 1 | 0.003978 | 0.00003958 | 6(a) | (83) |
| oxolan-2-one + n-nonadecane | − | 0.00267 | − | 0 | 1 | 0.03086 | 0.0003080 | 6(a) | (83) |
| system s (1 + 2) | T/K range | P/MPa range | x1 range | NDs,p | Ntotals,p | %AADsTaz | AADsTaz/K | figure | ref |
|---|---|---|---|---|---|---|---|---|---|
| oxolan-2-one + n-octane | − | 0.101 | − | 0 | 1 | 0.01256 | 0.05 | 6(b) | (83) |
| oxolan-2-one + n-undecane | − | 0.00267 | − | 0 | 1 | 1.106 | 3.85 | 6(b) | (83) |
| oxolan-2-one + n-tridecane | − | 0.00267 | − | 0 | 1 | 0.7870 | 2.85 | 6(b) | (83) |
| oxolan-2-one + n-pentadecane | − | 0.00267 | − | 0 | 1 | 1.332 | 4.85 | 6(b) | (83) |
| oxolan-2-one + n-heptadecane | − | 0.00267 | − | 0 | 1 | 1.051 | 3.85 | 6(b) | (83) |
| oxolan-2-one + n-nonadecane | − | 0.00267 | − | 0 | 1 | 0.7762 | 2.85 | 6(b) | (83) |
| system s (1 + 2) | T/K range | P/MPa range | x1 range | NDs,p | Ntotals,p | %AADsxLLE1 | AADsxLLE1 | figure | ref |
|---|---|---|---|---|---|---|---|---|---|
| oxolan-2-one + cyclohexane | 298 | 0.101 | − | 2 | 2 | 165.3 | 0.04311 | 5(a) | (84) |
| oxepan-2-one + cyclohexane | 293–303 | 0.101 | − | 2 | 2 | 178.3 | 0.1261 | 5(b) | (85) |
| 5-methyloxolan-2-one + cyclohexane | 288–330 | 0.101 | − | 17 | 17 | 57.78 | 0.2114 | − | (31) |
| oxolan-2-one + n-hexane | 293–298 | 0.101 | − | 3 | 3 | 44.26 | 0.02430 | 5(c) | (84,86) |
| oxepan-2-one + n-hexane | 293–323 | 0.101 | − | 4 | 4 | 15.25 | 0.005918 | 5(d) | (85) |
| oxolan-2-one + n-heptane | 298 | 0.101 | − | 2 | 2 | 53.51 | 0.01953 | − | (84) |
| oxepan-2-one + n-heptane | 293–323 | 0.101 | − | 4 | 4 | 23.57 | 0.02007 | − | (85) |
| 5-methyloxolan-2-one + n-heptane | 288–364 | 0.101 | − | 22 | 22 | 66.47 | 0.1179 | − | (31) |
| 5-methyloxolan-2-one + n-decane | 288–358 | 0.101 | − | 0 | 18 | 135.2 | 0.07116 | − | (31) |
| 5-methyloxolan-2-one + n-dodecane | 283–358 | 0.101 | − | 0 | 19 | 163.3 | 0.06151 | − | (31) |
| oxolan-2-one + n-tridecane | 293–368 | 0.101 | − | 0 | 10 | 120.4 | 0.02407 | − | (83) |
| 5-methyloxolan-2-one + n-tridecane | 283–333 | 0.101 | − | 0 | 20 | 180.6 | 0.08207 | − | (87) |
| system s (1 + 2) | T/K range | P/MPa range | x1 range | NDs,p | Ntotals,p | %AADsxsat1 | AADsxsat1 | figure | ref |
|---|---|---|---|---|---|---|---|---|---|
| oxepan-2-one in cyclohexane | 267–272 | 0.101 | − | 0 | 4 | 29.60 | 0.2510 | 5(b) | (66) |
| cyclohexane in oxepan-2-one | 270–279 | 0.101 | − | 0 | 7 | 256.6 | 0.5212 | 5(b) | (66) |
| system s (1+2) | T/K range | P/MPa range | x1 range | NDs,p | Ntotals,p | %AADs Δhmix | AADs Δhmix/(J/mol) | figure | ref |
|---|---|---|---|---|---|---|---|---|---|
| oxolan-2-one + cyclohexane | 298 | 0.101 | 0.982–0.995 | 6 | 6 | 64.96 | 68.13 | − | (88) |
| oxolan-2-one + n-hexane | 298 | 0.101 | 0.0048–0.014 | 8 | 8 | 6.082 | 6.705 | − | (88) |
| oxolan-2-one + n-heptane | 298–318 | 0.101 | 0.003–0.9968 | 11 | 43 | 32.59 | 42.10 | − | (89) |
Isobaric temperature–composition phase diagrams for a number of mixtures of lactones (oxolan-2-one or oxepan-2-one) and hydrocarbons (cyclohexane, n-hexane, or n-octane) are shown in Figure 5, in which SAFT-γ Mie calculations and the limited experimental data available can be compared. Specifically, the experimental LLE data for mixtures of oxolan-2-one and cyclohexane,84 oxolan-2-one and n-hexane,84,86 and oxepan-2-one and n-hexane85 can be seen in the figures. Good overall agreement is observed, as indicated by the low AADs summarized in Table 8. The small values of the LLE mole fractions cause some large %AADs, for example, for oxolan-2-one + cyclohexane (165.3%), despite a small corresponding AAD (0.04311). Experimental data for LLE85 and solid–liquid–liquid equilibrium66 (SLLE) are shown for the mixture of oxepan-2-one and cyclohexane in Figure 5b. The model allows for the correct prediction of the existence and the extent of the LLE region for this system but fails in predicting the composition of the eutectic point (xSAFToxepan-2-one = 0.084 and xexpoxepan-2-one = 0.847), in part as a consequence of the small difference in the SLLE temperature and the eutectic temperature. The temperature of the eutectic point predicted by SAFT-γ Mie with the estimated parameters is TSAFTeutectic = 264 K, while the experimental value66 is Texpeutectic = 267 K.
Figure 5.
Isobaric phase diagrams of ring lactones + hydrocarbons: oxolan-2-one (light blue) and oxepan-2-one (dark red) at atmospheric pressure. The curves represent the calculations with SAFT-γ Mie. The letters V, L and S indicate vapor, liquid, and solid phases, respectively. Experimental data used in the estimation of group-interaction parameters are represented with filled symbols, and those not used are represented with open symbols. (a) Oxolan-2-one + cyclohexane, with experimental data for the LLE.84 (b) Oxepan-2-one + cyclohexane, with experimental data for the LLE85 and SLE.66 (c) Oxolan-2-one + n-hexane, with experimental data for the LLE.84,86 (d) Oxepan-2-one + n-hexane, with experimental data for LLE.85 (e) Oxolan-2-one + n-octane, with experimental data for the azeotrope.83 Thermodynamic conditions and the accuracy of the calculations are detailed in Table 8 and in the Zenodo datafile.
Several azeotrope data are available for mixtures of oxolan-2-one and linear alkanes.83 This allows us to study the influence of the alkane chain length on the azeotrope composition and temperature at 2666.4 Pa. Related experimental data are available for systems containing alkanes from n-undecane (C11H24) to n-nonadecane (C19H40). SAFT-γ Mie calculations are carried out for n-hexane (C6H14) to n-eicosane (C20H42). The azeotrope composition xazoxolan-2-one increases with an increase in the alkane length (Figure 6a) and is found to be greater than 0.5 for oxolan-2-one + n-dodecane (C12H26) and longer alkanes, both from the experimental data and the predictions. The azeotrope temperature also increases with an increase in the alkane length at a fixed pressure (Figure 6b). The agreement between the experimental data and SAFT-γ Mie predictions is excellent both for the azeotrope compositions and temperatures, with the corresponding %AADs smaller than 2% for all the mixtures at 2.6664 kPa (cf. Table 8). For 101.3 kPa, only one azeotrope temperature has been reported83 for the VLE of oxolan-2-one + n-octane (Figures 5e and 6a,b), and the SAFT-γ Mie predictions are found to be in excellent agreement with these data. It also can be seen in Figure 6 that the azeotrope temperature of a given mixture increases significantly with an increase in the pressure, while the compositions remain quite similar. Other %AADs and ADDs associated with the mixtures of lactones and hydrocarbons are summarized in Table 8.
Figure 6.
(a) Azeotrope compositions given as the mole fraction of oxolan-2-one (xazoxolan-2-one) and (b) azeotrope temperatures (Taz) for mixtures of oxolan-2-one + linear alkanes. The number of carbons corresponds to the length of the alkane (six for n-hexane, seven for n-heptane, etc.). Black “×” symbols and blue “+” symbols represent the SAFT-γ Mie calculations. Black squares and blue diamonds represent the experimental points.83 Black points and blue points correspond to results at 2.6664 and 101.3 kPa, respectively. Thermodynamic conditions and the accuracy of the calculations are detailed in Table 8 and in the Zenodo datafile.
3.2. Binary Mixtures of Lactones + Alcohols
3.2.1. Lactone + Primary Alcohol Mixtures: cCOO–CH3OH and cCOO–CH2OH Interactions
Mixtures of lactones and primary
alcohols, from methanol to decan-1-ol,
are studied in this section. Methanol is represented by a single SAFT-γ
Mie molecular group,51 denoted as CH3OH. Longer primary alcohols (ethanol, propan-1-ol, butan-1-ol,
etc.) are modeled with a CH3 group, a number of CH2 groups appropriate for the length of the alkanol, and a CH2OH36 group (cf. Table 2). The CH3OH and
CH2OH groups include one site of type H, and two e sites
(labeled e1) correspond to the lone pairs of the oxygen
atom. In mixtures with lactones, an association interaction between
the H site of the hydroxyl groups and the e1 site of the
cCOO group is accounted for. The related parameters, characterized
here, are 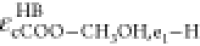 ,
, 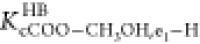 ,
, 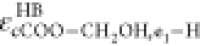 , and
, and  ; in addition, the unlike dispersion energy
parameters
; in addition, the unlike dispersion energy
parameters 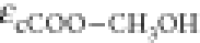 and
and  are also determined (cf. Tables 5 and 6).
are also determined (cf. Tables 5 and 6).
The unlike group interaction parameters are estimated from VLE,92−95 SLE,66 single-phase density,96−98 and excess enthalpy99,100 experimental data. In particular, the corresponding isobaric VLE data95 are shown in Figure 7a for 5-methyloxolan-2-one + methanol and 5-methyloxolan-2-ol + ethanol. No azeotrope is found in these phase diagrams. SLE data (Figure 7b) are available for mixtures of oxepan-2-one + methanol and oxepan-2-one + propan-1-ol; these are used to characterize the interaction parameters with more accuracy. Characteristic nonideal behavior is observed in the experimental density data97,98 of mixtures of oxolan-2-one and several linear primary alcohols (Figure 7c) at 298.15 K, with a concave shape for the shorter alcohols and a convex shape for the longer alcohols, as a function of mole fraction. The highest densities for xoxolan-2-one < 0.1 are obtained for the longest chains (the longer/heavier alcohols), while the highest densities for xoxolan-2-one > 0.1 are seen for the smallest chains. An inversion is observed for xoxolan-2-one ≈ 0.1 in the mixtures considered, including the mixture of oxolan-2-one + methanol. Excess molar enthalpy data99,100 at 298.15 K and calculations are shown in Figure 7d. As can be seen, the excess molar enthalpies of the oxolan-2-one + long primary alcohol mixtures exhibit a similar trend and order of magnitude, with a maximum of approximately 2 kJ/mol at xoxolan-2-one ≈ 0.5. The calculated excess enthalpy for oxolan-2-one + methanol presents a lower maximum; we note the limited experimental data available for this system.
Figure 7.
Selected isobaric thermodynamic properties at atmospheric pressure for lactones + primary alcohols: methanol (black), ethanol (dark gray), propan-1-ol (light gray), butan-1-ol (dark red), pentan-1-ol (red), hexan-1-ol (orange), heptan-1-ol (yellow), octan-1-ol (purple), nonan-1-ol (dark blue), and decan-1-ol (light blue). The curves represent the calculations with SAFT-γ Mie. Experimental data used in the estimation of group-interaction parameters are represented with filled symbols, and those not used are represented with open symbols. (a) Isobaric vapor–liquid equilibria of 5-methyloxolan-2-one + primary alcohols, with experimental data for methanol95 and ethanol.95 (b) Isobaric solid–liquid equilibria of oxepan-2-one + primary alcohols, with experimental data for methanol66 and propan-1-ol.66 (c) Density of oxolan-2-one + linear primary alcohols at 298.15 K, with experimental data for methanol,97 ethanol,97 butan-1-ol,97 and octan-1-ol.97 (d) Excess enthalpy of oxolan-2-one + primary alcohols at 298.15 K, with experimental data for methanol,100 hexan-1-ol,96 heptan-1-ol,96 octan-1-ol,96 and decan-1-ol.96 Thermodynamic conditions and the accuracy of the calculations are detailed in Table 9 and in the Zenodo datafile.
Azeotrope experimental data83 for mixtures of oxolan-2-one and linear primary alcohols are also available (Figure 8) for mixtures containing linear primary alcohols from pentan-1-ol (C5H11OH) to undecan-1-ol (C11H23OH) but are not used for the parameter estimation. The azeotrope compositions xazoxolan-2-one at 2666.4 Pa increase with an increase in the alcohol chain length (Figure 8a) and they are higher than 0.5 for oxolan-2-one + octan-1-ol (C8H17OH) and oxolan-2-one + longer alcohols. As noted earlier, the azeotrope temperatures also increase with an increase in the alkane chain length (Figure 8b) such that the results for the azeotrope compositions and temperatures are qualitatively similar for both oxolan-2-one + linear primary alcohols and oxolan-2-one + linear alkanes (Figure 6). We note, however, that the azeotrope compositions are higher in the mixtures with alcohols than in the mixtures with the alkanes for a given number of carbons in the chain.
Figure 8.
(a) Azeotrope compositions given as the mole fraction of oxolan-2-one (xazoxolan-2-one) and (b) azeotrope temperatures (Taz) for mixtures of oxolan-2-one + linear primary alcohols. The number of carbons corresponds to the length of the linear primary alcohol (six for hexan-1-ol, seven for heptan-1-ol, etc.). Black “×” symbols and blue “+” symbols represent the calculations with SAFT-γ Mie. Black squares and blue diamonds represent the experimental points.83 Black and blue points correspond to results at 2.6664 and 101.3 kPa, respectively. Thermodynamic conditions and the accuracy of the calculations are detailed in Table 9 and in the Zenodo datafile.
Excellent agreement between the experimental data and the SAFT-γ Mie calculation is obtained for the VLE, with %AADs of 0.7520 and 0.1422% for the bubble temperatures and 0.4562 and 0.3411% for the dew temperatures of 5-methyloxolan-2-one + methanol and 5-methyloxolan-2-one + ethanol, respectively. The solubility of oxepan-2-one (i.e., the SLE curves for T > 200 K in Figure 7b) is determined with accuracy both in methanol (%AAD = 1.702%) and propan-1-ol (%AAD = 4.388%). Densities are also correctly described with SAFT-γ Mie. In particular, the characteristics of the curves shown in Figure 7c, for example, the concave/convex shapes and the intersection of the curves, are in excellent quantitative agreement with the experimental data. The highest %AAD is only 3.438% for oxolan-2-one + octan-1-ol. A concave shape is found for all of the excess enthalpy curves, as shown in Figure 7d. Good agreement is obtained with experiment,99,100 and all %AADs for excess enthalpy are smaller than 10% except for oxolan-2-one + decan-1-ol (11.06%). The prediction of the excess enthalpy of oxolan-2-one + methanol is significantly different in comparison with the other mixtures containing alcohol, as suggested by the experimental data (the predicted maximum is around 1 kJ/mol only).
The influence of the length of the alcohol chain on the VLE, SLE, densities, and excess enthalpies can also be gleaned from Figure 7 with additional predictions made for several mixtures for which no experimental data are available. We also predict the azeotrope composition and temperature with SAFT-γ Mie for mixtures of oxolan-2-one + linear primary alcohols until pentadecan-1-ol (C15H31OH). The overall predictions are in excellent agreement with the experiment (%AADs and AAD are detailed in Table 9). An azeotrope is mentioned in the experimental data83 for oxolan-2-one + pentan-1-ol at 2666.4 Pa with an unusually small composition (xaz,expoxolan-2-one = 0.002) compared with the other data for the azeotropes considered here, while no azeotrope is predicted with SAFT-γ Mie for that mixture (which corresponds to %AAD = 100% and AAD = 0.002).
Table 9. Overview of the of Accuracy SAFT-γ Mie in the Calculation of Azeotrope Compositions xazoxolan-2-one and Temperatures Taz, Bubble Temperatures Tbub, Dew Temperatures Tdew, Bubble Pressures Pbub, Solubilities xsat1, Densities ρ, and Molar Excess Enthalpies Δhmix for Mixtures of Lactones and Primary Alcohols, Where NDs,p Is the Number of Experimental Data Used in the the Parameter Estimation, and ND,totals,p Is the Number of Experimental Data Used to Calculate %AADsp and AADsp for System s and Property p.
| system s (1 + 2) | T/K range | P/MPa range | x1 range | NDs,p | Ntotals,p | %AADsxazoxolan-2-one | AADsxazoxolan-2-one | figure | ref |
|---|---|---|---|---|---|---|---|---|---|
| oxolan-2-one + pentan-1-ol | − | 0.00267 | − | 0 | 1 | 100.0 | 0.002 | 8(a) | (83) |
| oxolan-2-one + hexan-1-ol | − | 0.00267 | − | 0 | 1 | 67.48 | 0.083 | 8(a) | (83) |
| oxolan-2-one + heptan-1-ol | − | 0.00267 | − | 0 | 1 | 17.30 | 0.06800 | 8(a) | (83) |
| oxolan-2-one + octan-1-ol | − | 0.00267 | − | 0 | 1 | 6.716 | 0.04365 | 8(a) | (83) |
| oxolan-2-one + nonan-1-ol | − | 0.00267 | − | 0 | 1 | 1.698 | 0.01444 | 8(a) | (83) |
| oxolan-2-one + decan-1-ol | − | 0.00267–0.101 | − | 0 | 2 | 12.03 | 0.1173 | 8(a) | (83) |
| oxolan-2-one + undecan-1-ol | − | 0.101 | − | 0 | 1 | 11.38 | 0.113 | 8(a) | (83) |
| system s (1 + 2) | T/K range | P/MPa range | x1 range | NDs,p | Ntotals,p | %AADsTaz | AADsTaz/K | figure | ref |
|---|---|---|---|---|---|---|---|---|---|
| oxolan-2-one + pentan-1-ol | − | 0.00267 | − | 0 | 1 | 0.1874 | 0.6167 | 8(b) | (83) |
| oxolan-2-one + hexan-1-ol | − | 0.00267 | − | 0 | 1 | 0.4756 | 1.632 | 8(b) | (83) |
| oxolan-2-one + heptan-1-ol | − | 0.00267 | − | 0 | 1 | 0.3069 | 1.090 | 8(b) | (83) |
| oxolan-2-one + decan-1-ol | − | 0.00267–0.101 | − | 0 | 2 | 0.5516 | 2.357 | 8(b) | (83) |
| oxolan-2-one + undecan-1-ol | − | 0.101 | − | 0 | 1 | 0.0879 | 0.4210 | 8(b) | (83) |
| system s (1 + 2) | T/K range | P/MPa range | x1 range | NDs,p | Ntotals,p | %AADsTbub | AADsTbub/K | figure | ref |
|---|---|---|---|---|---|---|---|---|---|
| oxolan-2-one +1,4-butanediol | − | 0.030–0.070 | 0.00–1.00 | 18 | 36 | 0.8126 | 3.792 | − | (94) |
| 5-methyloxolan-2-one + methanol | − | 0.101 | 0.00–0.82 | 18 | 18 | 0.3492 | 1.269 | 7(a) | (95) |
| 5-methyloxolan-2-one + ethanol | − | 0.101 | 0.00–0.82 | 12 | 35 | 0.1422 | 0.5184 | 7(a) | (95) |
| system s (1 + 2) | T/K range | P/MPa range | x1 range | NDs,p | Ntotals,p | %AADsTdew | AADsTdew/K | figure | ref |
|---|---|---|---|---|---|---|---|---|---|
| oxolan-2-one +1,4-butanediol | − | 0.030–0.070 | 0.00–1.00 | 18 | 36 | 0.8611 | 3.998 | − | (94) |
| 5-methyloxolan-2-one + methanol | − | 0.101 | 0.00–0.03 | 6 | 18 | 0.3080 | 1.112 | 7(a) | (95) |
| 5-methyloxolan-2-one + ethanol | − | 0.101 | 0.00–0.05 | 12 | 35 | 0.3411 | 1.261 | 7(a) | (95) |
| system s (1 + 2) | T/K range | P/MPa range | x1 range | NDs,p | Ntotals,p | %AADsPbub | AADsPbub/Pa | figure | ref |
|---|---|---|---|---|---|---|---|---|---|
| oxolan-2-one +1,4-butanediol | 373–423 | − | 0.00–1.00 | 32 | 32 | 14.73 | 795.3 | − | (92,93) |
| system s (1 + 2) | T/K range | P/MPa range | x1 range | NDs,p | Ntotals,p | %AADsxsat1 | AADsxsat1 | figure | ref |
|---|---|---|---|---|---|---|---|---|---|
| oxepan-2-one in methanol | 204–272 | 0.101 | − | 21 | 22 | 1.702 | 0.007757 | 7(b) | (66) |
| oxepan-2-one in propanol | 204–272 | 0.101 | − | 19 | 20 | 4.388 | 0.01220 | 7(b) | (66) |
| system s (1 + 2) | T/K range | P/MPa range | x1 range | NDs,p | Ntotals,p | %AADs ρ | AADs ρ/(kg/m3) | figure | ref |
|---|---|---|---|---|---|---|---|---|---|
| oxolan-2-one + methanol | 298 | 0.101 | 0.00–1.00 | 11 | 11 | 0.5953 | 6.281 | 7(c) | (97) |
| oxolan-2-one + ethanol | 298 | 0.101 | 0.00–1.00 | 11 | 11 | 0.9588 | 8.877 | 7(c) | (97) |
| oxolan-2-one + butan-1-ol | 293–303 | 0.101 | 0.00–1.00 | 24 | 59 | 1.209 | 11.29 | 7(c) | (97,98) |
| oxolan-2-one + octan-1-ol | 298 | 0.101 | 0.00–1.00 | 0 | 11 | 3.438 | 31.92 | 7(c) | (97) |
| oxolan-2-one + 2-methyl-1-propanol | 303 | 0.101 | 0.00–1.00 | 10 | 10 | 1.367 | 12.39 | − | (96) |
| oxolan-2-one + 3-methyl-1-butanol | 303 | 0.101 | 0.00–1.00 | 10 | 10 | 1.384 | 12.59 | − | (96) |
| system s (1 + 2) | T/K range | P/MPa range | x1 range | NDs,p | Ntotals,p | %AADs Δhmix | AADs Δhmix/(J/mol) | figure | ref |
|---|---|---|---|---|---|---|---|---|---|
| oxolan-2-one + methanol | 298 | 0.101 | 0.89–0.99 | 5 | 5 | 4.694 | 12.56 | 7(d) | (100) |
| oxolan-2-one + hexan-1-ol | 298 | 0.101 | 0.12–0.94 | 12 | 12 | 7.594 | 113.3 | 7(d) | (99) |
| oxolan-2-one + heptan-1-ol | 298 | 0.101 | 0.15–0.95 | 12 | 12 | 4.447 | 74.57 | 7(d) | (99) |
| oxolan-2-one + octan-1-ol | 298 | 0.101 | 0.17–0.95 | 0 | 12 | 9.077 | 172.5 | 7(d) | (99) |
| oxolan-2-one + decan-1-ol | 298 | 0.101 | 0.21–0.96 | 0 | 12 | 11.06 | 206.2 | 7(d) | (99) |
Primary alcohols with a branched carbon chain are also considered in order to estimate the unlike interaction between the cCOO group and the CH group.51 Very good accuracy is obtained for the density of oxolan-2-one + 2-methyl-1-propanol (%AAD = 1.367%) and oxolan-2-one +3-methyl-1-butanol (%AAD = 1.384%). The corresponding unlike group parameters are detailed in Table 5, and the association parameters are listed in Table 6. The overall accuracy for all of these systems can be found in Table 9.
3.2.2. Lactone + Secondary Alcohol Mixtures: cCOO–CHOH and cCH–CHOH Interactions
We now consider the modeling
of lactones and secondary alcohols by incorporating the CHOH group,11 which is modeled with two sites of type e1 and one site of type H. The H site of the CHOH group interacts
with the e1 sites of the cCOO group. The unlike group parameters
characterized in this section are εcCOO–CHOH, 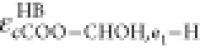 and
and  (cf. Tables 5 and 6).
(cf. Tables 5 and 6).
Experimental VLE data,95 shown in Figure 9a, are available for 5-methyloxolan-2-one + propan-2-ol at atmospheric pressure for a large range of mole fractions for the bubble temperature (0.00 ≤ x5-methyloxolan-2-one ≤ 0.77) and a small range for the dew temperature (0.00 ≤ x5-methyloxolan-2-one ≤ 0.045). Experimental density data can be seen in Figure 9b for oxolan-2-one + propan-2-ol96 and oxolan-2-one + butan-2-ol.98 The accuracy for the description of mixtures of lactones and secondary alcohols is very good for both VLE and density. The corresponding %AAD is only 0.3007% for the bubble temperature of 5-methyloxolan-2-one + propan-2-ol, and 0.2153% for the related dew temperature. The overall agreement for the density is also very good and includes a crossing of curves at x5-methyloxolan-2-one ∼ 0.15 seen both from experimental data and the SAFT-γ Mie calculations.
Figure 9.
Selected isobaric thermodynamic properties of lactones + secondary alcohols: propan-2-ol (black), butan-2-ol (dark gray), pentan-2-ol (light gray), hexan-2-ol (dark red), and heptan-2-ol (red) at atmospheric pressure. The curves represent the calculations with SAFT-γ Mie. Experimental data used in the estimation of group-interaction parameters are represented with filled symbols, and those not used are represented with open symbols. (a) Isobaric vapor–liquid equilibria of 5-methyloxolan-2-one + secondary alcohols, with experimental data for propan-2-ol.95 (b) Density of oxolan-2-one + secondary alcohols at 303.15 K, with experimental data for propan-2-ol96 and butan-2-ol.98 Thermodynamic conditions and the accuracy of the calculations are detailed in Table 10 and in the Zenodo datafile.
Predictions for the VLE of mixtures of 5-methyloxolan-2-one + butan-2-ol, + pentan-2-ol, + hexan-2-ol, and + heptan-2-ol are also shown in Figure 9a. No azeotrope is predicted for these systems at atmospheric pressure. Additional density predictions for oxolan-2-one + secondary alcohols are shown in Figure 9b, even if experimental data are not available for all the considered mixtures. The density is found to be more ideal for lactones + secondary alcohols than for lactones + primary alcohols (cf. Figure 7c). Other relevant information is summarized in Table 10.
Table 10. Overview of the Accuracy of SAFT-γ Mie in the Calculation of Bubble Temperatures Tbub, Dew Temperatures Tdew, and Densities ρ for Mixtures of Lactones and Secondary Alcohols, Where NDs,p Is the Number of Experimental Data Used in the Parameter Estimation, and ND,totals,p Is the Number of Experimental Data Used to Calculate %AADspand AADsp for System s and Property p.
| system s (1 + 2) | T/K range | P/MPa range | x1 range | NDs,p | Ntotals,p | %AADsTbub | AADsTbub/K | figure | ref |
|---|---|---|---|---|---|---|---|---|---|
| 5-methyloxolan-2-one + propan-2-ol | − | 0.101 | 0.00–0.77 | 16 | 31 | 0.3007 | 1.094 | 9(a) | (95) |
| system s (1 + 2) | T/K range | P/MPa range | x1 range | NDs,p | Ntotals,p | %AADsTdew | AADsTdew/K | figure | ref |
|---|---|---|---|---|---|---|---|---|---|
| 5-methyloxolan-2-one + propan-2-ol | − | 0.101 | 0.00–0.045 | 8 | 31 | 0.2153 | 0.7907 | 9(a) | (95) |
3.3. Mixtures of Lactones + 2-Ketones: cCOO–CH3COCH3 and cCOO–CH3CO Interactions
We now consider
binary mixtures of lactones + 2-ketones, including
acetone. SAFT-γ Mie models for acetone, as well as for 2-ketones,
have been presented in previous work,39,51 and the same
models are adopted here. Acetone is modeled as a single molecular
group51 denoted by CH3COCH3, while other 2-ketones are modeled by using the CH3CO group39 together with CH2 and CH3 groups. No unlike association is considered between
the cCOO group and ketone groups; thus, the only parameters that need
to be estimated here are 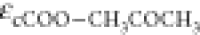 and
and 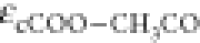 . Limited experimental data are available,
which include VLE data101 at atmospheric
pressure for 5-methyloxolan-2-one + acetone for a small range of x5-methyloxolan-2-one values
only and SLE data66 of oxepan-2-one + pentan-2-one
with a eutectic point at 194.46 K. As can be seen in Table 11, most of the experimental
data available are used to characterize the parameters.
. Limited experimental data are available,
which include VLE data101 at atmospheric
pressure for 5-methyloxolan-2-one + acetone for a small range of x5-methyloxolan-2-one values
only and SLE data66 of oxepan-2-one + pentan-2-one
with a eutectic point at 194.46 K. As can be seen in Table 11, most of the experimental
data available are used to characterize the parameters.
Table 11. Overview of the Accuracy of SAFT-γ Mie in the Calculation of Bubble Temperatures Tbub, Dew Temperatures Tdew, and Solubilities xsat1 for Binary Mixtures of Lactones + 2-Ketones, Where NDs,p Is the Number of Experimental Data Used in Parameter Estimation, and ND,totals,p is the Number of Experimental Data Used to Calculate %AADs,p and AADs,p for System s and Property p.
| system s (1 + 2) | T/K range | P/MPa range | x1 range | NDs,p | Ntotals,p | %AADsTbub | AADsTbub/K | figure | ref |
|---|---|---|---|---|---|---|---|---|---|
| 5-methyloxolan-2-one + acetone | − | 0.101 | 0.00–0.42 | 30 | 30 | 0.02819 | 0.09421 | 10(a) | (101) |
| system s (1 + 2) | T/K range | P/MPa range | x1 range | NDs,p | Ntotals,p | %AADsTdew | AADsTdew/K | figure | ref |
|---|---|---|---|---|---|---|---|---|---|
| 5-methyloxolan-2-one + acetone | − | 0.101 | 0–0.0062 | 15 | 30 | 1.300 | 4.360 | 10(a) | (101) |
Both the VLE of 5-methyloxolan-2-one + acetone and the SLE of oxepan-2-one + pentan-2-one are accurately described with the resulting SAFT-γ Mie model (Figure 10). The corresponding AADs are small, as are the %AADs, which are below 4% for all the available properties (Table 11). Additional VLE diagrams at atmospheric pressure are predicted for binary mixtures of 5-methyloxolan-2-one + butan-2-one, pentan-2-one, and hexan-2-one. No azeotrope is predicted for these systems. The SLE phase diagrams of oxepan-2-one + acetone, + butan-2-one, and + hexan-2-one are also predicted. All of these systems have a eutectic point, as can be seen for oxepan-2-one + pentan-2-one both from experiments and the SAFT calculations. These VLE and SLE predictions can also be seen in Figure 10.
Figure 10.
Isobaric phase diagrams of lactones + 2-ketones: acetone (black), butan-2-one (dark gray), pentan-2-one (light gray), hexan-2-one (dark red), heptan-2-one (red), and octan-2-one (orange) at atmospheric pressure. The curves represent the calculations with SAFT-γ Mie. Experimental data used in the estimation of group-interaction parameters are represented with filled symbols, and those not used are represented with open symbols. (a) Vapor–liquid equilibria of 5-methyloxolan-2-one + 2-ketones, with experimental data for acetone.101 (b) Solid–liquid equilibria of oxepan-2-one + 2-ketones, with experimental data for pentan-2-one.66 Thermodynamic conditions and accuracy are detailed in Table 11 and in the Zenodo datafile.
3.4. Mixtures of Lactones + Linear Esters: cCOO–COO Interactions
Experimental data of mixtures of lactones and linear esters are available for several properties, including VLE,70,101 SLE,70 density,102 and molar excess enthalpy103 (see Figure 11). In particular, VLE data at atmospheric pressure are available for the mixture of 5-methyloxolan-2-one + ethyl acetate.101 SLE data for oxolan-2-one + diethylbutanedioate70 are also available, with a eutectic point at xoxolan-2-one ≈ 0.78 and Teutectic ≈ 210 K. Density data at 298.15 K and 101.3 kPa are available for oxolan-2-one + methyl acetate and oxolan-2-one + ethyl acetate102 for xoxolan-2-one ∈ [0.0, 1.0]. Excess molar enthalpy data at 298.15 K and 101.3 kPa are available for oxolan-2-one + methyl acetate103 for the small range xoxolan-2-one ∈ [0.89, 0.97] with the largest value of only 35.7 J/mol (for xoxolan-2-one = 0.89).
Figure 11.
Isobaric thermodynamic properties of lactones + linear esters at atmospheric pressure: methyl acetate (black), ethyl acetate (dark gray), propyl acetate (light gray), butyl acetate (dark red), pentyl acetate (red), and diethylbutanedioate (green). The curves represent the calculations with SAFT-γ Mie. The dashed curves are determined with Δhfus, estimateddiethylbutanedioate, as explained in the text. Experimental data used in the estimation of group-interaction parameters are represented with filled symbols, and those not used are represented with open symbols. (a) Vapor–liquid equilibria of 5-methyloxolan-2-one + esters, with experimental data for ethyl acetate.101 (b) Solid–liquid equilibria of oxolan-2-one + esters, with experimental data for diethylbutanedioate.70 (c) Density of oxolan-2-one + esters at 298.15 K, with experimental data for methyl acetate102 and ethyl acetate.102 (d) Excess molar enthalpy of oxolan-2-one + esters at 298.15 K, with experimental data for methyl acetate.103 Thermodynamic conditions and the accuracy of the calculations are detailed in Table 12 and in the Zenodo datafile.
The characterization of the interaction parameters between the cCOO and COO8 groups in the SAFT-γ Mie modeling is performed by considering the VLE, density, and excess enthalpy data available. SLE data are not used to estimate the parameters here. The resulting agreement between the calculations and the experimental data is excellent for all of the properties. In particular, no azeotrope is found in the VLE of 5-methyloxolan-2-one + ethyl acetate at atmospheric pressure. The density at 298.15 K is larger for oxolan-2-one + methyl acetate than for oxolan-2-one + ethyl acetate, for all values of xoxolan-2-one, which is qualitatively consistent with the experimental findings. The agreement for the excess molar enthalpy of oxolan-2-one + methyl acetate is also very good despite the small values found for this property (quantitatively, we obtain %AAD = 16.86%, which corresponds to an AAD of 3.536 J/mol).
The resulting group parameters are used to make additional predictions of the VLE, SLE, density, and excess molar enthalpy for binary mixtures of lactones and methyl, ethyl, propyl, and pentyl acetates; these are shown in Figure 11. It is of interest to note the “S” shape predicted for the molar excess enthalpy curves shown in Figure 11d, with positive values for lactone-rich phases and negative values for ester-rich phases. For oxolan-2-one + pentyl acetate, the predicted excess enthalpy is always positive, although highly asymmetric. More experimental data would be useful to confirm or disprove these predictions.
The SLE of oxolan-2-one + diethylbutanedioate for xoxolan-2-one > 0.78 is correctly predicted by using the melting temperature and the enthalpy of fusion of oxolan-2-one56 (cf. Table 1). The melting temperature of diethylbutanedioate61 is reported as Tfusdiethylbutanedioate = 252.55 K (cf. Table 1); however, to the best of our knowledge, there is no experimental value of the corresponding enthalpy of fusion. The %AAD for the SLE shown in Figure 11b as a dashed curve for xoxolan-2-one < 0.78 can be minimized by estimating the value of the enthalpy of fusion, which yields Δhfus, estimateddiethylbutanedioate = 23 kJ/mol (such that %AAD = 6.238% and AAD = 0.01237). The value of Δhfus, estimateddiethylbutanedioate is close to the value obtained from the Joback group-contribution method:104 Δhfus, Jobackdiethylbutanedioate = 20.03 kJ/mol (we note that both values are higher than the values reported in Table 1 for other compounds). The eutectic composition and temperature are also correctly predicted, as xpredictedoxolan-2-one ∼ 0.75, and Tpredictedeutectic ∼ 211 K with the estimated enthalpy of fusion. Additional information about the accuracy of the SAFT-γ Mie approach for these systems is summarized in Table 12.
Table 12. Overview of the Accuracy of SAFT-γ Mie in the Calculation of Bubble Temperatures Tbub, Dew Temperatures Tdew, Solubilities xsat1, Densities ρ, and Excess Molar Enthalpies Δhmix for Binary Mixtures of Lactones + Esters, Where NDs,p Is the Number of Experimental Data Used in the Parameter Estimation, and ND,totals,p Is the Number of Experimental Data Used to Calculate %AADsp and AADsp for System s and Property p.
| system s (1 + 2) | T/K range | P/MPa range | x1 range | NDs,p | Ntotals,p | %AADsTbub | AADsTbub/K | figure | ref |
|---|---|---|---|---|---|---|---|---|---|
| oxolan-2-one + diethyl butanedioate | − | 0.012 | 0.00–1.00 | 21 | 24 | 2.152 | 8.871 | − | (70) |
| 5-methyloxolan-2-one + ethyl acetate | − | 0.101 | 0.00–0.69 | 36 | 36 | 0.5151 | 1.917 | 11(a) | (101) |
| system s (1 + 2) | T/K range | P/MPa range | x1 range | NDs,p | Ntotals,p | %AADsTdew | AADsTdew/K | figure | ref |
|---|---|---|---|---|---|---|---|---|---|
| oxolan-2-one + diethyl butanedioate | − | 0.012 | 0.00–1.00 | 21 | 24 | 2.362 | 9.723 | − | (70) |
| 5-methyloxolan-2-one + ethyl acetate | − | 0.101 | 0.00–0.03 | 36 | 36 | 2.495 | 9.005 | 11(a) | (101) |
| system s (1 + 2) | T/K range | P/MPa range | x1 range | NDs,p | Ntotals,p | %AADsxsat1 | AADsxsat1 | figure | ref |
|---|---|---|---|---|---|---|---|---|---|
| oxolan-2-one in diethyl butanedioate | 210–252 | 0.101 | − | 0 | 8 | 6.238 | 0.01237 | 11(b) | (70) |
| diethyl butanedioate in oxolan-2-one | 210–229 | 0.101 | − | 0 | 7 | 3.099 | 0.02592 | 11(b) | (70) |
| system s (1 + 2) | T/K range | P/MPa range | x1 range | NDs,p | Ntotals,p | %AADs ρ | AADs ρ/(kg/m3) | figure | ref |
|---|---|---|---|---|---|---|---|---|---|
| oxolan-2-one + methyl acetate | 298 | 0.101 | 0.00–1.00 | 19 | 19 | 1.312 | 13.50 | 11(c) | (102) |
| oxolan-2-one + ethyl acetate | 298 | 0.101 | 0.00–1.00 | 19 | 19 | 0.4436 | 4.634 | 11(c) | (102) |
3.5. Mixtures of Lactones + Aromatic Compounds: cCOO–aCH, cCOO–aCCH3, and cCOO–aCCH2 Interactions
The aromatic compounds are modeled with specific aromatic groups, denoted as aCH, aCCH3, and aCCH2. For instance, benzene is composed of six aCH groups.51 One of the aCH groups of benzene is replaced by an aCCH3 group37,90 to model toluene or replaced by an aCCH2 group51 bonded to a CH3 group to model ethylbenzene. There is no association between the cCOO group and the aromatic groups, such that only the unlike interaction parameters εkl and λrkl need to be characterized (Table 5) to describe binary mixtures of lactones + aromatic compounds.
Bubble-pressure data105 at 293 and 313 K are used in the characterization of the unlike parameters considering mixtures of benzene + oxolan-2-one, + oxan-2-one, + oxepan-2-one, and + 5-methyloxolan-2-one. The VLE of these mixtures can be seen in Figure 12a for a given temperature; the markedly different vapor pressures of the pure lactones (some hundreds of Pa, as shown in Figures 2–4) and pure benzene105 (10.03 kPa at 293 K and 24.38 kPa at 313 K) give rise to clear nonideality in the phase diagrams. We also use density data106 for mixtures of oxolan-2-one + benzene, + toluene, and + ethylbenzene to characterize the unlike parameters (cf. Figure 13a). Excess molar enthalphy data,105,107 shown in Figure 13b–d, represent the most abundant set of data for the mixtures of lactones (oxolan-2-one, oxan-2-one, and 5-methyloxolan-2-one) and aromatic compounds (benzene, toluene, and ethylbenzene). The reported values are positive, as well as negative, depending on the mixture and are remarkably small with a maximum value of only 413 J/mol for an equimolar mixture of oxolan-2-one + ethylbenzene. The shape of some of the excess-enthalpy curves is also unusual; for example, the excess enthalpy of oxolan-2-one + benzene has an “M” shape105 (cf. Figure 13b) with positive values for xoxolan-2-one < 0.21 and xoxolan-2-one > 0.48, negative values otherwise, and a maximum of about 30 J/mol. SLE data are also available for mixtures of lactones and aromatic compounds66,108,109 but are not used in the characterization of group interactions.
Figure 12.
Phase diagrams of lactones + aromatic compounds. The curves represent the calculations with SAFT-γ Mie. Experimental data used in the estimation of group-interaction parameters are represented with filled symbols, and those not used are represented with open symbols. (a) Isothermal vapor–liquid equilibria of lactones + benzene: oxolan-2-one (light blue), oxan-2-one (red), oxepan-2-one (dark red), and 5-methyloxolan-2-one (dark blue) at 293 and 313 K, with experimental data for oxolan-2-one,105 oxan-2-one,105 oxepan-2-one,105 and 5-methyloxolan-2-one.105 (b) Isobaric solid–liquid equilibria at atmospheric pressure of compounds (1) + (2): oxolan-2-one + benzene (black), oxolan-2-one + toluene (gray), oxepan-2-one + benzene (red), oxepan-2-one + toluene (yellow), 5-methyloxolan-2-one + benzene (dark blue), and 5-methyloxolan-2-one + toluene (light blue), with experimental data for oxolan-2-one + benzene,108 oxepan-2-one + benzene,66 oxepan-2-one + toluene,66 and 5-methyloxolan-2-one + benzene.109 Thermodynamic conditions and the accuracy of the calculations are detailed in Table 13 and in the Zenodo datafile.
Figure 13.
Isobaric thermodynamic properties of binary mixtures of lactone + aromatic compound: benzene (black), toluene (dark gray), and ethylbenzene (light gray) at atmospheric pressure. The curves represent calculations with SAFT-γ Mie. Experimental data used in the estimation of group-interaction parameters are represented with filled symbols, and those not used are represented with open symbols. (a) Density of oxolan-2-one + aromatic compounds at 293.15 K, with experimental data for benzene,106 toluene,106 and ethylbenzene.106 (b) Excess molar enthalpy of oxolan-2-one + aromatic compounds at 293.15 K, with experimental data for benzene,105 toluene,105 and ethylbenzene.105 (c) Excess enthalpy of oxan-2-one + aromatic compounds at 293.15 K, with experimental data for benzene,107 toluene,107 and ethylbenzene.107 (d) Excess enthalpy of 5-methyloxolan-2-one + aromatic compounds at 293.15 K, with experimental data for benzene,107 toluene,107 and ethylbenzene.107 Thermodynamic conditions and the accuracy of the calculations are detailed in Table 13 and in the Zenodo datafile.
The SAFT-γ Mie calculations using the optimized parameters are also shown in Figures 12 and 13. While the agreement for the bubble-pressure and density curves is excellent, the agreement for the excess enthalpy curves is not always quantitatively accurate. The sign is not correct for two of the nine mixtures considered (for oxan-2-one + toluene and 5-methyloxolan-2-one + ethylbenzene), although we note that the highest values obtained from the calculations and the experimental data are always of the order of a few hundred J/mol only. Encouragingly, the “M” shape of the excess enthalpy curve for oxolan-2-one + benzene is qualitatively obtained with SAFT.
The transferability of the parameters characterized is assessed for the prediction of the SLE (Figure 12b). As can be seen in the figure, the eutectic points of oxolan-2-one + benzene and 5-methyloxolan-2-one + benzene are correctly predicted. The corresponding %AADs and AAD for the systems66,105−109 shown in Figures 12 and 13 (and additional systems110−113) can be found in Table 13.
Table 13. Overview of the Accuracy of SAFT-γ Mie in the Calculation of Bubble Pressures Pbub, Solubilities xsat1, Densities ρ, and Excess Enthalpies Δhmix for Binary Mixtures of Lactones + Aromatic Compounds, Where NDs,p Is the Number of Experimental Data Used in the Parameter Estimation, and ND,totals,p Is the Number of Experimental Data Used to Calculate %AADsp and AADsp for System s and Property p.
| system s (1 + 2) | T/K range | P/MPa range | x1 range | NDs,p | Ntotals,p | %AADsPbub | AADsPbub/Pa | figure | ref |
|---|---|---|---|---|---|---|---|---|---|
| oxolan-2-one + benzene | 292–313 | − | 0.00–1.00 | 31 | 65 | 5.442 | 534.9 | 12(a) | (105) |
| oxan-2-one + benzene | 292–313 | − | 0.00–1.00 | 32 | 68 | 14.17 | 1093 | 12(a) | (105) |
| oxepan-2-one + benzene | 292–313 | − | 0.00–1.00 | 33 | 70 | 20.81 | 1327 | 12(a) | (105) |
| 5-methyloxolan-2-one + benzene | 292–313 | − | 0.00–1.00 | 37 | 77 | 22.81 | 1793 | 12(a) | (105) |
| system s (1 + 2) | T/K range | P/MPa range | x1 range | NDs,p | Ntotals,p | %AADsxsat1 | AADsxsat1 | figure | ref |
|---|---|---|---|---|---|---|---|---|---|
| oxolan-2-one in benzene | 217 | 0.101 | − | 0 | 1 | 20.75 | 0.1784 | 12(b) | (108) |
| oxepan-2-one in benzene | 248–272 | 0.101 | − | 0 | 10 | 1.671 | 0.01045 | 12(b) | (66) |
| benzene in oxepan-2-one | 245–279 | 0.101 | − | 0 | 11 | 6.771 | 0.04391 | 12(b) | (66) |
| oxepan-2-one in toluene | 211–272 | 0.101 | − | 0 | 19 | 20.99 | 0.05076 | 12(b) | (66) |
| 5-methyloxolan-2-one in benzene | 226–241 | 0.101 | − | 0 | 7 | 12.01 | 0.09369 | 12(b) | (109) |
| benzene in 5-methyloxolan-2-one | 234–279 | 0.101 | − | 0 | 14 | 10.72 | 0.05832 | 12(b) | (109) |
| system s (1 + 2) | T/K range | P/MPa range | x1 range | NDs,p | Ntotals,p | %AADs ρ | AADs ρ/(kg/m3) | figure | ref |
|---|---|---|---|---|---|---|---|---|---|
| oxolan-2-one + benzene | 293–343 | 0.101 | 0.00–1.00 | 32 | 102 | 0.6534 | 6.233 | 13(a) | (106) |
| oxolan-2-one + toluene | 293–353 | 0.101 | 0.00–1.00 | 0 | 119 | 0.4534 | 4.454 | 13(a) | (106) |
| oxolan-2-one +1,2-dimethylbenzene | 293–308 | 0.101 | 0.00–1.00 | 0 | 44 | 1.183 | 11.55 | − | (110) |
| oxolan-2-one +1,4-dimethylbenzene | 293–308 | 0.101 | 0.00–1.00 | 0 | 44 | 0.4880 | 4.829 | − | (111) |
| oxolan-2-one +1,2,4-trimethylbenzene | 288–308 | 0.101 | 0.00–1.00 | 0 | 85 | 0.7613 | 7.468 | − | (112) |
| oxolan-2-one +1,3,5-trimethylbenzene | 288–308 | 0.101 | 0.00–1.00 | 0 | 85 | 0.3751 | 3.721 | − | (112) |
| oxolan-2-one + ethylbenzene | 293–353 | 0.101 | 0.00–1.00 | 24 | 119 | 1.152 | 10.88 | 13(a) | (106) |
| 5-methyloxolan-2-one + benzene | 298 | 0.101 | 0.0008–0.006 | 0 | 5 | 1.814 | 15.86 | − | (113) |
| system s (1 + 2) | T/K range | P/MPa range | x1 range | NDs,p | Ntotals,p | %AADs Δhmix | AADs Δhmix/(J/mol) | figure | ref |
|---|---|---|---|---|---|---|---|---|---|
| oxolan-2-one + benzene | 293 | 0.101 | 0.0036–0.97 | 12 | 56 | 286.9 | 22.58 | 13(b) | (105) |
| oxolan-2-one + toluene | 293 | 0.101 | 0.0082–0.99 | 31 | 31 | 129.3 | 183.2 | 13(b) | (105) |
| oxolan-2-one + ethylbenzene | 293 | 0.101 | 0.017–0.98 | 36 | 36 | 116.7 | 314.0 | 13(b) | (105) |
| oxan-2-one + benzene | 293 | 0.101 | 0.0021–0.99 | 11 | 31 | 1741 | 159.1 | 13(c) | (107) |
| oxan-2-one + toluene | 293 | 0.101 | 0.0068–0.97 | 32 | 32 | 166.7 | 99.55 | 13(c) | (107) |
| oxan-2-one + ethylbenzene | 293 | 0.101 | 0.015–0.98 | 24 | 25 | 7.572 | 9.043 | 13(c) | (107) |
| 5-methyloxolan-2-one + benzene | 293 | 0.101 | 0.0047–0.98 | 9 | 35 | 1780 | 390.8 | 13(d) | (107) |
| 5-methyloxolan-2-one + toluene | 293 | 0.101 | 0.010–0.97 | 31 | 31 | 444.7 | 318.6 | 13(d) | (107) |
| 5-methyloxolan-2-one + ethylbenzene | 293 | 0.101 | 0.0054–0.98 | 33 | 33 | 141.4 | 259.8 | 13(d) | (107) |
3.6. Mixtures of Lactones + Water: cCOO–H2O Interactions
In the SAFT-γ
Mie approach,
water is modeled by an H2O molecular group9,10 that includes two association sites of type e1 (one for
each lone pair of electrons of the oxygen atom) and two sites of type
H (corresponding to the hydrogen atoms). The H2O–H2O e1–H interactions are incorporated into
the pure-water model. In mixtures with lactones, hydrogen bonding
interactions between the H sites in the H2O group and the
e1 sites of the cCOO group are also accounted for. The
cCOO–H2O unlike group interaction, thus, includes
three parameters (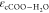 ,
, 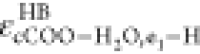 , and
, and 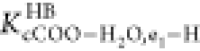 ); these are characterized
in this section.
); these are characterized
in this section.
The VLE114 and SLE70 experimental data found for oxolan-2-one + water are represented in Figure 14a. No azeotropic or liquid–liquid demixing behavior is seen, but we note the eutectic point in the SLE region. Densities115−117 at 298.15 K and atmospheric pressure are presented in Figure 14b for binary mixtures of oxolan-2-one + water and 5-methyloxolan-2-one + water, and the excess molar enthalpies73,118 for the same mixtures are shown in Figure 14c. A highly asymmetric “S” shape can be seen for the two curves, with positive excess enthalpies for xwater < 0.9 and small negative values for xwater > 0.9. The highest values are about 1 kJ/mol for xwater ≈ 0.4 for the two systems. As can be gleaned from the figures, very good agreement is obtained for the bubble temperature of oxolan-2-one + water (%AAD = 0.7953%, and AAD = 2.978 K), the solubility of oxolan-2-one in water (%AAD = 0.3427%, and AAD = 0.003086), and the solubility of water in oxolan-2-one (%AAD = 3.168%, and AAD = 0.01049). The experimental70 eutectic composition and temperature are also accurately predicted. The calculated densities decrease with an increase in the length of the lactone side chain, and the agreement with experimental data115−117 is very good for water + oxolan-2-one and reasonable for water +5-methyloxolan-2-one. The corresponding %AADs and AADs are found to be small (cf. Table 14). Furthermore, the “S” shape of the excess enthalpy curves is correctly reproduced by the SAFT-γ Mie calculation. The corresponding %AADs are rather large (251.2% for water + oxolan-2-one, and 31.32% for water + 5-methyloxolan-2-one), although we note that these large values are due to the very small enthalpies in the water-rich phase (we have considered all the experimental data73,118,119 found for the %AAD calculation and not only the points shown in Figure 14c, including data for different temperatures and data at infinite dilution). The corresponding AADs, which are relatively small (43.33 J/mol for water + oxolan-2-one and 129.4 J/mol for water + 5-methyloxolan-2-one), provide a more appropriate measure of the quality of the model and confirm the good agreement seen in Figure 14c. Additional information on the accuracy of the calculations for the systems considered in this section compared with experimental data from the literature70,73,114−122 can be found in Table 14.
Figure 14.
Isobaric thermodynamic properties of lactones + water at atmospheric pressure: oxolan-2-one (light blue) and 5-methyloxolan-2-one (dark blue). The curves represent the calculations with SAFT-γ Mie. Experimental data used in the estimation of group-interaction parameters are represented with filled symbols, and those not used are represented with open symbols. (a) Isobaric vapor–liquid equilibrium and solid–liquid equilibrium of oxolan-2-one + water, with experimental data for the bubble temperature114 and solid–liquid equilibrium.70 (b) Density of lactones + water at 298.15 K, with experimental data for oxolan-2-one116 and 5-methyloxolan-2-one.117 (c) Excess molar enthalpy of oxolan-2-one + water at 299.15 K and 5-methyloxolan-2-one + water at 303.15 K, with experimental data for oxolan-2-one + water118 and 5-methyloxolan-2-one + water.73 Thermodynamic conditions and the accuracy of the calculations are detailed in Table 14 and in the Zenodo datafile.
Table 14. Overview of the Accuracy of SAFT-γ Mie in the Calculation of Bubble Temperatures Tbub, Dew Temperatures Tdew, Liquid–Liquid Equilibrium Compositions xLLE1, Solubilities xsat1, Densities ρ, and Excess Molar Enthalpies Δhmix for Binary Mixtures of Lactones + Water, Where NDs,p Is the number of Experimental Data Used in the Parameter Estimation, and ND,totals,p Is the Number of Experimental Data Used to Calculate %AADsp and AADsp for System s and Property p.
| system s (1 + 2) | T/K range | P/MPa range | x1 range | NDs,p | Ntotals,p | %AADsTbub | AADsTbub/K | figure | ref |
|---|---|---|---|---|---|---|---|---|---|
| oxolan-2-one + water | − | 0.012–0.101 | 0.02–1.00 | 11 | 76 | 0.7953 | 2.978 | 14(a) | (70,114,120) |
| 5-methyloxolan-2-one + water | − | 0.010–0.101 | 0.00–1.00 | 8 | 42 | 0.3850 | 1.456 | − | (121) |
| system s (1 + 2) | T/K range | P/MPa range | x1 range | NDs,p | Ntotals,p | %AADsTdew | AADsTdew/K | figure | ref |
|---|---|---|---|---|---|---|---|---|---|
| oxolan-2-one + water | − | 0.012–0.080 | 0.009–1.00 | 0 | 65 | 0.9717 | 3.623 | 14(a) | (70,120) |
| 5-methyloxolan-2-one + water | − | 0.010–0.101 | 0.00–1.00 | 0 | 42 | 0.8737 | 3.171 | − | (121) |
| system s (1 + 2) | T/K range | P/MPa range | x1 range | NDs,p | Ntotals,p | %AADsxLLE1 | AADsxLLE1 | figure | ref |
|---|---|---|---|---|---|---|---|---|---|
| 5-pentyloxolan-2-one + water | 323–373 | 0.101 | − | 6 | 6 | 89.81 | 0.0009193 | − | (122) |
| system s (1 + 2) | T/K range | P/MPa range | x1 range | NDs,p | Ntotals,p | %AADsxsat1 | AADsxsat1 | figure | ref |
|---|---|---|---|---|---|---|---|---|---|
| oxolan-2-one in water | 225–229 | 0.101 | − | 3 | 4 | 0.3427 | 0.003086 | 14(a) | (70) |
| water in oxolan-2-one | 225–273 | 0.101 | − | 0 | 12 | 3.168 | 0.01049 | 14(a) | (70) |
| system s (1 + 2) | T/K range | P/MPa range | x1 range | NDs,p | Ntotals,p | %AADs ρ | AADs ρ/(kg/m3) | figure | ref |
|---|---|---|---|---|---|---|---|---|---|
| oxolan-2-one + water | 298–343 | 0.101 | 0.00–1.00 | 0 | 43 | 0.6222 | 6.664 | 14(b) | (115,116) |
| 5-methyloxolan-2-one + water | 298–323 | 0.101 | 0.00–1.00 | 12 | 12 | 1.338 | 13.63 | 14(b) | (117) |
| 5-ethyloxolan-2-one + water | 288–318 | 0.101 | 0.00081–0.0048 | 8 | 48 | 0.3988 | 3.983 | − | (119) |
| 6-methyloxan-2-one + water | 288–318 | 0.101 | 0.0012–0.0050 | 10 | 39 | 0.3811 | 3.806 | − | (119) |
| system s (1 + 2) | T/K range | P/MPa range | x1 range | NDs,p | Ntotals,p | %AADs Δhmix | AADs Δhmix/(J/mol) | figure | ref |
|---|---|---|---|---|---|---|---|---|---|
| oxolan-2-one + water | 288–318 | 0.101 | 0.0012–0.88 | 7 | 51 | 251.2 | 43.33 | 14(c) | (118,119) |
| 5-methyloxolan-2-one + water | 303–323 | 0.101 | 0.0019–0.90 | 14 | 28 | 31.32 | 129.4 | 14(c) | (73) |
| 5-ethyloxolan-2-one + water | 288–318 | 0.101 | 0.00081–0.0048 | 12 | 48 | 49.08 | 3.420 | − | (119) |
| 6-methyloxan-2-one + water | 288–318 | 0.101 | 0.0012–0.0050 | 10 | 39 | 58.61 | 11.35 | − | (119) |
3.7. Mixtures of Lactones + Carbon Dioxide: cCOO–CO2 Interactions
Carbon
dioxide is modeled with the
CO2 molecular group in SAFT-γ Mie.90 One association site of type e1 and one of e2 are incorporated in this group, and these are active in mixtures
of CO2 with water or amines;13,42 they are not,
however, assumed to interact with the e1 sites of the cCOO
lactone group. Thus, the only unlike group parameters that need to
be determined to characterize the cCOO–CO2 interactions
are 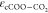 and
and 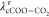 .
.
Experimental-bubble pressure data for mixtures of lactones + carbon dioxide are available,123−126 although we note that inconsistencies have been reported for some of the data related to these mixtures.125 We use the most recent set of data125 to estimate the cCOO–CO2 interaction parameters and present a representative sample of the results in Figure 15. Bubble pressures at 333 K for several binary lactone + carbon dioxide mixtures are shown in Figure 15a, and the influence of temperature is shown in Figure 15b for the bubble pressure of oxepan-2-one + carbon dioxide. For this system, vapor–liquid–liquid equilibrium (VLLE) can be seen at 303 K.125 At temperatures slightly higher than the critical point of CO2 (303 K), an upper critical end point signals the end of the three-phase line, and continuous behavior, from VLE at low pressure to LLE at higher pressure, can be seen (in the figure, this behavior is observed at T ≥ 313 K). The calculations are in very good agreement with the experimental data, although the critical pressure is overestimated in the case of the oxolan-2-one mixture (Figure 15a). The critical pressures are also slightly overestimated, but the overall agreement in terms of the VLLE (at 303 K) and the high-pressure fluid-phase equilibria (at higher temperatures) shown in Figure 15b is very good. The corresponding %AADs and AADs are detailed in Table 15. When inconsistent sets of data are found, we calculate the %AADs and AADs for the references taken together (denoted as † in the table) or taken separately (denoted as ††).
Figure 15.
Isothermal bubble and dew pressures of lactone + carbon dioxide binary mixtures. The curves represent the calculations with SAFT-γ Mie. Experimental data used in the estimation of group-interaction parameters are represented with filled symbols, and those not used are represented with open symbols. (a) Fluid−phase equilibria of lactones + carbon dioxide: oxolan-2-one (light blue), 5-methyloxolan-2-one, 5-ethyloxolan-2-one, 5-propyloxolan-2-one, 5-butyloxolan-2-one, 5-pentyloxolan-2-one, and 5-hexyloxolan-2-one (from dark blue to pale blue) at 333 K. Experimental data are represented by triangles for oxolan-2-one + carbon dioxide,124 diamonds for 5-methyloxolan-2-one + carbon dioxide,126 and squares for 5-ethyloxolan-2-one + carbon dioxide.125 (b) Fluid−phase equilibria of oxepan-2-one + carbon dioxide at 303 K (black), 313 K (dark gray), 323 K (light gray), 333 K (dark red), and 343 K (red). Experimental data are represented by triangles.125 Thermodynamic conditions and the accuracy of the calculations are detailed in Table 15 and in the Zenodo datafile.
Table 15. Overview of the Accuracy of SAFT-γ Mie in the Calculation of Bubble Pressures Pbub, Dew Pressures Pdew, and Densities ρ for Mixtures of Lactones and Carbon Dioxide, Where NDs,p Is the Number of Experimental Data Used in the Parameter Estimation, and ND,totals,p Is the Number of Experimental Data Used to Calculate %AADsp and AADsp for System s and Property pa.
| system s (1 + 2) | T/K range | P/MPa range | x1 range | NDs,p | Ntotals,p | %AADsPbub | AADsPbub/MPa | figure | ref |
|---|---|---|---|---|---|---|---|---|---|
| oxolan-2-one + carbon dioxide | 273–363 | − | 0.00–0.767 | 0 | 147 | 9.537 | 1.266 | − | (123,124)† |
| 313–363 | − | 0.144–0.494 | 0 | 59 | 16.70 | 2.785 | 15(a) | (124)†† | |
| 273–313 | − | 0.00–0.767 | 0 | 88 | 4.815 | 0.2649 | − | (123)†† | |
| oxepan-2-one + carbon dioxide | 303–363 | − | 0.0199–0.770 | 7 | 106 | 24.03 | 3.190 | − | (124,125)† |
| 303–343 | − | 0.0199–0.770 | 7 | 50 | 17.51 | 1.389 | 15(b) | (125)†† | |
| 313–363 | − | 0.129–0.560 | 0 | 56 | 29.86 | 4.799 | − | (124)†† | |
| 5-methyloxolan-2-one + carbon dioxide | 313–373 | − | 0.211–0.945 | 0 | 32 | 8.679 | 0.6585 | 15(a) | (126) |
| 5-ethyloxolan-2-one + carbon dioxide | 303–363 | − | 0.0199–0.606 | 0 | 102 | 13.54 | 1.617 | − | (124,125)† |
| 303–343 | − | 0.0199–0.606 | 0 | 55 | 8.733 | 0.7446 | 15(a) | (125)†† | |
| 323–363 | − | 0.140–0.513 | 0 | 47 | 19.16 | 2.637 | − | (124)†† | |
| 5-hexyloxolan-2-one + carbon dioxide | 333–363 | − | 0.081–0.372 | 0 | 57 | 16.74 | 2.513 | − | (124) |
| 6-methyloxan-2-one + carbon dioxide | 303–343 | − | 0.141–0.472 | 0 | 35 | 9.415 | 0.8300 | − | (125) |
| system s (1 + 2) | T/K range | P/MPa range | x1 range | NDs,p | Ntotals,p | %AADsPdew | AADsPdew/MPa | figure | ref |
|---|---|---|---|---|---|---|---|---|---|
| oxolan-2-one + carbon dioxide | 313–363 | − | 0.018–0.0379 | 0 | 63 | 3.916 | 0.5872 | 15(a) | (124) |
| oxepan-2-one + carbon dioxide | 313–363 | − | 0.0125–0.0888 | 0 | 74 | 5.303 | 0.7419 | − | (124,125)† |
| 313–343 | − | 0.0199–0.0888 | 0 | 22 | 4.903 | 0.8137 | 15(b) | (125)†† | |
| 313–363 | − | 0.0125–0.0240 | 0 | 52 | 5.450 | 0.7157 | − | (124)†† | |
| 5-methyloxolan-2-one + carbon dioxide | 323–363 | − | 0.0140–0.0265 | 0 | 40 | 3.245 | 0.4545 | − | (124) |
| 5-ethyloxolan-2-one + carbon dioxide | 313–343 | − | 0.0199–0.0637 | 0 | 10 | 5.968 | 0.8196 | 15(a) | (125) |
| 5-hexyloxolan-2-one + carbon dioxide | 323–363 | − | 0.0078–0.0150 | 0 | 35 | 6.850 | 0.9009 | − | (124) |
| 6-methyloxan-2-one + carbon dioxide | 313–343 | − | 0.0282–0.114 | 0 | 20 | 8.166 | 1.092 | − | (125) |
| system s (1 + 2) | T/K range | P/MPa range | x1 range | NDs,p | Ntotals,p | %AADs ρ | AADs ρ/(kg/m3) | figure | ref |
|---|---|---|---|---|---|---|---|---|---|
| oxolan-2-one + carbon dioxide | 273–303 | 0.101 | 0.0416–0.571 | 0 | 16 | 1.0088 | 9.691 | − | (123) |
The dagger symbols indicate that several sets of experimental data can be considered for the %ADD and AAD calculations and are taken together (†) or separately (††).
3.8. Overall Deviations
As a summary of the accuracy of the calculation of the thermodynamic properties and phase equilibria obtained with the SAFT-γ Mie models presented, we collate in Table 16 and Figure 16 the overall deviations of the predicted and calculated data for each property considered. Deviations for temperature, composition, pressure, density, and enthalpy data types are presented in Figure 16 a–e, respectively. As can be seen, the values of the deviations calculated for points not used in parameter estimation (%AADprediction and AADprediction) are found to be similar to those calculated for points used in parameter estimation (%AADestimation and AADestimation), thereby confirming the robustness of the models. Moreover, in the case of bubble and dew temperatures (Figure 16a), as well as for densities for pure fluids and mixtures (Figure 16d), the %AADprediction values are found to be smaller than those of the %AADestimation. Azeotrope temperature data are not used in parameter estimation, and we thus report only the corresponding %AADprediction and AADprediction; these deviations are found to be similar to those for bubble and dew temperatures. In terms of the composition deviations, it is important to note that the %AADs for compositions in binary mixtures (i.e., xLLE1 and xsat1) depend on the choice of compound 1 as a reference. The AADs provide a better metric of performance because these do not depend on the reference compound and they can be compared with the full range of mole fraction values (i.e., from 0 to 1). We find that the AADestimation and AADprediction values of the LLE and SLE compositions are small and of similar order of magnitude (Figure 16b). Similarly, in the case of the excess molar enthalpies, the overall %AADs are rather large, while the AADs are reasonably small; this is because of the experimental data values close to zero leading to very large %AADs. In particular, it is interesting to note that %AADprediction is higher than %AADestimation for the excess molar enthalpy (470.8% and 181.8%, respectively), while the corresponding AADprediction is lower than AADestimation (92.24 J/mol and 153.7 J/mol, respectively).
Table 16. Overview of the Accuracy of SAFT-γ Mie Calculations for the Pure Lactones and the Binary Mixtures That Contain Lactones Considered in Our Worka.
| property p | Nestimationp | Npredictionp | %AADestimation | %AADprediction | AADestimation | AADprediction |
|---|---|---|---|---|---|---|
| vapor pressure | 109 | 176 | 18.06 | 24.81 | 416.1 Pa | 393.4 Pa |
| liquid density (pure compounds) | 34 | 425 | 1.646 | 1.147 | 16.82 kg/m3 | 12.04 kg/m3 |
| enthalpy of vaporization | 110 | 152 | 2.623 | 3.071 | 1.600 kJ/mol | 1.859 kJ/mol |
| bubble temperature | 170 | 158 | 0.6427 | 0.5584 | 2.593 K | 2.170 K |
| dew temperature | 116 | 201 | 1.626 | 0.7560 | 6.217 K | 2.828 K |
| azeotrope temperature | 0 | 24 | − | 0.6022 | − | 2.231 K |
| azeotrope composition | 0 | 36 | − | 13.76 | − | 0.03520 |
| LLE composition | 62 | 66 | 65.57 | 154.4 | 0.1088 | 0.06470 |
| SLE composition | 73 | 95 | 3.087 | 30.76 | 0.01025 | 0.09023 |
| bubble pressure | 172 | 619 | 15.30 | 14.97 | 58.50 kPa | 1410 kPa |
| dew pressure | 0 | 242 | − | 5.083 | − | 708.4 kPa |
| liquid density (binary mixtures) | 220 | 765 | 0.8953 | 0.7271 | 8.618 kg/m3 | 7.063 kg/m3 |
| excess molar enthalpy | 322 | 269 | 181.8 | 470.8 | 0.1537 kJ/mol | 0.09224 kJ/mol |
Nestimationp is the number of experimental data used in parameter estimation for property p. Npredictionp is the number of experimental data not used in parameter estimation (prediction only) for property p. We calculated the corresponding %AADestimation, %AADprediction, AADestimation, and AADprediction.
Figure 16.
Overall %AAD and AAD for the properties considered in our current work. The results for the data used in the parameter estimation are presented in dark blue, and the results for the predictions are in pale blue. (a) Bubble, dew, and azeotrope temperatures. (b) Azeotrope, LLE, and SLE compositions. (c) Vapor pressure for pure fluids and bubble and dew pressures for mixtures. (d) Density for pure fluids and for mixtures. (e) Enthalpy of vaporization for pure fluids and excess molar enthalpy for mixtures.
4. Conclusions
The thermodynamic properties and phase behavior of small saturated lactones have been modeled with the SAFT-γ Mie group-contribution approach. A total of 86 systems have been considered, which correspond to 13 pure lactones and 73 binary mixtures: 21 with saturated hydrocarbons, 20 with alcohols, 2 with ketones, 4 with esters, 15 with aromatic compounds, 5 with water, and 6 with carbon dioxide.
A new SAFT-γ Mie cCOO group has been introduced, and the relevant like cCOO–cCOO and 17 unlike group interactions have been characterized. The accuracy of the calculations has been assessed by comparison with experimental data graphically with phase diagrams over broad thermodynamic conditions and by calculating the appropriate %AADs and AADs. The overall agreement between the experimental values and the SAFT-γ Mie calculations is found to be very good for all of the mixtures and properties studied.
A number of interesting regular features in the thermodynamic properties are found from the comparison between the available experimental data and the SAFT-γ Mie calculations. The VLE for the mixtures of 5-methyloxolan-2-one and several solvents,95,101,105,108 including alcohols (Figures 7a and 9a), ketones (Figure 10a), esters (Figure 11a), aromatic compounds (Figure 12a), and carbon dioxide (Figure 15), do not present azeotropes. In the case of the solubility of oxepan-2-one in ketones (Figure 10b) and aromatic compounds (Figure 12b), eutectic points are found. The density of oxolan-2-one mixtures is abundantly documented,96−98,102,106,116 and we have presented results for mixtures with alcohols (Figures 7c and 9b), esters (Figure 11c), aromatic compounds (Figure 13a), and water (Figure 14b). The density is found to be nonideal in most of the cases considered, with a concave or convex shape as a function of mole fraction. The values found for the excess molar enthalpy, both in the literature88,89,96,100,103,105,118 and from the SAFT-γ Mie calculations, are generally small as can be seen for the mixtures of oxolan-2-one with hydrocarbons (Table 8), alcohols (Figure 7d), esters (Figure 11d), aromatic compounds (Figure 13b), and water (Figure 14c).
The parameters characterized in this work are transferable to other lactones, given the group-contribution nature of the SAFT-γ Mie equation of state, such that more complex molecules modeled with the cCOO group can be considered in future work. In particular, the new interaction parameters pave the way for the modeling of a wide range of compounds, for example, unsaturated lactones, ascorbic acid (vitamin C), and active pharmaceutical ingredients (e.g., simvastatin and lovastatin) of current interest.
Acknowledgments
We acknowledge support from the EPSRC and the Future Manufacturing Research Hub in Continuous Manufacturing and Advanced Crystallization (Grants ref: EP/P006965/1 and EP/I033459/1) for funding this work. We also acknowledge financial support from the Engineering and Physical Sciences Research Council (EPSRC) of the UK (grants GR/T17595, GR/N35991, EP/E016340, EP/P006965, and EP/J014958/1) to the Molecular Systems Engineering group. A.G. is thankful to the Royal Academy of Engineering and Eli Lilly and Company for support of a Research Chair (Grant RCSRF18193). We wish to acknowledge the use of the EPSRC-funded Physical Sciences Data-science Service hosted by the University of Southampton and STFC under grant number EP/S020357/1. We also gratefully acknowledge support from Eli Lilly and Company through the PharmaSEL Programme and joint EPSRC/Lilly Prosperity Partnership (EP/T005556/1).
Data Availability Statement
Data underlying this article can be accessed on Zenodo at DOI: 10.5281/zenodo.8268756 and used under the Creative Commons Attribution license.
Author Present Address
‡ Pfizer R&D UK Limited, Sandwich, Kent CT13 9NJ, United Kingdom
Author Present Address
¶ Equinor ASA, Fornebu 1330, Norway
The authors declare no competing financial interest.
References
- Sartori S. K.; Diaz M. A. N.; Diaz-Muñoz G. Lactones: classification, synthesis, biological activities, and industrial applications. Tetrahedron 2021, 84, 132001. 10.1016/j.tet.2021.132001. [DOI] [Google Scholar]
- Maga J. A.; Katz I. Lactones in foods. CRC Crit. Rev. Food Sci. Nutr. 1976, 8, 1–56. 10.1080/10408397609527216. [DOI] [PubMed] [Google Scholar]
- Dufossé L.; Latrasse A.; Spinnler H. E. Importance of lactones in food flavours: structure, distribution, sensory properties and biosynthesis. Sciences des Aliments 1994, 14, 17–50. [Google Scholar]
- Gatfield I. L.Biotechnology of Aroma Compounds; Springer Berlin Heidelberg, 1997; pp 221–238. [Google Scholar]
- Schrader J.Chapter 23: Microbial flavour production. In Flavours and fragrances; Springer, 2007; pp 555–561. [Google Scholar]
- Marella E. R.; Dahlin J.; Dam M. I.; ter Horst J.; Christensen H. B.; Sudarsan S.; Wang G.; Holkenbrink C.; Borodina I. A single-host fermentation process for the production of flavor lactones from non-hydroxylated fatty acids. Metab. Eng. 2020, 61, 427–436. 10.1016/j.ymben.2019.08.009. [DOI] [PubMed] [Google Scholar]
- Schwarz W.; Schossig J.; Rossbacher R.; Pinkos R.; Höke H.. Butyrolactone. In Ullmann’s encyclopedia of industrial chemistry; American Cancer Society, 2019; pp 1–7. [Google Scholar]
- Papaioannou V.; Lafitte T.; Avendaño C.; Adjiman C. S.; Jackson G.; Müller E. A.; Galindo A. Group contribution methodology based on the statistical associating fluid theory for heteronuclear molecules formed from Mie segments. J. Chem. Phys. 2014, 140, 54107. 10.1063/1.4851455. [DOI] [PubMed] [Google Scholar]
- Dufal S.; Lafitte T.; Haslam A. J.; Galindo A.; Clark G. N. I.; Vega C.; Jackson G. The A in SAFT: developing the contribution of association to the Helmholtz free energy within a Wertheim TPT1 treatment of generic Mie fluids. Mol. Phys. 2015, 113, 948–984. 10.1080/00268976.2015.1029027. [DOI] [Google Scholar]
- Dufal S.; Lafitte T.; Haslam A. J.; Galindo A.; Clark G. N. I.; Vega C.; Jackson G. Corrigendum: The A in SAFT: developing the contribution of association to the Helmholtz free energy within a Wertheim TPT1 treatment of generic Mie fluids. Mol. Phys. 2018, 116, 283–285. 10.1080/00268976.2017.1402604. [DOI] [Google Scholar]
- Haslam A. J.; Gonzalez-Perez A.; Di Lecce S.; Khalit S. H.; Perdomo F. A.; Kournopoulos S.; Kohns M.; Lindeboom T.; Wehbe M.; Febra S. A.; Jackson G.; Adjiman C. S.; Galindo A. Expanding the applications of the SAFT-γ Mie group-contribution equation of state: prediction of thermodynamic properties and phase behaviour of mixtures. J. Chem. Eng. Data 2020, 65, 5862–5890. 10.1021/acs.jced.0c00746. [DOI] [Google Scholar]
- Watson O. L.; Jonuzaj S.; McGinty J.; Sefcik J.; Galindo A.; Jackson G.; Adjiman C. S. Computer aided design of solvent blends for hybrid cooling and antisolvent crystallization of active pharmaceutical ingredients. Org. Process Res. Dev. 2021, 25, 1123–1142. 10.1021/acs.oprd.0c00516. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee Y. S.; Galindo A.; Jackson G.; Adjiman C. S. Enabling the direct solution of challenging computer-aided molecular and process design problems: chemical absorption of carbon dioxide. Comput. Chem. Eng. 2023, 174, 108204. 10.1016/j.compchemeng.2023.108204. [DOI] [Google Scholar]
- Lee Y. S.; Galindo A.; Jackson G.; Adjiman C. S.. A predictive modelling approach for CO2 chemical absorption-desorption processes: linking solvent structure to techno-economic performance. Chem. Eng. Res. Des. 2023, submitted. [Google Scholar]
- Chapman W. G.; Gubbins K. E.; Jackson G.; Radosz M. SAFT: equation-of-state solution model for associating fluids. Fluid Phase Equilib. 1989, 52, 31–38. 10.1016/0378-3812(89)80308-5. [DOI] [Google Scholar]
- Chapman W. G.; Gubbins K. E.; Jackson G.; Radosz M. New reference equation of state for associating liquids. Ind. Eng. Chem. Res. 1990, 29, 1709–1721. 10.1021/ie00104a021. [DOI] [Google Scholar]
- Jackson G.; Chapman W. G.; Gubbins K. E. Phase equilibria of associating fluids: spherical molecules with multiple bonding sites. Mol. Phys. 1988, 65, 1–31. 10.1080/00268978800100821. [DOI] [Google Scholar]
- Chapman W. G.; Jackson G.; Gubbins K. E. Phase equilibria of associating fluids. Mol. Phys. 1988, 65, 1057–1079. 10.1080/00268978800101601. [DOI] [Google Scholar]
- Müller E. A.; Gubbins K. E. Molecular-based equations of state for associating fluids: a review of SAFT and related approaches. Ind. Eng. Chem. Res. 2001, 40, 2193–2211. 10.1021/ie000773w. [DOI] [Google Scholar]
- McCabe C.; Galindo A.. Chapter 8: SAFT associating fluids and fluid mixture. In Applied thermodynamics of fluids; The Royal Society of Chemistry, 2010. [Google Scholar]
- Gil-Villegas A.; Galindo A.; Whitehead P. J.; Mills S. J.; Jackson G.; Burgess A. N. Statistical associating fluid theory for chain molecules with attractive potentials of variable range. J. Chem. Phys. 1997, 106, 4168–4186. 10.1063/1.473101. [DOI] [Google Scholar]
- Blas F. J.; Vega L. F. Thermodynamic behaviour of homonuclear and heteronuclear Lennard-Jones chains with association sites from simulation and theory. Mol. Phys. 1997, 92, 135–150. 10.1080/00268979709482082. [DOI] [Google Scholar]
- Pàmies J. C.; Vega L. F. Vapor-liquid equilibria and critical behavior of heavy n-alkanes using transferable parameters from the soft-SAFT equation of state. Ind. Eng. Chem. Res. 2001, 40, 2532–2543. 10.1021/ie000944x. [DOI] [Google Scholar]
- Llovell F.; Pàmies J. C.; Vega L. F. Thermodynamic properties of Lennard-Jones chain molecules: renormalization-group corrections to a modified statistical associating fluid theory. J. Chem. Phys. 2004, 121, 10715–10724. 10.1063/1.1809112. [DOI] [PubMed] [Google Scholar]
- Llovell F.; Vega L. F. Global fluid phase equilibria and critical phenomena of selected mixtures using the crossover soft-SAFT equation. J. Phys. Chem. B 2006, 110, 1350–1362. 10.1021/jp0551465. [DOI] [PubMed] [Google Scholar]
- Llovell F.; Vega L. F. Prediction of thermodynamic derivative properties of pure fluids through the soft-SAFT equation of state. J. Phys. Chem. B 2006, 110, 11427–11437. 10.1021/jp0608022. [DOI] [PubMed] [Google Scholar]
- Lafitte T.; Apostolakou A.; Avendaño C.; Galindo A.; Adjiman C. S.; Müller E. A.; Jackson G. Accurate statistical associating fluid theory for chain molecules formed from Mie segments. J. Chem. Phys. 2013, 139, 154504. 10.1063/1.4819786. [DOI] [PubMed] [Google Scholar]
- Gross J.; Sadowski G. Perturbed-Chain SAFT: an equation of state based on a perturbation theory for chain molecules. Ind. Eng. Chem. Res. 2001, 40, 1244–1260. 10.1021/ie0003887. [DOI] [Google Scholar]
- Cameretti L. F.; Sadowski G.; M?llerup J. M. Modeling of aqueous electrolyte solutions with Perturbed-Chain Statistical Associated Fluid Theory. Ind. Eng. Chem. Res. 2005, 44, 3355–3362. 10.1021/ie0488142. [DOI] [Google Scholar]
- Gross J.; Vrabec J. An equation-of-state contribution for polar components: dipolar molecules. AIChE J. 2006, 52, 1194–1204. 10.1002/aic.10683. [DOI] [Google Scholar]
- Klajmon M.; Řehák K.; Morávek P.; Matoušová M. Binary liquid–liquid equilibria of γ-valerolactone with some hydrocarbons. J. Chem. Eng. Data 2015, 60, 1362–1370. 10.1021/je501074b. [DOI] [Google Scholar]
- Baird Z. S.; Uusi-Kyyny P.; Pokki J.-P.; Pedegert E.; Alopaeus V. Vapor pressures, densities, and PC-SAFT parameters for 11 bio-compounds. Int. J. Thermophys. 2019, 40, 102. 10.1007/s10765-019-2570-9. [DOI] [Google Scholar]
- Mayer D. A.; Rebelatto E. A.; Girardi D. G. L.; Ndiaye P. M.; Lanza M.; de Oliveira D.; Ulson de Souza S. M. A. G.; Oliveira J. V. Effect of different polymer molar mass on the phase behavior of carbon dioxide + dichloromethane + ε-caprolactone + poly(ε-caprolactone) system. Fluid Phase Equilib. 2020, 521, 112687. 10.1016/j.fluid.2020.112687. [DOI] [Google Scholar]
- Nascimento J. C.; Rebelatto E. A.; Mayer D. A.; Girardi D. G. L.; Ndiaye P. M.; Oliveira J. V.; Lanza M. Phase behavior of carbon dioxide + chloroform + ω-pentadecalactone + poly(ω-pentadecalactone) system: experimental data and PC-SAFT modeling. Fluid Phase Equilib. 2020, 521, 112736. 10.1016/j.fluid.2020.112736. [DOI] [Google Scholar]
- Müller E. A.; Jackson G. Force-field parameters from the SAFT-γ equation of state for use in coarse-grained molecular simulations. Annu. Rev. Chem. Biomol. Eng. 2014, 5, 405. 10.1146/annurev-chembioeng-061312-103314. [DOI] [PubMed] [Google Scholar]
- Hutacharoen P.; Dufal S.; Papaioannou V.; Shanker R. M.; Adjiman C. S.; Jackson G.; Galindo A. Predicting the solvation of organic compounds in aqueous environments: from alkanes and alcohols to pharmaceuticals. Ind. Eng. Chem. Res. 2017, 56, 10856–10876. 10.1021/acs.iecr.7b00899. [DOI] [Google Scholar]
- Hutacharoen P.Prediction of partition coefficients and solubilities of active pharmaceutical ingredients with the SAFT-γ Mie group-contribution approach. Ph.D. Thesis, Imperial College London, 2017. [Google Scholar]
- Di Lecce S.; Lazarou G.; Khalit S. H.; Adjiman C. S.; Jackson G.; Galindo A.; McQueen L. Modelling and prediction of the thermophysical properties of aqueous mixtures of choline geranate and geranic acid (CAGE) using SAFT-γ Mie. RSC Adv. 2019, 9, 38017–38031. 10.1039/C9RA07057E. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Febra S. A.; Bernet T.; Mack C.; McGinty J.; Onyemelukwe I. I.; Urwin S. J.; Sefcik J.; ter Horst J. H.; Adjiman C. S.; Jackson G.; Galindo A. Extending the SAFT-γ Mie approach to model benzoic acid, diphenylamine, and mefenamic acid: solubility prediction and experimental measurement. Fluid Phase Equilib. 2021, 540, 113002. 10.1016/j.fluid.2021.113002. [DOI] [Google Scholar]
- Wehbe M.; Haslam A. J.; Jackson G.; Galindo A. Phase behaviour and pH-solubility profile prediction of aqueous buffered solutions of ibuprofen and ketoprofen. Fluid Phase Equilib. 2022, 560, 113504. 10.1016/j.fluid.2022.113504. [DOI] [Google Scholar]
- Perdomo F. A.; Khalit S. H.; Adjiman C. S.; Galindo A.; Jackson G. Description of the thermodynamic properties and fluid-phase behavior of aqueous solutions of linear, branched, and cyclic amines. AIChE J. 2021, 67, e17194 10.1002/aic.17194. [DOI] [Google Scholar]
- Perdomo F. A.; Khalit S. H.; Graham E. J.; Tzirakis F.; Papadopoulos A. I.; Tsivintzelis I.; Seferlis P.; Adjiman C. S.; Jackson G.; Galindo A. A predictive group-contribution framework for the thermodynamic modelling of CO2 absorption in cyclic amines, alkyl polyamines, alkanolamines and phase-change amines: New data and SAFT-γ Mie parameters. Fluid Phase Equilib. 2023, 566, 113635. 10.1016/j.fluid.2022.113635. [DOI] [Google Scholar]
- Walker P. J.; Yew H.-W.; Riedemann A. Clapeyron.jl: an extensible, open-source fluid thermodynamics toolkit. Ind. Eng. Chem. Res. 2022, 61, 7130–7153. 10.1021/acs.iecr.2c00326. [DOI] [Google Scholar]
- Crespo E. A.; Coutinho J. A. P.. Insights into the limitations of parameter transferability in heteronuclear SAFT-type equations of state. arXiv, November 8, 2022, 2211.04606, ver. 1. 10.48550/arXiv.2211.04606. [DOI]
- Shaahmadi F.; Hurter R. M.; Burger A. J.; Cripwell J. T. Improving the SAFT-γ Mie equation of state to account for functional group interactions in a structural (s-SAFT-γ Mie) framework: linear and branched alkanes. J. Chem. Phys. 2021, 154, 244102. 10.1063/5.0048315. [DOI] [PubMed] [Google Scholar]
- Schulze-Hulbe A.; Shaahmadi F.; Burger A. J.; Cripwell J. T. Extending the structural (s)-SAFT-γ Mie equation of state to primary alcohols. Ind. Eng. Chem. Res. 2022, 61, 12208–12228. 10.1021/acs.iecr.2c00198. [DOI] [Google Scholar]
- Shaahmadi F.; Smith S. A. M.; Schwarz C. E.; Burger A. J.; Cripwell J. T. Group-contribution SAFT equations of state: a review. Fluid Phase Equilib. 2023, 565, 113674. 10.1016/j.fluid.2022.113674. [DOI] [Google Scholar]
- Longster G. F.; Walker E. E. Effect of permanent dipoles on the cohesive energy and solvent action of some highly polar substances. Trans. Faraday Soc. 1953, 49, 228–233. 10.1039/tf9534900228. [DOI] [Google Scholar]
- Rumble J. R.CRC Handbook of Chemistry and Physics, 102nd ed.; CRC, 2021. [Google Scholar]
- Searles S.; Tamres M.; Barrow G. M. Hydrogen-bonding of esters and lactones. Site of bonding and effect of ring size. J. Am. Chem. Soc. 1953, 75, 71–73. 10.1021/ja01097a019. [DOI] [Google Scholar]
- Dufal S.; Papaioannou V.; Sadeqzadeh M.; Pogiatzis T.; Chremos A.; Adjiman C. S.; Jackson G.; Galindo A. Prediction of thermodynamic properties and phase behavior of fluids and mixtures with the SAFT-γ Mie group-contribution equation of state. J. Chem. Eng. Data 2014, 59, 3272–3288. 10.1021/je500248h. [DOI] [Google Scholar]
- Sadeqzadeh M.; Papaioannou V.; Dufal S.; Adjiman C. S.; Jackson G.; Galindo A. The development of unlike induced association-site models to study the phase behaviour of aqueous mixtures comprising acetone, alkanes and alkyl carboxylic acids with the SAFT-γ Mie group contribution methodology. Fluid Phase Equilib. 2016, 407, 39–57. 10.1016/j.fluid.2015.07.047. [DOI] [Google Scholar]
- Do H. T.; Chua Y. Z.; Habicht J.; Klinksiek M.; Hallermann M.; Zaitsau D.; Schick C.; Held C. Melting properties of peptides and their solubility in water. Part 1: dipeptides based on glycine or alanine. RSC Adv. 2019, 9, 32722–32734. 10.1039/C9RA05730G. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Do H. T.; Chua Y. Z.; Kumar A.; Pabsch D.; Hallermann M.; Zaitsau D.; Schick C.; Held C. Melting properties of amino acids and their solubility in water. RSC Adv. 2020, 10, 44205–44215. 10.1039/D0RA08947H. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Febra S. A.Ring formation in a statistical associating fluid theory framework. Ph.D. Thesis, Imperial College London, 2018. [Google Scholar]
- Gmehling J.Pure compound data from DDB. 1983. [Google Scholar]
- Lebedev B. V.; Yevstropov A. A. Thermodynamics of β-propiolactone, γ-butyrolactone, δ-valerolactone, and ε-caprolactone from 13.8 to 340 K. J. Chem. Thermodyn. 1983, 15, 115–128. 10.1016/0021-9614(83)90150-7. [DOI] [Google Scholar]
- Pokorný V.; Štejfa V.; Fulem M.; Červinka C.; Růžička K. Vapor pressures and thermophysical properties of ethylene carbonate, propylene carbonate, γ-valerolactone, and γ-butyrolactone. J. Chem. Eng. Data 2017, 62, 4174–4186. 10.1021/acs.jced.7b00578. [DOI] [Google Scholar]
- Wilhoit R. C.; Zwolinski B. J. Physical and thermodynamic properties of aliphatic alcohols. J. Phys. Chem. Ref. Data 1973, 2, 1–420. [Google Scholar]
- Andon R. J. L.; Counsell J. F.; Martin J. F. Thermodynamic properties of organic oxygen compounds. Part XX. The low-temperature heat capacity and entropy of C4 and C5 ketones. J. Chem. Soc. A 1968, 1894–1897. 10.1039/j19680001894. [DOI] [Google Scholar]
- Liessmann G.; Schmidt W.; Reiffarth S.. Recommended thermophysical data. Data Compilation of the Saechische Olefinwerke Boehlen Germany 1995. [Google Scholar]
- Nan Z.-D.; Tan Z.-C. Thermodynamic investigation of the azeotropic mixture composed of water and benzene. Chin. J. Chem. 2004, 22, 4–8. 10.1002/cjoc.20040220103. [DOI] [Google Scholar]
- Hopfe D.Thermophysical data of Pure Substances. Data Compilation of FIZ CHEMIE Germany 1990. [Google Scholar]
- gPROMS. https://www.psenterprise.com/products/gproms (accessed 2023-06-06).
- Mejía A.; Müller E. A.; Chaparro Maldonado G. SGTPy: a Python code for calculating the interfacial properties of fluids based on the square gradient theory using the SAFT-VR Mie equation of state. J. Chem. Inf. Model. 2021, 61, 1244–1250. 10.1021/acs.jcim.0c01324. [DOI] [PubMed] [Google Scholar]
- Wittig R.; Constantinescu D.; Gmehling J. Binary solid–liquid equilibria of organic systems containing ε-caprolactone. J. Chem. Eng. Data 2001, 46, 1490–1493. 10.1021/je0101552. [DOI] [Google Scholar]
- Gmehling J.; Li J.; Schiller M. A modified UNIFAC model. 2. Present parameter matrix and results for different thermodynamic properties. Ind. Eng. Chem. Res. 1993, 32, 178–193. 10.1021/ie00013a024. [DOI] [Google Scholar]
- Bernet T.; Paliwal S.; Alyazidi A.; Haslam A. J.; Adjiman C. S.; Jackson G.; Galindo A.. Modeling the thermodynamic properties of cyclic alcohols with the SAFT-γ Mie approach: application to cyclohexanol and menthol systems. 2023, in preparation. [Google Scholar]
- Turovtsev V. V.; Emel’yanenko V. N.; Orlov Y. D. Thermodynamic functions of lactones in the gaseous state. Russ. Chem. Bull. 2016, 65, 82–90. 10.1007/s11172-016-1268-4. [DOI] [Google Scholar]
- Mathuni T.; Kim J.-I.; Park S.-J. Phase equilibrium and physical properties for the purification of propylene carbonate (PC) and γ-butyrolactone (GBL). J. Chem. Eng. Data 2011, 56, 89–96. 10.1021/je100803e. [DOI] [Google Scholar]
- Emel’yanenko V. N.; Kozlova S. A.; Verevkin S. P.; Roganov G. N. Vapour pressures and enthalpies of vaporization of a series of δ-lactones. J. Chem. Thermodyn. 2007, 39, 10–15. 10.1016/j.jct.2006.06.010. [DOI] [Google Scholar]
- Emel’yanenko V. N.; Verevkin S. P.; Stepurko E. N.; Roganov G. N.; Georgieva M. K. Thermodynamical properties of ε-caprolactone. Russ. J. Phys. Chem. 2010, 84, 356–363. 10.1134/S0036024410030039. [DOI] [Google Scholar]
- Zaitseva A.; Pokki J.-P.; Le H. Q.; Alopaeus V.; Sixta H. Vapor–liquid equilibria, excess enthalpy, and density of aqueous γ-valerolactone solutions. J. Chem. Eng. Data 2016, 61, 881–890. 10.1021/acs.jced.5b00724. [DOI] [Google Scholar]
- Emel’yanenko V. N.; Kozlova S. A.; Verevkin S. P.; Roganov G. N. Vapour pressures and enthalpies of vapourization of a series of the γ-lactones. J. Chem. Thermodyn. 2008, 40, 911–916. 10.1016/j.jct.2008.02.002. [DOI] [Google Scholar]
- Kozlovskiy M.; Gobble C.; Chickos J. Vapor pressures and enthalpies of vaporization of a series of γ and δ-lactones by correlation gas chromatography. J. Chem. Thermodyn. 2014, 73, 262–268. 10.1016/j.jct.2014.01.016. [DOI] [Google Scholar]
- Demakhin A.; Ponomarenko S. M.; Yudina O. Y.. Physico-chemical properties of some aprotic dipolar solvents. I. Dependence of bulk properties on temperature. Deposited Doc. 1991 NIITEKHIM N233-khp91 23 1991; p 23. [Google Scholar]
- Ihmels E. C.; Gmehling J. Liquid densities of γ-butyrolactone and N-methyl-2-pyrrolidone from 273 to 473 K and at pressures up to 40 MPa. J. Chem. Eng. Data 2002, 47, 1547–1552. 10.1021/je0255877. [DOI] [Google Scholar]
- Fornefeld-Schwarz U.; Klein A.; Svejda P. Densities and isothermal compressibilities of liquid mixtures of γ-butyrolactone, γ-valerolactone, δ-valerolactone, or ε-caprolactone + benzene, toluene, or ethylbenzene at 293.15 K and pressures up to 10 MPa. ELDATA Int. Electron. J. Phys. Chem. Data 1997, 3, 131–148. [Google Scholar]
- Boodida S.; Bachu R. K.; Patwari M. K.; Nallani S. Volumetric and transport properties of binary liquid mixtures of N-methylacetamide with lactones at temperatures (303.15 to 318.15) K. J. Chem. Thermodyn. 2008, 40, 1422–1427. 10.1016/j.jct.2008.05.004. [DOI] [Google Scholar]
- Papovic S.; Gadžurić S.; Tot A.; Bešter-Rogač M.; Pavlović K.; Vraneš M. A comparative study on the interactions of [bmim][NTf2] ionic liquid with selected four- to seven-membered-ring lactones. J. Chem. Thermodyn. 2017, 107, 170–181. 10.1016/j.jct.2016.12.032. [DOI] [Google Scholar]
- Delaby R.; Lecomte J. Absorption spectra of ethylenic compounds. III. Acids and lactones. Bull. Soc. Chim. Fr. Mem. 1937, 4, 1007–1017. [Google Scholar]
- Kuhn R.; Kum K. On the absolute configuration of sorbic oil. Chem. Ber. 1962, 95, 2009–2011. 10.1002/cber.19620950823. [DOI] [Google Scholar]
- Smogorzhevskaya M. V.; Kushner T. M. Azeotropes in systems formed by γ-butyrolacetone with alcohols and hydrocarbons. Zh. Prikl. Khim. 1989, 62, 1887–1890. [Google Scholar]
- Sevgili L. M. Liquid phase equilibria for mixtures of (an aliphatic hydrocarbon + toluene + γ-butyrolactone) at 298.2 K and atmospheric pressure. Fluid Phase Equilib. 2010, 287, 106–110. 10.1016/j.fluid.2009.09.019. [DOI] [Google Scholar]
- Koroleva L. V.; Kurochkina M. I.; Vauchskii Y. P.; Lunev V. D. Extractive separation of ε-caprolactone - polycaprolactone. Zh. Prikl. Khim. 1973, 46, 670–672. [Google Scholar]
- Hutton D. G.; Jones J. H. Extraction of cyclic ethers from mixtures containing hydrocarbons. J. Chem. Eng. Data 1963, 8, 617–620. 10.1021/je60019a049. [DOI] [Google Scholar]
- Falcchi Corrêa L. F.; de Pelegrini Soares R.; Ceriani R. Solubility behavior of γ-valerolactone + n-tetradecane or diesel mixtures at different temperatures. Fluid Phase Equilib. 2019, 484, 239–244. 10.1016/j.fluid.2018.11.012. [DOI] [Google Scholar]
- Kedrina N. N.; Semenov L. V.; Gaile A. A.; Kaifadzhyan E. A.. Enthalpy of mixing of hydrocarbons C5-C6 with polar solvents. Deposited Doc. 1985 VINITI N348–85 dep 1985; p 19. [Google Scholar]
- Belonsov V. P.; Shutin S. G. Calorimetric study of binary Systems with a solubility gap. 1. n-heptane + methanol, + γ-butyrolactone, + furfural. Z. Phys. Chem. Leipzig 1988, 269, 689–695. 10.1515/zpch-1988-26974. [DOI] [Google Scholar]
- Papaioannou V.; Calado F.; Lafitte T.; Dufal S.; Sadeqzadeh M.; Jackson G.; Adjiman C. S.; Galindo A. Application of the SAFT-γ Mie group contribution equation of state to fluids of relevance to the oil and gas industry. Fluid Phase Equilib. 2016, 416, 104–119. 10.1016/j.fluid.2015.12.041. [DOI] [Google Scholar]
- Lindeboom T.Molecular origins of the thermodynamic properties, phase separation behaviour and structure of biomolecules in aqueous solutions. PhD Thesis, Imperial College London, 2019. [Google Scholar]
- Doering K. E. Vapor pressures of 1,4-butanediol – butyrolactone mixtures. FIZ. Report 1965, 7261. [Google Scholar]
- Giles N. F.; Wilson G. M. Vapor–liquid equilibria on Seven binary systems: ethylene oxide + 2-methylpropane; acetophenone + phenol; cis-1,3-dichloropropene + 1,2-dichloropropane; 1,5-hexadiene + allyl chloride; isopropyl acetate + acetonitrile; vinyl chloride + methyl chloride; and 1,4-butanediol + γ-butyrolactone. J. Chem. Eng. Data 2006, 51, 1954–1962. 10.1021/je050317k. [DOI] [Google Scholar]
- Yang Q.; Jin F.; Feng X.; Zhi J.; Yang C. Isobaric vapor–liquid equilibrium for two binary systems (n-butanol + 1,4-butanediol and γ-butyrolactone + 1,4-butanediol) at p = (30.0, 50.0, and 70.0) kPa. J. Chem. Eng. Data 2016, 61, 3034–3040. 10.1021/acs.jced.6b00088. [DOI] [Google Scholar]
- Havasi D.; Pátzay G.; Kolarovszki Z.; Mika L. T. Isobaric vapor–liquid equilibria for binary mixtures of γ-valerolactone + methanol, ethanol, and 2-propanol. J. Chem. Eng. Data 2016, 61, 3326–3333. 10.1021/acs.jced.6b00384. [DOI] [Google Scholar]
- Rambabu K.; Raman G. K. Excess viscosities of binary mixtures of γ-butyrolactone with isoalcohols. Asian J. Chem. 1991, 3, 164–168. [Google Scholar]
- Ritzoulis G.; Missopolinou D.; Doulami S.; Panayiotou C. Relative permittivities, densities, refractive indices and ultrasound velocities of the binary systems of γ-butyrolactone with methanol, ethanol, 1-butanol, and 1-octanol. J. Chem. Eng. Data 2000, 45, 636–641. 10.1021/je990226l. [DOI] [Google Scholar]
- Farhan A. M.; Awwad A. M. Relative permittivities, refractive indices, and densities of dihydrofuran-2(3H)-one + butan-1-ol and + butan-2-ol at T = (293.15, 298.15, 303.15, and 313.15) K. J. Chem. Eng. Data 2010, 55, 1035–1038. 10.1021/je900503p. [DOI] [Google Scholar]
- Rambabu K.; Raman G. K.; Ramakrishna M. Excess enthalpies of binary solvent mixtures of γ-butyrolactone with hexan-1-ol, heptan-1-ol, octan-1-ol and decan-1-ol. Phys. Chem. Liq. 1990, 22, 61–64. 10.1080/00319109008036411. [DOI] [Google Scholar]
- Sitnyakovskii I. B.; Gaile A. A.; Semenov L. V.; Koldobskaya L. L.; Chupyra O. S. Intermolecular interaction in dilute solutions of non-electrolytes in methanol. Zh. Obshch. Khim. 1991, 61, 2405–2410. [Google Scholar]
- Yim J.-H.; Choo Y.-S.; Byun H.-S. Phase behaviour for the (CO2 + 1-butyl-2-pyrrolidone) and (CO2 + 1-octyl-2-pyrrolidone) systems at temperatures from (313.2 to 393.2) K and pressures up to 28 MPa. J. Chem. Thermodyn. 2019, 130, 140–146. 10.1016/j.jct.2018.10.002. [DOI] [Google Scholar]
- Lu H.; Wang J.; Zhao Y.; Xuan X.; Zhuo K. Excess molar volumes and viscosities for binary mixtures of γ-butyrolactone with methyl formate, ethyl formate, methyl acetate, ethyl acetate, and acetonitrile at 298.15 K. J. Chem. Eng. Data 2001, 46, 631–634. 10.1021/je0003290. [DOI] [Google Scholar]
- Sitnyakovskii I. B.; Gaile A. A.; Semenov L. V.; Koldobskaya L. L. Intermolecular interactions of dilute solutions of methylacetate on non-electrolytes. Zh. Obshch. Khim. 1992, 62, 1745–1750. [Google Scholar]
- Joback K. G.; Reid R. C. Estimation of pure-component properties from group-contributions. Chem. Eng. Commun. 1987, 57, 233–243. 10.1080/00986448708960487. [DOI] [Google Scholar]
- Bjola B. S.; Siddiqi M. A.; Svejda P. Excess enthalpies of binary liquid mixtures of γ-butyrolactone + benzene, + toluene, + ethylbenzene, and + carbon tetrachloride, and excess volume of the γ-butyrolactone + carbon tetrachloride liquid mixture. J. Chem. Eng. Data 2001, 46, 1167–1171. 10.1021/je010091v. [DOI] [Google Scholar]
- Yang S.-K.; Peng S.-J.; Huang J.-H.; Fan L.-Q.; Yang F.-X. A study on densities and excess volumes in the (γ-butyrolactone + aromatic hydrocarbon) system at various temperatures. J. Chem. Thermodyn. 2007, 39, 773–780. 10.1016/j.jct.2006.10.005. [DOI] [Google Scholar]
- Bjola B. S.; Siddiqi M. A.; Svejda P. Molar excess enthalpies of binary liquid mixtures of γ-valerolactone or δ-valerolactone + benzene, + toluene, or + ethylbenzene at 293.15 K and atmospheric pressure. J. Chem. Eng. Data 2002, 47, 254–257. 10.1021/je010244e. [DOI] [Google Scholar]
- Makitra P. G.; Tsikanchuk Y. M.; Lukyanets V. M. Interaction of benzene and o-xylene with dimethylformamide and some other selective solvents. Zh. Obshch. Khim. 1978, 48, 1220–1225. [Google Scholar]
- UNIFAC Consortium . Experimental data, measured for the UNIFAC Consortium; UNIFAC Consortium Research Report, 2016. [Google Scholar]
- Moumouzias G.; Ritzoulis G. Relative permittivities and refractive indices of γ-butyrolactone with o-xylene and m-xylene. J. Chem. Eng. Data 1999, 44, 1273–1278. 10.1021/je990119r. [DOI] [Google Scholar]
- Avraam T.; Moumouzias G.; Ritzoulis G. A study on excess volumes and dielectric properties in the γ-butyrolactone + p-xylene system at various temperatures. J. Chem. Eng. Data 1998, 43, 51–54. 10.1021/je9701487. [DOI] [Google Scholar]
- Yang S.-K. Excess volumes and densities of binary mixtures of γ-butyrolactone + 1,3,5-trimethylbenzene or 1,2,4-trimethylbenzene at several temperatures. J. Mol. Liq. 2008, 140, 45–47. 10.1016/j.molliq.2008.01.002. [DOI] [Google Scholar]
- Bock E.; Iwacha D. Dipole moments of some molecules in dilute benzene solutions. Can. J. Chem. 1968, 46, 523–526. 10.1139/v68-086. [DOI] [Google Scholar]
- Ramkumar D. H. S.; Odak S. V.; Kudchadker A. P. Mixture properties of the water + γ-butyrolactone + tetrahydrofuran system. Part 3. Isobaric vapor-liquid equilibrium of water + γ-butyrolactone and tetrahydrofuran + γ-butyrolactone at 1.013 bar. J. Chem. Eng. Data 1989, 34, 466–467. 10.1021/je00058a028. [DOI] [Google Scholar]
- Ramkumar D. H. S.; Kudchadker A. P. Mixture properties of the water + γ-butyrolactone + tetrahydrofuran system. Part 1: Densities of γ-butyrolactone + water at 303.15-to 343.15 K and of tetrahydrofuran + γ-butyrolactone at 278.15-to 298.15 K; and ultrasonic velocities at 298.15 K for the three binary systems inclusive of tetrahydrofuran + water and the ternary system tetrahydrofuran + water + γ-butyrolactone. J. Chem. Eng. Data 1989, 34, 459–463. 10.1021/je00058a026. [DOI] [Google Scholar]
- Werblan L.; Lesinski J. Phase velocity of sound, viscosity and density in mixtures of gamma-butyrolactone with water and ethers - 1,1-dimethoxyethane and 1,2-dimethoxyethane. Polym. J. Chem. 1980, 54, 507–516. [Google Scholar]
- Kurnakov N. S.; Voskresenskaya N. K.; Goltsman M.; Shuvalov M. The viscosimetry of double liquid systems containing bromine or water and organic substances. Izv. Akad. Nauk SSSR Otd. Mater. Estestv. Nauk 1938, 2, 379–390. [Google Scholar]
- Ramkumar D. H. S.; Kudchadker A. P.; Deshpande D. D. Enthalpies of mixing of tetrahydrofuran + γ-butyrolactone and water + γ-butyrolactone systems at 299.15 K. J. Chem. Eng. Data 1985, 30, 491–492. 10.1021/je00042a037. [DOI] [Google Scholar]
- Dohnal V.; Řehák K.; Morávek P. Thermal and volumetric properties of five lactones at infinite dilution in water. J. Chem. Eng. Data 2019, 64, 1577–1585. 10.1021/acs.jced.8b01146. [DOI] [Google Scholar]
- Yarym-Agaev N. L.; Kalinichenko V. P. Liquid-vapor equilibrium in the system gamma-butyrolactone - water. J. Appl. Chem. USSR 1981, 54, 962–963. [Google Scholar]
- Havasi D.; Mizsey P.; Mika L. T. Vapor–liquid equilibrium study of the gamma-valerolactone–water binary system. J. Chem. Eng. Data 2016, 61, 1502–1508. 10.1021/acs.jced.5b00849. [DOI] [Google Scholar]
- Hertel M. O.; Scheuren H.; Sommer K. Solubilities of hexanal, benzaldehyde, 2-furfural, 2-phenylethanol, phenylethanal, and γ-nonalactone in water at temperatures between (50 and 100) ◦C. J. Chem. Eng. Data 2007, 52, 2143–2145. 10.1021/je700122y. [DOI] [Google Scholar]
- Matvienko V. G.; Yarym-Agaev N. L. Liquid-vapor equilibrium and volume properties of the liquid phase in the gamma-butyrolactone - Carbon dioxide system at elevated pressures. Zh. Prikl. Khim. 1999, 72, 1085–1090. [Google Scholar]
- Xu Q.; Wagner K.-D.; Dahmen N. Vapor-liquid equilibria of different lactones in supercritical carbon dioxide. J. Supercrit. Fluid 2003, 26, 83–93. 10.1016/S0896-8446(02)00157-2. [DOI] [Google Scholar]
- Bender J. P.; Feitein M.; Franceschi E.; Corazza M. L.; Oliveira J. V. Phase behaviour of binary systems of lactones in carbon dioxide. J. Chem. Thermodyn. 2010, 42, 48–53. 10.1016/j.jct.2009.07.003. [DOI] [Google Scholar]
- Granero Fernandez E.Fluides supercritiques et solvants biosourcés: propriétés physicochimiques des systèmes expansés par du CO2. Ph.D. Thesis, Université de Toulouse, 2018; pp 1–195.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Citations
- Crespo E. A.; Coutinho J. A. P.. Insights into the limitations of parameter transferability in heteronuclear SAFT-type equations of state. arXiv, November 8, 2022, 2211.04606, ver. 1. 10.48550/arXiv.2211.04606. [DOI]
Data Availability Statement
Data underlying this article can be accessed on Zenodo at DOI: 10.5281/zenodo.8268756 and used under the Creative Commons Attribution license.

















