Figure 2.

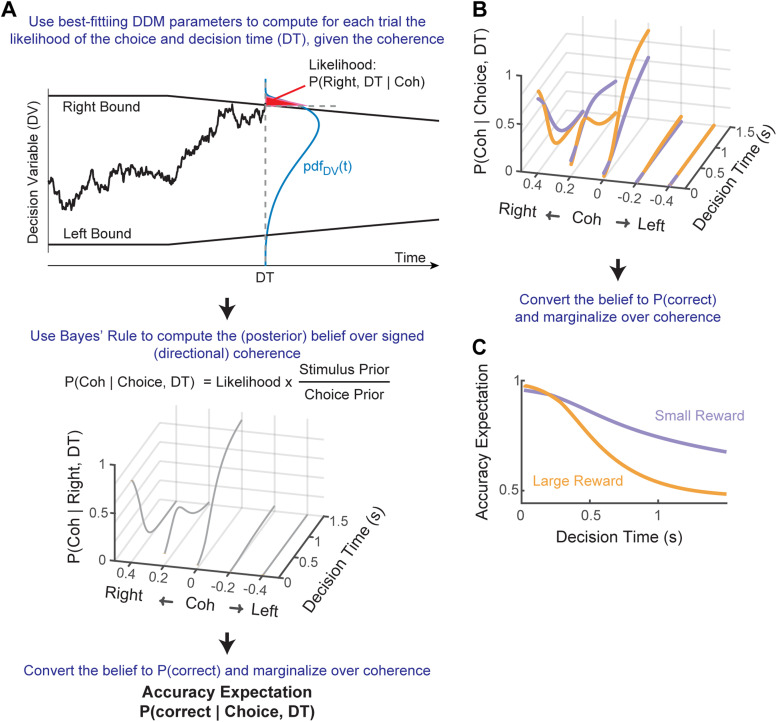
Computing accuracy expectation. A, General framework for computing accuracy expectation. For a given set of DDM parameters fitted to monkeys’ choice and RT data, the probability density function of the DV can be derived for a given time and coherence level: pdf_DV(t). In this example, the likelihood of reaching a Right choice at time t is the area under the pdf_DV(t) curve (red patch) beyond the Right Bound. The likelihoods are used to compute the posterior belief of the stimulus state (i.e., signed coherence). Using the mapping between signed coherence and correct choice, the posterior belief is converted to the probability of being correct and marginalized over coherence to compute accuracy expectation. B, C, Illustration of how asymmetric-reward contexts can influence posterior belief (B) and accuracy expectation (C). For the illustrations, five coherence levels (0, ±0.2, and ±0.4) and the average DDM parameters, separately for the two reward contexts, from all caudate recordings were used.