What Cannot Be Seen Correctly in 2D Visualizations Of Single-Cell ‘Omics Data?

Abstract

A common strategy for exploring single-cell ‘omics data is visualizing 2D nonlinear projections that aim to preserve high-dimensional data properties such as neighborhoods. Alternatively, mathematical theory and other computational tools can directly describe data geometry, while also showing that neighborhoods and other properties cannot be well-preserved in any 2D projection.

Introduction

With the arrival and establishment of single-cell ‘omics techniques over the past decade^1,2, in which a sizable number of cells (10³ – 10⁶) can each be measured for a sizable number of features (10² – 10⁵), biological studies increasingly face the challenges of “big data”. In dealing with high-dimensional data, explorative tools are indispensable for initial data analysis, visualization being perhaps the most obvious form. In the familiar case of low-dimensional (often 2D) data, examining scatter plots or curves immediately narrows down the relevant concepts for further study based on the shape/geometry of data, e.g. whether a studied phenomenon is more categorical or continuous, or whether it is underlain by a linear, sinusoidal, or sigmoidal function. However, in higher dimensions, direct visualization of N-D data shape is infeasible, prompting various strategies for indirectly visualizing the data.

In the field of single-cell ‘omics analysis, a prominent strategy for visualization is to compute low-dimensional representations of N-D data points, in the hopes that the representation produced by such procedures will preserve at least certain aspects of the N-D data’s geometry (we use “representation” herein to mean the image of a one-to-one function from the set of N-D data points to a low-dimensional, often 2D, Euclidean space). Commonly employed computational methods include Principal Component Analysis (PCA), Multi-Dimensional Scaling (MDS), Isomap, t-Stochastic Neighborhood Embedding (tSNE), Uniform Manifold Approximation and Projection (UMAP), and variations thereof, each based on slightly different philosophies of what geometries are key to preserve (e.g. inter-point distances, global topology of points, or density of data points). While there are many efforts towards refining low-dimensional representations of N-D data geometry, alongside critical evaluations of whether these representations are meaningful³, in this work we highlight aspects of N-D data geometry that are fundamentally impossible to represent in low dimensions and hence must be “visualized” in other ways, without mapping data points into a 2D plane.

The impossibility of properly representing high-dimensional geometry in lower dimensions is a well-known phenomenon in the familiar example of representing the Earth’s surface (i.e. 3D points lying on a 2D surface) as a cartographic map (i.e. 2D visualization on the Euclidean plane), which necessarily leads to local and global distortions no matter the map convention. For example, shortest paths on the Earth’s surface often become nonlinear curves on a map (such as the red path between two cyan locations in Fig 1A) instead of the usual straight lines suggested by the cartographic visualization. Even relative distance relationships between points cannot be realized on the map, e.g. it is possible for four points to be equidistant on the Earth’s surface (shown in Fig 1B with either 3D Euclidean distances in red or shortest paths along the surface in blue), whereas no map can have more than three points be equidistant, leading at least one point to be arbitrarily placed farther or closer to the others compared to reality. Furthermore, no map can preserve even the neighborhood relations of all points: there will always be points immediately adjacent in reality that appear in disjoint regions of a map, such as those highlighted in red in Fig 1C. Thus, there exists no 2D visualization of the Earth’s surface that can faithfully represent quantitative, relative, or even qualitative notions of local and global relationships. In general, the extent of problems with 2D data visualizations grows worse as the original dimensions grow higher, and just as 2D cartographic maps need to be understood in context after analyzing the Earth’s surface geometry in 3D space, 2D data visualizations need to be understood after first analyzing single-cell ‘omics data geometry in high-dimensional space.

Figure 1. Quantitative paths and relative distances of data points are misrepresented in 2D.

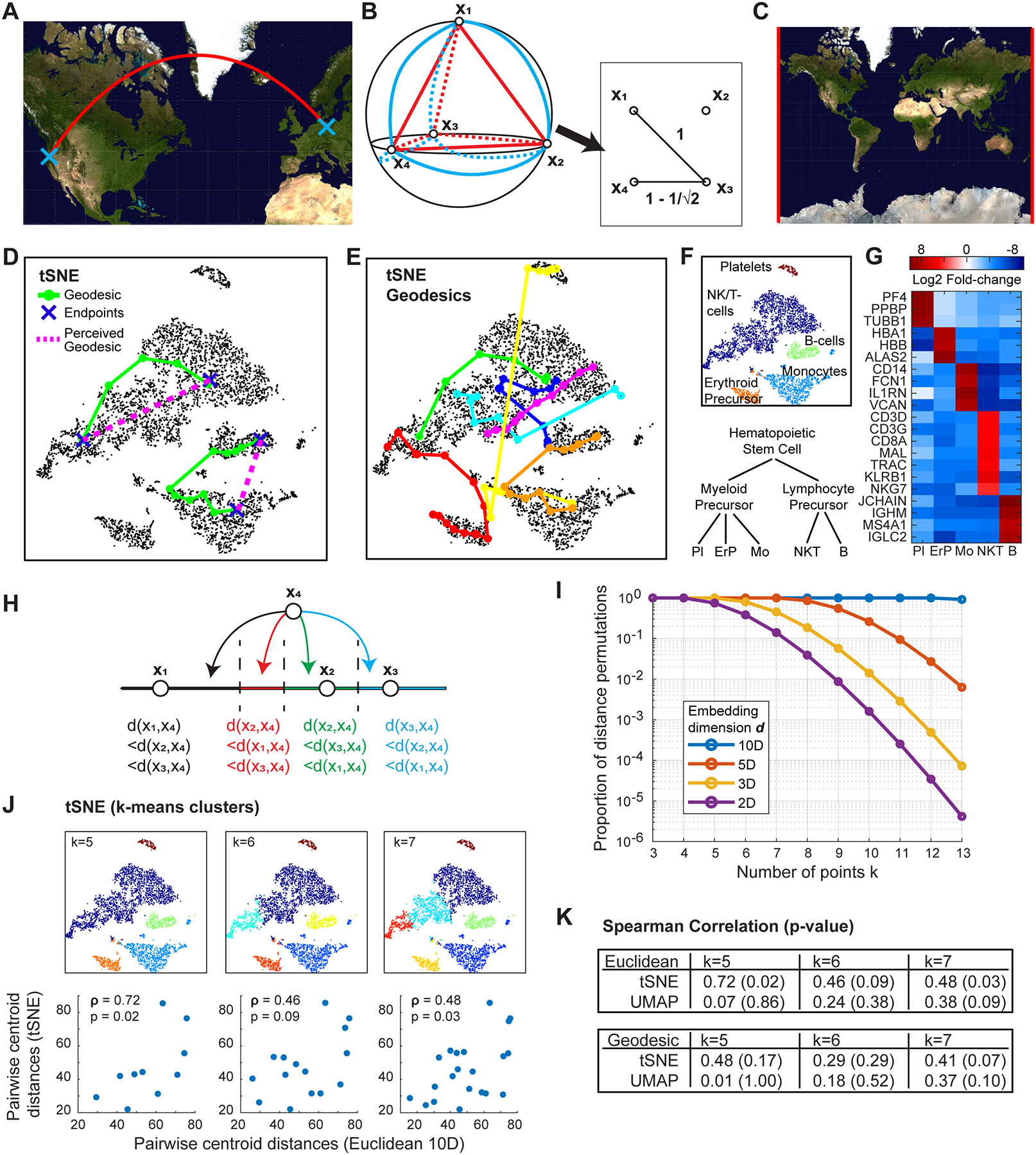
A) Example of shortest path between two locations on Earth, appearing as a curve on a Mercator projection map. See https://github.com/shuwang543/what_cannot_be_seen_in_2D for methods of determining when geodesics are inevitably curved in 2D representations.

B) Four equidistant points in a tetrahedron (red), which are simultaneously equidistant on the sphere (blue). In the plane, four points can be arranged in a square to minimize their deviation from equidistance.

C) Examples (in red) of adjacent regions of the Earth that are discontinuous on a map. Image of Mercator projection obtained from Wikimedia Commons, based on NASA’s Earth Observatory “Blue Marble”.

D) Two geodesics (green) of the 10-PC PBMC data (black) projected onto the tSNE map. The endpoints of the geodesics are indicated in blue, with intermediate nodes shown as circles. The usual straight-line geodesics on the Euclidean plane of the tSNE map are shown in magenta.

E) Several randomly chosen geodesics of the 10-PC neighborhood graph (same as D) shown in color. Pairs of points were chosen at random, and if a geodesic was shorter than 5 nodes, the pair of points were rejected for visualization purposes.

F) (Top) Cell-types of each single-cell cluster. Clusters given by k-means clustering for k=5. (Bottom) Canonical lineage relation between the identified cell-types (Pl: platelets, ErP: erythroid precursor, Mo: monocytes, NKT: natural killer/T-cells, B: B-cells).

G) Selected differentially expressed genes (p<10⁻¹⁰) of each cluster that identify cell-types.

H) Given three points x₁, x₂, x₃ on the 1D Euclidean space, a fourth point can be placed into one of four relative arrangements demarcated by dotted lines.

I) Proportion of possible permutations for placing a k’th point in a Euclidean space of dimension d. See https://github.com/shuwang543/what_cannot_be_seen_in_2D for methods of counting permutations.

J) K-means clustering results for k=5, 6, 7 of PBMC data shown as coloring in tSNE space, with scatter plots of the pairwise distance between cluster centroids shown below when calculated in tSNE space or 10-PC space. Spearman correlation ρ of the pairwise distances are shown alongside p-values.

K) Spearman correlations and p-values for pairwise distances in either the tSNE or UMAP space, relative to either the Euclidean distance in 10-PC space or the geodesic distance. To compute geodesic distances between cluster centroids, the nearest data point to each cluster’s centroid was taken as the centroid’s representative, and geodesics were computed subsequently between these representative data points.

The intuitive problems about local and global relationships of points in Fig 1A–C are relevant to single-cell ‘omics data analysis, since the organization of single-cell expression is often interpreted as indications of cell states and types, developmental landscapes, or disease progression. To avoid both being misled by 2D visualizations as well as neglecting biologically insightful geometric data features, various concepts from geometry and topology can be used to understand the high-dimensional geometry of the data directly. However, such a solution will not take the simple form of a single standalone computational package: to generalize all the intuitive visual notions in 2D that are immediately obvious to the eye at a glance, the field of mathematics had to develop entire subfields of geometry and topology just to understand particular notions rigorously in higher dimensions. For example, the three problems exhibited in Fig 1A–C are respectively motivated by general results from the separate subfields of differential geometry, discrete geometry, and algebraic topology. These subfields not only pinpoint general conditions under which local relations are inevitably distorted in low-dimensional representations of high-dimensional objects, but also provide a rigorous descriptive language for geometrical features existing exclusively in higher dimensions, for which some data-oriented computational tools have recently become available, such as from the disciplines of Manifold Learning and Topological Data Analysis (TDA). Thus, rigorous analysis of high-dimensional data geometry requires carefully defining the specific visual notion that is of biological interest, and applying the corresponding mathematical definition and computational tools that generalize that visual notion. To describe the complete “shape” of a high-dimensional dataset, one would then inevitably need multiple tools and packages based on different subfields of geometry and topology.

As a practical example, we analyze herein an existing public single-cell RNA sequencing dataset of ~5000 peripheral blood mononuclear cells (PBMCs) from a single patient, available at the 10x Genomics website (https://www.10xgenomics.com/resources/datasets/pbmcs-3p_acda_sepmate-3-1-standard). The dataset comes with UMAP and tSNE visualizations, predefined k-means clusters and differential gene expression (DGE) analysis, and a dimensionality reduction of the data to the first 10 principal components (PC) that we take as ground truth. Applying data analysis tools based on differential geometry, discrete geometry, and algebraic topology onto the PBMC dataset, we detect and describe features of the single patient PBMC expression that are exclusively high-dimensional. Consequently, every possible 2D visualization of even this simple dataset on a Euclidean plane necessarily distorts local and global relations at quantitative, relative, and qualitative levels analogous to maps of the Earth’s surface. In general, we anticipate that distinct insights into the organization of single-cell data may exist exclusively in the high-dimensional geometry of data, and are theoretically invisible or misrepresented during the common practice of finding 2D representations of single-cell data points.

Particular Issues

1. Quantitative distances and paths are distorted – differential geometry and curvature

The concept of data “manifolds” already appears frequently in discussions of single-cell ‘omics data to roughly denote the idea that the N features in high-dimensional data are not independent, and therefore can be specified with fewer than N parameters, e.g. the x, y, z- coordinates of points on a sphere can be specified using two angles (here we use manifold to denote both manifolds and manifolds-with-boundary). Nonlinear dependencies often (although not always) produce intrinsically curved geometries that are quantified by differential geometry concepts such as metrics or curvature, the same objects describing the curved space-times of general relativity. Many tools that model data manifolds, such as Isomap or UMAP, also estimate differential geometric objects like the metric as an algorithmic step. However, most features occurring in intrinsically curved manifolds cannot be captured in a 2D plane, which is intrinsically flat. The spherical surface of the Earth is a standard example of an intrinsically curved manifold, in which distances, angles, areas, etc. cannot be preserved in any representation on a flat plane. For nonlinear data manifolds in general, we expect the shortest paths (geodesics) to manifest in 2D visualizations as curves, akin to those on the Earth in Fig 1A, leading to distorted perceptions of which points are closer or farther apart from one another at both the local and global scale. Thus, if one is interested in paths or trajectories in expression space, e.g. to investigate cell-fate differentiation or disease progression, it is vital to compute paths in high-dimensional space as opposed to tracing them by eye on a 2D visualization.

The PBMC dataset, thought of as points sampled from a manifold, faces this exact issue when mapped onto a 2D plane, e.g. by tSNE as in Fig 1D. Geodesics on a manifold can be estimated from sampled data by first defining a neighborhood graph on the data points (e.g. by connecting points with an edge if they are within the first k neighbors of one or the other, and assigning distance as an edge weight), and then computing the shortest path between two points on this graph. We computed a neighborhood graph for the PBMC dataset in the 10-PC space, choosing a neighborhood size of k=30. Two examples of geodesics in the PBMC dataset are shown in Fig 1D projected onto tSNE space, in which two data points (blue) were chosen at random and the shortest path on the neighborhood graph is shown in green along with intermediate nodes shown as circles. While pairs of endpoints visually appear as if the geodesic between them might be the straight magenta lines, the true geodesics are instead curved, just as in the case of the Earth’s surface in Fig 1A. Plotting additional geodesics onto the tSNE map in Fig 1E, we see that besides the magenta one, geodesics of the 10-PC PBMC data are mostly not straight lines on these planar representations. These symptoms are not a particular drawback of tSNE, but rather suggest that even this simple PBMC dataset may have intrinsically curved geometry both within and between clusters that cannot be visualized on a plane, inevitably leading to distorted neighborhoods at various scales.

From a biological standpoint, the geodesics shown in Fig 1E are reminiscent of canonical hematopoietic relationships between PBMCs that cannot be seen from the 2D representation alone. Clustering by k-means for k=5 (Fig 1F) identifies platelets, erythroid precursors, monocytes, a mixture of natural killer and T-cells, and B-cells, as determined by DGE (Fig 1G), and the geodesics between the cell-types are consistent with their relative positions on the simplified hematopoiesis lineage tree shown in Fig 1F. For example, the yellow geodesic jumps across the lymphocytes in Fig 1E to connect the platelets with the monocytes and erythroid precursors, reflecting their common myeloid ancestry. The red and orange geodesics each connect a lymphocyte cluster to a myeloid cluster, and both geodesics take a path through the same neighborhood that connects the three myeloid cell-types, in agreement with the tree in Fig 1F indicating that any differentiation path between lymphocytes and myeloid cells would not skip over a myeloid precursor state. In general, high-dimensional distances and paths in single-cell expression data, e.g. as represented by geodesics in the PBMC dataset, are often considered to be indicative of relationships between cell-types. These high-dimensional paths are best characterized using experimental data from different stages of development, although various methods for trajectory inference assume that certain high-dimensional paths or geodesics represent developmental relations⁴ absent such data. Manifolds and geodesics also underlie quantitative analyses of phylogenetic trees⁵, and manifold learning techniques based on studying quantities such as Laplacians or diffusion maps can be used to leverage the high-dimensional geometry of ‘omics datasets to enable continuous versions of differential gene expression analysis⁶.

2. Relative distances are distorted – discrete geometry and combinatorics

Whereas concerns are occasionally raised about distorted quantitative distances in low-dimensional representations as a warning against over-interpreting visualizations, one might hope that at least some notion of relative proximity is preserved at local or global scales. Unfortunately, even relative proximities of high-dimensional points are nearly impossible to preserve in lower dimensions. We saw in Fig 1B that four points can be equidistant on the sphere but not in the plane, and in general it is possible to have at most N+1 equidistant points in an N-D Euclidean space. Thus, k>3 high-dimensional points may well be equidistant, yet any representation of those points in the plane will arbitrarily make some points closer or farther (the situation can be worse if one considers non-Euclidean metrics in the high-dimensional space). In other words, given a planar representation of k N-D points, many points will seem closer or farther apart even under a null hypothesis that the N-D points are equally dissimilar.

Instead of equidistant arrangements of points, one could alternatively consider whether it is possible to arrange k points x_i in the plane so that the Euclidean distances d(x_i, x_j) follow any particular rank ordering, i.e. an arrangement of relative proximities, such as d(x₁, x₂) < d(x₁, x₃) < d(x₂, x₃). This is related to the possibility of representing the original ordering of each point’s nearest neighbors faithfully in a low-dimensional representation, and such an ordering might be used to infer the relative similarities of single cells or disease states. Given $r=\left(\begin{array}{c}k\\ 2\end{array}\right)$ pairwise distances, there exist potentially r! permutations of the d(x_i, x_j)’s that each define a distinct ordering. Unfortunately, while all the r! orderings are possible in high dimensions, most of them are impossible in the Euclidean plane. To see this in a simpler way, consider the possible permutations of only the terms d(x_i, x_k)’s for a fixed x_k : intuitively this is equivalent to placing x_k a certain relative distance from every other x_i. For example, given 3 points x₁, x₂, x₃ on a line such as Fig 1H, a fourth point x₄ can achieve only four out of six possible permutations of d(x₁, x₄), d(x₂, x₄), d(x₃, x₄), each corresponding to one of the regions in Fig 1H demarcated by dotted lines (since x₂ is between x₁ and x₃, d(x₂,x₄) can never be the largest distance). In other words, in a 1D representation of 4 high-dimensional points, there is a 33% chance that the relative proximity of the fourth point is impossible to represent on a line, and therefore inevitably misrepresented no matter how it is placed.

For the general case of placing the point x_k into an existing arrangement of k-1 points x_i in an N-D Euclidean space, the exact number of permutations of the d(x_i, x_k) terms can be computed. In Fig 1I, we show the proportion of possible permutations for various values of k and embedding dimension d. The proportions drop rapidly with increasing k, and at k=10, only 0.16% of permutations are possible in a 2D representation. Thus, it is practically impossible that the relative proximities of k=10³-10⁵ high-dimensional points are preserved in low-dimensional representations. Even less ambitious criteria may be impossible to satisfy with low-dimensional representations: suppose that instead of preserving relative distances of all the data points, we wish to preserve only the relative distances of one data point X to several points of interest, e.g. points in or outside of X’s local neighborhood. For k = 10 such points including X, we would again only have a 0.16% chance of representing X’s relative position to the other nine correctly. Or at a global scale, suppose we wished to preserve the relative distances between centroids of clusters; again, there is only a 0.16% chance of representing the relative position of one centroid to the other nine correctly.

In the PBMC dataset, we evaluated whether tSNE or UMAP were able to reproduce the relative proximity of cluster centroids computed by k-means. Specifically, for k=5, 6, 7, we computed pairwise Euclidean distances of the k cluster centroids in the 10-PC space, as well as the tSNE or UMAP space, and evaluated the Spearman rank correlation ρ between the two sets of pairwise distances (plots in Fig 1J show results for tSNE). A faithful reproduction of relative proximities would correspond to a rank correlation of exactly 1, but actual correlation values were only 0.72, 0.46, and 0.48 for tSNE, while UMAP did much worse (Fig 1K). We also computed rank correlations by replacing the Euclidean 10-PC distance with the geodesic distances used in the previous section (Fig 1K), and correlations did not improve. Overall, the resulting correlations corresponded to p-values ranging from 0.02 to 0.86. Thus, not only are relative proximities of cluster centroids not reproduced exactly, but in some cases it is statistically unclear whether the relative proximities represented in tSNE or UMAP even correlate with ground truth. Retrospectively, this is a sensible result since only a tiny proportion of distance permutations can possibly be represented in the Euclidean plane. So in general, one must avoid interpreting even the relative proximity of points on 2D visualizations, and biological questions that pertain to the relative arrangement of points ought to be addressed by computing high-dimensional distances (using Euclidean, geodesic, or whatever metric is most meaningful to a given study).

While discrete geometry can be used to reason about the qualitative properties of visualizations, many discrete tools can also be used for directly describing the high-dimensional data itself. In single-cell ‘omics analysis, clustering is perhaps the most prevalent form of discrete geometric analysis, in which data distributions are effectively summarized as a collection of categories. However, it is also valuable to simultaneously characterize the distribution of data points both within and between clusters, e.g. characterizing major axes of variation, and one approach is to fit polygons (polytopes in higher dimensions) to data. The simplest class of polytopes that can be readily fit to data are simplices (or a union of simplices called a simplicial complex): isolated vertices are 0-simplices, a line segment is a 1-simplex, a triangle a 2-simplex, a tetrahedron a 3-simplex, etc. and in general a k-simplex may be defined inductively as a k-dimensional object with k+1 vertices and boundaries composed of (k-1)-simplices (as in Fig 2A). For example, a single-cell RNA sequencing data analysis package called PARTI⁷ applies algorithms for fitting a k-simplex to data and interprets the resulting k+1 vertices of the k-simplex as extremal archetypes of expression, in analogy to cell-types determined by clustering. But in addition, the 1D edges, 2D faces, etc. of the k-simplex can also be used to describe the distribution of data points between archetypes, which may correspond to differentiation trajectories or cells that transition continuously between different functional states, which can be further investigated experimentally.

Figure 2. Combinatorial and topological descriptors of high-dimensional data shape.

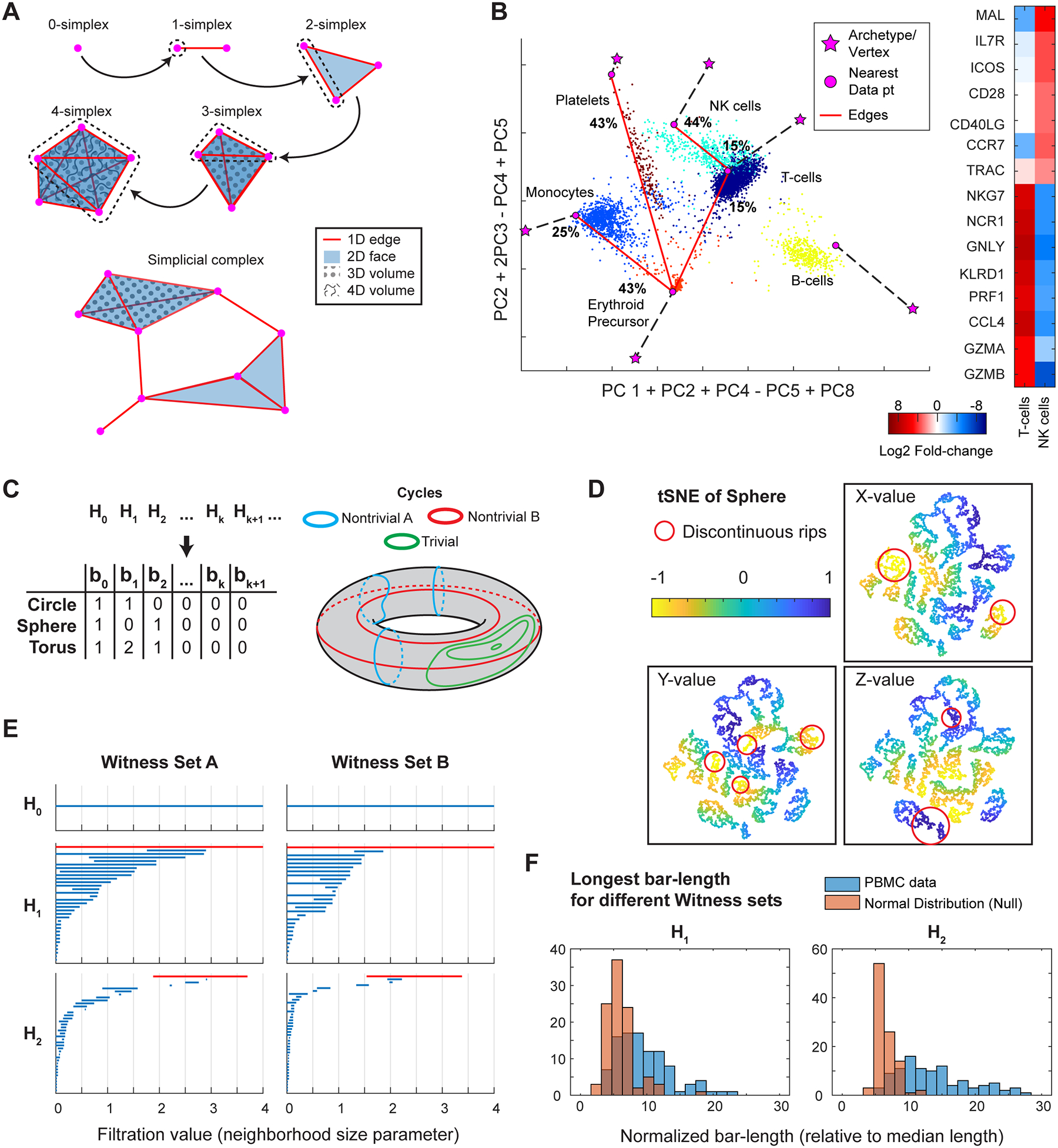
A) Examples of k-simplices, their inductive relation to (k+1)-simplices, and simplicial complexes.

B) (Top) Projection of PBMC data onto a manually selected plane guided by PARTI analysis. Projections of the six vertices of the 5-simplex fit by PARTI shown as magenta stars, alongside their respective nearest data points in 10-PC Euclidean space. Cells colored by k-means clustering for k=6. Red lines indicate edges along which particular clusters have a substantial percent-total-variance. The edge with the greatest variance for each cluster is labeled with the percent-total-variance. (Bottom) Selected differentially expressed genes (p<10⁻¹⁰) of the NK cell and T-cell clusters.

C) The homology groups H_k, which are summarized by Betti numbers b_k, categorize the k-dimensional cycles on a manifold. Betti numbers for the circle, sphere, and torus are listed. Various 1-dimensional cycles on the torus are shown. Cycles that can be continuously deformed into one another, and therefore belong to a common category, are shown in the same color. The green cycles are trivial, because they can be deformed into a point. Therefore, only the blue and red categories contribute non-trivially to H₁, each contributing 1 to the Betti number b₁ of the torus. More details for computing homology groups can be found at https://github.com/shuwang543/what_cannot_be_seen_in_2D

D) Points sampled uniformly from the sphere shown in tSNE space, colored by the original X, Y, or Z-values of the points in 3D. Examples of points belonging to the same neighborhood on the sphere but ripped apart on tSNE are marked by red circles. Other instances of manifolds whose neighborhoods are inevitably ripped apart can be found at https://github.com/shuwang543/what_cannot_be_seen_in_2D.

E) Two instances of barcode plots of the persistent homology of the PBMC dataset, each with a different set of 100 randomly sampled landmark points used in the Witness-complex estimation method of the javaPlex package (http://appliedtopology.github.io/javaplex/). Longest bars in H₁ and H₂ are highlighted in red. Witness complexes were computed with maximum dimension of 3, maximum filtration value of 4, for 200 different filtration values. Homology groups were computed with coefficients over ${\mathbb{Z}}_2$.

F) Maximal interval lengths normalized by the median length of all intervals in a given barcode plot, for 100 different sets of 100 random landmark points. Distributions are shown for both the PBMC data (blue) and normal distribution (orange) with the same covariance matrix as the 10-PC PBMC data as a null.

PARTI suggested a 5-simplex model for the PBMC data based on explained variability. While a complete representation of the 5-dimensional PARTI model in 2D is impossible, we manually found a linear projection (Fig 2B) for the PBMC data to visually convey the information captured by the 1-simplices (edges) of the model. Data points are colored by k-means clustering for k=6, which splits the previous, continuous NK/T-cell cluster into NK cells and T-cells as defined by DGE (Fig 2B). The 6 clusters happen to correspond to the 6 vertices (magenta stars) fit by PARTI, suggesting that we might interpret the 6 vertices as these classical immune cell-types. However, the cells themselves are distributed between vertices, as shown in Fig 2B, and cells in each cluster appear to distribute only along specific edges or faces, e.g. the platelets distribute substantially in the direction of the erythroid precursor, comprising 43% of the cluster’s total 10-PC variance. Specifically, we computed the percent-total-variance of each cluster along the direction of other cell-types, defining the direction in 10-PC space using pairs of nearest data points (represented as magenta circles in Fig 2B) to the vertices, i.e. 1D edges of the simplex. We found that each cluster, except for B-cells, had substantial variance (>10%) in the direction of other cell-types, and the largest of those directions are shown in Fig 2B as red edges labeled with corresponding percentage values (T-cells had two tied directions with 15%). In other words, a substantial portion of cell-type heterogeneity is along directions pointed towards other specific cell-types, as might be expected from hematopoiesis. Furthermore, we note that the 5-simplex model detects that the continuous NK/T-cell cluster is “bent”/V-shaped along the Erythroid-T-cell edge and the NK-T-cell edge. Thus, while the distinction between NK cells and T-cells in expression-space did not manifest geometrically as disjoint clustering, it did manifest as a nonlinear feature within a continuous cluster, which could be detected from the 1-simplices fit by PARTI. Retrospectively, this nonlinear cluster also contained curved geodesics in Fig 1E, in concordance with the expectation that intrinsic curvature in the PBMC data leads to curved geodesics.

We note that the visualization in Fig 2B is neither necessary nor sufficient for reaching these conclusions: the key steps were fitting a 5-simplex model to capture the PBMC data variability using a simple discrete object, characterizing the vertices of the model as cell-types, and quantifying the variance between vertices, which can all be done in any dimension. PARTI has been applied in the literature to understand continuums of cell-type tasks in intestinal villi and liver hepatocytes⁸, and simplices have also been used to understand the micro-environmental cell-type composition archetypes in breast cancer⁹. Beyond simplices, more general polytopes have even been used to describe high-dimensional fitness landscapes in the context of epistatic interactions¹⁰. In general, just as clustering in high-dimensions first before visualizing clusters in a 2D representation is preferable to clustering directly on the 2D representation, various other kinds of discrete relations between data points can be described and computed using other tools from discrete geometry.

3. Neighborhoods are qualitatively distorted – algebraic topology and homology groups

Of the geometric features that one might hope are well represented in low-dimensional visualizations, perhaps the least demanding requirement is for points that are neighbors to continue being neighbors in a low-dimensional representation, even if relative order of local neighbors are off. In other words, we would like the data and its low-dimensional representation to have some notion of topological equivalence. There are different possible technical definitions, but here we will mean homotopy equivalence, which roughly means that there is a way to continuously deform (i.e. no ripping apart of neighboring points and no gluing together of distant points) the original data to its low-dimensional representation and vice versa. We saw, however, in Fig 1C that this is impossible for even the Earth’s surface; note this is a clear instance in which the global shape of high-dimensional data has consequences for the local shape of low-dimensional representations, and so “local” and “global” features are not decoupled. From the perspective of algebraic topology, the key to understanding why no planar map can be homotopy equivalent to the Earth’s surface is the hole inside the hollow sphere, which has no equivalent inside the 2D plane.

In general, all manifolds can be classified by the holes they contain, or more precisely by the cycles on a manifold that envelope those holes. For example, circles and loops are 1-dimensional cycles, whereas spheres and ellipsoids are 2-dimensional cycles. Without referring to exact definitions here, all the k-dimensional cycles are further classified into a set of categories H_k called a homology group, based on which cycles can be deformed continuously into each other. Often, each group is simply characterized by a Betti number b_k, which essentially counts the number of k-dimensional holes in the manifold, with b₀ counting the number of connected components. For example, the Betti numbers of the circle, sphere, and torus are listed in Fig 2C. The torus shown in Fig 2C has non-zero Betti numbers b₂=1, b₁=2, and b₀=1, where three categories of 1-dimensional cycles are shown in red, blue, and green. Since the green cycles can be deformed to a single point, there is no hole, and they do not contribute to the Betti number b₁. However, the red and blue cycles can neither be deformed to a point nor to each other, and therefore correspond to two different holes resulting in the Betti number b₁ = 2.

One application for knowing the homology groups of a manifold is that in order for two manifolds to be homotopy equivalent, it is necessary for them to have matching Betti numbers. Unfortunately, any manifold contained in a 2D plane will always have b_i=0 for i>1, explaining why the Earth’s surface (b₂=1) cannot be homotopy equivalent to any set of points on a map, and will therefore always be ripped apart discontinuously in a planar representation. For example, Fig 2D shows a tSNE map of 10,000 points sampled uniformly from a spherical surface, with red circles highlighting some of the neighborhoods from the sphere that have been ripped apart on the map.

Describing the homology of data points has been a major goal of TDA. However, to define the topology of a finite set of data points, one typically has to choose free parameters (e.g., a distance cutoff), so for a given set of data points a resulting homology may be parameter-dependent. Thus, in TDA one is instead concerned with persistent homology – homology groups that persist over large ranges of parameters – as an indication of the robustness of any resulting description of the data homology. Applying the javaPlex package¹¹ for computing persistent homology on the PBMC dataset’s 10-PC space, we computed the first 3 persistent homology groups using the Witness-complex approach to define topology. Briefly, this approach builds a simplicial complex (Fig 2A) to model the data, selecting a random subset of data points as the 0-simplices (vertices), and connecting them into k-simplices if there are sufficient data points (“witnesses”) occupying the space between any subset of k+1 vertices (defined by a distance cutoff relative to other vertices). The distance cutoff can be tweaked with a filtration parameter which increases all cutoffs globally by a fixed amount. The resulting groups are shown in Fig 2E as barcode plots for two instances of the Witness-complex computation (not to be confused with the experimental barcodes used in sequencing preparation), in which each blue bar corresponds to a hole/homology group that persists over a range of distances (the filtration parameter).

The barcodes in Fig 2E suggest that the data has non-zero Betti numbers in all three computed homology groups, judging from the bars highlighted in red that are substantially longer than the short bars arising from holes that appear briefly due to random fluctuations. We computed barcodes for 100 instances of Witness-complexes; compared to a normal distribution with the same covariance matrix as the PBMC data (a null model with no interesting topology and therefore trivial homology), the longest bars were significantly longer on average for H₁ and H₂ in the PBMC data (Fig 2F). Specifically, Fig 2F shows the histograms of the longest bar length divided by the median bar length of a given barcode. A non-zero b₂ is sufficient to show that any 2D representation of the data will be discontinuously ripped, analogous to the discontinuous edges of cartographic maps. This may also explain why the yellow, cyan, or blue geodesics shown in Fig 1E suddenly jump across the tSNE space; there would always be continuous paths of cell expression that are ripped apart into disjoint path segments on any 2D map. In general, one must be cautious when interpreting the visual neighborhoods of a 2D representation, because if the topology of the high-dimensional data is even slightly complex (i.e. b_i > 0 for i>1), at least some local neighborhoods will inevitably be misrepresented and ripped apart like in Fig 2D. Thus, biological questions concerning the neighborhoods or topology of data should be approached by analyzing the high-dimensional neighborhood graphs (e.g. k-nearest-neighbors), or using tools from TDA like persistent homology.

We have found that 2D representations can generally be inadequate for recapturing even the topology of single-cell ‘omics data, even when topology is being defined by the relatively forgiving notion of homotopy equivalence. In the plane, where the only non-zero Betti numbers are b₁ and b₀, the only kinds of global shapes that can be represented are essentially branching trees, possibly with cycles, and amorphous blobs. In the PBMC dataset, the presence of non-zero b₁ and b₂ support the idea that the developmental relations between these immune cells do not form a literal tree in the graph-theoretical sense¹², but contain cycles of various dimensions. Cycles have also been identified in the context of evolution, resulting from horizontal exchange of genetic material between lineages that would otherwise only form a tree¹³, and other TDA tools have also been used to identify novel candidate cancer-associated genes in various tumor types¹⁴ by using the topology of high-dimensional tumor expression data as context. In general, the zoo of possible topological shapes is much bigger than just the shapes that we can visualize in the plane, and using tools from TDA such as persistent homology, we can explore these high-dimensional topologies and their biological implications.

Discussion

Single-cell ‘omics data provide rich information for biological studies, but the high-dimensional nature of such data makes it difficult to explore the data by visual inspection. Many methods such as tSNE and UMAP aim to find low-dimensional representations of data in the Euclidean plane that can be directly visualized, hoping to preserve geometric features of interest. However, certain kinds of important high-dimensional geometric features are, unfortunately, mathematically impossible to represent in the 2D Euclidean plane, no matter what method is used, leading to distorted visualizations and missed geometric – potentially biological – insights at both local and global scales. As an easily interpretable example of general mathematical principles, we have shown herein that the single-cell RNA sequencing data of even a single patient’s PBMC displayed various geometrical features exclusive to high dimensions. As an expected consequence, proximity of data points in tSNE and UMAP plots is distorted at quantitative (geodesic), relative (pairwise distance orderings), and qualitative (homotopy equivalence) levels at both local and global scales. In more complicated datasets, exclusively high-dimensional geometric features could easily be even more abundant. Thus, it is important not to over-interpret 2D visual representations of high-dimensional data without actually performing quantitative analysis in the original (or relevant) higher dimensions, just as one interprets maps of the Earth only after fully grasping its spherical properties in 3D. Clustering in higher dimensions as opposed to on a 2D representation is perhaps a common example currently in practice, but many other high-dimensional methods for understanding data shape can play a similar role of replacing visual inspection in 2D with more rigorous analysis.

Alternatively, concepts from topology and geometry can directly characterize the high-dimensional features of the data, offering complementary approaches to visual inspection in lower dimensions. Within biology, these concepts have been employed in studies of cellular expression, spatial organization, and evolution, and here we touched upon three different subfields of mathematics for which there exist computational tools suited to general data analysis. While these tools open the door to high-dimensional descriptions of data, it is important to remember that any particular computational implementation comes with assumptions that may or may not be appropriate for the original context of a dataset. For example, in spite of the myriad existing single-cell analysis methods appealing to the concept of a data manifold, in theory there always exist infinitely many manifolds that are consistent with any given finite set of data points, in the same way that one can choose different regression models to fit a set of data points. Thus, understanding the assumptions of particular manifold-methods can be critical, as it determines what variation in the data is considered “noise” as opposed to “signal”. In some methods, measurement noise is not even considered explicitly, yet its presence can heavily affect the ability to recover manifolds from data (see https://github.com/shuwang543/what_cannot_be_seen_in_2D).

There exist other subfields of geometry and topology which also provide rigorous systems of analysis for generalizing particular aspects of visual intuition to higher dimensions. For example, algebraic geometry allows for generalizing intuitions about the different types of shapes traced out by different types of equations (e.g. linear, quadratic, sigmoidal), and we have used algebro-geometric results to infer biochemical reaction properties from single-cell multiplex data¹⁵, in analogy to how one characterizes ultrasensitivity of ligand-binding based on the shape of a Hill curve. However, not every subfield of geometry or topology currently has well-developed computational tools meant for data analysis that not only handle the challenge of generalizing visual intuitions to high dimensions, but also the additional challenges of accounting for experimentally noisy, sampled data. Thus, if the vast array of subfields in geometry and topology are any indication, many aspects of high-dimensional data geometry - and their potential biological insights - have remained unexplored by 2D visualizations, and form a vast array of rich subjects for future research.

Data statement:

This paper analyzes existing, publicly available data from the 10x Genomics website: https://www.10xgenomics.com/resources/datasets/pbmcs-3p_acda_sepmate-3-1-standard.