Use of Stochastic Models To Assess the Effect of Environmental Factors on Microbial Growth

Abstract

We present a novel application of a stochastic ecological model to the study and analysis of microbial growth dynamics as influenced by environmental conditions in an extensive experimental data set. The model proved to be useful in bridging the gap between theoretical ideas in ecology and an applied problem in microbiology. The data consisted of recorded growth curves of Escherichia coli grown in triplicate in a base medium with all 32 possible combinations of five supplements: glucose, NH₄Cl, HCl, EDTA, and NaCl. The potential complexity of 2⁵ experimental treatments and their effects was reduced to 2² as just the metal chelator EDTA, the presumed osmotic pressure imposed by NaCl, and the interaction between these two factors were enough to explain the variability seen in the data. The statistical analysis showed that the positive and negative effects of the five chemical supplements and their combinations were directly translated into an increase or decrease in time required to attain stationary phase and the population size at which the stationary phase started. The stochastic ecological model proved to be useful, as it effectively explained and summarized the uncertainty seen in the recorded growth curves. Our findings have broad implications for both basic and applied research and illustrate how stochastic mathematical modeling coupled with rigorous statistical methods can be of great assistance in understanding basic processes in microbial ecology.

Mathematical modeling coupled with rigorous statistical methods can be of great assistance in understanding the interaction of organisms with their physical and biological environment (8, 47, 48, 50, 52, 56). Studies in the field of predictive microbiology have shown that successful modeling requires both adequate models and thorough data sets (57; for extensive reviews, see references 10, 42, and 55). In predictive microbiology a two-step modeling approach is used (reference 55 and citations therein). Primary models describe the basic rules of how microbial numbers change over time (52). Next, these simple models are used to derive secondary models that account for the effect of a set of factors in microbial growth.

The forces of the environment and the events of reproduction and growth are themselves stochastic in nature (3, 21, 24, 32, 36, 39, 44, 45, 51, 53), yet simple ecological models, such as the Verhulst logistic equation, result in deterministic predictions. However, smooth convergence to asymptotic results is not what is usually seen, even in rigorous experimental settings (17, 31). Hence, a more realistic alternative to population growth modeling is to confront stochastic equations with the data at hand (references 5, 14, and 17 and citations therein and references 41 and 47).

In this paper, we describe a novel application of a stochastic population model to analyze how environmental conditions influence microbial growth dynamics using an extensive experimental data set. The primary model used was the stochastic Ricker (SR) equation (27, 51). Our secondary model was a novel use and application of the SR model in an analysis of variance (ANOVA)-like format to account for differences between and within experimental conditions. We use rigorous statistical methods to characterize the effects of chemical supplements on the following aspects of bacterial growth: the rate of attaining stationary phase, the population density at which stationary phase occurs, and the variability associated with the growth process. The experimental data were time series measures of Escherichia coli growth in a basal medium amended with all 32 possible combinations of five supplements, namely, glucose, NH₄Cl, HCl, EDTA, and NaCl (Fig. 1). All supplement combinations were tested in triplicate. The methods and results presented here have broad implications and can be applied to any situation in which the experimentalist wishes to determine the factors that affect growth responses of microbial isolates.

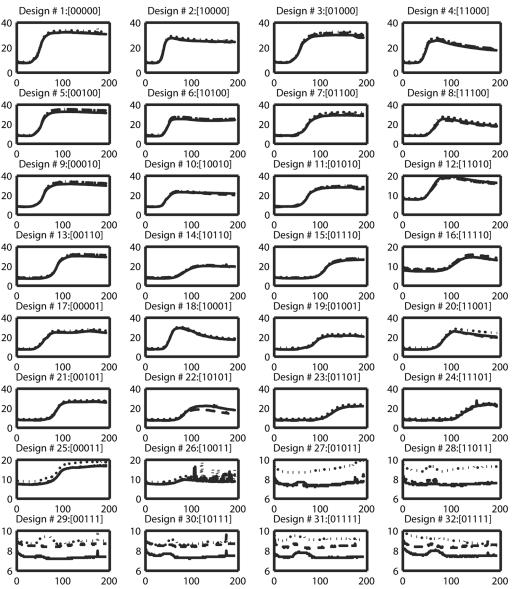
FIG. 1.

Plotted are the three replicated growth curves (OD × 100 as a function of time [min]) of each of the 32 design types (or treatment combinations). Each replicated growth curve is marked with a different line type. In the titles above each plot, the factors present or absent are indicated by 0 or 1, respectively, with the sequence of treatments being glucose, NH₄Cl, HCl, EDTA, and NaCl.

The organization of this paper is as follows. In the first section, we present the experimental procedures used. Next, we present a theoretical background section that is divided into three parts. In the first part, we provide a brief description of the SR model and maximum-likelihood parameter estimation methods. In the second part, we present details of how we derived various secondary models to explain the data. Among those models, the best one was chosen using information theoretic criteria (1, 15, 54). This model selection procedure is described in the third part of the theoretical background section. After presenting the results, we discuss how the SR model compares to other stochastic models and how it can be used to approach the following important problems in predictive microbiology: (i) building a stochastic lag phase model and accounting for the three main phases of microbial growth, (ii) accounting for time-varying environmental factors, (iii) accounting for microbial interactions in the model predictions, and (iv) using an adequate model selection tool that accounts for overparameterization and considers all the models simultaneously instead of stepwise.

MATERIALS AND METHODS

Growth curve experiments.

The organism used for the experiments was Escherichia coli HB101. As a basal medium, a diluted and modified Luria-Bertani (LB) broth was used (1 g/liter tryptone, 0.5 g/liter yeast extract, and 10 g/liter NaCl). The basal medium was supplemented with all 32 possible combinations of five chemicals in the following concentrations: glucose, 8 g/liter; NH₄Cl, 10 g/liter; HCl, 0.0005 M; Na₂EDTA · 2H₂O, 0.05 g/liter; and NaCl, 20 g/liter. Each growth medium was inoculated with a 10⁻³ dilution of an overnight (22-h) culture of the organism grown in undiluted LB broth at 37°C and shaken at 200 rpm. A 2⁵ factorial design with 32 experimental treatments was achieved by transferring triplicate 200-μl aliquots of each medium to a 96-well microtiter plate. This plate was sealed with a breathable membrane (Breathe-Easy; Diversified Biotech, Boston, Mass.) and incubated in an automated plate reader (PowerWave HT; Bio-Tek Instruments, Inc., Winooski, Vt.). The plate was continuously shaken between readings at level 4, and optical density (OD) values of the cultures were measured at 15-min intervals. Thus, 96 growth curves, each consisting of 193 measurements, were obtained. The experimental design is summarized in the plot titles in Fig. 1. Since the maximum recorded OD value was 0.362, we assume a linear relationship between OD and population size throughout this work.

Theoretical background. (i) Primary model: the SR model.

We modeled the growth dynamics of each treatment combination using a stochastic logistic growth model based on the Ricker model (51). The Ricker model has a long history in population ecology modeling (35) and has been used as a discrete version of the well-known Verhulst logistic differential equation (40). The Ricker equation expresses the one-step-ahead population size as a function of the current population size and includes a density-dependent effect:

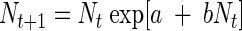(1)

Let N_t be the population size at time t. The parameter a can be thought of as the speed at which equilibrium is reached (mathematically, it is the eigenvalue of the Jacobian matrix, found after linearization around the equilibrium [39, 40]). The parameter b represents the effect of the current population size on the rate of growth. For example, if b is <0, then the current population size has a negative effect on growth, thus expressing density dependence. In that case, the model has a nontrivial stable equilibrium whose position is given by N_∞ = −a/b. The dynamic behavior of this model up to and including chaos is well known (17, 27, 40).

A stochastic version of this model bridges the gap between theoretical ideas and available data sets. The stochastic formulation of the deterministic model leads to a hypothesis that explains how the departures from the deterministic predictions occur in a given time series of population growth (17). The sources of variability may come from observational error or from process error. Observational error relates to the fact that at a given time, the total number of individuals cannot be known exactly, and the experimenter's estimate is based on a sample. Process error comes from uncertainty inherent in the process of growth itself. Population dynamics theory further subdivides the process error into “demographic” and “environmental” stochasticity. Demographic stochasticity represents the variability due to random contributions of births, deaths, and migrations of individuals in the population (17, 33). Environmental stochasticity represents the effect of external factors on the individuals of the population (23). For example, in Baranyi's stochastic models (5, 6, 7), the equations' coefficients are random variables that represent the biological variability between the individual cells in the population. In the ecological theory context, this is a model for demographic stochasticity (23). Cushing et al. (17) have shown that considering both demographic and environmental stochasticity is essential to adequate population dynamics modeling but that integrating both sources of uncertainty in a single model is not an easy task.

Because we were dealing with an experiment in which a given environment was imposed on bacterial populations, we chose to model environmental stochasticity alone. The stochastic Ricker model is written as follows (27):

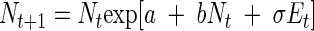(2)

where σE_t is a random shock to the population growth rate at time t, and the E_t are independent and normally distributed with mean zero and variance one. Because the current population size depends on the previous observation, this model has the Markov property and in the log scale it becomes a first-order nonlinear autoregressive model:

(3)

where X_t = ln N_t.

Setting a equal to 0 and b equal to 0 defines a discrete-time Brownian motion process with zero drift where there is no population density feedback typical of ecological processes (11, 23, 27). When a is not equal to 0 and b is equal to 0, the model is also a discrete-time Brownian motion with added drift. If a is not equal to 0 and b is not equal to 0, the model includes (positive or negative) density dependence. In particular, the model in which a is not equal to 0 and b is <0 represents a stochastic logistic growth. Under this model, the population no longer attains a single deterministic equilibrium, as in the Ricker equation, but instead, it approaches a “cloud of points” (60), a stationary distribution which can be approximated by a gamma probability density function (20, 24) whose mean is −a/b. The point −a/b represents a center for return tendencies: it is the population abundance at which the average change is N_t, conditional on N_t−1 being zero, thus accounting for the stationary phase. Note that the stochastic Ricker model does not include a term to account for the lag and death phases of bacterial growth in a batch culture, but as will be shown, the model serves as a very good approximation of these growth phases during the monitored period, despite the fact that the death phase is often evident. We later propose and briefly explore simple modifications to the stochastic Ricker model and other models to account for the processes occurring during these two phases of bacterial growth in batch cultures.

The problem of connecting a time series of observations with the proposed model in equation 2 requires the specification of a likelihood function. For each of the treatments, we estimated the corresponding parameters of the SR model as follows: suppose population abundances of a single culture are observed from time 0 to q. The likelihood function is a function of the unknown model parameters θ = [a, b, σ²]′. It is the joint probability density function for the vector of random variables X = [X₁, X₂, …, X_q]′ conditional on X₀ = x₀ and evaluated at the recorded vector of values x = [ln n₀, ln n₁, …, ln n_q]′ = [x₀, x₁, …, x_q]′ (25, 27). Because of the Markov property, the joint probability density function of the observed data, given our proposed model, is just the product of the individual transition density functions. The maximum-likelihood parameter estimates (MLEs) are the parameter values that make the observed data “most probable” or “most likely,” i.e., they maximize the likelihood function for time series data, which is given by (27):

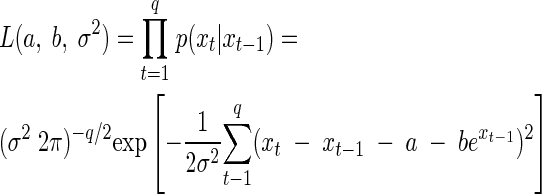(4)

Let Y_t = X_t − X_t−1 denote the one-step differences of the logarithmic population size. Dennis and Taper (27) show that the MLEs of a, b, and σ² under this model are identical to the least-squares estimates obtained by a linear regression of the observed y_t on n_t−1, where t = 1,2, …, q. This makes parameter estimation a straightforward task, and many commercial statistical packages can be used. We note that the confidence intervals returned by those packages are not correct in this case, because the observations at each time step are not independent of each other. Furthermore, the value b = 0 is at the edge of the set of values b < 0 for which the stochastic process N_t is ergodic, thus violating one of the regularity conditions under which a χ² approximation to the likelihood ratio test is valid. Using the χ² approximation thus yields inflated type I error rates (27). Instead, confidence intervals for the parameter estimates have to be found using the parametric bootstrap (PB) (29, 38). The PB of a stochastic model of population dynamics involves the following steps (26, 27). From a given data set, the ML estimates of the parameters are calculated for the chosen stochastic model and used to simulate many time series data sets (e.g., 2,000) of the same length as the original data set, using the same model. The ML estimates are then found for each of these data sets. Their histogram (or kernel density estimate) represents an estimate of their sampling distribution, from which various descriptive statistics can be obtained (e.g., the 2.5 and 97.5 percentiles).

(ii) Secondary model: an ANOVA variant of the SR model.

In predictive microbiology, secondary models describe the dependence of primary-model parameters on environmental factors. Here, the primary-model parameters are contained in the stochastic growth rate function (i.e., the terms in brackets in equation 2). Hence, the natural way to rigorously determine whether a certain combination of environmental factors affects the growth rate is to adopt an approach that is conceptually “ANOVA-like” and test whether there are differences in the estimated model parameters within and between experimental scenarios. Inference using this approach was greatly facilitated in this study because our data set was a perfect 2⁵ factorial design with three replicates of each experimental treatment. If the general hypothesis that each of the 32 treatments has a distinct effect on the population dynamics of bacteria is supported by the data, then the speed of attaining stationary phase, the population size around which the cell counts vary in stationary phase, and the variability of the process (i.e., each of the SR model parameters) should differ between the 32 experimental treatments. To estimate the model parameters for a single treatment, the joint likelihood of the three replicated time series has to be considered. Because a treatment's replicates were independent, the likelihood function for a given experimental treatment was taken as the product of the individual likelihoods. Note that although the ideal situation is having a full factorial design, just like in the traditional ANOVA methods, the overall procedure could be modified to account for unbalanced designs.

Various hypotheses were contained in the general hypothesis described above, and modified multivariate techniques can be used to identify patterns in the SR model parameter space. If there is no difference between the model parameters found in, e.g., two experimental treatments, the data for these two treatments can be pooled and the SR model parameters can be estimated anew. In that fashion, the total number of possible treatment effects, combinations, and interactions can be reduced and the main factors that drive the system dynamics can be identified. The patterns of variation in the 96 data sets were summarized in order to propose a set of competing hypotheses consistent with the observations and to group the data accordingly. To do so, the model parameters for each of the 96 data sets were calculated as described before. These values were used as coordinates in a three-dimensional space. Canonical-variates analysis was used to identify patterns of variation among treatments. The design types were plotted in a two-dimensional canonical-variates space. A careful inspection of the canonical-variates plot allowed the formulation of seven hypotheses that were consistent with the data. Each hypothesis grouped all of the 32 experimental treatments in a particular way and proposed that distinct population dynamics occurred within each group. We then tested and compared the degree to which each of the seven hypotheses was in agreement with the observed patterns of variation. Confidence intervals using a PB were calculated for the model parameters under each hypothesis (see reference 27 for details).

(iii) Model selection.

Statistical theory and evidence from many biological disciplines (15) show that traditional stepwise regression methods based on a series of likelihood ratio tests may miss the best model or hypothesis consistent with the data. Also, a series of pairwise comparisons can lead to erroneous P values in likelihood ratio tests and inflated type I errors. Therefore, we relied here on the Akaike information criterion (AIC) (1) and on the Bayesian information criterion (BIC) (54) to simultaneously assess the quality of each of those hypotheses to explain the data.

The use of the AIC and BIC for hypothesis selection has a strong theoretical rooting in information theory. For a given data set, the AIC gives an estimate of the expected, relative, directed distance between the fitted model and the unknown true mechanism that generated the data (15). Thus, the decision rule for model selection using those statistics is to choose the model with the lowest AIC or BIC. For a fixed data set, adding more parameters to the model reduces that distance but further increases uncertainty in the estimation process. That trade-off between underfitting and overfitting is directly expressed in both the AIC and BIC as a term that penalizes their scores as a function of the number of estimated parameters in the model. We note that Schwarz (54) showed that if the true model is within the suite of evaluated models, then the BIC is guaranteed to find it. Hence, we used both statistics to derive the conclusions of the hypothesis selection. For the stochastic Ricker model, the AIC is equal to:

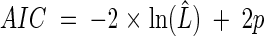(5)

where ln(L̂) is the likelihood function evaluated at the MLEs and p is the number of model parameters. The BIC is calculated with:

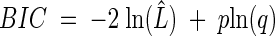(6)

where q is the number of data points used in the parameter estimation process. A disagreement between the two statistics would indicate that there is not enough evidence in the data to support the best model, and a decision would have to be taken after investigating the type I error rates of each model using extensive simulations (26, 33a).

Finally, an evaluation of the quality of the best-fitted model was done via a residual analysis. Under the proposed model, the residuals should be normally distributed, centered around zero, and nonautocorrelated. A strong deviation from normality, if it appears, is an indicator that the current model mechanism is insufficient to explain the available data. All the calculations were done using MATLAB 6.5.1, release 13 (The MathWorks, Inc., Natick, Mass.).

RESULTS

Growth curve experiments.

A biological data set was obtained by growing E. coli in a microtiter plate in a base medium that contained all 32 possible combinations of five supplements (glucose, NH₄Cl, HCl, EDTA, and NaCl) in triplicate. The growth that occurred with each supplement combination was recorded using an automated plate reader. Figure 1 shows how the recorded population size (OD × 100) varies for each of the 32 treatments.

Primary model: the SR model.

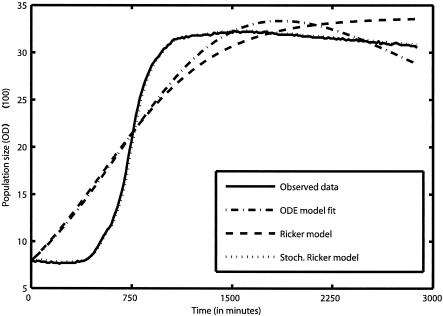
The SR model predictions found through a process error fit were superior to those generated by alternative models using an observation error fit, as is clearly illustrated in Fig. 2. In fact, even improved observation error models including a death phase do not fit as well as the SR model. This figure also illustrates the fact that a process error model fit is conceptually different from an observation error fit in that it naturally yields a stochastic one-step-ahead prediction of future population sizes. The advantage of this becomes evident while plotting the predictions from both types of statistical fit (Fig. 2). The residuals obtained by an observation error fit of the Ricker model were at least 1 order of magnitude larger than the process error fit residuals. A typical deterministic prediction using an observation error fit differs dramatically from the one-step-ahead predictions generated using the stochastic Ricker model parameter estimates.

FIG. 2.

Stochastic (Stoch.) Ricker model predictions compared to the observed data, an observation error fit of the Ricker equation, and an observation error fit of an ordinary differential equation (ODE) model that accounts for the rate of substrate consumption. In the ODE model, n is the population abundance, r is the resource variable, and φ_max, k, μ, and α are constants:

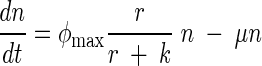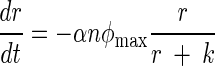This model assumes that a population is growing according to the well-known Monod function and that individuals are dying at a rate μn.

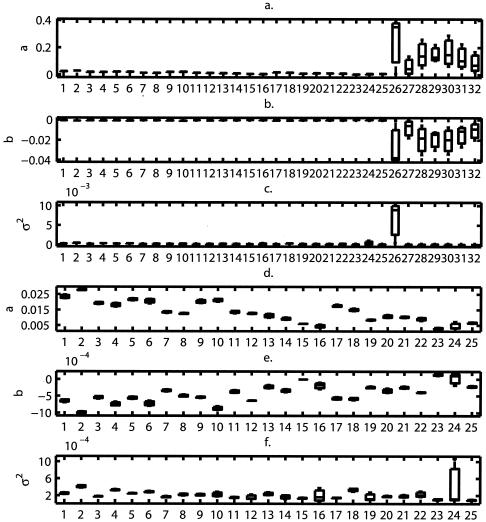
The estimates of the parameters a, b, and σ² of the stochastic logistic growth models fitted to each of the experimental growth curves are reported in Fig. 3a to c. In Fig. 3d to f, the parameters for supplement combinations 26 through 32 were omitted for clarity.

FIG. 3.

Box plots of the stochastic Ricker model parameter estimates as a function of the design type for treatments 1 to 32 (a, b, and c) and for designs 1 to 25 (d, e, and f). The bar inside the box indicates the median, the boxes delimit the interquartile range, and the vertical lines extend to the maximum and minimum.

Secondary model: an ANOVA variant of the stochastic Ricker model.

After estimating the parameters using the population dynamics modeling approach for each of the 96 growth curves, we grouped the data in various ways to establish how the data could best be explained. We used a graphical approach to develop seven hypotheses to explain the treatment groupings. Further data analysis showed that not all of the 32 different chemical supplement combinations had a significant effect on the population dynamics of the microbial cultures. The data were best explained with just four distinct dynamics, corresponding to the cases in which either NaCl or EDTA was present, both were present, and both were absent. Furthermore, we found a positive interaction effect between these two supplements.

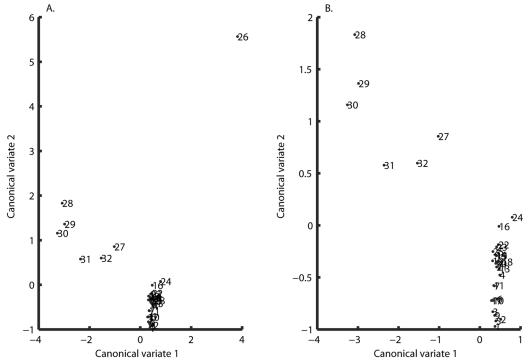
The MLEs of the stochastic Ricker model for each of the 96 data sets were used to run a canonical-variate analysis. Fisher's discriminant function based on the estimated parameter values of the stochastic Ricker models identified the vectors in the multidimensional space on which, when the data points were orthogonally projected, the experimental designs were maximally separated (34). The test for the relative contributions of the three selected eigenvalues and the total canonical structure extracted by Fisher's discriminant function indicated that only the first two eigenvalues were significant (P values of < 0.001, < 0.001, and 0.0684, respectively). Furthermore, they cumulatively explained 87.26% of the variation in the three-dimensional space of [a,b,σ²]. A closer examination of the canonical structure indicated that the extracted canonical variate number 3 was not very useful to explain the variation in the three-dimensional space. The plot of the designs in the discriminant space (Fig. 4) was used to identify possible design groupings and to formulate the following hypotheses.

FIG. 4.

(Left) Experimental treatments plotted in a two-dimensional space according to their mean coordinate values in canonical variates 1 and 2. (Right) Same as before, but treatment 26 is excluded for clarity. The two canonical variates represent the two axes in the three-dimensional space of a, b, and σ² along which the highest separation of the data points is obtained, i.e., these are the vectors along which most of the variability seen in the values of the model parameters occurs. Hence, two treatments for which the biochemical environment leads to similar growth patterns will appear closer when plotted in the two-canonical-variates space.

(i) Hypothesis 0.

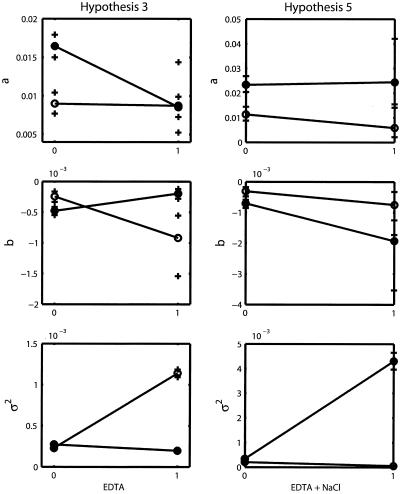
Only two groups (A and B) can be identified: group A consists of designs 26 to 32, and group B consists of designs 1 to 25. The first group corresponds to the case where EDTA and NaCl are both present at the same time regardless of any other supplement addition. The second group corresponds to the case where EDTA and NaCl are not present at the same time (Fig. 1). Group A dramatically increased the value of a, the rate at which stationary phase is reached (Fig. 3a), and lowered the mean level (−a/b) at which this occurred by decreasing the value of b (Fig. 3b).

(ii) Hypothesis 1.

Because the variability in the data coming from design 26 was much higher than the rest (Fig. 3c), this design can be separated from the rest and constitute another treatment by itself, besides the two proposed by hypothesis 0. Hence, this hypothesis proposes to divide the designs into three groups, corresponding to three separate population dynamics types.

(iii) Hypothesis 2.

Four groups explain the data: designs 27 to 32, in which EDTA and NaCl are both present and at least one of NH₄Cl and HCl is present; design 26; designs 16 and 24; and all other designs.

(iv) Hypothesis 3.

Four experimental groups defined by just two supplements explain the data. The treatments are EDTA and NaCl, and the experimental groups are as follows: EDTA and NaCl absent, EDTA present and NaCl absent, EDTA absent and NaCl present, and both present. This hypothesis suggests that there is a significant interaction between EDTA and NaCl and that the effects of that interaction drive the dynamics of the system.

(v) Hypothesis 4.

Hypothesis 4 considers the same experimental groups as in hypothesis 3 but also includes the presence or absence of glucose as a factor. Hence, a total of eight experimental groups are proposed by this hypothesis.

(vi) Hypothesis 5.

All of the supplements except glucose have an effect, and interactions exist between EDTA plus NaCl and NH₄Cl plus HCl. There are a total of 16 experimental groups.

(vii) Hypothesis 6: full model.

The data at hand can be best explained by proposing 32 distinct types of population dynamics types corresponding to each of the 32 experimental treatments with three replicates each.

Model selection.

To evaluate the consistency of each hypothesis with the data, the BIC and AIC statistics were calculated from the likelihood of each hypothesis evaluated at the MLEs. To estimate the parameters under each hypothesis, we pooled the replicates of designs contained within each group proposed by the seven hypotheses. The joint likelihood function for each group was computed as the product of the individual time series likelihoods.

Both the AIC and the BIC clearly favored hypothesis 3 (Table 1), implying that a good explanation of the changes in a, b, and σ² was obtained while considering just the presence or absence of EDTA and NaCl. With the parameter estimates and confidence intervals obtained using PB (Table 2), interaction plots were drawn (Fig. 5). The interaction plots show that the order of the effect of NaCl changed as the state of the EDTA treatment changed. Thus, the effects of these two factors were not simply additive. When the data coming from the treatments with the above-mentioned interaction were excluded, then the effects of the other factors became visible (Fig. 3d to f). The BIC values of hypotheses 0, 1, 2, 4, and 5 show that even when other tentative explanations may be valid and better than the full model, the patterns of variation in the time series cannot be explained as well as with hypothesis 3. The confidence intervals obtained with a PB of hypothesis 5 showed that the interactions between NaCl plus EDTA and NH₄Cl plus HCl were not significant (Fig. 5). Thus, in hypotheses 4 to 6, the treatment effects were just additive and could not generate as much variation as the one generated by the interaction between EDTA and NaCl. The second-best hypothesis was the reduced hypothesis (hypothesis 0), which considered just two groups. This hypothesis had the benefit of a reduced number of parameters to estimate. However, with just two groups it is not possible to estimate the interaction effects.

TABLE 1.

Hypothesis selection^a

Hypothesis	BIC	AIC
0	47,749.02	47,702.08
1	52,180.67	52,110.27
2	52,286.17	52,192.31
3	47,484.81	47,390.95
4	49,538.95	49,351.22
5	52,093.93	51,718.49
6	53,879.65	53,128.76

^aBIC and AIC values of the seven hypotheses proposed and defined in Results. The decision rule is to pick the hypothesis with the lowest AIC and BIC. The hypothesis that explains the variation in the stochastic Ricker model parameter estimates best is hypothesis 3.

TABLE 2.

Stochastic Ricker model parameter estimates and PB confidence intervals for the model specified by hypothesis 3^a

Groupa	ÂLCL	Â	ÂUCL	b̂LCL	b̂	b̂UCL	σ̂2LCL	σ̂2	σ̂2UCL
1	1.500E-02	1.645E-02	1.792E-02	−5.496E-04	−4.802E-04	−4.164E-04	2.598E-04	2.713E-04	2.820E-04
2	7.261E-03	8.539E-03	9.896E-03	−2.781E-04	−1.955E-04	−1.206E-04	1.885E-04	1.967E-04	2.047E-04
3	7.680E-03	8.977E-03	1.042E-02	−3.351E-04	−2.453E-04	−1.647E-04	2.185E-04	2.279E-04	2.369E-04
4	5.231E-03	8.722E-03	1.439E-02	−1.542E-03	−9.183E-04	−5.546E04	1.091E-03	1.139E-03	1.185E-03

^aThe data are best explained by considering the following four experimental groups: 1, both EDTA and NaCl absent; 2, EDTA present and NaCl absent; 3, EDTA absent and NaCl present; 4, both EDTA and NaCl present. LCL and UCL are the lower and upper confidence limits, respectively. Â, b̂, and σ̂² are the estimates of the stochastic Ricker model parameters.

FIG. 5.

Interaction plots for hypothesis 3 and hypothesis 5. (Left) Closed circles represent absence of NaCl, open circles, presence of NaCl. (Right) Open circles represent absence of both NH₄Cl and HCl, closed circles, presence of both chemicals. Parametric bootstrap confidence limits are marked with crosses.

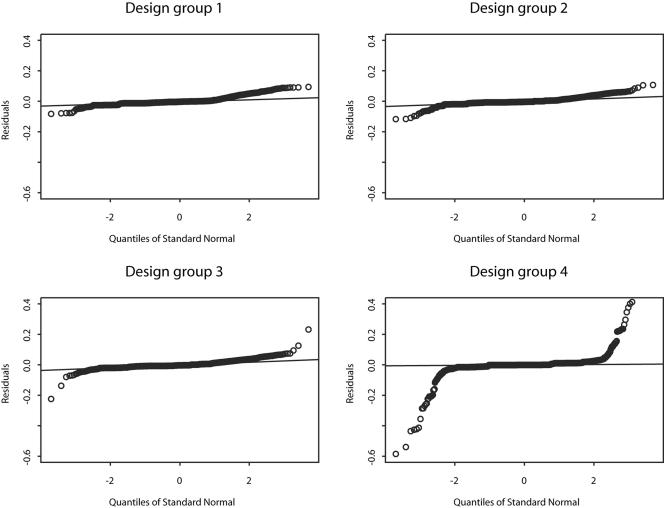
Once chosen, the best hypothesis was further scrutinized via a residual analysis. The model residuals for the best hypothesis, hypothesis 3, were approximately normally distributed and centered around zero, suggesting that the stochastic Ricker model was a good first approximation to differentiate between various population dynamics (Fig. 6). However, some deviations from the assumptions occurred in the extreme data points; at the early stage of the process, during the lag phase; and as expected, at the late stage of the process, during the death phase. Those deviations were accompanied in some cases with an autocorrelation pattern, which suggested a significant effect of an observational error.

FIG. 6.

Plotted are the quantile-quantile graphs of the residuals for each of the four experimental design groups in hypothesis 3 (see “Model selection” for details). The points far from the straight lines in the lower right plot represent the individual model residuals that deviated from the model normality assumption.

DISCUSSION

Uncertainty in the trajectories of population growth seen in our 96 microbial growth curves was effectively explained and summarized by the stochastic Ricker model. It was shown that the positive and negative effects of the five supplements and combinations of them directly resulted in an increase or decrease in the time required to attain stationary phase and the population size at which the stationary phase started. Furthermore, the potential complexity of 2⁵ experimental treatments and their effects was reduced to 2², as just the metal chelator EDTA, the presumed osmotic pressure imposed by NaCl, and the interaction between these two factors were enough to explain the variability seen in the data. These findings seem to be in agreement with previous studies (30, 49, 57).

Model selection via the AIC and BIC overcomes two major problems reported in the literature. The first one is overparameterization. In the search for more mechanistic models, many parameters are introduced, for example, to model the probability of growth as a long nonlinear function (57). Baranyi et al. (9) have already warned about the effects of overparameterization in predictive microbiology. Our results show that by using the AIC or BIC, a good compromise between the number of parameters included in the model and the quality of the predictions is reached. The second problem is stepwise regression as a model selection tool. As mentioned before, it has been repeatedly shown that stepwise regression can lead to an erroneous choice of the best available model. The information criteria used here overcome that problem by evaluating all the models at the same time, thereby allowing a proper identification of the best available model.

Process error fitting is a more realistic and mechanistic modeling approach. It is a realistic approach because it aims to explain the variability seen in time series of population abundance by proposing stepwise stochastic changes in the growth rate as a function of the experimental medium (Fig. 2). It is a mechanistic approach because it effectively explains and reproduces the observed growth patterns through proposed biological processes well rooted in first principles. Our model basically states that exponential growth and density-dependent effects are random and change as a function of the growth medium. The effects of the environmental factors were directly translated into changes in the basic growth characteristics.

Modeling the process error is not a mere fitting technique. Deterministic mathematical models (e.g., Gompertz and logistic equations) are often proposed as the true underlying “perfect” mechanism and fitted to the data via nonlinear fitting techniques (8, 13, 16, 19, 52, 59). Deviations from the deterministic predictions are accounted for as observational uncertainty. On the other hand, the SR model asserts that the process of population growth is stochastic by nature and can be modeled with a Markov process. The transition probability density function of this Markov process is used to predict trends and also as a natural tool for parameter estimation via ML. In the presence of substantial observation error, the process error model ML parameter estimates and predictions are biased, and the converse is also true (25, 28, 43, 46). However, in the context of this paper, because the microtiter plate reader is highly accurate (coefficient of variation = standard deviation/mean = 1.08%) and large populations are being sampled, observation error can be neglected. Further evidence supporting the use of the SR model was given here by the quantile residual plots (Fig. 6), in which generally the assumptions of normally distributed errors were met. However, we saw deviations from the normal model at the early stages (lag phase) and toward the end (death phase). Early deviations can possibly be additionally affected by the detectability limitations of the use of OD as a surrogate for population size (18), as well as by a lag phase.

The SR model can be modified to accurately predict more complex biological phenomena of bacterial batch cultures, such as the lag and death phases, the effect of time-varying environmental factors, and multiple-species microbial interactions. Well-known ideas in ecology can be translated into stochastic population models to explain the data. As an example, suppose that at small initial population sizes bacteria cannot grow well due to harsh environmental conditions, e.g., low pH values. This situation might change at larger population sizes, as metabolic products could increase the pH. That is, at intermediate population sizes, the population might grow much better than at small population sizes. Furthermore, a critical initial population size might exist below which bacteria cannot grow and above which they succeed. This phenomenon is well known in ecology as the Allee effect (2, 20), and stochastic population models exist in the literature that account for it (20, 21). A stochastic modeling approach to this problem could, for instance, lead to accurate estimates of that critical initial population size below which bacteria fail to grow.

To account for environmental stochasticity and the fluctuations over time in resources and in the concentrations of the chemical supplements, the stochastic Ricker model could be easily modified. To include the main effects of the chemical factors without the interactions, the growth function in the exponential term of the stochastic Ricker model could be written as follows:

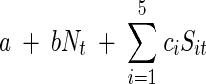where c₁,c₂,…,c₅ are parameters to be estimated and S_it is the concentration of the chemical supplement S_i at time t. This model has been successfully used to model long trends in populations whose growth depends on climatic fluctuations, such as “El Niño” rainfall (26). In the model described above, the chemical supplements are included as covariates that may enhance or suppress bacterial growth, depending on the values of the constants c_i. This model has the advantage that it takes into account the variation of the concentration of the supplements over time, and substrate depletion can be easily accounted for. However, to estimate the parameters in this model, the concentration of each chemical supplement and substrate at each time step is needed (12). In the context of our experiment, measuring these concentrations was not experimentally feasible. We opted to sacrifice the number of variables recorded in order to have a large number of data points and a perfectly balanced factorial design. From the point of view of improving statistical power, it is preferable to have many replicates of the same univariate process rather than to gather data on a large multivariate process with small sample sizes. Another extension of the model would be to consider several levels of the initial concentration of the supplements, and like most ANOVA models, our current approach can be easily expanded in such a way.

Accounting for the population lag phase (in the sense of Baranyi [5]) is also straightforward using the SR model. During lag phase, bacterial numbers seem to fluctuate randomly around the initial density. However, the case of zero growth is just a special case of the SR model. Indeed, no growth is equivalent to setting a equal to 0 and b equal to 0 in equation 2 (see “Theoretical background” above). Then, accounting for the lag phase amounts to specifying what is known in the statistics literature as a stochastic change point problem. While our model effectively accounts for the pattern of variability seen in the data, there are other aspects of growth dynamics that could be modeled in future work. For example, delay differential equation models, like the one proposed by Baker et al. (4), are useful in estimating the fraction of cells that are dividing, the degree of initial synchronization of the cells, and the initial distribution of cells in the cell cycle. It would be interesting to extend Baker's model to a stochastic differential equation and properly account for stochastic effects. However, parameter estimation via ML for stochastic differential equation models is a wide-open research area and presents many challenging statistical problems. These topics constitute materials for future research.

Finally, another of the latest concerns in predictive microbiology is the consideration of microbial interactions (37, 58). A two-species deterministic discrete Ricker model exists in the literature (40). This model can be easily transformed into a stochastic model in the form of equation 2 (22, 28). Preliminary results not presented here show that this competition model can be effectively used to analyze the seminal data set of Gause (31).

Stochastic modeling techniques are maturing, and there is no reason why theoretical and applied studies in microbiology should be deprived of such useful mathematical statistics tools and concepts. The results of this paper have broad implications for both basic and applied research and can be regarded as a different starting point to fulfill the urgent need of simple stochastic models of microbial growth.