A polymerization-depolymerization model that accurately generates the self-sustained oscillatory system involved in bacterial division site placement

Abstract

Determination of the proper site for division in Escherichia coli and other bacteria involves a unique spatial oscillatory system in which membrane-associated structures composed of the MinC, MinD and MinE proteins oscillate rapidly between the two cell poles. In vitro evidence indicates that this involves ordered cycles of assembly and disassembly of MinD polymers. We propose a mathematical model to explain this behavior. Unlike previous attempts, the present approach is based on the expected behavior of polymerization-depolymerization systems and incorporates current knowledge of the biochemical properties of MinD and MinE. Simulations based on the model reproduce all of the known topological and temporal characteristics of the in vivo oscillatory system.

Most bacteria divide by forming a division septum at the midpoint of the cell. Accurate placement of the division site is required to permit the equidistribution of genetic and cytoplasmic components between daughter cells. In Escherichia coli and related organisms, placement of the septum is regulated by a system of negative control, mediated by the three proteins of the MinCDE system (reviewed in ref. 1). The Min system prevents septation at potential division sites near cell poles without blocking septum formation at the desired midcell location. The MinC protein is responsible for the septation block. MinD and MinE prevent MinC from blocking division at the desired midcell site while permitting it to act at other potential division sites, thereby giving topological specificity to the division inhibitor. This process involves a unique oscillatory system in which membrane-associated MinC, -D, and -E oscillate rapidly from pole to pole.

The oscillation process is initiated by assembly of a membrane-associated polar zone consisting of MinC, MinD, and MinE (2-5), which first appears near a cell pole and grows toward midcell (Fig. 1). As the growing polar zone approaches midcell, MinE forms an annular structure (the E-ring) at its leading edge. The polar zone then disassembles, retracting from midcell back to the original pole. The E-ring remains associated with the medial edge of the zone during the disassembly stage (6, 7).

Fig. 1.

MinDE oscillation cycle. See text for description.

As the polar zone retracts from one pole, a new cycle of assembly and disassembly is initiated at the opposite end of the cell. In this way, MinC, -D, and -E oscillate from pole-to-pole with a periodicity of ≈1 min (2, 4-7). As a result, the time-averaged concentration of the MinC division inhibitor is kept low at midcell, thereby permitting assembly of the new septum at this site. Although MinC normally accompanies MinD throughout the oscillation cycle, MinC is not required for the oscillation phenomenon, which requires only MinD and MinE (2, 3).

In vitro, MinD binds to phospholipid vesicles in the presence of ATP (8). MinE destabilizes the phospholipid-MinD-ATP interaction by binding to the vesicle-bound MinD; this activates the MinD ATPase (9), leading to release of MinD-ADP and MinE from the vesicles.

MinD forms filamentous structures in vitro in the presence of ATP or GTP (10), or ATP and phospholipid vesicles (8), suggesting that MinD polymerizes when it associates with the cytoplasmic membrane in vivo. A role for MinD polymerization in vivo is also implied by the finding that MinD within the polar zone is organized into extended cytoskeletal-like structures (11) that coil around the cell and are believed to be composed of bundles of MinD protofilaments.

Previous attempts to model this interesting self-sustaining oscillatory system (12-15) did not take into consideration the polymeric nature of the MinD structures that comprise the polar zones. We describe here a mathematical model in which the polymerization-depolymerization behavior of MinD is the key element. The model incorporates many mechanistic suggestions from the experimental literature, especially those of Hu and Lutkenhaus (9), and assumes binding and dissociation kinetics consistent with published experimental data. Simulations show that the model faithfully reproduces the spatial and temporal variation in distribution of membrane-bound MinD and MinE and the other characteristic features of the oscillatory cycle.

Modeling the Min System

The model is founded on three assumptions regarding the binding of Min molecules: (i) initial association of MinD with the membrane can only occur at or near a cell pole; (ii) membrane-associated MinD recruits cytoplasmic MinD to form polymers that extend from the initial polar binding site toward midcell; (iii) MinE is able to bind to both internal and terminal MinD units of the polymers, but the binding affinity for terminal MinD is significantly greater than for internal MinD units.

Step 1. MinD binds to the membrane at the pole and recruits MinD from the cytoplasm to form a linear array of membrane-associated MinD molecules. We assume that only MinD-ATP is capable of binding to the membrane (8). The MinD at the growing end of the polymer acts as a site for addition of the next MinD unit. The attachment reaction is written as

[1]

where MinD^m represents a membrane-associated MinD molecule, MinD^c is a MinD-ATP molecule in the cytoplasm, (MinD^m)_n MinD^t represents a MinD array of length n (n = 0, 1,...), with MinD^t being the terminal MinD in the array. This reaction is implemented as 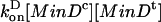, where [MinD^c] is the concentration of cytoplasmic MinD-ATP and [MinD^t] the number of terminal MinD sites in a cross-sectional slice at position x along the length of the cell.

Step 2. MinE can bind to the terminal MinD (Eq. 2a) or to an internal MinD within the chain (Eq. 2b). The two reactions have different association constants, although they are likely to use the same MinD-binding site within MinE (16). MinE bound to the terminal MinD acts as a chain blocker that prevents elongation of the polymer chain. This reaction is written as

[2a]

where [MinE^c] denotes the concentration of cytoplasmic MinE, and MinE^t is MinE that is bound to the terminal MinD in the chain. This is implemented as a reaction with rate , where 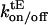are the rate constants for association and dissociation of a MinE unit at the end of a chain. Whether MinD or MinE binds to the end of a chain is a function of the different equilibrium constants of the two binding reactions (Eqs. 1 and 2a) and the relative cytoplasmic concentrations of the two proteins at the location of the chain end.

When MinE binds to internal MinD units the reaction is written as

[2b]

where MinEⁱ is MinE attached to an internal MinD unit in a chain. This is implemented as a reaction with rate 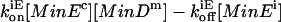. Whether MinE binds to a terminal MinD or an internal MinD is a function of the different equilibrium constants of the two binding reactions (Eqs. 2a and 2b).

Step 3. MinE can bind to MinE molecules at the end of the chain. This reaction is written as

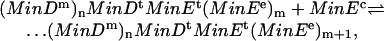[3]

where n, m = 0, 1,..., and MinE^e represent MinE attached to another MinE unit. This is implemented as a reaction with rate 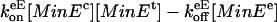. The reactions included in Eqs. 2a and 3 are responsible for formation of the E-ring.

Step 4. Terminal MinD is released from the chain in a reaction that is activated by MinE^e. This presumably reflects the MinE-mediated activation of MinD ATPase activity (9). On release of MinD^t, the terminal MinE assembly transfers to the next MinD in the array without passing through the cytoplasm. This is represented as

[4]

where MinD⁰ is cytoplasmic MinD-ADP. It is implemented as a reaction with rate 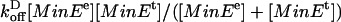. This reaction rate is proportional to [MinE^e] when there are few MinE^e molecules, and saturates at [MinE^t] when there are many MinE^e molecules. Internal MinE is released when the MinD to which it is attached is released. When the last MinD in the chain is released, the associated MinE molecules are also released into the cytoplasm.

Step 5. MinD-ADP released from the membrane is reactivated in the cytoplasm to the active ATP-bound form which is competent to rebind to the membrane (8). The regeneration reaction is represented as

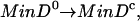where MinD⁰ and MinD^c represent the inactive and active forms of MinD within the cytoplasm, respectively. The reaction is implemented as k_act[MinD⁰].

Mathematical Implementation

We consider the E. coli cell to be a cylinder in which the cylinder wall (”membrane”) delimits a homogeneous internal compartment (”cytoplasm”). The MinD and MinE concentrations in membrane and cytoplasm can vary with time and with the axial spatial coordinate. We assume that MinD and MinE move in the cytoplasm by diffusion.

The reaction-diffusion equations for MinDE polymer dynamics take the form

[5a]

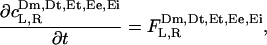[5b]

where C^D,E,D0 represents the concentrations in the cytoplasm of MinD^c, MinE^c, and MinD⁰; represents the concentrations on the membrane near the left (L) or right (R) pole, of MinD^m, MinD^t, MinE^t, MinE^e, and MinEⁱ; and represents the respective diffusivities. The reaction rates F^{D,E,0,Dm,Dt,Et,Ee,Ei} are complicated by the fact that the polymerization reaction occurs one molecular length from the distal end of the polymer. For example, the binding of a MinD to the polymer end at location x can only happen if there is a MinD^t one molecular length toward the pole, and results in changing that terminal MinD from MinD^t to MinD^m.

The spatial redistribution events that follow from steps 1-5 are implemented numerically by discretizing in the spatial variable x along the axis of the cell. Thus, we assume that for each Min protein M, in any of its states, k = c, m, t, e, i [M^k](x, τ) ≅ [M^k]_i(τ), where τ is time, and the spatial coordinate is discretized as x = iΔx. The cell is discretized with 60 axial grid locations, and the time step is taken to be 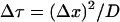. Assuming a cell length of 3 μm and a diffusivity of 2.5 (μm)²/s (17) gives Δτ = 0.001 s.

With the relevant association and dissociation parameters taken to be constants, the system failed to show sustained oscillations. Initial asymmetric distributions of the MinD and MinE proteins quickly converged to steady-state distributions. These distributions represent a situation where each individual chain is growing, then shrinking, but doing so in such a way that the overall distribution does not change. This process occurs in other polymerizing systems (e.g., microtubules), and is called “dynamic instability” when referring to individual microtubules, and on a statistically steady sense can be thought of as tread-milling.

Consequently, we focused on nonlinear interactions. Instead of fixed rate constants for each reaction, we allowed the rate constants of key binding and unbinding reactions to be affected by the local membrane concentrations of MinD or MinE (Eq. 6). The implementation takes the general form

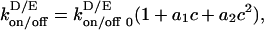[6]

where represents any of the membrane association disassociation rate constants or and 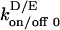is the corresponding basal rate constant. a_1,2 represents the effect of the local concentration c of some membrane-associated species on the basal rate constant. When implemented for MinD (i.e., c = MinD^m), changes in c reflect differences in the number of MinD chains within the specified volume segment. We also introduce a nonlinear dependence of the recruitment of MinE to the terminal MinE on the concentration of MinE^e, representing cooperativity of MinE^e formation.

To obtain sustained oscillations, it proved necessary to use conditions in which shorter MinD chains grow faster than longer chains. This step was necessary to ensure that all chains are more or less in register as they approach midcell so that subsequent polar zone disassembly occurs synchronously; this was accomplished by selecting values for parameters a₁ and a₂ (Eq. 6) whereby adjacent MinD chains: (i) increase the probability that cytoplasmic MinD will attach to the end of a MinD chain (Eq. 1); and (ii) decrease the probability that a terminal MinE will associate (Eq. 2a) and increase the probability that a terminal MinE will dissociate (Eq. 2a), thereby decreasing the likelihood that growing MinD chains will prematurely disassemble. The net effect of these factors is a growth advantage for short MinD chains. Other combinations of parameters that achieve the same effect might also be successful.

Testing the Model

To test the model, we used the discrete nonlinear system described above to simulate the time-dependent distribution pattern of MinD and MinE. The equations were incorporated into a Fortran-based code, and calculations were typically run for a few million explicit time steps, representing a few minutes of real time. For all simulations, the diffusivities of all cytoplasmic species were assumed to be the same (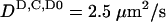) (17) and membrane-associated proteins were assumed to be nondiffusible within the plane of the membrane on the time scale of the simulations. The proteins were assumed not to be degraded or synthesized within the time frame of the simulations.

Under a range of starting conditions, a stable oscillatory pattern for MinDE polar zones was established after an initial transient and a variable lag period (Fig. 2 a and b and Table 1). The oscillatory behavior continued for as long as the simulation was run (up to 1,000 s). Within each cycle, MinD/MinE polar zones first appeared at the end of the cell and then grew progressively toward midcell (Fig. 2 c and d). A high concentration of MinE then appeared at the medial edge of the polar zone at the time of its maximal growth, presumably equivalent to the E-ring. This was followed by retraction of the polar zone to the original pole. Under the conditions described in Fig. 2, the oscillation period corresponded to a physical period of ≈1 min. In all of these characteristics, the system reproduced the in vivo behavior of the oscillatory system.

Fig. 2.

Simulation leading to a stable pole-to-pole oscillatory pattern. (a-d) The simulation was begun with all of the MinD and MinE in the cytoplasm. MinE concentration was uniform along the length of the cell; MinD concentration was uniform except for a fluctuation of 10^-2 between the two grid points adjacent to the right pole. Total cellular MinD and MinE were equivalent to 2,150 and 1,120 molecules per cell, based on a 3 × 1 μm unit cell. Values for the rate constants are given in Table 1 (x = 0 = “left” and x = 3 μm = “right” end). (a and b) Space-time contour plots of membrane-associated MinD (a) and MinE (b). The vertical axis shows space coordinates along the long axis of the cell; horizontal axis shows time units in seconds. One second of the simulation represents ≈1,200 iterations. Colors indicate concentrations of membrane-associated MinD (a) and MinE (b), in the order violet (zero)-blue-green-yellow-orange (highest). The colors represent relative values within the graph and cannot be compared from panel to panel. Arrowheads mark the time points used to obtain the data shown in c and d.(c and d) Concentration of membrane-associated MinD (c) and MinE (d) versus axial position. The curves represent information at the times indicated by the arrowheads in a and b, in the order red (first time point)-orange-blue-black-green-violet (last). The graph represents approximately one half of one complete oscillation cycle. As the sequence starts, the left polar zone is growing, and the right polar zone is shrinking. (e) Effect of MinE/MinD ratio on oscillation period. Simulations were performed as described above at varying starting cytoplasmic concentrations of MinE, expressed as molecules per cell (horizontal axis) and at three different concentrations of MinD, corresponding to 1,950 (green), 2,160 (red), and 2,370 (violet) molecules per 3 × 1 μm unit cell. Where no points appear, a stable oscillatory cycle was not observed. Vertical axis indicates the oscillation period as seconds per cycle; one cycle is defined as a single back-and-forth movement between the two cell poles. maple9 (Maplesoft) was used to convert numerical output from the Fortran code to graphical formats.

Table 1. Parameter values used in the numerical simulation.

Action	k0	a1 (MinD)	a2 (MinD)	a1 (MinEe)	a2 (MinEe)
MinDc on	0.33	0.00	150.00	0.00	0.00
MinEc on	1.00	−0.90	−1.00	0.00	0.00
MinEt off	0.06	0.00	6.00	0.00	0.00
MinDt off	1.50	0.00	0.00	0.00	0.00
MinD0 reactivation	0.05	0.00	0.00	0.00	0.00
MinEi on	1.00	0.00	0.00	0.00	0.00
MinEi off	5.00	0.00	0.00	0.00	0.00
MinEe on	6.00	0.00	0.00	0.00	10.00
MinEe off	1.00	−1.00	−1.00	0.00	0.00

The system oscillates as follows, as deduced from space-time analyses of membrane-associated MinD and MinE (Fig. 2 a and b) and from similar analyses of cytoplasmic MinD and MinE (data not shown). (i) A relative abundance of cytoplasmic MinD results in rapid attachment of MinD to the growing ends of MinD chains, leading to formation of a MinD polar zone that grows toward midcell. The high cytoplasmic MinD combined with the higher affinity of MinD than MinE for attachment to the ends of chains ensures that few chains are capped by MinE during the stage of extension of the polar zone. (ii) As the cytoplasmic MinD concentration falls to low levels because of its incorporation into the polar zone, and as cytoplasmic MinE concentration increases because of disassembly of the E-ring at the opposite end of the cell, MinE competes more effectively for binding to the terminal MinD of the chains. This leads to the appearance of a high concentration of MinE at the medial side of the MinD polar zone, corresponding to the MinE ring seen in vivo. (iii) After a short pause that is approximately proportional to the oscillation period, the polar zone and E-ring shrink back to the pole with release of MinD into the cytoplasm. This is not associated with a significant local increase in cytoplasmic MinE because the MinE molecules at the end of the chain reattach to the next MinD without passing through the bulk cytoplasmic compartment. (iv) As the proteins are released from the membrane, they rapidly diffuse to other parts of the cell.

When the simulation was initiated with all MinD and MinE in the cytoplasm, symmetrical bilateral polar zones were established in a very short time (Fig. 2 a and b). If the initial concentrations of MinD and MinE were uniform at all points along the length of the cell, the bilateral polar zones failed to oscillate (data not shown). Introduction of a small disturbance in the initial cytoplasmic MinD distribution, by increasing the concentration of MinD^c at one point and diminishing it by the same amount in the adjacent space interval, led to the development of stable oscillations after a variable lag period (e.g., Fig. 2 a and b). Sustained oscillations indistinguishable from those in Fig. 2 a and b were induced by perturbations as low as 10^-7 in local concentration of cytoplasmic MinD at any location within the cell. Perturbations below this level were not tested. The length of the lag period varied inversely with the extent of the initial perturbation, from 100 to 200 s for perturbations between 10^-2 (Fig. 2 a and b) and 10^-7.

It is not known what triggers the onset of oscillations at the end of the lag period. A very small asymmetry in the polar zones that is too slight to be visible in the graphics plots appears at the onset of the lag period and then progressively increases at a slow rate (unpublished data). It is possible that the slight asymmetry grows to a critical level that triggers the collapse of one of the polar zones and rapid progression to the self-perpetuating cycles of pole-to-pole oscillation. Further study will be needed to explain this intriguing behavior.

The oscillation period was significantly affected by the relative amounts of MinD and MinE in the cell (Fig. 2e). There were no oscillations at low MinE/MinD ratios. When total MinE was increased at constant MinD, oscillations were observed above a threshold MinE/MinD value of ≈0.4. As the MinE/MinD ratio was increased, the period decreased and the polar zones progressively shortened until finally the oscillations disappeared. A similar dependence of oscillation period on the level of expression of MinE relative to MinD has been observed in vivo (2), but the available in vivo data are insufficient to allow detailed comparison between the simulated and native systems.

No oscillations were observed when the MinD reactivation rate was lower than 0.035 per s, with other parameters unchanged. Above this value, the oscillation period and the length of the full-grown polar zone both increased progressively as the MinD reactivation rate was increased, although the pattern was otherwise unchanged. This presumably reflected a prolongation of the period of MinD chain growth, because of an increased ratio of MinD-ATP to MinE in the cytoplasm.

The species denoted as MinE^e and MinEⁱ were not essential to the oscillations. If these species were removed from the model and MinE^t was allowed to release MinD^t, a stable oscillatory system was still established, but only at MinE/MinD ratios below 0.1, a ratio lower than is likely to be present in growing cells (18).

Discussion

This model reproduces essentially all of the features of the MinDE oscillatory system in vivo, namely, growth of a MinD-MinE polar zone from the cell pole, formation of an E-ring at the medial edge of the polar zone, retraction of the polar zone and associated E-ring, and repetition of the sequence at the opposite pole. It yields self-organized oscillations that are relatively robust, in that moderate changes in parameters do not significantly change the general characteristics of the system. It is remarkable that a single local discontinuity in cytoplasmic MinD of 10^-7 can lead to a complex self-sustainable oscillatory system of this type. This finding implies that the characteristic oscillatory pattern could readily be triggered in vivo by the minor point-to-point fluctuations in solute concentrations that occur spontaneously in solutions at all relevant temperatures.

Several models have previously been proposed to explain the Min oscillatory system (12-15). These models generate a stable oscillatory system. The oscillation cycles show a periodic increase and decrease of membrane-associated MinD and MinE between midcell and the pole, together with formation of a MinE ring, but none of them show the characteristic growth of the polar zones from the pole to midcell (Fig. 1). They also do not show formation of MinE polar zones.

In contrast to previous treatments, the present model considers the system as a problem in polymer dynamics that is based on the assembly and disassembly of linear MinD polymers, rather than treating all membrane-associated MinD molecules as unspecified distributions of membrane-associated proteins. Based on in vivo and in vitro studies (9-11), each polymer is likely to represent a single protofilament of a bundle of protofilaments within an extended filamentous structure. Terminal MinD molecules are treated as a separate species that is the focal point of the key reactions. In view of the demonstration that membrane-associated MinD-ATP forms polymeric structures in vitro (8, 10) and that MinD is organized into extended membrane-associated structures in intact cells (11), we believe that a polymer dynamics model of this type is more likely to approximate the in vivo situation.

A second major difference between this and previous models is that polar zone formation is initiated specifically at nucleation sites at or near the cell pole. This observation implies that cell poles differ biochemically from other regions of the E. coli cell envelope. Consistent with this idea, a number of proteins are localized specifically to cell poles in E. coli and other organisms (19-22). If the localization of MinD and/or other polar proteins is initiated by interaction with specific nucleation sites, as predicated in the present model, the “site” could be either a protein or a function of local membrane phospholipid composition or organization. In this regard, it may be significant that the minor membrane phospholipid cardiolipin is concentrated specifically at cell poles (23), and that ATP-bound MinD binds preferentially to membrane vesicles containing cardiolipin or phosphatidylglycerol in vitro (24). The possibility should be considered that specific phospholipids, such as cardiolipin or phosphatidylglycerol, or a change in local membrane lipid organization, provide nucleation sites for polymer initiation, and possibly also for the polar localization of other proteins.

The mathematical treatment revealed several unexpected features. Amongst the most interesting was the observation that induction of a stable oscillatory pattern requires that most chains arrive near midcell at approximately the same time. Therefore, if chain initiation occurs stochastically, as in a probabilistic model of the type presented here, a mechanism is required to provide a growth advantage for the youngest (i.e., shortest) chains. One solution is proposed here, that the presence of neighboring (i.e., longer) chains affects the net rate at which subunits are added to the growing end of the shorter chain. This finding implies that interactions with neighboring polymer chains affect the properties of the termini of the shorter chains; this would provide a functional advantage to bundling of MinD polymers, such as occurs spontaneously during MinD polymerization in vitro (10). The same results might also be achieved in other ways, for example, if a signal to stop chain growth were produced at midcell.

It has been shown that oscillating MinDE zones analogous to polar zones are formed at approximately unit cell lengths in nonseptate filaments resulting from a block in cell division (2, 3, 6, 7). The question thus arises as to whether such filaments might contain “virtual poles” that could provide the postulated nucleation sites for initiation of polar zone formation. Several lines of evidence suggest that such virtual poles may indeed exist at potential division sites in filaments. Mileykovskaya and Dowhan (23) have shown that cardiolipin is concentrated at regular intervals along the cell body as well as at cell poles in filaments induced by cephalexin or by depletion of phosphatidylethanolamine, and we have shown a similar phenomenon in filaments induced by depletion of the essential division protein FtsZ (unpublished results). Similarly, Jonakiraman and Goldberg (19) have recently reported that the polar protein, IcsA, is also located at unit cell lengths along FtsZ- and aztreonam-induced filaments.

The basic mathematical treatment described here can, with appropriate modification, be used to test different scenarios for their effects on the self-sustaining oscillatory reactions. To more fully define the range of conditions under which the system can be established, the effects of placing nucleation sites at different locations and allowing alternative directionality of polymer growth could prove useful. We note that the theoretical formulation and mathematical implementation may also be useful in studying other biological systems that involve membrane-associated polymerization phenomena.