Luminescence Thermometry Beyond the Biological Realm

Benjamin Harrington; Ziyang Ye; Laura Signor; Andrea D Pickel

doi:10.1021/acsnanoscienceau.3c00051

. 2023 Dec 1;4(1):30–61. doi: 10.1021/acsnanoscienceau.3c00051

Luminescence Thermometry Beyond the Biological Realm

Benjamin Harrington ^†, Ziyang Ye ^†, Laura Signor ^‡, Andrea D Pickel ^§,^*

PMCID: PMC10885336 PMID: 38406316

Abstract

graphic file with name ng3c00051_0011.jpg

As the field of luminescence thermometry has matured, practical applications of luminescence thermometry techniques have grown in both frequency and scope. Due to the biocompatibility of most luminescent thermometers, many of these applications fall within the realm of biology. However, luminescence thermometry is increasingly employed beyond the biological realm, with expanding applications in areas such as thermal characterization of microelectronics, catalysis, and plasmonics. Here, we review the motivations, methodologies, and advances linked to nonbiological applications of luminescence thermometry. We begin with a brief overview of luminescence thermometry probes and techniques, focusing on those most commonly used for nonbiological applications. We then address measurement capabilities that are particularly relevant for these applications and provide a detailed survey of results across various application categories. Throughout the review, we highlight measurement challenges and requirements that are distinct from those of biological applications. Finally, we discuss emerging areas and future directions that present opportunities for continued research.

Keywords: luminescence thermometry, nanothermometry, thermal metrology, upconverting nanoparticles, color centers, ratiometric thermometry, measurement artifacts, batch calibration

1. Introduction

Temperature is a fundamental parameter across areas ranging from device reliability to catalytic efficiency to life-sustaining cellular processes, and with this broad relevance comes an inherent need for effective and reliable temperature measurements. As a result, a vast library of thermometry techniques has been developed, with options spanning a wide range of costs, compatibility with different operating environments, and spatial, temperature, and temporal resolution. Common thermometry techniques employed across consumer, industrial, and research settings include electrical sensors such as resistance temperature detectors, thermistors, and thermocouples, scanning probe methods like scanning thermal microscopy (SThM), and optical techniques including thermoreflectance, Raman, thermal radiation, and luminescence-based approaches. The continued downscaling of modern devices has led to an ongoing emphasis on temperature probes with micro to nanoscale spatial resolution.¹ A major advantage of optical thermometry techniques is their noninvasive or less invasive nature,² stemming from the fact that these methods use lasers or other illumination sources to remotely probe the sample or, in the case of thermal radiation-based approaches, rely on the thermal emission from the sample itself. Luminescence thermometry falls within this category of optical techniques, which are often referred to as “non-contact” methods, although luminescence thermometry has also been referred to as a “semi-contact”³ or “remote detection”⁴ method since the probe is placed directly on the sample while its emission is collected from the far field. Similar situations exist for some other optical thermometry techniques like thermoreflectance methods that require depositing a metal transducer layer on the sample surface^5,6 and Raman measurements on surfaces using molecular probes.⁷ Meanwhile, thermal radiation, certain Raman approaches based on solid materials,⁸ and emerging transducer-less thermoreflectance methods⁹⁻¹¹ can be considered truly noncontact.

Luminescence thermometry is deeply intertwined with biological imaging due to the fact that many luminescent thermometers were first developed as biological imaging probes. These probes have a variety of features that are particularly desirable for in vivo applications: many are excited or emit within the first and second biological windows, near-infrared (NIR) wavelength regions where absorption and scattering by biological tissue is minimized, and their surfaces are amenable to modifications that allow for diverse bioconjugation strategies. Furthermore, many luminescent thermometers possess the small probe size, high spatial resolution, and sub-1 K temperature resolution desired for probing temperature in cellular environments. While the advantages of luminescence thermometry for biological applications are clear, one might ask why luminescence thermometry would be selected over other optical techniques for nonbiological applications. In addition to the desirable properties that it shares with other optical thermometry methods, such as remote detection and submicron spatial resolution, luminescence thermometry has other features that can facilitate unique measurement capabilities and applications (Figure 1). Luminescent probes are thermally stable and can operate over exceptionally wide temperature ranges, from cryogenic temperatures up to ∼1000 K. Many luminescent probes are chemically inert and can operate during chemical reactions without perturbing the reaction. Luminescent thermometers have a broad and tunable range of excitation and emission wavelengths, providing excellent compatibility with applications where certain spectral regions must be avoided and enabling optical multiplexing. The nanoscale size and discrete nature of luminescent probes also offer unmatched flexibility in terms of how the probes can be distributed on the sample of interest, from dense layers or ensembles to single-particle measurements.

While luminescence thermometry has both longstanding ties to and continued promise for biological applications, a wide variety of nonbiological applications have emerged over the last several decades. Many of these applications require pushing the bounds of existing techniques to achieve broader operating temperature ranges or higher spatial and temporal resolution. In turn, these advanced capabilities drive the growth of new applications. Top row images, left to right: Reprinted from ref (12) with the permission of AIP Publishing. Reprinted from ref (13) with the permission of AIP Publishing. Reprinted with permission from ref (14) Copyright 2016, Springer Nature Limited. Reprinted with permission from ref (15) Copyright 2018 American Chemical Society. Bottom row images, left to right: Reprinted with permission from ref (16) Copyright 2011 WILEY-VCH Verlag GmbH & Co. KGaA, Weinheim. Reproduced from ref (17) with permission from the Royal Society of Chemistry. Reprinted with permission from ref (18) Copyright 2019 American Chemical Society. Reprinted with permission from ref (19) Copyright 2020 American Chemical Society. Reprinted with permission under a Creative Commons CC BY 4.0 license from ref (20) Copyright 2021 Springer Nature.

This review complements several other recent reviews on luminescence thermometry, some of which specifically focus on biological applications²¹⁻²⁴ and some of which also cover a subset of nonbiological applications.^{2−4,25−27} While a number of existing reviews provide excellent summaries of the different luminescent probes and signals that can be exploited for thermometry, here we largely focus on the applications enabled by these techniques. We also omit coverage of thermographic phosphors used primarily for combustion and industrial manufacturing applications,²⁸ which are typically applied as paints or thin film coatings and have been reviewed elsewhere,^29,30 and focus on luminescent nanomaterial-based thermometry. The review is organized as follows: we first provide an overview of upconverting nanoparticles (UCNPs) and related lanthanide-containing materials, nitrogen vacancy (NV) and other color centers, quantum dots (QDs), and other luminescent probes. These particular luminescent probes are the most commonly used materials across the literature we cover in the later section focused on applications of luminescence thermometry. Subsequently, we discuss several specific capabilities, including high-temperature and cryogenic thermometry, single-particle measurements, and time-resolved thermometry. We then present applications of luminescence thermometry to microelectronics and other devices, plasmonics, catalysis, optical trapping and levitation, pressure sensing, microfluidics, and additional selected applications. Finally, we discuss emerging areas such as the identification and mitigation of artifacts that can distort luminescence thermometry signals and the resulting temperature measurements, the application of advanced data analysis and machine learning (ML) methods to luminescence thermometry, and particle-to-particle uniformity of luminescence thermometry signals and the use of batch calibration procedures. Several of the emerging areas we cover were also highlighted in a very recent comprehensive review,⁴ underscoring the growing importance of these topics within the luminescence thermometry community. We end by summarizing the current status of the field and offer a perspective on future research directions. Throughout the review, we emphasize motivations and applications that largely fall within the physical sciences and nonbiological engineering disciplines. Nonetheless, given the strong ties between luminescence thermometry and biology and the fact that certain requirements are shared between biological and nonbiological applications, we inevitably also touch on work that is primarily biologically motivated.

2. Probes

2.1. Upconverting Nanoparticles (UCNPs) and Related Lanthanide-Containing Materials

UCNPs are rare earth-doped luminescent probes with diverse applications including biological imaging, theranostics, anticounterfeiting, lasing, and sensing of quantities including pH, viscosity, and temperature. UCNPs commonly consist of multiple rare earth dopants in fluoride, oxide, or other crystalline host matrices. Often, one lanthanide dopant serves as the sensitizer, which absorbs the excitation light and subsequently transfers energy to another dopant that serves as the activator, which then emits luminescence. The most common doping composition is 20% Yb³⁺ and 2% Er³⁺, but various other rare earth dopants including Nd³⁺,³¹⁻³⁴ Tm³⁺,³⁵⁻³⁹ Ho³⁺,^40,41 Eu³⁺,^42,43 Gd³⁺,^31,44,45 and Pr³⁺⁴⁵⁻⁴⁸ are also routinely employed. The most common host matrix material is hexagonal (β) phase NaYF₄, which has a low maximum phonon energy that minimizes nonradiative recombination. A range of other host matrix materials have also been explored. Other UCNP configurations beyond the sensitizer-activator model, such as an Er³⁺ sublattice that promotes thermally activated upconversion luminescence,⁴⁹ can also enable thermometry with very high temperature sensitivity. UCNPs traditionally absorb two or more NIR photons and emit a single photon in the visible or ultraviolet wavelength range. UCNPs that convert longer wavelength NIR excitation light to shorter wavelength NIR emission have also been developed. UCNPs are favorable for biological imaging and sensing due to their excitation and in some cases emission wavelengths falling within the biological transparency windows, lack of autofluorescence, and increased optical penetration depth in tissue relative to other common probes.⁵⁰ UCNPs also have desirable features for nonbiological applications such as wide operating temperature ranges, excellent thermal stability, and chemical inertness. Other features such as UCNPs’ lack of photobleaching or blinking and the broad tunability of their excitation and emission wavelengths are beneficial across all application categories. Related lanthanide-containing materials, such as lanthanide metal–organic frameworks (MOFs),⁵¹ also facilitate thermometry based on similar operating principles.

Many lanthanides have closely spaced, thermally coupled energy levels whose relative population is governed by Boltzmann statistics. As a result, the relative emission intensity corresponding to the transitions from each excited state to the ground state provides a convenient temperature-dependent metric.⁵² The emission wavelength range is typically divided into two bands, again corresponding to the transitions from each excited state to the ground state, and a luminescence intensity ratio r is defined as the integrated emission intensity from the higher energy, shorter wavelength band divided by that from the lower energy, longer wavelength band. r increases with temperature and can be calibrated to an Arrhenius-type relation of the form 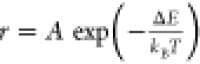Inline graphic , where A is a constant related to the radiative transition rates from each excited state to the ground state, ΔE is the energy gap between the two excited states, k_B is the Boltzmann constant, and T is temperature. This approach, known as “ratiometric” thermometry, is the most common UCNP thermometry method. Ratiometric sensing is advantageous over approaches based on absolute intensities since ratiometric signals are often insensitive to intensity variations resulting from sample absorption and scattering and day-to-day alignment variations, for example, although recent work discussed further in Section 5.1 (Measurement Artifacts) has demonstrated that parameters including the excitation laser intensity and surrounding environment can affect UCNP ratiometric thermometry signals under certain circumstances and caution must be taken.⁵³⁻⁵⁵ Ratiometric thermometry traditionally requires calibration using a temperature-controlled platform combined with a reference temperature probe, meaning that these approaches are by definition secondary thermometry methods. However, strategies for applying UCNPs for primary thermometry, in which temperature can be determined directly from a known physical law with no required calibration, have also been reported.⁵⁶

Figures of merit used to characterize the performance of luminescent thermometers include the absolute and relative thermal sensitivities, operating temperature range, repeatability, and spatial, temporal, and temperature resolution. Other reviews have provided extensive summaries of different UCNP compositions that have been used for thermometry and comparisons of the relevant figures of merit.^57,58 Similar summaries and comparisons of these figures of merit for other luminescent materials discussed in subsequent sections are also available in other review articles.^2,21,25 Here, we summarize a selection of recent, representative work on UCNP thermometry. The ²H_11/2 to ⁴I_15/2 and ⁴S_3/2 to ⁴I_15/2 transitions of Er³⁺ is the most common set used for ratiometric thermometry,⁵⁹ but numerous other dopants and transitions have also been employed to achieve higher sensitivities,^{36,39,40,47,48,60} broader operating temperature ranges,^33,41,45,46 and wide-ranging excitation and emission wavelengths. For example, Nd³⁺ sensitization³¹⁻³⁴ allows for excitation at 800 or 808 nm, where the absorption cross-section of water is much smaller than that at the 976 or 980 nm excitation wavelengths used for Yb³⁺-sensitized UCNPs. While UCNP-based ratiometric thermometry has most commonly relied on thermally coupled energy levels (TCLs), more recent work has also explored the use of nonthermally coupled levels (non-TCLs),⁶¹ which can provide higher sensitivities or extended operating temperature ranges. Stark sublevels of a single band have also been applied for ratiometric thermometry.^34,37 Other strategies that have been used to increase temperature sensitivity include applying inert coatings to the UCNPs,⁶² engineering the phonon energies of the host matrix,⁶³ and manipulating the temperature-dependent electron population through the use of an additional excitation laser.⁶⁴ An emerging alternative strategy is to increase sensitivity by defining new temperature-dependent metrics, such as the product of the luminescence intensity ratio based on emission from two thermally coupled energy levels and that based on the emission from a single band upon successive excitation of two TCLs⁴² or the product of multiple luminescence intensity ratios from different pairs of thermally coupled energy levels.⁶⁵ Recent work has also demonstrated how hardware considerations such as sensor noise can ultimately limit the temperature measurement precision.^66,67 Multiparametric sensing approaches that combine several temperature-dependent parameters can also be used to improve sensitivity and are discussed in further detail in Section 5.2 (Advanced Data Analysis and Machine Learning Approaches).

Beyond ratiometric signals, other temperature-dependent UCNP emission signatures such as spectral peak shifts⁶⁸ and luminescence lifetimes have also been used for thermometry. Several UCNP-based demonstrations of luminescence lifetime thermometry and other measurement schemes that enable real-time temperature measurements are discussed further in Section 3.4 (Time-Resolved Measurements).

2.2. Nitrogen Vacancy (NV) and Other Color Centers

NV centers are bright, photostable luminescent defects consisting of a substitutional nitrogen atom and an adjacent vacancy that are found in both bulk diamond and nanodiamonds. NV centers display magnetic sensitivity and long spin coherence times that are appealing for applications like magnetometry, quantum information processing, and quantum sensing. Due to these features, NV centers are more commonly employed for nonbiological applications than other luminescent probes; nonetheless, other features including their temperature sensitivity and amenability to surface functionalization are also attractive for biological applications such as nanoscale thermometry in a living cell.⁶⁹ Recent reviews dedicated exclusively to diamond thermometry provide detailed coverage of NV center thermometry fundamentals as well as biological and other applications.^70,71 The most common NV center thermometry approach is optically detected magnetic resonance (ODMR) thermometry, where the NV center spin state is manipulated using microwave pulses and the temperature-dependent zero-field splitting of the electronic ground state spin sublevels can be determined from the emitted luminescence.⁷² The temperature dependence of the zero-field splitting has been attributed to a combination of local thermal expansion and electron–phonon interactions.⁷³ Very recent work has put forth a physically motivated analytical expression where the zero-field splitting shifts in proportion to the occupation of two representative phonon modes, which matches experimental measurements from 15 to 500 K.⁷⁴

NV center thermometry with noise floors at or below 10 mK/Hz^1/2 and temperature resolution down to the mK level has been achieved,⁷⁵ in some cases using enhancement strategies such as those based on magnetic criticality⁷⁶ and spin coherence.^77,78 NV center thermometry is robust over an exceptionally wide temperature range, from cryogenic temperatures up to 600 K,⁷⁹ and both NV centers in bulk diamond and NV center-containing nanodiamonds are chemically inert and thermally stable at elevated temperatures. Single NV centers in high-quality bulk diamond typically achieve the highest temperature sensitivities. Meanwhile, nanodiamonds containing either single or multiple NV centers are advantageous in terms of their potential to reduce parasitic heat sinking effects, particularly given the high thermal conductivity of bulk diamond, and enable single-particle temperature measurements. ODMR thermometry has also been combined with other sensing modalities for multiplexing applications such as simultaneous magnetometry and thermometry.^80,81 Very recently, a hand-held device enabling ODMR thermometry was demonstrated, suggesting a path toward practical deployment of ODMR thermometry at macroscopic length scales in industrial or medical settings.⁸²

Because ODMR thermometry requires the use of a microwave antenna, which increases instrumentation complexity and can cause parasitic heating or otherwise disturb sensitive samples, alternative all-optical thermometry approaches have also been developed. Negatively charged NV centers display a zero-phonon line (ZPL) at approximately 638 nm, corresponding to the purely electronic transition. The ratio of the area under the ZPL relative to the total area under the emission band is known as the optical Debye–Waller factor and has been used for all-optical NV center thermometry,⁸³ along with a related approach based on the amplitude of the background emission at the ZPL center wavelength relative to the ZPL amplitude.⁸⁴ A limited number of studies have also explored the use of NV center excited state lifetimes for thermometry,^79,85,86 providing another all-optical approach, which is discussed further in Section 3.4 (Time-Resolved Measurements). More recently, other color centers beyond NV centers have gained traction for thermometry, such as silicon vacancy (SiV),⁸⁷⁻⁹¹ germanium vacancy (GeV),⁹²⁻⁹⁴ tin vacancy (SnV),⁹⁵ and magnesium vacancy (MgV)⁹⁴ centers, all of which enable all-optical thermometry. A diverse range of physical mechanisms gives rise to the temperature-dependent emission signals used for color center-based thermometry. Temperature-dependent zero-field splitting and changes to the ZPL peak position or width are common metrics for these other color centers in addition to NV centers. Other signals, such as anti-Stokes to Stokes photoluminescence intensity ratios whose temperature dependence originates from thermally activated anti-Stokes excitation⁹³ or the emission intensity resulting from thermally activated two-photon excitation,⁹¹ have also been employed.

2.3. Quantum Dots (QDs)

QDs are a class of nanoparticles with important applications across display technologies, solar cells, bioimaging, and in the sensing of pH, voltage, and temperature.⁹⁶⁻⁹⁹ Semiconductor-based QDs, particularly group II-VI QDs such as CdSe,^13,100−103 ZnS,^13,97,98,102 and CdTe,^100,104 are some of the most common types. QDs are typically spherical in nature, although related particles known as quantum rods, with an elongated length of up to ∼100 nm, have also been synthesized.¹⁰⁵ Alternatives such as carbon-based QDs^106−108 and group I-III-VI₂ compounds have been developed due to concerns over both the cellular and environmental toxicity of heavy metal QD materials.¹⁰⁶ Many groups have also developed multilayer QDs consisting of varying compositions of cores and multiple layers of shells^{99,103,109−111} and have incorporated QDs in composites with other types of nanoparticles.^112,113 Typical QDs are smaller than 20 nm in size and include only a few hundred or thousands of atoms within the lattice,⁹⁹ leading to quantum confinement effects since the characteristic size of the QD is comparable to the exciton Bohr radius.⁹⁹ QDs have a discrete valence and conduction band, which gives rise to a forbidden energy bandgap in between. Bound electron–hole pairs (excitons) are created across the valence and conduction bands and later recombine. Radiative recombination produces the QD luminescent response with emission energy determined by the bandgap of the material. QDs offer a high quantum yield¹⁰⁶ and good intensity stability compared to some other probes like organic dyes.¹⁰³ QDs are most commonly utilized for thermometry at biologically relevant temperatures since thermal quenching occurs at higher temperatures due to an increased rate of nonradiative transitions,⁹⁹ although work is being done to expand the operating temperature range of these probes.¹⁰⁰

The temperature-dependent luminescence response of QDs is typically modeled with the Varshni equation,^96,100,105 a widely used empirical expression that describes how the bandgap of a semiconductor changes with temperature. Modifications made to the physical structure of QDs including to the size, shape, and composition have also been shown to affect the bandgap and thus the temperature-dependent response.^96,99 A detailed summary of QD structural and compositional modifications and the resulting photophysical changes relevant for thermometry is available for further review.⁹⁸ On the one hand, the tunability of QDs enables access to a large range of possible emission wavelengths, but relatively unpredictable or unintended structural changes can introduce uncertainty in temperature measurements across experiments without proper calibration.¹⁰⁰ QDs exhibit several different temperature-dependent signals including photoluminescence (PL) lifetimes, PL intensity,¹¹¹ PL peak width, and PL peak wavelength.⁹⁹ CdSe QDs are commonly used for luminescence nanothermometry based only on the observed wavelength shift of their PL emission peak.^{13,101,102,105} More broadly, however, QD PL intensity changes and peak wavelength shifts have been found to be sensitive to nonthermal effects, making temperature readings difficult with these approaches alone.⁹⁹

Another thermometry approach for QDs utilizes the ratiometric intensity between the PL emission of a primary QD and a second emission signal^97,99 originating from other dopants, QD layers, or nanoparticles for improved sensitivity.⁹⁶ This “double emission” or “dual emission” technique is commonly achieved by doping the host QD with an additional emitter—typically Mn²⁺, Ag⁺, and Cu⁺ are used^98,99,114—or by layering additional QDs onto the primary QD in a core/shell approach.^99,109,110 Zhao et al.⁹⁹ provided a comprehensive review of work done to synthesize novel core/shell and core/shell/shell QDs for ratiometric thermometry. In a unique demonstration of the double emission approach, a hybrid nanocrystal incorporating PbS QDs and NaYbF₄:Tm³⁺ UCNPs utilized the ratiometric signal between the QDs and the UCNPs for nanothermometry.¹¹³ Because the emission overlapped in the spectral domain, time-resolved measurements were used to separate the signals from the two emitters based on differences in their luminescence lifetimes.

2.4. Other Probes

Beyond the three specific classes of probes described above, numerous other luminescent materials have also been applied for thermometry. Here, we cover a limited selection of other common luminescent thermometers that are relevant to work discussed in later sections. In recent years, transition metal (TM) ions such as chromium, manganese, vanadium, and titanium have also been applied for luminescence thermometry. TM-doped materials have much larger absorption cross-sections compared to those for lanthanide-doped materials, resulting in brighter luminescence intensity.¹¹⁵ Additionally, in contrast with lanthanide-doped materials whose temperature dependence is largely based on the selection of the rare earth elements, for TM-doped materials the host matrix and the resulting crystal field acting on the TM ions can dramatically affect the temperature-dependent emission.^116−118 Generally, the temperature-dependent emission originates from the temperature dependence of both the radiative and nonradiative relaxation rates, in contrast with lanthanide-doped materials where the radiative relaxation is typically assumed to be temperature independent.¹¹⁵ The temperature-dependent radiative and nonradiative relaxation rates can be indirectly observed via changes in parameters such as PL intensities and lifetimes. We highlight Cr³⁺ as one of the most frequently investigated TM ions. Here, common approaches include ratiometric thermometry based on the relative emission intensities of the bands corresponding to the ²E to ⁴A₂ and ⁴T₂ to ⁴A₂ transitions or thermometry based on the lifetimes of these excited states.^119−123 The same transitions have also been applied for thermometry using Mn³⁺ or Mn⁴⁺, another popular TM ion.¹²⁴

Another relevant class of compounds is organic thermometers such as fluorescent dyes, which are highly biocompatible and have longstanding applications for imaging, pH sensing, and thermometry in a biological context. Nonetheless, these same materials have also been used in nonbiological thermometry applications, some examples of which will be discussed in later sections. The temperature-dependent fluorescence emitted by organic molecules typically originates from the temperature dependence of nonradiative decay processes such as internal conversion or intersystem crossing.¹²⁵ In most cases, the fluorescence spectrum consists of a single broad peak, and the temperature dependence can manifest as changes in the fluorescence intensity^126,127 or lifetime.¹²⁸ For fluorescent dyes, the temperature dependence can also be influenced by processes such as Förster resonance energy transfer^129,130 or twisted intramolecular charge transfer.¹³¹ To circumvent the challenges associated with thermometry based on absolute fluorescence intensity, a common strategy is to use a ratiometric signal based on the emission intensities of two dyes with different temperature sensitivities.^132−134 A similar approach has been used to create a ratiometric thermometer based on two fluorescent proteins with different temperature sensitivities.¹³⁵ Ratiometric thermometry methods can also be developed for organic molecules by linking multiple emitting species via a MOF or a polymer matrix.^{118,136−139}

3. Capabilities

3.1. High-Temperature Measurements

Several of the emitters discussed thus far have been evaluated for use specifically in high-temperature environments. High-temperature measurements are of growing importance for studying high-power devices¹⁴⁰ and for investigating processes including metal alloy formation, sintering, and catalytic reactions.¹⁹ In the most extreme cases, relevant industrial applications for luminescence thermometry such as evaluating thermal barrier coatings for gas turbine blades can require operating temperatures as high as 1500 K.¹⁴¹ High-temperature measurements can also facilitate fundamental studies of material properties under extreme conditions. Many UCNPs suffer from catastrophic thermal quenching and host material degradation around 600 K,¹⁴² with noticeable sensitivity losses occurring at even lower temperatures.¹⁴³ Several studies have improved upon the high-temperature capabilities of UCNPs and related upconverting materials to measure temperatures as high as 1000 K.^19,140,141 Meanwhile, diamond has exceptional high-temperature stability, and temperature-dependent responses from NV centers including all-optical⁸⁶ and ODMR⁷⁹ signals remain robust up to approximately 700 K.

Geitenbeek et al.¹⁴¹ utilized bare NaYF₄:Yb³⁺,Er³⁺ UCNPs for high-temperature thermometry up to 600 K; however, above these temperatures the particles melted and fused together. Incorporating a SiO₂ shell around the UCNP core prevented this issue, thereby enabling thermometry up to 900 K. A similar study found that a SiO₂ shell enabled higher temperature measurements with LiLuF₄:Yb³⁺, Er³⁺ UCNPs up to 800 K.¹⁴⁰ As an alternative to the shell encapsulation technique, a study involving LiYF₄:Yb³⁺,Er³⁺ upconverting microcrystals used varying levels of Cu²⁺ doping to reinforce the crystalline host matrix, mitigate defects, and reduce thermal quenching of the luminescence response for thermometry up to 873 K.¹⁴² Recent work identified temperature-dependent cross-relaxation processes in Pr³⁺-doped Y₃GaO₆ as a mechanism for achieving ratiometric thermometry from room temperature up to approximately 800 K.¹⁴³ This study also found that varying the Pr³⁺ concentration modified the thermal sensitivity across the same temperature range. Other work involving UCNPs used a NIR ratiometric thermometry signal based on the ²F_5/2 to ²F_7/2 transition of Yb³⁺ and the ³H₄ to ³H₆ transition of Tm³⁺, which, notably, are non-TCLs, in YVO₄:Yb³⁺,Tm³⁺ UCNPs for thermometry up to 1000 K.¹⁹ The non-TCLs studied showed significantly better thermal sensitivity and temperature resolution compared to TCLs of Tm³⁺ at elevated temperatures, highlighting the possibility that underexamined luminescence signals lacking good resolution and sensitivity at room temperature could potentially be well-suited for high-temperature thermometry.^19,140

3.2. Cryogenic Measurements

Temperatures below 120 K are generally considered cryogenic, where research pertaining to the study of superconductivity, aerospace materials, and quantum devices often occurs.^144−146 Contact-based thermometry measurements for cryogenic systems can pose particular challenges due to the often-unavoidable heat transfer between the relatively hot probe and a cold sample. As a result, a variety of luminescent thermometers have been developed specifically for cryogenic thermometry. Fukami et al.¹⁴⁷ utilized the ZPL amplitude ratio of NV centers in nanodiamonds at temperatures ranging from 85 to 300 K. Across the cryogenic range, an important cutoff exists at 77 K, where liquid nitrogen cooling systems reach their lower temperature limit. Below this limit, helium-cooled systems are necessary as demonstrated by Chen et al.,¹⁴⁴ who used the temperature-dependent line width of GeV centers in nanodiamonds for thermometry from 5 to 35 K. Additional work in the ultralow temperature range was performed by Zhao et al.,¹⁴⁸ who demonstrated a Tb³⁺/Eu³⁺ MOF thermometer with tunable relative sensitivity for the 25 to 125 K range. A similar temperature range of 40 to 150 K was achieved using the ratiometric response from the thermally coupled ⁴T₂ to ⁴A₂ and ²E to ⁴A₂ transitions of Cr³⁺ in a CaHfO₃ perovskite host.¹¹⁹ Additional work has explored BiLaWO₆:Yb³⁺,Er³⁺,Tm³⁺¹⁴⁹ and BaGa₂O₄:Bi³⁺¹⁵⁰ for thermometry from 30 to 300 K and 7 to 300 K, respectively.

Oftentimes, a particle composition with an existing thermometry signal near room temperature can incorporate additional emitters with a cryogenic temperature response, such that the modified composition is capable of measurements across both temperature ranges. This strategy was demonstrated for core/multishell UCNPs consisting of NaYbF₄:Tm³⁺ cores and CaF₂/NaYF₄:Yb³⁺,Er³⁺/CaF₂ shells.¹⁸ The intensity ratio originating from thermally coupled Tm³⁺ Stark sublevels was used as a temperature-dependent signal between 10 to 150 K since the conventional Er³⁺ emission was barely detectable below 150 K. By utilizing both the Tm³⁺ and Er³⁺ thermometry signals, a particle composition with broad applicability for thermometry from 10 to 295 K was demonstrated. Additional work with a Tb³⁺/Eu³⁺ phosphonate dimer¹⁵¹ and several different compositions of Tb³⁺/Eu³⁺ MOFs has established that these dopants can facilitate sensitive thermometry from approximately 10 K up to room temperature.^145,146,152

In certain cases, a single emitter can provide thermometry capabilities across a wide range of temperatures. Brites et al.⁴⁶ developed a Sr₂GeO₄:Pr³⁺ thermometer that is particularly notable for its broad detection capabilities at cryogenic temperatures, near room temperature, and even into the high temperature region, enabled by two distinct ratiometric signals operating from 17 to 300 K and 300 to 600 K. Bolek et al.¹⁵³ likewise demonstrated thermometry between 17 and 700 K based on Y₃(Al,Ga)₅O₁₂:Pr³⁺ phosphors using multiple ratiometric signals and the luminescence decay time. A broad detection range of 4 to 500 K was also achieved with an erbium-chloride-silicate nanowire using ratiometric signals derived from several distinct NIR Er³⁺ Stark sublevels.¹⁵⁴

3.3. Single-Particle Measurements

In contrast with ensemble measurements that are fundamentally diffraction limited, single-particle thermometry can allow for temperature measurements with spatial resolution below the diffraction limit. When an isolated single particle is excited, the resulting temperature-dependent luminescence response corresponds solely to the location of that particle, and the spatial resolution of the temperature measurement is therefore determined by the particle size. Consequently, although single-particle measurements are technically demanding and challenges associated with particle-to-particle variation can play a larger role than in ensemble measurements,^155,156 a number of the probes discussed thus far have been employed for single-particle thermometry. Key to performing single-particle measurements is the dispersal of individual particles and subsequent validation that the particles are in fact spatially isolated. Dispersal is often accomplished by spin coating a dilute solution of particles on a sample surface.^17,66,84,157 Validation that a chosen particle is isolated (i.e., other particles are sufficiently far away such that only one particle falls within the excitation laser spot) is typically performed by observing the measurement region via scanning electron microscopy (SEM)^17,85,154 (Figure 2a). Methods for deterministically placing a single-particle thermometer at the location of interest on a sample surface include nanomanipulation techniques such as nanomanipulation using an atomic force microscope (AFM) tip⁸⁵ (Figure 2b). Lithographic approaches, including those based on lift-off processes¹⁵⁸ and nanofluidic confinement,¹⁵⁹ have successfully been used to position individual nanoparticles and thus offer another potential strategy for placing single-particle thermometers at desired locations. Optical trapping methods that can isolate and position single particles for thermometry have also been demonstrated and will be discussed later in Section 4.4 (Optical Trapping and Levitation). Single particles can also be attached to AFM tips and scanned over a sample.^12,16,160 In contrast with single-point measurements using a particle at a fixed location on a sample surface, this approach allows for temperature mapping, although such measurements retain some of the challenges associated with SThM measurements such as unknown thermal resistances and parasitic heat sinking.

(a) SEM and fluorescence images of the same pattern of NV center-containing nanodiamonds on a substrate. Such cross-validation is particularly important for confirming the presence of isolated single particles when there is substantial particle-to-particle variation in emission intensity, as in this example. Reprinted from ref (85) with the permission of AIP Publishing. (b) Another approach to performing single-particle thermometry is to deterministically place a single particle at the location of interest using a nanomanipulator tip. Reprinted with permission from A. Zimmers et al., PRL **110**, 056601 (2013). Copyright 2013 American Physical Society.

An early demonstration of thermometry via isolated single particles on a substrate was performed by Li et al.,¹⁰¹ who used the temperature-dependent spectral peak shifts of individual CdSe QDs nominally ∼7 to 12 nm in diameter. Zimmers et al.¹⁶¹ used an isolated, micron-wide Yb³⁺ and Er³⁺ codoped particle placed via nanomanipulation to study the insulator–metal transition of VO₂. Others have similarly used individual Yb³⁺ and Er³⁺ codoped particles hundreds of nm to microns in size for thermometry.^{66,142,157,162} Kilbane et al.¹⁷ showed that the temperature-dependent response of individual NaYF₄:Yb³⁺,Er³⁺ UCNPs was preserved for particles 20 × 20 × 40 nm³ in size, even though these small single particles require excitation intensities several orders of magnitude larger than those used for ensemble measurements. Pickel et al.⁵³ later demonstrated similar results for individual 50 × 50 × 50 nm³ NaYF₄:Yb³⁺,Er³⁺ UCNPs. Other morphologies have also been developed, such as elongated erbium-chloride-silicate nanowires with diameters of tens of nm up to microns and lengths over 100 μm. As discussed above in Section 3.2 (Cryogenic Measurements), Liang et al.¹⁵⁴ used these individual nanowires to demonstrate thermometry with a large operating temperature range based on several different NIR ratiometric signals. Beyond the spatial resolution advantage gained from single-particle measurements, other performance improvements and measurements capabilities have also been demonstrated at the single-particle level. Plakhotnik et al.⁸⁴ showed that all-optical ratiometric thermometry based on a single nanodiamond containing approximately 100 NV centers resulted in a noise floor an order of magnitude lower than prior all-optical measurements. Bommidi and Pickel⁸⁵ investigated the temperature-dependent excited state lifetimes of NV centers in individual nanodiamonds and demonstrated single-particle temperature measurements that combine ∼100 nm spatial resolution with ∼100 ns temporal resolution.

3.4. Time-Resolved Measurements

There is growing interest in developing thermometry techniques that demonstrate both good spatial and temporal resolution since smaller length scales naturally lead to faster thermal time constants. As a result, studies pertaining to heat dissipation in microelectronics and other nanoscale heating applications can greatly benefit from sensitive thermometry techniques with high spatial and temporal resolution. Luminescence lifetime thermometry measurements are one of the more common time-resolved techniques, given the signal’s robustness to variations in parameters such as particle size, morphology, and emitter concentration.¹⁶³ The lifetimes of most emitters decrease with increasing temperature due to the higher probability of phonon-assisted, nonradiative decay processes at elevated temperatures. Lifetime measurements typically involve a pulsed excitation laser and a time-gated photon monitor such as a camera or a photodetector.

Lifetime thermometry has been demonstrated using a number of UCNP compositions, including NaYF₄:Yb³⁺,Er³⁺,^53,164−166 other Yb³⁺ and Er³⁺ codoped hosts,^165,167,168 and compositions involving other dopants such as Tm³⁺ and Ho³⁺.^163,169 Because the transitions that give rise to UCNP luminescence are parity forbidden, UCNPs have long lifetimes on the order of hundreds of μs to ms, limiting the temporal resolution of UCNP-based lifetime thermometry. Luminescence lifetime thermometry using Mn³⁺ and Mn⁴⁺ codoped¹⁷⁰ and Cr³⁺-doped¹⁶³ nanoparticles with lifetimes on the order of ms and tens of ms, respectively, has also been reported. Other emitters intrinsically have much faster lifetimes, enabling higher temporal resolution measurements. For example, some QDs have temperature-sensitive lifetimes on the order of tens of ns.¹⁷¹ As noted previously, Bommidi and Pickel measured lifetimes on the order of tens of ns for NV centers in single nanodiamonds,⁸⁵ complementing prior lifetime measurements of nanodiamond ensembles.⁸⁶ While these techniques are suitable for single-point analysis, measuring lifetimes by scanning across a sample takes considerably longer.²⁰ To circumvent this challenge, several groups have developed wide-field imaging techniques to reduce the measurement time.^20,172 Liu et al.²⁰ explored the lifetimes of core/shell NaGdF₄:Yb³⁺,Er³⁺/NaGdF₄ UCNPs using single-shot photoluminescence lifetime imaging thermometry (SPLIT), enabling temperature mapping at a video rate of 20 Hz with 20 μm spatial resolution for a 1.5 × 1.5 mm² field of view. Yakunin et al.¹⁷² combined the highly temperature-sensitive, ns-level lifetimes of low-dimensional tin-halide perovskites with time-of-flight sensors to demonstrate video-rate thermography. Very recently, Li et al.¹⁷³ also reported highly sensitive lifetime-based thermometry using zero-dimensional Te⁴⁺-doped scandium-halide perovskites with μs-level lifetimes.

Another category of time-resolved techniques relies on the “real-time” monitoring (often referring to integration times on the order of hundreds of ms) of other common thermometry signals, including ratiometric^174−178 and ODMR signals.^179,180 Piñol et al.¹⁷⁶ developed composite nanoparticles containing iron oxide cores for magnetic induction heating functionalized with Eu³⁺ and Tb³⁺ complexes for ratiometric thermometry. The temperature of the nanoparticles was monitored with an integration time of 250 ms as AC magnetic field heating was switched on and off. Caixeta et al.¹⁷⁴ embedded GeO₂-Ta₂O₅:Yb³⁺,Er³⁺ UCNPs in poly(methyl methacrylate) films and performed ratiometric thermometry measurements with a 200 ms integration time that were in good agreement with simultaneous measurements from a thermocouple. Chen et al.¹⁷⁵ combined a ratiometric signal based on the Stokes and anti-Stokes fluorescence originating from SiV and GeV centers, respectively, in nanodiamonds with a parallel detection scheme relying on two photodetectors to demonstrate thermometry with a 200 ms integration time. Notably, Tzeng et al.¹⁷⁹ achieved ODMR thermometry using NV centers in nanodiamonds with temporal resolution better than 10 μs by monitoring the fluorescence intensity at only three frequencies rather than acquiring the entire ODMR spectrum. Yun et al.¹⁸⁰ later used a related six-frequency measurement approach to demonstrate thermometry with approximately 50 ns temporal resolution. Other work has taken advantage of time-resolved thermometry signals for purposes beyond increased temporal resolution. For example, Qiu et al.¹¹³ constructed a ratiometric signal based on PbS QDs with ns lifetimes and NaYbF₄:Tm³⁺ UCNPs with μs lifetimes by separating their spectrally overlapping emission in the time domain.

Many of the measurement capabilities described within this section and elsewhere in this review have specific instrumentation requirements. Figure 3 provides a graphical overview of custom imaging and spectroscopy systems that different researchers have constructed to perform luminescence thermometry measurements. As noted above, time-resolved luminescence thermometry measurements often involve pulsed lasers and required photodetectors or cameras with time gating capabilities (Figure 3a). Single-particle temperature measurements frequently require spectrometers coupled with highly sensitive charged-coupled device (CCD) sensors to detect weak emission signals (Figure 3b). ODMR thermometry requires a microwave source in addition to standard luminescence measurement components (Figure 3c). Optical fiber-based measurements can provide a convenient alternative to free-space excitation and collection of luminescence signals (Figure 3d). Measurements performed far from room temperature often require special heating or cooling stages and temperature control systems, with one example system for high-temperature measurements shown in Figure 3e.

(a) Major components for a time-resolved luminescence thermometry measurement. Reprinted with permission under a Creative Commons CC BY 4.0 license from ref (163) Copyright 2021 John Wiley and Sons. (b) Schematic of a single-particle luminescence thermometry measurement utilizing a spectrometer to record luminescence spectra. Reprinted with permission from ref (66) Copyright 2022 American Chemical Society. (c) Experimental setup including microwave sources for ODMR thermometry measurements. Reprinted with permission from ref (179) Copyright 2015 American Chemical Society. (d) Optical fiber technique used to perform luminescence thermometry measurements for particles dispersed in water. Reprinted with permission from ref (176) Copyright 2015 American Chemical Society. (e) Example experimental setup for high-temperature luminescence thermometry measurements using a solid immersion lens, integrated resistive heater, resistive temperature detector (RTD), and temperature controller. Reprinted with permission under a Creative Commons CC BY 3.0 license from ref (79) Copyright 2012 American Physical Society.

4. Applications

4.1. Electronics and Other Devices

The continued miniaturization of electronics and other devices has exhausted the spatial resolution of many existing thermometry techniques.¹⁰¹ Traditional probes with limited spatial resolution, such as thermocouples (∼100 μm)¹⁰¹ and IR microscopy (∼5 μm),¹⁸¹ cannot resolve temperature gradients or hotspots with smaller characteristic length scales. Many of the luminescence thermometry techniques discussed thus far have been applied to elucidate local temperature distributions in microelectronics and related devices.

One common strategy for demonstrating the ability to measure local temperature rises resulting from electrical heating is to Joule heat microfabricated metal structures or metallic wires (Figure 4a–f). Löw et al.¹⁸¹ used the temperature-dependent fluorescence intensity of Rhodamine B to produce surface temperature maps of a 2 μm wide, 80 μm long Ni line for different input current values. The Rhodamine B fluorescence intensity was quenched on and near the Ni line due to the local temperature increase, and stronger fluorescence quenching was observed for higher currents that produced larger temperature changes. In another example, two Joule-heated Au microwires 25 μm in diameter buried within a polymer film were studied.¹⁸² Both the steady-state temperature rise due to DC electrical heating and the time-dependent temperature response following pulsed heating were measured at different locations near the microwires using the ZPL shift of NV center-containing nanodiamonds embedded in the film.

(a) Microfabricated structure imaged via false-color SEM and fluorescence microscopy. NV center-containing nanodiamonds with both temperature- and magnetic field-dependent responses were imaged across the surface. Reprinted with permission from ref.⁸⁰ Copyright 2020 American Chemical Society. (b) A film of ZnCuInS/ZnSe/ZnS QDs was deposited over resistors attached to a printed circuit broad and the QD temperature response was mapped. Copyright IOP Publishing. Reproduced with permission from ref (111), all rights reserved. (c) The temperature rise due to an applied current was measured along a Ni line using the temperature-dependent fluorescence intensity of Rhodamine B. Reprinted with permission from ref (181) Copyright 2008 Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim. (d) An AFM tip with an attached luminescent nanocrystal was scanned across the surface of a Joule-heated structure with repeated constrictions to produce a temperature map. Reprinted with permission from ref (16) Copyright 2011 WILEY-VCH Verlag GmbH & Co. KGaA, Weinheim. (e) The temperature rise of a microcircuit was monitored via the temperature-dependent ZPL shift of color centers in hexagonal boron nitride flakes. Reprinted with permission from ref (183) Copyright 2020 American Chemical Society. (f) Nanodiamonds codoped with SiV and GeV centers were deposited onto a microfabricated structure. The temperature rise of the sample at four different points was measured based on the temperature response of the nanodiamonds and compared to a simulation. Reprinted with permission from ref (175) Copyright 2023 American Chemical Society. (g) The same NV center-containing nanodiamonds from (a) were used to produce temperature and magnetic field maps of the source-gate-drain region of a GaN HEMT. Reprinted with permission from ref (80) Copyright 2020 American Chemical Society. (h) The surface temperature profile of a GaN HEMT was measured using the temperature response of CdSe/CdS quantum rods. Reprinted with permission from ref (105) Copyright 2020 American Chemical Society. (i) The same nanodiamonds from (f) were used to measure the temperature rise at three different positions along an operating 2D MoTe₂ flake-based FET under various drain-source voltages. Reprinted with permission from ref (175) Copyright 2023 American Chemical Society.

In addition to Joule-heated metal lines and wires, more complicated geometries and materials have also been studied.^{16,54,80,183−185} Van Swieten et al.⁵⁴ used a Mo spiral microheater embedded in a Si₃N₄ membrane. By drop casting a layer of NaYF₄:Yb³⁺,Er³⁺ UCNPs approximately several μm in thickness onto the surface, the surface temperature was found to be homogeneous up to the edge of the microheater. An important finding on luminescence thermometry measurement artifacts from this work will be discussed later in Section 5.1 (Measurement Artifacts). Mi et al.¹⁸⁴ also used sandwich-structured NaYF₄:Yb³⁺,Nd³⁺/NaYF₄/NaYF₄:Yb³⁺,Er³⁺ upconverting nanorods to study the temperature rise at different positions along a Joule-heated magnetoresistive device. Another study mapped the temperature of several resistors in series on a printed circuit board surface using the temperature-dependent PL intensity of core/shell/shell ZnCuInS/ZnSe/ZnS QDs and compared the results to readings from an infrared (IR) thermal camera.¹¹¹ In many cases, the temperature response of the structure under consideration is also calculated analytically or numerically, allowing discrepancies between the measured and modeled temperature profiles to be investigated.^{16,80,101,105,181} In one study, the temperature profile of an Al microelectromechanical system (MEMS) heater was measured using CdSe QDs and calculated using a 1D electrothermal model.¹⁰¹ The experimental and modeled results were found to be in good agreement other than at the ends of the heater lines, where the measured temperature profiles indicated that the contact pads could heat above the ambient temperature, whereas the model assumed the pads remained at the ambient value.

In contrast with structures engineered to produce localized Joule heating, other work has studied devices where localized heating is a byproduct of device operation (Figure 4g–i). Such studies are motivated by technologies including microelectronics and optoelectronics where thermal management is required to mitigate local hotspots that can induce performance degradation and failure in operating devices. Chen et al.¹⁷⁵ used SiV and GeV centers in nanodiamonds to measure the temperature rise at three surface positions of an operating 2D MoTe₂ flake-based field-effect transistor (FET). The region near the metal-semiconductor junction experienced a large temperature rise of 44 K when the drain-source voltage was increased from 16 to 24 V, which was attributed to the Schottky barrier at the junction. Öner et al.¹⁰⁵ used the temperature-dependent spectral shift of emission from CdSe/CdS quantum rods to develop a temperature mapping technique called hyperspectral quantum rod thermal imaging (HQTI). Using HQTI, Öner et al. mapped the temperature rise of the passivation layer and source-drain metallization on the surface of a GaN high-electron mobility transistor (HEMT). The HQTI method revealed a temperature rise along the channel that was greater than at the surrounding metal contacts as expected, but no local hotspots or large thermal gradients within the channel were observed. Foy et al.⁸⁰ used ODMR measurements of ∼100 nm thick films of NV center-containing nanodiamonds to demonstrate simultaneous magnetic field and temperature mapping in a wide-field modality at high frame rates of 100 to 1000 Hz. Applying this technique to a GaN HEMT, Foy et al. measured a localized temperature rise near the gate and were also able to resolve a steep temperature drop at the end of the gate. Andrich et al.¹⁸⁶ developed a fabrication process to create ordered arrays of nanodiamonds containing NV centers in a polymer matrix and used ODMR thermometry to demonstrate temperature mapping of an operating Au coplanar waveguide. Finite element simulations with and without the polymer layer confirmed that the presence of the low thermal conductivity polymer layer did not alter the waveguide temperature profile. Given the numerous applications particularly for Si-based devices, Rodrigues et al.¹⁸⁷ developed self-assembled monolayers (SAMs) of temperature-sensitive Eu³⁺ and Tb³⁺ complexes that were formed on Si wafers with three different surface coatings, namely, monocrystalline Si, SiO₂, and polycrystalline Si. Rodrigues et al. also demonstrated that these SAMs could be used to create optical logic gates by taking advantage of bistability in their temperature-dependent ratiometric response.

While temperature mapping can be performed by monitoring many different particles spread over the surface of a device, other methods instead involve scanning a probe with attached emitters across a device. In a foundational demonstration of this concept, a Yb³⁺ and Er³⁺ codoped fluoride glass particle was glued to the end of an AFM tip.¹² A temperature map was recorded by scanning the particle across a 20 μm wide Joule-heated polysilicon resistor and measuring the ratiometric signal from the particle. Another study measured the temperature of two microheaters using a PbF₂:Yb³⁺,Er³⁺ nanocrystal on an AFM tip.¹⁶ Two Ti microheaters with repeated constrictions that increased the local current density were patterned on top of Si/SiO₂ substrates. One microheater had a 100 nm SiO₂ layer between the Si and Ti layers, while the other sample had a 1 μm thick layer. Temperature maps of the two devices revealed that the thicker SiO₂ layer increased the lateral heat spreading and reduced the temperature difference between the local hotspots and the surroundings when compared to the thinner SiO₂ layer. Laraoui et al.¹⁶⁰ developed a related approach to map thermal conductivity by mounting a nanodiamond containing an NV center on the end of an AFM tip. An electrical current was used to heat the tip and the ODMR signal from the NV center was used to measure the tip temperature, which changed in response to being brought in contact with surfaces of different thermal conductivities. Thermal conductivity mapping was demonstrated for an 18 nm thick Au structure patterned on a sapphire substrate. The thin-film Au thermal conductivity was measured to be below the bulk value, in accordance with prior measurements using other techniques.

Recognizing the pervasiveness of quick response (QR) codes and their ability to be read using ubiquitous smartphone hardware, Ramalho et al.¹⁸⁸ developed a luminescent QR code containing Eu³⁺ and Tb³⁺ codoped organic–inorganic hybrid materials with temperature-dependent emission. The green to red intensity ratio served as the temperature-dependent signal and could be detected using a standard smartphone camera. The results agreed well with emission spectra obtained by a more sophisticated spectrometer, important for advancements in the Internet of Things and on-demand thermal probing. In contrast to what has been discussed so far, where luminescent emitters are used to measure the temperature of a heater or device, Martínez et al.¹⁸⁹ demonstrated the opposite effect, where a device was heated specifically to modulate the emission from two different types of UCNPs varying in both size and shape. Silver nanowires in a poly(methyl methacrylate) layer were Joule heated using Au contacts. NaYF₄:Yb³⁺,Ln³⁺ and core/shell NaGdF₄:Yb³⁺,Ln³⁺/NaYF₄ (Ln = Tm, Er, Ho) UCNPs were deposited on the surface and their emission was selectively quenched or enhanced based on the surrounding temperature. The end result was an electrochromic device where the color output was determined by the local heating of the emitters.

4.2. Plasmonics

Plasmonic nanostructures, which are often composed of noble metals, interact resonantly with specific frequencies of light. These interactions lead to strong absorption, scattering, and localization of the electric field, which are known as plasmonic effects. Plasmonic nanostructures have wide-ranging applications in areas including photothermal therapy, solar energy conversion, and surface-enhanced Raman spectroscopy. Plasmonic nanostructures are also often used to enhance luminescence signals. Luminescence thermometry and plasmonic nanostructures can be combined for different purposes, such as thermometry and optical absorption measurements of the plasmonic nanostructures or thermal property measurements of other materials. While applying luminescence thermometry to plasmonic nanostructures requires careful validation, studies of some luminescent thermometers such as NaYF₄:Yb³⁺,Er³⁺ UCNPs have shown that common thermometry signals remain valid in a plasmonic environment.¹⁶⁴ Glais et al.¹⁹⁰ also showed that the temperature-dependent lifetime of Cr³⁺ measured from ZnGa₂O₄:Cr³⁺,Bi³⁺ nanoparticles was unaffected by a plasmonic environment.

Maestro et al.¹⁰² used QD thermometry to investigate the absorption and heating efficiency of different morphologies of gold nanoparticles (GNPs), namely, nanorods, nanocages, nanoshells, and nanostars (Figure 5a). The GNPs and CdSe QDs were both dispersed in purified water and excited by an 808 nm laser and a 488 nm laser, respectively. The GNP concentration was high enough to introduce a detectable temperature rise, while the QD concentration was low enough to avoid additional, non-negligible optical absorption. After measuring the extinction cross-sections via optical transmission experiments and the temperature rise at different excitation powers via QD thermometry, the heating efficiency and the absorption and scattering cross-sections of the GNPs were obtained by combining the experimental results with a thermal model. In addition to measuring the optical and thermal properties of plasmonic nanostructures, the combination of a plasmonic heat source and luminescence thermometry can be applied to measure the thermal properties of other materials, as demonstrated by Brites et al.¹⁹¹ Tb³⁺ and Eu³⁺ codoped organic–inorganic hybrid luminescent thermometers were deposited on top of silica and titania mesoporous nanolayers, while gold nanoparticles for plasmonic heating were deposited at the bottom of the silica mesoporous nanolayers or in the pores of the titania mesoporous nanolayers (Figure 5b). By combining the experimental temperature measurements with a thermal model, the thermal conductivities of the silica and titania mesoporous nanolayers were obtained. The calculated values were similar to previously reported literature values. This method also avoids the need to deposit a metal heater line on the sample surface, which is required by approaches such as the 3ω method.

(a) The temperature-dependent luminescence of CdSe QDs excited by a 488 nm laser was used to assess the absorption and heating efficiency of gold nanoparticles (GNPs) heated by an 808 nm laser. Reprinted with permission from ref (102) Copyright 2014 American Chemical Society. (b) Gold plasmonic nanoparticle heaters and Tb³⁺/Eu³⁺ codoped organic–inorganic hybrid thermometers were combined with a thermal model to determine the thermal conductivity of mesoporous nanolayers. Reprinted with permission from ref (191) Copyright 2017 American Chemical Society. (c) A maskless lithography process was developed based on plasmonic gold nanostars (AuNSs) tuned to absorb at the same wavelength as UCNPs used for temperature monitoring. Reprinted with permission from ref (194) Copyright 2019 American Chemical Society. (d) The temperature profile of a gold nanodot and its surroundings was measured by scanning optically trapped Er₂O₃ nanoparticle thermometers. Reprinted with permission from ref (196) Copyright 2016, Springer-Verlag Berlin Heidelberg.

Many reports of luminescence thermometry applied to plasmonic nanostructures use a combination of two lasers operating at different wavelengths. Experiments that use only one laser to excite both the plasmonic nanostructures and the luminescent thermometers are possible but require careful selection or design of the plasmonic nanostructures and luminescent thermometers. A one-beam system can overcome two potential disadvantages of a two-beam system: additional plasmonic heating due to the laser used to excite the luminescent thermometers and artifacts in the temperature measurements introduced by the laser used to excite the plasmonic nanostructures. However, the plasmonic absorption and luminescent thermometer excitation wavelengths must overlap to obtain the temperature readout and plasmonic heating simultaneously. With only one beam, Maestro et al.¹³ measured the temperature rise of an optical plasmonic recording medium, which contained CdSe QDs serving as luminescent thermometers and gold nanorods acting as plasmonic heat sources. Using two-photon excitation of the CdSe QDs, an 800 nm laser was able to excite both the gold nanorods and QDs. Taking a different approach, Rohani et al.¹⁹² tuned the plasmonic resonance of gold nanorods to match the 980 nm absorption wavelength of NaGdF₄:Yb³⁺,Er³⁺ UCNPs and demonstrated both plasmon-enhanced UCNP luminescence and a measured temperature rise of approximately 160 °C. Debasu et al.¹⁹³ combined (Gd,Yb,Er)₂O₃ nanorods with GNPs and showed that although the GNP absorbance was stronger in other spectral regions, it was sufficiently large at the 980 nm nanorod excitation wavelength to generate temperature rises of hundreds of degrees. Martínez et al.¹⁹⁴ deposited gold nanostars (AuNSs) on top of a polylactic acid (PLA) film, which has a glass transition temperature near 60 °C, embedded with NaGdYbErF₄/NaGdF₄ core/shell UCNPs (Figure 5c). The AuNS synthesis parameters were adjusted to match their plasmonic resonance to the 976 nm UCNP laser excitation wavelength. When locally heated above the PLA glass transition temperature, the AuNSs attach to the PLA surface and the unexposed PLA can subsequently be dissolved using acetone, behavior that was harnessed to develop a maskless lithography process. By sharing the same excitation laser, the UCNPs were able to probe the temperature rise resulting from plasmonic heating of the AuNSs and provide real-time monitoring of the lithography process. Huang et al.¹⁹⁵ instead tuned the plasmonic resonance of gold nanorod cores surrounded by upconverting NaYF₄:Yb³⁺,Er³⁺ shells to ∼ 650 nm to match the red Er³⁺ emission from the ⁴F_9/2 excited state. The gold nanorod cores generated heat upon absorbing this red upconverted emission, while the green upconverted Er³⁺ emission was used for thermometry.

Although most measurements characterize the temperature rise resulting from the collective contributions of many individual plasmonic nanoparticles, Baral et al.¹⁹⁶ reported an approach to measure the temperature profile near a single isolated gold nanostructure using the temperature-dependent emission from a small cluster of optically trapped Er₂O₃ nanoparticles (Figure 5d). Er₂O₃ nanoparticles ∼45 nm in size were suspended in water, optically trapped, and scanned to map the temperature rise of a gold nanodot 100 nm in diameter and its surroundings. From the measured temperature profile, the point spread function of the thermometer was estimated to be approximately 165 nm, suggesting that a small cluster of Er₂O₃ nanoparticles was trapped. While trapping and stabilizing a single Er₂O₃ nanoparticle of this size is challenging due to the weak optical forces in the case of laser trapping of small nanoparticles, trapping a cluster nonetheless allowed for temperature measurements with subdiffraction limited spatial resolution.

4.3. Catalysis

Catalysis improves chemical reaction rates by providing reaction pathways with lower activation energy barriers and is essential to critical industrial processes such as ammonia production, emerging green technologies like hydrogen production and carbon dioxide reduction, and myriad other areas. Temperature plays a fundamental role in catalysis, motivating the need for in situ temperature measurements during catalytic reactions. Reaction rates are generally improved by increasing the temperature, which can be understood from the Arrhenius equation. Common thermometry techniques such as thermocouples, nuclear magnetic resonance methods, and IR thermography have several drawbacks that include spatial resolution, complicated data analysis procedures, and requiring previous knowledge of the emissivity of the target surface. Meanwhile, luminescence thermometry has numerous advantages, such as enabling remote detection, requiring simpler calibration, and having high spatial resolution.

Different methods have been used to combine luminescent thermometers and catalytic materials. A convenient method is to physically mix the luminescent thermometers with the catalyst.^15,197 Geitenbeek et al.¹⁵ mixed NaYF₄:Yb³⁺,Er³⁺ microcrystals with a commercial solid catalyst, zeolite H-ZSM-5, to measure temperature in a fixed-bed reactor (Figure 6a). The temperature as a function of time at the top, middle, and bottom of the reactor bed was monitored during the methanol-to-hydrocarbons (MTH) reaction by using a fiber probe to collect luminescence spectra from the NaYF₄:Yb³⁺,Er³⁺ particles at three different heights. Meanwhile, several different types of hydrocarbons that form as reaction products were measured using online gas chromatography. Although the temperature uncertainty increased from approximately 0.3 to 22 K over the course of the reaction due to reduced luminescence intensity, the NaYF₄:Yb³⁺,Er³⁺ particles measured temperatures up to nearly 875 K, indicating excellent thermal stability. The temperature increases measured in the system matched the exothermic nature of the MTH reaction, and a moving temperature front observed during the reaction was also consistent with prior reports of coke deposition.

(a) The temperature at the top, middle, and bottom of a fixed-bed reactor was monitored using NaYF₄:Yb³⁺,Er³⁺ microcrystals mixed with a solid catalyst during the methanol-to-hydrocarbons reaction, revealing a moving temperature front. Reprinted with permission from ref (15) Copyright 2018 American Chemical Society. (b) NaYF₄:Yb³⁺,Er³⁺ nanothermometers were grown inside hollow bipyridine-ethane periodic mesoporous organosilica hosts to avoid catalytic activity loss that can result from blocking catalyst surface area with nanothermometer materials. Reprinted with permission from ref (200) Copyright 2022 American Chemical Society. (c) EuOCl was applied as both a catalyst and thermometer for the exothermic methane oxychlorination reaction. Reprinted with permission under a Creative Commons CC BY 4.0 license from ref (203) Copyright 2022 John Wiley and Sons. (d) Microcrystalline NaYF₄:Yb³⁺,Er³⁺ thermometers revealed temperature gradients and deviations from the set temperature on MEMS reactors. Reprinted with permission from ref (204) Copyright 2019 The Authors. Published by Wiley-VCH Verlag GmbH & Co. KGaA. (e) A single 808 nm laser was used to both photocatalyze a chemical reaction and excite NaYF₄:Nd³⁺,Yb³⁺,Er³⁺ UCNP thermometers, enabling simultaneous temperature and reaction monitoring during plasmonic photocatalysis. Reprinted with permission from ref (206) Copyright 2023 Wiley-VCH GmbH.

Another strategy is to realize the dual functions of thermometer and catalyst in a composite material. Jena et al.¹⁹⁸ created nanocomposites consisting of Yb³⁺ and Er³⁺ codoped or Yb³⁺ and Tm³⁺ codoped UCNPs combined with UiO-66-NH₂ MOFs. The presence of the UCNP thermometers did not prevent catalytic activity during the esterification of lauric acid with methanol, although a longer reaction time was required than for pristine MOFs due to the reduction in available surface area. The temperature-dependent UCNP spectral features also remained effective for thermometry. Krishnaraj et al.¹⁹⁹ developed composites consisting of covalent organic frameworks (COFs) grown around UCNPs and subsequently grafted with Cu ions for catalysis, an architecture that avoided any loss of COF surface area. Similarly, Sun et al.²⁰⁰ grew NaYF₄:Yb³⁺,Er³⁺ nanothermometers inside hollow bipyridine-ethane periodic mesoporous organosilica hosts to avoid catalytic activity loss (Figure 6b).

In some cases, the luminescent thermometer itself can serve as a catalyst. Kaczmarek et al.²⁰¹ grafted lanthanide ions to covalent organic frameworks (COFs), enabling simultaneous temperature measurements and catalysis using a single material. Gomez et al.²⁰² demonstrated the synthesis, temperature sensing, and catalytic properties of a series of lanthanide MOFs based on lanthanide ions and 2-phenylsuccinate. The MOFs were able to catalyze a cyanosilylation reaction (CSR), suggesting the possibility of using these materials to investigate the influence of temperature on CSRs. In another example reported by Terlingen et al.,²⁰³ EuOCl served as both a thermometer and catalyst for the exothermic methane oxychlorination reaction (Figure 6c). A temperature rise of 16 K over the oven temperature was recorded due to the exothermic nature of the reaction, while no measurable temperature gradient was observed between the top and bottom of the reactor.

Beyond measuring the temperature at selected locations along a reactor bed, incorporating microscopy capabilities can enable higher spatial resolution temperature mapping to correlate the temperature and reaction activity more precisely. Van Ravenhorst et al.²⁰⁴ mapped the temperature distribution in a 300 μm MEMS reactor with approximately 10 μm resolution (Figure 6d). Rather than monitoring the temperature and reaction simultaneously, microcrystalline NaYF₄:Yb³⁺,Er³⁺ particles for thermometry and Co/TiO₂ catalyst particles were deposited on separate MEMS reactors. A 200 °C temperature gradient between the center and edge of the reactor was measured in vacuum, consistent with separate scanning transmission X-ray microscopy measurements that showed variations in catalytic activity for individual catalytic particles at different locations on the reactor surface. Additional luminescence thermometry measurements performed in air and in the presence of flowing gases showed deviations from the set reactor temperature, suggesting that accurate temperature measurements can play a key role in optimizing the catalyst and reactor design.

In addition to online gas chromatography or mass spectrometry, surface-enhanced Raman spectroscopy is a powerful tool for monitoring chemical bond formation and can offer detailed information about the reaction process. Because NIR-excited Raman signals remain within several hundred nm of their excitation wavelength while NIR-excited UCNP luminescence is typically anti-Stokes shifted to the visible wavelength range, UCNP thermometry and Raman-based reaction monitoring can be performed concurrently. Hartman et al.²⁰⁵ developed multifunctional sensors consisting of shell-isolated nanoparticles for Raman signal enhancement, core/shell NaYF₄:Yb³⁺/Er³⁺ UCNPs for luminescence thermometry, and Rh catalysts, allowing for operando thermometry and reaction monitoring at the single catalyst particle level. A 980 nm laser was used to excite the UCNPs and a 785 nm laser was used for Raman spectroscopy. The luminescence thermometry measurements revealed differences between the set and measured temperatures that were attributed to heat dissipation into the flowing gas, with a higher thermal conductivity gas resulting in a larger discrepancy. Ye et al.²⁰⁶ combined UCNP thermometry and Raman-based reaction monitoring to investigate thermal contributions to plasmonic photocatalysis (Figure 6e). Here, a single 808 nm laser was used to both photocatalyze the chemical reaction and excite NaYF₄:Nd³⁺,Yb³⁺,Er³⁺ UCNP thermometers. Local laser-induced temperature rises over 40 K were recorded, yet heating alone could not catalyze the reaction, indicating the potential of luminescence thermometry to further elucidate plasmonic photocatalysis mechanisms.

4.4. Optical Trapping and Levitation

In optical trapping, the power density of the trapping laser must be sufficiently high for stable trapping of micro to nanoscale targets, making it possible to induce an unwanted temperature rise. This undesirable heating can damage optically trapped targets or increase their Brownian motion, resulting in loss of the target. Therefore, quantitative investigation is required to assess the temperature rise of trapped objects. Fluorescence correlation spectroscopy was applied to quantify local heating in different solutions (ethylene glycol, ethanol, and water) under optical trapping conditions over a decade ago.²⁰⁷ Jiang et al.²⁰⁸ later used three different temperature-dependent fluorescence parameters—the intensity, diffusion time, and lifetime of Alexa Fluor 647— to study the local temperature rise due to a 1064 nm trapping beam focused on single and double nanoholes milled in gold films, which are plasmonic nanostructures commonly used for optical trapping (Figure 7a). The temperatures measured using these three independent parameters were in excellent agreement with one another and with numerical simulations, demonstrating that even at a moderate power density of 2 mW μm^–2 the temperature rise could reach nearly 10 °C.

(a) Three different temperature-dependent fluorescence signals from Alexa Fluor 647 were applied to measure the laser-induced temperature rise in plasmonic nanohole structures used for optical trapping. Reprinted with permission from ref (208) Copyright 2019 American Chemical Society. (b) The luminescence intensity ratio, optical rotation rate, and trap stiffness were all used to measure the temperature of an optically trapped microscale upconverting particle, allowing the measured internal and center-of-mass temperatures to be compared. Reprinted with permission from ref (210) Copyright 2018 American Chemical Society. (c) A silica microsphere was used to focus the trapping laser below the diffraction limit and create a “photonic nanojet,” enabling stable trapping of a single sub-10 nm UCNP in water from 20 to 90 °C. Reprinted with permission from ref (212) Copyright 2021 Wiley-VCH GmbH. (d) ODMR thermometry based on NV centers was used to measure the temperature rise of an optically levitated nanodiamond in low vacuum due to laser absorption by impurities, which exceeded 150 K. Reprinted with permission under a Creative Commons CC BY 4.0 license from ref (216) Copyright 2016 Springer Nature. (e) ODMR thermometry was used to demonstrate that optically levitated nanodiamonds containing single NV centers remained close to room temperature even in low vacuum. Reprinted with permission from ref (218) Copyright The Optical Society.

While laser heating during optical trapping is often considered a parasitic side effect, in other cases it offers fundamental information about heat transfer, Brownian dynamics, and optical forces at small length scales. Rodríguez-Sevilla et al.²⁰⁹ used ratiometric luminescence thermometry based on microscale upconverting NaYF₄:Yb³⁺,Er³⁺ particles trapped in water to investigate the optical spinning behavior of the particles themselves, a capability enabled by their intrinsic birefringence, as a function of laser power. This study enabled the subsequent development of upconverting particle-based mechanical microthermometers with thermal sensitivity two times that of the luminescence-based thermometry. In another study, Rodríguez-Sevilla et al.²¹⁰ used three different signals to measure the temperature of optically trapped microscale upconverting particles in water, namely, the luminescence intensity ratio, the optical rotation rate, and the trap stiffness, facilitating comparison of the measured internal and center-of-mass temperatures (Figure 7b). Lu et al.²¹¹ also measured the temperature-dependent diffusive velocity of a single optically trapped NaYF₄:Yb³⁺,Er³⁺ UCNP and compared their results with the predictions of the Stokes–Einstein relation. Thermometry using optically trapped upconverting particles with nanoscale characteristic dimensions can enable higher spatial resolution measurements, but such measurements are difficult due to the weak optical trapping forces and small luminescent signals. Lu et al.²¹² overcame these challenges by using a silica microsphere to focus the trapping laser below the diffraction limit and create a “photonic nanojet,” which allowed for stable trapping of a single sub-10 nm UCNP in water from 20 to 90 °C (Figure 7c).

Another commonly investigated material for optical trapping and thermal sensing is NV centers in nanodiamonds. Optically levitated nanodiamonds (i.e., nanodiamonds trapped in vacuum or in a gas) are appealing for quantum sensing and metrology and for creating spin-optomechanical hybrid systems.²¹³ Heating caused by the trapping laser is often unfavorable since it can lead to quantum decoherence and result in the loss of the nanodiamond from the trap or of the fluorescence signal. Rahman et al.²¹⁴ demonstrated that nanodiamonds levitated in air burn at subatmospheric pressures and graphitize in nitrogen below 10 mbar, which was attributed to absorption of the 1064 nm trapping laser by impurities in the nanodiamonds and amorphous carbon present on their surfaces. Frangeskou et al.²¹⁵ later showed that nanodiamonds created by milling ultrahigh purity diamond displayed no detectable heating below 5 mbar as determined from their center-of-mass motion.

Hoang et al.²¹⁶ demonstrated electronic spin control and ODMR thermometry of NV centers in a nanodiamond that was optically levitated using a 1550 nm laser rather than the common 1064 nm trapping wavelength to increase the percentage of trapped nanodiamonds with a strong fluorescence signal (Figure 7d). In low vacuum, temperature rises over 150 K were measured, which was again attributed to impurities in the nanodiamonds. Delord et al.²¹⁷ recorded ODMR spectra from NV centers in levitated nanodiamonds at pressures down to 0.2 mbar by using a Paul trap rather than an optical dipole trap and showed that the 532 nm laser used for NV center thermometry could induce temperatures rises of tens of degrees for laser powers on the order of tens of μW at these low pressures. Pettit et al.²¹⁸ demonstrated stable optical levitation of nanodiamonds containing single NV centers at both atmospheric pressure and in low vacuum (Figure 7e). ODMR thermometry indicated that the nanodiamond temperature was maintained near room temperature for the range of pressures and trapping powers considered. The transverse spin coherence time was also shown to remain robust. Rivière et al.²¹⁹ used simultaneous ODMR and center-of-mass motion thermometry to study the Brownian motion of NV center-containing nanodiamonds heated by a 1550 nm trapping laser, another example of harnessing laser heating of optically trapped particles for fundamental studies of heat transfer and Brownian dynamics.

4.5. Pressure Sensing

Studies of matter at high pressures of tens to hundreds of GPa are relevant across areas including geology, astrophysics, and materials synthesis, motivating the development of methods to access these extreme conditions in a laboratory setting. Tribology studies can likewise involve lubricants that experience pressures in the range of several GPa. These high-pressure environments are often coupled with elevated temperatures. Intuitively, remote detection is advantageous for sensing quantities like pressure and temperature under these conditions. The diamond anvil cell (DAC) is a commonly employed device capable of generating pressures of hundreds of GPa. While luminescence-based pressure sensing is common for DACs, accurate, simultaneous temperature and pressure measurements have remained elusive until recently.²²⁰ YF₃:Yb³⁺,Er³⁺ upconverting microparticles were used in a DAC to measure pressures up to ∼8 GPa based on the spectral shift of the red Er³⁺ peak near ∼665 nm due to Stark sublevel position changes caused by increased crystal field splitting at higher pressures; meanwhile, temperature was measured up to ∼473 K via the common ratiometric signal based on the green Er³⁺ emission.²²⁰ The pressure and temperature responses showed only minor interdependence, and the measured pressure and temperature values were in good agreement with reference measurements from ruby emission and a thermocouple, respectively. Zheng et al.²²¹ demonstrated stabilization of the less common divalent oxidation state of Tm (i.e., Tm²⁺) in a SrB₄O₇ matrix and used this probe for separate temperature and pressure measurements in a DAC at pressures up to ∼13 GPa. Pressure sensing was performed based on both the spectral shift and broadening of a Tm²⁺ emission peak. Zheng et al. also demonstrated thermometry using four different Tm²⁺ luminescence signals (peak width, spectral peak shift, intensity ratio of two vibronic components in the emission spectra, and lifetime) over a wide temperature range of approximately 10 to 400 K.

Other work on luminescence-based thermometry and pressure sensing conducted within DACs has been motivated by tribology applications involving comparatively modest pressures. Albrahani et al.²²² calibrated the spectral shift of the emission peak from CdSe/CdS/ZnS core/shell/shell QDs between 295 and 373 K and at pressures up to 1.1 GPa. The peak shifts to shorter wavelengths at higher pressures, in agreement with prior pressure-dependent studies of CdSe. The temperature rise due to shear heating of a liquid film flowing between two parallel plates was also studied. Seoudi et al.²²³ later applied QDs of the same composition to measure the temperature rise and pressure of lubricants in elastohydrodynamic contacts following calibration in a DAC. Recently, Zhou et al.²²⁴ also used GdVO₄:Yb³⁺,Er³⁺ UCNPs suspended in an ester-based oil lubricant to demonstrate ratiometric thermometry up to 473 K at pressures up to approximately 1.1 GPa in a DAC, suggesting a path toward tribology applications of UCNP thermometry.

Recent work has also demonstrated the adaptation of proven luminescence thermometry probes for optical pressure sensing in low-pressure and vacuum systems. Runowski et al.²²⁵ showed that ratiometric thermometry could be used to measure increased laser-induced heating of YVO₄:Yb³⁺,Er³⁺ UCNPs at vacuum pressures that results from decreased heat dissipation into the surrounding air. The temperature rise can be calibrated as a function of pressure and subsequently used for pressure sensing. A similar strategy was demonstrated using glass microspheres containing Nd³⁺-doped nanoperovskites that act as whispering gallery mode resonators.²²⁶ In addition to the luminescence intensity ratio and the temperature-dependent spectral shifts and broadening of the Nd³⁺ emission peaks, the temperature dependence of the whispering gallery mode spectral shift was evaluated and found to result in a pressure sensitivity almost twice as high. The techniques discussed thus far have focused on optimizing a pressure-dependent signal for either low- or high-pressure environments. Runowski et al.²²⁷ demonstrated an upconverting YPO₄:Yb³⁺,Er³⁺ probe that combines low- and high-pressure sensing capabilities, using laser heating measured by Er³⁺-based ratiometric thermometry to extract low pressures and the pressure-dependent spectral shift of a NIR Er³⁺ peak in the high-pressure range. With this approach, pressures spanning 9 orders of magnitude, from 10^–8 GPa to 10 GPa, could be determined.

4.6. Microfluidics and Nanofluids

While many thermal studies of microfluidic devices are biologically motivated, other motivating applications include evaluating the performance of microchannel heat sinks, optimizing nanomaterial synthesis procedures, and monitoring chemical reactions. Chamarthy et al.²²⁸ used a ratiometric technique based on Rhodamine B and Rhodamine 110 fluorescence to map temperature nonuniformities in a silicon microchannel heat sink resulting from flow maldistribution. Geitenbeek et al.²²⁹ fabricated microfluidic devices with different material compositions and performed temperature measurements using the ratiometric signal from NaYF₄:Yb³⁺,Er³⁺ UCNPs dispersed in fluids that were in good agreement with readings from platinum resistance temperature detectors (RTDs) (Figure 8a). Unlike RTDs, which can only provide temperature readings at fixed locations, UCNPs enable remote readout of the temperature at any location on the device. Using a polydimethylsiloxane (PDMS)/glass chip, the temperature rise due to the exothermic reaction of hydrochloric acid and ammonia was locally monitored at the end of the microchannel where the reaction took place with a fiber probe. A temperature gradient imposed along a glass/glass chip was measured with spatial resolution down to ∼9 μm using confocal microscopy. Brites et al.²³⁰ also used Eu³⁺/Tb³⁺ codoped nanoparticles suspended in water to measure the temperature gradient imposed along a capillary tube with ∼65 μm spatial resolution (Figure 8b). Zhu et al.²³¹ recently demonstrated 2D thermometry in microchannels using the temperature-dependent PL intensity of octylamine substituted CsPbBr₃ perovskite QDs, including transient measurements of laminar water flow, with ∼10 μm spatial resolution and 200 ms temporal resolution. As a potential strategy for thermometry in microfluidic devices that would not require dispersing luminescent nanomaterials in the fluid, Savchuk et al.²³² developed PDMS/NaYF₄:Yb³⁺,Er³⁺ composites suitable for ratiometric thermometry that also maintain the transparency of PDMS.

(a) Several examples of microfluidic devices studied under various conditions using the temperature-dependent luminescence from NaYF₄:Yb³⁺,Er³⁺ UCNPs. A glass/glass microfluidic device was used to study the temperature profile that developed across a fluid channel with one heated side, and a PDMS/glass device was used to observe temperature changes due to the mixing of reactants as part of an exothermic reaction. Reproduced from ref (229) with permission from the Royal Society of Chemistry. (b) Temperature mapping of a nanofluid containing Eu³⁺/Tb³⁺ codoped particles. Reproduced from ref (230) with permission from the Royal Society of Chemistry. (c) Color images of an ethanol solution containing microwave-heated thermochromic zinc-based MOFs, which were used to generate temperature maps of the fluid across different heating times. Reprinted with permission from ref (234) Copyright 2022 Elsevier, Ltd. All rights reserved.

Other nanofluid-based luminescence thermometry studies extend beyond microfluidic device applications. Brites et al.¹⁴ imposed temperature gradients along solutions of NaYF₄:Yb³⁺,Er³⁺ UCNPs dispersed in water and chloroform and used ratiometric thermometry to record the time-dependent UCNP temperature rise at different positions, from which instantaneous Brownian velocities of the UCNPs were extracted. Luminescence thermometry has also been used to monitor the temperature rise of liquids heated by magnetic induction and by microwave irradiation, the latter of which has applications in areas including chemical synthesis, separations, and catalysis. Many magnetic induction heating studies have been driven by therapeutic hyperthermia applications, although additional motivating applications include catalysis and water purification.²³³ Shen et al.²³⁴ dispersed microwave-transparent thermochromic zinc-based MOFs in an ethanolic solution that was distributed in a 10 × 10 × 1 cm³ matrix consisting of 100 individual plastic cells (Figure 8c). When heated in a microwave cavity, temperature variations attributed to the nonuniform electric field were observed across the matrix.

Interestingly, a number of studies have reported local hotspots resulting from microwave or magnetic induction heating of nanofluids. These results are in contrast with heat transfer analysis demonstrating that the local temperature rise near electromagnetically heated nanoparticles is negligible, although the overall temperature rise for a macroscopic region can be appreciable due to the combined contributions of many individual nanoparticles.²³⁵ For example, Zhao et al.²³⁶ recently used microwave-absorbing carbon particles coated with Eu³⁺/Tb³⁺ mixed-metal organic complexes to measure the temperature rise in n-propanol and glycol-water solutions. The temperature in the n-propanol solution measured by ratiometric thermometry was 12 °C higher than that measured by a fiber-optic thermometer, which was taken as evidence of microwave-induced local hotspots. In another representative example, Dong and Zink²³⁷ encapsulated NaYF₄:Yb³⁺,Er³⁺ UCNPs and superparamagnetic Fe₃O₄ nanocrystals together in mesoporous silica nanoparticles and used ratiometric thermometry to measure a temperature rise of 42 °C in an aqueous solution. Conversely, experiments using separate Fe₃O₄ nanocrystals and UCNPs in solution resulted in a measured temperature rise of only 19 °C, which was likewise considered indicative of local hotspots arising from magnetic induction heating. Similarly, Gu et al.²³⁸ recently reported an intracellular temperature rise of 8.0 °C measured by Sm³⁺/Eu³⁺ ratiometric luminescent thermometers chemically linked to magnetically heated Fe₂O₃ nanoparticles, whereas Sm³⁺/Eu³⁺ thermometers located near (but not chemically linked to) the Fe₂O₃ nanoparticles indicated an intracellular temperature rise of only 5.9 °C and the measured extracellular temperature was essentially unchanged. Further investigation is warranted to resolve this apparent contradiction between modeling and experimental results, as also highlighted recently by others.²³⁹

4.7. Other Applications

Finally, we briefly highlight a nonexhaustive selection of other emerging luminescence thermometry applications that do not fall fully within one of the categories covered previously and where the relevant literature may be less extensive. Given the micro to nanoscale spatial resolution of many luminescence thermometry techniques, fundamental studies of heat transfer at these length scales are a natural application. Although the existing work that will be discussed momentarily has largely focused on heat conduction scenarios in which Fourier’s law remains valid, experimental exploration of deviations from Fourier’s law are a logical next frontier.²⁴⁰ Savchuk et al.²⁴¹ used time-resolved ratiometric thermometry measurements combined with a lumped capacitance model to determine the thermal resistance associated with heat dissipation in a laser-heated KLu(WO₄)₂:Ho³⁺,Tm³⁺ UCNP powder surrounded by air. Also using time-resolved ratiometric thermometry measurements, Rafiei Miandashti et al.¹⁷⁸ studied the transient heating and cooling of gold-decorated NaYF₄:Yb³⁺,Er³⁺ UCNPs on glass substrates surrounded by air or water and compared their results with the predictions of both analytical and finite element models.

Lin et al.¹¹² developed nanocomposites consisting of Au nanoparticles that acted as heat sources and NaYbF₄:Er³⁺/NaYF₄ core/shell UCNPs and Ag₂S QDs that served as thermometers with spectrally distinct temperature-dependent emission signatures. Surprisingly, a measured steady-state temperature difference of 30 °C across the ∼55 nm average distance separating the UCNPs and QDs was reported for nanocomposites in solution, and both the UCNPs and QDs measured temperatures tens of degrees higher than a thermocouple placed in the solution. These results are in contrast with analysis of similar scenarios showing that the local temperature rise of individual nanoparticles is negligible under continuous wave laser heating²³⁵ and that individual nanoparticles can be treated as thermally lumped to an excellent approximation.^53,176 The times to reach a steady-state temperature as measured by the UCNPs, QDs, and thermocouple were also all on the order of tens to hundreds of seconds, at odds with the much faster time scale expected for heating of an individual nanoparticle but in line with the time scale expected for collective heating of the solution,²³⁵ suggesting that these measurements may call for closer examination.

Luminescence thermometry has also been applied to phase transitions such as the metal–insulator transition of VO₂, where the question of whether the DC voltage- or current-induced phase transition is thermally or electronically driven has been strongly contested. To elucidate the role of Joule heating, Zimmers et al.¹⁶¹ used a single ∼1 μm Yb³⁺/Er³⁺ codoped fluoride glass particle to measure the local temperature rise, as noted in Section 3.3 (Single-Particle Measurements). The measured temperature consistently reached the phase transition temperature as the insulator to metal transition occurred, indicating that Joule heating plays a critical role. Brites et al.²⁴² reported a geometric phase transition in water at ∼330 K that was identified using temperature-dependent instantaneous Brownian velocity measurements of NaYF₄:Yb³⁺,Er³⁺ UCNPs.

Next-generation devices beyond those covered in prior sections may have different operating principles and, as a result, distinct metrology requirements. Errulat et al.²⁴³ demonstrated a Dy³⁺-based single-molecule magnet that also functioned as a luminescent thermometer under magnetic fields as high as 7 T, a potentially useful capability for temperature monitoring in future optomagnetic devices. Additional work in this growing area includes Dy³⁺-based single-molecule magnets that enable simultaneous luminescence thermometry and magnetic field sensing,²⁴⁴ as well as thermometry with enhanced temperature sensitivity achieved by combining temperature-dependent optical and magnetic signals,²⁴⁵ and Tb³⁺-based single-molecule magnets with luminescence thermometry capabilities.²⁴⁶ Thermal management and metrology of lithium-ion batteries is another ongoing challenge. Li et al.²⁴⁷ integrated an optical fiber sensor containing NaYF₄:Yb³⁺,Er³⁺/NaYF₄ core/shell UCNPs into a rechargeable lithium-ion battery and monitored the battery temperature in real time for different discharge rates. Luminescence thermometry has also been applied to inform thermal management strategies for optoelectronics and integrated photonics²⁴⁸ and guide the design of thermally actuated photonic devices;²⁴⁹ alternatively, optoelectronic devices themselves can also serve as thermometers.²⁵⁰ While UCNPs have longstanding anticounterfeiting applications based on their unique optical properties, Maturi et al.²⁵¹ recently reported QR codes containing NaGdF₄:Yb³⁺,Er³⁺ UCNPs that rely on emission changes resulting from laser-induced heating as part of a two-step verification process.

Although quantum coherence control typically requires low temperatures, Liu et al.²⁵² demonstrated coherent control of the electron spins of NV centers in nanodiamonds at temperatures near ∼1000 K using pulsed laser heating. Microwave pulses much shorter than the nanodiamond thermal time constant were used to manipulate the NV center spin state immediately following the laser heating, such that the nanodiamond remained near its peak temperature. To estimate nanodiamond temperatures above 700 K, where fluorescence quenching prevents ODMR thermometry, ODMR measurements were performed after allowing the nanodiamond to partially cool. The peak temperature was subsequently calculated using an analytical transient heat transfer model. In contrast with studies of laser-induced heating, Roder et al.²⁵³ used ratiometric thermometry to assess the temperature decrease of optically trapped upconverting YLF:Yb³⁺,Er³⁺ nanocrystals in liquid media resulting from laser refrigeration. Due to particle-to-particle variation in the ratiometric thermometry signal and the inability to calibrate the trapped particle, quantitative ratiometric thermometry measurements were not feasible, but the luminescence intensity ratio was shown to increase as a function of 975 nm laser excitation intensity (indicative of heating) and decrease as a function of 1020 nm laser excitation intensity (indicative of cooling). These final two works exemplify demanding applications that have taken advantage of luminescence thermometry capabilities such as high-temperature and single-particle measurements, while simultaneously underscoring opportunities for continued materials and technique development to address challenging metrology needs.

5. Emerging Areas

5.1. Measurement Artifacts

The growth of luminescence thermometry applications has been accompanied by an increasing number of reports identifying various measurement artifacts that, without careful calibration and correction, can lead to errors in the measured temperature values often on the order of tens of degrees or more. Artifacts specific to biological applications have been reported, such as spectral distortions due to tissue absorption and scattering,^113,254 and Bednarkiewicz et al.²⁵⁵ reviewed different sources of such artifacts and offered guidelines for avoiding or mitigating artifacts in a biological context. Luminescence thermometry artifacts relevant to both biological and nonbiological applications were also discussed in detail in a recent review by Brites et al.⁴ Below, we summarize research on luminescence thermometry measurement artifacts relevant to a broad array of applications, the majority of which pertains to the commonly used ratiometric thermometry signal of Yb³⁺/Er³⁺ codoped UCNPs.

One potential source of artifacts is the optical instrumentation used to perform the luminescence measurements, such as spectral distortions caused by high numerical aperture objective lenses⁴ or noise from the CCD sensor used to record spectra.^66,67 The resulting temperature errors reported in these cases ranged from less than one degree up to tens of degrees. Optical misalignment can also introduce artifacts. For example, deviations on the order of several degrees were observed during temperature mapping via NaYF₄:Yb³⁺,Er³⁺ UCNPs over scan distances of ∼100 μm.²⁵⁶

Artifacts can also originate from the photonic environment in which the nanoparticle thermometers are placed. Van Swieten et al.⁵⁴ demonstrated temperature readout errors of more than 10 K from NaYF₄:Yb³⁺,Er³⁺ UCNPs on a Mo spiral microheater embedded in a Si₃N₄ membrane due to reflectivity differences between Mo and Si₃N₄ (Figure 9a). The microheater surface acted as a mirror, leading to interference between the direct emission from the UCNPs and the reflected emission. Because the emission wavelengths for the two Er³⁺ transitions used for ratiometric thermometry vary slightly, this interference affects the emission from each transition differently, thereby altering the temperature-dependent ratio. Later, Vonk et al.⁵⁵ fabricated samples consisting of UCNP monolayers located at controlled, variable distances from Au mirrors and showed that in this scenario, the same interference phenomenon could lead to temperature errors of up to ∼100 K for Yb³⁺/Er³⁺ codoped UCNPs and ∼250 K for Ho³⁺-doped UCNPs (Figure 9b). Photonic artifacts caused by scattering from purely dielectric polystyrene microspheres that resulted in temperature errors of ∼10 K were also demonstrated.

(a) Metallic surfaces such as the Mo spiral microheater shown here can act as a mirror, resulting in interference between the direct emission of the luminescent thermometers and the reflected emission. This phenomenon led the NaYF₄:Yb³⁺,Er³⁺ UCNPs on the spiral microheater surface to erroneously report a lower temperature than those off the heater, an artifact that must be corrected to obtain accurate temperature measurements. Reprinted with permission from ref (54) Copyright 2021 American Chemical Society. (b) Fabricating samples consisting of UCNP monolayers located at controlled, variable distances from Au mirrors later allowed for systematic studies of the same interference phenomenon described in (a), which demonstrated how the measured temperature oscillates as a function of the emitter-mirror distance. Reprinted with permission from ref (55) Copyright 2023 American Chemical Society. (c) Apparent temperature rises exceeding 50 K were measured using individual NaYF₄:Yb³⁺,Er³⁺ UCNPs at the high excitation intensities required for single-particle measurements. However, this apparent self-heating was unaffected by manipulating the UCNP heat dissipation pathways or absorption cross-section, indicating that this effect is a nonthermal artifact. Reprinted with permission under a Creative Commons CC BY 4.0 license from ref (53) Copyright 2018 Springer Nature. (d) The emission intensity from Yb³⁺/Er³⁺ codoped UCNPs remains constant with laser power in the first portion of the wavelength range corresponding to the ⁴S_3/2 to ⁴I_15/2 Er³⁺ transition but increases in the second portion due to undesirable contributions from the ²H_9/2 to ⁴I_13/2 transition. Consequently, calculations of the temperature-dependent ratio that include both portions of this wavelength band can lead to erroneous measurements of decreasing temperatures as a function of laser irradiance. Reprinted with permission from ref (260) Copyright 2021 Elsevier B.V. All rights reserved.

Various artifacts caused by raising the laser excitation intensity have been reported. Pickel et al.⁵³ observed an increase in the ratiometric thermometry signal for individual NaYF₄:Yb³⁺,Er³⁺ UCNPs that would indicate a temperature rise over 50 K if interpreted as thermal (Figure 9c). Directly manipulating the UCNP heat dissipation pathways and absorption cross-section had no effect on this apparent temperature rise, demonstrating that the effect is nonthermal. Complementary rate equation modeling instead showed that a combination of radiative and nonradiative relaxation from higher-lying Er³⁺ energy levels that become heavily populated at high single-particle excitation intensities increases the temperature-dependent ratio. Working in a lower excitation intensity range, Nguyen et al.²⁵⁷ instead identified a decrease in the ratio with excitation intensity that was attributed to decreased population of the ²H_11/2 excited state. Several works have identified emission from the ²H_9/2 to ⁴I_13/2 transition of Er³⁺, which is frequently observed at higher excitation intensities and overlaps spectrally with the ⁴S_3/2 to ⁴I_15/2 Er³⁺ transition used for ratiometric thermometry, as a source of measurement artifacts.^{162,258−260} Because the ²H_9/2 to ⁴I_13/2 transition results from a three-photon upconversion process, the emission from this transition displays a different excitation intensity scaling than the Er³⁺ transitions used for ratiometric thermometry that originate from two-photon upconversion processes, leading to errors in temperature measurements where the excitation intensity is varied (Figure 9d).

The appropriate correction methodology depends on the source of the artifacts. Some excitation intensity-dependent artifacts can be avoided or mitigated by working at fixed or low excitation intensities. Another approach is to correct the ratio by subtracting or dividing out an excitation intensity-dependent term.^257,261 Martins et al.²⁵⁸ also demonstrated the disappearance of the emission from the ²H_9/2 to ⁴I_13/2 transition when the excitation wavelength was switched from 980 to 808 nm. Alternatively, deconvolution²⁵⁸ or experimental procedures^54,162 can be applied to separate and subsequently remove the emission originating from the ²H_9/2 to ⁴I_13/2 transition prior to calculating the ratio.

Beyond artifacts related to the ratiometric thermometry signal for Yb³⁺/Er³⁺codoped UCNPs, other artifacts relevant to this composition have also been identified. For example, Yb³⁺/Er³⁺codoped UCNP lifetimes have been shown to display nonthermal dependence on excitation intensity⁵³ and proximity to a dielectric interface.¹⁶⁶ Furthermore, in addition to artifacts and correction methods specific to Yb³⁺/Er³⁺ codoped UCNPs, artifacts related to other UCNP compositions and alternative strategies to avoid artifacts have been identified. Labrador-Páez et al.²⁶² reported errors in temperature measurements based on IR emitting Tm³⁺-doped and Nd³⁺-doped luminescent thermometers caused by variations in parameters including the excitation intensity, local concentration of the thermometers, optical path length, and optical absorption of the surrounding medium. Another strategy to avoid artifacts related to wavelength-dependent spectral distortions is to perform ratiometric thermometry using two spectrally overlapping emission bands that can be separated along another axis. Qiu et al.¹¹³ reported a novel nanothermometer based on a hybrid structure composed of PbS QDs and NaYbF₄:Tm³⁺ UCNPs both emitting near 810 nm. Because the PbS QDs have ns lifetimes while the NaYbF₄:Tm³⁺ UCNPs have μs lifetimes, the two emission signals could be separated via time-gated spectroscopy.

5.2. Advanced Data Analysis and Machine Learning (ML) Approaches

In contrast with extracting temperature from a single temperature-dependent luminescence feature such as spectral peak intensity, peak width, lifetime, or the intensity ratio of two emission bands, advanced data analysis and ML techniques can combine multiple features to enhance temperature sensitivity and measurement accuracy. Approaches such as multiparametric sensing, multiple linear regression, dimensionality reduction, and neural networks (NNs) can transform original data into quantities that have no interpretable physical meaning, but have the potential to require fewer calibration temperatures and produce temperature readouts with smaller uncertainty than traditional calibration methods.

Choi et al.⁸⁸ performed multiparametric analysis based on a linear combination of the peak position, width, and relative amplitude of the ZPL for nanodiamonds containing a high concentration of SiV centers. A noise floor of 13 mK/Hz^1/2 was achieved, resulting in a readout speed orders of magnitude faster than other all-optical methods with similar spatial resolution and temperature uncertainty. Chen et al.²⁶³ used multiple linear regression to improve the temperature sensitivity and reduce the temperature uncertainty of Mn²⁺/Tb³⁺ codoped Ca₂LaTaO₆ luminescent thermometers. Maturi et al.²⁶⁴ applied multiparametric analysis and multiple linear regression to thermometry based on green fluorescent protein and Ag₂S nanoparticles, demonstrating temperature uncertainties as low as 0.05 K. Ximendes et al.²⁶⁵ applied a dimensionality reduction approach to calibration data sets obtained from nanoparticles containing Yb³⁺, Nd³⁺, and Er³⁺ and Ag₂S nanoparticles. For the rare earth-containing nanoparticles, two intensity ratios and one peak intensity were calibrated as a function of temperature and both linear and nonlinear transformations (principle component analysis and t-distributed stochastic neighbor embedding, respectively) were applied to the data. These dimensionality reduction approaches reduced the temperature uncertainty to 0.09 °C compared to 0.15 °C for a conventional approach.

Stone et al.²⁶⁶ synthesized nanodiamonds containing GeV and SiV centers and used the temperature dependence of the ZPL position and width for both types of colors centers as inputs to a ML multifeature regression model. Using only three to five temperature-dependent features and three calibration temperatures for a set of five nanodiamonds, their model was able to predict the temperature of any other nanodiamond with 1.5 K uncertainty and a noise floor of 1.1 K/Hz^1/2. Liu et al.²⁶⁷ reported the application of NN recognition to extract the temperature from the magnitude and shape of Rhodamine B fluorescence spectra. Here, two different types of NNs were trained, one based on the integrated intensity and peak intensity, and the other based on the normalized spectra, which represented the spectral shape. The shape-based NN performed better than the intensity-based NN in measurement accuracy by a factor of 3 (noise floor of 4.2 mK/Hz^1/2 vs 13 mK/Hz^1/2). This improved performance resulted from eliminating the effect of fluorescence intensity fluctuations and using a greater number of temperature-dependent features to determine the temperature. Later, the same methodology and material were applied in a transient study to measure the temperature rise due to heating from a pulsed laser. A pump–probe approach was implemented to achieve 10 ns temporal resolution and the results were well-described by a 1D thermal diffusion model.²⁶⁸ Munro et al.¹⁰³ further optimized NN inputs and found that NNs trained on a combination of peak intensity-based and shaped-based inputs offered better accuracy than peak intensity-based or shaped-based inputs alone. In addition to spectral features, lifetime decay curves can also be incorporated as inputs. Lewis et al.¹⁰⁰ combined normalized spectra and lifetime decay curves of CdTe QDs in a microfluidic device. Different NNs were established, such as a conventional NN, a dense fully connected neural network (DNN) that was fed only spectra or lifetime decay curves, and a DNN that was fed both spectra and lifetime decay curves in separate branches. Compared to the other NNs, the DNN that was fed spectra and lifetime decay curves together yielded the lowest error. Applications of other new ML models such as convolutional NNs²⁶⁹ and automated ML tools²⁷⁰ to luminescence thermometry have also been reported, and further research in this burgeoning area will undoubtedly follow.

5.3. Batch Calibration and Particle-to-Particle Uniformity

As discussed in Section 5.1 (Measurement Artifacts), growing recognition of various ways in which the surrounding environment and excitation conditions can influence luminescence thermometry signals has led to the development of alternative calibration procedures to either account for or avoid these effects. A related challenge that has received less attention is errors or uncertainty resulting from applying the calibration curve obtained for a given particle or ensemble either to different particles from the same batch or another batch of nominally identical particles. Such issues are particularly relevant for single-particle measurements, where there is no averaging among particles and particle-to-particle heterogeneity is inherently important. However, these concerns are also relevant for ensemble measurements. The motivations for applying a given calibration curve to other particles from the same batch or to a new batch are both practical and fundamental: performing a separate calibration for every measurement can be tedious and decreases the appeal of the technique and its potential for broader deployment. Furthermore, in certain applications, prior calibration of same particles used for the final temperature measurement may be impractical or impossible. For example, in catalysis applications where the goal is to measure the local temperature rise during a chemical reaction, calibration of the exact particles used for these measurements is often impossible since raising the sample temperature could inadvertently catalyze the reaction, an irreversible process.²⁰⁶ Similarly, in optical trapping and levitation experiments, particles are trapped at random and thus cannot be calibrated beforehand.

While many of the thermometry metrics described previously should in theory be uniform across different particles and batches of the same nominal composition, some variation is frequently observed in practice, even for probes like UCNPs with high particle-to-particle uniformity. Kilbane et al.¹⁷ calibrated the ratiometric thermometry signal for five individual NaYF₄:Yb³⁺,Er³⁺ nanoparticles and evaluated both the smallest detectable temperature change for a single particle and the temperature uncertainty associated with applying these prior calibrations to another particle from the same batch (Figure 10a). The single-particle detection limits were estimated to be ±0.3 K at 296 K, ±1.4 K at 350 K, and ±3.3 K at 400 K., while the uncertainties associated with applying a batch calibration based on the five particles to another particle from the same batch were estimated to be ±1.2 K at 296 K, ±3.3 K at 350 K, and ±7.2 K at 400 K. Pickel et al.⁵³ performed a similar analysis in which slopes obtained from fitting the measured ln(r) vs 1/T (a linear relationship) data for five individual NaYF₄:Yb³⁺,Er³⁺ nanoparticles were used to evaluate uncertainties in the apparent temperature rise recorded for other single particles from the same batch. De Oliveira Lima et al.¹⁵⁷ also performed ratiometric thermometry calibrations of two individual KGd₃F₁₀:Yb³⁺, Er³⁺ nanoparticles and calculated the relative sensitivity as a function of temperature for both particles.

(a) Luminescence intensity ratio vs temperature calibration for five individual 20 × 20 × 40 nm³ NaYF₄:Yb³⁺,Er³⁺ UCNPs. Calibrating multiple single particles allows for estimation of the temperature uncertainty associated with batch calibration, in which previously measured calibration curves for particles from a given batch are applied to an uncalibrated particle from the same batch. Reproduced from ref (17) with permission from the Royal Society of Chemistry. (b) Individually calibrating the temperature-dependent zero-field splitting for NV center-containing nanodiamonds used for ODMR thermometry reduces the temperature uncertainty compared with uncalibrated measurements. Reprinted with permission from ref (80) Copyright 2020 American Chemical Society. (c) Luminescence intensity ratio vs temperature calibrations for three different batches of Tb³⁺ and Eu³⁺ codoped MOFs, showing similar temperature-dependent responses across the three batches. Reproduced from ref (272) with permission from the Royal Society of Chemistry.

Foy et al.⁸⁰ used a wide-field technique that allows for simultaneous measurements of hundreds of NV center-containing nanodiamonds in parallel and evaluated the temperature-dependent zero-field splitting for 2573 nanodiamonds between 23.5 and 150 °C. The mean standard deviation of the thermal response across all temperatures was found to be 3.88 °C, greater than the 2.17 °C ± 0.46 °C uncertainty expected from measurement error, which is indicative of variations in the thermal responses of individual nanodiamonds. Applying individual calibrations to each nanodiamond improved the mean temperature uncertainty to 2.6 °C per ∼1 × 1 μm² pixel (Figure 10b). As noted in Section 5.2 (Advanced Data Analysis and Machine Learning Approaches), Stone et al.²⁶⁶ demonstrated an alternative strategy based on a multifeature regression ML algorithm to facilitate all-optical thermometry using uncalibrated nanodiamonds codoped with GeV and SiV centers. Training the algorithm with as a few as five nanodiamonds enabled temperature measurements with 1.5 K uncertainty and a noise floor of 1.1 K/Hz^1/2 for uncalibrated nanodiamonds. Although other approaches achieve lower temperature uncertainties and noise floors, this method offers a practical strategy for thermometry using uncalibrated nanodiamonds that minimizes the required number of prior calibration measurements. Bommidi and Pickel⁸⁵ measured the excited state lifetimes of NV centers in five individual nanodiamonds each on silicon and glass substrates between 300 and 500 K. They evaluated nanodiamond-to-nanodiamond variation in the absolute lifetime values at a given temperature as well as in the change in lifetime over the temperature range investigated and the associated linearized temperature coefficients.

Other have evaluated variation among different batches of luminescent thermometers with the same nominal composition rather than within a single batch. Rao at el.²⁷¹ demonstrated that three different batches of Tb³⁺ and Eu³⁺ codoped MOFs display similar temperature-dependent intensity ratios. Yang et al.²⁷² reported comparable results for another Tb³⁺ and Eu³⁺ codoped MOF system (Figure 10c). Additional work has explored thermometry signals that are robust against changes in parameters like doping concentration, which may vary slightly across batches. Stefanska et al.²⁷³ showed that single-band ratiometric thermometry based on LaF₃:Pr³⁺ powders is essentially independent of the Pr³⁺ doping for concentrations between 0.06% and 4.43%. Renero-Lecuna et al.²⁷⁴ evaluated the ratiometric thermometry signal based on emission from Stark sublevels in LaOCl:Nd³⁺ nanoparticles for Nd³⁺ concentrations between 1% and 10% and found that the slopes of the fitted ln(r) vs 1/T data were similar for all doping concentrations.

Although relatively few studies have considered particle-to-particle variation, it is clear that such variation frequently represents a non-negligible or even dominant source of uncertainty if temperature measurements are performed using particles that have not been previously calibrated. For single-particle studies, calibration measurements using multiple single particles should be reported. Similar strategies may also be applicable and relevant for ensemble measurements. For example, temperature calibrations can be performed at multiple spatial locations in the case of particles dispersed on a substrate or other solid sample. In temperature mapping applications, a pixel-by-pixel calibration may be required to achieve the highest possible accuracy. Emerging ML methods also represent an alternative strategy to overcome uncertainty and errors stemming from the use of uncalibrated luminescence thermometers while simultaneously avoiding practical challenges associated with performing numerous calibration measurements.

6. Summary and Outlook

While luminescence thermometry has both longstanding ties to and continued promise for biological applications, this applications-driven review has highlighted an extensive body work from the last several decades that demonstrates how luminescence thermometry can address challenges in many other areas. Identifying micro to nanoscale hotspots in electronics, an early device-oriented application of luminescence thermometry, remains a frontier opportunity, with increasingly important technologies such as wide bandgap devices presenting a new set of thermal challenges and metrology needs.^11,275 Devices for quantum computing applications, many of which operate well below room temperature, similarly benefit from thermal characterization²⁷⁶ and are a prime example of applications that could take advantage of the wide operating temperature range of luminescent thermometers. Various applications in catalysis have appeared in recent years, indicating opportunities to optimize reactor conditions, delineate photothermal and photochemical mechanisms, and characterize the temperature rise resulting from heat generated by exothermic reactions.

Emerging areas of focus point to both opportunities and challenges for the field of luminescence thermometry. ML and other advanced data analysis methods suggest a path toward luminescence thermometry approaches that offer improved sensitivity and reliability while simultaneously requiring fewer calibration tasks. Increasing recognition of artifacts that can distort measured temperature values calls for carefully considered strategies to both identify and mitigate the effects of these artifacts, areas that are being addressed by a growing number of publications. While the presence of artifacts naturally raises questions about the robustness of luminescence thermometry and its ultimate potential for deployment in industrial or commercial settings, well-established and widely used techniques like resistance thermometry must also contend with confounding factors such as self-heating and strain-induced resistance changes, and strategies have been established to compensate and account for these effects.²⁷⁷ We have also emphasized challenges related to particle-to-particle uniformity and the resulting implications for batch calibration methods as a less-examined area that merits further consideration with an eye toward practical applications.

Luminescence thermometry frequently benefits from innovations in probe materials, and parallel developments in this area suggest intriguing possibilities. For example, recent advances in highly doped UCNPs²⁷⁸ have led to a variety of applications including bright probes for single-molecule studies,²⁷⁹ multiple super-resolution imaging modalities,^280−283 and optical multiplexing schemes.²⁸⁴ Future exploration of these probes for thermometry applications may likewise yield exciting new capabilities. Avalanching nanoparticles^280,281 offer particularly intriguing possibilities for thermometry since avalanche phenomena are highly sensitive to environmental perturbations like temperature changes, and simulations exploring the temperature-dependent processes involved in photon avalanching have yielded promising results.²⁸⁵ The confluence of advances in probe materials, instrumentation, and data analysis, combined with ongoing thermal characterization needs stemming from both established and early stage application categories, should provide a diverse set of impactful research directions for luminescence thermometry researchers to pursue in the years ahead.

Acknowledgments

This material is based upon work supported by the National Science Foundation under Grant No. 2142140. The authors also acknowledge support from the U.S. Department of Education Graduate Assistance in Areas of National Need (GAANN) fellowship program and the University of Rochester.

Author Contributions

^∥ These authors contributed equally to this paper. CRediT: Benjamin Harrington conceptualization, visualization, writing-original draft, writing-review & editing; Ziyang Ye conceptualization, visualization, writing-original draft, writing-review & editing; Laura Signor writing-review & editing; Andrea D. Pickel conceptualization, funding acquisition, project administration, supervision, visualization, writing-original draft, writing-review & editing.

The authors declare no competing financial interest.

References

Yue Y.; Wang X. Nanoscale thermal probing. Nano Reviews 2012, 3 (1), 11586. 10.3402/nano.v3i0.11586. [DOI] [PMC free article] [PubMed] [Google Scholar]
Bradac C.; Lim S. F.; Chang H.-C.; Aharonovich I. Optical Nanoscale Thermometry: From Fundamental Mechanisms to Emerging Practical Applications. Advanced Optical Materials 2020, 8 (15), 2000183. 10.1002/adom.202000183. [DOI] [Google Scholar]
Dramićanin M. D. Trends in luminescence thermometry. J. Appl. Phys. 2020, 128, 040902. 10.1063/5.0014825. [DOI] [Google Scholar]
Brites C. D. S.; Marin R.; Suta M.; Carneiro Neto A. N.; Ximendes E.; Jaque D.; Carlos L. D. Spotlight on Luminescence Thermometry: Basics, Challenges, and Cutting-Edge Applications. Adv. Mater. 2023, 35 (36), 2302749. 10.1002/adma.202302749. [DOI] [PubMed] [Google Scholar]
Jiang P.; Qian X.; Yang R. Tutorial: Time-domain thermoreflectance (TDTR) for thermal property characterization of bulk and thin film materials. J. Appl. Phys. 2018, 124, 161103. 10.1063/1.5046944. [DOI] [Google Scholar]
Yang J.; Maragliano C.; Schmidt A. J. Thermal property microscopy with frequency domain thermoreflectance. Rev. Sci. Instrum. 2013, 84, 104904. 10.1063/1.4824143. [DOI] [PubMed] [Google Scholar]
Pozzi E. A.; Zrimsek A. B.; Lethiec C. M.; Schatz G. C.; Hersam M. C.; Van Duyne R. P. Evaluating Single-Molecule Stokes and Anti-Stokes SERS for Nanoscale Thermometry. The Journal of Physical Chemistry C 2015, 119 (36), 21116–21124. 10.1021/acs.jpcc.5b08054. [DOI] [Google Scholar]
Xu S.; Fan A.; Wang H.; Zhang X.; Wang X. Raman-based Nanoscale Thermal Transport Characterization: A Critical Review. Int. J. Heat Mass Transfer 2020, 154, 119751. 10.1016/j.ijheatmasstransfer.2020.119751. [DOI] [Google Scholar]
Olson D. H.; Braun J. L.; Hopkins P. E. Spatially resolved thermoreflectance techniques for thermal conductivity measurements from the nanoscale to the mesoscale. J. Appl. Phys. 2019, 126, 150901. 10.1063/1.5120310. [DOI] [Google Scholar]
Warkander S.; Wu J. Transducerless time domain reflectance measurement of semiconductor thermal properties. J. Appl. Phys. 2022, 131, 025101. 10.1063/5.0069360. [DOI] [Google Scholar]
Yuan C.; Hanus R.; Graham S. A review of thermoreflectance techniques for characterizing wide bandgap semiconductors’ thermal properties and devices’ temperatures. J. Appl. Phys. 2022, 132, 220701. 10.1063/5.0122200. [DOI] [Google Scholar]
Aigouy L.; Tessier G.; Mortier M.; Charlot B. Scanning thermal imaging of microelectronic circuits with a fluorescent nanoprobe. Appl. Phys. Lett. 2005, 87, 184105. 10.1063/1.2123384. [DOI] [Google Scholar]
Maestro L. M.; Zhang Q.; Li X.; Jaque D.; Gu M. Quantum-dot based nanothermometry in optical plasmonic recording media. Appl. Phys. Lett. 2014, 105, 181110. 10.1063/1.4901258. [DOI] [Google Scholar]
Brites C. D. S.; Xie X.; Debasu M. L.; Qin X.; Chen R.; Huang W.; Rocha J.; Liu X.; Carlos L. D. Instantaneous ballistic velocity of suspended Brownian nanocrystals measured by upconversion nanothermometry. Nature Nanotechnology 2016, 11, 851–856. 10.1038/nnano.2016.111. [DOI] [PubMed] [Google Scholar]
Geitenbeek R. G.; Nieuwelink A.-E.; Jacobs T. S.; Salzmann B. B. V.; Goetze J.; Meijerink A.; Weckhuysen B. M. In Situ Luminescence Thermometry To Locally Measure Temperature Gradients during Catalytic Reactions. ACS Catalysis 2018, 8 (3), 2397–2401. 10.1021/acscatal.7b04154. [DOI] [PMC free article] [PubMed] [Google Scholar]
Saïdi E.; Babinet N.; Lalouat L.; Lesueur J.; Aigouy L.; Volz S.; Labéguerie-Egéa J.; Mortier M. Tuning Temperature and Size of Hot Spots and Hot-Spot Arrays. Small 2011, 7 (2), 259–264. 10.1002/smll.201001476. [DOI] [PubMed] [Google Scholar]
Kilbane J. D.; Chan E. M.; Monachon C.; Borys N. J.; Levy E. S.; Pickel A. D.; Urban J. J.; Schuck P. J.; Dames C. Far-field optical nanothermometry using individual sub-50 nm upconverting nanoparticles. Nanoscale 2016, 8 (22), 11611–11616. 10.1039/C6NR01479H. [DOI] [PubMed] [Google Scholar]
Shang Y.; Han Q.; Hao S.; Chen T.; Zhu Y.; Wang Z.; Yang C. Dual-Mode Upconversion Nanoprobe Enables Broad-Range Thermometry from Cryogenic to Room Temperature. ACS Applied Materials & Interfaces 2019, 11 (45), 42455–42461. 10.1021/acsami.9b11751. [DOI] [PubMed] [Google Scholar]
Runowski M.; Woźny P.; Stopikowska N.; Martín I. R.; Lavín V.; Lis S. Luminescent Nanothermometer Operating at Very High Temperature—Sensing up to 1000 K with Upconverting Nanoparticles (Yb³⁺/Tm³⁺). ACS Applied Materials & Interfaces 2020, 12 (39), 43933–43941. 10.1021/acsami.0c13011. [DOI] [PMC free article] [PubMed] [Google Scholar]
Liu X.; Skripka A.; Lai Y.; Jiang C.; Liu J.; Vetrone F.; Liang J. Fast wide-field upconversion luminescence lifetime thermometry enabled by single-shot compressed ultrahigh-speed imaging. Nature Communications 2021, 12, 6401. 10.1038/s41467-021-26701-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
Bednarkiewicz A.; Drabik J.; Trejgis K.; Jaque D.; Ximendes E.; Marciniak L. Luminescence based temperature bio-imaging: Status, challenges, and perspectives. Applied Physics Reviews 2021, 8, 011317. 10.1063/5.0030295. [DOI] [Google Scholar]
del Rosal B.; Ximendes E.; Rocha U.; Jaque D. In Vivo Luminescence Nanothermometry: from Materials to Applications. Advanced Optical Materials 2017, 5 (1), 1600508. 10.1002/adom.201600508. [DOI] [Google Scholar]
Nexha A.; Carvajal J. J.; Pujol M. C.; Díaz F.; Aguiló M. Lanthanide doped luminescence nanothermometers in the biological windows: strategies and applications. Nanoscale 2021, 13 (17), 7913–7987. 10.1039/D0NR09150B. [DOI] [PubMed] [Google Scholar]
Zhou J.; del Rosal B.; Jaque D.; Uchiyama S.; Jin D. Advances and challenges for fluorescence nanothermometry. Nature Methods 2020, 17, 967–980. 10.1038/s41592-020-0957-y. [DOI] [PubMed] [Google Scholar]
Brites C. D. S.; Balabhadra S.; Carlos L. D. Lanthanide-Based Thermometers: At the Cutting-Edge of Luminescence Thermometry. Advanced Optical Materials 2019, 7 (5), 1801239. 10.1002/adom.201801239. [DOI] [Google Scholar]
Zhang B.; Guo X.; Zhang Z.; Fu Z.; Zheng H. Luminescence thermometry with rare earth doped nanoparticles: Status and challenges. J. Lumin. 2022, 250, 119110. 10.1016/j.jlumin.2022.119110. [DOI] [Google Scholar]
Jia M.; Chen X.; Sun R.; Wu D.; Li X.; Shi Z.; Chen G.; Shan C. Lanthanide-based ratiometric luminescence nanothermometry. Nano Research 2023, 16, 2949–2967. 10.1007/s12274-022-4882-7. [DOI] [Google Scholar]
Rosso L.; Tabandeh S.; Beltramino G.; Fernicola V. Validation of phosphor thermometry for industrial surface temperature measurements. Measurement Science and Technology 2020, 31, 034002. 10.1088/1361-6501/ab4b6b. [DOI] [Google Scholar]
Aldén M.; Omrane A.; Richter M.; Särner G. Thermographic phosphors for thermometry: A survey of combustion applications. Prog. Energy Combust. Sci. 2011, 37 (4), 422–461. 10.1016/j.pecs.2010.07.001. [DOI] [Google Scholar]
Brübach J.; Pflitsch C.; Dreizler A.; Atakan B. On surface temperature measurements with thermographic phosphors: A review. Prog. Energy Combust. Sci. 2013, 39 (1), 37–60. 10.1016/j.pecs.2012.06.001. [DOI] [Google Scholar]
Klier D. T.; Kumke M. U. Upconversion NaYF₄:Yb:Er nanoparticles co-doped with Gd³⁺ and Nd³⁺ for thermometry on the nanoscale. RSC Advances 2015, 5 (82), 67149–67156. 10.1039/C5RA11502G. [DOI] [Google Scholar]
Marciniak L.; Pilch A.; Arabasz S.; Jin D.; Bednarkiewicz A. Heterogeneously Nd³⁺ doped single nanoparticles for NIR-induced heat conversion, luminescence, and thermometry. Nanoscale 2017, 9 (24), 8288–8297. 10.1039/C7NR02630G. [DOI] [PubMed] [Google Scholar]
Marciniak L.; Prorok K.; Francés-Soriano L.; Pérez-Prieto J.; Bednarkiewicz A. A broadening temperature sensitivity range with a core-shell YbEr@YbNd double ratiometric optical nanothermometer. Nanoscale 2016, 8 (9), 5037–5042. 10.1039/C5NR08223D. [DOI] [PubMed] [Google Scholar]
Skripka A.; Morinvil A.; Matulionyte M.; Cheng T.; Vetrone F. Advancing neodymium single-band nanothermometry. Nanoscale 2019, 11 (23), 11322–11330. 10.1039/C9NR02801C. [DOI] [PubMed] [Google Scholar]
Du P.; Luo L.; Yu J. S. Controlled synthesis and upconversion luminescence of Tm³⁺-doped NaYbF₄ nanoparticles for non-invasion optical thermometry. J. Alloys Compd. 2018, 739, 926–933. 10.1016/j.jallcom.2017.12.260. [DOI] [Google Scholar]
Liu H.; Yan L.; Huang J.; An Z.; Sheng W.; Zhou B. Ultrasensitive Thermochromic Upconversion in Core-Shell-Shell Nanoparticles for Nanothermometry and Anticounterfeiting. The Journal of Physical Chemistry Letters 2022, 13 (10), 2306–2312. 10.1021/acs.jpclett.2c00005. [DOI] [PubMed] [Google Scholar]
Pereira A. F.; Kumar K. U.; Silva W. F.; Santos W. Q.; Jaque D.; Jacinto C. Yb³⁺/Tm³⁺ co-doped NaNbO₃ nanocrystals as three-photon-excited luminescent nanothermometers. Sensors and Actuators B: Chemical 2015, 213, 65–71. 10.1016/j.snb.2015.01.136. [DOI] [Google Scholar]
Savchuk O. A.; Carvajal J. J.; Cascales C.; Massons J.; Aguiló M.; Díaz F. Thermochromic upconversion nanoparticles for visual temperature sensors with high thermal, spatial and temporal resolution. J. Mater. Chem. C 2016, 4 (27), 6602–6613. 10.1039/C6TC01841F. [DOI] [Google Scholar]
Zheng T.; Runowski M.; Stopikowska N.; Skwierczyńska M.; Lis S.; Du P.; Luo L. Dual-center thermochromic Bi₂MoO₆:Yb³⁺, Er³⁺, Tm³⁺ phosphors for ultrasensitive luminescence thermometry. J. Alloys Compd. 2022, 890, 161830. 10.1016/j.jallcom.2021.161830. [DOI] [Google Scholar]
Runowski M.; Goderski S.; Przybylska D.; Grzyb T.; Lis S.; Martín I. R. Sr₂LuF₇:Yb³⁺-Ho³⁺-Er³⁺ Upconverting Nanoparticles as Luminescent Thermometers in the First, Second, and Third Biological Windows. ACS Applied Nano Materials 2020, 3 (7), 6406–6415. 10.1021/acsanm.0c00839. [DOI] [Google Scholar]
van Swieten T. P.; Yu D.; Yu T.; Vonk S. J. W.; Suta M.; Zhang Q.; Meijerink A.; Rabouw F. T. A Ho³⁺-Based Luminescent Thermometer for Sensitive Sensing over a Wide Temperature Range. Advanced Optical Materials 2021, 9 (1), 2001518. 10.1002/adom.202001518. [DOI] [Google Scholar]
Ćirić A.; Marciniak Ł.; Dramićanin M. D.. Luminescence intensity ratio squared—A new luminescence thermometry method for enhanced sensitivity. J. Appl. Phys. 2022, 131 ( (11), ) 10.1063/5.0086807. [DOI] [Google Scholar]
van Swieten T. P.; Steenhoff J. M.; Vlasblom A.; de Berg R.; Mattern S. P.; Rabouw F. T.; Suta M.; Meijerink A. Extending the dynamic temperature range of Boltzmann thermometers. Light: Science & Applications 2022, 11, 343. 10.1038/s41377-022-01028-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
Netzsch P.; Hämmer M.; Turgunbajew E.; van Swieten T. P.; Meijerink A.; Höppe H. A.; Suta M. Beyond the Energy Gap Law: The Influence of Selection Rules and Host Compound Effects on Nonradiative Transition Rates in Boltzmann Thermometers. Advanced Optical Materials 2022, 10 (11), 2200059. 10.1002/adom.202200059. [DOI] [Google Scholar]
Yu D.; Li H.; Zhang D.; Zhang Q.; Meijerink A.; Suta M. One ion to catch them all: Targeted high-precision Boltzmann thermometry over a wide temperature range with Gd³⁺. Light: Science & Applications 2021, 10, 236. 10.1038/s41377-021-00677-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
Brites C. D. S.; Fiaczyk K.; Ramalho J. F. C. B.; Sójka M.; Carlos L. D.; Zych E. Widening the Temperature Range of Luminescent Thermometers through the Intra- and Interconfigurational Transitions of Pr³⁺. Advanced Optical Materials 2018, 6 (10), 1701318. 10.1002/adom.201701318. [DOI] [Google Scholar]
Gao Y.; Huang F.; Lin H.; Xu J.; Wang Y. Intervalence charge transfer state interfered Pr³⁺ luminescence: A novel strategy for high sensitive optical thermometry. Sensors and Actuators B: Chemical 2017, 243, 137–143. 10.1016/j.snb.2016.11.143. [DOI] [Google Scholar]
Runowski M.; Woźny P.; Martín I. R.; Lavín V.; Lis S. Praseodymium doped YF₃:Pr³⁺ nanoparticles as optical thermometer based on luminescence intensity ratio (LIR) - Studies in visible and NIR range. J. Lumin. 2019, 214, 116571. 10.1016/j.jlumin.2019.116571. [DOI] [Google Scholar]
Yan L.; Huang J.; An Z.; Zhang Q.; Zhou B. Activating Ultrahigh Thermoresponsive Upconversion in an Erbium Sublattice for Nanothermometry and Information Security. Nano Letters 2022, 22 (17), 7042–7048. 10.1021/acs.nanolett.2c01931. [DOI] [PubMed] [Google Scholar]
Vetrone F.; Naccache R.; Zamarrón A.; Juarranz de la Fuente A.; Sanz-Rodríguez F.; Martinez Maestro L.; Martín Rodriguez E.; Jaque D.; García Solé J.; Capobianco J. A. Temperature Sensing Using Fluorescent Nanothermometers. ACS Nano 2010, 4 (6), 3254–3258. 10.1021/nn100244a. [DOI] [PubMed] [Google Scholar]
Zhou Y.; Yan B.; Lei F. Postsynthetic lanthanide functionalization of nanosized metal-organic frameworks for highly sensitive ratiometric luminescent thermometry. Chemical Communications 2014, 50 (96), 15235–15238. 10.1039/C4CC07038K. [DOI] [PubMed] [Google Scholar]
Fischer L. H.; Harms G. S.; Wolfbeis O. S. Upconverting Nanoparticles for Nanoscale Thermometry. Angewandte Chemie International Edition 2011, 50 (20), 4546–4551. 10.1002/anie.201006835. [DOI] [PubMed] [Google Scholar]
Pickel A. D.; Teitelboim A.; Chan E. M.; Borys N. J.; Schuck P. J.; Dames C. Apparent self-heating of individual upconverting nanoparticle thermometers. Nature Communications 2018, 9, 4907. 10.1038/s41467-018-07361-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
van Swieten T. P.; van Omme T.; van den Heuvel D. J.; Vonk S. J. W.; Spruit R. G.; Meirer F.; Garza H. H. P.; Weckhuysen B. M.; Meijerink A.; Rabouw F. T.; Geitenbeek R. G. Mapping Elevated Temperatures with a Micrometer Resolution Using the Luminescence of Chemically Stable Upconversion Nanoparticles. ACS Applied Nano Materials 2021, 4 (4), 4208–4215. 10.1021/acsanm.1c00657. [DOI] [PMC free article] [PubMed] [Google Scholar]
Vonk S. J. W.; van Swieten T. P.; Cocina A.; Rabouw F. T. Photonic Artifacts in Ratiometric Luminescence Nanothermometry. Nano Letters 2023, 23 (14), 6560–6566. 10.1021/acs.nanolett.3c01602. [DOI] [PMC free article] [PubMed] [Google Scholar]
Balabhadra S.; Debasu M. L.; Brites C. D. S.; Ferreira R. A. S.; Carlos L. D. Upconverting Nanoparticles Working As Primary Thermometers In Different Media. The Journal of Physical Chemistry C 2017, 121 (25), 13962–13968. 10.1021/acs.jpcc.7b04827. [DOI] [Google Scholar]
Wang Q.; Liao M.; Lin Q.; Xiong M.; Mu Z.; Wu F. A review on fluorescence intensity ratio thermometer based on rare-earth and transition metal ions doped inorganic luminescent materials. J. Alloys Compd. 2021, 850, 156744. 10.1016/j.jallcom.2020.156744. [DOI] [Google Scholar]
Zhao Y.; Wang X.; Zhang Y.; Li Y.; Yao X. Optical temperature sensing of up-conversion luminescent materials: Fundamentals and progress. J. Alloys Compd. 2020, 817, 152691. 10.1016/j.jallcom.2019.152691. [DOI] [Google Scholar]
Sedlmeier A.; Achatz D. E.; Fischer L. H.; Gorris H. H.; Wolfbeis O. S. Photon upconverting nanoparticles for luminescent sensing of temperature. Nanoscale 2012, 4 (22), 7090–7096. 10.1039/c2nr32314a. [DOI] [PubMed] [Google Scholar]
Zheng K.; Song W.; He G.; Yuan Z.; Qin W. Five-photon UV upconversion emissions of Er³⁺ for temperature sensing. Opt. Express 2015, 23 (6), 7653–7658. 10.1364/OE.23.007653. [DOI] [PubMed] [Google Scholar]
Wang C.; Jin Y.; Zhang R.; Yao Q.; Hu Y. A review and outlook of ratiometric optical thermometer based on thermally coupled levels and non-thermally coupled levels. J. Alloys Compd. 2022, 894, 162494. 10.1016/j.jallcom.2021.162494. [DOI] [Google Scholar]
Savchuk O. A.; Carvajal J. J.; Cascales C.; Aguiló M.; Díaz F. Benefits of Silica Core-Shell Structures on the Temperature Sensing Properties of Er,Yb:GdVO₄ Up-Conversion Nanoparticles. ACS Applied Materials & Interfaces 2016, 8 (11), 7266–7273. 10.1021/acsami.6b01371. [DOI] [PubMed] [Google Scholar]
Suo H.; Guo C.; Zheng J.; Zhou B.; Ma C.; Zhao X.; Li T.; Guo P.; Goldys E. M. Sensitivity Modulation of Upconverting Thermometry through Engineering Phonon Energy of a Matrix. ACS Applied Materials & Interfaces 2016, 8 (44), 30312–30319. 10.1021/acsami.6b12176. [DOI] [PubMed] [Google Scholar]
Wang J.; Lin H.; Cheng Y.; Cui X.; Gao Y.; Ji Z.; Xu J.; Wang Y. A novel high-sensitive upconversion thermometry strategy: Utilizing synergistic effect of dual-wavelength lasers excitation to manipulate electron thermal distribution. Sensors and Actuators B: Chemical 2019, 278, 165–171. 10.1016/j.snb.2018.09.086. [DOI] [Google Scholar]
Wang Y.; Sun Y.; Xia Z. Energy Gap Linear Superposition of Thermally Coupled Levels toward Enhanced Relative Sensitivity of Ratiometric Thermometry. The Journal of Physical Chemistry Letters 2023, 14 (1), 178–182. 10.1021/acs.jpclett.2c03587. [DOI] [PubMed] [Google Scholar]
Pessoa A. R.; Galindo J. A. O.; Serge-Correales Y. E.; Amaral A. M.; Ribeiro S. J. L.; Menezes L. d. S. 2D Thermal Maps Using Hyperspectral Scanning of Single Upconverting Microcrystals: Experimental Artifacts and Image Processing. ACS Appl. Mater. Interfaces 2022, 14 (33), 38311–38319. 10.1021/acsami.2c08709. [DOI] [PubMed] [Google Scholar]
van Swieten T. P.; Meijerink A.; Rabouw F. T. Impact of Noise and Background on Measurement Uncertainties in Luminescence Thermometry. ACS Photonics 2022, 9 (4), 1366–1374. 10.1021/acsphotonics.2c00039. [DOI] [PMC free article] [PubMed] [Google Scholar]
Rocha U.; Jacinto da Silva C.; Ferreira Silva W.; Guedes I.; Benayas A.; Martínez Maestro L.; Acosta Elias M.; Bovero E.; van Veggel F. C. J. M.; García Solé J. A.; Jaque D. Subtissue Thermal Sensing Based on Neodymium-Doped LaF₃ Nanoparticles. ACS Nano 2013, 7 (2), 1188–1199. 10.1021/nn304373q. [DOI] [PubMed] [Google Scholar]
Kucsko G.; Maurer P. C.; Yao N. Y.; Kubo M.; Noh H. J.; Lo P. K.; Park H.; Lukin M. D. Nanometre-scale thermometry in a living cell. Nature 2013, 500, 54–58. 10.1038/nature12373. [DOI] [PMC free article] [PubMed] [Google Scholar]
Fujiwara M.; Shikano Y. Diamond quantum thermometry: from foundations to applications. Nanotechnology 2021, 32, 482002. 10.1088/1361-6528/ac1fb1. [DOI] [PubMed] [Google Scholar]
Sotoma S.; Zhong C.; Kah J. C. Y.; Yamashita H.; Plakhotnik T.; Harada Y.; Suzuki M. In situ measurements of intracellular thermal conductivity using heater-thermometer hybrid diamond nanosensors. Science Advances 2021, 7 (3), eabd7888 10.1126/sciadv.abd7888. [DOI] [PMC free article] [PubMed] [Google Scholar]
Acosta V. M.; Bauch E.; Ledbetter M. P.; Waxman A.; Bouchard L. S.; Budker D. Temperature Dependence of the Nitrogen-Vacancy Magnetic Resonance in Diamond. Phys. Rev. Lett. 2010, 104, 070801. 10.1103/PhysRevLett.104.070801. [DOI] [PubMed] [Google Scholar]
Doherty M. W.; Acosta V. M.; Jarmola A.; Barson M. S. J.; Manson N. B.; Budker D.; Hollenberg L. C. L. Temperature shifts of the resonances of the NV^– center in diamond. Physical Review B 2014, 90, 041201. 10.1103/PhysRevB.90.041201. [DOI] [Google Scholar]
Cambria M. C.; Thiering G.; Norambuena A.; Dinani H. T.; Gardill A.; Kemeny I.; Lordi V.; Gali A.; Maze J. R.; Kolkowitz S. Physically motivated analytical expression for the temperature dependence of the zero-field splitting of the nitrogen-vacancy center in diamond. Phys. Rev. B 2023, 108 (18), 102. 10.1103/PhysRevB.108.L180102. [DOI] [PubMed] [Google Scholar]
Neumann P.; Jakobi I.; Dolde F.; Burk C.; Reuter R.; Waldherr G.; Honert J.; Wolf T.; Brunner A.; Shim J. H.; et al. High-Precision Nanoscale Temperature Sensing Using Single Defects in Diamond. Nano Letters 2013, 13 (6), 2738–2742. 10.1021/nl401216y. [DOI] [PubMed] [Google Scholar]
Wang N.; Liu G.-Q.; Leong W.-H.; Zeng H.; Feng X.; Li S.-H.; Dolde F.; Fedder H.; Wrachtrup J.; Cui X.-D.; et al. Magnetic Criticality Enhanced Hybrid Nanodiamond Thermometer under Ambient Conditions. Physical Review X 2018, 8, 011042. 10.1103/PhysRevX.8.011042. [DOI] [Google Scholar]
Toyli D. M.; de las Casas C. F.; Christle D. J.; Dobrovitski V. V.; Awschalom D. D. Fluorescence thermometry enhanced by the quantum coherence of single spins in diamond. Proceedings of the National Academy of Sciences 2013, 110 (21), 8417–8421. 10.1073/pnas.1306825110. [DOI] [PMC free article] [PubMed] [Google Scholar]
Wang J.; Feng F.; Zhang J.; Chen J.; Zheng Z.; Guo L.; Zhang W.; Song X.; Guo G.; Fan L.; et al. High-sensitivity temperature sensing using an implanted single nitrogen-vacancy center array in diamond. Physical Review B 2015, 91, 155404. 10.1103/PhysRevB.91.155404. [DOI] [Google Scholar]
Toyli D. M.; Christle D. J.; Alkauskas A.; Buckley B. B.; Van de Walle C. G.; Awschalom D. D. Measurement and Control of Single Nitrogen-Vacancy Center Spins above 600 K. Physical Review X 2012, 2, 031001. 10.1103/PhysRevX.2.031001. [DOI] [Google Scholar]
Foy C.; Zhang L.; Trusheim M. E.; Bagnall K. R.; Walsh M.; Wang E. N.; Englund D. R. Wide-Field Magnetic Field and Temperature Imaging Using Nanoscale Quantum Sensors. ACS Applied Materials & Interfaces 2020, 12 (23), 26525–26533. 10.1021/acsami.0c01545. [DOI] [PubMed] [Google Scholar]
Shim J. H.; Lee S.-J.; Ghimire S.; Hwang J. I.; Lee K.-G.; Kim K.; Turner M. J.; Hart C. A.; Walsworth R. L.; Oh S. Multiplexed Sensing of Magnetic Field and Temperature in Real Time Using a Nitrogen-Vacancy Ensemble in Diamond. Physical Review Applied 2022, 17, 014009. 10.1103/PhysRevApplied.17.014009. [DOI] [Google Scholar]
Abrahams G. J.; Ellul E.; Robertson I. O.; Khalid A.; Greentree A. D.; Gibson B. C.; Tetienne J.-P. Handheld Device for Noncontact Thermometry via Optically Detected Magnetic Resonance of Proximate Diamond Sensors. Physical Review Applied 2023, 19, 054076. 10.1103/PhysRevApplied.19.054076. [DOI] [Google Scholar]
Plakhotnik T.; Doherty M. W.; Cole J. H.; Chapman R.; Manson N. B. All-Optical Thermometry and Thermal Properties of the Optically Detected Spin Resonances of the NV- Center in Nanodiamond. Nano Letters 2014, 14 (9), 4989–4996. 10.1021/nl501841d. [DOI] [PubMed] [Google Scholar]
Plakhotnik T.; Aman H.; Chang H.-C. All-optical single-nanoparticle ratiometric thermometry with a noise floor of 0.3 K Hz^–1/2. Nanotechnology 2015, 26, 245501. 10.1088/0957-4484/26/24/245501. [DOI] [PubMed] [Google Scholar]
Bommidi D. K.; Pickel A. D. Temperature-dependent excited state lifetimes of nitrogen vacancy centers in individual nanodiamonds. Appl. Phys. Lett. 2021, 119, 254103. 10.1063/5.0072357. [DOI] [Google Scholar]
Plakhotnik T.; Gruber D. Luminescence of nitrogen-vacancy centers in nanodiamonds at temperatures between 300 and 700 K: perspectives on nanothermometry. Phys. Chem. Chem. Phys. 2010, 12, 9751–9756. 10.1039/c001132k. [DOI] [PubMed] [Google Scholar]
Anisimov A. N.; Simin D.; Soltamov V. A.; Lebedev S. P.; Baranov P. G.; Astakhov G. V.; Dyakonov V. Optical thermometry based on level anticrossing in silicon carbide. Scientific Reports 2016, 6, 33301. 10.1038/srep33301. [DOI] [PMC free article] [PubMed] [Google Scholar]
Choi S.; Agafonov V. N.; Davydov V. A.; Plakhotnik T. Ultrasensitive All-Optical Thermometry Using Nanodiamonds with a High Concentration of Silicon-Vacancy Centers and Multiparametric Data Analysis. ACS Photonics 2019, 6 (6), 1387–1392. 10.1021/acsphotonics.9b00468. [DOI] [Google Scholar]
Fujiwara M.; Uchida G.; Ohki I.; Liu M.; Tsurui A.; Yoshikawa T.; Nishikawa M.; Mizuochi N. All-optical nanoscale thermometry based on silicon-vacancy centers in detonation nanodiamonds. Carbon 2022, 198, 57–62. 10.1016/j.carbon.2022.06.076. [DOI] [Google Scholar]
Nguyen C. T.; Evans R. E.; Sipahigil A.; Bhaskar M. K.; Sukachev D. D.; Agafonov V. N.; Davydov V. A.; Kulikova L. F.; Jelezko F.; Lukin M. D. All-optical nanoscale thermometry with silicon-vacancy centers in diamond. Appl. Phys. Lett. 2018, 112, 203102. 10.1063/1.5029904. [DOI] [Google Scholar]
Zhang J.; He H.; Zhang T.; Wang L.; Gupta M.; Jing J.; Wang Z.; Wang Q.; Li K. H.; Wong K. K.-Y.; Chu Z. Two-Photon Excitation of Silicon-Vacancy Centers in Nanodiamonds for All-Optical Thermometry with a Noise Floor of 6.6 mK·Hz^–-1/2. The Journal of Physical Chemistry C 2023, 127 (6), 3013–3019. 10.1021/acs.jpcc.2c06966. [DOI] [Google Scholar]
Fan J.-W.; Cojocaru I.; Becker J.; Fedotov I. V.; Alkahtani M. H. A.; Alajlan A.; Blakley S.; Rezaee M.; Lyamkina A.; Palyanov Y. N.; et al. Germanium-Vacancy Color Center in Diamond as a Temperature Sensor. ACS Photonics 2018, 5 (3), 765–770. 10.1021/acsphotonics.7b01465. [DOI] [Google Scholar]
Tran T. T.; Regan B.; Ekimov E. A.; Mu Z.; Zhou Y.; Gao W.-b.; Narang P.; Solntsev A. S.; Toth M.; Aharonovich I.; Bradac C. Anti-Stokes excitation of solid-state quantum emitters for nanoscale thermometry. Science Advances 2019, 5 (5), eaav9180 10.1126/sciadv.aav9180. [DOI] [PMC free article] [PubMed] [Google Scholar]
Osmic E.; Pezzagna S.; Lühmann T.; Böhlmann W.; Meijer J. Unusual temperature dependence of the photoluminescence emission of MgV centers in diamond. Appl. Phys. Lett. 2022, 121, 084101. 10.1063/5.0100409. [DOI] [Google Scholar]
Alkahtani M.; Cojocaru I.; Liu X.; Herzig T.; Meijer J.; Küpper J.; Lühmann T.; Akimov A. V.; Hemmer P. R. Tin-vacancy in diamonds for luminescent thermometry. Appl. Phys. Lett. 2018, 112, 241902. 10.1063/1.5037053. [DOI] [Google Scholar]
Chern M.; Kays J. C.; Bhuckory S.; Dennis A. M. Sensing with photoluminescent semiconductor quantum dots. Methods and Applications in Fluorescence 2019, 7, 012005. 10.1088/2050-6120/aaf6f8. [DOI] [PMC free article] [PubMed] [Google Scholar]
Conceição P.; Barata J. F. B.; Hernández-Rodríguez M. A.; Lacerda P. S. S.; Neves M. G. P. M. S.; Carlos L. D.; Trindade T. Ratiometric nanothermometry via porphyrin inner filter effect applied to colloidal ZnS quantum dots. Sensors and Actuators A: Physical 2023, 357, 114382. 10.1016/j.sna.2023.114382. [DOI] [Google Scholar]
Kumbhakar P.; Roy Karmakar A.; Das G. P.; Chakraborty J.; Tiwary C. S.; Kumbhakar P. Reversible temperature-dependent photoluminescence in semiconductor quantum dots for the development of a smartphone-based optical thermometer. Nanoscale 2021, 13 (5), 2946–2954. 10.1039/D0NR07874C. [DOI] [PubMed] [Google Scholar]
Zhao H.; Vomiero A.; Rosei F. Tailoring the Heterostructure of Colloidal Quantum Dots for Ratiometric Optical Nanothermometry. Small 2020, 16 (28), 2000804. 10.1002/smll.202000804. [DOI] [PubMed] [Google Scholar]
Lewis C.; Erikson J. W.; Sanchez D. A.; McClure C. E.; Nordin G. P.; Munro T. R.; Colton J. S. Use of Machine Learning with Temporal Photoluminescence Signals from CdTe Quantum Dots for Temperature Measurement in Microfluidic Devices. ACS Applied Nano Materials 2020, 3 (5), 4045–4053. 10.1021/acsanm.0c00065. [DOI] [PMC free article] [PubMed] [Google Scholar]
Li S.; Zhang K.; Yang J.-M.; Lin L.; Yang H. Single Quantum Dots as Local Temperature Markers. Nano Letters 2007, 7 (10), 3102–3105. 10.1021/nl071606p. [DOI] [PubMed] [Google Scholar]
Maestro L. M.; Haro-González P.; Sánchez-Iglesias A.; Liz-Marzán L. M.; García Solé J.; Jaque D. Quantum Dot Thermometry Evaluation of Geometry Dependent Heating Efficiency in Gold Nanoparticles. Langmuir 2014, 30 (6), 1650–1658. 10.1021/la403435v. [DOI] [PubMed] [Google Scholar]
Munro T.; Liu L.; Glorieux C.; Ban H. CdSe/ZnS quantum dot fluorescence spectra shape-based thermometry via neural network reconstruction. J. Appl. Phys. 2016, 119, 214903. 10.1063/1.4953223. [DOI] [Google Scholar]
Maestro L. M.; Jacinto C.; Silva U. R.; Vetrone F.; Capobianco J. A.; Jaque D.; Solé J. G. CdTe Quantum Dots as Nanothermometers: Towards Highly Sensitive Thermal Imaging. Small 2011, 7 (13), 1774–1778. 10.1002/smll.201002377. [DOI] [PubMed] [Google Scholar]
Öner B.; Pomeroy J. W.; Kuball M. Submicrometer Resolution Hyperspectral Quantum Rod Thermal Imaging of Microelectronic Devices. ACS Applied Electronic Materials 2020, 2 (1), 93–102. 10.1021/acsaelm.9b00575. [DOI] [Google Scholar]
Han Y.; Liu Y.; Zhao H.; Vomiero A.; Li R. Highly efficient ratiometric nanothermometers based on colloidal carbon quantum dots. Journal of Materials Chemistry B 2021, 9 (20), 4111–4119. 10.1039/D1TB00224D. [DOI] [PubMed] [Google Scholar]
Sehrawat P.; Abid; Islam S. S. An ultrafast quantum thermometer from graphene quantum dots. Nanoscale Advances 2019, 1 (5), 1772–1783. 10.1039/C8NA00361K. [DOI] [PMC free article] [PubMed] [Google Scholar]
Wang C.; Hu T.; Thomas T.; Song S.; Wen Z.; Wang C.; Song Q.; Yang M. Surface state-controlled C-dot/C-dot based dual-emission fluorescent nanothermometers for intra-cellular thermometry. Nanoscale 2018, 10 (46), 21809–21817. 10.1039/C8NR07445C. [DOI] [PubMed] [Google Scholar]
Fanizza E.; Zhao H.; De Zio S.; Depalo N.; Rosei F.; Vomiero A.; Curri M. L.; Striccoli M. Encapsulation of Dual Emitting Giant Quantum Dots in Silica Nanoparticles for Optical Ratiometric Temperature Nanosensors. Applied Sciences 2020, 10, 2767. 10.3390/app10082767. [DOI] [Google Scholar]
Liu J.; Zhang H.; Selopal G. S.; Sun S.; Zhao H.; Rosei F. Visible and Near-Infrared, Multiparametric, Ultrasensitive Nanothermometer Based on Dual-Emission Colloidal Quantum Dots. ACS Photonics 2019, 6 (10), 2479–2486. 10.1021/acsphotonics.9b00763. [DOI] [Google Scholar]
Liu W.; Zhang Y.; Wu H.; Feng Y.; Zhang T.; Gao W.; Chu H.; Yin J.; Cui T.; Wang Y.; et al. Planar temperature sensing using heavy-metal-free quantum dots with micrometer resolution. Nanotechnology 2014, 25, 285501. 10.1088/0957-4484/25/28/285501. [DOI] [PubMed] [Google Scholar]
Lin X.; Kong M.; Wu N.; Gu Y.; Qiu X.; Chen X.; Li Z.; Feng W.; Li F. Measurement of Temperature Distribution at the Nanoscale with Luminescent Probes Based on Lanthanide Nanoparticles and Quantum Dots. ACS Applied Materials & Interfaces 2020, 12 (47), 52393–52401. 10.1021/acsami.0c15697. [DOI] [PubMed] [Google Scholar]
Qiu X.; Zhou Q.; Zhu X.; Wu Z.; Feng W.; Li F. Ratiometric upconversion nanothermometry with dual emission at the same wavelength decoded via a time-resolved technique. Nature Communications 2020, 11, 4. 10.1038/s41467-019-13796-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
Cao S.; Zheng J.; Zhao J.; Yang Z.; Shang M.; Li C.; Yang W.; Fang X. Robust and Stable Ratiometric Temperature Sensor Based on Zn-In-S Quantum Dots with Intrinsic Dual-Dopant Ion Emissions. Advanced Functional Materials 2016, 26 (40), 7224–7233. 10.1002/adfm.201603201. [DOI] [Google Scholar]
Marciniak L.; Kniec K.; Elżbieciak-Piecka K.; Trejgis K.; Stefanska J.; Dramićanin M. Luminescence thermometry with transition metal ions. A review. Coord. Chem. Rev. 2022, 469, 214671. 10.1016/j.ccr.2022.214671. [DOI] [Google Scholar]
Kniec K.; Ledwa K.; Maciejewska K.; Marciniak L. Intentional modification of the optical spectral response and relative sensitivity of luminescent thermometers based on Fe³⁺,Cr³⁺,Nd³⁺ co-doped garnet nanocrystals by crystal field strength optimization. Materials Chemistry Frontiers 2020, 4 (6), 1697–1705. 10.1039/D0QM00097C. [DOI] [Google Scholar]
Qin Y.; Zhong F.; Bian Y.; Hariyani S.; Cao Y.; Brgoch J.; Seto T.; Brik M. G.; Srivastava A. M.; Wang X.; Wang Y. Sensitive and Reliable Fluorescent Thermometer Based on a Red-Emitting Li2MgHfO4:Mn4+ Phosphor. Inorganic Chemistry 2022, 61 (21), 8126–8134. 10.1021/acs.inorgchem.1c03971. [DOI] [PubMed] [Google Scholar]
Wang Q.; Liao M.; Mu Z.; Zhang X.; Dong H.; Liang Z.; Luo J.; Yang Y.; Wu F. Ratiometric Optical Thermometer with High Sensitivity Based on Site-Selective Occupancy of Mn2+ Ions in Li5Zn8Al5Ge9O36 under Controllable Synthesis Atmosphere. The Journal of Physical Chemistry C 2020, 124 (1), 886–895. 10.1021/acs.jpcc.9b09379. [DOI] [Google Scholar]
Back M.; Ueda J.; Brik M. G.; Tanabe S. Pushing the Limit of Boltzmann Distribution in Cr³⁺-Doped CaHfO₃ for Cryogenic Thermometry. ACS Applied Materials & Interfaces 2020, 12 (34), 38325–38332. 10.1021/acsami.0c08965. [DOI] [PubMed] [Google Scholar]
Glais E.; Pellerin M.; Castaing V.; Alloyeau D.; Touati N.; Viana B.; Chanéac C. Luminescence properties of ZnGa₂O₄:Cr³⁺,Bi³⁺ nanophosphors for thermometry applications. RSC Advances 2018, 8 (73), 41767–41774. 10.1039/C8RA08182D. [DOI] [PMC free article] [PubMed] [Google Scholar]
Kabański A.; Ptak M.; Stefańska D. Metal-Organic Framework Optical Thermometer Based on Cr³⁺ Ion Luminescence. ACS Applied Materials & Interfaces 2023, 15 (5), 7074–7082. 10.1021/acsami.2c19957. [DOI] [PMC free article] [PubMed] [Google Scholar]
Pflitsch C.; Viefhaus D.; Atakan B. CVD of Thin Ruby Films on Si(100) and Stainless Steel for Surface Temperature Sensor Applications. Chemical Vapor Deposition 2007, 13 (8), 420–426. 10.1002/cvde.200606564. [DOI] [Google Scholar]
Ueda J.; Back M.; Brik M. G.; Zhuang Y.; Grinberg M.; Tanabe S. Ratiometric optical thermometry using deep red luminescence from ⁴T₂ and ²E states of Cr³⁺ in ZnGa₂O₄ host. Optical Materials 2018, 85, 510–516. 10.1016/j.optmat.2018.09.013. [DOI] [Google Scholar]
Glais E.; Đorđević V.; Papan J.; Viana B.; Dramićanin M. D. MgTiO₃:Mn⁴⁺ a multi-reading temperature nanoprobe. RSC Advances 2018, 8 (33), 18341–18346. 10.1039/C8RA02482K. [DOI] [PMC free article] [PubMed] [Google Scholar]
Qin T.; Liu B.; Zhu K.; Luo Z.; Huang Y.; Pan C.; Wang L. Organic fluorescent thermometers: Highlights from 2013 to 2017. Trends in Analytical Chemistry 2018, 102, 259–271. 10.1016/j.trac.2018.03.003. [DOI] [Google Scholar]
Jung W.; Kim Y. W.; Yim D.; Yoo J. Y. Microscale surface thermometry using SU8/Rhodamine-B thin layer. Sensors and Actuators A: Physical 2011, 171, 228–232. 10.1016/j.sna.2011.06.025. [DOI] [Google Scholar]
Ross D.; Gaitan M.; Locascio L. E. Temperature Measurement in Microfluidic Systems Using a Temperature-Dependent Fluorescent Dye. Anal. Chem. 2001, 73 (17), 4117–4123. 10.1021/ac010370l. [DOI] [PubMed] [Google Scholar]
Benninger R. K. P.; Koç Y.; Hofmann O.; Requejo-Isidro J.; Neil M. A. A.; French P. M. W.; deMello A. J. Quantitative 3D Mapping of Fluidic Temperatures within Microchannel Networks Using Fluorescence Lifetime Imaging. Anal. Chem. 2006, 78 (7), 2272–2278. 10.1021/ac051990f. [DOI] [PubMed] [Google Scholar]
Cai H.; Lu W.; Yang C.; Zhang M.; Li M.; Che C.-M.; Li D. Tandem Förster Resonance Energy Transfer Induced Luminescent Ratiometric Thermometry in Dye-Encapsulated Biological Metal-Organic Frameworks. Advanced Optical Materials 2019, 7 (2), 1801149. 10.1002/adom.201801149. [DOI] [Google Scholar]
Huang Z.; Li N.; Zhang X.; Xiao Y. Mitochondria-Anchored Molecular Thermometer Quantitatively Monitoring Cellular Inflammations. Anal. Chem. 2021, 93 (12), 5081–5088. 10.1021/acs.analchem.0c04547. [DOI] [PubMed] [Google Scholar]
Cao C.; Liu X.; Qiao Q.; Zhao M.; Yin W.; Mao D.; Zhang H.; Xu Z. A twisted-intramolecular-charge-transfer (TICT) based ratiometric fluorescent thermometer with a mega-Stokes shift and a positive temperature coefficient. Chemical Communications 2014, 50 (99), 15811–15814. 10.1039/C4CC08010F. [DOI] [PubMed] [Google Scholar]
Ebert S.; Travis K.; Lincoln B.; Guck J. Fluorescence ratio thermometry in a microfluidic dual-beam laser trap. Opt. Express 2007, 15 (23), 15493–15499. 10.1364/OE.15.015493. [DOI] [PubMed] [Google Scholar]
Fogg D.; David M.; Goodson K. Non-invasive measurement of void fraction and liquid temperature in microchannel flow boiling. Experiments in Fluids 2009, 46, 725–736. 10.1007/s00348-008-0604-3. [DOI] [Google Scholar]
Natrajan V. K.; Christensen K. T. Two-color laser-induced fluorescent thermometry for microfluidic systems. Measurement Science and Technology 2009, 20, 015401. 10.1088/0957-0233/20/1/015401. [DOI] [Google Scholar]
Nakano M.; Arai Y.; Kotera I.; Okabe K.; Kamei Y.; Nagai T. Genetically encoded ratiometric fluorescent thermometer with wide range and rapid response. PLOS ONE 2017, 12 (2), e0172344 10.1371/journal.pone.0172344. [DOI] [PMC free article] [PubMed] [Google Scholar]
Gong M.; Li Z.; Wang Q.; Xiang W.; Xia T.; Zhao D. Encapsulating Rhodamine B in the NbO-type metal-organic framework to construct dual-emitting ratiometric thermometer. J. Solid State Chem. 2022, 311, 123147. 10.1016/j.jssc.2022.123147. [DOI] [Google Scholar]
Peng M.; Kaczmarek A. M.; Van Hecke K. Ratiometric Thermometers Based on Rhodamine B and Fluorescein Dye-Incorporated (Nano) Cyclodextrin Metal-Organic Frameworks. ACS Applied Materials & Interfaces 2022, 14 (12), 14367–14379. 10.1021/acsami.2c01332. [DOI] [PubMed] [Google Scholar]
Zhang H.; Lin C.; Sheng T.; Hu S.; Zhuo C.; Fu R.; Wen Y.; Li H.; Su S.; Wu X. A Luminescent Metal-Organic Framework Thermometer with Intrinsic Dual Emission from Organic Lumophores. Chem.-Eur. J. 2016, 22 (13), 4460–4468. 10.1002/chem.201504432. [DOI] [PubMed] [Google Scholar]
Wan Y.; Yu L.; Xia T. A dye-loaded nonlinear metal-organic framework as self-calibrated optical thermometer. Dyes and Pigments 2022, 202, 110234. 10.1016/j.dyepig.2022.110234. [DOI] [Google Scholar]
Kaczmarek A. M.; Suta M.; Rijckaert H.; van Swieten T. P.; Van Driessche I.; Kaczmarek M. K.; Meijerink A. High temperature (nano)thermometers based on LiLuF₄:Er³⁺,Yb³⁺ nano- and microcrystals. Confounded results for core-shell nanocrystals. Journal of Materials Chemistry C 2021, 9 (10), 3589–3600. 10.1039/D0TC05865C. [DOI] [Google Scholar]
Geitenbeek R. G.; Prins P. T.; Albrecht W.; van Blaaderen A.; Weckhuysen B. M.; Meijerink A. NaYF4:Er³⁺,Yb³⁺/SiO₂ Core/Shell Upconverting Nanocrystals for Luminescence Thermometry up to 900 K. The Journal of Physical Chemistry C 2017, 121 (6), 3503–3510. 10.1021/acs.jpcc.6b10279. [DOI] [PMC free article] [PubMed] [Google Scholar]
Yuan M.; Han K.; Wang L.; Yang X.; Yang Z.; Wang H.; Xu X. Highly thermally stable upconversion in copper(II)-doped LiYF₄:Yb,Er microcrystals toward ultrahigh temperature (micro)thermometers. J. Alloys Compd. 2022, 919, 165844. 10.1016/j.jallcom.2022.165844. [DOI] [Google Scholar]
Li H.; Wang S.; Pang R.; Jiang L.; Li D.; Zhang S.; Li C.; Zhang H. Pr³⁺ doped Y₃GaO₆ luminescent thermometer for high temperature conditions. Mater. Res. Bull. 2023, 165, 112297. 10.1016/j.materresbull.2023.112297. [DOI] [Google Scholar]
Chen Y.; White S.; Ekimov E. A.; Bradac C.; Toth M.; Aharonovich I.; Tran T. T. Ultralow-Power Cryogenic Thermometry Based on Optical-Transition Broadening of a Two-Level System in Diamond. ACS Photonics 2023, 10 (8), 2481–2487. 10.1021/acsphotonics.2c01622. [DOI] [Google Scholar]
Liu X.; Akerboom S.; Jong M. d.; Mutikainen I.; Tanase S.; Meijerink A.; Bouwman E. Mixed-Lanthanoid Metal-Organic Framework for Ratiometric Cryogenic Temperature Sensing. Inorganic Chemistry 2015, 54 (23), 11323–11329. 10.1021/acs.inorgchem.5b01924. [DOI] [PubMed] [Google Scholar]
N’Dala-Louika I.; Ananias D.; Latouche C.; Dessapt R.; Carlos L. D.; Serier-Brault H. Ratiometric mixed Eu-Tb metal-organic framework as a new cryogenic luminescent thermometer. Journal of Materials Chemistry C 2017, 5 (42), 10933–10937. 10.1039/C7TC03223D. [DOI] [Google Scholar]
Fukami M.; Yale C. G.; Andrich P.; Liu X.; Heremans F. J.; Nealey P. F.; Awschalom D. D. All-Optical Cryogenic Thermometry Based on Nitrogen-Vacancy Centers in Nanodiamonds. Physical Review Applied 2019, 12, 014042. 10.1103/PhysRevApplied.12.014042. [DOI] [Google Scholar]
Zhao D.; Yue D.; Zhang L.; Jiang K.; Qian G. Cryogenic Luminescent Tb/Eu-MOF Thermometer Based on a Fluorine-Modified Tetracarboxylate Ligand. Inorganic Chemistry 2018, 57 (20), 12596–12602. 10.1021/acs.inorgchem.8b01746. [DOI] [PubMed] [Google Scholar]
Pavani K.; Neves A. J.; Pinto R. J. B.; Freire C. S. R.; Soares M. J.; Graça M. P. F.; Kumar K. U.; Jakka S. K. BiLaWO₆: Er³⁺/Tm³⁺/Yb³⁺ phosphor: Study of multiple fluorescence intensity ratiometric thermometry at cryogenic temperatures. Ceram. Int. 2022, 48 (21), 31344–31353. 10.1016/j.ceramint.2022.06.316. [DOI] [Google Scholar]
Li H.; Wu H.; Pang R.; Liu G.; Zhang S.; Jiang L.; Li D.; Li C.; Feng J.; Zhang H. Investigation on the photoluminescence and thermoluminescence of BaGa₂O₄:Bi³⁺ at extremely low temperatures. Journal of Materials Chemistry C 2021, 9 (5), 1786–1793. 10.1039/D0TC05122E. [DOI] [Google Scholar]
Ren M.; Brites C. D. S.; Bao S.-S.; Ferreira R. A. S.; Zheng L.-M.; Carlos L. D. A cryogenic luminescent ratiometric thermometer based on a lanthanide phosphonate dimer. Journal of Materials Chemistry C 2015, 3 (33), 8480–8484. 10.1039/C5TC01468A. [DOI] [Google Scholar]
Cui Y.; Zou W.; Song R.; Yu J.; Zhang W.; Yang Y.; Qian G. A ratiometric and colorimetric luminescent thermometer over a wide temperature range based on a lanthanide coordination polymer. Chemical Communications 2014, 50 (6), 719–721. 10.1039/C3CC47225F. [DOI] [PubMed] [Google Scholar]
Bolek P.; Zeler J.; Brites C. D. S.; Trojan-Piegza J.; Carlos L. D.; Zych E. Ga-modified YAG:Pr³⁺ dual-mode tunable luminescence thermometers. Chemical Engineering Journal 2021, 421, 129764. 10.1016/j.cej.2021.129764. [DOI] [Google Scholar]
Liang Z.; Wu J.; Cui Y.; Sun H.; Ning C.-Z. Self-optimized single-nanowire photoluminescence thermometry. Light: Science & Applications 2023, 12, 36. 10.1038/s41377-023-01070-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
Casar J. R.; McLellan C. A.; Siefe C.; Dionne J. A. Lanthanide-Based Nanosensors: Refining Nanoparticle Responsiveness for Single Particle Imaging of Stimuli. ACS Photonics 2021, 8 (1), 3–17. 10.1021/acsphotonics.0c00894. [DOI] [PMC free article] [PubMed] [Google Scholar]
Zhou J.; Chizhik A. I.; Chu S.; Jin D. Single-particle spectroscopy for functional nanomaterials. Nature 2020, 579, 41–50. 10.1038/s41586-020-2048-8. [DOI] [PubMed] [Google Scholar]
de Oliveira Lima K.; dos Santos L. F.; Galvão R.; Tedesco A. C.; de Souza Menezes L.; Gonçalves R. R. Single Er³⁺, Yb³⁺: KGd₃F₁₀ Nanoparticles for Nanothermometry. Frontiers in Chemistry 2021, 9, 712659.Original Research. 10.3389/fchem.2021.712659. [DOI] [PMC free article] [PubMed] [Google Scholar]
Xie W.; Gomes R.; Aubert T.; Bisschop S.; Zhu Y.; Hens Z.; Brainis E.; Van Thourhout D. Nanoscale and Single-Dot Patterning of Colloidal Quantum Dots. Nano Letters 2015, 15 (11), 7481–7487. 10.1021/acs.nanolett.5b03068. [DOI] [PubMed] [Google Scholar]
Fringes S.; Schwemmer C.; Rawlings C. D.; Knoll A. W. Deterministic Deposition of Nanoparticles with Sub-10 nm Resolution. Nano Letters 2019, 19 (12), 8855–8861. 10.1021/acs.nanolett.9b03687. [DOI] [PubMed] [Google Scholar]
Laraoui A.; Aycock-Rizzo H.; Gao Y.; Lu X.; Riedo E.; Meriles C. A. Imaging thermal conductivity with nanoscale resolution using a scanning spin probe. Nature Communications 2015, 6, 8954. 10.1038/ncomms9954. [DOI] [PMC free article] [PubMed] [Google Scholar]
Zimmers A.; Aigouy L.; Mortier M.; Sharoni A.; Wang S.; West K. G.; Ramirez J. G.; Schuller I. K. Role of Thermal Heating on the Voltage Induced Insulator-Metal Transition in VO₂. Phys. Rev. Lett. 2013, 110, 056601. 10.1103/PhysRevLett.110.056601. [DOI] [PubMed] [Google Scholar]
Pessoa A. R.; Galindo J. A. O.; dos Santos L. F.; Goncalves R. R.; Maier S. A.; Menezes L. d. S.; Amaral A. M. Correction Due to Nonthermally Coupled Emission Bands and Its Implications on the Performance of Y₂O₃:Yb³⁺ /Er³⁺ Single-Particle Thermometers. J. Phys. Chem. C 2023, 127 (20), 9673–9680. 10.1021/acs.jpcc.3c00522. [DOI] [Google Scholar]
Avram D.; Porosnicu I.; Patrascu A.; Tiseanu C. Real-Time Thermal Imaging based on the Simultaneous Rise and Decay Luminescence Lifetime Thermometry. Advanced Photonics Research 2022, 3 (6), 2100208. 10.1002/adpr.202100208. [DOI] [Google Scholar]
Rafiei Miandashti A.; Kordesch M. E.; Richardson H. H. Effect of Temperature and Gold Nanoparticle Interaction on the Lifetime and Luminescence of NaYF4:Yb³⁺:Er³⁺ Upconverting Nanoparticles. ACS Photonics 2017, 4 (7), 1864–1869. 10.1021/acsphotonics.7b00512. [DOI] [Google Scholar]
Savchuk O. A.; Haro-González P.; Carvajal J. J.; Jaque D.; Massons J.; Aguiló M.; Díaz F. Er:Yb:NaY₂F₅O up-converting nanoparticles for sub-tissue fluorescence lifetime thermal sensing. Nanoscale 2014, 6 (16), 9727–9733. 10.1039/C4NR02305F. [DOI] [PubMed] [Google Scholar]
Zhou X.; Xia X.; Smith B. E.; Lim M. B.; Bard A. B.; Pant A.; Pauzauskie P. J. Interface-Dependent Radiative Lifetimes of Yb³⁺, Er³⁺ Co-doped Single NaYF₄ Upconversion Nanowires. ACS Applied Materials & Interfaces 2019, 11 (25), 22817–22823. 10.1021/acsami.8b17271. [DOI] [PubMed] [Google Scholar]
Jiang Y.; Tong Y.; Chen S.; Zhang W.; Hu F.; Wei R.; Guo H. A three-mode self-referenced optical thermometry based on up-conversion luminescence of Ca₂MgWO₆:Er³⁺,Yb³⁺ phosphors. Chemical Engineering Journal 2021, 413, 127470. 10.1016/j.cej.2020.127470. [DOI] [Google Scholar]
Savchuk O. A.; Carvajal J. J.; Pujol M. C.; Massons J.; Haro-González P.; Martínez O.; Jiménez J.; Aguiló M.; Díaz F. New strategies invonving upconverting nanoparticles for determining moderate temperatures by luminescence thermometry. J. Lumin. 2016, 169, 711–716. 10.1016/j.jlumin.2015.05.016. [DOI] [Google Scholar]
Raab M. E.; Maurizio S. L.; Capobianco J. A.; Prasad P. N. Lifetime of the ³H₄ Electronic State in Tm³⁺-Doped Upconverting Nanoparticles for NIR Nanothermometry. The Journal of Physical Chemistry B 2021, 125 (48), 13132–13136. 10.1021/acs.jpcb.1c07659. [DOI] [PubMed] [Google Scholar]
Marciniak L.; Trejgis K. Luminescence lifetime thermometry with Mn³⁺-Mn⁴⁺ co-doped nanocrystals. Journal of Materials Chemistry C 2018, 6 (26), 7092–7100. 10.1039/C8TC01981A. [DOI] [Google Scholar]
Haro-González P.; Martínez-Maestro L.; Martín I. R.; García-Solé J.; Jaque D. High-Sensitivity Fluorescence Lifetime Thermal Sensing Based on CdTe Quantum Dots. Small 2012, 8 (17), 2652–2658. 10.1002/smll.201102736. [DOI] [PubMed] [Google Scholar]
Yakunin S.; Benin B. M.; Shynkarenko Y.; Nazarenko O.; Bodnarchuk M. I.; Dirin D. N.; Hofer C.; Cattaneo S.; Kovalenko M. V. High-resolution remote thermometry and thermography using luminescent low-dimensional tin-halide perovskites. Nat. Mater. 2019, 18, 846–852. 10.1038/s41563-019-0416-2. [DOI] [PubMed] [Google Scholar]
Li G.; Chen X.; Wang M.; Cheng S.; Yang D.; Wu D.; Han Y.; Jia M.; Li X.; Zhang Y.; et al. Regulating Exciton De-trapping of Te⁴⁺-doped Zero-Dimensional Scandium-Halide Perovskite for Fluorescence Thermometry with Record High Time-Resolved Thermal Sensitivity. Adv. Mater. 2023, 35, 2305495. 10.1002/adma.202305495. [DOI] [PubMed] [Google Scholar]
Caixeta F. J.; Bastos A. R. N.; Botas A. M. P.; Rosa L. S.; Souza V. S.; Borges F. H.; Neto A. N. C.; Ferrier A.; Goldner P.; Carlos L. D.; et al. High-Quantum-Yield Upconverting Er³⁺/Yb³⁺-Organic-Inorganic Hybrid Dual Coatings for Real-Time Temperature Sensing and Photothermal Conversion. The Journal of Physical Chemistry C 2020, 124 (37), 19892–19903. 10.1021/acs.jpcc.0c03874. [DOI] [Google Scholar]
Chen Y.; Li C.; Yang T.; Ekimov E. A.; Bradac C.; Ha S. T.; Toth M.; Aharonovich I.; Tran T. T. Real-Time Ratiometric Optical Nanoscale Thermometry. ACS Nano 2023, 17 (3), 2725–2736. 10.1021/acsnano.2c10974. [DOI] [PubMed] [Google Scholar]
Piñol R.; Brites C. D. S.; Bustamante R.; Martínez A.; Silva N. J. O.; Murillo J. L.; Cases R.; Carrey J.; Estepa C.; Sosa C.; et al. Joining Time-Resolved Thermometry and Magnetic-Induced Heating in a Single Nanoparticle Unveils Intriguing Thermal Properties. ACS Nano 2015, 9 (3), 3134–3142. 10.1021/acsnano.5b00059. [DOI] [PubMed] [Google Scholar]
Xiang G.; Xia Q.; Liu X.; Wang Y.; Jiang S.; Li L.; Zhou X.; Ma L.; Wang X.; Zhang J. Upconversion nanoparticles modified by Cu₂S for photothermal therapy along with real-time optical thermometry. Nanoscale 2021, 13 (15), 7161–7168. 10.1039/D0NR09115D. [DOI] [PubMed] [Google Scholar]
Rafiei Miandashti A.; Khosravi Khorashad L.; Govorov A. O.; Kordesch M. E.; Richardson H. H. Time-Resolved Temperature-Jump Measurements and Theoretical Simulations of Nanoscale Heat Transfer Using NaYF₄:Yb³⁺:Er³⁺ Upconverting Nanoparticles. The Journal of Physical Chemistry C 2019, 123 (6), 3770–3780. 10.1021/acs.jpcc.8b11215. [DOI] [Google Scholar]
Tzeng Y.-K.; Tsai P.-C.; Liu H.-Y.; Chen O. Y.; Hsu H.; Yee F.-G.; Chang M.-S.; Chang H.-C. Time-Resolved Luminescence Nanothermometry with Nitrogen-Vacancy Centers in Nanodiamonds. Nano Letters 2015, 15 (6), 3945–3952. 10.1021/acs.nanolett.5b00836. [DOI] [PubMed] [Google Scholar]
Yun J.; Kim K.; Park S.; Kim D. Temperature Selective Thermometry with Sub-Microsecond Time Resolution Using Dressed-Spin States in Diamond. Advanced Quantum Technologies 2021, 4 (11), 2100084. 10.1002/qute.202100084. [DOI] [Google Scholar]
Löw P.; Kim B.; Takama N.; Bergaud C. High-Spatial-Resolution Surface-Temperature Mapping Using Fluorescent Thermometry. Small 2008, 4 (7), 908–914. 10.1002/smll.200700581. [DOI] [PubMed] [Google Scholar]
Hui Y. Y.; Chen O. Y.; Azuma T.; Chang B.-M.; Hsieh F.-J.; Chang H.-C. All-Optical Thermometry with Nitrogen-Vacancy Centers in Nanodiamond-Embedded Polymer Films. The Journal of Physical Chemistry C 2019, 123 (24), 15366–15374. 10.1021/acs.jpcc.9b04496. [DOI] [Google Scholar]
Chen Y.; Tran T. N.; Duong N. M. H.; Li C.; Toth M.; Bradac C.; Aharonovich I.; Solntsev A.; Tran T. T. Optical Thermometry with Quantum Emitters in Hexagonal Boron Nitride. ACS Applied Materials & Interfaces 2020, 12 (22), 25464–25470. 10.1021/acsami.0c05735. [DOI] [PubMed] [Google Scholar]
Mi C.; Zhou J.; Wang F.; Lin G.; Jin D. Ultrasensitive Ratiometric Nanothermometer with Large Dynamic Range and Photostability. Chem. Mater. 2019, 31 (22), 9480–9487. 10.1021/acs.chemmater.9b03466. [DOI] [Google Scholar]
Brites C. D. S.; Lima P. P.; Silva N. J. O.; Millán A.; Amaral V. S.; Palacio F.; Carlos L. D. A Luminescent Molecular Thermometer for Long-Term Absolute Temperature Measurements at the Nanoscale. Adv. Mater. 2010, 22 (40), 4499–4504. 10.1002/adma.201001780. [DOI] [PubMed] [Google Scholar]
Andrich P.; Li J.; Liu X.; Heremans F. J.; Nealey P. F.; Awschalom D. D. Microscale-Resolution Thermal Mapping Using a Flexible Platform of Patterned Quantum Sensors. Nano Letters 2018, 18 (8), 4684–4690. 10.1021/acs.nanolett.8b00895. [DOI] [PubMed] [Google Scholar]
Rodrigues M.; Piñol R.; Antorrena G.; Brites C. D. S.; Silva N. J. O.; Murillo J. L.; Cases R.; Díez I.; Palacio F.; Torras N.; et al. Implementing Thermometry on Silicon Surfaces Functionalized by Lanthanide-Doped Self-Assembled Polymer Monolayers. Advanced Functional Materials 2016, 26 (2), 200–209. 10.1002/adfm.201503889. [DOI] [Google Scholar]
Ramalho J. F. C. B.; Correia S. F. H.; Fu L.; António L. L. F.; Brites C. D. S.; André P. S.; Ferreira R. A. S.; Carlos L. D. Luminescence Thermometry on the Route of the Mobile-Based Internet of Things (IoT): How Smart QR Codes Make It Real. Advanced Science 2019, 6 (19), 1900950. 10.1002/advs.201900950. [DOI] [PMC free article] [PubMed] [Google Scholar]
Martínez E. D.; Brites C. D. S.; Carlos L. D.; García-Flores A. F.; Urbano R. R.; Rettori C. Electrochromic Switch Devices Mixing Small- and Large-Sized Upconverting Nanocrystals. Advanced Functional Materials 2019, 29 (8), 1807758. 10.1002/adfm.201807758. [DOI] [Google Scholar]
Glais E.; Maître A.; Viana B.; Chanéac C. Experimental measurement of local high temperature at the surface of gold nanorods using doped ZnGa₂O₄ as a nanothermometer. Nanoscale Advances 2021, 3 (10), 2862–2869. 10.1039/D1NA00010A. [DOI] [PMC free article] [PubMed] [Google Scholar]
Brites C. D. S.; Fuertes M. C.; Angelomé P. C.; Martínez E. D.; Lima P. P.; Soler-Illia G. J. A. A.; Carlos L. D. Tethering Luminescent Thermometry and Plasmonics: Light Manipulation to Assess Real-Time Thermal Flow in Nanoarchitectures. Nano Letters 2017, 17 (8), 4746–4752. 10.1021/acs.nanolett.7b01433. [DOI] [PubMed] [Google Scholar]
Rohani S.; Quintanilla M.; Tuccio S.; De Angelis F.; Cantelar E.; Govorov A. O.; Razzari L.; Vetrone F. Enhanced Luminescence, Collective Heating, and Nanothermometry in an Ensemble System Composed of Lanthanide-Doped Upconverting Nanoparticles and Gold Nanorods. Advanced Optical Materials 2015, 3 (11), 1606–1613. 10.1002/adom.201500380. [DOI] [Google Scholar]
Debasu M. L.; Ananias D.; Pastoriza-Santos I.; Liz-Marzán L. M.; Rocha J.; Carlos L. D. All-In-One Optical Heater-Thermometer Nanoplatform Operative From 300 to 2000 K Based on Er³⁺ Emission and Blackbody Radiation. Adv. Mater. 2013, 25 (35), 4868–4874. 10.1002/adma.201300892. [DOI] [PubMed] [Google Scholar]
Martínez E. D.; Urbano R. R.; Rettori C. Thermoplasmonic Maskless Lithography on Upconverting Nanocomposites Assisted by Gold Nanostars. ACS Applied Nano Materials 2019, 2 (11), 6889–6897. 10.1021/acsanm.9b01355. [DOI] [Google Scholar]
Huang Y.; Rosei F.; Vetrone F. A single multifunctional nanoplatform based on upconversion luminescence and gold nanorods. Nanoscale 2015, 7 (12), 5178–5185. 10.1039/C4NR07369J. [DOI] [PubMed] [Google Scholar]
Baral S.; Johnson S. C.; Alaulamie A. A.; Richardson H. H. Nanothermometry using optically trapped erbium oxide nanoparticle. Appl. Phys. A: Mater. Sci. Process. 2016, 122, 340. 10.1007/s00339-016-9886-0. [DOI] [Google Scholar]
Geitenbeek R. G.; Salzmann B. B. V.; Nieuwelink A.-E.; Meijerink A.; Weckhuysen B. M. Chemically and thermally stable lanthanide-doped Y₂O₃ nanoparticles for remote temperature sensing in catalytic environments. Chem. Eng. Sci. 2019, 198, 235–240. 10.1016/j.ces.2018.10.004. [DOI] [Google Scholar]
Jena H. S.; Rijckaert H.; Krishnaraj C.; Van Driessche I.; Van Der Voort P.; Kaczmarek A. M. Hybrid Nanocomposites Formed by Lanthanide Nanoparticles in Zr-MOF for Local Temperature Measurements during Catalytic Reactions. Chem. Mater. 2021, 33 (20), 8007–8017. 10.1021/acs.chemmater.1c02126. [DOI] [Google Scholar]
Krishnaraj C.; Rijckaert H.; Jena H. S.; Van Der Voort P.; Kaczmarek A. M. Upconverting Er³⁺-Yb³⁺ Inorganic/Covalent Organic Framework Core-Shell Nanoplatforms for Simultaneous Catalysis and Nanothermometry. ACS Applied Materials & Interfaces 2021, 13 (39), 47010–47018. 10.1021/acsami.1c11314. [DOI] [PubMed] [Google Scholar]
Sun J.; Rijckaert H.; Maegawa Y.; Inagaki S.; Van Der Voort P.; Kaczmarek A. M. Luminescent Nanorattles Based on Bipyridine Periodic Mesoporous Organosilicas for Simultaneous Thermometry and Catalysis. Chem. Mater. 2022, 34 (8), 3770–3780. 10.1021/acs.chemmater.2c00215. [DOI] [Google Scholar]
Kaczmarek A. M.; Jena H. S.; Krishnaraj C.; Rijckaert H.; Veerapandian S. K. P.; Meijerink A.; Van Der Voort P. Luminescent Ratiometric Thermometers Based on a 4f-3d Grafted Covalent Organic Framework to Locally Measure Temperature Gradients During Catalytic Reactions. Angewandte Chemie International Edition 2021, 60 (7), 3727–3736. 10.1002/anie.202013377. [DOI] [PubMed] [Google Scholar]
Gomez G. E.; Kaczmarek A. M.; Van Deun R.; Brusau E. V.; Narda G. E.; Vega D.; Iglesias M.; Gutierrez-Puebla E.; Monge M. Á. Photoluminescence, Unconventional-Range Temperature Sensing, and Efficient Catalytic Activities of Lanthanide Metal-Organic Frameworks. Eur. J. Inorg. Chem. 2016, 2016 (10), 1577–1588. 10.1002/ejic.201501402. [DOI] [Google Scholar]
Terlingen B. J. P.; Arens T.; van Swieten T. P.; Rabouw F. T.; Prins P. T.; de Beer M. M.; Meijerink A.; Ahr M. P.; Hutter E. M.; van Lare C. E. J.; Weckhuysen B. M. Bifunctional Europium for Operando Catalyst Thermometry in an Exothermic Chemical Reaction. Angewandte Chemie International Edition 2022, 61 (52), e202211991 10.1002/anie.202211991. [DOI] [PMC free article] [PubMed] [Google Scholar]
van Ravenhorst I. K.; Geitenbeek R. G.; van der Eerden M. J.; Tijn van Omme J.; Peréz Garza H. H.; Meirer F.; Meijerink A.; Weckhuysen B. M. In Situ Local Temperature Mapping in Microscopy Nano-Reactors with Luminescence Thermometry. ChemCatChem 2019, 11 (22), 5505–5512. 10.1002/cctc.201900985. [DOI] [Google Scholar]
Hartman T.; Geitenbeek R. G.; Whiting G. T.; Weckhuysen B. M. Operando monitoring of temperature and active species at the single catalyst particle level. Nature Catalysis 2019, 2, 986–996. 10.1038/s41929-019-0352-1. [DOI] [Google Scholar]
Ye Z.; Bommidi D. K.; Pickel A. D. Dual-Mode Operando Raman Spectroscopy and Upconversion Thermometry for Probing Thermal Contributions to Plasmonic Photocatalysis. Advanced Optical Materials 2023, 11, 2300824. 10.1002/adom.202300824. [DOI] [Google Scholar]
Ito S.; Sugiyama T.; Toitani N.; Katayama G.; Miyasaka H. Application of Fluorescence Correlation Spectroscopy to the Measurement of Local Temperature in Solutions under Optical Trapping Condition. The Journal of Physical Chemistry B 2007, 111 (9), 2365–2371. 10.1021/jp065156l. [DOI] [PubMed] [Google Scholar]
Jiang Q.; Rogez B.; Claude J.-B.; Baffou G.; Wenger J. Temperature Measurement in Plasmonic Nanoapertures Used for Optical Trapping. ACS Photonics 2019, 6 (7), 1763–1773. 10.1021/acsphotonics.9b00519. [DOI] [Google Scholar]
Rodriguez-Sevilla P.; Lee T.; Liang L.; Haro-González P.; Lifante G.; Liu X.; Jaque D. Light-Activated Upconverting Spinners. Advanced Optical Materials 2018, 6 (12), 1800161. 10.1002/adom.201800161. [DOI] [Google Scholar]
Rodríguez-Sevilla P.; Arita Y.; Liu X.; Jaque D.; Dholakia K. The Temperature of an Optically Trapped, Rotating Microparticle. ACS Photonics 2018, 5 (9), 3772–3778. 10.1021/acsphotonics.8b00822. [DOI] [Google Scholar]
Lu D.; Labrador-Páez L.; Ortiz-Rivero E.; Frades P.; Antoniak M. A.; Wawrzyńczyk D.; Nyk M.; Brites C. D. S.; Carlos L. D.; Garcıa Solé J. A.; et al. Exploring Single-Nanoparticle Dynamics at High Temperature by Optical Tweezers. Nano Letters 2020, 20 (11), 8024–8031. 10.1021/acs.nanolett.0c02936. [DOI] [PubMed] [Google Scholar]
Lu D.; Pedroni M.; Labrador-Páez L.; Marqués M. I.; Jaque D.; Haro-González P. Nanojet Trapping of a Single Sub-10 nm Upconverting Nanoparticle in the Full Liquid Water Temperature Range. Small 2021, 17 (7), 2006764. 10.1002/smll.202006764. [DOI] [PubMed] [Google Scholar]
Castelletto S.; Rosa L.; Boretti A. Micro-manipulation of nanodiamonds containing NV centers for quantum applications. Diamond Relat. Mater. 2020, 106, 107840. 10.1016/j.diamond.2020.107840. [DOI] [Google Scholar]
Rahman A. T. M. A.; Frangeskou A. C.; Kim M. S.; Bose S.; Morley G. W.; Barker P. F. Burning and graphitization of optically levitated nanodiamonds in vacuum. Scientific Reports 2016, 6, 21633. 10.1038/srep21633. [DOI] [PMC free article] [PubMed] [Google Scholar]
Frangeskou A. C.; Rahman A. T. M. A.; Gines L.; Mandal S.; Williams O. A.; Barker P. F.; Morley G. W. Pure nanodiamonds for levitated optomechanics in vacuum. New Journal of Physics 2018, 20, 043016. 10.1088/1367-2630/aab700. [DOI] [Google Scholar]
Hoang T. M.; Ahn J.; Bang J.; Li T. Electron spin control of optically levitated nanodiamonds in vacuum. Nature Communications 2016, 7, 12250. 10.1038/ncomms12250. [DOI] [PMC free article] [PubMed] [Google Scholar]
Delord T.; Nicolas L.; Bodini M.; Hétet G. Diamonds levitating in a Paul trap under vacuum: Measurements of laser-induced heating via NV center thermometry. Appl. Phys. Lett. 2017, 111, 013101. 10.1063/1.4991670. [DOI] [Google Scholar]
Pettit R. M.; Neukirch L. P.; Zhang Y.; Nick Vamivakas A. Coherent control of a single nitrogen-vacancy center spin in optically levitated nanodiamond. J. Opt. Soc. Am. B 2017, 34 (6), C31–C35. 10.1364/JOSAB.34.000C31. [DOI] [Google Scholar]
Rivière F.; de Guillebon T.; Raynal D.; Schmidt M.; Lauret J.-S.; Roch J.-F.; Rondin L. Hot Brownian Motion of Optically Levitated Nanodiamonds. ACS Photonics 2022, 9 (2), 420–425. 10.1021/acsphotonics.1c01642. [DOI] [Google Scholar]
Goderski S.; Runowski M.; Woźny P.; Lavín V.; Lis S. Lanthanide Upconverted Luminescence for Simultaneous Contactless Optical Thermometry and Manometry-Sensing under Extreme Conditions of Pressure and Temperature. ACS Applied Materials & Interfaces 2020, 12 (36), 40475–40485. 10.1021/acsami.0c09882. [DOI] [PMC free article] [PubMed] [Google Scholar]
Zheng T.; Sójka M.; Runowski M.; Woźny P.; Lis S.; Zych E. Tm²⁺ Activated SrB₄O₇ Bifunctional Sensor of Temperature and Pressure—Highly Sensitive, Multi-Parameter Luminescence Thermometry and Manometry. Advanced Optical Materials 2021, 9 (22), 2101507. 10.1002/adom.202101507. [DOI] [Google Scholar]
Albahrani S. M. B.; Seoudi T.; Philippon D.; Lafarge L.; Reiss P.; Hajjaji H.; Guillot G.; Querry M.; Bluet J.-M.; Vergne P. Quantum dots to probe temperature and pressure in highly confined liquids. RSC Advances 2018, 8 (41), 22897–22908. 10.1039/C8RA03652G. [DOI] [PMC free article] [PubMed] [Google Scholar]
Seoudi T.; Philippon D.; Fillot N.; Lafarge L.; Devaux N.; Mondelin A.; Vergne P. CdSe-Based Quantum Dots as In Situ Pressure and Temperature Non-intrusive Sensors in Elastohydrodynamic Contacts. Tribology Letters 2020, 68, 73. 10.1007/s11249-020-01312-x. [DOI] [Google Scholar]
Zhou Y.; Ledoux G.; Bois L.; Descartes S.; Bouscharain N.; Chassagneux F.; Martini M.; Bakary Y. M.; Journet C.; Philippon D. Er³⁺ doped nanoparticles as upconversion thermometer probes in confined fluids. Phys. Chem. Chem. Phys. 2023, 25 (28), 19254–19265. 10.1039/D3CP02218H. [DOI] [PubMed] [Google Scholar]
Runowski M.; Woźny P.; Lis S.; Lavín V.; Martín I. R. Optical Vacuum Sensor Based on Lanthanide Upconversion—Luminescence Thermometry as a Tool for Ultralow Pressure Sensing. Advanced Materials Technologies 2020, 5 (4), 1901091. 10.1002/admt.201901091. [DOI] [Google Scholar]
Soler-Carracedo K.; Martin I. R.; Runowski M.; Martín L. L.; Lahoz F.; Lozano-Gorrín A. D.; Paz-Buclatin F. Luminescent Nd³⁺-Based Microresonators Working as Optical Vacuum Sensors. Advanced Optical Materials 2020, 8 (19), 2000678. 10.1002/adom.202000678. [DOI] [Google Scholar]
Runowski M.; Woźny P.; Martín I. R. Optical pressure sensing in vacuum and high-pressure ranges using lanthanide-based luminescent thermometer-manometer. Journal of Materials Chemistry C 2021, 9 (13), 4643–4651. 10.1039/D1TC00709B. [DOI] [Google Scholar]
Chamarthy P.; Garimella S. V.; Wereley S. T. Measurement of the temperature non-uniformity in a microchannel heat sink using microscale laser-induced fluorescence. Int. J. Heat Mass Transfer 2010, 53 (15), 3275–3283. 10.1016/j.ijheatmasstransfer.2010.02.052. [DOI] [Google Scholar]
Geitenbeek R. G.; Vollenbroek J. C.; Weijgertze H. M. H.; Tregouet C. B. M.; Nieuwelink A.-E.; Kennedy C. L.; Weckhuysen B. M.; Lohse D.; van Blaaderen A.; van den Berg A.; et al. Luminescence thermometry for in situ temperature measurements in microfluidic devices. Lab on a Chip 2019, 19 (7), 1236–1246. 10.1039/C8LC01292J. [DOI] [PubMed] [Google Scholar]
Brites C. D. S.; Lima P. P.; Silva N. J. O.; Millán A.; Amaral V. S.; Palacio F.; Carlos L. D. Ratiometric highly sensitive luminescent nanothermometers working in the room temperature range. Applications to heat propagation in nanofluids. Nanoscale 2013, 5 (16), 7572–7580. 10.1039/c3nr02335d. [DOI] [PubMed] [Google Scholar]
Zhu Y.; Buitenhuis J.; Förster B.; Vetrano M. R.; Koos E. Development of Perovskite Quantum Dots for Two-Dimensional Temperature Sensors. ACS Applied Nano Materials 2023, 6 (6), 4661–4671. 10.1021/acsanm.3c00144. [DOI] [Google Scholar]
Savchuk O. A.; Carvajal J. J.; Massons J.; Cascales C.; Aguiló M.; Díaz F. Novel low-cost, compact and fast signal processing sensor for ratiometric luminescent nanothermometry. Sensors and Actuators A: Physical 2016, 250, 87–95. 10.1016/j.sna.2016.08.031. [DOI] [Google Scholar]
da Silva Moura N.; Bajgiran K. R.; Melvin A. T.; Dooley K. M.; Dorman J. A. Direct Probing of Fe₃O₄ Nanoparticle Surface Temperatures during Magnetic Heating: Implications for Induction Catalysis. ACS Applied Nano Materials 2021, 4 (12), 13778–13787. 10.1021/acsanm.1c03168. [DOI] [Google Scholar]
Shen X.; Li H.; Zhao Z.; Li X.; Liu K.; Gao X. Imaging of liquid temperature distribution during microwave heating via thermochromic metal organic frameworks. Int. J. Heat Mass Transfer 2022, 189, 122667. 10.1016/j.ijheatmasstransfer.2022.122667. [DOI] [Google Scholar]
Keblinski P.; Cahill D. G.; Bodapati A.; Sullivan C. R.; Taton T. A.. Limits of localized heating by electromagnetically excited nanoparticles. J. Appl. Phys. 2006, 100 ( (5), ) 10.1063/1.2335783. [DOI] [Google Scholar]
Zhao Z.; Shen X.; Li H.; Liu K.; Wu H.; Li X.; Gao X. Watching Microwave-Induced Microscopic Hot Spots via the Thermosensitive Fluorescence of Europium/Terbium Mixed-Metal Organic Complexes. Angewandte Chemie International Edition 2022, 61 (6), e202114340 10.1002/anie.202114340. [DOI] [PubMed] [Google Scholar]
Dong J.; Zink J. I. Taking the Temperature of the Interiors of Magnetically Heated Nanoparticles. ACS Nano 2014, 8 (5), 5199–5207. 10.1021/nn501250e. [DOI] [PMC free article] [PubMed] [Google Scholar]
Gu Y.; Piñol R.; Moreno-Loshuertos R.; Brites C. D. S.; Zeler J.; Martínez A.; Maurin-Pasturel G.; Fernández-Silva P.; Marco-Brualla J.; Téllez P.; et al. Local Temperature Increments and Induced Cell Death in Intracellular Magnetic Hyperthermia. ACS Nano 2023, 17 (7), 6822–6832. 10.1021/acsnano.3c00388. [DOI] [PMC free article] [PubMed] [Google Scholar]
Moreno Maldonado A. C.; Goya G. F. Comment on “Local Temperature Increments and Induced Cell Death in Intracellular Magnetic Hyperthermia”. ACS Nano 2023, 17 (16), 15217–15218. 10.1021/acsnano.3c04393. [DOI] [PubMed] [Google Scholar]
Chen G. Non-Fourier phonon heat conduction at the microscale and nanoscale. Nature Reviews Physics 2021, 3, 555–569. 10.1038/s42254-021-00334-1. [DOI] [Google Scholar]
Savchuk O. A.; Carvajal J. J.; Brites C. D. S.; Carlos L. D.; Aguilo M.; Diaz F. Upconversion thermometry: a new tool to measure the thermal resistance of nanoparticles. Nanoscale 2018, 10 (14), 6602–6610. 10.1039/C7NR08758F. [DOI] [PubMed] [Google Scholar]
Brites C. D. S.; Zhuang B.; Debasu M. L.; Ding D.; Qin X.; Maturi F. E.; Lim W. W. Y.; Soh D. W.; Rocha J.; Yi Z.; et al. Decoding a Percolation Phase Transition of Water at ∼ 330 K with a Nanoparticle Ruler. The Journal of Physical Chemistry Letters 2020, 11 (16), 6704–6711. 10.1021/acs.jpclett.0c02147. [DOI] [PubMed] [Google Scholar]
Errulat D.; Marin R.; Gálico D. A.; Harriman K. L. M.; Pialat A.; Gabidullin B.; Iikawa F.; Couto O. D. D. Jr.; Moilanen J. O.; Hemmer E.; et al. A Luminescent Thermometer Exhibiting Slow Relaxation of the Magnetization: Toward Self-Monitored Building Blocks for Next-Generation Optomagnetic Devices. ACS Central Science 2019, 5 (7), 1187–1198. 10.1021/acscentsci.9b00288. [DOI] [PMC free article] [PubMed] [Google Scholar]
Ferreira R. A. S.; Mamontova E.; Botas A. M. P.; Shestakov M.; Vanacken J.; Moshchalkov V.; Guari Y.; Chibotaru L. F.; Luneau D.; André P. S.; et al. Synchronous Temperature and Magnetic Field Dual-Sensing by Luminescence in a Dysprosium Single-Molecule Magnet. Advanced Optical Materials 2021, 9 (24), 2101495. 10.1002/adom.202101495. [DOI] [Google Scholar]
Zanella S.; Aragon-Alberti M.; Brite C. D. S.; Salles F.; Carlos L. D.; Long J. Luminescent Single-Molecule Magnets as Dual Magneto-Optical Molecular Thermometers. Angewandte Chemie International Edition 2023, 62 (35), e202306970 10.1002/anie.202306970. [DOI] [PubMed] [Google Scholar]
Wang J.; Zakrzewski J. J.; Zychowicz M.; Xin Y.; Tokoro H.; Chorazy S.; Ohkoshi S.-i. Desolvation-Induced Highly Symmetrical Terbium(III) Single-Molecule Magnet Exhibiting Luminescent Self-Monitoring of Temperature. Angewandte Chemie International Edition 2023, 62 (35), e202306372 10.1002/anie.202306372. [DOI] [PubMed] [Google Scholar]
Li H.; Wei F.; Li Y.; Yu M.; Zhang Y.; Liu L.; Liu Z. Optical fiber sensor based on upconversion nanoparticles for internal temperature monitoring of Li-ion batteries. Journal of Materials Chemistry C 2021, 9 (41), 14757–14765. 10.1039/D1TC03701C. [DOI] [Google Scholar]
He R.; Vázquez de Aldana J. R.; Pedrola G. L.; Chen F.; Jaque D. Two-photon luminescence thermometry: towards 3D high-resolution thermal imaging of waveguides. Opt. Express 2016, 24 (14), 16156–16166. 10.1364/OE.24.016156. [DOI] [PubMed] [Google Scholar]
Ferreira R. A. S.; Brites C. D. S.; Vicente C. M. S.; Lima P. P.; Bastos A. R. N.; Marques P. G.; Hiltunen M.; Carlos L. D.; André P. S. Photonic-on-a-chip: a thermal actuated Mach-Zehnder interferometer and a molecular thermometer based on a single di-ureasil organic-inorganic hybrid. Laser & Photonics Reviews 2013, 7 (6), 1027–1035. 10.1002/lpor.201300080. [DOI] [Google Scholar]
Ding H.; Lv G.; Cai X.; Chen J.; Cheng Z.; Peng Y.; Tang G.; Shi Z.; Xie Y.; Fu X.; et al. An Optoelectronic thermometer based on microscale infrared-to-visible conversion devices. Light: Science & Applications 2022, 11, 130. 10.1038/s41377-022-00825-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
Maturi F. E.; Brites C. D. S.; Silva R. R.; Nigoghossian K.; Wilson D.; Ferreira R. A. S.; Ribeiro S. J. L.; Carlos L. D. Sustainable Smart Tags with Two-Step Verification for Anticounterfeiting Triggered by the Photothermal Response of Upconverting Nanoparticles. Advanced Photonics Research 2022, 3 (6), 2100227. 10.1002/adpr.202100227. [DOI] [Google Scholar]
Liu G.-Q.; Feng X.; Wang N.; Li Q.; Liu R.-B. Coherent quantum control of nitrogen-vacancy center spins near 1000 kelvin. Nature Communications 2019, 10, 1344. 10.1038/s41467-019-09327-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
Roder P. B.; Smith B. E.; Zhou X.; Crane M. J.; Pauzauskie P. J. Laser refrigeration of hydrothermal nanocrystals in physiological media. Proceedings of the National Academy of Sciences 2015, 112 (49), 15024–15029. 10.1073/pnas.1510418112. [DOI] [PMC free article] [PubMed] [Google Scholar]
Shen Y.; Lifante J.; Fernández N.; Jaque D.; Ximendes E. In Vivo Spectral Distortions of Infrared Luminescent Nanothermometers Compromise Their Reliability. ACS Nano 2020, 14 (4), 4122–4133. 10.1021/acsnano.9b08824. [DOI] [PubMed] [Google Scholar]
Bednarkiewicz A.; Marciniak L.; Carlos L. D.; Jaque D. Standardizing luminescence nanothermometry for biomedical applications. Nanoscale 2020, 12 (27), 14405–14421. 10.1039/D0NR03568H. [DOI] [PubMed] [Google Scholar]
Martínez E. D.; Brites C. D. S.; Urbano R. R.; Rettori C.; Carlos L. D. Hyperspectral imaging thermometry assisted by upconverting nanoparticles: Experimental artifacts and accuracy. Physica B: Physics of Condensed Matter 2022, 629, 413639. 10.1016/j.physb.2021.413639. [DOI] [Google Scholar]
Nguyen V. N.; Lee Y. H.; Le-Vu T. T.; Lin J.-Y.; Kan H.-C.; Hsu C.-C. Impact of Excitation Intensity-Dependent Fluorescence Intensity Ratio of Upconversion Nanoparticles on Wide-Field Thermal Imaging. ACS Applied Nano Materials 2022, 5 (10), 15172–15182. 10.1021/acsanm.2c03303. [DOI] [Google Scholar]
Martins J. C.; Bastos A. R. N.; Ferreira R. A. S.; Wang X.; Chen G.; Carlos L. D. Primary Luminescent Nanothermometers for Temperature Measurements Reliability Assessment. Advanced Photonics Research 2021, 2 (5), 2000169. 10.1002/adpr.202000169. [DOI] [Google Scholar]
Rühl P.; Wang D.; Garwe F.; Müller R.; Haase M.; Krämer K. W.; Paa W.; Heintzmann R.; Heinemann S. H.; Stafast H. Notes on thermometric artefacts by Er³⁺ luminescence band interference. J. Lumin. 2021, 232, 117860. 10.1016/j.jlumin.2020.117860. [DOI] [Google Scholar]
Xia X.; Volpi A.; Roh J. Y. D.; De Siena M. C.; Gamelin D. R.; Hehlen M. P.; Pauzauskie P. J. The impact of ²H_9/2 → ⁴I_13/2 emission from Er³⁺ ions on ratiometric optical temperature sensing with Yb³⁺/Er³⁺ co-doped upconversion materials. J. Lumin. 2021, 236, 118006. 10.1016/j.jlumin.2021.118006. [DOI] [Google Scholar]
Pickel A. D.; Dames C. Size and shape effects on the measured peak temperatures of nanoscale hotspots. J. Appl. Phys. 2020, 128, 045103. 10.1063/5.0012167. [DOI] [Google Scholar]
Labrador-Páez L.; Pedroni M.; Speghini A.; García-Solé J.; Haro-González P.; Jaque D. Reliability of rare-earth-doped infrared luminescent nanothermometers. Nanoscale 2018, 10 (47), 22319–22328. 10.1039/C8NR07566B. [DOI] [PubMed] [Google Scholar]
Chen Y.; Li G.; Ding Y.; Mao Q.; Liu M.; Wang C.; Zheng R.; Su B.-L.; Zhong J. Antithermal Quenching and Multiparametric Temperature Sensing from Mn²⁺/Tb³⁺-Codoped Ca₂LaTaO₆ Phosphor. Advanced Photonics Research 2023, 4 (6), 2300106. 10.1002/adpr.202300106. [DOI] [Google Scholar]
Maturi F. E.; Brites C. D. S.; Ximendes E. C.; Mills C.; Olsen B.; Jaque D.; Ribeiro S. J. L.; Carlos L. D. Going Above and Beyond: A Tenfold Gain in the Performance of Luminescence Thermometers Joining Multiparametric Sensing and Multiple Regression. Laser & Photonics Reviews 2021, 15 (11), 2100301. 10.1002/lpor.202100301. [DOI] [Google Scholar]
Ximendes E.; Marin R.; Carlos L. D.; Jaque D. Less is more: dimensionality reduction as a general strategy for more precise luminescence thermometry. Light: Science & Applications 2022, 11, 237. 10.1038/s41377-022-00932-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
Stone D. G.; Chen Y.; Ekimov E. A.; Tran T. T.; Bradac C. Diamond Nanothermometry Using a Machine Learning Approach. ACS Applied Optical Materials 2023, 1 (4), 898–905. 10.1021/acsaom.3c00059. [DOI] [Google Scholar]
Liu L.; Creten S.; Firdaus Y.; Agustin Flores Cuautle J. J.; Kouyaté M.; Van der Auweraer M.; Glorieux C. Fluorescence spectra shape based dynamic thermometry. Appl. Phys. Lett. 2014, 104, 031902. 10.1063/1.4862921. [DOI] [Google Scholar]
Liu L.; Zhong K.; Munro T.; Alvarado S.; Côte R.; Creten S.; Fron E.; Ban H.; Van der Auweraer M.; Roozen N. B.; et al. Wideband fluorescence-based thermometry by neural network recognition: Photothermal application with 10 ns time resolution. J. Appl. Phys. 2015, 118, 184906. 10.1063/1.4935277. [DOI] [Google Scholar]
Cui J.; Xu W.; Yao M.; Zheng L.; Hu C.; Zhang Z.; Sun Z. Convolutional neural networks open up horizons for luminescence thermometry. J. Lumin. 2023, 256, 119637. 10.1016/j.jlumin.2022.119637. [DOI] [Google Scholar]
Santos E. P.; Pugina R. S.; Hilário E. G.; Carvalho A. J. A.; Jacinto C.; Rego-Filho F. A. M. G.; Canabarro A.; Gomes A. S. L.; Caiut J. M. A.; Moura A. L. Towards accurate real-time luminescence thermometry: an automated machine learning approach. Sens. Actuators A 2023, 362, 114666. 10.1016/j.sna.2023.114666. [DOI] [Google Scholar]
Rao X.; Song T.; Gao J.; Cui Y.; Yang Y.; Wu C.; Chen B.; Qian G. A Highly Sensitive Mixed Lanthanide Metal-Organic Framework Self-Calibrated Luminescent Thermometer. J. Am. Chem. Soc. 2013, 135 (41), 15559–15564. 10.1021/ja407219k. [DOI] [PubMed] [Google Scholar]
Yang Y.; Huang H.; Wang Y.; Qiu F.; Feng Y.; Song X.; Tang X.; Zhang G.; Liu W. A family of mixed-lanthanide metal-organic framework thermometers in a wide temperature range. Dalton Transactions 2018, 47 (38), 13384–13390. 10.1039/C8DT03182G. [DOI] [PubMed] [Google Scholar]
Stefanska J.; Maciejewska K.; Marciniak L. Blue-emitting single band ratiometric luminescent thermometry based on LaF3:Pr³⁺. New J. Chem. 2021, 45 (27), 11898–11904. 10.1039/D1NJ01869H. [DOI] [Google Scholar]
Renero-Lecuna C.; Herrero A.; Jimenez de Aberasturi D.; Martínez-Flórez M.; Valiente R.; Mychinko M.; Bals S.; Liz-Marzán L. M. Nd³⁺-Doped Lanthanum Oxychloride Nanocrystals as Nanothermometers. The Journal of Physical Chemistry C 2021, 125 (36), 19887–19896. 10.1021/acs.jpcc.1c05828. [DOI] [PMC free article] [PubMed] [Google Scholar]
Choi S.; Graham S.; Chowdhury S.; Heller E. R.; Tadjer M. J.; Moreno G.; Narumanchi S. A perspective on the electro-thermal co-design of ultra-wide bandgap lateral devices. Appl. Phys. Lett. 2021, 119, 170501. 10.1063/5.0056271. [DOI] [Google Scholar]
Choi A. Y.; Esho I.; Gabritchidze B.; Kooi J.; Minnich A. J. Characterization of self-heating in cryogenic high electron mobility transistors using Schottky thermometry. J. Appl. Phys. 2021, 130, 155107. 10.1063/5.0063331. [DOI] [Google Scholar]
Childs P. R. N.; Greenwood J. R.; Long C. A. Review of temperature measurement. Rev. Sci. Instrum. 2000, 71, 2959–2978. 10.1063/1.1305516. [DOI] [Google Scholar]
Wen S.; Zhou J.; Zheng K.; Bednarkiewicz A.; Liu X.; Jin D. Advances in highly doped upconversion nanoparticles. Nature Communications 2018, 9, 2415. 10.1038/s41467-018-04813-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
Gargas D. J.; Chan E. M.; Ostrowski A. D.; Aloni S.; Altoe M. V. P.; Barnard E. S.; Sanii B.; Urban J. J.; Milliron D. J.; Cohen B. E.; Schuck P. J. Engineering bright sub-10-nm upconverting nanocrystals for single-molecule imaging. Nature Nanotechnology 2014, 9, 300–305. 10.1038/nnano.2014.29. [DOI] [PubMed] [Google Scholar]
Lee C.; Xu E. Z.; Kwock K. W. C.; Teitelboim A.; Liu Y.; Park H. S.; Ursprung B.; Ziffer M. E.; Karube Y.; Fardian-Melamed N.; et al. Indefinite and bidirectional near-infrared nanocrystal photoswitching. Nature 2023, 618, 951–958. 10.1038/s41586-023-06076-7. [DOI] [PubMed] [Google Scholar]
Lee C.; Xu E. Z.; Liu Y.; Teitelboim A.; Yao K.; Fernandez-Bravo A.; Kotulska A. M.; Nam S. H.; Suh Y. D.; Bednarkiewicz A.; et al. Giant nonlinear optical responses from photon-avalanching nanoparticles. Nature 2021, 589, 230–235. 10.1038/s41586-020-03092-9. [DOI] [PubMed] [Google Scholar]
Liu Y.; Lu Y.; Yang X.; Zheng X.; Wen S.; Wang F.; Vidal X.; Zhao J.; Liu D.; Zhou Z.; et al. Amplified stimulated emission in upconversion nanoparticles for super-resolution nanoscopy. Nature 2017, 543, 229–233. 10.1038/nature21366. [DOI] [PubMed] [Google Scholar]
Zhan Q.; Liu H.; Wang B.; Wu Q.; Pu R.; Zhou C.; Huang B.; Peng X.; Ågren H.; He S. Achieving high-efficiency emission depletion nanoscopy by employing cross relaxation in upconversion nanoparticles. Nature Communications 2017, 8, 1058. 10.1038/s41467-017-01141-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
Lu Y.; Zhao J.; Zhang R.; Liu Y.; Liu D.; Goldys E. M.; Yang X.; Xi P.; Sunna A.; Lu J.; et al. Tunable lifetime multiplexing using luminescent nanocrystals. Nature Photonics 2014, 8, 32–36. 10.1038/nphoton.2013.322. [DOI] [Google Scholar]
Szalkowski M.; Dudek M.; Korczak Z.; Lee C.; Marciniak Ł.; Chan E. M.; Schuck P. J.; Bednarkiewicz A. Predicting the impact of temperature dependent multi-phonon relaxation processes on the photon avalanche behavior in Tm³⁺: NaYF₄ nanoparticles. Optical Materials: X 2021, 12, 100102. 10.1016/j.omx.2021.100102. [DOI] [Google Scholar]

[ref1] Yue Y.; Wang X. Nanoscale thermal probing. Nano Reviews 2012, 3 (1), 11586. 10.3402/nano.v3i0.11586. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref2] Bradac C.; Lim S. F.; Chang H.-C.; Aharonovich I. Optical Nanoscale Thermometry: From Fundamental Mechanisms to Emerging Practical Applications. Advanced Optical Materials 2020, 8 (15), 2000183. 10.1002/adom.202000183. [DOI] [Google Scholar]

[ref3] Dramićanin M. D. Trends in luminescence thermometry. J. Appl. Phys. 2020, 128, 040902. 10.1063/5.0014825. [DOI] [Google Scholar]

[ref4] Brites C. D. S.; Marin R.; Suta M.; Carneiro Neto A. N.; Ximendes E.; Jaque D.; Carlos L. D. Spotlight on Luminescence Thermometry: Basics, Challenges, and Cutting-Edge Applications. Adv. Mater. 2023, 35 (36), 2302749. 10.1002/adma.202302749. [DOI] [PubMed] [Google Scholar]

[ref5] Jiang P.; Qian X.; Yang R. Tutorial: Time-domain thermoreflectance (TDTR) for thermal property characterization of bulk and thin film materials. J. Appl. Phys. 2018, 124, 161103. 10.1063/1.5046944. [DOI] [Google Scholar]

[ref6] Yang J.; Maragliano C.; Schmidt A. J. Thermal property microscopy with frequency domain thermoreflectance. Rev. Sci. Instrum. 2013, 84, 104904. 10.1063/1.4824143. [DOI] [PubMed] [Google Scholar]

[ref7] Pozzi E. A.; Zrimsek A. B.; Lethiec C. M.; Schatz G. C.; Hersam M. C.; Van Duyne R. P. Evaluating Single-Molecule Stokes and Anti-Stokes SERS for Nanoscale Thermometry. The Journal of Physical Chemistry C 2015, 119 (36), 21116–21124. 10.1021/acs.jpcc.5b08054. [DOI] [Google Scholar]

[ref8] Xu S.; Fan A.; Wang H.; Zhang X.; Wang X. Raman-based Nanoscale Thermal Transport Characterization: A Critical Review. Int. J. Heat Mass Transfer 2020, 154, 119751. 10.1016/j.ijheatmasstransfer.2020.119751. [DOI] [Google Scholar]

[ref9] Olson D. H.; Braun J. L.; Hopkins P. E. Spatially resolved thermoreflectance techniques for thermal conductivity measurements from the nanoscale to the mesoscale. J. Appl. Phys. 2019, 126, 150901. 10.1063/1.5120310. [DOI] [Google Scholar]

[ref10] Warkander S.; Wu J. Transducerless time domain reflectance measurement of semiconductor thermal properties. J. Appl. Phys. 2022, 131, 025101. 10.1063/5.0069360. [DOI] [Google Scholar]

[ref11] Yuan C.; Hanus R.; Graham S. A review of thermoreflectance techniques for characterizing wide bandgap semiconductors’ thermal properties and devices’ temperatures. J. Appl. Phys. 2022, 132, 220701. 10.1063/5.0122200. [DOI] [Google Scholar]

[ref12] Aigouy L.; Tessier G.; Mortier M.; Charlot B. Scanning thermal imaging of microelectronic circuits with a fluorescent nanoprobe. Appl. Phys. Lett. 2005, 87, 184105. 10.1063/1.2123384. [DOI] [Google Scholar]

[ref13] Maestro L. M.; Zhang Q.; Li X.; Jaque D.; Gu M. Quantum-dot based nanothermometry in optical plasmonic recording media. Appl. Phys. Lett. 2014, 105, 181110. 10.1063/1.4901258. [DOI] [Google Scholar]

[ref14] Brites C. D. S.; Xie X.; Debasu M. L.; Qin X.; Chen R.; Huang W.; Rocha J.; Liu X.; Carlos L. D. Instantaneous ballistic velocity of suspended Brownian nanocrystals measured by upconversion nanothermometry. Nature Nanotechnology 2016, 11, 851–856. 10.1038/nnano.2016.111. [DOI] [PubMed] [Google Scholar]

[ref15] Geitenbeek R. G.; Nieuwelink A.-E.; Jacobs T. S.; Salzmann B. B. V.; Goetze J.; Meijerink A.; Weckhuysen B. M. In Situ Luminescence Thermometry To Locally Measure Temperature Gradients during Catalytic Reactions. ACS Catalysis 2018, 8 (3), 2397–2401. 10.1021/acscatal.7b04154. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref16] Saïdi E.; Babinet N.; Lalouat L.; Lesueur J.; Aigouy L.; Volz S.; Labéguerie-Egéa J.; Mortier M. Tuning Temperature and Size of Hot Spots and Hot-Spot Arrays. Small 2011, 7 (2), 259–264. 10.1002/smll.201001476. [DOI] [PubMed] [Google Scholar]

[ref17] Kilbane J. D.; Chan E. M.; Monachon C.; Borys N. J.; Levy E. S.; Pickel A. D.; Urban J. J.; Schuck P. J.; Dames C. Far-field optical nanothermometry using individual sub-50 nm upconverting nanoparticles. Nanoscale 2016, 8 (22), 11611–11616. 10.1039/C6NR01479H. [DOI] [PubMed] [Google Scholar]

[ref18] Shang Y.; Han Q.; Hao S.; Chen T.; Zhu Y.; Wang Z.; Yang C. Dual-Mode Upconversion Nanoprobe Enables Broad-Range Thermometry from Cryogenic to Room Temperature. ACS Applied Materials & Interfaces 2019, 11 (45), 42455–42461. 10.1021/acsami.9b11751. [DOI] [PubMed] [Google Scholar]

[ref19] Runowski M.; Woźny P.; Stopikowska N.; Martín I. R.; Lavín V.; Lis S. Luminescent Nanothermometer Operating at Very High Temperature—Sensing up to 1000 K with Upconverting Nanoparticles (Yb³⁺/Tm³⁺). ACS Applied Materials & Interfaces 2020, 12 (39), 43933–43941. 10.1021/acsami.0c13011. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref20] Liu X.; Skripka A.; Lai Y.; Jiang C.; Liu J.; Vetrone F.; Liang J. Fast wide-field upconversion luminescence lifetime thermometry enabled by single-shot compressed ultrahigh-speed imaging. Nature Communications 2021, 12, 6401. 10.1038/s41467-021-26701-1. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref21] Bednarkiewicz A.; Drabik J.; Trejgis K.; Jaque D.; Ximendes E.; Marciniak L. Luminescence based temperature bio-imaging: Status, challenges, and perspectives. Applied Physics Reviews 2021, 8, 011317. 10.1063/5.0030295. [DOI] [Google Scholar]

[ref22] del Rosal B.; Ximendes E.; Rocha U.; Jaque D. In Vivo Luminescence Nanothermometry: from Materials to Applications. Advanced Optical Materials 2017, 5 (1), 1600508. 10.1002/adom.201600508. [DOI] [Google Scholar]

[ref23] Nexha A.; Carvajal J. J.; Pujol M. C.; Díaz F.; Aguiló M. Lanthanide doped luminescence nanothermometers in the biological windows: strategies and applications. Nanoscale 2021, 13 (17), 7913–7987. 10.1039/D0NR09150B. [DOI] [PubMed] [Google Scholar]

[ref24] Zhou J.; del Rosal B.; Jaque D.; Uchiyama S.; Jin D. Advances and challenges for fluorescence nanothermometry. Nature Methods 2020, 17, 967–980. 10.1038/s41592-020-0957-y. [DOI] [PubMed] [Google Scholar]

[ref25] Brites C. D. S.; Balabhadra S.; Carlos L. D. Lanthanide-Based Thermometers: At the Cutting-Edge of Luminescence Thermometry. Advanced Optical Materials 2019, 7 (5), 1801239. 10.1002/adom.201801239. [DOI] [Google Scholar]

[ref26] Zhang B.; Guo X.; Zhang Z.; Fu Z.; Zheng H. Luminescence thermometry with rare earth doped nanoparticles: Status and challenges. J. Lumin. 2022, 250, 119110. 10.1016/j.jlumin.2022.119110. [DOI] [Google Scholar]

[ref27] Jia M.; Chen X.; Sun R.; Wu D.; Li X.; Shi Z.; Chen G.; Shan C. Lanthanide-based ratiometric luminescence nanothermometry. Nano Research 2023, 16, 2949–2967. 10.1007/s12274-022-4882-7. [DOI] [Google Scholar]

[ref28] Rosso L.; Tabandeh S.; Beltramino G.; Fernicola V. Validation of phosphor thermometry for industrial surface temperature measurements. Measurement Science and Technology 2020, 31, 034002. 10.1088/1361-6501/ab4b6b. [DOI] [Google Scholar]

[ref29] Aldén M.; Omrane A.; Richter M.; Särner G. Thermographic phosphors for thermometry: A survey of combustion applications. Prog. Energy Combust. Sci. 2011, 37 (4), 422–461. 10.1016/j.pecs.2010.07.001. [DOI] [Google Scholar]

[ref30] Brübach J.; Pflitsch C.; Dreizler A.; Atakan B. On surface temperature measurements with thermographic phosphors: A review. Prog. Energy Combust. Sci. 2013, 39 (1), 37–60. 10.1016/j.pecs.2012.06.001. [DOI] [Google Scholar]

[ref31] Klier D. T.; Kumke M. U. Upconversion NaYF₄:Yb:Er nanoparticles co-doped with Gd³⁺ and Nd³⁺ for thermometry on the nanoscale. RSC Advances 2015, 5 (82), 67149–67156. 10.1039/C5RA11502G. [DOI] [Google Scholar]

[ref32] Marciniak L.; Pilch A.; Arabasz S.; Jin D.; Bednarkiewicz A. Heterogeneously Nd³⁺ doped single nanoparticles for NIR-induced heat conversion, luminescence, and thermometry. Nanoscale 2017, 9 (24), 8288–8297. 10.1039/C7NR02630G. [DOI] [PubMed] [Google Scholar]

[ref33] Marciniak L.; Prorok K.; Francés-Soriano L.; Pérez-Prieto J.; Bednarkiewicz A. A broadening temperature sensitivity range with a core-shell YbEr@YbNd double ratiometric optical nanothermometer. Nanoscale 2016, 8 (9), 5037–5042. 10.1039/C5NR08223D. [DOI] [PubMed] [Google Scholar]

[ref34] Skripka A.; Morinvil A.; Matulionyte M.; Cheng T.; Vetrone F. Advancing neodymium single-band nanothermometry. Nanoscale 2019, 11 (23), 11322–11330. 10.1039/C9NR02801C. [DOI] [PubMed] [Google Scholar]

[ref35] Du P.; Luo L.; Yu J. S. Controlled synthesis and upconversion luminescence of Tm³⁺-doped NaYbF₄ nanoparticles for non-invasion optical thermometry. J. Alloys Compd. 2018, 739, 926–933. 10.1016/j.jallcom.2017.12.260. [DOI] [Google Scholar]

[ref36] Liu H.; Yan L.; Huang J.; An Z.; Sheng W.; Zhou B. Ultrasensitive Thermochromic Upconversion in Core-Shell-Shell Nanoparticles for Nanothermometry and Anticounterfeiting. The Journal of Physical Chemistry Letters 2022, 13 (10), 2306–2312. 10.1021/acs.jpclett.2c00005. [DOI] [PubMed] [Google Scholar]

[ref37] Pereira A. F.; Kumar K. U.; Silva W. F.; Santos W. Q.; Jaque D.; Jacinto C. Yb³⁺/Tm³⁺ co-doped NaNbO₃ nanocrystals as three-photon-excited luminescent nanothermometers. Sensors and Actuators B: Chemical 2015, 213, 65–71. 10.1016/j.snb.2015.01.136. [DOI] [Google Scholar]

[ref38] Savchuk O. A.; Carvajal J. J.; Cascales C.; Massons J.; Aguiló M.; Díaz F. Thermochromic upconversion nanoparticles for visual temperature sensors with high thermal, spatial and temporal resolution. J. Mater. Chem. C 2016, 4 (27), 6602–6613. 10.1039/C6TC01841F. [DOI] [Google Scholar]

[ref39] Zheng T.; Runowski M.; Stopikowska N.; Skwierczyńska M.; Lis S.; Du P.; Luo L. Dual-center thermochromic Bi₂MoO₆:Yb³⁺, Er³⁺, Tm³⁺ phosphors for ultrasensitive luminescence thermometry. J. Alloys Compd. 2022, 890, 161830. 10.1016/j.jallcom.2021.161830. [DOI] [Google Scholar]

[ref40] Runowski M.; Goderski S.; Przybylska D.; Grzyb T.; Lis S.; Martín I. R. Sr₂LuF₇:Yb³⁺-Ho³⁺-Er³⁺ Upconverting Nanoparticles as Luminescent Thermometers in the First, Second, and Third Biological Windows. ACS Applied Nano Materials 2020, 3 (7), 6406–6415. 10.1021/acsanm.0c00839. [DOI] [Google Scholar]

[ref41] van Swieten T. P.; Yu D.; Yu T.; Vonk S. J. W.; Suta M.; Zhang Q.; Meijerink A.; Rabouw F. T. A Ho³⁺-Based Luminescent Thermometer for Sensitive Sensing over a Wide Temperature Range. Advanced Optical Materials 2021, 9 (1), 2001518. 10.1002/adom.202001518. [DOI] [Google Scholar]

[ref42] Ćirić A.; Marciniak Ł.; Dramićanin M. D.. Luminescence intensity ratio squared—A new luminescence thermometry method for enhanced sensitivity. J. Appl. Phys. 2022, 131 ( (11), ) 10.1063/5.0086807. [DOI] [Google Scholar]

[ref43] van Swieten T. P.; Steenhoff J. M.; Vlasblom A.; de Berg R.; Mattern S. P.; Rabouw F. T.; Suta M.; Meijerink A. Extending the dynamic temperature range of Boltzmann thermometers. Light: Science & Applications 2022, 11, 343. 10.1038/s41377-022-01028-8. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref44] Netzsch P.; Hämmer M.; Turgunbajew E.; van Swieten T. P.; Meijerink A.; Höppe H. A.; Suta M. Beyond the Energy Gap Law: The Influence of Selection Rules and Host Compound Effects on Nonradiative Transition Rates in Boltzmann Thermometers. Advanced Optical Materials 2022, 10 (11), 2200059. 10.1002/adom.202200059. [DOI] [Google Scholar]

[ref45] Yu D.; Li H.; Zhang D.; Zhang Q.; Meijerink A.; Suta M. One ion to catch them all: Targeted high-precision Boltzmann thermometry over a wide temperature range with Gd³⁺. Light: Science & Applications 2021, 10, 236. 10.1038/s41377-021-00677-5. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref46] Brites C. D. S.; Fiaczyk K.; Ramalho J. F. C. B.; Sójka M.; Carlos L. D.; Zych E. Widening the Temperature Range of Luminescent Thermometers through the Intra- and Interconfigurational Transitions of Pr³⁺. Advanced Optical Materials 2018, 6 (10), 1701318. 10.1002/adom.201701318. [DOI] [Google Scholar]

[ref47] Gao Y.; Huang F.; Lin H.; Xu J.; Wang Y. Intervalence charge transfer state interfered Pr³⁺ luminescence: A novel strategy for high sensitive optical thermometry. Sensors and Actuators B: Chemical 2017, 243, 137–143. 10.1016/j.snb.2016.11.143. [DOI] [Google Scholar]

[ref48] Runowski M.; Woźny P.; Martín I. R.; Lavín V.; Lis S. Praseodymium doped YF₃:Pr³⁺ nanoparticles as optical thermometer based on luminescence intensity ratio (LIR) - Studies in visible and NIR range. J. Lumin. 2019, 214, 116571. 10.1016/j.jlumin.2019.116571. [DOI] [Google Scholar]

[ref49] Yan L.; Huang J.; An Z.; Zhang Q.; Zhou B. Activating Ultrahigh Thermoresponsive Upconversion in an Erbium Sublattice for Nanothermometry and Information Security. Nano Letters 2022, 22 (17), 7042–7048. 10.1021/acs.nanolett.2c01931. [DOI] [PubMed] [Google Scholar]

[ref50] Vetrone F.; Naccache R.; Zamarrón A.; Juarranz de la Fuente A.; Sanz-Rodríguez F.; Martinez Maestro L.; Martín Rodriguez E.; Jaque D.; García Solé J.; Capobianco J. A. Temperature Sensing Using Fluorescent Nanothermometers. ACS Nano 2010, 4 (6), 3254–3258. 10.1021/nn100244a. [DOI] [PubMed] [Google Scholar]

[ref51] Zhou Y.; Yan B.; Lei F. Postsynthetic lanthanide functionalization of nanosized metal-organic frameworks for highly sensitive ratiometric luminescent thermometry. Chemical Communications 2014, 50 (96), 15235–15238. 10.1039/C4CC07038K. [DOI] [PubMed] [Google Scholar]

[ref52] Fischer L. H.; Harms G. S.; Wolfbeis O. S. Upconverting Nanoparticles for Nanoscale Thermometry. Angewandte Chemie International Edition 2011, 50 (20), 4546–4551. 10.1002/anie.201006835. [DOI] [PubMed] [Google Scholar]

[ref53] Pickel A. D.; Teitelboim A.; Chan E. M.; Borys N. J.; Schuck P. J.; Dames C. Apparent self-heating of individual upconverting nanoparticle thermometers. Nature Communications 2018, 9, 4907. 10.1038/s41467-018-07361-0. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref54] van Swieten T. P.; van Omme T.; van den Heuvel D. J.; Vonk S. J. W.; Spruit R. G.; Meirer F.; Garza H. H. P.; Weckhuysen B. M.; Meijerink A.; Rabouw F. T.; Geitenbeek R. G. Mapping Elevated Temperatures with a Micrometer Resolution Using the Luminescence of Chemically Stable Upconversion Nanoparticles. ACS Applied Nano Materials 2021, 4 (4), 4208–4215. 10.1021/acsanm.1c00657. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref55] Vonk S. J. W.; van Swieten T. P.; Cocina A.; Rabouw F. T. Photonic Artifacts in Ratiometric Luminescence Nanothermometry. Nano Letters 2023, 23 (14), 6560–6566. 10.1021/acs.nanolett.3c01602. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref56] Balabhadra S.; Debasu M. L.; Brites C. D. S.; Ferreira R. A. S.; Carlos L. D. Upconverting Nanoparticles Working As Primary Thermometers In Different Media. The Journal of Physical Chemistry C 2017, 121 (25), 13962–13968. 10.1021/acs.jpcc.7b04827. [DOI] [Google Scholar]

[ref57] Wang Q.; Liao M.; Lin Q.; Xiong M.; Mu Z.; Wu F. A review on fluorescence intensity ratio thermometer based on rare-earth and transition metal ions doped inorganic luminescent materials. J. Alloys Compd. 2021, 850, 156744. 10.1016/j.jallcom.2020.156744. [DOI] [Google Scholar]

[ref58] Zhao Y.; Wang X.; Zhang Y.; Li Y.; Yao X. Optical temperature sensing of up-conversion luminescent materials: Fundamentals and progress. J. Alloys Compd. 2020, 817, 152691. 10.1016/j.jallcom.2019.152691. [DOI] [Google Scholar]

[ref59] Sedlmeier A.; Achatz D. E.; Fischer L. H.; Gorris H. H.; Wolfbeis O. S. Photon upconverting nanoparticles for luminescent sensing of temperature. Nanoscale 2012, 4 (22), 7090–7096. 10.1039/c2nr32314a. [DOI] [PubMed] [Google Scholar]

[ref60] Zheng K.; Song W.; He G.; Yuan Z.; Qin W. Five-photon UV upconversion emissions of Er³⁺ for temperature sensing. Opt. Express 2015, 23 (6), 7653–7658. 10.1364/OE.23.007653. [DOI] [PubMed] [Google Scholar]

[ref61] Wang C.; Jin Y.; Zhang R.; Yao Q.; Hu Y. A review and outlook of ratiometric optical thermometer based on thermally coupled levels and non-thermally coupled levels. J. Alloys Compd. 2022, 894, 162494. 10.1016/j.jallcom.2021.162494. [DOI] [Google Scholar]

[ref62] Savchuk O. A.; Carvajal J. J.; Cascales C.; Aguiló M.; Díaz F. Benefits of Silica Core-Shell Structures on the Temperature Sensing Properties of Er,Yb:GdVO₄ Up-Conversion Nanoparticles. ACS Applied Materials & Interfaces 2016, 8 (11), 7266–7273. 10.1021/acsami.6b01371. [DOI] [PubMed] [Google Scholar]

[ref63] Suo H.; Guo C.; Zheng J.; Zhou B.; Ma C.; Zhao X.; Li T.; Guo P.; Goldys E. M. Sensitivity Modulation of Upconverting Thermometry through Engineering Phonon Energy of a Matrix. ACS Applied Materials & Interfaces 2016, 8 (44), 30312–30319. 10.1021/acsami.6b12176. [DOI] [PubMed] [Google Scholar]

[ref64] Wang J.; Lin H.; Cheng Y.; Cui X.; Gao Y.; Ji Z.; Xu J.; Wang Y. A novel high-sensitive upconversion thermometry strategy: Utilizing synergistic effect of dual-wavelength lasers excitation to manipulate electron thermal distribution. Sensors and Actuators B: Chemical 2019, 278, 165–171. 10.1016/j.snb.2018.09.086. [DOI] [Google Scholar]

[ref65] Wang Y.; Sun Y.; Xia Z. Energy Gap Linear Superposition of Thermally Coupled Levels toward Enhanced Relative Sensitivity of Ratiometric Thermometry. The Journal of Physical Chemistry Letters 2023, 14 (1), 178–182. 10.1021/acs.jpclett.2c03587. [DOI] [PubMed] [Google Scholar]

[ref66] Pessoa A. R.; Galindo J. A. O.; Serge-Correales Y. E.; Amaral A. M.; Ribeiro S. J. L.; Menezes L. d. S. 2D Thermal Maps Using Hyperspectral Scanning of Single Upconverting Microcrystals: Experimental Artifacts and Image Processing. ACS Appl. Mater. Interfaces 2022, 14 (33), 38311–38319. 10.1021/acsami.2c08709. [DOI] [PubMed] [Google Scholar]

[ref67] van Swieten T. P.; Meijerink A.; Rabouw F. T. Impact of Noise and Background on Measurement Uncertainties in Luminescence Thermometry. ACS Photonics 2022, 9 (4), 1366–1374. 10.1021/acsphotonics.2c00039. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref68] Rocha U.; Jacinto da Silva C.; Ferreira Silva W.; Guedes I.; Benayas A.; Martínez Maestro L.; Acosta Elias M.; Bovero E.; van Veggel F. C. J. M.; García Solé J. A.; Jaque D. Subtissue Thermal Sensing Based on Neodymium-Doped LaF₃ Nanoparticles. ACS Nano 2013, 7 (2), 1188–1199. 10.1021/nn304373q. [DOI] [PubMed] [Google Scholar]

[ref69] Kucsko G.; Maurer P. C.; Yao N. Y.; Kubo M.; Noh H. J.; Lo P. K.; Park H.; Lukin M. D. Nanometre-scale thermometry in a living cell. Nature 2013, 500, 54–58. 10.1038/nature12373. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref70] Fujiwara M.; Shikano Y. Diamond quantum thermometry: from foundations to applications. Nanotechnology 2021, 32, 482002. 10.1088/1361-6528/ac1fb1. [DOI] [PubMed] [Google Scholar]

[ref71] Sotoma S.; Zhong C.; Kah J. C. Y.; Yamashita H.; Plakhotnik T.; Harada Y.; Suzuki M. In situ measurements of intracellular thermal conductivity using heater-thermometer hybrid diamond nanosensors. Science Advances 2021, 7 (3), eabd7888 10.1126/sciadv.abd7888. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref72] Acosta V. M.; Bauch E.; Ledbetter M. P.; Waxman A.; Bouchard L. S.; Budker D. Temperature Dependence of the Nitrogen-Vacancy Magnetic Resonance in Diamond. Phys. Rev. Lett. 2010, 104, 070801. 10.1103/PhysRevLett.104.070801. [DOI] [PubMed] [Google Scholar]

[ref73] Doherty M. W.; Acosta V. M.; Jarmola A.; Barson M. S. J.; Manson N. B.; Budker D.; Hollenberg L. C. L. Temperature shifts of the resonances of the NV^– center in diamond. Physical Review B 2014, 90, 041201. 10.1103/PhysRevB.90.041201. [DOI] [Google Scholar]

[ref74] Cambria M. C.; Thiering G.; Norambuena A.; Dinani H. T.; Gardill A.; Kemeny I.; Lordi V.; Gali A.; Maze J. R.; Kolkowitz S. Physically motivated analytical expression for the temperature dependence of the zero-field splitting of the nitrogen-vacancy center in diamond. Phys. Rev. B 2023, 108 (18), 102. 10.1103/PhysRevB.108.L180102. [DOI] [PubMed] [Google Scholar]

[ref75] Neumann P.; Jakobi I.; Dolde F.; Burk C.; Reuter R.; Waldherr G.; Honert J.; Wolf T.; Brunner A.; Shim J. H.; et al. High-Precision Nanoscale Temperature Sensing Using Single Defects in Diamond. Nano Letters 2013, 13 (6), 2738–2742. 10.1021/nl401216y. [DOI] [PubMed] [Google Scholar]

[ref76] Wang N.; Liu G.-Q.; Leong W.-H.; Zeng H.; Feng X.; Li S.-H.; Dolde F.; Fedder H.; Wrachtrup J.; Cui X.-D.; et al. Magnetic Criticality Enhanced Hybrid Nanodiamond Thermometer under Ambient Conditions. Physical Review X 2018, 8, 011042. 10.1103/PhysRevX.8.011042. [DOI] [Google Scholar]

[ref77] Toyli D. M.; de las Casas C. F.; Christle D. J.; Dobrovitski V. V.; Awschalom D. D. Fluorescence thermometry enhanced by the quantum coherence of single spins in diamond. Proceedings of the National Academy of Sciences 2013, 110 (21), 8417–8421. 10.1073/pnas.1306825110. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref78] Wang J.; Feng F.; Zhang J.; Chen J.; Zheng Z.; Guo L.; Zhang W.; Song X.; Guo G.; Fan L.; et al. High-sensitivity temperature sensing using an implanted single nitrogen-vacancy center array in diamond. Physical Review B 2015, 91, 155404. 10.1103/PhysRevB.91.155404. [DOI] [Google Scholar]

[ref79] Toyli D. M.; Christle D. J.; Alkauskas A.; Buckley B. B.; Van de Walle C. G.; Awschalom D. D. Measurement and Control of Single Nitrogen-Vacancy Center Spins above 600 K. Physical Review X 2012, 2, 031001. 10.1103/PhysRevX.2.031001. [DOI] [Google Scholar]

[ref80] Foy C.; Zhang L.; Trusheim M. E.; Bagnall K. R.; Walsh M.; Wang E. N.; Englund D. R. Wide-Field Magnetic Field and Temperature Imaging Using Nanoscale Quantum Sensors. ACS Applied Materials & Interfaces 2020, 12 (23), 26525–26533. 10.1021/acsami.0c01545. [DOI] [PubMed] [Google Scholar]

[ref81] Shim J. H.; Lee S.-J.; Ghimire S.; Hwang J. I.; Lee K.-G.; Kim K.; Turner M. J.; Hart C. A.; Walsworth R. L.; Oh S. Multiplexed Sensing of Magnetic Field and Temperature in Real Time Using a Nitrogen-Vacancy Ensemble in Diamond. Physical Review Applied 2022, 17, 014009. 10.1103/PhysRevApplied.17.014009. [DOI] [Google Scholar]

[ref82] Abrahams G. J.; Ellul E.; Robertson I. O.; Khalid A.; Greentree A. D.; Gibson B. C.; Tetienne J.-P. Handheld Device for Noncontact Thermometry via Optically Detected Magnetic Resonance of Proximate Diamond Sensors. Physical Review Applied 2023, 19, 054076. 10.1103/PhysRevApplied.19.054076. [DOI] [Google Scholar]

[ref83] Plakhotnik T.; Doherty M. W.; Cole J. H.; Chapman R.; Manson N. B. All-Optical Thermometry and Thermal Properties of the Optically Detected Spin Resonances of the NV- Center in Nanodiamond. Nano Letters 2014, 14 (9), 4989–4996. 10.1021/nl501841d. [DOI] [PubMed] [Google Scholar]

[ref84] Plakhotnik T.; Aman H.; Chang H.-C. All-optical single-nanoparticle ratiometric thermometry with a noise floor of 0.3 K Hz^–1/2. Nanotechnology 2015, 26, 245501. 10.1088/0957-4484/26/24/245501. [DOI] [PubMed] [Google Scholar]

[ref85] Bommidi D. K.; Pickel A. D. Temperature-dependent excited state lifetimes of nitrogen vacancy centers in individual nanodiamonds. Appl. Phys. Lett. 2021, 119, 254103. 10.1063/5.0072357. [DOI] [Google Scholar]

[ref86] Plakhotnik T.; Gruber D. Luminescence of nitrogen-vacancy centers in nanodiamonds at temperatures between 300 and 700 K: perspectives on nanothermometry. Phys. Chem. Chem. Phys. 2010, 12, 9751–9756. 10.1039/c001132k. [DOI] [PubMed] [Google Scholar]

[ref87] Anisimov A. N.; Simin D.; Soltamov V. A.; Lebedev S. P.; Baranov P. G.; Astakhov G. V.; Dyakonov V. Optical thermometry based on level anticrossing in silicon carbide. Scientific Reports 2016, 6, 33301. 10.1038/srep33301. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref88] Choi S.; Agafonov V. N.; Davydov V. A.; Plakhotnik T. Ultrasensitive All-Optical Thermometry Using Nanodiamonds with a High Concentration of Silicon-Vacancy Centers and Multiparametric Data Analysis. ACS Photonics 2019, 6 (6), 1387–1392. 10.1021/acsphotonics.9b00468. [DOI] [Google Scholar]

[ref89] Fujiwara M.; Uchida G.; Ohki I.; Liu M.; Tsurui A.; Yoshikawa T.; Nishikawa M.; Mizuochi N. All-optical nanoscale thermometry based on silicon-vacancy centers in detonation nanodiamonds. Carbon 2022, 198, 57–62. 10.1016/j.carbon.2022.06.076. [DOI] [Google Scholar]

[ref90] Nguyen C. T.; Evans R. E.; Sipahigil A.; Bhaskar M. K.; Sukachev D. D.; Agafonov V. N.; Davydov V. A.; Kulikova L. F.; Jelezko F.; Lukin M. D. All-optical nanoscale thermometry with silicon-vacancy centers in diamond. Appl. Phys. Lett. 2018, 112, 203102. 10.1063/1.5029904. [DOI] [Google Scholar]

[ref91] Zhang J.; He H.; Zhang T.; Wang L.; Gupta M.; Jing J.; Wang Z.; Wang Q.; Li K. H.; Wong K. K.-Y.; Chu Z. Two-Photon Excitation of Silicon-Vacancy Centers in Nanodiamonds for All-Optical Thermometry with a Noise Floor of 6.6 mK·Hz^–-1/2. The Journal of Physical Chemistry C 2023, 127 (6), 3013–3019. 10.1021/acs.jpcc.2c06966. [DOI] [Google Scholar]

[ref92] Fan J.-W.; Cojocaru I.; Becker J.; Fedotov I. V.; Alkahtani M. H. A.; Alajlan A.; Blakley S.; Rezaee M.; Lyamkina A.; Palyanov Y. N.; et al. Germanium-Vacancy Color Center in Diamond as a Temperature Sensor. ACS Photonics 2018, 5 (3), 765–770. 10.1021/acsphotonics.7b01465. [DOI] [Google Scholar]

[ref93] Tran T. T.; Regan B.; Ekimov E. A.; Mu Z.; Zhou Y.; Gao W.-b.; Narang P.; Solntsev A. S.; Toth M.; Aharonovich I.; Bradac C. Anti-Stokes excitation of solid-state quantum emitters for nanoscale thermometry. Science Advances 2019, 5 (5), eaav9180 10.1126/sciadv.aav9180. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref94] Osmic E.; Pezzagna S.; Lühmann T.; Böhlmann W.; Meijer J. Unusual temperature dependence of the photoluminescence emission of MgV centers in diamond. Appl. Phys. Lett. 2022, 121, 084101. 10.1063/5.0100409. [DOI] [Google Scholar]

[ref95] Alkahtani M.; Cojocaru I.; Liu X.; Herzig T.; Meijer J.; Küpper J.; Lühmann T.; Akimov A. V.; Hemmer P. R. Tin-vacancy in diamonds for luminescent thermometry. Appl. Phys. Lett. 2018, 112, 241902. 10.1063/1.5037053. [DOI] [Google Scholar]

[ref96] Chern M.; Kays J. C.; Bhuckory S.; Dennis A. M. Sensing with photoluminescent semiconductor quantum dots. Methods and Applications in Fluorescence 2019, 7, 012005. 10.1088/2050-6120/aaf6f8. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref97] Conceição P.; Barata J. F. B.; Hernández-Rodríguez M. A.; Lacerda P. S. S.; Neves M. G. P. M. S.; Carlos L. D.; Trindade T. Ratiometric nanothermometry via porphyrin inner filter effect applied to colloidal ZnS quantum dots. Sensors and Actuators A: Physical 2023, 357, 114382. 10.1016/j.sna.2023.114382. [DOI] [Google Scholar]

[ref98] Kumbhakar P.; Roy Karmakar A.; Das G. P.; Chakraborty J.; Tiwary C. S.; Kumbhakar P. Reversible temperature-dependent photoluminescence in semiconductor quantum dots for the development of a smartphone-based optical thermometer. Nanoscale 2021, 13 (5), 2946–2954. 10.1039/D0NR07874C. [DOI] [PubMed] [Google Scholar]

[ref99] Zhao H.; Vomiero A.; Rosei F. Tailoring the Heterostructure of Colloidal Quantum Dots for Ratiometric Optical Nanothermometry. Small 2020, 16 (28), 2000804. 10.1002/smll.202000804. [DOI] [PubMed] [Google Scholar]

[ref100] Lewis C.; Erikson J. W.; Sanchez D. A.; McClure C. E.; Nordin G. P.; Munro T. R.; Colton J. S. Use of Machine Learning with Temporal Photoluminescence Signals from CdTe Quantum Dots for Temperature Measurement in Microfluidic Devices. ACS Applied Nano Materials 2020, 3 (5), 4045–4053. 10.1021/acsanm.0c00065. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref101] Li S.; Zhang K.; Yang J.-M.; Lin L.; Yang H. Single Quantum Dots as Local Temperature Markers. Nano Letters 2007, 7 (10), 3102–3105. 10.1021/nl071606p. [DOI] [PubMed] [Google Scholar]

[ref102] Maestro L. M.; Haro-González P.; Sánchez-Iglesias A.; Liz-Marzán L. M.; García Solé J.; Jaque D. Quantum Dot Thermometry Evaluation of Geometry Dependent Heating Efficiency in Gold Nanoparticles. Langmuir 2014, 30 (6), 1650–1658. 10.1021/la403435v. [DOI] [PubMed] [Google Scholar]

[ref103] Munro T.; Liu L.; Glorieux C.; Ban H. CdSe/ZnS quantum dot fluorescence spectra shape-based thermometry via neural network reconstruction. J. Appl. Phys. 2016, 119, 214903. 10.1063/1.4953223. [DOI] [Google Scholar]

[ref104] Maestro L. M.; Jacinto C.; Silva U. R.; Vetrone F.; Capobianco J. A.; Jaque D.; Solé J. G. CdTe Quantum Dots as Nanothermometers: Towards Highly Sensitive Thermal Imaging. Small 2011, 7 (13), 1774–1778. 10.1002/smll.201002377. [DOI] [PubMed] [Google Scholar]

[ref105] Öner B.; Pomeroy J. W.; Kuball M. Submicrometer Resolution Hyperspectral Quantum Rod Thermal Imaging of Microelectronic Devices. ACS Applied Electronic Materials 2020, 2 (1), 93–102. 10.1021/acsaelm.9b00575. [DOI] [Google Scholar]

[ref106] Han Y.; Liu Y.; Zhao H.; Vomiero A.; Li R. Highly efficient ratiometric nanothermometers based on colloidal carbon quantum dots. Journal of Materials Chemistry B 2021, 9 (20), 4111–4119. 10.1039/D1TB00224D. [DOI] [PubMed] [Google Scholar]

[ref107] Sehrawat P.; Abid; Islam S. S. An ultrafast quantum thermometer from graphene quantum dots. Nanoscale Advances 2019, 1 (5), 1772–1783. 10.1039/C8NA00361K. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref108] Wang C.; Hu T.; Thomas T.; Song S.; Wen Z.; Wang C.; Song Q.; Yang M. Surface state-controlled C-dot/C-dot based dual-emission fluorescent nanothermometers for intra-cellular thermometry. Nanoscale 2018, 10 (46), 21809–21817. 10.1039/C8NR07445C. [DOI] [PubMed] [Google Scholar]

[ref109] Fanizza E.; Zhao H.; De Zio S.; Depalo N.; Rosei F.; Vomiero A.; Curri M. L.; Striccoli M. Encapsulation of Dual Emitting Giant Quantum Dots in Silica Nanoparticles for Optical Ratiometric Temperature Nanosensors. Applied Sciences 2020, 10, 2767. 10.3390/app10082767. [DOI] [Google Scholar]

[ref110] Liu J.; Zhang H.; Selopal G. S.; Sun S.; Zhao H.; Rosei F. Visible and Near-Infrared, Multiparametric, Ultrasensitive Nanothermometer Based on Dual-Emission Colloidal Quantum Dots. ACS Photonics 2019, 6 (10), 2479–2486. 10.1021/acsphotonics.9b00763. [DOI] [Google Scholar]

[ref111] Liu W.; Zhang Y.; Wu H.; Feng Y.; Zhang T.; Gao W.; Chu H.; Yin J.; Cui T.; Wang Y.; et al. Planar temperature sensing using heavy-metal-free quantum dots with micrometer resolution. Nanotechnology 2014, 25, 285501. 10.1088/0957-4484/25/28/285501. [DOI] [PubMed] [Google Scholar]

[ref112] Lin X.; Kong M.; Wu N.; Gu Y.; Qiu X.; Chen X.; Li Z.; Feng W.; Li F. Measurement of Temperature Distribution at the Nanoscale with Luminescent Probes Based on Lanthanide Nanoparticles and Quantum Dots. ACS Applied Materials & Interfaces 2020, 12 (47), 52393–52401. 10.1021/acsami.0c15697. [DOI] [PubMed] [Google Scholar]

[ref113] Qiu X.; Zhou Q.; Zhu X.; Wu Z.; Feng W.; Li F. Ratiometric upconversion nanothermometry with dual emission at the same wavelength decoded via a time-resolved technique. Nature Communications 2020, 11, 4. 10.1038/s41467-019-13796-w. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref114] Cao S.; Zheng J.; Zhao J.; Yang Z.; Shang M.; Li C.; Yang W.; Fang X. Robust and Stable Ratiometric Temperature Sensor Based on Zn-In-S Quantum Dots with Intrinsic Dual-Dopant Ion Emissions. Advanced Functional Materials 2016, 26 (40), 7224–7233. 10.1002/adfm.201603201. [DOI] [Google Scholar]

[ref115] Marciniak L.; Kniec K.; Elżbieciak-Piecka K.; Trejgis K.; Stefanska J.; Dramićanin M. Luminescence thermometry with transition metal ions. A review. Coord. Chem. Rev. 2022, 469, 214671. 10.1016/j.ccr.2022.214671. [DOI] [Google Scholar]

[ref116] Kniec K.; Ledwa K.; Maciejewska K.; Marciniak L. Intentional modification of the optical spectral response and relative sensitivity of luminescent thermometers based on Fe³⁺,Cr³⁺,Nd³⁺ co-doped garnet nanocrystals by crystal field strength optimization. Materials Chemistry Frontiers 2020, 4 (6), 1697–1705. 10.1039/D0QM00097C. [DOI] [Google Scholar]

[ref117] Qin Y.; Zhong F.; Bian Y.; Hariyani S.; Cao Y.; Brgoch J.; Seto T.; Brik M. G.; Srivastava A. M.; Wang X.; Wang Y. Sensitive and Reliable Fluorescent Thermometer Based on a Red-Emitting Li2MgHfO4:Mn4+ Phosphor. Inorganic Chemistry 2022, 61 (21), 8126–8134. 10.1021/acs.inorgchem.1c03971. [DOI] [PubMed] [Google Scholar]

[ref118] Wang Q.; Liao M.; Mu Z.; Zhang X.; Dong H.; Liang Z.; Luo J.; Yang Y.; Wu F. Ratiometric Optical Thermometer with High Sensitivity Based on Site-Selective Occupancy of Mn2+ Ions in Li5Zn8Al5Ge9O36 under Controllable Synthesis Atmosphere. The Journal of Physical Chemistry C 2020, 124 (1), 886–895. 10.1021/acs.jpcc.9b09379. [DOI] [Google Scholar]

[ref119] Back M.; Ueda J.; Brik M. G.; Tanabe S. Pushing the Limit of Boltzmann Distribution in Cr³⁺-Doped CaHfO₃ for Cryogenic Thermometry. ACS Applied Materials & Interfaces 2020, 12 (34), 38325–38332. 10.1021/acsami.0c08965. [DOI] [PubMed] [Google Scholar]

[ref120] Glais E.; Pellerin M.; Castaing V.; Alloyeau D.; Touati N.; Viana B.; Chanéac C. Luminescence properties of ZnGa₂O₄:Cr³⁺,Bi³⁺ nanophosphors for thermometry applications. RSC Advances 2018, 8 (73), 41767–41774. 10.1039/C8RA08182D. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref121] Kabański A.; Ptak M.; Stefańska D. Metal-Organic Framework Optical Thermometer Based on Cr³⁺ Ion Luminescence. ACS Applied Materials & Interfaces 2023, 15 (5), 7074–7082. 10.1021/acsami.2c19957. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref122] Pflitsch C.; Viefhaus D.; Atakan B. CVD of Thin Ruby Films on Si(100) and Stainless Steel for Surface Temperature Sensor Applications. Chemical Vapor Deposition 2007, 13 (8), 420–426. 10.1002/cvde.200606564. [DOI] [Google Scholar]

[ref123] Ueda J.; Back M.; Brik M. G.; Zhuang Y.; Grinberg M.; Tanabe S. Ratiometric optical thermometry using deep red luminescence from ⁴T₂ and ²E states of Cr³⁺ in ZnGa₂O₄ host. Optical Materials 2018, 85, 510–516. 10.1016/j.optmat.2018.09.013. [DOI] [Google Scholar]

[ref124] Glais E.; Đorđević V.; Papan J.; Viana B.; Dramićanin M. D. MgTiO₃:Mn⁴⁺ a multi-reading temperature nanoprobe. RSC Advances 2018, 8 (33), 18341–18346. 10.1039/C8RA02482K. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref125] Qin T.; Liu B.; Zhu K.; Luo Z.; Huang Y.; Pan C.; Wang L. Organic fluorescent thermometers: Highlights from 2013 to 2017. Trends in Analytical Chemistry 2018, 102, 259–271. 10.1016/j.trac.2018.03.003. [DOI] [Google Scholar]

[ref126] Jung W.; Kim Y. W.; Yim D.; Yoo J. Y. Microscale surface thermometry using SU8/Rhodamine-B thin layer. Sensors and Actuators A: Physical 2011, 171, 228–232. 10.1016/j.sna.2011.06.025. [DOI] [Google Scholar]

[ref127] Ross D.; Gaitan M.; Locascio L. E. Temperature Measurement in Microfluidic Systems Using a Temperature-Dependent Fluorescent Dye. Anal. Chem. 2001, 73 (17), 4117–4123. 10.1021/ac010370l. [DOI] [PubMed] [Google Scholar]

[ref128] Benninger R. K. P.; Koç Y.; Hofmann O.; Requejo-Isidro J.; Neil M. A. A.; French P. M. W.; deMello A. J. Quantitative 3D Mapping of Fluidic Temperatures within Microchannel Networks Using Fluorescence Lifetime Imaging. Anal. Chem. 2006, 78 (7), 2272–2278. 10.1021/ac051990f. [DOI] [PubMed] [Google Scholar]

[ref129] Cai H.; Lu W.; Yang C.; Zhang M.; Li M.; Che C.-M.; Li D. Tandem Förster Resonance Energy Transfer Induced Luminescent Ratiometric Thermometry in Dye-Encapsulated Biological Metal-Organic Frameworks. Advanced Optical Materials 2019, 7 (2), 1801149. 10.1002/adom.201801149. [DOI] [Google Scholar]

[ref130] Huang Z.; Li N.; Zhang X.; Xiao Y. Mitochondria-Anchored Molecular Thermometer Quantitatively Monitoring Cellular Inflammations. Anal. Chem. 2021, 93 (12), 5081–5088. 10.1021/acs.analchem.0c04547. [DOI] [PubMed] [Google Scholar]

[ref131] Cao C.; Liu X.; Qiao Q.; Zhao M.; Yin W.; Mao D.; Zhang H.; Xu Z. A twisted-intramolecular-charge-transfer (TICT) based ratiometric fluorescent thermometer with a mega-Stokes shift and a positive temperature coefficient. Chemical Communications 2014, 50 (99), 15811–15814. 10.1039/C4CC08010F. [DOI] [PubMed] [Google Scholar]

[ref132] Ebert S.; Travis K.; Lincoln B.; Guck J. Fluorescence ratio thermometry in a microfluidic dual-beam laser trap. Opt. Express 2007, 15 (23), 15493–15499. 10.1364/OE.15.015493. [DOI] [PubMed] [Google Scholar]

[ref133] Fogg D.; David M.; Goodson K. Non-invasive measurement of void fraction and liquid temperature in microchannel flow boiling. Experiments in Fluids 2009, 46, 725–736. 10.1007/s00348-008-0604-3. [DOI] [Google Scholar]

[ref134] Natrajan V. K.; Christensen K. T. Two-color laser-induced fluorescent thermometry for microfluidic systems. Measurement Science and Technology 2009, 20, 015401. 10.1088/0957-0233/20/1/015401. [DOI] [Google Scholar]

[ref135] Nakano M.; Arai Y.; Kotera I.; Okabe K.; Kamei Y.; Nagai T. Genetically encoded ratiometric fluorescent thermometer with wide range and rapid response. PLOS ONE 2017, 12 (2), e0172344 10.1371/journal.pone.0172344. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref136] Gong M.; Li Z.; Wang Q.; Xiang W.; Xia T.; Zhao D. Encapsulating Rhodamine B in the NbO-type metal-organic framework to construct dual-emitting ratiometric thermometer. J. Solid State Chem. 2022, 311, 123147. 10.1016/j.jssc.2022.123147. [DOI] [Google Scholar]

[ref137] Peng M.; Kaczmarek A. M.; Van Hecke K. Ratiometric Thermometers Based on Rhodamine B and Fluorescein Dye-Incorporated (Nano) Cyclodextrin Metal-Organic Frameworks. ACS Applied Materials & Interfaces 2022, 14 (12), 14367–14379. 10.1021/acsami.2c01332. [DOI] [PubMed] [Google Scholar]

[ref138] Zhang H.; Lin C.; Sheng T.; Hu S.; Zhuo C.; Fu R.; Wen Y.; Li H.; Su S.; Wu X. A Luminescent Metal-Organic Framework Thermometer with Intrinsic Dual Emission from Organic Lumophores. Chem.-Eur. J. 2016, 22 (13), 4460–4468. 10.1002/chem.201504432. [DOI] [PubMed] [Google Scholar]

[ref139] Wan Y.; Yu L.; Xia T. A dye-loaded nonlinear metal-organic framework as self-calibrated optical thermometer. Dyes and Pigments 2022, 202, 110234. 10.1016/j.dyepig.2022.110234. [DOI] [Google Scholar]

[ref140] Kaczmarek A. M.; Suta M.; Rijckaert H.; van Swieten T. P.; Van Driessche I.; Kaczmarek M. K.; Meijerink A. High temperature (nano)thermometers based on LiLuF₄:Er³⁺,Yb³⁺ nano- and microcrystals. Confounded results for core-shell nanocrystals. Journal of Materials Chemistry C 2021, 9 (10), 3589–3600. 10.1039/D0TC05865C. [DOI] [Google Scholar]

[ref141] Geitenbeek R. G.; Prins P. T.; Albrecht W.; van Blaaderen A.; Weckhuysen B. M.; Meijerink A. NaYF4:Er³⁺,Yb³⁺/SiO₂ Core/Shell Upconverting Nanocrystals for Luminescence Thermometry up to 900 K. The Journal of Physical Chemistry C 2017, 121 (6), 3503–3510. 10.1021/acs.jpcc.6b10279. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref142] Yuan M.; Han K.; Wang L.; Yang X.; Yang Z.; Wang H.; Xu X. Highly thermally stable upconversion in copper(II)-doped LiYF₄:Yb,Er microcrystals toward ultrahigh temperature (micro)thermometers. J. Alloys Compd. 2022, 919, 165844. 10.1016/j.jallcom.2022.165844. [DOI] [Google Scholar]

[ref143] Li H.; Wang S.; Pang R.; Jiang L.; Li D.; Zhang S.; Li C.; Zhang H. Pr³⁺ doped Y₃GaO₆ luminescent thermometer for high temperature conditions. Mater. Res. Bull. 2023, 165, 112297. 10.1016/j.materresbull.2023.112297. [DOI] [Google Scholar]

[ref144] Chen Y.; White S.; Ekimov E. A.; Bradac C.; Toth M.; Aharonovich I.; Tran T. T. Ultralow-Power Cryogenic Thermometry Based on Optical-Transition Broadening of a Two-Level System in Diamond. ACS Photonics 2023, 10 (8), 2481–2487. 10.1021/acsphotonics.2c01622. [DOI] [Google Scholar]

[ref145] Liu X.; Akerboom S.; Jong M. d.; Mutikainen I.; Tanase S.; Meijerink A.; Bouwman E. Mixed-Lanthanoid Metal-Organic Framework for Ratiometric Cryogenic Temperature Sensing. Inorganic Chemistry 2015, 54 (23), 11323–11329. 10.1021/acs.inorgchem.5b01924. [DOI] [PubMed] [Google Scholar]

[ref146] N’Dala-Louika I.; Ananias D.; Latouche C.; Dessapt R.; Carlos L. D.; Serier-Brault H. Ratiometric mixed Eu-Tb metal-organic framework as a new cryogenic luminescent thermometer. Journal of Materials Chemistry C 2017, 5 (42), 10933–10937. 10.1039/C7TC03223D. [DOI] [Google Scholar]

[ref147] Fukami M.; Yale C. G.; Andrich P.; Liu X.; Heremans F. J.; Nealey P. F.; Awschalom D. D. All-Optical Cryogenic Thermometry Based on Nitrogen-Vacancy Centers in Nanodiamonds. Physical Review Applied 2019, 12, 014042. 10.1103/PhysRevApplied.12.014042. [DOI] [Google Scholar]

[ref148] Zhao D.; Yue D.; Zhang L.; Jiang K.; Qian G. Cryogenic Luminescent Tb/Eu-MOF Thermometer Based on a Fluorine-Modified Tetracarboxylate Ligand. Inorganic Chemistry 2018, 57 (20), 12596–12602. 10.1021/acs.inorgchem.8b01746. [DOI] [PubMed] [Google Scholar]

[ref149] Pavani K.; Neves A. J.; Pinto R. J. B.; Freire C. S. R.; Soares M. J.; Graça M. P. F.; Kumar K. U.; Jakka S. K. BiLaWO₆: Er³⁺/Tm³⁺/Yb³⁺ phosphor: Study of multiple fluorescence intensity ratiometric thermometry at cryogenic temperatures. Ceram. Int. 2022, 48 (21), 31344–31353. 10.1016/j.ceramint.2022.06.316. [DOI] [Google Scholar]

[ref150] Li H.; Wu H.; Pang R.; Liu G.; Zhang S.; Jiang L.; Li D.; Li C.; Feng J.; Zhang H. Investigation on the photoluminescence and thermoluminescence of BaGa₂O₄:Bi³⁺ at extremely low temperatures. Journal of Materials Chemistry C 2021, 9 (5), 1786–1793. 10.1039/D0TC05122E. [DOI] [Google Scholar]

[ref151] Ren M.; Brites C. D. S.; Bao S.-S.; Ferreira R. A. S.; Zheng L.-M.; Carlos L. D. A cryogenic luminescent ratiometric thermometer based on a lanthanide phosphonate dimer. Journal of Materials Chemistry C 2015, 3 (33), 8480–8484. 10.1039/C5TC01468A. [DOI] [Google Scholar]

[ref152] Cui Y.; Zou W.; Song R.; Yu J.; Zhang W.; Yang Y.; Qian G. A ratiometric and colorimetric luminescent thermometer over a wide temperature range based on a lanthanide coordination polymer. Chemical Communications 2014, 50 (6), 719–721. 10.1039/C3CC47225F. [DOI] [PubMed] [Google Scholar]

[ref153] Bolek P.; Zeler J.; Brites C. D. S.; Trojan-Piegza J.; Carlos L. D.; Zych E. Ga-modified YAG:Pr³⁺ dual-mode tunable luminescence thermometers. Chemical Engineering Journal 2021, 421, 129764. 10.1016/j.cej.2021.129764. [DOI] [Google Scholar]

[ref154] Liang Z.; Wu J.; Cui Y.; Sun H.; Ning C.-Z. Self-optimized single-nanowire photoluminescence thermometry. Light: Science & Applications 2023, 12, 36. 10.1038/s41377-023-01070-0. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref155] Casar J. R.; McLellan C. A.; Siefe C.; Dionne J. A. Lanthanide-Based Nanosensors: Refining Nanoparticle Responsiveness for Single Particle Imaging of Stimuli. ACS Photonics 2021, 8 (1), 3–17. 10.1021/acsphotonics.0c00894. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref156] Zhou J.; Chizhik A. I.; Chu S.; Jin D. Single-particle spectroscopy for functional nanomaterials. Nature 2020, 579, 41–50. 10.1038/s41586-020-2048-8. [DOI] [PubMed] [Google Scholar]

[ref157] de Oliveira Lima K.; dos Santos L. F.; Galvão R.; Tedesco A. C.; de Souza Menezes L.; Gonçalves R. R. Single Er³⁺, Yb³⁺: KGd₃F₁₀ Nanoparticles for Nanothermometry. Frontiers in Chemistry 2021, 9, 712659.Original Research. 10.3389/fchem.2021.712659. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref158] Xie W.; Gomes R.; Aubert T.; Bisschop S.; Zhu Y.; Hens Z.; Brainis E.; Van Thourhout D. Nanoscale and Single-Dot Patterning of Colloidal Quantum Dots. Nano Letters 2015, 15 (11), 7481–7487. 10.1021/acs.nanolett.5b03068. [DOI] [PubMed] [Google Scholar]

[ref159] Fringes S.; Schwemmer C.; Rawlings C. D.; Knoll A. W. Deterministic Deposition of Nanoparticles with Sub-10 nm Resolution. Nano Letters 2019, 19 (12), 8855–8861. 10.1021/acs.nanolett.9b03687. [DOI] [PubMed] [Google Scholar]

[ref160] Laraoui A.; Aycock-Rizzo H.; Gao Y.; Lu X.; Riedo E.; Meriles C. A. Imaging thermal conductivity with nanoscale resolution using a scanning spin probe. Nature Communications 2015, 6, 8954. 10.1038/ncomms9954. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref161] Zimmers A.; Aigouy L.; Mortier M.; Sharoni A.; Wang S.; West K. G.; Ramirez J. G.; Schuller I. K. Role of Thermal Heating on the Voltage Induced Insulator-Metal Transition in VO₂. Phys. Rev. Lett. 2013, 110, 056601. 10.1103/PhysRevLett.110.056601. [DOI] [PubMed] [Google Scholar]

[ref162] Pessoa A. R.; Galindo J. A. O.; dos Santos L. F.; Goncalves R. R.; Maier S. A.; Menezes L. d. S.; Amaral A. M. Correction Due to Nonthermally Coupled Emission Bands and Its Implications on the Performance of Y₂O₃:Yb³⁺ /Er³⁺ Single-Particle Thermometers. J. Phys. Chem. C 2023, 127 (20), 9673–9680. 10.1021/acs.jpcc.3c00522. [DOI] [Google Scholar]

[ref163] Avram D.; Porosnicu I.; Patrascu A.; Tiseanu C. Real-Time Thermal Imaging based on the Simultaneous Rise and Decay Luminescence Lifetime Thermometry. Advanced Photonics Research 2022, 3 (6), 2100208. 10.1002/adpr.202100208. [DOI] [Google Scholar]

[ref164] Rafiei Miandashti A.; Kordesch M. E.; Richardson H. H. Effect of Temperature and Gold Nanoparticle Interaction on the Lifetime and Luminescence of NaYF4:Yb³⁺:Er³⁺ Upconverting Nanoparticles. ACS Photonics 2017, 4 (7), 1864–1869. 10.1021/acsphotonics.7b00512. [DOI] [Google Scholar]

[ref165] Savchuk O. A.; Haro-González P.; Carvajal J. J.; Jaque D.; Massons J.; Aguiló M.; Díaz F. Er:Yb:NaY₂F₅O up-converting nanoparticles for sub-tissue fluorescence lifetime thermal sensing. Nanoscale 2014, 6 (16), 9727–9733. 10.1039/C4NR02305F. [DOI] [PubMed] [Google Scholar]

[ref166] Zhou X.; Xia X.; Smith B. E.; Lim M. B.; Bard A. B.; Pant A.; Pauzauskie P. J. Interface-Dependent Radiative Lifetimes of Yb³⁺, Er³⁺ Co-doped Single NaYF₄ Upconversion Nanowires. ACS Applied Materials & Interfaces 2019, 11 (25), 22817–22823. 10.1021/acsami.8b17271. [DOI] [PubMed] [Google Scholar]

[ref167] Jiang Y.; Tong Y.; Chen S.; Zhang W.; Hu F.; Wei R.; Guo H. A three-mode self-referenced optical thermometry based on up-conversion luminescence of Ca₂MgWO₆:Er³⁺,Yb³⁺ phosphors. Chemical Engineering Journal 2021, 413, 127470. 10.1016/j.cej.2020.127470. [DOI] [Google Scholar]

[ref168] Savchuk O. A.; Carvajal J. J.; Pujol M. C.; Massons J.; Haro-González P.; Martínez O.; Jiménez J.; Aguiló M.; Díaz F. New strategies invonving upconverting nanoparticles for determining moderate temperatures by luminescence thermometry. J. Lumin. 2016, 169, 711–716. 10.1016/j.jlumin.2015.05.016. [DOI] [Google Scholar]

[ref169] Raab M. E.; Maurizio S. L.; Capobianco J. A.; Prasad P. N. Lifetime of the ³H₄ Electronic State in Tm³⁺-Doped Upconverting Nanoparticles for NIR Nanothermometry. The Journal of Physical Chemistry B 2021, 125 (48), 13132–13136. 10.1021/acs.jpcb.1c07659. [DOI] [PubMed] [Google Scholar]

[ref170] Marciniak L.; Trejgis K. Luminescence lifetime thermometry with Mn³⁺-Mn⁴⁺ co-doped nanocrystals. Journal of Materials Chemistry C 2018, 6 (26), 7092–7100. 10.1039/C8TC01981A. [DOI] [Google Scholar]

[ref171] Haro-González P.; Martínez-Maestro L.; Martín I. R.; García-Solé J.; Jaque D. High-Sensitivity Fluorescence Lifetime Thermal Sensing Based on CdTe Quantum Dots. Small 2012, 8 (17), 2652–2658. 10.1002/smll.201102736. [DOI] [PubMed] [Google Scholar]

[ref172] Yakunin S.; Benin B. M.; Shynkarenko Y.; Nazarenko O.; Bodnarchuk M. I.; Dirin D. N.; Hofer C.; Cattaneo S.; Kovalenko M. V. High-resolution remote thermometry and thermography using luminescent low-dimensional tin-halide perovskites. Nat. Mater. 2019, 18, 846–852. 10.1038/s41563-019-0416-2. [DOI] [PubMed] [Google Scholar]

[ref173] Li G.; Chen X.; Wang M.; Cheng S.; Yang D.; Wu D.; Han Y.; Jia M.; Li X.; Zhang Y.; et al. Regulating Exciton De-trapping of Te⁴⁺-doped Zero-Dimensional Scandium-Halide Perovskite for Fluorescence Thermometry with Record High Time-Resolved Thermal Sensitivity. Adv. Mater. 2023, 35, 2305495. 10.1002/adma.202305495. [DOI] [PubMed] [Google Scholar]

[ref174] Caixeta F. J.; Bastos A. R. N.; Botas A. M. P.; Rosa L. S.; Souza V. S.; Borges F. H.; Neto A. N. C.; Ferrier A.; Goldner P.; Carlos L. D.; et al. High-Quantum-Yield Upconverting Er³⁺/Yb³⁺-Organic-Inorganic Hybrid Dual Coatings for Real-Time Temperature Sensing and Photothermal Conversion. The Journal of Physical Chemistry C 2020, 124 (37), 19892–19903. 10.1021/acs.jpcc.0c03874. [DOI] [Google Scholar]

[ref175] Chen Y.; Li C.; Yang T.; Ekimov E. A.; Bradac C.; Ha S. T.; Toth M.; Aharonovich I.; Tran T. T. Real-Time Ratiometric Optical Nanoscale Thermometry. ACS Nano 2023, 17 (3), 2725–2736. 10.1021/acsnano.2c10974. [DOI] [PubMed] [Google Scholar]

[ref176] Piñol R.; Brites C. D. S.; Bustamante R.; Martínez A.; Silva N. J. O.; Murillo J. L.; Cases R.; Carrey J.; Estepa C.; Sosa C.; et al. Joining Time-Resolved Thermometry and Magnetic-Induced Heating in a Single Nanoparticle Unveils Intriguing Thermal Properties. ACS Nano 2015, 9 (3), 3134–3142. 10.1021/acsnano.5b00059. [DOI] [PubMed] [Google Scholar]

[ref177] Xiang G.; Xia Q.; Liu X.; Wang Y.; Jiang S.; Li L.; Zhou X.; Ma L.; Wang X.; Zhang J. Upconversion nanoparticles modified by Cu₂S for photothermal therapy along with real-time optical thermometry. Nanoscale 2021, 13 (15), 7161–7168. 10.1039/D0NR09115D. [DOI] [PubMed] [Google Scholar]

[ref178] Rafiei Miandashti A.; Khosravi Khorashad L.; Govorov A. O.; Kordesch M. E.; Richardson H. H. Time-Resolved Temperature-Jump Measurements and Theoretical Simulations of Nanoscale Heat Transfer Using NaYF₄:Yb³⁺:Er³⁺ Upconverting Nanoparticles. The Journal of Physical Chemistry C 2019, 123 (6), 3770–3780. 10.1021/acs.jpcc.8b11215. [DOI] [Google Scholar]

[ref179] Tzeng Y.-K.; Tsai P.-C.; Liu H.-Y.; Chen O. Y.; Hsu H.; Yee F.-G.; Chang M.-S.; Chang H.-C. Time-Resolved Luminescence Nanothermometry with Nitrogen-Vacancy Centers in Nanodiamonds. Nano Letters 2015, 15 (6), 3945–3952. 10.1021/acs.nanolett.5b00836. [DOI] [PubMed] [Google Scholar]

[ref180] Yun J.; Kim K.; Park S.; Kim D. Temperature Selective Thermometry with Sub-Microsecond Time Resolution Using Dressed-Spin States in Diamond. Advanced Quantum Technologies 2021, 4 (11), 2100084. 10.1002/qute.202100084. [DOI] [Google Scholar]

[ref181] Löw P.; Kim B.; Takama N.; Bergaud C. High-Spatial-Resolution Surface-Temperature Mapping Using Fluorescent Thermometry. Small 2008, 4 (7), 908–914. 10.1002/smll.200700581. [DOI] [PubMed] [Google Scholar]

[ref182] Hui Y. Y.; Chen O. Y.; Azuma T.; Chang B.-M.; Hsieh F.-J.; Chang H.-C. All-Optical Thermometry with Nitrogen-Vacancy Centers in Nanodiamond-Embedded Polymer Films. The Journal of Physical Chemistry C 2019, 123 (24), 15366–15374. 10.1021/acs.jpcc.9b04496. [DOI] [Google Scholar]

[ref183] Chen Y.; Tran T. N.; Duong N. M. H.; Li C.; Toth M.; Bradac C.; Aharonovich I.; Solntsev A.; Tran T. T. Optical Thermometry with Quantum Emitters in Hexagonal Boron Nitride. ACS Applied Materials & Interfaces 2020, 12 (22), 25464–25470. 10.1021/acsami.0c05735. [DOI] [PubMed] [Google Scholar]

[ref184] Mi C.; Zhou J.; Wang F.; Lin G.; Jin D. Ultrasensitive Ratiometric Nanothermometer with Large Dynamic Range and Photostability. Chem. Mater. 2019, 31 (22), 9480–9487. 10.1021/acs.chemmater.9b03466. [DOI] [Google Scholar]

[ref185] Brites C. D. S.; Lima P. P.; Silva N. J. O.; Millán A.; Amaral V. S.; Palacio F.; Carlos L. D. A Luminescent Molecular Thermometer for Long-Term Absolute Temperature Measurements at the Nanoscale. Adv. Mater. 2010, 22 (40), 4499–4504. 10.1002/adma.201001780. [DOI] [PubMed] [Google Scholar]

[ref186] Andrich P.; Li J.; Liu X.; Heremans F. J.; Nealey P. F.; Awschalom D. D. Microscale-Resolution Thermal Mapping Using a Flexible Platform of Patterned Quantum Sensors. Nano Letters 2018, 18 (8), 4684–4690. 10.1021/acs.nanolett.8b00895. [DOI] [PubMed] [Google Scholar]

[ref187] Rodrigues M.; Piñol R.; Antorrena G.; Brites C. D. S.; Silva N. J. O.; Murillo J. L.; Cases R.; Díez I.; Palacio F.; Torras N.; et al. Implementing Thermometry on Silicon Surfaces Functionalized by Lanthanide-Doped Self-Assembled Polymer Monolayers. Advanced Functional Materials 2016, 26 (2), 200–209. 10.1002/adfm.201503889. [DOI] [Google Scholar]

[ref188] Ramalho J. F. C. B.; Correia S. F. H.; Fu L.; António L. L. F.; Brites C. D. S.; André P. S.; Ferreira R. A. S.; Carlos L. D. Luminescence Thermometry on the Route of the Mobile-Based Internet of Things (IoT): How Smart QR Codes Make It Real. Advanced Science 2019, 6 (19), 1900950. 10.1002/advs.201900950. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref189] Martínez E. D.; Brites C. D. S.; Carlos L. D.; García-Flores A. F.; Urbano R. R.; Rettori C. Electrochromic Switch Devices Mixing Small- and Large-Sized Upconverting Nanocrystals. Advanced Functional Materials 2019, 29 (8), 1807758. 10.1002/adfm.201807758. [DOI] [Google Scholar]

[ref190] Glais E.; Maître A.; Viana B.; Chanéac C. Experimental measurement of local high temperature at the surface of gold nanorods using doped ZnGa₂O₄ as a nanothermometer. Nanoscale Advances 2021, 3 (10), 2862–2869. 10.1039/D1NA00010A. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref191] Brites C. D. S.; Fuertes M. C.; Angelomé P. C.; Martínez E. D.; Lima P. P.; Soler-Illia G. J. A. A.; Carlos L. D. Tethering Luminescent Thermometry and Plasmonics: Light Manipulation to Assess Real-Time Thermal Flow in Nanoarchitectures. Nano Letters 2017, 17 (8), 4746–4752. 10.1021/acs.nanolett.7b01433. [DOI] [PubMed] [Google Scholar]

[ref192] Rohani S.; Quintanilla M.; Tuccio S.; De Angelis F.; Cantelar E.; Govorov A. O.; Razzari L.; Vetrone F. Enhanced Luminescence, Collective Heating, and Nanothermometry in an Ensemble System Composed of Lanthanide-Doped Upconverting Nanoparticles and Gold Nanorods. Advanced Optical Materials 2015, 3 (11), 1606–1613. 10.1002/adom.201500380. [DOI] [Google Scholar]

[ref193] Debasu M. L.; Ananias D.; Pastoriza-Santos I.; Liz-Marzán L. M.; Rocha J.; Carlos L. D. All-In-One Optical Heater-Thermometer Nanoplatform Operative From 300 to 2000 K Based on Er³⁺ Emission and Blackbody Radiation. Adv. Mater. 2013, 25 (35), 4868–4874. 10.1002/adma.201300892. [DOI] [PubMed] [Google Scholar]

[ref194] Martínez E. D.; Urbano R. R.; Rettori C. Thermoplasmonic Maskless Lithography on Upconverting Nanocomposites Assisted by Gold Nanostars. ACS Applied Nano Materials 2019, 2 (11), 6889–6897. 10.1021/acsanm.9b01355. [DOI] [Google Scholar]

[ref195] Huang Y.; Rosei F.; Vetrone F. A single multifunctional nanoplatform based on upconversion luminescence and gold nanorods. Nanoscale 2015, 7 (12), 5178–5185. 10.1039/C4NR07369J. [DOI] [PubMed] [Google Scholar]

[ref196] Baral S.; Johnson S. C.; Alaulamie A. A.; Richardson H. H. Nanothermometry using optically trapped erbium oxide nanoparticle. Appl. Phys. A: Mater. Sci. Process. 2016, 122, 340. 10.1007/s00339-016-9886-0. [DOI] [Google Scholar]

[ref197] Geitenbeek R. G.; Salzmann B. B. V.; Nieuwelink A.-E.; Meijerink A.; Weckhuysen B. M. Chemically and thermally stable lanthanide-doped Y₂O₃ nanoparticles for remote temperature sensing in catalytic environments. Chem. Eng. Sci. 2019, 198, 235–240. 10.1016/j.ces.2018.10.004. [DOI] [Google Scholar]

[ref198] Jena H. S.; Rijckaert H.; Krishnaraj C.; Van Driessche I.; Van Der Voort P.; Kaczmarek A. M. Hybrid Nanocomposites Formed by Lanthanide Nanoparticles in Zr-MOF for Local Temperature Measurements during Catalytic Reactions. Chem. Mater. 2021, 33 (20), 8007–8017. 10.1021/acs.chemmater.1c02126. [DOI] [Google Scholar]

[ref199] Krishnaraj C.; Rijckaert H.; Jena H. S.; Van Der Voort P.; Kaczmarek A. M. Upconverting Er³⁺-Yb³⁺ Inorganic/Covalent Organic Framework Core-Shell Nanoplatforms for Simultaneous Catalysis and Nanothermometry. ACS Applied Materials & Interfaces 2021, 13 (39), 47010–47018. 10.1021/acsami.1c11314. [DOI] [PubMed] [Google Scholar]

[ref200] Sun J.; Rijckaert H.; Maegawa Y.; Inagaki S.; Van Der Voort P.; Kaczmarek A. M. Luminescent Nanorattles Based on Bipyridine Periodic Mesoporous Organosilicas for Simultaneous Thermometry and Catalysis. Chem. Mater. 2022, 34 (8), 3770–3780. 10.1021/acs.chemmater.2c00215. [DOI] [Google Scholar]

[ref201] Kaczmarek A. M.; Jena H. S.; Krishnaraj C.; Rijckaert H.; Veerapandian S. K. P.; Meijerink A.; Van Der Voort P. Luminescent Ratiometric Thermometers Based on a 4f-3d Grafted Covalent Organic Framework to Locally Measure Temperature Gradients During Catalytic Reactions. Angewandte Chemie International Edition 2021, 60 (7), 3727–3736. 10.1002/anie.202013377. [DOI] [PubMed] [Google Scholar]

[ref202] Gomez G. E.; Kaczmarek A. M.; Van Deun R.; Brusau E. V.; Narda G. E.; Vega D.; Iglesias M.; Gutierrez-Puebla E.; Monge M. Á. Photoluminescence, Unconventional-Range Temperature Sensing, and Efficient Catalytic Activities of Lanthanide Metal-Organic Frameworks. Eur. J. Inorg. Chem. 2016, 2016 (10), 1577–1588. 10.1002/ejic.201501402. [DOI] [Google Scholar]

[ref203] Terlingen B. J. P.; Arens T.; van Swieten T. P.; Rabouw F. T.; Prins P. T.; de Beer M. M.; Meijerink A.; Ahr M. P.; Hutter E. M.; van Lare C. E. J.; Weckhuysen B. M. Bifunctional Europium for Operando Catalyst Thermometry in an Exothermic Chemical Reaction. Angewandte Chemie International Edition 2022, 61 (52), e202211991 10.1002/anie.202211991. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref204] van Ravenhorst I. K.; Geitenbeek R. G.; van der Eerden M. J.; Tijn van Omme J.; Peréz Garza H. H.; Meirer F.; Meijerink A.; Weckhuysen B. M. In Situ Local Temperature Mapping in Microscopy Nano-Reactors with Luminescence Thermometry. ChemCatChem 2019, 11 (22), 5505–5512. 10.1002/cctc.201900985. [DOI] [Google Scholar]

[ref205] Hartman T.; Geitenbeek R. G.; Whiting G. T.; Weckhuysen B. M. Operando monitoring of temperature and active species at the single catalyst particle level. Nature Catalysis 2019, 2, 986–996. 10.1038/s41929-019-0352-1. [DOI] [Google Scholar]

[ref206] Ye Z.; Bommidi D. K.; Pickel A. D. Dual-Mode Operando Raman Spectroscopy and Upconversion Thermometry for Probing Thermal Contributions to Plasmonic Photocatalysis. Advanced Optical Materials 2023, 11, 2300824. 10.1002/adom.202300824. [DOI] [Google Scholar]

[ref207] Ito S.; Sugiyama T.; Toitani N.; Katayama G.; Miyasaka H. Application of Fluorescence Correlation Spectroscopy to the Measurement of Local Temperature in Solutions under Optical Trapping Condition. The Journal of Physical Chemistry B 2007, 111 (9), 2365–2371. 10.1021/jp065156l. [DOI] [PubMed] [Google Scholar]

[ref208] Jiang Q.; Rogez B.; Claude J.-B.; Baffou G.; Wenger J. Temperature Measurement in Plasmonic Nanoapertures Used for Optical Trapping. ACS Photonics 2019, 6 (7), 1763–1773. 10.1021/acsphotonics.9b00519. [DOI] [Google Scholar]

[ref209] Rodriguez-Sevilla P.; Lee T.; Liang L.; Haro-González P.; Lifante G.; Liu X.; Jaque D. Light-Activated Upconverting Spinners. Advanced Optical Materials 2018, 6 (12), 1800161. 10.1002/adom.201800161. [DOI] [Google Scholar]

[ref210] Rodríguez-Sevilla P.; Arita Y.; Liu X.; Jaque D.; Dholakia K. The Temperature of an Optically Trapped, Rotating Microparticle. ACS Photonics 2018, 5 (9), 3772–3778. 10.1021/acsphotonics.8b00822. [DOI] [Google Scholar]

[ref211] Lu D.; Labrador-Páez L.; Ortiz-Rivero E.; Frades P.; Antoniak M. A.; Wawrzyńczyk D.; Nyk M.; Brites C. D. S.; Carlos L. D.; Garcıa Solé J. A.; et al. Exploring Single-Nanoparticle Dynamics at High Temperature by Optical Tweezers. Nano Letters 2020, 20 (11), 8024–8031. 10.1021/acs.nanolett.0c02936. [DOI] [PubMed] [Google Scholar]

[ref212] Lu D.; Pedroni M.; Labrador-Páez L.; Marqués M. I.; Jaque D.; Haro-González P. Nanojet Trapping of a Single Sub-10 nm Upconverting Nanoparticle in the Full Liquid Water Temperature Range. Small 2021, 17 (7), 2006764. 10.1002/smll.202006764. [DOI] [PubMed] [Google Scholar]

[ref213] Castelletto S.; Rosa L.; Boretti A. Micro-manipulation of nanodiamonds containing NV centers for quantum applications. Diamond Relat. Mater. 2020, 106, 107840. 10.1016/j.diamond.2020.107840. [DOI] [Google Scholar]

[ref214] Rahman A. T. M. A.; Frangeskou A. C.; Kim M. S.; Bose S.; Morley G. W.; Barker P. F. Burning and graphitization of optically levitated nanodiamonds in vacuum. Scientific Reports 2016, 6, 21633. 10.1038/srep21633. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref215] Frangeskou A. C.; Rahman A. T. M. A.; Gines L.; Mandal S.; Williams O. A.; Barker P. F.; Morley G. W. Pure nanodiamonds for levitated optomechanics in vacuum. New Journal of Physics 2018, 20, 043016. 10.1088/1367-2630/aab700. [DOI] [Google Scholar]

[ref216] Hoang T. M.; Ahn J.; Bang J.; Li T. Electron spin control of optically levitated nanodiamonds in vacuum. Nature Communications 2016, 7, 12250. 10.1038/ncomms12250. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref217] Delord T.; Nicolas L.; Bodini M.; Hétet G. Diamonds levitating in a Paul trap under vacuum: Measurements of laser-induced heating via NV center thermometry. Appl. Phys. Lett. 2017, 111, 013101. 10.1063/1.4991670. [DOI] [Google Scholar]

[ref218] Pettit R. M.; Neukirch L. P.; Zhang Y.; Nick Vamivakas A. Coherent control of a single nitrogen-vacancy center spin in optically levitated nanodiamond. J. Opt. Soc. Am. B 2017, 34 (6), C31–C35. 10.1364/JOSAB.34.000C31. [DOI] [Google Scholar]

[ref219] Rivière F.; de Guillebon T.; Raynal D.; Schmidt M.; Lauret J.-S.; Roch J.-F.; Rondin L. Hot Brownian Motion of Optically Levitated Nanodiamonds. ACS Photonics 2022, 9 (2), 420–425. 10.1021/acsphotonics.1c01642. [DOI] [Google Scholar]

[ref220] Goderski S.; Runowski M.; Woźny P.; Lavín V.; Lis S. Lanthanide Upconverted Luminescence for Simultaneous Contactless Optical Thermometry and Manometry-Sensing under Extreme Conditions of Pressure and Temperature. ACS Applied Materials & Interfaces 2020, 12 (36), 40475–40485. 10.1021/acsami.0c09882. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref221] Zheng T.; Sójka M.; Runowski M.; Woźny P.; Lis S.; Zych E. Tm²⁺ Activated SrB₄O₇ Bifunctional Sensor of Temperature and Pressure—Highly Sensitive, Multi-Parameter Luminescence Thermometry and Manometry. Advanced Optical Materials 2021, 9 (22), 2101507. 10.1002/adom.202101507. [DOI] [Google Scholar]

[ref222] Albahrani S. M. B.; Seoudi T.; Philippon D.; Lafarge L.; Reiss P.; Hajjaji H.; Guillot G.; Querry M.; Bluet J.-M.; Vergne P. Quantum dots to probe temperature and pressure in highly confined liquids. RSC Advances 2018, 8 (41), 22897–22908. 10.1039/C8RA03652G. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref223] Seoudi T.; Philippon D.; Fillot N.; Lafarge L.; Devaux N.; Mondelin A.; Vergne P. CdSe-Based Quantum Dots as In Situ Pressure and Temperature Non-intrusive Sensors in Elastohydrodynamic Contacts. Tribology Letters 2020, 68, 73. 10.1007/s11249-020-01312-x. [DOI] [Google Scholar]

[ref224] Zhou Y.; Ledoux G.; Bois L.; Descartes S.; Bouscharain N.; Chassagneux F.; Martini M.; Bakary Y. M.; Journet C.; Philippon D. Er³⁺ doped nanoparticles as upconversion thermometer probes in confined fluids. Phys. Chem. Chem. Phys. 2023, 25 (28), 19254–19265. 10.1039/D3CP02218H. [DOI] [PubMed] [Google Scholar]

[ref225] Runowski M.; Woźny P.; Lis S.; Lavín V.; Martín I. R. Optical Vacuum Sensor Based on Lanthanide Upconversion—Luminescence Thermometry as a Tool for Ultralow Pressure Sensing. Advanced Materials Technologies 2020, 5 (4), 1901091. 10.1002/admt.201901091. [DOI] [Google Scholar]

[ref226] Soler-Carracedo K.; Martin I. R.; Runowski M.; Martín L. L.; Lahoz F.; Lozano-Gorrín A. D.; Paz-Buclatin F. Luminescent Nd³⁺-Based Microresonators Working as Optical Vacuum Sensors. Advanced Optical Materials 2020, 8 (19), 2000678. 10.1002/adom.202000678. [DOI] [Google Scholar]

[ref227] Runowski M.; Woźny P.; Martín I. R. Optical pressure sensing in vacuum and high-pressure ranges using lanthanide-based luminescent thermometer-manometer. Journal of Materials Chemistry C 2021, 9 (13), 4643–4651. 10.1039/D1TC00709B. [DOI] [Google Scholar]

[ref228] Chamarthy P.; Garimella S. V.; Wereley S. T. Measurement of the temperature non-uniformity in a microchannel heat sink using microscale laser-induced fluorescence. Int. J. Heat Mass Transfer 2010, 53 (15), 3275–3283. 10.1016/j.ijheatmasstransfer.2010.02.052. [DOI] [Google Scholar]

[ref229] Geitenbeek R. G.; Vollenbroek J. C.; Weijgertze H. M. H.; Tregouet C. B. M.; Nieuwelink A.-E.; Kennedy C. L.; Weckhuysen B. M.; Lohse D.; van Blaaderen A.; van den Berg A.; et al. Luminescence thermometry for in situ temperature measurements in microfluidic devices. Lab on a Chip 2019, 19 (7), 1236–1246. 10.1039/C8LC01292J. [DOI] [PubMed] [Google Scholar]

[ref230] Brites C. D. S.; Lima P. P.; Silva N. J. O.; Millán A.; Amaral V. S.; Palacio F.; Carlos L. D. Ratiometric highly sensitive luminescent nanothermometers working in the room temperature range. Applications to heat propagation in nanofluids. Nanoscale 2013, 5 (16), 7572–7580. 10.1039/c3nr02335d. [DOI] [PubMed] [Google Scholar]

[ref231] Zhu Y.; Buitenhuis J.; Förster B.; Vetrano M. R.; Koos E. Development of Perovskite Quantum Dots for Two-Dimensional Temperature Sensors. ACS Applied Nano Materials 2023, 6 (6), 4661–4671. 10.1021/acsanm.3c00144. [DOI] [Google Scholar]

[ref232] Savchuk O. A.; Carvajal J. J.; Massons J.; Cascales C.; Aguiló M.; Díaz F. Novel low-cost, compact and fast signal processing sensor for ratiometric luminescent nanothermometry. Sensors and Actuators A: Physical 2016, 250, 87–95. 10.1016/j.sna.2016.08.031. [DOI] [Google Scholar]

[ref233] da Silva Moura N.; Bajgiran K. R.; Melvin A. T.; Dooley K. M.; Dorman J. A. Direct Probing of Fe₃O₄ Nanoparticle Surface Temperatures during Magnetic Heating: Implications for Induction Catalysis. ACS Applied Nano Materials 2021, 4 (12), 13778–13787. 10.1021/acsanm.1c03168. [DOI] [Google Scholar]

[ref234] Shen X.; Li H.; Zhao Z.; Li X.; Liu K.; Gao X. Imaging of liquid temperature distribution during microwave heating via thermochromic metal organic frameworks. Int. J. Heat Mass Transfer 2022, 189, 122667. 10.1016/j.ijheatmasstransfer.2022.122667. [DOI] [Google Scholar]

[ref235] Keblinski P.; Cahill D. G.; Bodapati A.; Sullivan C. R.; Taton T. A.. Limits of localized heating by electromagnetically excited nanoparticles. J. Appl. Phys. 2006, 100 ( (5), ) 10.1063/1.2335783. [DOI] [Google Scholar]

[ref236] Zhao Z.; Shen X.; Li H.; Liu K.; Wu H.; Li X.; Gao X. Watching Microwave-Induced Microscopic Hot Spots via the Thermosensitive Fluorescence of Europium/Terbium Mixed-Metal Organic Complexes. Angewandte Chemie International Edition 2022, 61 (6), e202114340 10.1002/anie.202114340. [DOI] [PubMed] [Google Scholar]

[ref237] Dong J.; Zink J. I. Taking the Temperature of the Interiors of Magnetically Heated Nanoparticles. ACS Nano 2014, 8 (5), 5199–5207. 10.1021/nn501250e. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref238] Gu Y.; Piñol R.; Moreno-Loshuertos R.; Brites C. D. S.; Zeler J.; Martínez A.; Maurin-Pasturel G.; Fernández-Silva P.; Marco-Brualla J.; Téllez P.; et al. Local Temperature Increments and Induced Cell Death in Intracellular Magnetic Hyperthermia. ACS Nano 2023, 17 (7), 6822–6832. 10.1021/acsnano.3c00388. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref239] Moreno Maldonado A. C.; Goya G. F. Comment on “Local Temperature Increments and Induced Cell Death in Intracellular Magnetic Hyperthermia”. ACS Nano 2023, 17 (16), 15217–15218. 10.1021/acsnano.3c04393. [DOI] [PubMed] [Google Scholar]

[ref240] Chen G. Non-Fourier phonon heat conduction at the microscale and nanoscale. Nature Reviews Physics 2021, 3, 555–569. 10.1038/s42254-021-00334-1. [DOI] [Google Scholar]

[ref241] Savchuk O. A.; Carvajal J. J.; Brites C. D. S.; Carlos L. D.; Aguilo M.; Diaz F. Upconversion thermometry: a new tool to measure the thermal resistance of nanoparticles. Nanoscale 2018, 10 (14), 6602–6610. 10.1039/C7NR08758F. [DOI] [PubMed] [Google Scholar]

[ref242] Brites C. D. S.; Zhuang B.; Debasu M. L.; Ding D.; Qin X.; Maturi F. E.; Lim W. W. Y.; Soh D. W.; Rocha J.; Yi Z.; et al. Decoding a Percolation Phase Transition of Water at ∼ 330 K with a Nanoparticle Ruler. The Journal of Physical Chemistry Letters 2020, 11 (16), 6704–6711. 10.1021/acs.jpclett.0c02147. [DOI] [PubMed] [Google Scholar]

[ref243] Errulat D.; Marin R.; Gálico D. A.; Harriman K. L. M.; Pialat A.; Gabidullin B.; Iikawa F.; Couto O. D. D. Jr.; Moilanen J. O.; Hemmer E.; et al. A Luminescent Thermometer Exhibiting Slow Relaxation of the Magnetization: Toward Self-Monitored Building Blocks for Next-Generation Optomagnetic Devices. ACS Central Science 2019, 5 (7), 1187–1198. 10.1021/acscentsci.9b00288. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref244] Ferreira R. A. S.; Mamontova E.; Botas A. M. P.; Shestakov M.; Vanacken J.; Moshchalkov V.; Guari Y.; Chibotaru L. F.; Luneau D.; André P. S.; et al. Synchronous Temperature and Magnetic Field Dual-Sensing by Luminescence in a Dysprosium Single-Molecule Magnet. Advanced Optical Materials 2021, 9 (24), 2101495. 10.1002/adom.202101495. [DOI] [Google Scholar]

[ref245] Zanella S.; Aragon-Alberti M.; Brite C. D. S.; Salles F.; Carlos L. D.; Long J. Luminescent Single-Molecule Magnets as Dual Magneto-Optical Molecular Thermometers. Angewandte Chemie International Edition 2023, 62 (35), e202306970 10.1002/anie.202306970. [DOI] [PubMed] [Google Scholar]

[ref246] Wang J.; Zakrzewski J. J.; Zychowicz M.; Xin Y.; Tokoro H.; Chorazy S.; Ohkoshi S.-i. Desolvation-Induced Highly Symmetrical Terbium(III) Single-Molecule Magnet Exhibiting Luminescent Self-Monitoring of Temperature. Angewandte Chemie International Edition 2023, 62 (35), e202306372 10.1002/anie.202306372. [DOI] [PubMed] [Google Scholar]

[ref247] Li H.; Wei F.; Li Y.; Yu M.; Zhang Y.; Liu L.; Liu Z. Optical fiber sensor based on upconversion nanoparticles for internal temperature monitoring of Li-ion batteries. Journal of Materials Chemistry C 2021, 9 (41), 14757–14765. 10.1039/D1TC03701C. [DOI] [Google Scholar]

[ref248] He R.; Vázquez de Aldana J. R.; Pedrola G. L.; Chen F.; Jaque D. Two-photon luminescence thermometry: towards 3D high-resolution thermal imaging of waveguides. Opt. Express 2016, 24 (14), 16156–16166. 10.1364/OE.24.016156. [DOI] [PubMed] [Google Scholar]

[ref249] Ferreira R. A. S.; Brites C. D. S.; Vicente C. M. S.; Lima P. P.; Bastos A. R. N.; Marques P. G.; Hiltunen M.; Carlos L. D.; André P. S. Photonic-on-a-chip: a thermal actuated Mach-Zehnder interferometer and a molecular thermometer based on a single di-ureasil organic-inorganic hybrid. Laser & Photonics Reviews 2013, 7 (6), 1027–1035. 10.1002/lpor.201300080. [DOI] [Google Scholar]

[ref250] Ding H.; Lv G.; Cai X.; Chen J.; Cheng Z.; Peng Y.; Tang G.; Shi Z.; Xie Y.; Fu X.; et al. An Optoelectronic thermometer based on microscale infrared-to-visible conversion devices. Light: Science & Applications 2022, 11, 130. 10.1038/s41377-022-00825-5. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref251] Maturi F. E.; Brites C. D. S.; Silva R. R.; Nigoghossian K.; Wilson D.; Ferreira R. A. S.; Ribeiro S. J. L.; Carlos L. D. Sustainable Smart Tags with Two-Step Verification for Anticounterfeiting Triggered by the Photothermal Response of Upconverting Nanoparticles. Advanced Photonics Research 2022, 3 (6), 2100227. 10.1002/adpr.202100227. [DOI] [Google Scholar]

[ref252] Liu G.-Q.; Feng X.; Wang N.; Li Q.; Liu R.-B. Coherent quantum control of nitrogen-vacancy center spins near 1000 kelvin. Nature Communications 2019, 10, 1344. 10.1038/s41467-019-09327-2. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref253] Roder P. B.; Smith B. E.; Zhou X.; Crane M. J.; Pauzauskie P. J. Laser refrigeration of hydrothermal nanocrystals in physiological media. Proceedings of the National Academy of Sciences 2015, 112 (49), 15024–15029. 10.1073/pnas.1510418112. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref254] Shen Y.; Lifante J.; Fernández N.; Jaque D.; Ximendes E. In Vivo Spectral Distortions of Infrared Luminescent Nanothermometers Compromise Their Reliability. ACS Nano 2020, 14 (4), 4122–4133. 10.1021/acsnano.9b08824. [DOI] [PubMed] [Google Scholar]

[ref255] Bednarkiewicz A.; Marciniak L.; Carlos L. D.; Jaque D. Standardizing luminescence nanothermometry for biomedical applications. Nanoscale 2020, 12 (27), 14405–14421. 10.1039/D0NR03568H. [DOI] [PubMed] [Google Scholar]

[ref256] Martínez E. D.; Brites C. D. S.; Urbano R. R.; Rettori C.; Carlos L. D. Hyperspectral imaging thermometry assisted by upconverting nanoparticles: Experimental artifacts and accuracy. Physica B: Physics of Condensed Matter 2022, 629, 413639. 10.1016/j.physb.2021.413639. [DOI] [Google Scholar]

[ref257] Nguyen V. N.; Lee Y. H.; Le-Vu T. T.; Lin J.-Y.; Kan H.-C.; Hsu C.-C. Impact of Excitation Intensity-Dependent Fluorescence Intensity Ratio of Upconversion Nanoparticles on Wide-Field Thermal Imaging. ACS Applied Nano Materials 2022, 5 (10), 15172–15182. 10.1021/acsanm.2c03303. [DOI] [Google Scholar]

[ref258] Martins J. C.; Bastos A. R. N.; Ferreira R. A. S.; Wang X.; Chen G.; Carlos L. D. Primary Luminescent Nanothermometers for Temperature Measurements Reliability Assessment. Advanced Photonics Research 2021, 2 (5), 2000169. 10.1002/adpr.202000169. [DOI] [Google Scholar]

[ref259] Rühl P.; Wang D.; Garwe F.; Müller R.; Haase M.; Krämer K. W.; Paa W.; Heintzmann R.; Heinemann S. H.; Stafast H. Notes on thermometric artefacts by Er³⁺ luminescence band interference. J. Lumin. 2021, 232, 117860. 10.1016/j.jlumin.2020.117860. [DOI] [Google Scholar]

[ref260] Xia X.; Volpi A.; Roh J. Y. D.; De Siena M. C.; Gamelin D. R.; Hehlen M. P.; Pauzauskie P. J. The impact of ²H_9/2 → ⁴I_13/2 emission from Er³⁺ ions on ratiometric optical temperature sensing with Yb³⁺/Er³⁺ co-doped upconversion materials. J. Lumin. 2021, 236, 118006. 10.1016/j.jlumin.2021.118006. [DOI] [Google Scholar]

[ref261] Pickel A. D.; Dames C. Size and shape effects on the measured peak temperatures of nanoscale hotspots. J. Appl. Phys. 2020, 128, 045103. 10.1063/5.0012167. [DOI] [Google Scholar]

[ref262] Labrador-Páez L.; Pedroni M.; Speghini A.; García-Solé J.; Haro-González P.; Jaque D. Reliability of rare-earth-doped infrared luminescent nanothermometers. Nanoscale 2018, 10 (47), 22319–22328. 10.1039/C8NR07566B. [DOI] [PubMed] [Google Scholar]

[ref263] Chen Y.; Li G.; Ding Y.; Mao Q.; Liu M.; Wang C.; Zheng R.; Su B.-L.; Zhong J. Antithermal Quenching and Multiparametric Temperature Sensing from Mn²⁺/Tb³⁺-Codoped Ca₂LaTaO₆ Phosphor. Advanced Photonics Research 2023, 4 (6), 2300106. 10.1002/adpr.202300106. [DOI] [Google Scholar]

[ref264] Maturi F. E.; Brites C. D. S.; Ximendes E. C.; Mills C.; Olsen B.; Jaque D.; Ribeiro S. J. L.; Carlos L. D. Going Above and Beyond: A Tenfold Gain in the Performance of Luminescence Thermometers Joining Multiparametric Sensing and Multiple Regression. Laser & Photonics Reviews 2021, 15 (11), 2100301. 10.1002/lpor.202100301. [DOI] [Google Scholar]

[ref265] Ximendes E.; Marin R.; Carlos L. D.; Jaque D. Less is more: dimensionality reduction as a general strategy for more precise luminescence thermometry. Light: Science & Applications 2022, 11, 237. 10.1038/s41377-022-00932-3. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref266] Stone D. G.; Chen Y.; Ekimov E. A.; Tran T. T.; Bradac C. Diamond Nanothermometry Using a Machine Learning Approach. ACS Applied Optical Materials 2023, 1 (4), 898–905. 10.1021/acsaom.3c00059. [DOI] [Google Scholar]

[ref267] Liu L.; Creten S.; Firdaus Y.; Agustin Flores Cuautle J. J.; Kouyaté M.; Van der Auweraer M.; Glorieux C. Fluorescence spectra shape based dynamic thermometry. Appl. Phys. Lett. 2014, 104, 031902. 10.1063/1.4862921. [DOI] [Google Scholar]

[ref268] Liu L.; Zhong K.; Munro T.; Alvarado S.; Côte R.; Creten S.; Fron E.; Ban H.; Van der Auweraer M.; Roozen N. B.; et al. Wideband fluorescence-based thermometry by neural network recognition: Photothermal application with 10 ns time resolution. J. Appl. Phys. 2015, 118, 184906. 10.1063/1.4935277. [DOI] [Google Scholar]

[ref269] Cui J.; Xu W.; Yao M.; Zheng L.; Hu C.; Zhang Z.; Sun Z. Convolutional neural networks open up horizons for luminescence thermometry. J. Lumin. 2023, 256, 119637. 10.1016/j.jlumin.2022.119637. [DOI] [Google Scholar]

[ref270] Santos E. P.; Pugina R. S.; Hilário E. G.; Carvalho A. J. A.; Jacinto C.; Rego-Filho F. A. M. G.; Canabarro A.; Gomes A. S. L.; Caiut J. M. A.; Moura A. L. Towards accurate real-time luminescence thermometry: an automated machine learning approach. Sens. Actuators A 2023, 362, 114666. 10.1016/j.sna.2023.114666. [DOI] [Google Scholar]

[ref271] Rao X.; Song T.; Gao J.; Cui Y.; Yang Y.; Wu C.; Chen B.; Qian G. A Highly Sensitive Mixed Lanthanide Metal-Organic Framework Self-Calibrated Luminescent Thermometer. J. Am. Chem. Soc. 2013, 135 (41), 15559–15564. 10.1021/ja407219k. [DOI] [PubMed] [Google Scholar]

[ref272] Yang Y.; Huang H.; Wang Y.; Qiu F.; Feng Y.; Song X.; Tang X.; Zhang G.; Liu W. A family of mixed-lanthanide metal-organic framework thermometers in a wide temperature range. Dalton Transactions 2018, 47 (38), 13384–13390. 10.1039/C8DT03182G. [DOI] [PubMed] [Google Scholar]

[ref273] Stefanska J.; Maciejewska K.; Marciniak L. Blue-emitting single band ratiometric luminescent thermometry based on LaF3:Pr³⁺. New J. Chem. 2021, 45 (27), 11898–11904. 10.1039/D1NJ01869H. [DOI] [Google Scholar]

[ref274] Renero-Lecuna C.; Herrero A.; Jimenez de Aberasturi D.; Martínez-Flórez M.; Valiente R.; Mychinko M.; Bals S.; Liz-Marzán L. M. Nd³⁺-Doped Lanthanum Oxychloride Nanocrystals as Nanothermometers. The Journal of Physical Chemistry C 2021, 125 (36), 19887–19896. 10.1021/acs.jpcc.1c05828. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref275] Choi S.; Graham S.; Chowdhury S.; Heller E. R.; Tadjer M. J.; Moreno G.; Narumanchi S. A perspective on the electro-thermal co-design of ultra-wide bandgap lateral devices. Appl. Phys. Lett. 2021, 119, 170501. 10.1063/5.0056271. [DOI] [Google Scholar]

[ref276] Choi A. Y.; Esho I.; Gabritchidze B.; Kooi J.; Minnich A. J. Characterization of self-heating in cryogenic high electron mobility transistors using Schottky thermometry. J. Appl. Phys. 2021, 130, 155107. 10.1063/5.0063331. [DOI] [Google Scholar]

[ref277] Childs P. R. N.; Greenwood J. R.; Long C. A. Review of temperature measurement. Rev. Sci. Instrum. 2000, 71, 2959–2978. 10.1063/1.1305516. [DOI] [Google Scholar]

[ref278] Wen S.; Zhou J.; Zheng K.; Bednarkiewicz A.; Liu X.; Jin D. Advances in highly doped upconversion nanoparticles. Nature Communications 2018, 9, 2415. 10.1038/s41467-018-04813-5. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref279] Gargas D. J.; Chan E. M.; Ostrowski A. D.; Aloni S.; Altoe M. V. P.; Barnard E. S.; Sanii B.; Urban J. J.; Milliron D. J.; Cohen B. E.; Schuck P. J. Engineering bright sub-10-nm upconverting nanocrystals for single-molecule imaging. Nature Nanotechnology 2014, 9, 300–305. 10.1038/nnano.2014.29. [DOI] [PubMed] [Google Scholar]

[ref280] Lee C.; Xu E. Z.; Kwock K. W. C.; Teitelboim A.; Liu Y.; Park H. S.; Ursprung B.; Ziffer M. E.; Karube Y.; Fardian-Melamed N.; et al. Indefinite and bidirectional near-infrared nanocrystal photoswitching. Nature 2023, 618, 951–958. 10.1038/s41586-023-06076-7. [DOI] [PubMed] [Google Scholar]

[ref281] Lee C.; Xu E. Z.; Liu Y.; Teitelboim A.; Yao K.; Fernandez-Bravo A.; Kotulska A. M.; Nam S. H.; Suh Y. D.; Bednarkiewicz A.; et al. Giant nonlinear optical responses from photon-avalanching nanoparticles. Nature 2021, 589, 230–235. 10.1038/s41586-020-03092-9. [DOI] [PubMed] [Google Scholar]

[ref282] Liu Y.; Lu Y.; Yang X.; Zheng X.; Wen S.; Wang F.; Vidal X.; Zhao J.; Liu D.; Zhou Z.; et al. Amplified stimulated emission in upconversion nanoparticles for super-resolution nanoscopy. Nature 2017, 543, 229–233. 10.1038/nature21366. [DOI] [PubMed] [Google Scholar]

[ref283] Zhan Q.; Liu H.; Wang B.; Wu Q.; Pu R.; Zhou C.; Huang B.; Peng X.; Ågren H.; He S. Achieving high-efficiency emission depletion nanoscopy by employing cross relaxation in upconversion nanoparticles. Nature Communications 2017, 8, 1058. 10.1038/s41467-017-01141-y. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref284] Lu Y.; Zhao J.; Zhang R.; Liu Y.; Liu D.; Goldys E. M.; Yang X.; Xi P.; Sunna A.; Lu J.; et al. Tunable lifetime multiplexing using luminescent nanocrystals. Nature Photonics 2014, 8, 32–36. 10.1038/nphoton.2013.322. [DOI] [Google Scholar]

[ref285] Szalkowski M.; Dudek M.; Korczak Z.; Lee C.; Marciniak Ł.; Chan E. M.; Schuck P. J.; Bednarkiewicz A. Predicting the impact of temperature dependent multi-phonon relaxation processes on the photon avalanche behavior in Tm³⁺: NaYF₄ nanoparticles. Optical Materials: X 2021, 12, 100102. 10.1016/j.omx.2021.100102. [DOI] [Google Scholar]

PERMALINK

Luminescence Thermometry Beyond the Biological Realm

Benjamin Harrington

Ziyang Ye

Laura Signor

Andrea D Pickel

Abstract

1. Introduction

Figure 1.

2. Probes

2.1. Upconverting Nanoparticles (UCNPs) and Related Lanthanide-Containing Materials

2.2. Nitrogen Vacancy (NV) and Other Color Centers

2.3. Quantum Dots (QDs)

2.4. Other Probes

3. Capabilities

3.1. High-Temperature Measurements

3.2. Cryogenic Measurements

3.3. Single-Particle Measurements

Figure 2.

3.4. Time-Resolved Measurements

Figure 3.

4. Applications

4.1. Electronics and Other Devices

Figure 4.

4.2. Plasmonics

Figure 5.

4.3. Catalysis

Figure 6.

4.4. Optical Trapping and Levitation

Figure 7.

4.5. Pressure Sensing

4.6. Microfluidics and Nanofluids

Figure 8.

4.7. Other Applications

5. Emerging Areas

5.1. Measurement Artifacts

Figure 9.

5.2. Advanced Data Analysis and Machine Learning (ML) Approaches

5.3. Batch Calibration and Particle-to-Particle Uniformity

Figure 10.

6. Summary and Outlook

Acknowledgments

Author Contributions

References

ACTIONS

PERMALINK

RESOURCES

Similar articles

Cited by other articles

Links to NCBI Databases