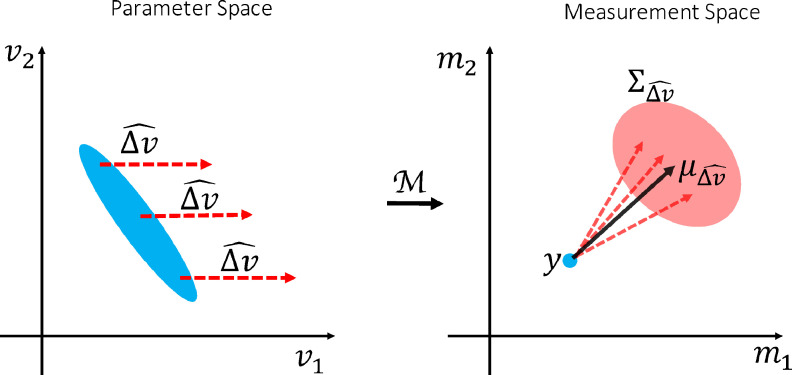
Fig. 2.

Distribution of derivatives. The way measurements change as a result of a particular change in the parameters can only be calculated if we know the baseline parameters. When we are only given the measurements, there are several instances of equally likely derivative directions depending on the underlying baseline parameters. We model all of these derivatives given the baseline measurements as a random variable with a presumed distribution. This allows us to transfer the uncertainty due to the inverse model degeneracy into the measurement space. The blue oval in the parameter space (left) represents all the parameter settings that map onto the same blue point in the measurement space(right). Each of these parameter settings can produce a different derivative direction in the measurements space. The collection of such derivatives of change $\widehat{\Delta v}$ for the measurement $y$ are modelled as a Gaussian distribution with mean ${\mu }_{\widehat{\Delta v}}\left(y\right)$ and covariance ${\Sigma }_{\widehat{\Delta v}}\left(y\right)$. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)