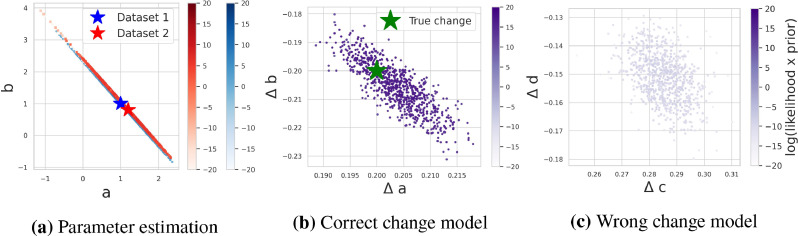
Fig. 13.

a) Parameter estimation. Each set of dots shows parameter estimates for one instance of the model using MCMC and intensities represent the log posterior probability. The parameter estimates for each data set are highly correlated and all of the points on the lines explain the data equally well, i.e. the models are degenerate and it is not possible to directly compare the parameter estimates. B) Inferred change with the correct model. We ran MCMC with the assumption that change has a particular shape (only a and b changed). The estimated values for $\Delta a$ and $\Delta b$ are centred around the correct change (green star) and the unnormalized posterior probabilities are comparatively high. C) Inferred change using a wrong model. We run a similar MCMC but this time assuming $c$ and $d$ can change. In this case the estimated posterior probabilities are much smaller compared to the previous change model, i.e. this model of change cannot explain the change in the measurements as well as the model in (b). (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)