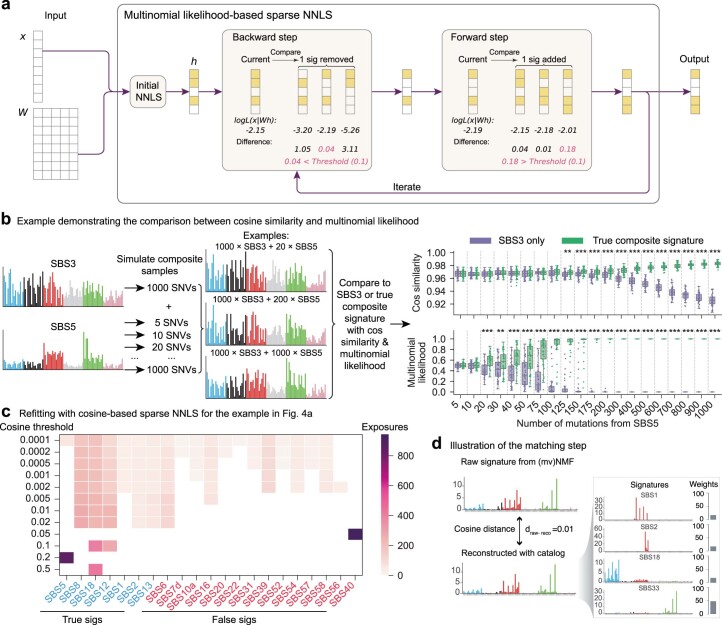
Extended Data Fig. 5. Matching and refitting with multinomial likelihood-based sparse NNLS.

a. Diagram of the likelihood-based sparse NNLS algorithm. See Methods for details. b. An example demonstrating that multinomial likelihood is more powerful than cosine similarity for separating similar signatures. SBS3 and SBS5 are used to simulate synthetic samples. All samples contain 1000 SNVs contributed by SBS3 as well as varying numbers of SNVs from SBS5. Multinomial likelihood and cosine similarity are then applied to distinguish whether the sample spectra are generated from the correct (SBS3 + SBS5 with appropriate weights) or incorrect (pure SBS3) underlying signatures. The problem is expected to be difficult with few SNVs from SBS5, as the sample spectra will be dominated by SBS3. Indeed, cosine similarity fails to separate the two underlying signatures when there are less than 100 SNVs from SBS5, corresponding to an SBS5 exposure of 100/(100 + 1000) = 9%. By comparison, multinomial likelihood achieves statistically significant separation down to 20 SNVs from SBS5, corresponding to an SBS5 exposure of 2%. *: p < 0.05. **: p < 0.005. ***: p < 0.0005. p-values are calculated with two-sided t-tests. c. Same as Fig. 4b, but refitting is performed using cosine similarity combined with the same bidirectional stepwise algorithm as in (a). Notably, there is no threshold with which the set of active signatures is identified correctly. Also, solutions with cosine similarity do not possess the desired property of continuity as in Fig. 4b. For example, even when the threshold is overly small, true signatures (for example, SBS5) can be missed, while when the threshold is overly large, false signatures (for example, SBS40) can be discovered instead of the strongest true signatures. d. Illustration of the matching step. MuSiCal uses the same likelihood-based sparse NNLS for the matching step, where a de novo signature is decomposed as a non-negative mixture of known signatures in the catalog.