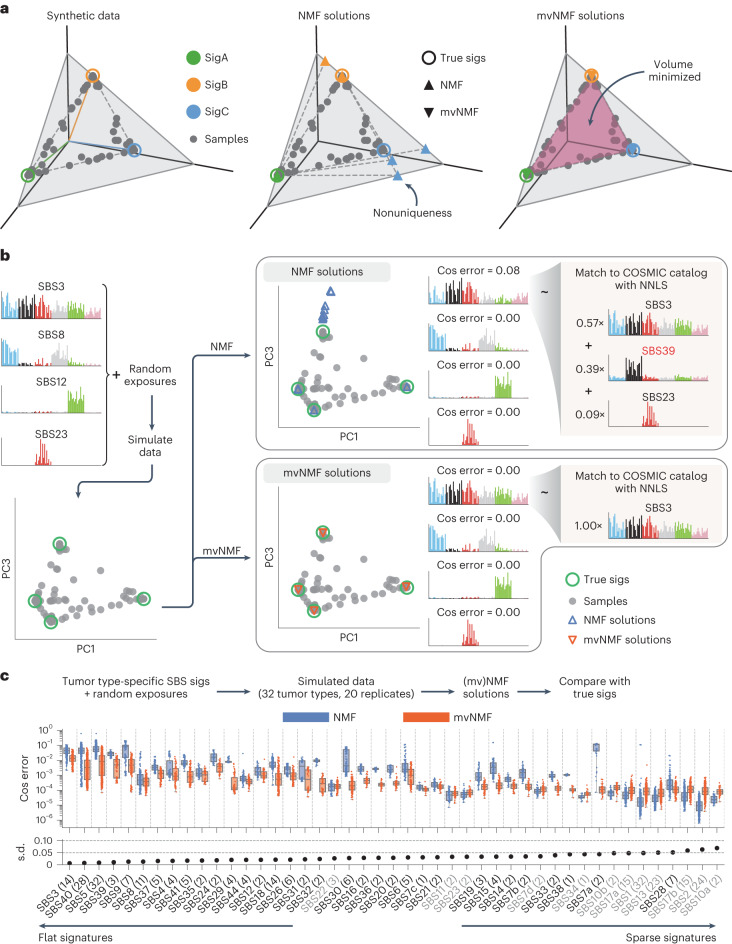
Fig. 2. mvNMF improves the accuracy of de novo signature discovery by inducing unique solutions.

a, An example demonstrating the nonuniqueness of NMF solutions and uniqueness of mvNMF solutions. Synthetic samples are simulated from signatures with three mutation channels (represented by the three axes x, y and z). NMF and mvNMF are then applied to recover the signatures with three different initializations (shared between NMF and mvNMF). Both signatures and samples are normalized and subsequently visualized on the plane x + y + z = 1. b, A similar example with real SBS signatures. Example solutions are plotted for NMF and mvNMF. The NMF solution for SBS3 receives a relatively large cosine error, and when decomposed using COSMIC signatures by NNLS (with a relative exposure cutoff of 0.05), it is identified as a composite signature involving the false SBS39. By comparison, mvNMF is able to recover SBS3 accurately. c, Cosine errors of NMF and mvNMF solutions in tumor type-specific simulations with real SBS signatures. The number in parentheses after each signature name indicates the number of tumor types where the corresponding signature is present. The number of data points in each box plot equals this number multiplied by 20 (independent simulations). mvNMF improves the accuracy of de novo signature discovery for most SBS signatures, especially for relatively flat ones characterized by small standard deviations (s.d., shown below the box plot). Although NMF outperforms mvNMF for some sparse signatures (marked by gray signature labels), the cosine errors for both algorithms are much smaller than 0.001 in those cases and thus negligible. Note that the apparent similar or larger spread of cosine errors for mvNMF is because of the log scale on the y axis. Solutions from mvNMF are in fact more stable, producing smaller standard deviations in the cosine errors overall. In all panels, random exposures are generated from symmetric Dirichlet distributions with a concentration parameter of α = 0.1, which is a representative value according to real exposure matrices obtained by the PCAWG Consortium⁵ (Supplementary Fig. 3). sigs, signatures.