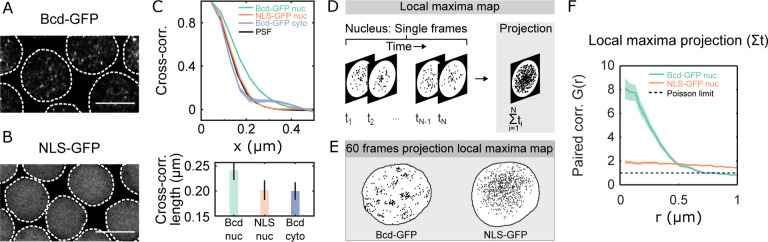
FIG. 1. Quantitative characterization of nuclear Bcd heterogeneity.

(A-B) Confocal (Zeiss-Airyscan) images of cross-sections of Bcd-GFP (A), and NLS-GFP (B) expressing blastoderm nuclei in living Drosophila embryos (NC14). Scale bars are $5\mu m$. The broken lines represent a guide to the eye for the nuclear boundaries. (C) (TOP) Spatial cross-correlations computed on the nuclear pixels in 2D nuclear cross-section images expressing Bcd-GFP (green, 44 nuclei from 5 embryos) and NLS-GFP (orange, 27 nuclei from 3 embryos); and from pixels within the cytoplasm of Bcd-GFP expressing embryos (grey, 5 embryos). For comparison, the point-spread-function (PSF) of the objective is in black. Bottom panel shows mean and standard deviations of the computed correlation lengths: nucleoplasmic Bcd-GFP: $0.24\pm 0.02\mu m$; nucleoplasmic NLS-GFP: $0.20\pm 0.02\mu m$; and cytoplasmic Bcd-GFP: $0.20\pm 0.02\mu m$. (D) Schematic showing a map of local fluorescence intensity maxima inside a nucleus (left). The local maxima maps are extracted from individual frames of $~30s$ long videos (60 frames) of nuclear cross sections ($1\mu m$ thick). All maps from a given video are projected onto a single frame to form the local maxima map (right). See also METHODS and FIG. S3. (E) Representative local maxima maps for a Bcd-GFP nucleus (left) and an NLS-GFP nucleus (right). (F) Radial distribution function (or pair-correlation function, $\left(r\right)$) for the local maxima distribution expressed as a function of distance $r$ from the center. $G\left(r\right)$ was calculated on time-projected (60 frames each) local intensity maxima centroid maps, averaged over multiple nuclei (same nuclei and embryo counts as in C). A distinct peak in G(r) indicates temporally persistent confinement of the local maxima, as seen for Bcd-GFP expressing nuclei. For NLS-GFP, the gradual reduction in the radial function indicates a gradual decline in intensity near the nuclear edges without the existence of any sub-micron accumulations. ($G\left(r\right)=1$ corresponds to a perfectly uniform distribution).