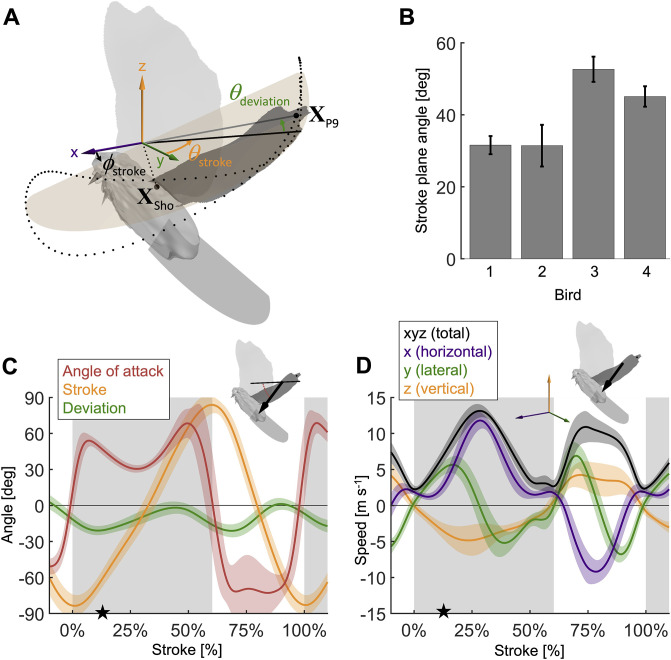
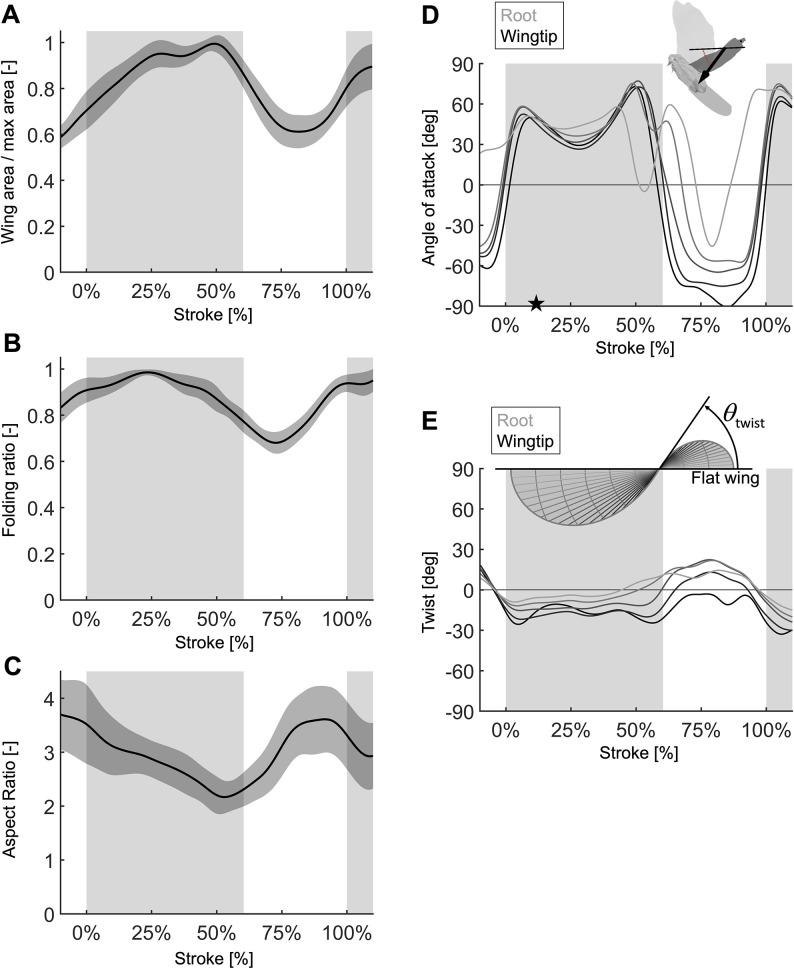
Figure 2. Measured wingbeat kinematics show wing area, extension, and speed are maximal mid-downstroke, while the wing angle of attack reaches a local minimum.

(A) The stroke plane (light orange) fits the path of the vector originating from the shoulder joint and extending to the ninth primary feather tip (${\displaystyle {\mathbf{X}}_{\mathrm{P}9}}$) during the wingbeat, which we use to define wing kinematics with three angles: (1) the stroke plane angle ${\displaystyle {\varphi }_{\mathrm{s}\mathrm{t}\mathrm{r}\mathrm{o}\mathrm{k}\mathrm{e}}}$, (2) the wing stroke angle ${\displaystyle {\theta }_{\mathrm{s}\mathrm{t}\mathrm{r}\mathrm{o}\mathrm{k}\mathrm{e}}}$, and (3) the deviation of the stroke angle from the stroke plane ${\displaystyle {\theta }_{\mathrm{d}\mathrm{e}\mathrm{v}\mathrm{i}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}}}$. (B) The average stroke plane differs across the four doves while being consistent for each individual dove. (C) The wing stroke angle (orange), stroke deviation angle (green), and wing angle of attack (red) are consistent (low variance) across all flights and all four individuals. The only exception is the angle of attack during the upstroke. The avatar shows the angle of attack (red dotted arc), the angle between the wing chord (thin) and velocity vector (thick), at 17% of the second wingbeat (star in panels C and D). (D) The net wing speed (black) peaks mid-downstroke and mid-upstroke. The x-velocity component dominates net speed. The avatar shows the 3D wing velocity vector.

Figure 2—figure supplement 1. Stroke-resolved wing morphing parameters during the second wingbeat, measured using 3D wing surface reconstruction.

N = 4 doves; n = 5 flights each; gray region indicates second downstroke after takeoff. (A) The wing surface area normalized with the fully extended area reaches a plateau between mid-downstroke and the start of the upstroke. (B) The wing folding ratio shows wingspan reduction relative to the fully extended wing mid-downstroke. (C) The aspect ratio of the wing was computed using Equation S4 and quantifies the ratio of the wingspan squared and the wing surface area. Hence, the normalized aspect ratio is (B) squared divided by (A). The aspect ratio peak near the end of the upstroke corresponds to the dove beginning to re-extend its wing to prepare for the downstroke, even while its feathers are still splayed to maintain low-surface area. (D) The angle of attack induced by flapping motion varies through the stroke, and in a lesser degree, along the span. We computed the angle of attack for each blade element as the angle between the chordline of the blade element (avatar: thin black line) and the velocity vector (avatar: thick black line) and plot the results at 20% (labeled as root), 40%, 60%, 80%, and 100% (labeled as tip) of the wing radius. (E) Wing twist, the angle between the chord vector at the root and the chord vector along the span of the wing, is plotted at 20% (labeled as root), 40%, 60%, 80%, and 100% (labeled as tip) of the wing radius. The diagram shows a twisted elliptical wing viewed with the wingspan axis out of the page.