Abstract
Aneuploidy is common in eukaryotes, often leading to decreased fitness. However, evidence from fungi and human tumur cells suggests that specific aneuploidies can be beneficial under stressful conditions and facilitate adaptation. In a previous evolutionary experiment with yeast, populations evolving under heat stress became aneuploid, only to later revert to euploidy after beneficial mutations accumulated. It was therefore suggested that aneuploidy is a “stepping stone” on the path to adaptation. Here, we test this hypothesis. We use Bayesian inference to fit an evolutionary model with both aneuploidy and mutation to the experimental results. We then predict the genotype frequency dynamics during the experiment, demonstrating that most of the evolved euploid population likely did not descend from aneuploid cells, but rather from the euploid wild-type population. Our model shows how the beneficial mutation supply—the product of population size and beneficial mutation rate–determines the evolutionary dynamics: with low supply, much of the evolved population descends from aneuploid cells; but with high supply, beneficial mutations are generated fast enough to outcompete aneuploidy due to its inherent fitness cost. Our results suggest that despite its potential fitness benefits under stress, aneuploidy can be an evolutionary “diversion” rather than a “stepping stone”: it can delay, rather than facilitate, the adaptation of the population, and cells that become aneuploid may leave less descendants compared to cells that remain diploid.
Keywords: whole-chromosome duplication, evolutionary model, adaptive evolution
Introduction
Aneuploidy is an imbalance in the number of chromosomes in the cell: an incorrect karyotype. Evidence suggests that aneuploidy is very common in eukaryotes, e.g. animals (Santaguida and Amon 2015; Naylor and van Deursen 2016; Bakhoum and Landau 2017) and fungi (Pavelka et al. 2010; Zhu et al. 2016; Robbins et al. 2017; Todd et al. 2017). Aneuploidy has been implicated in cancer formation, progression, and drug resistance (Boveri 2008; Schvartzman et al. 2010; Santaguida and Amon 2015; Rutledge et al. 2016; Ippolito et al. 2021; Lukow et al. 2021). It is also common in protozoan pathogens of the Leishmania genus, a major global health concern (Mannaert et al. 2012), and contributes to the emergence of drug resistance (Selmecki et al. 2009) and virulence (Möller et al. 2018) in fungal pathogens, which are under-studied (Rodrigues and Albuquerque 2018), despite infecting a billion people per year, causing significant morbidity in million and death in million people per year (Selmecki et al. 2009; Rodrigues and Albuquerque 2018).
Experiments with human and mouse embryos found that most germ-line aneuploidies are lethal. Aneuploidies are also associated with developmental defects and lethality in other multicellular organisms (Sheltzer and Amon 2011). For example, aneuploid mouse embryonic cells grow slower than euploid cells (Williams et al. 2008). Similarly, in unicellular eukaryotes growing in benign conditions, aneuploidy usually leads to slower growth and decreased overall fitness, in part due to proteotoxic stress due to increased expression, gene dosage imbalance, and hypo-osmotic-like stress (Niwa et al. 2006; Torres et al. 2007; Pavelka et al. 2010; Sheltzer and Amon 2011; Santaguida et al. 2015; Kasuga et al. 2016; Zhu et al. 2018; Tsai et al. 2019; Yang et al. 2021; Robinson et al. 2023).
However, aneuploidy can be beneficial under stressful conditions due to the wide range of phenotypes it can produce, some of which are advantageous (Pavelka et al. 2010; Yang et al. 2021). Indeed, in a survey of 1,011 yeast strains, aneuploidy has been detected in about 19% (Peter et al. 2018). Thus, aneuploidy can lead to rapid adaptation in unicellular eukaryotes (Rancati et al. 2008; Torres et al. 2010; Hong and Gresham 2014; Gerstein et al. 2015), as well as to rapid growth of somatic tumor cells (Schvartzman et al. 2010; Sheltzer et al. 2017). For example, aneuploidy in Saccharomyces cerevisiae facilitates adaptation to a variety of stressful conditions like heat and pH (Yona et al. 2012), copper (Covo et al. 2014; Gerstein et al. 2015), salt (Dhar et al. 2011; Robinson et al. 2023), and nutrient limitation (Dunham et al. 2002; Gresham et al. 2008; Avecilla et al. 2022), with similar results in Candida albicans (Yang et al. 2021). Importantly, aneuploidy can also lead to drug resistance in pathogenic fungi such as C. albicans (Selmecki et al. 2008, 2010; Gerstein and Berman 2020) and Cryptococcus neoformans (Sionov et al. 2010), which cause candidiasis and meningoencephalitis, respectively. Although we focus here on aneuploidy, a similar phenomena of adaptation via gene duplication or amplification has been observed in yeast (Lauer et al. 2018), bacteria (Sonti and Roth 1989), and DNA viruses (Elde et al. 2012).
Yona et al. (2012) demonstrated experimentally the importance of aneuploidy in adaptive evolution. They evolved populations of S. cerevisiae under strong heat stress. The populations adapted to the heat stress within 450 generations, and this adaptation was determined to be due a duplication of chromosome III. Later on, after more than 1,500 generations, the populations reverted back to an euploid state, while remaining adapted to the heat stress. Aneuploidy was therefore suggested to be a transient adaptive solution, because it can rapidly appear and take over the population under stressful conditions, and can then be rapidly lost when the cost of aneuploidy outweighs its benefit—after the stress is removed, or after refined beneficial mutations appear and fix (Yona et al. 2012). Furthermore, it has been suggested that aneuploidy is an evolutionary “stepping stone” that facilitates future adaptation by genetic mutations, which require more time to evolve (Yona et al. 2012, 2015).
Here, we test the hypothesis that aneuploidy is an evolutionary “stepping stone” that facilitates adaptive evolution by genetic mutations (Yona et al. 2012). We develop an evolutionary genetic model and fit it to the experimental results of Yona et al. (2012) to predict the genotype frequency dynamics in the experimental populations, thereby estimating the frequency of evolved euploid cells that descended from aneuploid cells. Our results show that although aneuploidy reached high frequencies in the experimental populations, the majority of cells in the evolved euploid population likely did not descend from aneuploid cells, but rather directly from wild-type euploid cells. These suggest that at the lineage level, aneuploidy may be an “evolutionary diversion”, rather than a “stepping stone”, on the path to adaptation.
Results
In the heat-stress experiment of Yona et al. (2012), four populations of S. cerevisiae evolved under 39 °C. Aneuploidy reached high frequency () in all four experimental repetitions in the first 450 generations. Two of the repetitions, marked and , carried no large-scale duplications other than a chromosome III trisomy. These two repetitions continued to evolve under the same conditions, wherein aneuploidy was eliminated by generation 1,700 and 2,350 in and , respectively.
Evolutionary genetic model
To explore the dynamics during the evolutionary experiments, we developed an evolutionary genetic model, fitted the model to empirical data, and used it to predict the genotype frequency dynamics, or specifically, the fraction of the evolved euploid population descended from aneuploid cells.
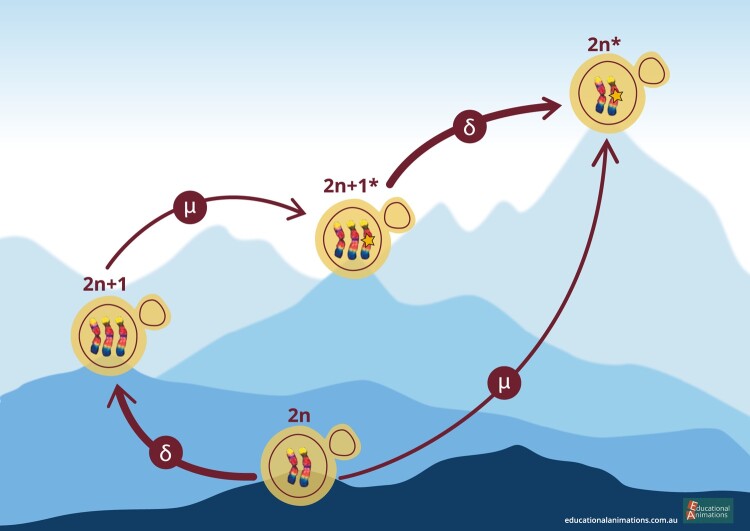
The model includes the effects of natural selection, genetic drift, aneuploidy, and mutation (i.e. other genetic variants) and follows a population of cells characterized by their genotype: euploid wild-type, , is the ancestral diploid genotype; euploid mutant, , has a diploid karyotype and a single beneficial mutation; aneuploid wild-type, , has an extra chromosome due to a chromosome duplication event; and aneuploid mutant, , has an extra chromosome (like ) and a beneficial mutation (like ). Note that “mutation” here refers to point mutations and other genetic variants unrelated to aneuploidy. Fitness values of the different genotypes are denoted by , , , and , and the rate of mutation and aneuploidy are denoted by μ and δ, respectively. See Fig. 1 for an illustration of the model.
Fig. 1.
Model illustration. There are four genotypes in our model: euploid wild-type, ; euploid mutant, ; aneuploid wild-type, ; and aneuploid mutant, . Overall there are two possible trajectories from to . Arrows denote transitions between genotypes, with transition rates μ for the beneficial mutation rate and δ for the aneuploidy rate. Elevation differences illustrate the expected, rather than the assumed, fitness differences between the genotypes.
We fitted this model to the experimental results (Yona et al. 2012)—time for fixation (frequency ) and for loss (frequency ) of aneuploidy—using approximate Bayesian computation with sequential Monte-Carlo (ABC-SMC; Sisson et al. 2007), thereby inferring the model parameters: rates of aneuploidy (i.e. mis-segregation, non-disjunction) and mutation and the fitness of all genotypes. We then sampled posterior predictions for the genotype frequency dynamics using the estimated parameter values and compared different versions of the model to test additional hypotheses about the evolutionary process.
Estimated rates and fitness effects of aneuploidy and mutation
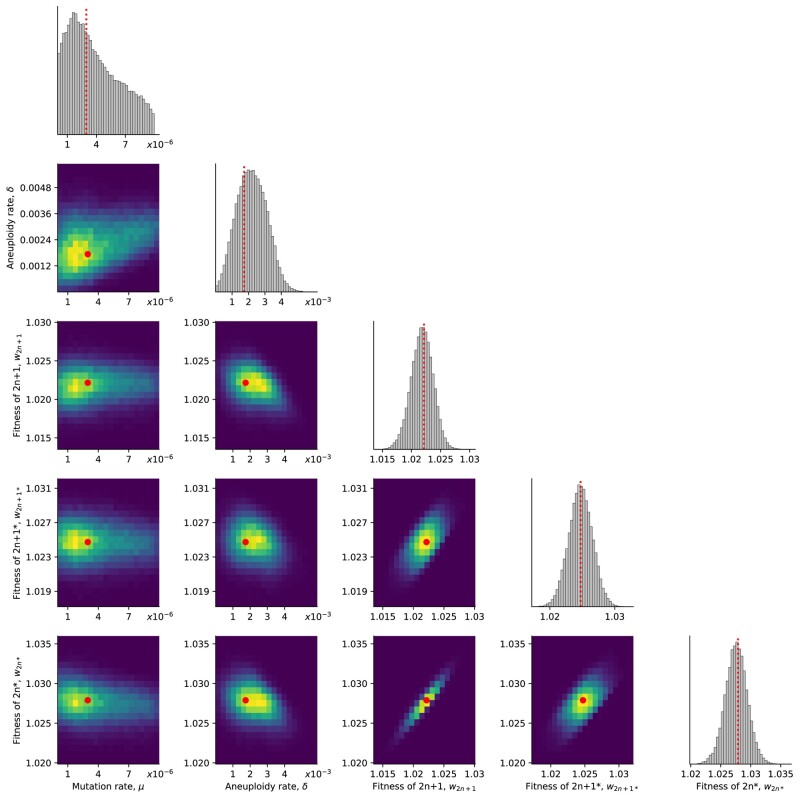
We inferred the posterior distribution of model parameters (Fig. 2). We report parameter estimates using the maximum a posteriori (MAP) and providing the 50% highest density interval (HDI) in square brackets. See Supplementary material online for sensitivity analysis.
Fig. 2.
Posterior distribution of model parameters. On the diagonal, the marginal posterior distribution of each model parameter. Below the diagonal, the joint posterior distribution of pairs of model parameters (dark and bright for low and high density, respectively). Markers and lines for the joint MAP estimate (which may differ from the marginal MAP, as the marginal distribution integrates over all other parameters).
The estimated beneficial mutation rate is per genome per generation (that is, roughly three out of cell divisions produce a mutant cell with a fitness advantage). From the literature, the mutation rate per base pair is roughly (Lynch et al. 2008; Zhu et al. 2014), but it may be higher under heat stress, as several stresses (Heidenreich 2007), including heat (Huang et al. 2018), may cause hypermutation in yeast. If we assume a 10-fold increase over the mutation rate reported in the literature, then the estimated beneficial mutation rate can be explained by a genomic target size of 1,000 base pairs (that is, 1,000 base pairs across the genome in which a mutation would provide a fitness advantage): . Supporting this, Jarolim et al. (2013) found 279 genes that contributed to survival after a sudden shift from 30 °C to 50 °C, and Flynn et al. (2020) used a deep mutational scan of a single protein, Hsp90, to find 465 amino-acid variants (out of 14,160) that significantly increased growth rate in 37 °C. Furthermore, Yona et al. (2012) found at least 10 genes on chromosome III that increased heat tolerance when over-expressed. Assuming that other chromosomes also have a similar number of heat-tolerance genes (and even more, as chromosome III is one of the smallest chromosomes; Gilchrist and Stelkens 2019), we estimate a total of 160 heat-tolerance genes in the genome. Indeed, mutations were found in 97 genes in an evolutionary experiment with yeast under heat stress (Huang et al. 2018). Thus, to get a genomic target size of 1,000, it is enough that the average gene target size (number of base pairs in a gene in which a mutation is beneficial) is 6.25 base pairs. For example, Kohn and Anderson (2014) found a target size of 11 in a proton exporter gene (PMA1) that contributes to high-salt adaptation.
The estimated rate of aneuploidy (i.e. mis-segregation, non-disjunction), –, is higher than in previous studies: for chromosome III in diploid S. cerevisiae, Zhu et al. (2014) estimated chromosome gain events per generation, and Kumaran et al. (2013) estimate – chromosome loss events per generation (95% confidence interval). However, this difference may be partly explained by an increased rate of aneuploidy during heat stress: heat shock can increase the rate of chromosome fragment loss by 2–3 orders of magnitude (Chen et al. 2012).
The estimated fitness values are – , –, and –, all relative to the fitness of , which is set to . If we allow for transitions (mutation, chromosome loss and gain) to less-fit genotypes (e.g. to ), then we infer similar but slightly different values, see Supplementary material online.
Model comparison and goodness-of-fit
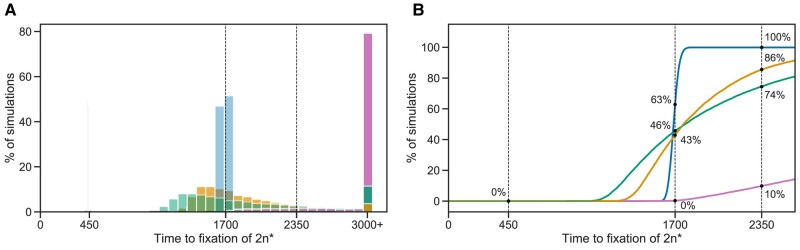
To assess the fit of our model to the data, we use posterior predictive checks, in which we simulate the frequency dynamics using MAP parameter estimates and compare them to the data. Our model fits the data well: fixed in 63% of simulations by generation 1,700 and in 100% of simulations by generation 2,350 (Fig. 3).
Fig. 3.
Model fit with and without aneuploidy. The distribution of time to fixation of (i.e. adaptation time) in simulations using MAP parameters of the model with beneficial aneuploidy (blue; ) compared to alternative models: a model with the same parameter values but without aneuploidy (gray, , concentrated at ); a model fitted to the data assuming no aneuploidy (green, ); a model fitted to the data assuming neutral aneuploidy (yellow, ); and a model with beneficial aneuploidy and an extended prior distribution (pink). In the experiment by Yona et al. (2012), one population lost aneuploidy by generation 1,700 and another by generation 2,350 (dashed lines) but not before generation 450. Thus, the blue distribution has a better fit compared to the other distributions (the gray distribution has a particularly poor fit). The MAP likelihood (equation 4) is 0.84, 0.78, 0.67, and 0.14 for the models represented by blue, yellow, green, and pink distributions, respectively. A) Histogram of the time to fixation of . The last bin contains all values equal or greater than 3,000. B) Cumulative distribution of the time to fixation.
However, a model without aneuploidy (where the aneuploidy rate is fixed at zero, ) fails to explain the experimental observations (Fig. 3). The estimated mutation rate without aneuploidy is –, much lower compared to a model with aneuploidy. The fitness of the mutant is also much lower at –. This is because, without aneuploidy, a high mutation rate or fitness effect will lead to faster appearance and fixation of than in the experimental observations.
We also checked a model in which aneuploidy occurs but is adaptively neutral compared to the wild-type, that is, and but . This model fits the data better than the model with no aneuploidy (in which ), but worse than a model with positive selection for aneuploidy, in which (Fig. 3).
Model predictions of genotype frequency dynamics
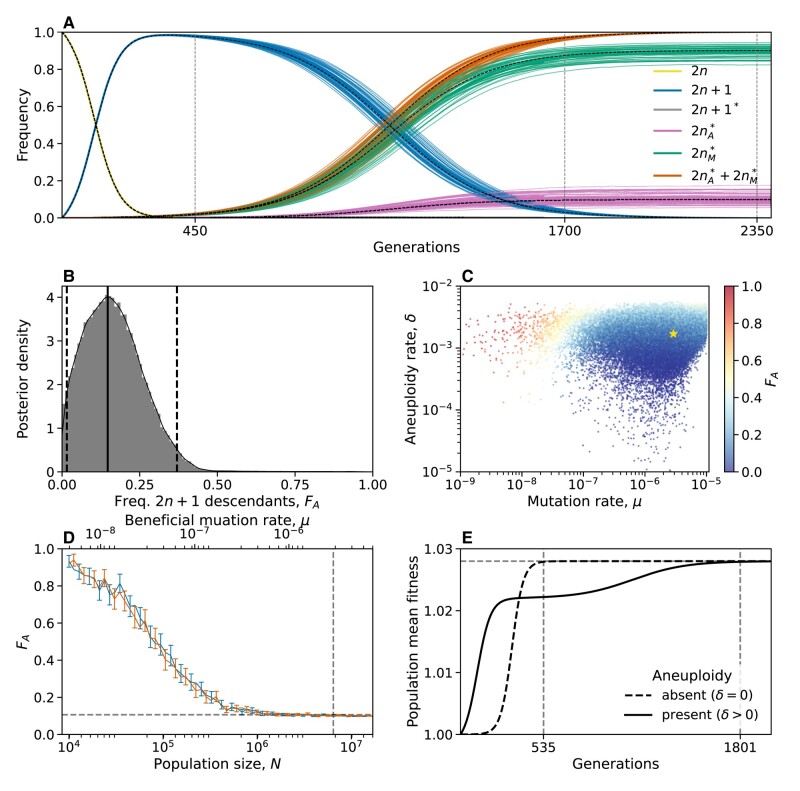
We simulated 50 replicate genotype frequency dynamics using the MAP estimate parameters. Figure 4A shows the simulated frequencies of the four genotypes (, , , and ), as well as the frequencies of cells that arose from either cells via a sequences of mutation and chromosome loss events () or directly from cells via a mutation event (). We find that never reaches substantial frequency as it is quickly replaced by in a process similar to stochastic tunneling (Komarova et al. 2003; Iwasa et al. 2004).
Fig. 4.
Predicted frequency of aneuploid-descended cells. A) Posterior predicted genotype frequencies over time, including the source of : arose from , whereas arose directly from . Colored curves are 50 simulations using the MAP estimate parameters. Black dashed curves are the expected genotype frequencies without genetic drift (from a deterministic model). See supplementary fig. S9, Supplementary Material online, for log–log scale, in which the sequence of events is easier to observe. B) Posterior distribution of , the expected frequency of cells descended from cells, computed as the average frequency at the end of 100 simulations for 100,000 samples from the parameter posterior distribution. Solid and dashed lines show the mode and 95% CI. C) values (color coded) from panel B, with their corresponding mutation rate μ on x-axis and aneuploidy rate δ on the y-axis. Yellow star shows the MAP estimate. See also supplementary fig. S10, Supplementary Material online. D) as a function of the population size (N, bottom x-axis) and the beneficial mutation rate (μ, top x-axis) in posterior predictions with MAP parameters. Markers show in 250 simulations per population size or mutation rate value. Error bars show mean with 95% CI (bootstrap, ). Blue and red bars for varying population size and mutation rate, respectively. Vertical dashed line for population size in the experiment, , and the MAP mutation rate, . Horizontal line for . E) Population mean fitness in a model without drift using MAP estimate parameters. Solid lines for mean fitness with aneuploidy (), where the population reaches adaptation (mean fitness at 99.99% of maximum value) at generation 1,802. Dashed lines for mean fitness without aneuploidy (), where the population adapts much earlier, at generation 535.
To test the hypothesis that aneuploidy facilitates adaptation, we estimated , the expected frequency of that arose from , computed as the average frequency of such cells at the end of simulations using the MAP estimate parameters. Surprisingly, we observe that the majority of cells are , a product of a direct mutation in cells, rather than descending from cells (, average end point of 50 purple lines in Fig. 4A). This is despite the fact that the genotype reaches high frequencies in the population (at least 0.98; Fig. 4A).
This result is not unique to the MAP parameter estimate. We simulated genotype frequency dynamics using parameter samples from the posterior distribution, and computed the posterior distribution of (Fig. 4B). The posterior mode was just 0.147 [0.0154–0.370 95% CI] and only in 489 of 100,000 posterior samples (0.489%), was larger than 0.5 (see Supporting Material for results when transitions to less-fit genotypes are allowed, such as to ). Thus, if we sample a random cell from the evolved population, it is more likely to have descended directly from an euploid cell than from an aneuploid cell. The probability of descending from () increases with the aneuploidy rate, δ, and decreases with both the population size N and the mutation rate, μ (Fig. 4C and D). In some cases it can also be affected by the fitness parameters (supplementary fig. S10, Supplementary Material online).
Genetic instability in aneuploid cells
It has been suggested that aneuploidy increases genomic instability: Sheltzer et al. (2011) have demonstrated a fold increase of between 2.2 and 7.1 in the mutation rate of disomic yeast (rather than trisomic yeast, the focus of our analysis). Therefore, we inferred model parameters under the assumption that the mutation rate increases in aneuploid cells by a factor , 33/32 (due to an additional chromosome), 2, 5, 10, or 100 (due to genetic instability). We found that the posterior distribution was similar for , 33/32, 2, and 5 (supplementary fig. S4, Supplementary Material online). Furthermore, we computed the WAIC (widely applicable information criterion), a criterion for model selection (see Methods). The WAIC values were similar for all τ values (supplementary table S1, Supplementary Material online).
Assuming a strong increase of the mutation rate in aneuploid cells, i.e. , the inferred mutation rate was – , and the inferred aneuploidy rate was –. Compared to inference made assuming no effect of aneuploidy on the mutation rate, these rates were about 7–8-fold and 2–3-fold lower for μ and δ, respectively. Assuming , the inferred mutation rate was only slightly lower compared to ( – ).
Therefore, we do not find evidence of an increase in mutation rate in aneuploid cells. This may be because, unless the increase is strong (), it does not seem to affect our inference or because chromosome III is one of the smallest chromosomes (Gilchrist and Stelkens 2019). We also checked the differences in genotype frequency dynamics for different τ values. We observe that could be distinguished if accurate data were available for the waiting time for the frequency of to decrease below 95% (supplementary fig. S5A, Supplementary Material online) or for the waiting time for the frequency of to either reach or go below 95% (supplementary fig. S5B, Supplementary Material online).
Similarly, we did not find evidence for an increase in the rate of chromosome loss in aneuploid cells (Sheltzer et al. 2011), probably due to lack of statistical power. Nevertheless, increasing the rate of chromosome loss (transitions from to ) without increasing the rate of chromosome gain (transitions from to ) increases (supplementary fig. S11B, Supplementary Material online), but not to the same extent as increasing the rate of chromosome gain (supplementary fig. S10, Supplementary Material online). In contrast, increasing the mutation rate in aneuploid cells can have a marked effect on the dynamics: when using the MAP parameter estimates, increases from 0.1 to 0.52 when the mutation rate in aneuploid cells increases 10-fold (supplementary fig. S11C, Supplementary Material online).
Discussion
In a study on the role of chromosome duplication in adaptive evolution, Yona et al. (2012) found that a chromosome III trisomy was acquired by S. cerevisiae populations evolving under heat stress, only to be later replaced by euploid mutant cells that carry “refined” solutions to the stress. Additionally, such a replacement also occurred when they initiated evolutionary experiments with a population in which all cells carry a chromosome III trisomy. They hypothesized that aneuploidy is a “useful yet short-lived intermediate that facilitates further adaptation”, suggesting that the euploid mutant cells evolved by heat-resistance mutations in aneuploid cells followed by reversion of trisomy due to a chromosome loss event.
We developed an evolutionary genetic model of adaptive evolution by aneuploidy and mutation (Fig. 1), fitted it to the experimental results of Yona et al. (2012), and used it to predict the genotype frequency dynamics. The model predicted that only about 10–15% of the evolved euploid population descended from aneuploid cells by acquiring a mutation and losing the extra chromosome—that is, the majority of the euploid population are not descended from aneuploid cells, but rather are direct descendants of the ancestral wild-type population (Fig. 4).
This happens despite aneuploidy reaching a high frequency in the population (). Conventional wisdom might suggest that once the aneuploid genotype reaches high frequency, it will have a better chance at producing “refined” solutions via mutations, and its descendants will come to dominate the population: the frequency of (which arises from ) will be higher than the frequency of (which arises directly from ).
So how does prevail? Initially, the supply rates of and are and , respectively (assuming MAP parameter estimates). Therefore, both genotypes are expected to appear immediately at the beginning of the experiment (supplementary fig. S9, Supplementary Material online). However, appears at a much higher frequency as by 2–3 orders of magnitude. After they first appear, has higher fitness. But as long as the frequency of is high, the supply rate of is higher than that of , again due to . However, supply rates of both genotypes decrease with the frequency of . Therefore, when the latter decreases, mainly due to the increase in the frequency of , both supply rates diminish. At this stage, the higher fitness of comes into play and it starts to take over the population, which is mainly composed of . For the aneuploid lineage to compete with the mutant lineage, it must produce via a mutation followed by chromosome loss. Although this is a stochastic process (due to drift), our results show that the time until reaches a frequency of 0.1% is roughly 450 generations, without much variation (intersection of purple lines and vertical dashed line in supplementary fig. S9, Supplementary Material online). However, by that time, is already at a roughly 10-fold higher frequency (1.86%), and since both mutants have the same fitness, their relative frequency remains roughly the same until the end of the experiment.
Predictions for small populations and low mutation rates
We examined the effect of the population size, N, and the beneficial mutation rate, μ, on the frequency of descendants in the evolved population, . We found that is expected to decrease as the population size or mutation rate increase (Fig. 4D), ranging from when the population size is 10,000 or the mutation rate is , to about 10% when the population size is above 1,000,000 (less than the experimental population size, which was 6,425,000) or the mutation rate is above (less than the inferred mutation rate, which is ). Thus, our model provides a testable prediction: if the experiment was repeated under a lower population size (via stronger daily dilutions or in a smaller volume) or a lower mutation rate (via a non-mutagenic stress or stress with a smaller target size such as an antifungal drug), then the fraction of the population descending from aneuploid cells would be much higher.
Aneuploidy delays rather than facilitates adaptation
An additional interesting result of our study is that aneuploidy increases, rather than decreases, the adaptation time (Fig. 4E). This happens despite the fact that the mean fitness initially increases faster in the presence of aneuploidy (Fig. 4E). Aneuploidy increases adaptation time because once is common, selection for the mutant strain ( or ) is weaker compared to when competes directly with . This is an interesting example of clonal interference (Good et al. 2012) but between fast and slow mutational processes (Kronholm and Collins 2016).
Rate and fitness effect of aneuploidy and mutation
We inferred the rates of aneuploidy and mutation and their effects on fitness. We estimate that the aneuploidy rate (i.e. number of chromosome gains per generation) is , higher than a previous estimate of (Zhu et al. 2016). This may be due to genetic instability caused by heat stress (Chen et al. 2012), but we note that there is a general scarcity of empirical data on aneuploidy rates. In addition, we did not find evidence for increased mutation rates in aneuploid cells. Previous empirical studies have suggested that genetic instability (e.g. elevated mutation rates) in aneuploid cells is due to stress associated with the aneuploid state (Bouchonville et al. 2009; Chen et al. 2012; Zhu et al. 2012; Ippolito et al. 2021). However, in the experiment of Yona et al. (2012), both the wild-type and the aneuploid were under heat stress, which may explain why we did not find evidence for an increased mutation rate specifically in aneuploid cells.
Effect of ploidy
The evolutionary dynamics may change in haploid yeast, in which aneuploidy results in a second, rather than third, chromosome copy. For example, it has been demonstrated that drug resistance mainly evolves via recessive mutations and aneuploidy in haploid yeast (Soncini et al. 2020), whereas in diploid yeast it evolves via dominant mutations, aneuploidy, and gene/segmental duplications (Barney et al. 2021). Thus, the second chromosome copy of disomic yeast may facilitate further adaptation via duplications, rearrangements, and increased mutational tolerance (Avecilla et al. 2023), while decreasing the chance for adaptation via recessive mutations. Future models and experiments can consider how ploidy and other genomic contexts affect the role of aneuploidy in adaptive evolution.
Conclusions
Here, we tested the hypothesis that aneuploid cells are an evolutionary “stepping stone”, or adaptive intermediate, between wild-type euploid cells and mutant euploid cells in the evolutionary experiment of Yona et al. (2012). Our results suggest that, although it seems the population goes from euploid to aneuploid and back, this is not the case at the individual level. We estimate that only about 10–15% of the euploid cells descended from aneuploid cells, whereas the rest are direct descendants of the wild-type euploid cells. Thus, aneuploidy can delay, rather than accelerate, adaptation, and cells that become aneuploid may leave less descendants than cells that remain euploid. This surprising result reinforces the importance of mathematical models when interpreting evolutionary dynamics. Moreover, our study emphasizes the unintuitive outcomes of clonal interference between mechanisms for generation of variation that differ in their rate of formation and distribution of fitness effects, including mutation, copy number variation, horizontal gene transfer, and epigenetic modifications.
Models and Methods
Evolutionary genetic model
We model the evolution of a population of cells using a Wright–Fisher model (Otto and Day 2007), assuming a constant effective population size N, non-overlapping generations, and including the effects of natural selection, genetic drift, aneuploidy, and mutation. We focus on beneficial genetic modifications, neglecting the effects of deleterious and neutral mutations or karyotypic changes. The model allows for a single aneuploid karyotype (e.g. chromosome III duplication) and a single mutation to accumulate in the genotype. Thus, the model follows four genotypes (Fig. 1): euploid wild-type, ; the initial genotype; euploid mutant, , with the standard karyotype and a single beneficial mutation; aneuploid wild-type, , with an extra chromosome, i.e. following chromosome duplication; and aneuploid mutant, , with an extra chromosome and a beneficial mutation.
Transitions between the genotypes occur as follows (Fig. 1): beneficial mutations from to and from to occur with probability μ, the mutation rate. We neglect back-mutations (i.e. from to and from to ). Aneuploidy is formed by chromosome mis-segregation, so that cells transition from to and from to with probability δ, the aneuploidy rate. That is, we assume chromosomes are gained and lost at the same rate, and we neglect events that form a less-fit genotype (i.e. to and to ). A model that assumes an increased rate of chromosome loss in aneuploid cells [as in Sheltzer et al. (2011)] did not perform well, probably due to lack of statistical power, and was abandoned.
In the experiment by Yona et al. (2012), the population was grown every day from cells until reaching stationary phase and then diluted 1:120. Thus, we set the population size to , the harmonic mean of (Crow and Kimura 1970). The initial population has N cells with genotype . The effect of natural selection on the frequency of genotype is given by
| (1) |
where is the fitness of genotype i and is the population mean fitness. The effect of mutation and aneuploidy on genotype frequencies is given by
| (2) |
Finally, random genetic drift is modeled using a multinomial distribution (Otto and Day 2007):
| (3) |
where are the frequencies of the genotypes after mutation and aneuploidy, are the genotype frequencies in the next generation, and is a multinomial distribution parameterized by the population size N and the genotype frequencies . Overall, the change in genotype frequencies from one generation to the next is given by the transformation .
Empirical data for model inference
We use the results of evolutionary experiments reported by Yona et al. (2012). In their heat-stress experiment, four populations of S. cerevisiae evolved under 39 °C. Aneuploidy fixed (frequency ) in all four population in the first 450 generations. Hereafter, fixation or elimination of a genotype by generation t means that more than 95% or less than 5% of the population carry the genotype at generation t, and possibly earlier. In the original analysis of Yona et al. (2012), samples were routinely extracted from the evolving populations and tested for indication of heat-shock tolerance. The first generation in which such indication was found was generation 200. Therefore, we determine that aneuploidy did not reach high frequency before generation 200. The experiment continued with two populations, in which aneuploidy was eliminated by generation 1,700 and 2,350 while still under the same conditions of elevated heat (39 °C).
Likelihood function
Because our model, just like the Wright–Fisher model, is non-linear and stochastic, computing the distribution of fixation time of genotype g for use in the likelihood function is intractable (it is even hard to use a diffusion-equation approximation due to the model having multiple genotypes, rather than just two). We overcome this problem by approximating the likelihood using simulations. We simulate 1,000 experiments per parameter vector , resulting in a set of simulated observations . We then compute the approximate likelihood:
| (4) |
where is the “logical not” operator, is the fourth power of , and all probabilities are approximated from the results of the simulations . For example, is approximated by taking simulations in which fixed (reached ) before generation 450 but not before generation 200, and computing the fraction of such simulations in which did not fix by generation 1,700, and hence aneuploidy did not extinct (reach ) before generation 1,700. Supplementary fig. S1, Supplementary Material online, compares results with less and more simulated experiments, demonstrating that 1,000 simulations are likely sufficient.
For a model without aneuploidy (that is, when the aneuploidy rate is fixed at zero, ), we disregard the increased expression in chromosome III and the growth advantage measured in generation 450, and focus on the growth advantage measured in later generations, presumably due to a beneficial mutation. Therefore, the likelihood is approximated by
| (5) |
Parameter inference
To infer model parameters, we use ABC-SMC (Sisson et al. 2007) implemented in the pyABC Python package (Klinger et al. 2018, pyabc.readthedocs.io). This approach uses numerical stochastic simulations of the model to infer a posterior distribution over the model parameters. It is a method of likelihood-free, simulation-based inference (Cranmer et al. 2020), that is, for estimating a posterior distribution when a likelihood function cannot be directly computed. It is therefore suitable in our case, in which the likelihood function can only be approximated from simulations, and cannot be directly computed.
The ABC-SMC algorithm employs sequential importance sampling over multiple iterations (Toni et al. 2009; Klinger and Hasenauer 2017; Syga et al. 2021). In iteration t of the algorithm, a set of parameter vectors, , also called particles, are constructed in the following way. A proposal particle, , is sampled from a proposal distribution, and is either accepted or rejected, until particles are accepted. The number of particles, , is adapted at every iteration t using the adaptive population strategy (Klinger et al. 2018, pyabc.readthedocs.io). For , the proposal particle is sampled from the prior distribution, . For , the proposal particle is sampled from the particles accepted in the previous iteration, , each with a probability relative to its weight (see below). The proposal particle is then perturbed using a kernel perturbation kernel, , where θ is the sample from the previous iteration. Then, a set of synthetic observations is simulated, and the proposal particle is accepted if its approximate likelihood (equation 4) is high enough, (or more commonly, if ), where is the acceptance threshold, as higher values of allow more particles to be accepted. The acceptance threshold is chosen as the median of the of the particles accepted in the previous iteration, , and . For each accepted particle , a weight is assigned: for , , and for , , where is the prior density of θ and is the probability of a perturbation from θ to . is a multivariate normal distribution, fitted at iteration t to the particles from the previous iteration, , and their weights, .
Acceptance is determined according to the approximate likelihood (equation 4), which has a maximum value of (giving a minimal value of ). We terminated the inference iterations when the change in value from one iteration to the next was small. With our standard prior and model, we reached (or ) after six iterations, with accepted parameter vectors and effective sample size 651 (supplementary fig. S2, Supplementary Material online). Running the inference algorithm with different initialization seeds and less or more simulations for approximating the likelihood produced similar posterior distributions (supplementary fig. S1, Supplementary Material online).
After producing a set of weighted particles from the posterior distribution using the above ABC-SMC algorithm, we approximate the posterior using kernel density estimation (KDE) with Gaussian kernels. We truncate the estimated posterior to avoid positive posterior density for values with zero prior density. The MAP estimate is computed as the maximum of the estimated joint posterior density. We then draw samples from the posterior distribution to compute the HDI and draw samples to visualize the posterior distribution with histograms.
Model comparison
We examine several versions of our evolutionary models, e.g. without aneuploidy or with increased mutation rate in aneuploid cells, as well as several different prior distributions (see below). To compare these, we plot posterior predictions: for each model we execute simulations using the MAP parameter estimates and plot the distributions of time to fixation of , one of the key properties of the model likelihood. These plots visualize the fit of each model to the data. Also, for similar models, we plot the marginal and joint posterior distributions of the parameters; if these are similar, we consider the models interchangeable. We validate this by comparing HDI of posterior distributions.
Where posterior plots are very similar and the number of parameters is the same, we use WAIC, or the widely applicable information criterion (Gelman et al. 2013), defined as
| (6) |
where θ is a parameter vector, and and are the expectation and variance taken over the posterior distribution, which in practice are approximated using 50,000 samples from the posterior KDE. We validated that upon resampling WAIC values do not significantly change and that differences in WAIC between models are preserved. WAIC values are scaled as a deviance measure: lower values imply higher predictive accuracy.
Prior distributions
We used informative prior distributions for , , and (we set ), which we estimated from growth curves data from mono-culture growth experiments previously reported by Yona et al. (2012, Figs. 3C, 4A, and S2). We used Curveball, a method for predicting results of competition experiments from growth curve data (Ram et al. 2019, curveball.yoavram.com). Briefly, Curveball takes growth curves of two strains growing separately in mono-culture and predicts how they would grow in a mixed culture, that is, it predicts the results of a competition assay. From these predictions, relative fitness values can be computed. Because Curveball uses a maximum-likelihood approach to estimate model parameters, we were able to estimate a distribution of relative fitness values to be used as a prior distribution by sampling 10,000 samples from a truncated multivariate normal distribution defined by the maximum-likelihood covariance matrix (supplementary fig. S3, Supplementary Material online).
We used growth curves of and in 39 °C to estimate an informative prior distribution for (supplementary fig. S3D, Supplementary Material online, assuming ). In this prior distribution, we used the same prior for and . To increase computational efficiency, we also assumed ; running the inference without this assumption produced similar results. See Supporting Material online for an extended informative prior distribution that uses growth curves of and growing in 39 °C; this prior distribution proved to be less useful.
As a control, we tested an uninformative uniform prior with , for (i) all , , , or (ii) only for , , using the above informative prior for . In these cases, the inference algorithm failed to converge.
For the mutation rate, μ, and aneuploidy rate, δ, we used uninformative uniform priors, and . A wider mutation rate prior, , produced similar results.
Supplementary Material
Acknowledgements
We thank Lilach Hadany, Judith Berman, David Gresham, Shay Covo, Martin Kupiec, Uri Obolski, Daniel Weissman, and Tal Simon for discussions and comments. This work was supported in part by the Israel Science Foundation (ISF, Y.R. 552/19), the US–Israel Binational Science Foundation (BSF, Y.R. 2021276), Minerva Center for Live Emulation of Evolution in the Lab (Y.R., Y.P.), Minerva Stiftung Short-Term Research Grant (M.P.), the National Institutes of Health R01 (A.S. AI143689), the Burroughs Wellcome Fund Investigators in the Pathogenesis of Infectious Diseases (A.S. 1020388), and the Jane Coffin Childs Memorial Fund (P.V.Z.).
Contributor Information
Ilia Kohanovski, School of Zoology, Faculty of Life Sciences, Tel Aviv University, Tel Aviv, Israel; School of Computer Science, Reichman University, Herzliya, Israel.
Martin Pontz, School of Zoology, Faculty of Life Sciences, Tel Aviv University, Tel Aviv, Israel.
Pétra Vande Zande, Department of Microbiology and Immunology, University of Minnesota Medical School, Minneapolis, MN, USA.
Anna Selmecki, Department of Microbiology and Immunology, University of Minnesota Medical School, Minneapolis, MN, USA.
Orna Dahan, Department of Molecular Genetics, Weizmann Institute of Science, Rehovot, Israel.
Yitzhak Pilpel, Department of Molecular Genetics, Weizmann Institute of Science, Rehovot, Israel.
Avihu H Yona, Institute of Biochemistry, Food Science and Nutrition, Robert H. Smith Faculty of Agriculture, Food and Environment, The Hebrew University of Jerusalem, Rehovot, Israel.
Yoav Ram, School of Zoology, Faculty of Life Sciences, Tel Aviv University, Tel Aviv, Israel.
Supplementary Material
Supplementary material is available at Molecular Biology and Evolution online.
References
- Avecilla G, Chuong JN, Li F, Sherlock G, Gresham D, Ram Y. Neural networks enable efficient and accurate simulation-based inference of evolutionary parameters from adaptation dynamics. PLoS Biol. 2022:20(5):e3001633. 10.1371/journal.pbio.3001633. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Avecilla G, Spealman P, Matthews J, Caudal E, Schacherer J, Gresham D. Copy number variation alters local and global mutational tolerance. Genome Res. 2023:33:1340–1353. 10.1101/gr.277625.122. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bakhoum SF, Landau DA. Chromosomal instability as a driver of tumor heterogeneity and evolution. Cold Spring Harb Perspect Med. 2017:7(6):1–14. 10.1101/cshperspect.a029611. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barney JB, Chandrashekarappa DG, Soncini SR, Schmidt MC. Drug resistance in diploid yeast is acquired through dominant alleles, haploinsufficiency, gene duplication and aneuploidy. PLoS Genet. 2021:17(9):e1009800. 10.1371/journal.pgen.1009800. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bouchonville K, Forche A, Tang KES, Semple CAM, Berman J. Aneuploid chromosomes are highly unstable during DNA transformation of Candida albicans. Eukaryot Cell. 2009:8(10):1554–1566. 10.1128/EC.00209-09. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boveri T. Concerning the origin of malignant tumours. J Cell Sci. 2008:121(Supplement_1):1–84. 10.1242/jcs.025742. [DOI] [PubMed] [Google Scholar]
- Chen G, Bradford WD, Seidel CW, Li R. Hsp90 stress potentiates rapid cellular adaptation through induction of aneuploidy. Nature. 2012:482(7384):246–250. 10.1038/nature10795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen G, Rubinstein B, Li R. Whole chromosome aneuploidy: big mutations drive adaptation by phenotypic leap. BioEssays. 2012:34(10):893–900. 10.1002/bies.v34.10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Covo S, Puccia CM, Argueso JL, Gordenin DA, Resnick MA. The sister chromatid cohesion pathway suppresses multiple chromosome gain and chromosome amplification. Genetics. 2014:196(2):373–384. 10.1534/genetics.113.159202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cranmer K, Brehmer J, Louppe G. The frontier of simulation-based inference. Proc Natl Acad Sci U S A. 2020:117(48):30055–30062. 10.1073/pnas.1912789117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crow JF, Kimura M. An introduction to population genetics theory. Minneapolis (MN): Burgess Pub. Co.; 1970. [Google Scholar]
- Dhar R, Sägesser R, Weikert C, Yuan J, Wagner A. Adaptation of Saccharomyces cerevisiae to saline stress through laboratory evolution. J Evol Biol. 2011:24(5):1135–1153. 10.1111/jeb.2011.24.issue-5. [DOI] [PubMed] [Google Scholar]
- Dunham MJ, Badrane H, Ferea T, Adams J, Brown PO, Rosenzweig F, Botstein D. Characteristic genome rearrangements in experimental evolution of Saccharomyces cerevisiae. Proc Natl Acad Sci U S A. 2002:99(25):16144–16149. 10.1073/pnas.242624799. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elde NC, Child SJ, Eickbush MT, Kitzman JO, Rogers KS, Shendure J, Geballe AP, Malik HS. Poxviruses deploy genomic accordions to adapt rapidly against host antiviral defenses. Cell. 2012:150(4):831–841. 10.1016/j.cell.2012.05.049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Flynn JM, Rossouw A, Cote-Hammarlof P, Fragata I, Mavor D, Hollins C, Bank C, Bolon DN. Comprehensive fitness maps of Hsp90 show widespread environmental dependence. Elife. 2020:9:1–25. 10.7554/eLife.53810. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gelman A, Carlin JB, Stern HS, Dunson DB, Vehtari A, Rubin DB. Bayesian data analysis. 3rd ed. New York: Taylor & Francis; 2013. Chapman & Hall/CRC Texts in Statistical Science. [Google Scholar]
- Gerstein AC, Berman J. Candida albicans genetic background influences mean and heterogeneity of drug responses and genome stability during evolution in fluconazole. mSphere. 2020:5(3):e00480-20. 10.1128/mSphere.00480-20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gerstein AC, Ono J, Lo DS, Campbell ML, Kuzmin A, Otto SP. Too much of a good thing: the unique and repeated paths toward copper adaptation. Genetics. 2015:199(2):555–571. 10.1534/genetics.114.171124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gilchrist C, Stelkens R. Aneuploidy in yeast: segregation error or adaptation mechanism? Yeast. 2019:36(9):525–539. 10.1002/yea.v36.9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Good BH, Rouzine IM, Balick DJ, Hallatschek O, Desai MM. Distribution of fixed beneficial mutations and the rate of adaptation in asexual populations. Proc Natl Acad Sci U S A. 2012:109(13):4950–4955. 10.1073/pnas.1119910109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gresham D, Desai MM, Tucker CM, Jenq HT, Pai DA, Ward A, DeSevo CG, Botstein D, Dunham MJ. The repertoire and dynamics of evolutionary adaptations to controlled nutrient-limited environments in yeast. PLoS Genet. 2008:4(12):e1000303. 10.1371/journal.pgen.1000303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heidenreich E. Adaptive mutation in Saccharomyces cerevisiae. Crit Rev Biochem Mol Biol. 2007:42(4):285–311. 10.1080/10409230701507773. [DOI] [PubMed] [Google Scholar]
- Hong J, Gresham D. Molecular specificity, convergence and constraint shape adaptive evolution in nutrient-poor environments. PLoS Genet. 2014:10(1):e1004041. 10.1371/journal.pgen.1004041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang CJ, Lu MY, Chang YW, Li WH. Experimental evolution of yeast for high-temperature tolerance. Mol Biol Evol. 2018:35(8):1823–1839. 10.1093/molbev/msy077. [DOI] [PubMed] [Google Scholar]
- Ippolito MR, Martis V, Martin S, Tijhuis AE, Hong C, Wardenaar R, Dumont M, Zerbib J, Spierings DC, Fachinetti D, et al. Gene copy-number changes and chromosomal instability induced by aneuploidy confer resistance to chemotherapy. Dev Cell. 2021:56(17):2440–2454.e6. 10.1016/j.devcel.2021.07.006. [DOI] [PubMed] [Google Scholar]
- Iwasa Y, Michor F, Nowak MA. Stochastic tunnels in evolutionary dynamics. Genetics. 2004:166(3):1571–1579. 10.1534/genetics.166.3.1571. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jarolim S, Ayer A, Pillay B, Gee AC, Phrakaysone A, Perrone GG, Breitenbach M, Dawes IW. Saccharomyces cerevisiae genes involved in survival of heat shock. G3 Genes Genom Genet. 2013:3(12):2321–2333. 10.1534/g3.113.007971. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kasuga T, Bui M, Bernhardt E, Swiecki T, Aram K, Cano LM, Webber J, Brasier C, Press C, Grünwald NJ, et al. Host-induced aneuploidy and phenotypic diversification in the Sudden Oak Death pathogen Phytophthora ramorum. BMC Genom. 2016:17(1):1–17. 10.1186/s12864-016-2717-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klinger E, Hasenauer J. A scheme for adaptive selection of population sizes in approximate Bayesian computation—sequential Monte Carlo. In: Feret J, Koeppl H, editors. Computational methods in systems biology, Vol. 10545. Springer International Publishing; 2017. p. 128–144. Series Title: Lecture Notes in Computer Science.
- Klinger E, Rickert D, Hasenauer J. pyabc: distributed, likelihood-free inference. Bioinformatics. 2018:34(20):3591–3593. 10.1093/bioinformatics/bty361. [DOI] [PubMed] [Google Scholar]
- Kohn LM, Anderson JB. The underlying structure of adaptation under strong selection in 12 experimental yeast populations. Eukaryot Cell. 2014:13(9):1200–1206. 10.1128/EC.00122-14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Komarova NL, Sengupta A, Nowak MA. Mutation-selection networks of cancer initiation: tumor suppressor genes and chromosomal instability. J Theor Biol. 2003:223(4):433–450. 10.1016/S0022-5193(03)00120-6. [DOI] [PubMed] [Google Scholar]
- Kronholm I, Collins S. Epigenetic mutations can both help and hinder adaptive evolution. Mol Ecol. 2016:25(8):1856–1868. 10.1111/mec.2016.25.issue-8. [DOI] [PubMed] [Google Scholar]
- Kumaran R, Yang S-Y, Leu J-Y. Characterization of chromosome stability in diploid, polyploid and hybrid yeast cells. PLoS One. 2013:8(7):e68094. 10.1371/journal.pone.0068094. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lauer S, Avecilla G, Spealman P, Sethia G, Brandt N, Levy SF, Gresham D. Single-cell copy number variant detection reveals the dynamics and diversity of adaptation. PLoS Biol. 2018:16(12):e3000069. 10.1371/journal.pbio.3000069. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lukow DA, Sausville EL, Suri P, Chunduri NK, Wieland A, Leu J, Smith JC, Girish V, Kumar AA, Kendall J, et al. Chromosomal instability accelerates the evolution of resistance to anti-cancer therapies. Dev Cell. 2021:56(17):2427–2439.e4. 10.1016/j.devcel.2021.07.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lynch M, Sung W, Morris K, Coffey N, Landry CR, Dopman EB, Dickinson WJ, Okamoto K, Kulkarni S, Hartl DL, et al. A genome-wide view of the spectrum of spontaneous mutations in yeast. Proc Natl Acad Sci U S A. 2008:105(27):9272–9277. 10.1073/pnas.0803466105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mannaert A, Downing T, Imamura H, Dujardin JC. Adaptive mechanisms in pathogens: universal aneuploidy in Leishmania. Trends Parasitol. 2012:28(9):370–376. 10.1016/j.pt.2012.06.003. [DOI] [PubMed] [Google Scholar]
- Möller M, Habig M, Freitag M, Stukenbrock EH. Extraordinary genome instability and widespread chromosome rearrangements during vegetative growth. Genetics. 2018:210(2):517–529. 10.1534/genetics.118.301050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Naylor RM, van Deursen JM. Aneuploidy in cancer and aging. Annu Rev Genet. 2016:50(1):45–66. 10.1146/genet.2016.50.issue-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Niwa O, Tange Y, Kurabayashi A. Growth arrest and chromosome instability in aneuploid yeast. Yeast. 2006:23(13):937–950. 10.1002/yea.v23:13. [DOI] [PubMed] [Google Scholar]
- Otto SP, Day T. A biologist’s guide to mathematical modeling in ecology and evolution. Princeton and Oxford: Princeton University Press; 2007. [Google Scholar]
- Pavelka N, Rancati G, Zhu J, Bradford WD, Saraf A, Florens L, Sanderson BW, Hattem GL, Li R. Aneuploidy confers quantitative proteome changes and phenotypic variation in budding yeast. Nature. 2010:468(7321):321–325. 10.1038/nature09529. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peter J, De Chiara M, Friedrich A, Yue JX, Pflieger D, Bergström A, Sigwalt A, Barre B, Freel K, Llored A, et al. Genome evolution across 1,011 Saccharomyces cerevisiae isolates. Nature. 2018:556(7701):339–344. 10.1038/s41586-018-0030-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ram Y, Dellus-Gur E, Bibi M, Karkare K, Obolski U, Feldman MW, Cooper TF, Berman J, Hadany L. Predicting microbial growth in a mixed culture from growth curve data. Proc Natl Acad Sci U S A. 2019:116(29):14698–14707. 10.1073/pnas.1902217116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rancati G, Pavelka N, Fleharty B, Noll A, Trimble R, Walton K, Perera A, Staehling-Hampton K, Seidel CW, Li R. Aneuploidy underlies rapid adaptive evolution of yeast cells deprived of a conserved cytokinesis motor. Cell. 2008:135(5):879–893. 10.1016/j.cell.2008.09.039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robbins N, Caplan T, Cowen LE. Molecular evolution of antifungal drug resistance. Annu Rev Microbiol. 2017:71(1):753–775. 10.1146/micro.2017.71.issue-1. [DOI] [PubMed] [Google Scholar]
- Robinson D, Vanacloig-Pedros E, Cai R, Place M, Hose J, Gasch AP. Gene-by-environment interactions influence the fitness cost of gene copy-number variation in yeast. G3 Genes Genomes Genetics. 2023:13(10):jkad159. 10.1093/g3journal/jkad159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rodrigues ML, Albuquerque PC. Searching for a change: the need for increased support for public health and research on fungal diseases. PLoS Negl Trop Dis. 2018:12(6):1–5. 10.1371/journal.pntd.0006479. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rutledge SD, Douglas TA, Nicholson JM, Vila-Casadesús M, Kantzler CL, Wangsa D, Barroso-Vilares M, Kale SD, Logarinho E, Cimini D. Selective advantage of trisomic human cells cultured in non-standard conditions. Sci Rep. 2016:6(1):22828. 10.1038/srep22828. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Santaguida S, Amon A. Short- and long-term effects of chromosome mis-segregation and aneuploidy. Nat Rev Mol Cell Biol. 2015:16(8):473–485. 10.1038/nrm4025. [DOI] [PubMed] [Google Scholar]
- Santaguida S, Vasile E, White E, Amon A. Aneuploidy-induced cellular stresses limit autophagic degradation. Genes Dev. 2015:29(19):2010–2021. 10.1101/gad.269118.115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schvartzman JM, Sotillo R, Benezra R. Mitotic chromosomal instability and cancer: mouse modelling of the human disease. Nat Rev Cancer. 2010:10(2):102–115. 10.1038/nrc2781. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Selmecki AM, Dulmage K, Cowen LE, Anderson JB, Berman J. Acquisition of aneuploidy provides increased fitness during the evolution of antifungal drug resistance. PLoS Genet. 2009:5(10):e1000705. 10.1371/journal.pgen.1000705. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Selmecki AM, Forche A, Berman J. Genomic plasticity of the human fungal pathogen Candida albicans. Eukaryot Cell. 2010:9(7):991–1008. 10.1128/EC.00060-10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Selmecki AM, Gerami-Nejad M, Paulson C, Forche A, Berman J. An isochromosome confers drug resistance in vivo by amplification of two genes, ERG11 and TAC1. Mol Microbiol. 2008:68(3):624–641. 10.1111/mmi.2008.68.issue-3. [DOI] [PubMed] [Google Scholar]
- Sheltzer JM, Amon A. The aneuploidy paradox: costs and benefits of an incorrect karyotype. Trends Genet. 2011:27(11):446–453. 10.1016/j.tig.2011.07.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sheltzer JM, Blank HM, Pfau SJ, Tange Y, George BM, Humpton TJ, Brito IL, Hiraoka Y, Niwa O, Amon A. Aneuploidy drives genomic instability in yeast. Science. 2011:333(6045):1026–1030. 10.1126/science.1206412. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sheltzer JM, Ko JH, Replogle JM, Habibe Burgos NC, Chung ES, Meehl CM, Sayles NM, Passerini V, Storchova Z, Amon A. Single-chromosome gains commonly function as tumor suppressors. Cancer Cell. 2017:31(2):240–255. 10.1016/j.ccell.2016.12.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sionov E, Lee H, Chang YC, Kwon-Chung KJ. Cryptococcus neoformans overcomes stress of azole drugs by formation of disomy in specific multiple chromosomes. PLoS Pathog. 2010:6(4):e1000848. 10.1371/journal.ppat.1000848. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sisson SA, Fan Y, Tanaka MM. Sequential Monte Carlo without likelihoods. Proc Natl Acad Sci U S A. 2007:104(6):1760–1765. 10.1073/pnas.0607208104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Soncini SR, Chandrashekarappa DG, Augustine DA, Callahan KP, O’Donnell AF, Schmidt MC. Spontaneous mutations that confer resistance to 2-deoxyglucose act through Hxk2 and Snf1 pathways to regulate gene expression and HXT endocytosis. PLoS Genet. 2020:16(7):e1008484 10.1371/journal.pgen.1008484. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sonti RV, Roth JR. Role of gene duplications in the adaptation of Salmonella typhimurium to growth on limiting carbon sources. Genetics. 1989:123(1):19–28. 10.1093/genetics/123.1.19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Syga S, David-Rus D, Schälte Y, Hatzikirou H, Deutsch A. Inferring the effect of interventions on covid-19 transmission networks. Sci Rep. 2021:11(1):1–11. 10.1038/s41598-021-01407-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Todd RT, Forche A, Selmecki AM. Ploidy variation in fungi: polyploidy, aneuploidy, and genome evolution. Microbiol Spectr. 2017:5(4):1–20. 10.1128/microbiolspec.FUNK-0051-2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Toni T, Welch D, Strelkowa N, Ipsen A, Stumpf MP. Approximate Bayesian computation scheme for parameter inference and model selection in dynamical systems. J R Soc Interface. 2009:6(31):187–202. 10.1098/rsif.2008.0172. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Torres EM, Dephoure N, Panneerselvam A, Tucker CM, Whittaker CA, Gygi SP, Dunham MJ, Amon A. Identification of aneuploidy-tolerating mutations. Cell. 2010:143(1):71–83. 10.1016/j.cell.2010.08.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Torres EM, Sokolsky T, Tucker CM, Chan LY, Boselli M, Dunham MJ, Amon A. Effects of aneuploidy on cellular physiology and cell division in haploid yeast. Science. 2007:317(5840):916–924. 10.1126/science.1142210. [DOI] [PubMed] [Google Scholar]
- Tsai HJ, Nelliat AR, Choudhury MI, Kucharavy A, Bradford WD, Cook ME, Kim J, Mair DB, Sun SX, Schatz MC. Hypo-osmotic-like stress underlies general cellular defects of aneuploidy. Nature. 2019(570):117–121. 10.1038/s41586-019-1187-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Williams BR, Prabhu VR, Hunter KE, Glazier CM, Whittaker CA, Housman DE, Amon A. Aneuploidy affects proliferation and spontaneous immortalization in mammalian cells. Science. 2008:322(5902):703–709. 10.1126/science.1160058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang F, Todd RT, Selmecki A, Jiang YY, Cao YB, Berman J. The fitness costs and benefits of trisomy of each Candida albicans chromosome. Genetics. 2021:218(2):1–7. 10.1093/genetics/iyab056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yona AH, Frumkin I, Pilpel Y. A relay race on the evolutionary adaptation spectrum. Cell. 2015:163(3):549–559. 10.1016/j.cell.2015.10.005. [DOI] [PubMed] [Google Scholar]
- Yona AH, Manor YS, Herbst RH, Romano GH, Mitchell A, Kupiec M, Pilpel Y, Dahan O. Chromosomal duplication is a transient evolutionary solution to stress. Proc Natl Acad Sci U S A. 2012:109(51):21010–21015. 10.1073/pnas.1211150109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu J, Pavelka N, Bradford WD, Rancati G, Li R. Karyotypic determinants of chromosome instability in aneuploid budding yeast. PLoS Genet. 2012:8(5):e1002719. 10.1371/journal.pgen.1002719. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu YO, Sherlock G, Petrov DA. Whole genome analysis of 132 clinical Saccharomyces cerevisiae strains reveals extensive ploidy variation. G3 Genes Genom Genet. 2016:6(8):2421–2434. 10.1534/g3.116.029397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu YO, Siegal ML, Hall DW, Petrov DA. Precise estimates of mutation rate and spectrum in yeast. Proc Natl Acad Sci U S A. 2014:111(22):E2310–E2318. 10.1073/pnas.1323011111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu J, Tsai H-J, Gordon MR, Li R. Cellular stress associated with aneuploidy. Dev Cell. 2018:44(4):420–431. 10.1016/j.devcel.2018.02.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.