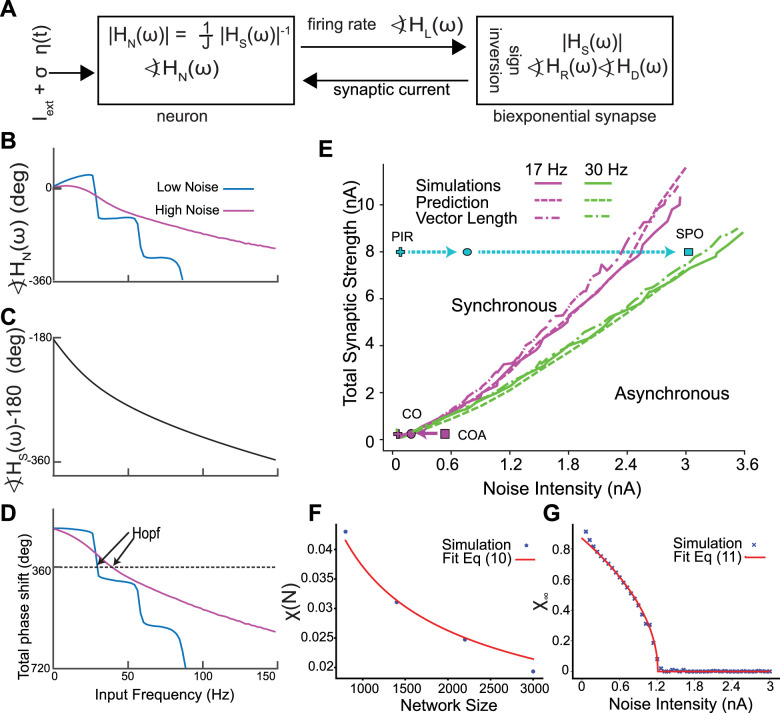
Figure 4.

Hopf bifurcation between stochastic asynchrony and synchrony. A, Self-consistent criterion for an oscillation in population rate. The sum of the phase shifts must equal −360°. B–D, Self-consistent phasic relationship for an oscillation in population rate. B, Numerically calculated neuronal phase shifts with $\sigma$ = 0.16 nA, for low noise and $\sigma$ = 2.8 nA for high noise. Iext is adjusted to maintain a constant firing rate of 30 Hz. C, Analytically calculated synaptic phase shift. D, The sum of the phase shifts must equal zero or a multiple of 360° (see Fig. 2) E, Projection of two curves onto the noise versus synaptic strength plane. Prediction, simulation result. The points corresponding to Figures 2 and 3 are depicted in cyan and purple, respectively. Dashed arrows depict transition in the synchronous region, full arrows correspond to asynchronous region. In E, we vary I_ext for each (${\sigma }_C$, J) to keep the mean firing rate constant. F, G, Finite-size scaling to find the Hopf bifurcation for Izhikevich model. F, Value of $\chi (N)$ for the four sizes of the network together with the fit of Equation 9. This fit gives a value of ${\chi }_{\mathrm{\infty }}$ for each J, $\sigma$ and I_ext. In this case J = 2 nA, $\sigma$ = 2 nA and I_ext= 2 nA. G, After finding ${\chi }_{\mathrm{\infty }}$, we find the noise value that destabilizes the asynchronous state for each value of J and I_ext. Thus, we end up with a set of values (J, I_ext, ${\sigma }_C$) which determines the Hopf bifurcation surface. J and I_ext are as (in F). All units are given per cm².