SUMMARY
To navigate, we must represent information about our place in the environment. Traditional research highlights the role of the hippocampal complex in this process. Spurred by recent research highlighting the widespread cortical encoding of cognitive and motor variables previously thought to have localized function, we hypothesized that navigational variables would be likewise encoded widely, especially in the prefrontal cortex, which is associated with volitional behavior. We recorded neural activity from six prefrontal regions while macaques performed a foraging task in an open enclosure. In all regions, we found strong encoding of allocentric position, allocentric head direction, boundary distance, and linear and angular velocity. These encodings were not accounted for by distance, time to reward, or motor factors. Strength of coding of all variables increases along a ventral-to-dorsal gradient. Together these results argue that encoding of navigational variables is not localized to the hippocampus and support the hypothesis that navigation is continuous with other forms of flexible cognition in the service of action.
Keywords: navigation, spatial selectivity, head direction tuning, mixed selectivity, prefrontal cortex
ETOC Blurb
Maisson et al., show that prefrontal brain areas in freely-moving rhesus macaques encode navigational variables with random, mixed selectivity. The strength of encoding increases along a ventral-to-dorsal gradient.
INTRODUCTION
To move in the world, organisms must represent where they are, where they are going, and where important features in the world are. In other words, they must navigate. The majority of research highlights the role of the hippocampus and adjacent structures in navigation1–6. This work supports a modular view of navigation, that is, that navigation results from computations in anatomically circumscribed circuits7, 8. An alternative view is that navigation relies on a suite of more general cognitive abilities, including generalized mapping functions, such as the encoding of task structure and latent environmental variables.
The modular approach to understanding functional neuroanatomy has been challenged by a growing set of studies that highlight the broad distribution of variables. These include motor signals9–12 and reward signals13–15. Such findings raise the possibility navigation may also be distributed16–19. Thus, evidence of widespread distribution of navigational codes would support their posited role in anchoring elements of cognition to maps of embodied space. In this view, navigation is a special case of the more general problem of representing conceptual linkages 5–7, 20, 21.
A growing body of research suggests that, at least in rodents, navigational functions exist outside the hippocampal complex, including within prefrontal areas22, 23. For example, neurons in somatosensory cortex, orbitofrontal cortex, and piriform cortex encode current and future spatial positions as well as the location of targets in the environment24–27. However, the distinct navigational strategies and preferred sensory modalities in rodents may not generalize to primates. Moreover, the extent to which rodent prefrontal areas serve as functional homologies to those of primates remains unclear28.
Theories about the function of prefrontal cortex seldom involve a navigational role. Instead, they typically involve functions that indirectly support navigation, including control of action, planning, resolving conflict, and comparing values17, 18, 29, 30. Often, however, these areas support more abstract mapping functions that augment space by anchoring to it an executive control-type function. For example, the roles for space typically assigned to PFC include the encoding of goal location, navigational action planning and landmark vector representations, and spatial working memory19, 20, 31–34. Yet, the direct involvement of PFC in navigational encoding remains unclear.
We developed a novel naturalistic paradigm for recording neural and behavioral data from freely-navigating macaques35. As macaques performed a freely-moving foraging task, we recorded neuronal activity in six regions: orbitofrontal cortex (OFC), dorsal anterior cingulate cortex (dACC), supplementary motor area (SMA), ventrolateral prefrontal cortex (vlPFC), dorsolateral prefrontal cortex (dlPFC), and dorsal premotor cortex (PMd). In all six, we found selectivity for navigational variables: allocentric position, allocentric head orientation, egocentric boundary distance, angular velocity, and linear velocity. Notably, this navigational tuning is not place-cell-like. Instead, it has a more unstructured pattern, even as it contains navigational information. Proportions of neurons responding were roughly the same as those encoding non-navigational variables, such as reward number and feeder identity. Neurons encoding navigational variables did not form functionally specialized subpopulations and these encodings were not accounted for by distance, time to reward, or motor factors. Finally, we found that distributed encoding of both navigational and non-navigational task variables followed functional gradients in which stronger coding was found in more dorsal areas. Together these results support the idea that navigational functions are supported by widespread activity of neurons, including those in several prefrontal structures.
RESULTS
Behavioral and neural recordings
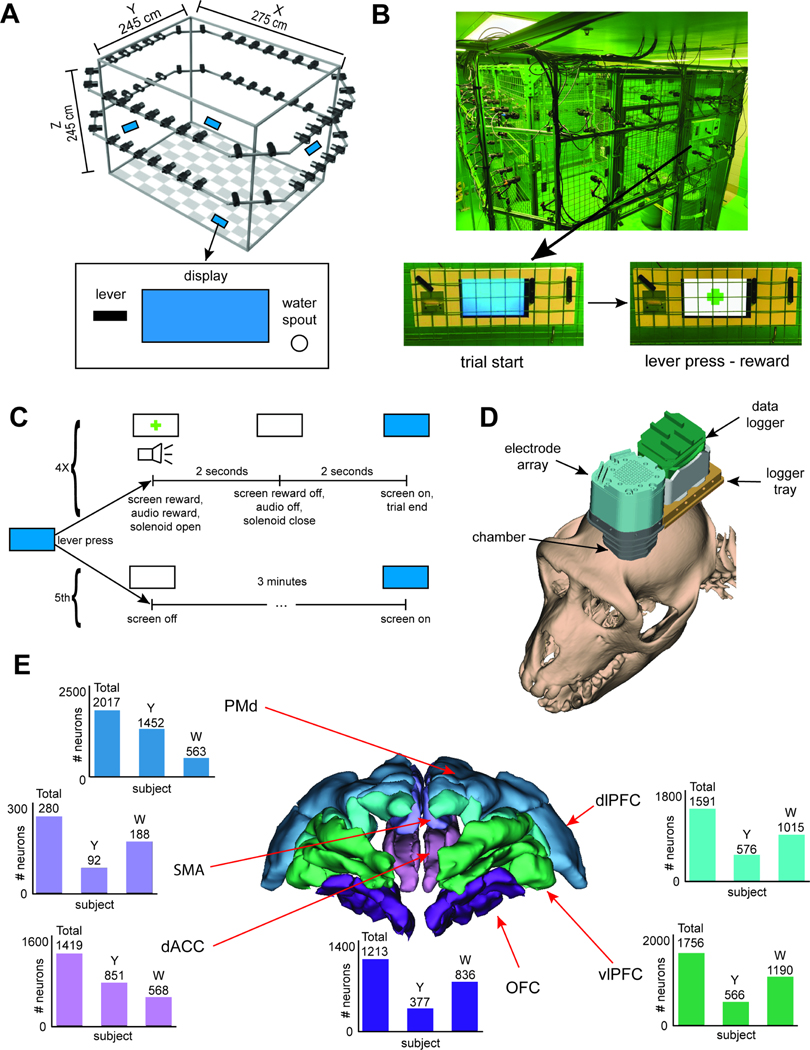
Rhesus macaques performed a novel freely-moving foraging task in a large (245 × 245 × 275 cm) enclosure with four barrels and up to four reward stations (Figure 1A and B, STAR Methods). If the subject approached a station (hereafter, a “patch”) and pressed the lever, a juice tube provided preferred liquid reward (1.5 mL) and the display changed from blue to white with green cross (Figure 1C). After two seconds, the screen returned to blue and the subject could repeat the process. After the fifth lever-press, the patch deactivated for 3 minutes. We used OpenMonkeyStudio35 to track subjects in space. We recorded neural activity from 128 electrodes (independently moveable, Figure 1D, STAR Methods). We recorded 8,276 neurons over 196 sessions from six structures in the prefrontal cortex (Figure 1E).
Figure 1. Behavior and neural recordings.
(A) Schematic of the arena. Checkerboard patterns indicate floor. Black rectangles denote cameras. Blue rectangles indicate the approximate locations of the feeding stations. The lower panel shows a cartoon depiction of the feeding station, with the display monitor at the center showing solid blue. (B) Photograph of the arena. (C) Schematic of the available, novel freely-moving foraging task. (D) 3D model of the recording system superimposed on a subject’s cranium. (E) 3D rendering of the prefrontal areas from which neural data were recorded. Bars: number of neurons recorded from each region.
Activity of prefrontal neurons can be fitted by a linear-nonlinear encoding model
We used a linear-nonlinear Poisson-distributed generalized additive model (LN-GAM) to estimate tuning functions for 8 distinct variables (method developed by Hardcastle et al.36 and used by others37–41: (1) lever pressing (vs. not pressing, equivalent to reward), (2) position of the body on the ground plane, (3) head elevation, (4) compass-wise head direction, (5) head tilt, (6) distance to enclosure boundaries, (7) angular velocity (speed of change in subjects’ compasswise orientation), and (8) linear velocity of the subject’s body. These variables were used in previous studies of navigational tuning in the macaque hippocampus, and were defined the same way37, 39. Note that this procedure includes a cross-validation procedure that controls for false positives by dividing each session into 10 partitions and performing 5-fold cross-validation within each partition. To characterize encoding of basic navigational variables, we considered the prevalence of tuning to each variable in turn across neurons in each structure (see Figure S1 and Table S1 for a summary).
Neurons in all six regions encode position
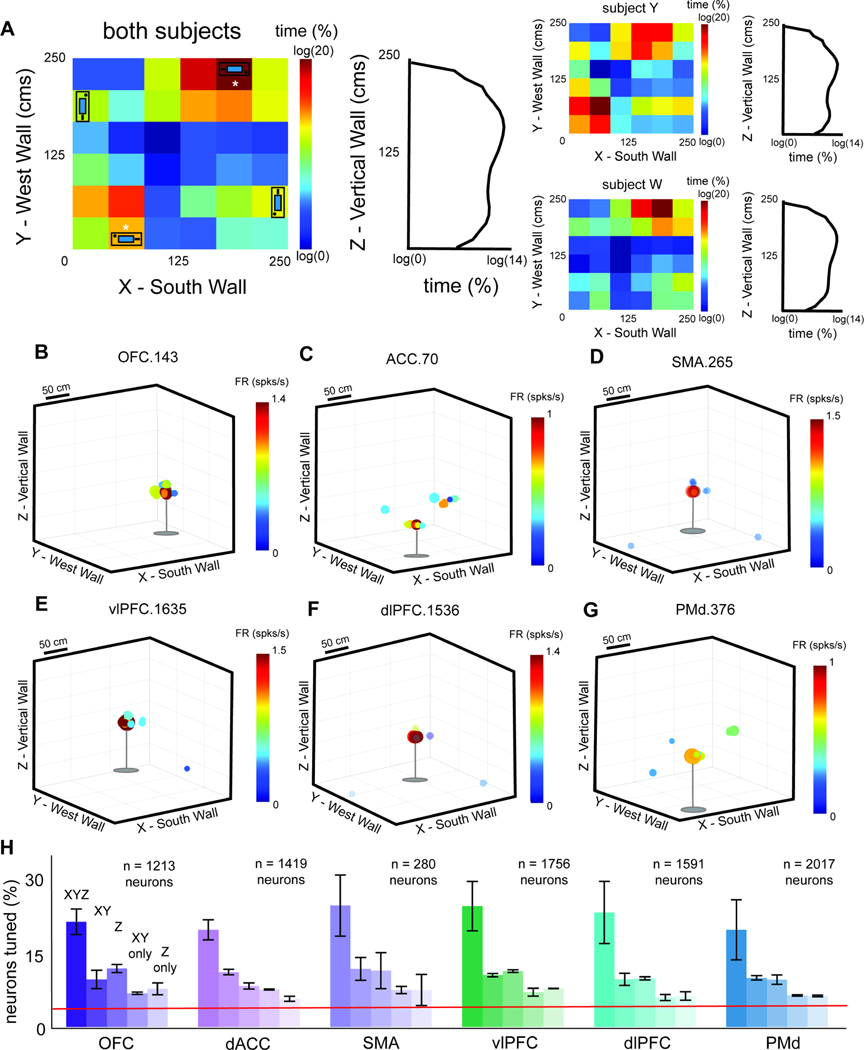
To quantify occupancy, we segmented the surface area of the arena into 36 ~50 cm2 bins. During each session, we computed the amount of time head position was within each bin (Figure 2A). Subjects visited the full range of the arena height, though they tended to favor an elevation between 100–200 cm.
Figure 2. Allocentric position encoding.
(A) Occupancy heat maps depicting the average proportion of time spent in each 50 cm2 bin across sessions. X: E-W axis of the arena; Y: N-S axis. Color: proportion of the session time in each bin; left: rectangular screens represent the approximate location of each patch feeder and white asterisks denote which ones were on top of barrels. right: occupancy plot for elevation axis. (B- G) Rate maps of a sample neuron from each structure that was determined to be significantly tuned to 3D allocentric position (2D position and tracked height, simultaneously). Color: neural activity, computed as the occupancy-normalized firing rate (spikes/second); Size: occupancy, computed as the time spent (s) in a bin. (H) The proportion of total recorded neurons in each structure (collapsed across subjects) tuned to 3D position (XYZ), 2D position (XY only), tracked height (Z only), single selectivity to 2D position alone, and single selectivity to height alone. Red line: chance. Bars indicate standard error of the mean. See also Figure S2.
We defined tuning to 3D position as the simultaneous selectivity to the head’s 2D position (X and Y-axes, Figure 1A) and elevation (Z-axis)39. Neurons in all six regions encode 3D position. For example, neuron OFC.143 showed increased firing when the subject entered the northeast corner (Figure 2B); neuron ACC.70 showed increased firing when the subject entered the southeast corner (Figure 2C). Responses of six neurons are shown in Figure 2B-G and Figure S2.
Spatial selectivity is common in all regions recorded. In OFC, 42.87% of neurons showed selectivity to position (Y: 50.13%; W: 39.59%). Overall, 21.35% (n = 259/1213) carry information about 3D position (p < 0.0001, binomial test). This pattern was observed in both subjects individually (Y: 24.93%; W: 19.74%). An additional 9.65% of OFC neurons were tuned to 2D position, but not head elevation (Y: 12.22%; W: 8.49%; p < 0.0001); 11.87% of OFC neurons were tuned to head elevation only (Y: 12.99%; W: 11.36%). Indeed, a statistically significant proportion of neurons showed selectivity for 3D position in all regions (Figure 2H). Note that in reporting the percent of neurons modulated by this variable, we do not mean to imply that this is the only variable that the neurons encode. Indeed, we later show that this is not true (see below). To confirm tuning stability, we computed correlation between encoding magnitudes for each neuron during the first and second half of the session. We found high correlations in all 6 structures (OFC: r = 0.903; ACC: r = 0.865; SMA: r = 0.504; vlPFC: r = 0.757; dlPFC: r = 0.608; PMd: r = 0.563; p < 0.0001, in all cases).
Neurons in all six regions encode allocentric head direction
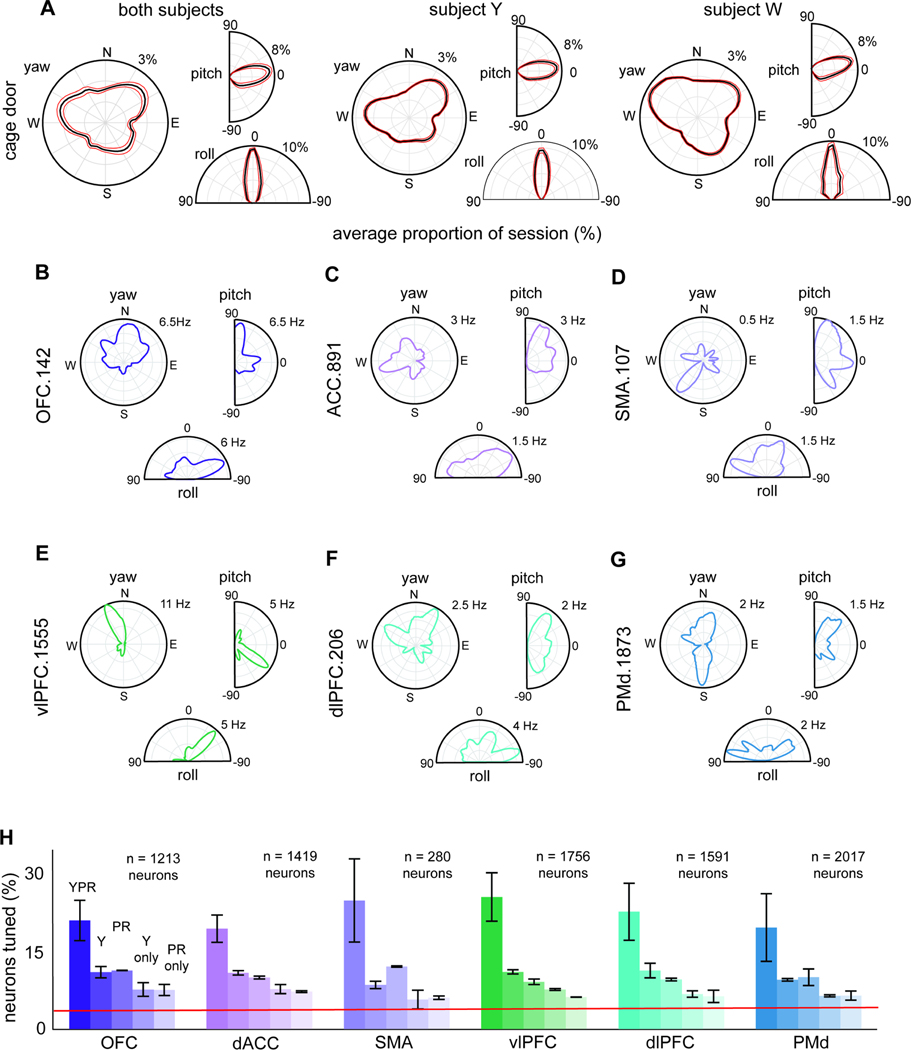
Head direction tuning has been observed in hippocampal formation and associated thalamic nuclei, including in macaques39, 42, 43. To confirm that subjects’ head positions varied, we segmented the allocentric yaw angles into 6-degree bins (n = 60 bins, from 0-degrees to 360-degrees, 0-degrees representing East). For each bin, during each session, we computed the amount of time during which head direction (yaw) was within each bin (Figure 3A). We did the same with pitch. Subjects favored (an average of 63.61 ± 0.59% of the session) angles between 72 and 132 degrees (Figure 3A). Subjects overwhelmingly favored (an average of 69.51 ± 0.09% of the session) orienting their heads at an angle between 60 and 120 degrees (Figure 3A). We found that individual neurons in the prefrontal cortex encode head direction. For example, neuron OFC.276 showed increased firing rates for northeast head direction (Figure 3B). Responses of six example neurons are shown in Figure 3D-G.
Figure 3. Allocentric head orientation coding in volumetric space.
(A) Occupancy histograms depicting the distribution across sessions of the proportion of the total orientations recorded. R: proportion orientation bins occupied at least once during a session; theta: orientation. (B- G) Polar rate maps of a sample neuron with significant tuning. R: occupancy-normalized firing rate (spikes/second). (H) Proportion of total recorded neurons in each structure (collapsed across subjects) tuned to 3D orientation (Y = yaw, P = pitch and R = roll), head direction (yaw only), head tilt (pitch and roll), single selectivity to head direction, and single selectivity to head tilt. Red line: chance.
Head direction selectivity was common. In OFC, 43.53% of neurons showed selectivity to 3D-orientation (Y: 47.48%; W: 41.75%). Overall, 21.12% (n = 256/1213) carry information about 3D orientation (p < 0.0001; Y: 26.52%; W: 18.66%). 11.05% of OFC neurons were tuned to head direction but not head tilt (Y: 9.55%; W: 11.72%) and 11.38% o were tuned to head tilt (Y: 11.41%; W: 11.36%). We found similar results across all 5 other structures (Figure 3H). To confirm stability, we computed correlation between encoding magnitudes during the first and second half of the session. We found positive correlations in all structures (OFC: r = 0.922; ACC: r = 0.846; SMA: r = 0.504; vlPFC: r = 0.774; dlPFC: r = 0.624; PMd: r = 0.548; p < 0.0001, in all cases). These findings suggest that allocentric head direction is encoded in all 6 prefrontal regions and this encoding is stable within sessions.
Encoding of boundary distance, linear velocity and angular velocity
We found neural encoding of egocentric boundary distance, linear velocity, and angular velocity in all six regions39 (Figure 4). Egocentric boundary distance is a subject’s current distance to the nearest boundary of the environment39. A significant proportion of neurons in all 6 regions show this encoding (Figure 4C-D and Figure 5A); tuning in the first and second halves of the session were correlated (OFC: r = 0.94; ACC: r = 0.93; SMA: r = 0.73; vlPFC: r = 0.86; dlPFC: r = 0.78; PMd: r = 0.74; p < 0.0001 in all cases).
Figure 4. Example tuning curves for neurons encoding angular velocity, egocentric boundary distance, and linear velocity.
A) The within-session distribution of angular velocities and B) the corresponding rate maps of a sample neuron from each brain area with significant tuning. C) The within-session distribution of egocentric boundary distance and D) the corresponding rate maps of a sample neuron with significant tuning. E) The tuning curve of a sample neuron with significant tuning to linear velocity. See also Figure S3.
Figure 5. Prefrontal encoding of other navigational and non-navigational variables.
A) A summary of the proportion of total recorded neurons tuned to egocentric boundary distance, angular velocity, and linear velocity collapsed across subjects. B) The proportion of neurons significantly tuned to task-related variables. Each bar indicates the proportion of tuned neurons in one of the six structures. Red line in (A) and (B): chance level for ɑ = 0.05. nSMA = 280, nPMd = 2017, ndlPFC = 1591, nvlPFC = 1756, nACC = 1419, nOFC = 1213. See also Table S2-3.
Linear velocity is the derivative of position (converted to cm/s). Significant portions of neurons encoded linear velocity in all areas (Figure 4E and Figure 5A); first/second half coding was correlated (OFC: r = 0.865; ACC: r = 0.865; SMA: r = 0.518; vlPFC: r = 0.757; dlPFC: r = 0.624; PMd: r = 0.548; p < 0.0001, in all cases).
We defined angular velocity as the change in orientation along yaw and pitch angles. We found a significant encoding proportion in all structures (p < 0.0001 in all cases; Figure 4A-B and Figure 5A) and positive first/second half correlations (OFC: r = 0.884; ACC: r = 0.865; SMA: r = 0.518; vlPFC: r = 0.774; dlPFC: r = 0.608; PMd: r = 0.563; p < 0.0001, in all cases). Figure S3 offers a visualization of the overlap between encoding of different navigational variables across all brain areas.
Relationship between encoding of navigational variables and task variables
Neurons in prefrontal cortex carry information related to key behavioral variables, such as reward and choice44–46. We wondered how robust encoding of navigational variables relates to the more familiar non-navigational task variable encoding methodology. We computed neural encoding for five task variables: (1) lever pressing (vs. not pressing; note that this is confounded with reward receipt), (2) number of rewards remaining throughout the environment, (3) number of rewards remaining at the current patch, (4) stay/leave choice after the previous trial, and (5) the predicted probability of stay/leave at each press given the number of presses remaining through the environment.
We found that, in OFC, 21.19% (n = 257/1213 neurons) showed selectivity to lever pressing. This proportion is significantly greater than chance (p < 0.0001; binomial test). We found similar and significant proportions in both subjects individually (Y: 22.55%, W: 20.69%). These proportions are roughly in line with the proportion observed in this region in other tasks47. We found similar results in all structures (Figure 5B and Table S2-3).
To measure variables 2–5, we segmented each lever press into individual trials, computed the average firing rates for each neuron per lever press, and regressed the averages on the four other task variables (comparable to the approach expected from a chaired-task paradigm). We found that a significant proportion of neurons in each region encoded the number of rewards remaining across the environment (Figure 5B). We found similar results for stay/leave choice (Figure 5B).
To measure the probability of leaving a given patch, we fitted a sigmoid function to choice by regressing the total number of presses remaining across all patches in the environment against the stay/leave decision (see STAR Methods). We then used the fitted function to estimate the probability of staying/leaving, based on the total number of presses available in the arena. We found a significant proportion of neurons encoded the probability of leaving the current patch, controlling for the rewards remaining at current patch (Figure 5B).
Finally, we found that a significant proportion of neurons encoded the probability of leaving the current patch, while controlling for the number of rewards remaining at the current patch in OFC, dACC, vlPFC, and dlPFC (Figure 5B). The proportion of neurons encoding the number of remaining rewards at the current patch failed to reach significance in the SMA (6.64%, p = 0.07, binomial test) and PMd (5.33%, p = 0.25, binomial test).
Variable encoding is distributed randomly among neurons within structures
To determine whether navigational and task variables are encoded in distinct subpopulations, we used elliptical Projection Angle Index of Response Similarity (ePAIRS) 48. We used the LN-GAM-generated variable weights to calculate estimated marginal means (EMMs), reduced the dimensionality, and computed a cluster index (Cidx) from the 10 best explanatory principal components (see STAR Methods and Raposo et al.49). The cluster index uses the angles between neural response vectors to compute similarities in tuning properties, so neurons that respond along the same dimensions will be categorized as more similar (even if their tuning curves are different) than neurons that respond along orthogonal dimensions. Given perfect clustering (Cidx = 1), the angle of each point is identical to its nearest neighbors. Conversely, given a perfectly random distribution of variables, Cidx = 0. A Cidx < 0 would indicate a smoother distribution in variable encoding than would be generated by the data-derived null distribution49. We found significantly negative ePAIRS score in all structures (Figure 6A). This result provides evidence against the hypothesis that neurons are clustered into functional subtypes.
Figure 6. Prefrontal encoding of navigational and task variables is distributed randomly among regional neurons.
(A) Weights for the first and second principal components from both subjects combined, which was produced by reducing the dimensionality of the LN-GAM derived navigational variable encoding. The roughly uniform circular distributions indicate a lack of encoding-based clustering in N-dimensional principal component space. The inlaid score indicated the clustering index from the ePAIRS analysis and an asterisk denotes significance at p < 0.05 (B) Accuracy of a linear decoder, a regression-based support vector machine, in using population neural activity to decode the 2D position of the subject. Each bar indicates the accuracy for decoding subject position based on neural activity in each structure. Gray: shuffled values. Bars: standard error across bootstrapped iterations. Red line: chance.
One advantage of multiplexing is that it allows the same population of neurons to meet distinct behavioral demands, while continuing to support simple linear combinations for downstream decoding49, 50. In one study, authors demonstrated that, despite the category-free coding they observed in the posterior parietal cortex, it was possible to nonetheless perform a linear readout of firing to estimate task variables, demonstrating that category-free coding does not result in a sacrifice in fidelity49. To confirm that the same applies to our own data, we performed the same control analysis described in that study. To do so, we asked whether we could use a linear decoder to accurately predict the position of the animal, based on the firing rates across the population (see STAR Methods). We segmented the arena into 9 zones, so chance-level decoding accuracy was 11.11% (i.e., 1/9). We compared the decoding accuracy from population activity in each structure with chance (correcting for multiple comparisons, ⍺ = 0.0083). Position was decodable from population neural activity in all structures (Figure 6B). These analyses were confirmed for both subjects individually (data not shown).
Coding of all measured variables grows along a ventral to dorsal gradient
We previously found a ventral-to-dorsal gradient in encoding of economic variables along the medial wall of the PFC46. We asked if a similar gradient is observed for navigational variables. We identified two distinct potential ventral-to-dorsal anatomical gradients in our data: a medial (OFC→dACC→SMA→PMd) and a lateral series (OFC→vlPFC→dlPFC→PMd). We found that position encoding increases along both gradients. Formally, the regression weight of response strength, computed for each neuron, increased with structure’s hierarchical position (medial: Spearman ρ2 = 0.067; lateral: ρ2 = 0.051; p < 0.0001 in both cases). We observed the same pattern using depth of electrode instead of brain areas (Figure 7, medial: Pearson r2 = 0.055; lateral: r2 = 0.065; p < 0.0001 in both cases).
Figure 7. Ventral-dorsal gradient of navigational tuning.
Average encoding strength as a function of electrode position for both subjects combined. Bubbles correspond to position bins. Color: strength of encoding. Size: number of neurons in bin.
We found a similar gradient for head direction with brain area (medial: ρ2 = 0.099; lateral: ρ2 = 0.078; p < 0.0001) and with electrode depth (medial: r2 = 0.081; lateral: r2 = 0.095; p < 0.0001). We found similar results for egocentric boundary distance (medial: ρ2 = 0.125; lateral: ρ2 = 0.099; p < 0.0001) and electrode depth (medial series: r2 = 0.098; lateral: r2 = 0.076; p < 0.0001). Likewise for angular velocity (medial: ρ2 = 0.125; lateral: ρ2 = 0.099; p < 0.0001) and electrode depth (medial: r2 = 0.098; lateral: r2 = 0.076; p < 0.0001). Likewise for linear velocity (medial: ρ2 = 0.118; lateral: ρ2 = 0.099; p < 0.0001) and electrode depth (medial: r2 = 0.097; lateral: r2 = 0.071; p < 0.0001).
We found similar patterns for our non-navigational variables. Encoding of stay/leave choice probability significantly increased along both gradients (medial: ρ2 = 0.071; lateral: ρ2 = 0.069; p < 0.0001). Unsigned weight of reward encoding, from the LN-GAM, increased along both (medial: ρ2 = 0.081; lateral: ρ2 = 0.067; p < 0.0001). These patterns were significant with electrode depth (p < 0.0001 in all cases). These results extend our previous findings of a ventral to dorsal gradient of encoding for economic variables to navigational variables.
DISCUSSION
In freely moving macaques, single neurons in six prefrontal areas encode several navigational variables. Navigational and non-navigational variables are encoded in the same set of neurons, using mixed selectivity49–51. The widespread encoding of navigational variables outside of hippocampus suggests that processing of navigational information may not be localized. These results tie into emerging theories that see navigation as a special case of associative mapping5–7, 20, 21. Indeed navigational information may be found in prefrontal regions because of their more general role as flexible encoders of associative information.
It is not clear whether these signals are generated within the regions we recorded, or whether they are generated elsewhere. Given the broad interconnections with prefrontal regions, it may be inevitable that information like this is observed broadly. Unfortunately, we cannot ascertain whether these navigational variables are endogenously or exogenously generated (or some combination). However, we do not believe it is logically necessary that the information will be observed everywhere. There are plentiful examples of cases in which information is generated in one region, but not shared in others. As such, it seems unlikely that different parts of the prefrontal cortex achieve a balance of encoding due to sharing of information. Having said that, we must also be careful about functional interpretations - the fact that we observe widespread correlates of navigational information in these regions does not prove they play a causal role in navigation.
Several reports in rodents have identified encoding of navigational variables beyond the hippocampal complex24–27. Likewise, a small literature in humans emphasizes the potential roles of non-hippocampal regions, especially prefrontal ones, in navigation22. Our report adds to this literature. Some of these results have proposed that navigational information outside of hippocampus may play a distinct role, such as linking space to value or changing plans; however, existing data are also consistent with the hypothesis that hippocampal and prefrontal regions play largely overlapping roles. Our results imply that navigational information can be found in the prefrontal cortex, just as it can be found in the hippocampal complex. It is worth emphasizing that the tuning for place that we find is not place-cell-like. In particular, it is not generally localized to a single position in space, nor does it have other hallmarks of place cells. On the other hand, it does clearly contain information about place, and it does resemble responses of non-Grid cells in medial entorhinal cortex. It is likely, in our view, that these differences reflect differences in the way space is encoded in prefrontal regions and in hippocampus. It is worth noting, however, that the spread-out responses we observe do qualitatively resemble those measured in two recent studies of primate hippocampus39, 52, suggesting that the difference may be, at least in part, a species difference, rather than a purely real one.
We observe no evidence for separate populations encoding navigational and nonnavigational information. These results are important because they indicate that navigational encoding is not part of specialized patches or neural subregions, nor of distinct neurons that were inaccessible in prior studies. This result is consistent with the growing body of research indicating that mixed selectivity is widespread and robust49, 51, 53. This mixed selectivity may allow for flexible yet robust coding and may allow for rapid recombination of information50.
The ventral-to-dorsal gradient in coding strength we report here resembles one we have found for the medial wall46. Why would we see stronger encoding more dorsally? We propose that information encoded in a format that is more accessible to the motor system (and likewise to our decoding analyses) in more ventral structures. In other words, more dorsal structures show information in a more untangled manner54. Conversely, these data argue against a functionally modular arrangement, in which each area has a specific nameable function, such as “evaluate,” “compare,” and “control”. At the same time, these data argue against a purely distributed view, in which all information is present in the same form across prefrontal cortex. Instead, they support a hierarchical view17, 18, 45, 55–57.
One interesting feature of our data is that firing rates are much lower than those typically observed in standard primate physiology experiments, and lower than those often reported in rodent studies of the navigational system. We suspect that the discrepancy is likely to reflect genuine differences in how neurons fire and differences in firing rate for neurons selected on-line and off-line. Specifically, we have noticed that as we move towards more naturalistic tasks, firing rates tend to decrease. Indeed, in our informal observations of these same subjects performing chaired tasks with the same recording system, firing rates are lower in our open-field paradigm. Moreover, we believe that when selecting neurons for recording, physiologists (including ourselves) tend to select higher tonically active neurons, simply because these are the ones we are more likely to notice. It remains an open question which of these two factors is more important, and whether other factors contribute as well.
One limitation of the present study is that we did not measure gaze direction. As such, we could not perform a disambiguation between tuning to facing location (where in the room the subject’s head is facing) and spatial view (where in the room the subject’s eyes are looking). In a recent, important paper, Mao et al.39 characterized navigational tuning in the hippocampus of freely moving primates. They showed the results of both a traditional tuning curve and the LN-GAM approach used here. The traditional tuning curve approach, using a single fitted variable at a time, yielded tuned proportions analogous to those commonly reported in the rodent HC. Critically, however, the LN-GAM approach included a variable for “facing location” and “spatial view” within the large, simultaneously fitted model. They demonstrated that hippocampal tuning was predominantly driven by facing location rather than spatial view, which underscores the importance of performing this disambiguation (see also Killian et al.58 and Jacobs et al.59). In future studies we hope to investigate the relationship between facing location and spatial view.
Another limitation is that we could not include 4 of the 5 non-navigational variables in the LN-GAM (rewards remaining at the current patch, rewards remaining in the environment, stay/leave choice, and stay/leave probability), so we could not perform any direct analyses to relate navigational encoding to the broader non-navigational encoding strengths beyond the one included in the LN-GAM (lever-pressing). One further limitation is that the lack of a rigid trial structure restricted our ability to compare navigational variable encoding when subjects were task-engaged vs not engaged. We conservatively defined a trial as the 2 second epoch after a lever press, a period in which subjects exhibited limited range of motion and which was highly confounded with reward receipt.
Ultimately, we believe that these results provide a strong argument for the use of naturalistic tasks. It is well known that natural behavior is continuous, complex (multi-effector), embedded (in an environment), and seldom isolated from other competing demands on attention and planning60–65. Nonetheless, most laboratory tasks, including the great bulk of our own past work, does not hew to these principles. Instead, they use overly simplified laboratory tasks. Simple laboratory tasks have great benefits, especially in tractability, but they have disadvantages. One is that they often do not manipulate variables that may, if manipulated, be found to be major drivers of neural activity. Ignoring that tuning may in turn obscure the broader and more general functions of neurons in regions of interest.
STAR★METHODS
RESOURCE AVAILABILITY
Lead contact
Further information and requests for resources and reagents should be directed to and will be fulfilled by the lead contact, Benjamin Hayden (benhayden@gmail.com).
Materials availability
The study did not generate new unique reagents.
Data and code availability
The processed data reported in this paper has been deposited on Zenodo and is publicly available as of the date of publication. The DOI is listed in the key resources table.
All original code has been deposited on Zenodo and is publicly available as of the date ofpublication. The DOI is listed in the key resources table.
Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.
KEY RESOURCES TABLE
| Resource | Source | Identifier |
|---|---|---|
| Deposited Data | ||
| Preprocessed data | Zenodo | DOI: 10.5281/zenodo.8067596 |
| Software and Algorithms | ||
| MATLAB analysis code | Zenodo | DOI: 10.5281/zenodo.8067596 |
EXPERIMENTAL MODEL AND SUBJECT DETAILS
Animal Model
Two male rhesus macaques (Macaca mulatta) served as subjects. Animals were habituated to laboratory conditions, trained to enter and exit an open arena, and then trained to operate water dispensers. The University Committee on Animal Resources at the University of Minnesota approved all animal procedures. Animal procedures were designed and conducted in compliance with the Public Health Service’s Guide for the Care and Use of Animals and approved by the institutional animal care and use committee (IACUC) of the University of Minnesota.
METHOD DETAILS
Surgical Procedures
We placed a cranium adherent form-fitted Gray Matter (Gray Matter Research) recording chamber and a 128-channel microdrive recording system over the area of interest. We used the same approach as Mao et al.39 to verify sites. Specifically, we used CT scans which were compared to corresponding CT studies performed following surgical implantation and placement of the electrodes. The hyperdense appearance of electrodes using the post-recording CT allowed us to verify that electrodes followed the trajectory of the pre-operative plan. In both cases (that is, for both subjects), the results of the CT show that this was the case. Specifically, these results indicate that our procedures provided co-registration with an error of less than 0.5 mm. Since electrodes were advanced incrementally not all locations are verified using this approach, but positions could be validly inferred using interpolation. In addition, we performed a second complementary method that also confirmed placement of the electrodes. Specifically, as we have done in many past studies, as we moved the electrodes down into the brain, we made note of the auditorily detectable change from gray to white matter, and reconciled this information with our preoperative CT scans. In all cases, the two matched. Animals received analgesics and antibiotics after all procedures. Procedures were designed and conducted in compliance with the Public Health Service’s Guide for the Care and Use of Animals and approved by the institutional animal care and use committee (IACUC) of the University of Minnesota.
Recording sites
We approached our brain regions by controlled and monitored advancement of individual electrodes, through reconciliation of measured thread-count against postoperative CT images. The implanted microdrive was connected through jumper cables and a head stage to a removable data logger (SpikeGadgets). The data logger was wirelessly triggered to store neural recordings onto a removable memory card from which it was then extracted at the end of each session.
We defined OFC as lying within the coronal planes situated between 39.6 and 23.9 mm rostral to the central sulcus, the horizontal planes situated between 23.3 and 45.7 mm from the brain’s dorsal surface, and the sagittal planes between 1.3 and 22.1 mm from the medial wall.
We defined dACC as lying within the coronal planes situated between 33.5 and 7.4 mm rostral to the central sulcus, the horizontal planes situated between 11.1 and 38.5 mm from the brain’s dorsal surface, and the sagittal planes between 0.4 and 6.7 mm from the medial wall.
We defined SMA as lying within the coronal planes situated between 30.4 and 13.1 mm rostral to the central sulcus, the horizontal planes situated between 16.2 and 34.3 mm from the brain’s dorsal surface, and the sagittal planes between 0.4 and 6.7 mm from the medial wall.
We defined vlPFC as lying within the coronal planes situated between 46.8 and 16.8 mm rostral to the central sulcus, the horizontal planes situated between 16.2 and 47.2 mm from the brain’s dorsal surface, and the sagittal planes between 1.1 and 19.4 mm from the medial wall.
We defined dlPFC as lying within the coronal planes situated between 36.4 and 12.3 mm rostral to the central sulcus, the horizontal planes situated between 17.4 and 48.9 mm from the brain’s dorsal surface, and the sagittal planes between 1.1 and 19.4 mm from the medial wall.
We defined PMd as lying within the coronal planes situated between 26.7 and 2.9 mm rostral to the central sulcus, the horizontal planes situated between 6.8 and 37.9 mm from the brain’s dorsal surface, and the sagittal planes between 1.9 and 23.7 mm from the medial wall.
Behavioral task
Each patch delivered a fixed amount of 1.5 mL. The first four presses were rewarded with fluid delivery. The fifth was unrewarded and led to a 3-minute deactivation. No reset or deactivation was applied if the animal left the patch. A patch was only reset if the subject pressed the lever a fifth time and waited 3 minutes. A trial consisted of a lever press at time 0, which changed the display to white with a green plus-sign in the center (0–2 seconds), an auditory cue was played (0–2 seconds), and a solenoid opened to dispense reward (0–1 second). After dispensing reward, the solenoid closed, the auditory cue ended, and the green plus-sign disappeared. The screen remained white for 2 additional seconds (2–4 seconds) before the screen turned blue again (total trial time = 4 seconds). The fifth lever press was followed by a white screen. Prior and concurrent chaired task training of these subjects included two risky choice tasks66–70 and a simpler choice task71, 72.
QUANTIFICATION AND STATISTICAL ANALYSIS
Behavioral analysis
There were 5–7 patch events recorded for each patch engagement: lever press, screen off (set to white), screen/auditory reward cue (rewarded presses only), solenoid open (rewarded presses only), solenoid close (rewarded presses only), screen off (set to white), timeout (deactivation press only), and screen reset. Lever press events that led to a reward were used to analyze the reward encoding. The final (unrewarded) press in the series was behaviorally special, so it was not suitable for use in comparison with the rewarded presses. We verified the accuracy of our system to subtle head movements in a previous manuscript35.
To measure the 3 angular axes of the head, we first centered the extracted nose and neck coordinates, placing the estimated head position at the volumetric axis-origin. For each frame, we applied Euler angle transformations on the head-fixed coplanar points to determine the yaw, pitch and roll angles between the origin and the current head orientation. We defined the head direction variable as a 1D vector for the yaw angle of the head. We defined the head tilt variable as a 2D vector consisting of the pitch and roll angles. We measured egocentric boundary in polar coordinates, defined as a 2D variable consisting of the radial distance between the subject and the nearest wall on the azimuthal plane and the angle of the subject relative to the center of the room. To measure angular velocity, we computed a two-dimensional variable, where the first dimension reflects the rotation speed of the head (degrees/second) along the yaw angle and the second dimension reflects the rotation along the pitch angle. To measure linear velocity, we computed the distance traveled (centimeters/second) in any direction.
Linear-Nonlinear Poisson-distributed Generalized Additive Model
We adapted a previously developed approach36, 37, 39, 40, 41, 73, 74. Briefly, recordings and variables were binned into 100-ms time bins. Neural data were fitted to multiple, nested linear-nonlinear-Poisson distributed generalized additive models. Data were divided into 10 tranches across the session. Within each, model estimates were computed using 5-fold cross-validation, by dividing each into 5 more subtranches. The process was repeated for each one. The estimated log-likelihood quantified the model performance, and the distribution of log-likelihood estimates was compared to a null distribution (one-sided Wilcoxon signed rank test, alpha = 0.05).
The best-fitting model was selected using an optimized forward search. Models containing only one variable (1st order models) were fitted first. If these models performed better than the null, models containing two variables (2nd order models) were fitted. The process was repeated until the performance of the newly fitted model no longer improved over the previous. A neuron was categorized as tuned to a given variable if that variable was included within the best-fitting model. We use the proportion of neurons tuned as a population level analysis because it suggests that a variable may be a particularly important feature of the neural code and that the population activity may be important for decoding that variable (as we show in the decoding analysis for Figure 6)75, 76. Since our significance threshold, alpha, was set at 0.05 for a one-sided Wilcoxon signed rank test, we consider any proportion of neurons above 5% to be significant (see Figure S1 and Table S1 for a summary of variable tuning). Importantly, the additive process for multiple terms was incorporated within the exponentiation used to compute the estimated firing, thus making selectivity to multiple variables a conjunctive (nonlinear) estimate. To assess tuning stability across a session, we computed Pearson’s correlation between encoding magnitudes for each neuron to a given variable during the first and second half of the session.
We validated the model on our data through a series of controls. After fitting the LN-GAM models, we randomly selected a neuron that was not significantly tuned to any combination of variables. We modified the spike train for that neuron to include a single spurious high firing event, once in each of 3 time periods. We also selected both 10 and 100 bins from each of 3 time periods to insert spurious high firing. Finally, we time-locked the insertion of 1, 10, and 100 simulated spurious events to consistent instances of the tracked position. We repeated this process across 20 randomly selected, untuned neurons from each structure, generating a set of 1200 synthetic datasets. We fitted each of these simulated time series against the original variables. We then determined the proportion of fitting processes that resulted in significant tuning. Only 8.08% (n = 97/1200) of control sets generated a statistically significant fit. These controls confirmed that the best-fitting models were not being influenced by random or spurious events, and instead reflected reliable tuning to the selected variables.
Stay/Leave choice probability and neural encoding
We adapted an approach commonly used in traditional neuroeconomics paradigms23, 46, 73. We leveraged the strictly timed structure of the foraging task to isolate the 2-second epoch during which subjects were rewarded for pressing a lever. Each lever press is necessarily separated from the next by a minimum of 4 seconds; 2 seconds of a reward period and 2 seconds of an intertrial interval. Therefore, each rewarded lever press was treated as a separate trial. We aggregated all trials for each feeder across the session. For each trial, we determined the number of rewarded presses remaining at both the current patch and all distal patches. We also determined whether the current trial occurred at the same or different patch from the previous trial. If it was the same as the previous patch, the subject was said to have made a “stay” choice on the previous trial. Conversely, if it was at a different patch, the subject was said to have made a “leave” choice on the previous trial. This binary choice variable was fitted to the total number of rewarded presses available across the distal patches, using a logistic regression. The resulting sigmoidal function was then used to estimate the stay/leave probability for each trial, based on how many rewarded presses were available elsewhere in the arena. Finally, for each neuron and each trial, an average firing rate was computed from the same post-press epoch. The trial-length vector of stay/leave probability was used to predict this trial-length vector of firing rates, using a linear regression that simultaneously controlled for the number of rewarded presses remaining at the current patch.
Distribution of variable encoding
We adapted an approach previously developed for estimating clustering in n-dimensions, the elliptical Projection Angle Index of Response Similarity (ePAIRS)48, 49. If neurons form specialized subpopulations, they should form clusters along a shared axis. Thus, reducing the dimensionality of the tuning conditions across the population code should elucidate a functional cluster. To define a tuning condition, we compute the estimated marginal means (EMMs) from the fully-fitted LN-GAM model. Estimates were computed using the minimum and maximum values for each variable in the design matrix. We used the fully-fitted model estimates because it reduces sparsity in the population matrix. The dimensions of the EMM matrix were n x c, where n is the number of neurons in a brain area and c are the EMMs for each condition (1022 conditions total). We then performed principal component analysis (PCA) on this matrix to generate an n x d matrix of scores for each neuron, where d is the 10 most explanatory PC scores. We then computed the relative angles of each point in 10-D PC space and compared the angular distance between all pairs of nearest neighbors. A functional cluster, therefore, should have relatively tight angles between nearest neighbors when compared to a random distribution. Statistical significance was computed using a rank sum test.
In each session, a given neuron might be more heavily tuned to one variable than another. That is, the EMMs reflect the distribution of preferred variables. We would expect these estimates to show clustering along the dimensions of the preferred variables. Therefore, as a positive control we performed the ePAIRS analysis on the EMMs and found significant clustering in all areas (p < 0.001, in all areas; two-tailed rank sum test).
Linear decoder
To determine if randomly distributed variable encoding continues to support downstream decodability, we implemented a regression-based SVM. Tracking data from each session was spatially binned into 9 continuous zones. We define a trial as an entry into the zone, followed by continuous zone occupancy until exiting the zone. We constructed a pseudo-population of pseudo-trials, 495-trials X n-neurons, by randomly selecting 55 trials from each zone for each neuron. We repeated the bootstrapping procedure to constitute one training set and one test set. We created two more matrices by shuffling the zone labels. A regression-based SVM model was trained on the training set and predictions were calculated by fitting the model to the test set. Accuracy was measured as the overall rate of successfully predicting the zone from the population neural activity in the test set. We repeated this process 500 times and averaged the classification accuracy across iterations. We then compared this average accuracy to that from the shuffled data.
Supplementary Material
Highlights.
Prefrontal regions encode navigational variables
Neurons encoding navigational variables exhibit random, mixed selectivity
Strength of navigational encoding increases along a ventral-to-dorsal gradient
ACKNOWLEDGMENTS
We thank the Hayden/Zimmermann lab for valuable discussions as well as Brenna Knaebe for help with animal care and preparation. This work was supported by NIH grants R01 MH128177 (JZ), P30 DA048742 (JZ, BH), R01 MH125377 (BH), T32 GM008244 (RLC), T32 MH115886 (RLC and DM), T32 NS105604 (RLC and DM), NSF 2024581 (JZ, BH) and a UMN AIRP award (JZ, BH) from the Digital Technologies Initiative (JZ), from the Minnesota Institute of Robotics (JZ).
Footnotes
DECLARATION OF INTERESTS
The authors declare no competing interests.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
REFERENCES
- 1.Hartley T, Lever C, Burgess N, & O’Keefe J. (2014). Space in the brain: How the hippocampal formation supports spatial cognition. Phil. Trans. R. Soc, B369(20120510). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Rolls ET, & Wirth S. (2018). Spatial representations in the primate hippocampus, and their functions in memory and navigation. Progress in neurobiology, 171, 90–113. [DOI] [PubMed] [Google Scholar]
- 3.Moser EI, Kropff E, & Moser MB (2008). Place cells, grid cells, and the brain’s spatial representation system. Annual review of neuroscience, 31(1), 69–89. [DOI] [PubMed] [Google Scholar]
- 4.McNaughton BL, Battaglia FP, Jensen O, Moser EI, & Moser MB (2006). Path integration and the neural basis of the ‘cognitive map’. Nature Reviews Neuroscience, 7(8), 663–678. [DOI] [PubMed] [Google Scholar]
- 5.Stachenfeld KL, Botvinick MM, & Gershman SJ (2017). The hippocampus as a predictive map. Nature neuroscience, 20(11), 1643–1653. [DOI] [PubMed] [Google Scholar]
- 6.Schuck NW, & Niv Y. (2019). Sequential replay of nonspatial task states in the human hippocampus. Science, 364(6447), eaaw5181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Epstein RA, Patai EZ, Julian JB, & Spiers HJ (2017). The cognitive map in humans: Spatial navigation and beyond. Nature Neuroscience, 20(11), Article 11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Poulter S, Hartley T, & Lever C. (2018). The neurobiology of mammalian navigation. Current Biology, 28(17), R1023–R1042. [DOI] [PubMed] [Google Scholar]
- 9.Musall S, Kaufman MT, Juavinett AL, Gluf S, & Churchland AK (2019a). Single-trial neural dynamics are dominated by richly varied movements. Nature Neuroscience, 22(10), Article 10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Musall S, Urai AE, Sussillo D, & Churchland AK (2019b). Harnessing behavioral diversity to understand neural computations for cognition. Current Opinion in Neurobiology, 58, 229–238 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Stringer C, Pachitariu M, Steinmetz N, Reddy CB, Carandini M, & Harris KD (2019). Spontaneous behaviors drive multidimensional, brainwide activity. Science, 364(6437), eaav7893. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Steinmetz NA, Zatka-Haas P, Carandini M, & Harris KD (2019). Distributed coding of choice, action and engagement across the mouse brain. Nature, 576(7786), Article 7786. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Vickery TJ, Chun MM, & Lee D. (2011). Ubiquity and Specificity of Reinforcement Signals throughout the Human Brain. Neuron, 72(1), 166–177. [DOI] [PubMed] [Google Scholar]
- 14.Shin EJ, Jang Y, Kim S, Kim H, Cai X, Lee H, Sul JH, Lee S-H, Chung Y, et al. (2021). Robust and distributed neural representation of action values. ELife, 10, e53045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Ottenheimer DJ, Hjort MM, Bowen AJ, Steinmetz NA, & Stuber GD (2022). A stable, distributed code for cue value in mouse cortex during reward learning [Preprint]. Neuroscience. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Fine JM, & Hayden BY (2022). The whole prefrontal cortex is premotor cortex. Philosophical Transactions of the Royal Society B, 377(1844), 20200524. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Fuster JM (2000). Executive frontal functions. Experimental Brain Research, 133(1), 66–70. [DOI] [PubMed] [Google Scholar]
- 18.Fuster JM (2001). The prefrontal cortex—an update: time is of the essence. Neuron, 30(2), 319–333. [DOI] [PubMed] [Google Scholar]
- 19.Yoo SBM, Sleezer BJ, & Hayden BY (2018). Robust Encoding of Spatial Information in Orbitofrontal Cortex and Striatum. Journal of Cognitive Neuroscience, 30(6), 898–913. [DOI] [PubMed] [Google Scholar]
- 20.Behrens TE, Muller TH, Whittington JC, Mark S, Baram AB, Stachenfeld KL, & Kurth-Nelson Z. (2018). What is a cognitive map? Organizing knowledge for flexible behavior. Neuron, 100(2), 490–509. [DOI] [PubMed] [Google Scholar]
- 21.Whittington JC, Muller TH, Mark S, Chen G, Barry C, Burgess N, & Behrens TE (2020). The Tolman-Eichenbaum machine: unifying space and relational memory through generalization in the hippocampal formation. Cell, 183(5), 1249–1263. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Patai EZ, & Spiers HJ (2021). The Versatile Wayfinder: Prefrontal Contributions to Spatial Navigation. Trends in Cognitive Sciences, 25(6), 520–533. [DOI] [PubMed] [Google Scholar]
- 23.Maisson DJ-N, Wikenheiser A, Noel J-PG, & Keinath AT (2022). Making sense of the multiplicity and dynamics of navigational codes in the brain. Journal of Neuroscience. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Basu R, Gebauer R, Herfurth T, Kolb S, Golipour Z, Tchumatchenko T, & Ito HT (2021). The orbitofrontal cortex maps future navigational goals. Nature, 1–4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Long X, & Zhang S-J (2021). A novel somatosensory spatial navigation system outside the hippocampal formation. Cell Research, 31(6), Article 6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Poo C, Agarwal G, Bonacchi N, & Mainen ZF (2022). Spatial maps in piriform cortex during olfactory navigation. Nature, 601(7894), Article 7894. [DOI] [PubMed] [Google Scholar]
- 27.Wikenheiser AM, Gardner MPH, Mueller LE, & Schoenbaum G. (2021). Spatial Representations in Rat Orbitofrontal Cortex. The Journal of Neuroscience, 41(32), 6933–6945. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Heilbronner SR, Rodriguez-Romaguera J, Quirk GJ, Groenewegen HJ, & Haber SN (2016). Circuit-based corticostriatal homologies between rat and primate. Biological Psychiatry, 80(7), 509–521. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Miller EK, & Cohen JD (2001). An integrative theory of prefrontal cortex function. Annual Review of Neuroscience, 24(1), 167–202. [DOI] [PubMed] [Google Scholar]
- 30.Knight RT, & Stuss DT (2002). Prefrontal cortex: The present and the future. Principles of frontal lobe function, 573–597. [Google Scholar]
- 31.Martinet L-E, Sheynikhovich D, Benchenane K, & Arleo A. (2011). Spatial learning and action planning in a prefrontal cortical network model. PLoS Computational Biology, 7(5), e1002045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Strait CE, Sleezer BJ, Blanchard TC, Azab H, Castagno MD, & Hayden BY (2016). Neuronal selectivity for spatial positions of offers and choices in five reward regions. Journal of Neurophysiology, 115(3), 1098–1111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Bicanski A, & Burgess N. (2020). Neuronal vector coding in spatial cognition. Nature Reviews Neuroscience, 21(9), 453–470. [DOI] [PubMed] [Google Scholar]
- 34.Ikkai A, & Curtis CE (2011). Common neural mechanisms supporting spatial working memory, attention and motor intention. Neuropsychologia, 49(6), 1428–1434. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Bala PC, Eisenreich BR, Yoo SBM, Hayden BY, Park HS, & Zimmermann J. (2020). Automated markerless pose estimation in freely moving macaques with OpenMonkeyStudio. Nature communications, 11(1), 1–12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Hardcastle K, Maheswaranathan N, Ganguli S, & Giocomo LM (2017). A Multiplexed, Heterogeneous, and Adaptive Code for Navigation in Medial Entorhinal Cortex. Neuron, 94(2), 375–387.e7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Laurens J, Abrego A, Cham H, Popeney B, Yu Y, Rotem N, Aarse J, Asprodini EK, Dickman JD, & Angelaki DE (2019). Multiplexed code of navigation variables in anterior limbic areas. BioRxiv, 684464. [Google Scholar]
- 38.Vinepinsky E, Perchik S, & Segev R. (2020). A Generalized Linear Model of a Navigation Network. Frontiers in Neural Circuits, 14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Mao D, Avila E, Caziot B, Laurens J, Dickman JD, & Angelaki DE (2021). Spatial modulation of hippocampal activity in freely moving macaques. Neuron, 109(21), 3521–3534.e6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Yoo SBM, Tu JC, Piantadosi ST, & Hayden BY (2020). The neural basis of predictive pursuit. Nature neuroscience, 23(2), 252–259. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Yoo SBM, Tu JC, & Hayden BY (2021). Multicentric tracking of multiple agents by anterior cingulate cortex during pursuit and evasion. Nature Communications, 12(1), 1985. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Taube JS, Muller RU, & Ranck JB (1990). Head-direction cells recorded from the postsubiculum in freely moving rats. I. Description and quantitative analysis. Journal of Neuroscience, 10(2), 420–435. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Taube JS (1998). Head direction cells and the neurophysiological basis for a sense of direction. Progress in Neurobiology, 55(3), 225–256. [DOI] [PubMed] [Google Scholar]
- 44.Kennerley SW, & Wallis JD (2009). Reward-dependent modulation of working memory in lateral prefrontal cortex. Journal of Neuroscience. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Rushworth MFS, Noonan MAP, Boorman ED, Walton ME, & Behrens TE (2011). Frontal Cortex and Reward-Guided Learning and Decision-Making. Neuron, 70(6), 1054–1069. [DOI] [PubMed] [Google Scholar]
- 46.Maisson DJ-N, Cash-Padgett TV, Wang MZ, Hayden BY, Heilbronner SR, & Zimmermann J. (2021). Choice-relevant information transformation along a ventrodorsal axis in the medial prefrontal cortex. Nature Communications, 12(1), 4830. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Padoa-Schioppa C. (2011). Neurobiology of Economic Choice: A Good-Based Model. Annual Review of Neuroscience, 34(1), 333–359. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Hirokawa J, Vaughan A, Masset P, Ott T, & Kepecs A. (2019). Frontal cortex neuron types categorically encode single decision variables. Nature, 576(7787), 446–451. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Raposo D, Kaufman MT, & Churchland AK (2014). A category-free neural population supports evolving demands during decision-making. Nature Neuroscience, 17(12), 1784–1792. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Fusi S, Miller EK, & Rigotti M. (2016). Why neurons mix: High dimensionality for higher cognition. Current Opinion in Neurobiology, 37, 66–74. [DOI] [PubMed] [Google Scholar]
- 51.Blanchard TC, Piantadosi ST, & Hayden BY (2018). Robust mixture modeling reveals category-free selectivity in reward region neuronal ensembles. Journal of neurophysiology, 119(4), 1305–1318. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Courellis HS, Nummela SU, Metke M, Diehl GW, Bussell R, Cauwenberghs G, & Miller CT (2019). Spatial encoding in primate hippocampus during free navigation. PLoS biology, 17(12), e3000546. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Kaufman MT, Benna MK, Rigotti M, Stefanini F, Fusi S, & Churchland AK (2022). The implications of categorical and category-free mixed selectivity on representational geometries. Current Opinion in Neurobiology, 77, 102644. [DOI] [PubMed] [Google Scholar]
- 54.Yoo SBM, & Hayden BY (2018). Economic choice as an untangling of options into actions. Neuron, 99(3), 434–447. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Hunt LT, Dolan RJ, & Behrens TE (2014). Hierarchical competitions subserving multi-attribute choice. Nature neuroscience, 17(11), 1613–1622. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Hunt LT, Malalasekera WM, de Berker AO, Miranda B, Farmer SF, Behrens TE, & Kennerley SW (2018). Triple dissociation of attention and decision computations across prefrontal cortex. Nature neuroscience, 21(10), 1471–1481. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Hunt LT, & Hayden BY (2017). A distributed, hierarchical and recurrent framework for reward-based choice. Nature Reviews Neuroscience, 18(3), 172–182. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Killian NJ, Jutras MJ, & Buffalo EA (2012). A map of visual space in the primate entorhinal cortex. Nature, 491(7426), 761–764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Jacobs J, Weidemann CT, Miller JF, Solway A, Burke JF, Wei XX, Suthana N, Sperling MR, Sharan, et al. (2013). Direct recordings of grid-like neuronal activity in human spatial navigation. Nature neuroscience, 16(9), 1188–1190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Brown AE, & De Bivort B. (2018). Ethology as a physical science. Nature Physics, 14(7), 653–657. [Google Scholar]
- 61.Datta SR, Anderson DJ, Branson K, Perona P, & Leifer A. (2019). Computational neuroethology: a call to action. Neuron, 104(1), 11–24. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Krakauer JW, Ghazanfar AA, Gomez-Marin A, MacIver MA, & Poeppel D. (2017). Neuroscience needs behavior: correcting a reductionist bias. Neuron, 93(3), 480-490. [DOI] [PubMed] [Google Scholar]
- 63.Matusz PJ, Dikker S, Huth AG, & Perrodin C. (2019). Are we ready for real-world neuroscience?. Journal of cognitive neuroscience, 31(3), 327–338. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Pearson JM, Watson KK, & Platt ML (2014). Decision making: the neuroethological turn. Neuron, 82(5), 950–965. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Yoo SBM, Hayden BY, & Pearson JM (2021). Continuous decisions. Philosophical Transactions of the Royal Society B, 376(1819), 20190664. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Azab H, & Hayden BY (2018). Correlates of economic decisions in the dorsal and subgenual anterior cingulate cortices. European Journal of Neuroscience, 47(8), 979–993. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Farashahi S, Donahue CH, Hayden BY, Lee D, & Soltani A. (2019). Flexible combination of reward information across primates. Nature human behaviour, 3(11), 1215–1224. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Yoo SBM, & Hayden BY (2020). The Transition from Evaluation to Selection Involves Neural Subspace Reorganization in Core Reward Regions. Neuron, 105(4), 712–724.e4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Wang MZ, & Hayden BY (2019). Monkeys are curious about counterfactual outcomes. Cognition, 189, 1–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Wang MZ, Hayden BY, & Heilbronner SR (2022). A structural and functional subdivision in central orbitofrontal cortex. Nature communications, 13(1), 1–12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Blanchard TC, Wolfe LS, Vlaev I, Winston JS, & Hayden BY (2014). Biases in preferences for sequences of outcomes in monkeys. Cognition, 130(3), 289–299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Ebitz RB, Sleezer BJ, Jedema HP, Bradberry CW, & Hayden BY (2019). Tonic exploration governs both flexibility and lapses. PLoS computational biology, 15(11), e1007475. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Balzani E, Lakshminarasimhan K, Angelaki D, & Savin C. (2020). Efficient estimation of neural tuning during naturalistic behavior. Advances in Neural Information Processing Systems, 33, 12604–12614. [Google Scholar]
- 74.Ledergerber D, Battistin C, Blackstad JS, Gardner RJ, Witter MP, Moser MB, Roudi Y, & Moser EI (2021). Task-dependent mixed selectivity in the subiculum. Cell reports, 35(8), 109175. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Saxena S, & Cunningham JP (2019). Towards the neural population doctrine. Current opinion in neurobiology, 55, 103–111. [DOI] [PubMed] [Google Scholar]
- 76.Ebitz RB, & Hayden BY (2021). The population doctrine in cognitive neuroscience. Neuron, 109(19), 3055–3068. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The processed data reported in this paper has been deposited on Zenodo and is publicly available as of the date of publication. The DOI is listed in the key resources table.
All original code has been deposited on Zenodo and is publicly available as of the date ofpublication. The DOI is listed in the key resources table.
Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.
KEY RESOURCES TABLE
| Resource | Source | Identifier |
|---|---|---|
| Deposited Data | ||
| Preprocessed data | Zenodo | DOI: 10.5281/zenodo.8067596 |
| Software and Algorithms | ||
| MATLAB analysis code | Zenodo | DOI: 10.5281/zenodo.8067596 |