Harmonizing florbetapir and PiB PET measurements of cortical Aβ plaque burden using multiple regions‐of‐interest and machine learning techniques: An alternative to the Centiloid approach

Abstract

INTRODUCTION

Machine learning (ML) can optimize amyloid (Aβ) comparability among positron emission tomography (PET) radiotracers. Using multi‐regional florbetapir (FBP) measures and ML, we report better Pittsburgh compound‐B (PiB)/FBP harmonization of mean‐cortical Aβ (mcAβ) than Centiloid.

METHODS

PiB‐FBP pairs from 92 subjects in www.oasis‐brains.org and 46 in www.gaain.org/centiloid‐project were used as the training/testing sets. FreeSurfer‐extracted FBP multi‐regional Aβ and actual PiB mcAβ in the training set were used to train ML models generating synthetic PiB mcAβ. The correlation coefficient (R) between the synthetic/actual PiB mcAβ in the testing set was assessed.

RESULTS

In the testing set, the synthetic/actual PiB mcAβ correlation R = 0.985 (R² = 0.970) using artificial neural network was significantly higher (p ≤ 6.6e‐4) than the FBP/PiB correlation R = 0.927 (R² = 0.860), improving total variance percentage (R²) from 86% to 97%. Other ML models such as partial least square, ensemble, and relevance vector regressions also improved R (p = 9.677e⁻⁰⁵/0.045/0.0017).

DISCUSSION

ML improved mcAβ comparability. Additional studies are needed for the generalizability to other amyloid tracers, and to tau PET.

Highlights

• Centiloid is a calibration of the amyloid scale, not harmonization.

• Centiloid unifies the amyloid scale without improving inter‐tracer association (R²).

• Machine learning (ML) can harmonize the amyloid scale by improving R².

• ML harmonization maps multi‐regional florbetapir SUVRs to PiB mean‐cortical SUVR.

• Artificial neural network ML increases Centiloid R² from 86% to 97%.

1. INTRODUCTION

The research community has the consensus that a standardized common scale is needed ¹ , ² , ³ , ⁴ , ⁵ for measuring cerebral β‐amyloid (Aβ) burden with various positron emission tomography (PET) tracers including C11 Pittsburgh compound (PiB), ⁶ , ⁷ , ⁸ , ⁹ , ¹⁰ F18 florbetapir (FBP), ¹¹ F18 florbetaben, ¹² F18 flutemetamol, ¹³ and F18 NAV4694. ⁴ The widely used amyloid measure is the standard uptake value ratio (SUVR), essentially the raw PET count ratio of region‐of‐interests (ROIs) over a reference region such as the cerebellum. ⁷ , ¹⁴ , ¹⁵ Based on predefined ROIs composed of cortical areas, the so‐called mean‐cortical SUVR (mcSUVR) was used as a measurement of global Aβ burden for a given tracer. ¹⁴ , ¹⁵ , ¹⁶ It is well recognized that the existence of different radioactive tracers and wide variation in PET data acquisition/processing introduce mcSUVR heterogeneity. ⁵ , ¹⁷ , ¹⁸ Even when great efforts are made to standardize image acquisition, processing, and analysis pipelines across multiple centers for a given study such as ADNI and other multisite clinical trials, ¹⁹ , ²⁰ , ²¹ , ²² heterogeneity still exists.

To meet this challenge, the Centiloid Working Group created the common Centiloid (CL) scale ⁵ via linear regression, scaling together with a calibration dataset for a given tracer and the reference PiB tracer to convert the tracer/pipeline‐specific mcSUVR into standard CL (see also Schwarz et al., 2018 ²³ ). With CL, the average amyloid burden measurement is 0 for young controls and 100 in typical Alzheimer's disease (AD) patients. ⁵ , ¹⁷ , ¹⁸ Ideally, CL can be used independently of tracer, scan protocol, and analysis pipeline. In a sense, the Aβ measures from one PET tracer “Y” are the same as from another PET tracer “X,” that is, Y = X in CL, or Y = kX + b with the slope k = 1 and intercept b = 0 statistically. The unit slope and zero intercept, however, has nothing to do with the goodness of fit (GOF) or how tightly the scaled mcSUVR pairs are scattered around Y = kX + b. ²³ GOF, defined as the square of the correlation coefficient, R², between two measures, is intrinsic to the data and would not be altered by a linear transformation such as CL. To facilitate discussion, we will refer to a process as “calibration” if it brings the amyloid measures to a common scale with their intrinsic fixed GOF. In contrast, we refer to a process as “harmonization” if it attempts to optimize GOF (reducing the scattering around the fitted curve). Thus, CL is only a process of calibration.

As such, CL has two related limitations: (1) the inconsistent amyloid positivity thresholds for two different tracers; and (2) the inconsistent Aβ burden reading from the two tracers. Based on a different dataset, the mcSUVR cutoff of 1.17 for FBP detects moderate‐to‐frequent brain amyloid burden determined pathologically ¹⁴ and can be converted to a CL cutoff of 37.1 ¹⁷ while the corresponding threshold is 20.1 CL for PiB ²⁴ and 19 CL for florbetaben. ²⁵ Using the head‐to‐head comparison data from the DIAN‐TU cohort and a common positivity cutoff criterion of 95% specificity, the positivity cutoff for PiB was 6.0 CL and 26.1 CL for FBP. If we apply the same approach to the PiB‐FBP Centiloid calibration dataset used in this study (see Methods below for details), the positivity cutoff for 95% specificity would be 10.2 CL for PiB and 19.1 CL for FBP. These differences are partially compounded also by the variation of the analysis pipeline and pathological assessment from different researchers. The second limitation is related to individual‐level deviation of the mcSUVR pair from the fitted Y = kX + b line. This will be especially problematic if the readings are close to the positivity threshold or if CL will be used as a clinical trial outcome measure. In fact, both limitations are related to the intrinsic GOF, with or without CL calibration.

Unlike the linear regression which only computes GOF, this study aims to use machine learning (ML) to improve GOF by harmonizing, not just calibrating, Aβ PET measurements over different tracers. We note that R² is complementary to the linear slope which reflects the magnitude of the specific amyloid signal of a tracer relative to PiB, ⁵ and that the slope can be scaled for a common range. Our harmonization strategy to improve R² involves utilizing multiple regional SUVRs for a tracer, in this case, FBP, to optimally map to PiB mcSUVR using ML techniques such as the artificial neural network.

2. METHODS

2.1. Subjects and image preprocessing

A training set of PiB‐FBP head‐to‐head comparison data was obtained from the Open Access Series of Imaging Studies (OASIS) in the OASIS‐3 release. ²⁶ The OASIS‐3 release incorporates data from 1098 participants covering the adult life span aged 42–95, including cognitively normal individuals and individuals with early‐stage AD dementia from the Knight Alzheimer Disease Research Center at Washington University St. Louis. The OASIS‐3 release includes T1‐weighted structural and functional MRI (magnetic resonance imaging), amyloid and metabolic PET imaging, neuropsychological testing, and clinical data. A total of 92 participants with both PiB and FBP collected within three months were included in this study.

The FBP‐PET data for these 92 participants were from the PET‐MR scanner. The version of the data used for sharing in OASIS and for our report was reconstructed using computed tomography (CT)‐based attenuation maps by the WashU team, the same as the PiB‐PET. ²⁷ The T1‐weighted structural MR image (T1w‐MRI) associated with each PET scan was used to provide anatomical reference and help analyze PET data. FreeSurfer (FS) v5.3 (http://surfer.nmr.mgh.harvard.edu/) software processed the T1w‐MRI and performed cortical parcellation and subcortical segmentation to define ROIs in individual space. ²⁸ Regional SUVR measurements of PiB and FBP uptake were obtained for each FS ROI and composite regions of the gyrus rectus, temporal cortex, occipital cortex, and prefrontal cortex using the cerebellar cortex as the reference region (commonly used but one of several choices) and our in‐house PET processing pipeline. ¹⁵ , ¹⁸ As the global index of amyloid burden, ¹⁵ the mcSUVR was calculated as the average SUVR of the gyrus rectus, temporal cortex, prefrontal cortex, and precuneus. A total of 90 regional, composite, and global SUVR measures were generated from our pipeline for each PET scan where corresponding left and right hemispheric regions were averaged. These measures were used as the input to the ML models to estimate synthetic PiB mcSUVR from FBP measurements. Alternatively, FS‐based regional SUVRs without averaging left and right brain regions were also examined in an exploratory analysis as the input to the ML models. Conversion to the CL scale was performed for the global mcSUVR measure as previously described, ¹⁸ , ²⁹ and performance evaluation was assessed based on the converted CL measures.

The Global Alzheimer's Association Interactive Network (GAAIN) PiB‐FBP CL calibration dataset from AVID with 13 young controls and 33 elderly subjects ¹⁷ was obtained from the GAAIN website (http://www.gaain.org/centiloid‐project), preprocessed the same way and used as an independent testing set. The demographic and clinical characteristics of the participants in these two datasets are summarized in Table 1.

TABLE 1.

Demographic and clinical characteristics of the study participants.

	OASIS (n = 92)	AVID (n = 46)	p‐value
Age at PiB scan (range)	68 ± 8.8 (43–88)	58 ± 21.4 (21–89)	9e‐05
Sex (M/F)	44/48	27/19	0.22
APOE genotype (NC/HT/HM)	60/27/5	31/13/2	0.95
MMSE	29.2 ± 1.0 (26–30)	25.8 ± 4.9 (8–30)	2e‐09

Abbreviations: APOE, apolipoprotein E gene, ε4 allele; AVID, the Centiloid project dataset downloaded from the GAAIN website (http://www.gaain.org/centiloid‐project); HM, homozygotes; HT, heterozygotes; MMSE, Mini‐Mental State Examination; NC, non‐carriers; OASIS, Open Access Series of Imaging Studies; PiB, Pittsburgh compound.

RESEARCH IN CONTEXT

1. Systematic review: The authors searched traditional sources (eg, PubMed) for all pertinent literature using keywords such as “Centiloid,” “amyloid PET harmonization,” “amyloid PET standardization,” “amyloid measure harmonization,” “harmonization,” “machine learning,” “artificial neural network,” and “artificial intelligence.”

2. Interpretation: Our results demonstrated improved performance with machine learning‐based amyloid harmonization compared to the Centiloid calibration. It not only brought the amyloid measurements from different PET tracers into a common scale, but it also improved the inter‐tracer amyloid measure consistency (measured as the squared correlation coefficient, R²). The generalizability of our harmonization method is demonstrated in an independent dataset.

3. Future directions: The manuscript proposes a framework for the harmonization between FBP and PiB amyloid measurements. Future studies will examine the framework's generalizability to other amyloid PET tracers, to perform harmonization for different tau tracers and to apply this cross‐sectional framework to longitudinal data.

2.2. ML methods

The larger dataset with 92 PiB‐FBP pairs from OASIS (https://www.oasis‐brains.org/) was used as the training set. The smaller independent dataset with 46 PiB‐FBP pairs from AVID was used as the testing set. Both FBP and PiB images were reconstructed using the CT‐derived attenuation map. ²⁷ We considered four ML methods: (1) partial least square regression (PLSR), (2) ensemble regression (ER), (3) relevance vector regression (RVR), and (4) artificial neural network (ANN). The Deep Learning and Statistics and Machine Learning toolboxes in MATLAB (release 2020a, www.mathworks.com) were used to carry out ER, PLSR, and ANN (see below for RVR). As a post hoc analysis, we switched the training and testing datasets, and repeated the assessment of the ML methods to further confirm our findings.

2.2.1. Partial least square regression (PLSR)

We have been using the partial least square procedure for analyzing dual‐modal imaging data to examine the covarying spatial patterns between imaging modalities and therefore to increase statistical power in the preclinical study of AD. ³⁰ , ³¹ Our use of PLSR in this study, however, is one of the means to map FBP multi‐regional SUVR values to the mcSUVR of PiB. Instead of the commonly used linear regression, the PLSR will account for the collinearity among the multiple regional SUVR measures. For our data, the collinearity exists not only because the number of subjects is less than the number of FS‐defined regions from which we extract the FBP SUVR data, but also from the fact that regional amyloid PET SUVRs are highly correlated. As essentially a linear mapping, PLSR gives a reference (baseline) metric to compare the performance of nonlinear mappings such as ANN, RVR, and ER. For carrying out PLSR in MATLAB, we chose the outputs of the first three components as the mapped outcome measures, consistent  with our previous studies. ³⁰ , ³¹ All other MATLAB settings for PLSR were default.

2.2.2. Ensemble regression (ER)

ER is another ML algorithmic method. ³² According to Moreira et al., ensemble learning (in our case, regression) is a process that uses a set of models, each of them obtained by applying a learning process to the given problem. ³³ This set of models (ensemble) is integrated in some way to obtain the final prediction. ER is based on a random forest with individual regression trees. ³² In this study, we ensembled these individual regression trees using the aggregation method of least‐square boosting (LSBoost) https://www.mathworks.com/help/stats/fitrensemble.html. With LSBoost at every step, the ensemble fits a new learner to the difference between the observed response and the aggregated prediction of all learners grown previously. The ensemble fits to minimize mean‐squared error. In carrying out the analysis, we turned on the hyperparameter auto‐determination feature, but all others were MATLAB default settings.

2.2.3. Relevance vector regression (RVR)

The general relevance vector machine (RVM) is an ML technique that uses Bayesian inference to obtain parsimonious solutions for both regression and probabilistic classification. ³⁴ RVM has previously been used to estimate continuous clinical scores from brain images. ³⁵ , ³⁶ For our application, we used it for regression (ie, RVR). The RVM has an identical functional form to the support vector machine/regression (SVM/SVR) with specified kernel functions but provides probabilistic classification/regression.

In this study, we ran the RVR MATLAB program downloaded from https://ww2.mathworks.cn/matlabcentral/fileexchange/69407‐relevance‐vector‐machine‐rvm and used a Gaussian kernel with a width of 7 and all other default settings. Though the Bayesian formulation of the RVM avoids the set of free parameters that the SVM usually requires for cross‐validation‐based post‐optimizations, the RVM uses an expectation maximization‐like learning method and is at risk of local minima. We thus also ran SVR (with fitrsvm implemented in MATLAB with all default settings) to compare the results. The RVM is patented in the United States by Microsoft, but expired September 4, 2019.

2.2.4. Artificial neural network (ANN)

Neural network methods are able to learn abstract and complex features from high dimensional input data sets based on partially analyzing the progressive layer‐to‐layer non‐linear transformations to learn the variable degrees of importance of these features and to find automatically the optimal way to combine them. Given the sample size and relatively simple question, we considered the use of shallow ANN. ³⁷ In contrast to the popular Deep Learning neural network which has many hidden layers, shallow ANN has only several hidden layers in addition to the input layer to which the regional FBP SUVRs from multi‐ROIs are fed, and an output layer which generates the synthetic PiB mcSUVR as a continuous variable.

There were a few hyperparameters to decide on prior to running the ANN, including the number of hidden layers and the number of neurons in each hidden layer. The maximal number of hidden layers in our investigation was set to be four, and the maximal number of neurons for each hidden layer was variable depending on the number of layers. For a system with two hidden layers, for example, the maximal number of neurons in each hidden layer was set to be 15. Similarly, for three, four, and five hidden layers, the maximal number of neurons in each hidden layer was set to be four. The loss function was the default mean squared error.

2.3. ML performance assessments and comparisons

The primary objective assessment is the improved correlation coefficient, R_ML, between the synthetic‐PiB mcSUVR and the PiB mcSUVR in comparison to the correlation coefficient R_CL between FBP mcSUVR and the PiB mcSUVR in the independent testing dataset. Note that the subscript ML in R_ML can indicate the correlation coefficient based on PLRS, RVR, ANN, or ER, and the subscript CL in R_CL stands for Centiloid as R_CL is invariant under the linear conversion from the mcSUVR to CL scale. To test if R_ML is significantly higher than R_CL, we used the Steiger test to compare correlation coefficients while accounting for the existing correlation—the multi‐regional FBP SUVR‐based mapping measures (synthetic‐PiB mcSUVR) and the FBP mcSUVR. In addition, we also report R_ML versus R_CL results in the training data set for the consistency of findings between the training and the testing datasets. Though our hypothesis is directional (R_ML is significantly higher than R_CL), our significance is two‐tailed at p = 0.05 to be statistically conservative. We also report the squared R (R_ML ² or R_CL ²) value as it is a measure of the GOF (how tightly the data dots are distributed around the fitted regression line) in our simple regression model, and it represents the percentage of the total variance the model explains. All the analyses in this study are based on the commonly used (ordinary) linear regression, although the Deming regression accounts for measurement errors in both tracers (treated as dependent or independent variable); it was found that the difference between the two approaches is negligible. ²³ Regardless, the R² or R values are not affected by the regression model choice.

3. RESULTS

Table 1 includes the participants’ demographic and clinical characteristics for the two datasets. As stated in the Methods, the training dataset consisted of 92 PiB‐FBP pairs obtained from OASIS in the OASIS‐3 release. ²⁶ The testing dataset consisted of 46 scans from the GAAIN PiB‐FBP Centiloid calibration study by AVID with 13 young controls and 33 elderly subjects. ¹⁷ We note that the two study cohorts differed in terms of age and Mini‐Mental State Examination (MMSE) scores; however, this mismatch is less a concern for this study as we are more interested in examining the generalizability of the results generated from one cohort to another.

Table 2 shows the results for each of the ML algorithms when the SUVR data from 90 ROIs were used as the input to each ML model. The values of R_CL in the training and testing datasets were 0.9047 and 0.9274, respectively, and were not statistically different from each other (p = 0.2232). They each were used as the reference value in the respective training and testing datasets to assess the correlation coefficient improvement by each ML algorithm.

TABLE 2.

ML results for left/right combined ROI data with OASIS/AVID as training/testing datasets.

	Training dataset (OASIS)		Testing dataset (AVID)
ML method	R	p‐value	R	p‐value
CL (ref)	0.9047	N/A	0.9274	N/A
ER	0.9862	<1e‐31	0.9536	0.04
PLSR	0.9651	1e‐08	0.9634	10e‐05
RVR	0.9623	10e‐08	0.9728	2e‐06
ANN (3)	0.9794	2e‐10	0.9745	4e‐07
ANN (2)	0.9905	<1e‐31	0.9847	8e‐08

Note: The Steiger test was used to compare the PiB/FBP correlation coefficient (R) between the Centiloid (as reference) and each ML method. The comparison was performed separately for the training and testing datasets.

Abbreviations: ANN(n), artificial neural network with n hidden layers; AVID, the Centiloid project dataset downloaded from the GAAIN website (http://www.gaain.org/centiloid‐project); CL (ref), Centiloid reference; ER, ensemble regression; FBP, florbetapir; ML, machine learning; OASIS, Open Access Series of Imaging Studies; PiB, Pittsburgh compound‐B; PLSR, partial least square regression; ROI, region of interest; RVR, relevance vector regression;.

Among the various ML models evaluated, using the Steiger test we found moderate but significant improvement of the correlation by ER in the testing dataset (R_ER = 0.9536, p = 0.04, vs R_ER = 0.9862 in the training dataset, p < 1e⁻³¹). We observed significant improvement for PLSR (with the first three components accounting for 96% of the total accumulative variation) in the testing dataset (R_PLSR = 0.9634 , p = 10e⁻⁰⁵, vs R_PLSR = 0.9651 in the training dataset, p = 1e⁻⁰⁸). For RVR with a single kernel, we observed R_RVR = 0.9728 in the testing dataset, p = 2e⁻⁰⁶, versus R_RVR = 0.9623 in the training dataset, p = 10e⁻⁰⁸. In comparison to the RVR, the SVR was R_SVR = 0.9530 in the testing dataset, p = 0.001, versus R_SVR = 0.9696 in the training dataset, p = 2e⁻¹³.

Among the shallow ANN models we evaluated with the number of layers ranging from one to four, Figure 1 illustrates the ANN model with two layers. ANN models performed better than the other ML models in general, with the R_ANN values ranging from 0.9762 to 0.9847 in the independent testing dataset. The better performance, however, was not associated with more layers. Corresponding to R_ANN = 0.9847 in the independent testing dataset and generated with two hidden layers (Figure 1), the value of R² or the shared variance percentage was R_ANN ² = 0.9696 (for the training dataset, R_ANN = 0.9905 and R_ANN ² = 0.9811). Figure 2 plots the linear regression with R and R² values for this ANN performance in the training (top of Figure 2) and testing (bottom of Figure 2) datasets. We used the CL scale in the graphs, noting the R and R² values are the same for mcSUVR and CL. The 97% of the total variance explained is in contrast with the 91% of the total variance for ER (R_ER = 0.95363 and R_ER ² = 91%, Table 2). More importantly, this 97% R² for ANN is an increase of more than 10% in contrast to the 86% of the total variance explained with the original CL approach (Table 2). Results in Table 3 for each of the ML algorithms when the SUVR data from the separate bilateral ROIs were used were similar to those in Table 2 with the combined left/right ROI data.

FIGURE 1.

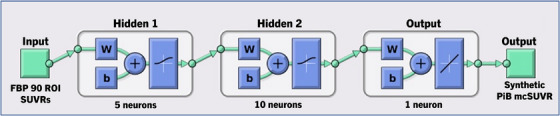
Artificial neural network (ANN) model configuration with two hidden layers. b, bias; FBP, florbetapir; mcSUVR, mean‐cortical SUVR; PiB, Pittsburgh compound‐B; ROI, region of interest; SUVR, standard uptake value ratio; W, weights.

FIGURE 2.

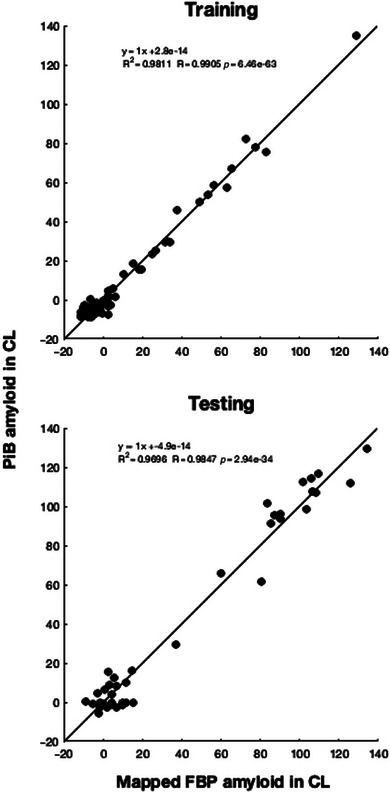
Linear regression plot with displayed R and R² values for artificial neural network (ANN) performance with two hidden layers in the training (top, OASIS) and testing (bottom, AVID) datasets. The regression relates the ANN mapped florbetapir (FBP) Aβ burden to PiB Aβ burden expressed in Centiloid (CL). Note that the R and R² values remain the same for mcSUVR and for CL. Aβ, β‐amyloid; AVID, the Centiloid project dataset downloaded from the GAAIN website (http://www.gaain.org/centiloid‐project); mcSUVR, mean‐cortical SUVR; OASIS, Open Access Series of Imaging Studies; Pittsburgh compound‐B (PiB).

TABLE 3.

ML results with separate left and right ROI data with OASIS/AVID as training/testing datasets.

	Training dataset (OASIS)		Testing dataset (AVID)
ML method	R	p‐value	R	p‐value
CL (ref)	0.9021	N/A	0.9273	N/A
ER	0.9936	<1e‐31	0.9532	0.03
PLSR	0.9654	9e‐09	0.9642	5e‐05
RVR	0.9750	2e‐12	0.9651	0.001
ANN (3)	0.9620	6e‐05	0.9838	7e‐07
ANN (2)	0.9653	1e‐05	0.9846	1e‐07

Note: The Steiger test was used to compare the PiB/FBP correlation coefficient (R) between Centiloid (as reference) and each ML method. The comparison was performed separately for the training and testing datasets.

Abbreviations: ANN(n), artificial neural network with n hidden layers; AVID, the Centiloid project dataset downloaded from the GAAIN website (http://www.gaain.org/centiloid‐project); CL (ref), Centiloid reference; ER, ensemble regression; FBP, florbetapir; ML, machine learning; OASIS, Open Access Series of Imaging Studies; PiB, Pittsburgh compound‐B; PLSR, partial least square regression; ROI, region of interest; RVR, relevance vector regression.

The performance of these ML methods was further confirmed when we switched the training and testing datasets for our post hoc analysis. For ANN in the switched independent testing dataset, R_ANN = 0.9721 and R_ANN ² = 0.945 (Figure S1 and Table S1). As shown in Table S1, significant improvements were also observed for PLSR and RVR, but not for ER. In addition to the improved R², we also explored the inter‐tracer bias issue which essentially led to the creation of the Centiloid. Between the ML‐based synthetic mcSUVR for FBP and the PiB mcSUVR, the inter‐tracer regression line's slope is closer to 1.0 and intercept closer to 0.0 prior to the level‐1 and level‐2 Centiloid conversion as shown in Figure S2 and Table S2. We observed that the original FBP mcSUVR values deviate the most from the target PiB mcSUVR particularly around the higher SUVR range on the y‐axis (eg, 1.2 and above), versus the tighter fit seen with the synthetic SUVRs generated from each ML algorithm.

4. DISCUSSION

This study introduces approaches to harmonize amyloid plaque burden measurements among different amyloid PET tracers. For FBP‐PiB tracer pairs, we showed stronger correlations, or equivalently, better GOF (ie, higher percentage of the total variance accounted for) between the FBP multi‐ROI SUVR mapped synthetic PiB mcSUVR and the actual PiB mcSUVR in contrast to the correlations between the two tracers using the Centiloid calibration approach. This significant improvement was observed using either OASIS or AVID as the testing dataset.

For this study, our goal was to harmonize the global mcSUVR between two tracers based on cortical amyloid burden SUVR measurements from one tracer (FBP) mapped to the mcSUVR of another (PiB as the reference). This method focuses directly on the global measure as the final outcome, as does the CL approach. The tracer uptake from multiple brain regions contains rich biological information of amyloid burden in the brain in addition to non‐specific binding and other factors that contribute to the tracer‐specific amyloid PET measures. Logically, this rich information contributed to the global mcSUVR estimation directly and indirectly by the ML algorithms which served implicitly as a filter to enforce the more adequate estimation of amyloid burden for the given tracer, as well as capture the commonality measured by different PET tracers such as FBP and PiB. In a related study, we also developed a harmonization approach directly operating on the imaging data themselves and generating synthetic PiB images from FBP data, and achieved significant improvement in the agreement in global mcSUVR, although to a lesser degree than accomplished by the methods proposed in the current approach. ³⁸ Further investigation of approaches that can achieve optimal harmonization at both voxel and global level is warranted.

Instead of simply calibrating different mcSUVRs to the common CL scale with GOF unchanged by Centiloid or by AMYQ ³⁹ (an alternative to Centiloid), our approach attempts to optimize the GOF measured as R² or equivalently R. In this regard, our harmonization approach is superior with 97% of the total variance explained via ANN versus the CL‐based approach (R² is 86% for testing the AVID dataset). The same conclusion was reached when we switched the training and testing datasets. Though in theory the ideal 100% of the total variance is not achievable, we expect better results when larger datasets are available which allow more comprehensive search of model configurations and the estimation of the model parameters. We acknowledge that the ML‐harmonized amyloid measures were standardized using the CL calibration procedure already established ⁵ ; so was the AMYQ ³⁹ performance which is compatible with Centiloid but easier to use as it does not require MRI or the definition of a priori reference and cortical ROIs.

The nonlinear mapping of a multi‐regional SUVR of one tracer to the mcSUVR of another tracer is one way to improve the harmonization of the global amyloid burden measure. Additionally, more adequate SUVR quantification and imaging preprocessing such as proper partial volume correction ¹⁸ could also improve the harmonization. For example, recent comparison studies demonstrated that the global amyloid burden measures between PiB and FBP have a shared variance (the R²) ranging from approximately 70% to 90% depending on the quantification pipelines and cohorts. ¹⁶ , ¹⁷ , ¹⁸ In general, adequate preprocessing can be used for CL alone or in conjunction with ML to achieve better results. Potentially, ML especially ANN may be robust enough to handle, to some degree, variability in acquisition, quantification, and preprocessing. Further studies are needed to assess such robustness or the need to build different ML models to handle such variability.

This study does not intend to address the differential contributions of regional SUVRs to the outcomes of ANN and other ML models. For our simple shallow ANN model, it is feasible to further explore such differential contributions, and consequently provide some insights on regions where specific or non‐specific bindings are seen and how they were used in the mapping to the mcSUVR of PiB. In general, numerous studies have demonstrated the power of the neural network approach in solving difficult problems when traditional methods, including some ML techniques assessed in this study, have failed. Continued efforts, including those to better understand of how a model behaves (such as the ones used in this study) and to explore more advanced models, will aid the field and make use of multiple amyloid tracers from multi‐center studies more feasible.

Our primary focus for this study is the improved harmonization (GOF), measured by R², between two tracers. The inter‐tracer bias issue was separated and adequately addressed by the integrated Centiloid level‐1 and level‐2 scaling/linear regression, so the inter‐tracer regression slope is 1.0 and intercept 0.0 in Centiloid scale. As part of our post hoc exploratory analysis, we examined the linear regression part of Centiloid standardization in terms of the slope and intercept between raw FBP mcSUVR and the PiB mcSUVR, between the synthetic PiB mcSUVR for FBP and the PiB mcSUVR. We noted bigger bias between raw FBP mcSUVR and PiB mcSUVR, with a slope of 1.622 and an intercept of −0.6900 as compared to, for example, ANN with two hidden layers, which has a slope of 1.0081 and an intercept of −0.0100. Future studies to examine the bias in a more systematic way are needed to see the consistent harmonization improvement and bias reduction.

While our datasets are small, they are adequate for the relatively simple ML algorithms we examined in the current study. Moreover, the separation of the two naturally independent datasets, one as training and the other as testing with the additional training/testing switch for cross‐validation, provides us with a certain level of assurance regarding the generalizability of our results. Nevertheless, for ML models to be adequate and generalizable, larger datasets are needed especially for more complex models (eg, more layers and/or a greater number of neurons in each layer for ANN) aiming for better results. New studies are being actively planned with adequate or even larger sample sizes, additional amyloid PET tracer pairs and/or different reference regions to confirm, generalize, and further improve our findings. Additionally, we also believe that our approach can be  easily adopted for tau PET tracer harmonization.

In summary, we demonstrated much improved inter‐tracer harmonization of PET measurement of amyloid burden with the use of the multi‐ROI amyloid measures of one tracer to map the global amyloid burden of another tracer and the use of ML techniques as compared to the linear regression‐based CL calibration approach.

CONFLICT OF INTEREST STATEMENT

The authors have no conflicts of interest to report. Author disclosures are available in the supporting information.

CONSENT STATEMENT

All studies were approved by their corresponding institutional review boards and written informed consent was obtained for each participant.

Supporting information

Supporting Information

Supporting Information

Supporting Information

Chen K, Ghisays V, Luo J, et al. Harmonizing florbetapir and PiB PET measurements of cortical Aβ plaque burden using multiple regions‐of‐interest and machine learning techniques: An alternative to the Centiloid approach. Alzheimer's Dement. 2024;20:2165–2172. 10.1002/alz.13677