Abstract
Reliable sensory discrimination must arise from high-fidelity neural representations and accurate communication between brain areas. However, the coding and communication strategies used by neocortex to overcome the substantial variability of neuronal sensory responses remain undetermined1–6. To examine these components of perception, we imaged neuronal activity in 8 neocortical areas concurrently and over 5 days in mice performing a visual discrimination task, yielding longitudinal recordings of >21,000 neurons. Our analyses revealed a sequence of events across neocortex starting from an initial resting state, to early stages of perception, and through formation of a task response. At rest, neocortex had one pattern of functional connections, identified via sets of brain areas that shared activity co-fluctuations7,8. Within ~200 ms after onset of a sensory stimulus, such connections rearranged, with different areas sharing co-fluctuations and task-related information. During this short-lived (~300 ms) state, inter-area transmission of sensory data and the redundancy of sensory encoding both peaked, stemming from a transient increase in correlated fluctuations among task-related neurons. By ~0.5 s after stimulus onset, the visual representation reached a more stable form, whose statistical structure made it robust to the prominent, day-to-day variations in individual cells’ responses. About ~1 s into stimulus presentation, a global fluctuation mode arose that was orthogonal to modes carrying sensory data and that conveyed the mouse’s upcoming response to every cortical area examined. Overall, neocortex supports sensory performance via brief elevations in the redundancy of sensory coding near the start of perception, neural population codes that are robust to cellular variability, and widespread, inter-area fluctuation modes that transmit sensory data and task responses in non-interfering channels.
Given a fixed sensory scene or object, sensory recognition is normally reliable. However, sensory cortical neurons have stochastic responses that vary over timescales from seconds to days1–4,6,9. These variations are often shared between cells and across cortical areas1–6, raising basic questions about how neural populations encode and transfer information reliably despite activity fluctuations over multiple spatiotemporal scales9–11.
Many studies have argued neurons’ shared fluctuations constrain the signaling capacity of cortical coding3,12–14, while perhaps also facilitating the decoding of transmitted messages6,15,16. However, the relationships between shared fluctuations, the redundancy of large-scale neural coding, and the reliability of sensory cortical representations remain poorly understood. Neural populations can show greater long-term coding stability than single cells, but the mechanism for stability and its relationship to shared fluctuations merit further examination17–20.
Human neuroimaging studies usually interpret co-fluctuations across brain areas as denoting functional connections for information transmission8,21. Neuronal recordings have shown inter-area fluctuations can reflect arousal, neuromodulatory levels, or spontaneous movements11,22,23 and might also communicate functional information10. However, whether cortex uses inter-area fluctuations to encode task-related sensory data has not been tested empirically.
To uncover neural coding and inter-area dynamics promoting reliable sensory processing, we recorded neuronal activity across the entire visual cortex in mice performing a visual task. We analyzed thousands of cells, how their visual representations attain coding redundancy and long-term stability, and whether brain areas share information via co-fluctuations.
Imaging neuronal activity across cortex
To study visual processing, we trained head-fixed mice to perform a GO/NO-GO task (Fig. 1a,b; Methods). On each trial, mice viewed a moving grating stimulus (2-s-duration) oriented either horizontally or vertically (respectively termed ‘GO’ and ‘NO-GO’ stimuli). A half-second after the offset of a GO stimulus, the mouse could receive a reward by licking a spout. Incorrect licking after a NO-GO stimulus elicited an aversive air-puff. To minimize motor-related neural activity during stimulus presentation, we trained mice to withhold licking until the response-period (Fig. 1b). Near the end of training and before brain-imaging began, we reduced the grating contrast so mice just surpassed 80% success on both trial-types.
Fig. 1. Cellular-level imaging across multiple cortical areas during a visual discrimination task.
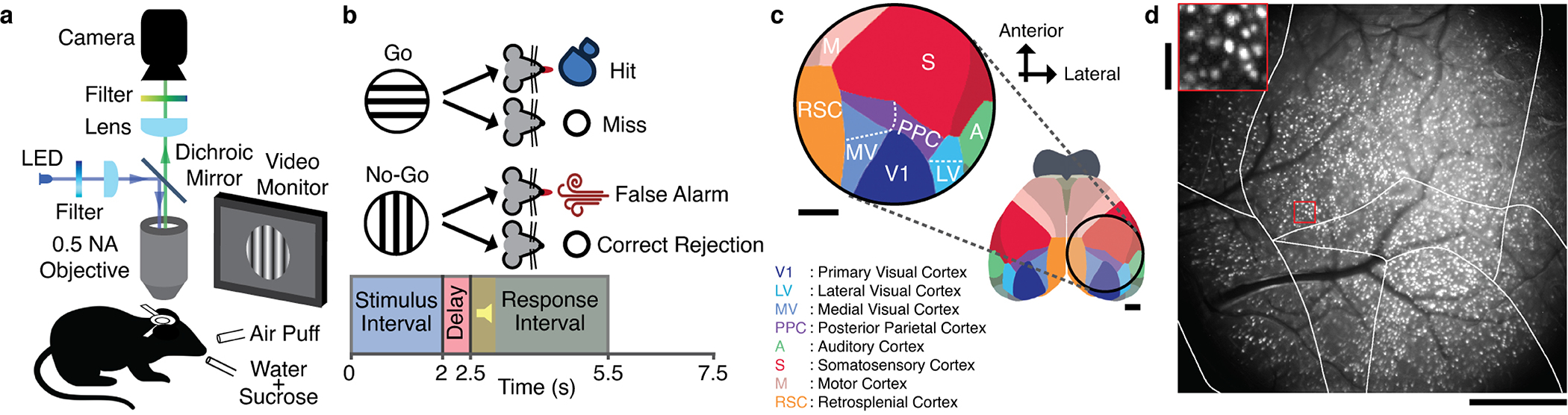
(a) A custom macroscope imaged Ca2+ activity in thousands of layer 2/3 pyramidal neurons.
(b) On each trial, mice viewed a moving grating (2 s duration). After a 0.5-s-delay, an auditory tone initiated a 3-s-long response period, when mice could respond by licking a spout. Responses to a horizontal grating (the ‘GO’ stimulus) elicited a water reward. If the mouse responded to a vertical grating, it received an air puff and an 8-s-timeout before the next trial. Mice performed 83±3% of trials correctly (mean±s.e.m.; 6 mice; Extended Data Fig. 1).
(c) Imaged brain areas (encircled). Scale bars: 1 mm. Same color scheme and abbreviations used in all subsequent figures. Inset: Magnified view.
(d) Maximum projection of a Ca2+-video (280-min-duration) with 5292 cells, overlaid with cortical area boundaries. Scale bar: 1 mm. Inset: Enlargement of red boxed area. Scale bar: 0.1 mm.
As mice performed the task, we used a macroscope (16 mm2 field-of-view) to image somatic Ca2+ dynamics in neocortical layer 2/3 pyramidal neurons (Fig. 1c,d; Supplementary Video 1). To avoid conflating locomotor-evoked and visual neural signals, we only analyzed trials in which locomotion remained <1 cm·s−1. Each recording spanned nearly all of primary and higher-order visual cortical areas, plus parts of somatosensory, auditory, posterior parietal, motor and retrosplenial cortex. By identifying cells within concatenated datasets, we tracked 21,570 neurons [3597±1082 (±s.d.) in 6 mice that performed 2000±415 trials over 5–7 days; Figs. 1d,2a; Extended Data Figs. 1,2a–d], thereby attaining unprecedented, long-term and concurrent access to neuronal dynamics in multiple cortical areas.
Fig. 2. Layer 2/3 cells exhibit diverse coding properties during visual discrimination.
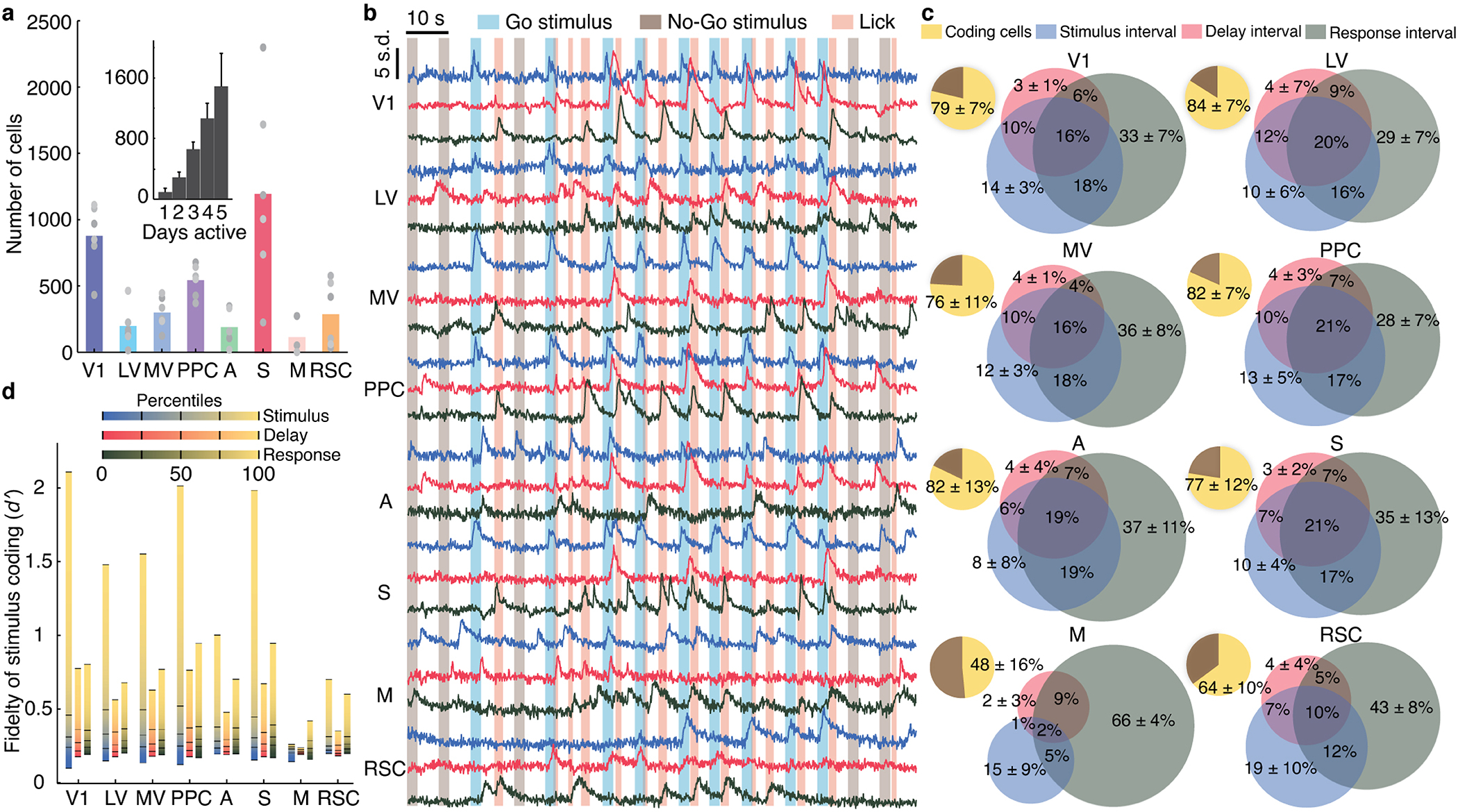
(a) Mean numbers of cells identified in each mouse and brain area [total cells: 3597±1082 (s.d.); 6 mice]. Gray points: data from individual mice. Inset: Histogram of the number of days each cell was active [error bars (s.d.) determined as counting errors].
(b) Ca2+ traces for 3 neurons from each of 8 areas. Traces of cells responding during stimulus, delay, or response intervals are blue, red, and black, respectively.
(c) Pie charts: percentages of cells in each area significantly encoding the stimulus-type (yellow; P<0.01; permutation test; 710–1340 trials) on correct trials, across all sessions. Venn diagrams: proportions of coding cells whose dynamics significantly encoded the stimulus-type during one or more of the intervals within correct trials. Errors: s.d. over 6 mice.
(d) For each area, we computed the distribution of cellular values for trial-type encoding on correct trials. Plots show values for each percentile of the distributions, averaged over 6 mice. Tick marks: 0, 25th, 50th, 75th and 100th percentiles.
Variability of cellular level coding
Across 8 cortical areas, many cells preferentially responded to one of the two stimuli, with variable time-dependencies across cells and areas (Extended Data Figs. 2e–h, 3a,b). To characterize cellular coding, we examined correctly performed trials and determined the statistical fidelity, , with which one could distinguish the two trial-types based on each cell’s dynamics during the stimulus, delay or response intervals. Notably, ( )2 relates to the Fisher information conveyed about trial-type12–14. In merged datasets across all days, most cells exhibited tuning to trial-type in at least one of the trial periods (16,682 cells with significant tuning; 10,329, 9204 and 11,958 in stimulus, delay and response periods, respectively; P<0.01; permutation test; 710–1,340 trials per mouse; Fig. 2b,c; Extended Data Fig. 2h). Fractions of cells tuned to trial-type were similar across visual areas, but the distributions of varied, especially due to outlier cells with large values (Fig. 2c,d).
Many cells had values and coding properties that changed within individual sessions, even while their Ca2+-traces retained high signal-to-noise ratios and stable event rates (Extended Data Fig. 1i–k). Some cells increased their values while others decreased theirs (Extended Data Fig. 2g,j). These bi-directional changes were balanced in magnitude, could not result from photobleaching, and were unlikely to reflect movement-induced effects, since movement nearly always increases pyramidal cell activity11,23,24.
To assess coding stability, we tested if cells concentrated their coding responses into sub-portions of the ~1 h imaging sessions by computing separately for the two halves of each session. We also analyzed shuffled datasets with random permutations of the trial order. If coding cells concentrate their responses into specific epochs, coding should vary more across half-sessions in real than trial-shuffled data, which indeed was so (Extended Data Fig. 2e), indicative of intra-session coding fluctuations.
Many cells also had variable coding fidelity across days (Extended Data Fig. 2f,h,i). However, as in past work20, only a minority flipped their coding preference (1.7±0.9% of coding cells) and these cells had tiny values (0.13±0.05, mean±s.d.; N=587 cells that flipped preference in 6 mice). Notably, fluctuations were correlated across time-scales; cells with variable intra-day coding were ~4-fold more likely to have variable across-day coding (Extended Data Fig. 2l). The anatomic comingling of cells with greater and lesser stability (Extended Data Fig. 2i) and correlations between short- and long-term fluctuations make it hard to argue coding variability arose from imperceptible changes in image quality or focal plane drift.
Time-invariant decoding strategies
Given the non-stationarities in cellular coding, would an area receiving such variable signals need to continually adjust its readout strategy to optimally extract stimulus information? Ongoing plasticity might enable such adjustments, or, alternatively, neural ensembles might achieve reliability via redundant signaling across multiple cells, information encoded in the correlation structure of neural population activity, or combinations thereof 5,9,14,15,19,25.
To explore, for each brain area we trained optimal linear decoders to distinguish the two types of correctly performed trials based on neural ensemble activity in 100-ms time-bins (Methods). These ‘instantaneous decoders’ accurately determined the trial-type, and, as previously3, had a stable form over the latter 1.5 s of the 2-s stimulus presentation (Fig. 3a,b; Extended Data Fig. 3c,f–h). Given this constancy, for the interval 0.5–2 s after stimulus onset we trained ‘consensus decoders’, whose performance matched or surpassed the instantaneous decoders in most time-bins (Extended Data Fig. 3g). Notably, the form of the consensus decoder was stable over days (Fig. 3c, inset), especially for visual areas (Extended Data Fig. 3i, insets).
Fig. 3. Accounting for correlated fluctuations among task-related cells facilitates stable representations of stimulus-type.
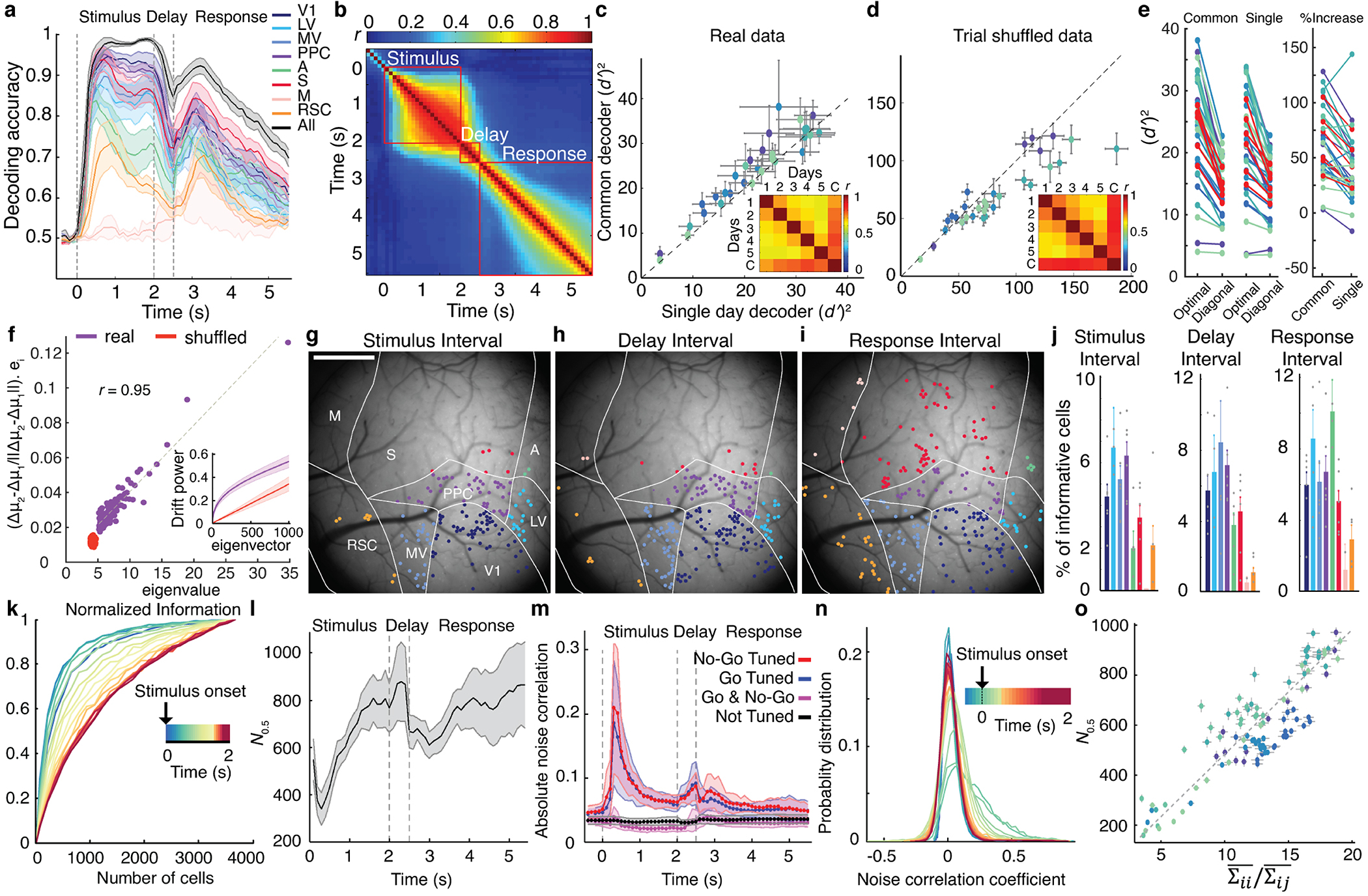
(a) Mean accuracies for inferring stimulus-identity using optimal instantaneous (100 ms time-bins) linear decoders of activity for individual (colored traces) or all brain areas (black trace) Dashed lines in a, l and m demarcate stimulus, delay and response intervals. Shading: s.e.m. across 6 mice.
(b) Mean similarities between all pairs of instantaneous decoders, assessed via correlation coefficients between pairs of decoder weights for all cells in each mouse (N=6 mice). Given the decoder constancy across stimulus presentation, in c–j we trained ‘consensus’ decoders, optimized for 0.5–2.0 s after stimulus onset. See also Extended Data Fig. 3f,h.
(c, d) To assess decoder stability, we trained ‘common’ consensus decoders on data from all days and compared them to consensus decoders trained on data from single days. We evaluated real, c, and trial-shuffled datasets, d, in which each cell’s Ca2+ traces were randomly permuted across trials of the same stimulus-type from the same day. Each blue shade in c–e denotes data from one mouse during stimulus presentation. Each datum in c,d is from one session and shows the stimulus-identity information ( )2 conveyed by common and single-day decoders given identical test datasets from individual days. On real datasets, common decoders outperformed single-day decoders, c. On trial-shuffled datasets, single-day decoders outperformed common decoders, d. Error bars: s.d. across 100 random divisions of each dataset into thirds, for dimensionality reduction, decoder training and testing. Insets: Correlation coefficients, r, between consensus decoders from individual days and the common decoder (‘C’), averaged over 6 mice. See also Extended Data Fig. 3i.
(e) Left: Optimal linear decoders outperformed diagonal decoders that ignore correlated fluctuations (68±6%, P<1.7×10−6 and 40±5%, P<2.3×10−6 mean±s.e.m. more information captured by optimal decoders of trial-type, respectively, for common and single-day decoders of activity during stimulus presentation; signed-rank test; N=30 sessions in 6 mice). Right: The superiority of optimal over diagonal decoders was greater for common than single-day decoders. Increases in ( )2 for optimal vs. diagonal decoders were 55±26% (s.e.m.) greater for common than single-day decoders; P<4.9×10−5; signed-rank test; N=30 sessions). Each connected pair of blue-shaded points shows results from one session and one mouse. Red points: mean values for individual mice.
(f) Day-to-day drifts in neural responses were aligned with within-day, trial-to-trial fluctuations. To assess day-to-day drift, we computed the unity normalized vector between the mean neural ensemble responses to each stimulus on consecutive days, (μ2–μ1)/(||μ2–μ1||). To characterize trial-to-trial fluctuations, we computed the noise covariance matrix of ensemble responses, averaged over both stimuli, for the first day of all consecutive pairs of days. We projected (μ2–μ1)/(||μ2–μ1||) onto this matrix’s eigenvectors and averaged over both stimuli and all pairs of consecutive days. Day-to-day drifts aligned with within-day, principal noise eigenvectors in real (purple points; r=0.95; P<10–50) but not trial-shuffled (red points; r=0.02; P=0.82) data. Inset: Cumulative plots of the fraction of the power of day-to-day variations lying within the subspace defined by the first n noise eigenvectors (where n is the abscissa value) for real (purple) and trial-shuffled (red) data.
(g–j) Cells contributing most to the performance of stimulus-only decoders were interspersed across cortex. Maps of these most-informative cells (with decoder weights that deviated >2 s.d. from the mean) are shown for one mouse, g–i, averaged over both response-types. Scale bars: 1 mm. j shows mean±s.e.m. (6 mice) percentages of most-informative cells in each area. Colors scheme as in a. Extended Data Fig. 4h–m show results for response-decoders.
(k) Coding redundancy peaked just after stimulus onset. For each time bin after stimulus onset (denoted in color), we measured the information conveyed about stimulus-identity by subsets of cells randomly chosen across all areas using instantaneous decoders. Plotted values are from one mouse and are averages over 100 different subsets of each size, normalized to the result for all cells. Extended Data Fig. 5b,c has results for all mice and the delay and response periods. s.e.m. values are not shown but are <8% for all points.
(l) Mean ensemble sizes, N0.5, at which ( )2 reached its half-maximum, estimated for each time bin using instantaneous decoders of activity across all imaged areas. Shading: s.e.m. across 6 mice.
(m) Traces show absolute values of mean noise correlations in Ca2+ event rates for pairs of most-informative cells (defined in g–j) both tuned to Go stimuli (blue trace), both tuned to No-Go stimuli (red trace), or oppositely tuned (magenta trace). Black trace: results for untuned cells. Shading: s.e.m. across 6 mice.
(n) Cell pairs with similar stimulus-tuning had their greatest noise correlation coefficients just after stimulus onset. Plotted are distributions of these coefficients at different times (denoted in color), pooled over 6 mice. Error bars (s.d.) are too small to be visible.
(o) N0.5 vs. the ratio of the mean of the noise covariance matrix’s diagonal elements to the mean of its non-diagonal elements, for most-informative neurons (see g–j) . Each datum is from one mouse and time-bin during stimulus presentation. Colors denote individual mice and reveal a linear relationship (r=0.9 ; P<1.4·10−25) consistent with mice having statistically similar neural connectivity matrices. Error bars: s.e.m. over 100 sub-samplings of cells (y-axis) or 51–296 cells (x-axis).
This across-day stability led us to train one decoder for each area, plus a separate one for all areas grouped together, which we termed ‘common decoders’ and optimized for the 0.5–2 s interval after stimulus onset using all correct trials from all sessions. Surprisingly, common decoders outperformed decoders optimized for single sessions; instead of yielding a suboptimal compromise between the best decoders for different days, common decoders benefited from training on multiple days’ data (Fig. 3c; Extended Data Fig. 3i). However, the existence of successful common decoders stemmed not just from greater training data, for when we trained them on equally sized datasets as single-day decoders, the two decoder-types performed equivalently (Extended Data Fig. 3l). Although, in principle, common decoders could use stimulus- or choice-related neural activity to discriminate between trial-types, in practice common decoders trained on stimulus-period data only used stimulus information (Extended Data Fig. 3j), implying their stability reflected that of stimulus representations.
To identify a basis for stability, we compared common and single-day decoders using trial-shuffled datasets, in which each cell’s responses were randomly permuted across trials of the same type from the same day (Fig. 3d). Trial-shuffling leaves individual cells’ statistical properties unchanged but eradicates correlated fluctuations between cells. Unlike for real data, common decoders trained on trial-shuffled data performed equivalently or worse than decoders optimized for single days (Fig. 3d). Further, with real datasets, accounting for noise correlations was important for extracting information optimally, as decoders ignoring noise correlations did much poorer, especially for common decoders (Fig. 3e). Altogether, accounting for correlated fluctuations was especially important for constructing decoders that were invariant across days (Extended Data Fig. 3i).
Why was accounting for noise correlations so beneficial to stable decoding performance? Strikingly, in real but not shuffled datasets, day-to-day changes in stimulus-evoked neural responses aligned to the principal eigenvectors of the noise covariance matrix describing trial-to-trial response fluctuations (Fig. 3f; Extended Data Fig. 4a). Mathematical modeling showed that this similarity between fluctuations on distinct time-scales allows common decoders to be naturally resistant to both forms of variability, instead of compromising between structures optimized for single days, and that this ‘dual robustness’ emerges even for simple feedforward networks in which activity fluctuations on different time-scales propagate through the same pathways (Appendix).
To examine how the mouse’s upcoming responses might have affected stimulus encoding, we trained ‘stimulus-only’ and ‘response-only’ consensus decoders that distinguished either the stimulus or the mouse’s upcoming response, with the other factor held fixed. For example, using trials on which mice withheld licking, we trained decoders to identify the stimulus-type. Cells making the largest contributions to stimulus- and response-only decoders were interspersed across cortex (Fig. 3g–j; Extended Data Fig. 4). Stimulus-only decoders attained high accuracy independently of the mouse’s upcoming response (P<0.7; signed-rank test; N=6 mice; Extended Data Figs. 3k,4), suggesting sensory cortex separably encodes stimulus- and choice-related signals. In accord, trial-type decoders for the stimulus period captured stimulus- not response-related information. Further, trial-to-trial variations in stimulus encoding were uncorrelated with the mouse’s responses (Extended Data Figs. 3j,6d), suggesting incorrect responses were not directly related to the quality of visual coding and instead stemmed from other factors.
Notably, response-only decoders attained significant accuracy during stimulus presentation on GO but not NO-GO trials (Extended Data Figs. 3k, 4). Thus, cortex exhibits signals related to the mouse’s decision or lick preparation on GO trials that are absent on NO-GO trials. This may reflect differences in how the brain couples a GO cue to a correct response versus a failure to suppress licking after a NO-GO cue. Prior studies have reported similar asymmetries26,27.
Modulation of visual coding redundancy
Since classic studies of motion perception5,28, neuroscientists have appreciated that neural ensembles with correlated fluctuations encode information redundantly, allowing subsets of cells to convey most of the same information as the full ensemble3,5,12–14,25. However, past work has not directly measured how the redundancy of large-scale neural coding relates to shared fluctuations, especially across brain areas.
We examined 3 inter-related facets of redundancy: resilience to a hypothetical loss of one cell; the number of cells, N0.5, needed to convey 50% of the stimulus-identity information conveyed by all cells; and levels of correlated fluctuations between cell pairs (Fig. 3k–o; Extended Data Fig. 5). Unexpectedly, correlated fluctuations and visual coding redundancy were time-varying throughout stimulus presentation. Both rose within 100 ms and crested ~200 ms after stimulus onset, at which time N0.5 had its minimum value, stimulus coding was most redundant, and correlated fluctuations peaked (Fig. 3k–n). These conditions persisted only ~300 ms; subsequently, correlated fluctuations and redundancy declined and neurons acted more independently. On average across mice, just after stimulus onset N0.5 was ~350 cells, but near stimulation offset N0.5 was ~800 cells (Fig. 3l). Within individual mice, the full range of redundancy (N0.5) variations was a factor of 3.5±0.5 (mean±s.e.m.; N=6 mice).
These changes arose from modulations in task-related neurons. Specifically, correlated fluctuations in similarly tuned stimulus-coding cells rose to a peak ~200 ms after stimulus onset (Fig. 3m). These correlation dynamics had greater amplitudes and distinct kinetics from those of single cell variability, arose within pairs of cells in the same or different areas, and could not be simply explained as due to changes in the activity rates of stimulus-coding cells (Extended Data Fig. 5e–k). Although some cells were modulated by the mouse’s upcoming response (11±3% of stimulus-coding cells; mean±s.e.m.; N=6 mice; P<0.01; permutation test), response-related modulations had slower kinetics than correlated fluctuations, and, at the neural ensemble level, were orthogonal to stimulus representations and did not affect stimulus-coding redundancy (N0.5) (Extended Data Fig. 6c,d). Throughout stimulus presentation, N0.5 varied inversely with correlated noise levels in similarly tuned cell pairs, with the same proportionality in all mice (r=0.9; P<1.4·10−25; Fig. 3o). Thus, the 3.5-fold variations in coding redundancy seen in individual mice reflected roughly comparable variations in correlated noise among task-related neurons. Since correlated fluctuations likely arise from cells’ shared inputs3,29, the invariant proportionality constant likely reflects invariant aspects of murine cortical connectivity. Overall, unlike in studies that assessed widespread noise correlations with lower time-resolution11, during passive viewing3,10,11, or without cellular resolution23, here noise correlations in task-related neurons rose in early phases of perception to more than triple the redundancy of sensory encoding.
We next examined how much of the information, ( )2, provided by our decoders was redundant across brain areas. Decoder outputs proved to be highly correlated between sensory areas; if on one trial stimulus encoding in one area was weaker or stronger than average, this was usually so in other areas (Fig. 4a–c; Extended Data Fig. 6). This interdependence and the resulting coding redundancy across areas had a similar time-dependence as the noise correlations among task-related cells. Within ~200 ms of stimulus onset, decoder score correlations peaked, yielding a ~3-fold redundancy across the brain areas examined (Fig. 4d). This was not just from replication of information within V1, since the full set of cells conveyed almost twice the information as those in V1 (Extended Data Fig. 4b), suggesting higher-order areas receive additional information from outside V1. After attaining their peak values, coding redundancy and decoder score correlations declined for the remainder of visual stimulation. Near stimulus offset, visual representations in different areas were almost mutually independent, consistent with the vanishing correlated noise levels between cell pairs (Figs. 3m,4d). Overall, time-varying co-fluctuations among task-related cells greatly impacted visual processing, leading to several-fold increases in coding resilience (Extended Data Fig. 5i), redundancy and inter-area correlations that peaked soon after stimulus onset.
Fig. 4. Inter-area fluctuations and stimulus encoding redundancy peaked ~200 ms after stimulus onset.

(a) Different sensory areas had strongly correlated decoder scores. To illustrate, for correctly performed trials we trained stimulus-type decoders using either V1 or S1 activity from 0.5–0.6 s after stimulus onset. Each datum shows the two decoder scores on one trial. See also Extended Data Fig. 6a.
(b, c) Correlation coefficients, r, for decoder scores peaked ~200 ms after stimulus onset. b shows time-varying mean±s.e.m. (6 mice) r-values between V1 and 7 other regions. c shows peak r-values across for all area pairs, averaged over mice. See also Extended Data Fig. 6b,d. Dashed lines in b,d demarcate stimulus, delay and response periods.
(d) Redundancy of stimulus encoding across cortex peaked ~200 ms after stimulus onset and then declined back toward unity. Shading: s.e.m. over 6 mice.
(e) Bottom: Raster plots of Ca2+ events in individual cells (from 8 areas in one mouse) with large contributions to inter-area co-fluctuation modes found by canonical-correlation analysis (CCA). Top: Colored traces show dynamics of the largest CCA modes between V1 and 7 other areas. V1 trace is an average over results from all 7 analyses. Cyan and gray shading respectively mark Go and No-Go stimulus presentations.
(f) Inter-area co-fluctuations comprised ~60% of the total power of cortical noise modes. Plot shows mean powers of the 10 largest CCA modes (red curve, left axis), averaged over all 28 area pairs and both areas per pair, and the mean power of the 10 largest noise modes (blue curve) found by principal component analysis (PCA) of fluctuations in each area, averaged over all 8 areas. Noise modes found by randomly shuffling weights from CCA (black curve) had far less power. Ratios of noise power in CCA and PCA modes (magenta curve, right axis) were consistently ~60%. Shading in f,g: s.e.m. over 6 mice.
(g) Distinct inter-area co-fluctuations arose during visual stimulation and inter-trial intervals (ITIs; 2-s-intervals preceding stimulus onsets). We separately applied CCA to ITIs and stimulus presentation periods. Plotted are time-varying correlation coefficients for the largest noise modes between V1 and 7 other areas (color-coded as in b,e). At stimulus onset, correlated activity rose sharply in modes found during visual stimulation, whereas activity in the ITI modes declined. See also Extended Data Fig. 8.
Communication via inter-area fluctuations
Activity co-fluctuations of cell ensembles are thought to reflect shared connectivity, such as common inputs, or direct interconnections10,30,31. In the absence of sensory stimuli, such fluctuations can reflect an animal’s spontaneous behavior11. During sensory tasks, prior studies examined shared fluctuations across pairs of electrodes32–35 and decoder score correlations across a pair of brain areas36, but the anatomic distributions and time-dependencies of neuronal co-fluctuations across multiple areas and how they relate to task performance remain unexplored10.
To identify co-fluctuating cell ensembles across pairs of areas, we applied canonical correlation analysis (CCA) to mean-subtracted neural activity traces, which represent trial-by-trial activity fluctuations. CCA identifies dimensions of shared activity and paired sets of dynamical or communication modes10 (‘CCA modes’) ranked by their levels of co-varying activity (Extended Data Figs. 7–9; Methods). During visual stimulation the number of CCA modes with significant co-fluctuations varied across different pairs of areas but generally was <20 in our datasets (Extended Data Fig. 7). Inter-area, CCA fluctuation modes comprised ~60% of the total power of all cortical fluctuations, implying a majority of fluctuation power during visual stimulation propagates across cortical regions (Fig. 4e,f).
Given the time-dependence of task-related cells’ correlated fluctuations, we compared the CCA modes arising during visual stimulation to those present just beforehand. Strikingly, by ~200 ms after stimulus onset, CCA modes present in inter-trial intervals had decayed and a new set of modes had activated (Fig. 4g; Extended Data Fig. 8). Thus, inter-area fluctuations in animals nominally at rest11,37 appear distinct from those during an active sensory task.
To characterize the spatial structure of inter-area fluctuations, for each choice of brain area as a source, we quantified the similarity of its CCA modes with each of the 7 other imaged areas. Strikingly, for every source area, the primary communication mode was nearly the same, irrespective of the target, implying there was a global mode of co-fluctuations (Fig. 5a,b). Secondary modes were more localized and shared across subsets of areas. For instance, V1 shared one secondary mode with areas A and S, and another with LV, MV and PPC (Fig. 5a–c). Thus, CCA revealed a hierarchical structure in which each area shared a global fluctuation mode with all other areas, and distinct secondary modes with different sets of areas.
Fig. 5. Orthogonal inter-area co-fluctuations communicate sensory data and the mouse’s upcoming response.
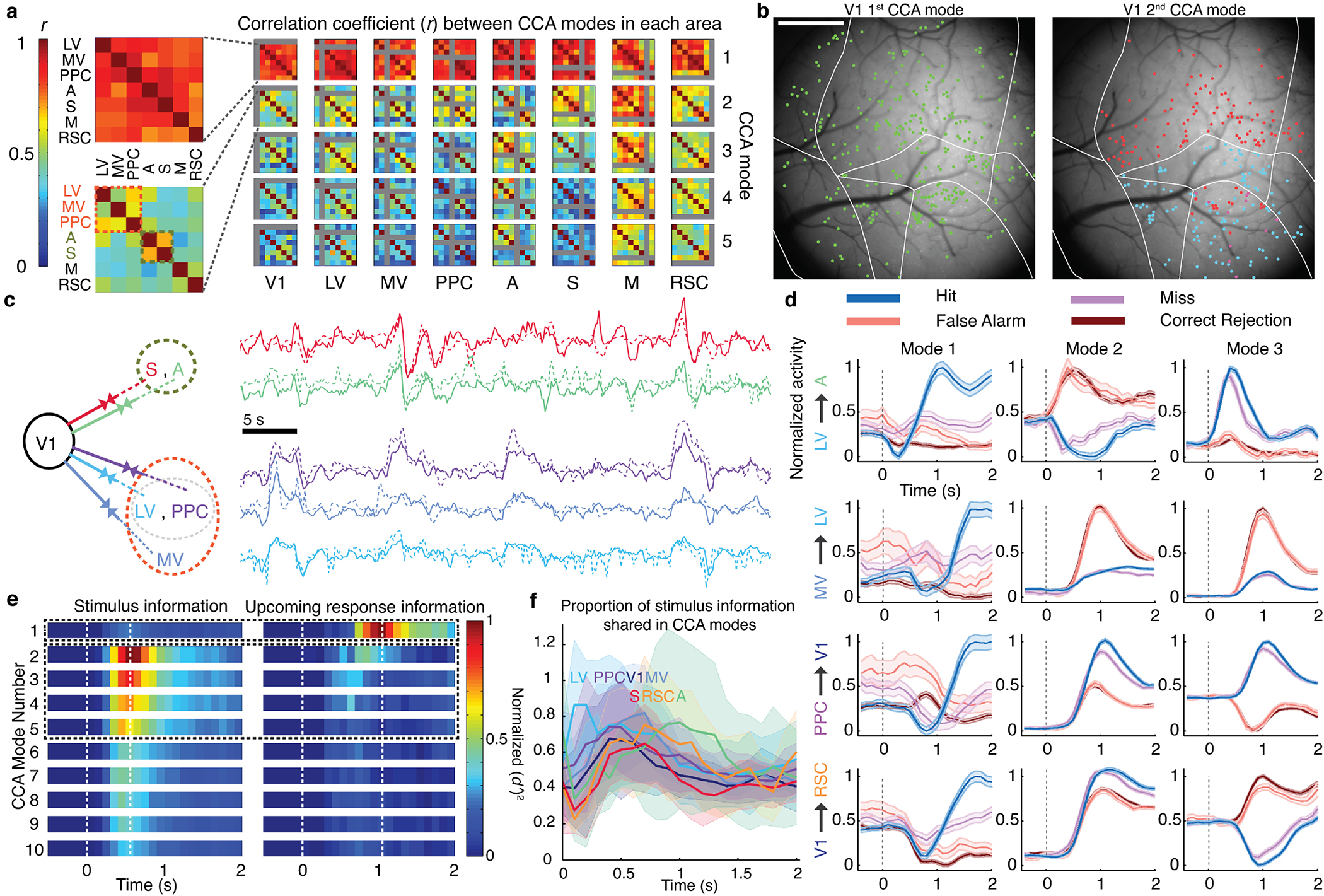
(a) Each matrix shows correlation coefficients, r, for CCA modes between one of 8 source areas (listed at bottom) and 2 target regions (arranged as in the insets). A large matrix element value indicates the source co-fluctuated with the 2 targets using a similar activity mode; small values imply distinct co-fluctuation modes. Results are shown for the 5 largest CCA modes for each source/target pair, averaged over 6 mice. The largest CCA mode (top row) was largely invariant to source/target choices and thus globally shared across areas (mean r-values of the largest modes for individual mice were 0.99, 0.95, 0.85, 0.91, 0.92, 0.68). Insets: Magnified views for the largest CCA modes involving V1 and one of 7 other areas (top), and the second-largest modes between V1 and these other areas (bottom). In 5 of 6 mice there were at least 2 clusters (orange and olive fonts) of secondary modes with moderate similarity (schematized in c). Modes involving V1 and either LV, MV or PPC comprised one cluster; modes involving V1 and either area A or S comprised another.
(b) Left, Map of neurons (green) contributing significantly (weights deviating >2 s.d. from mean values) to the global fluctuation mode in one mouse. Right, Map of neurons in the 2 clusters of second-largest CCA modes involving V1 (see a,c). Cells marked red contributed to co-fluctuations between V1 and either S or A. Cells marked cyan contributed to co-fluctuations between V1 and either LV, MV or PPC.
(c) Left, Clustering revealed 2 subsets of target areas with similar second-largest CCA modes in V1, as seen in a,b. Right, 10 example activity traces for these modes, colored to match areas at left. Solid traces: Activity within the CCA mode in V1. Dotted traces: activity in the target area’s CCA mode.
(d) Aggregate neural Ca2+ signals in one mouse within the population vector dimensions determined by the largest 3 CCA modes (columns), for 4 different area pairs (rows) and trial outcomes (colored traces). Dashed line: stimulus onset. Ordinate values are shifted and normalized to lie within [0,1]. Shading: s.e.m. (N=100–678 trials).
(e) Right, The global fluctuation mode, identified in (a), lies in the dimension encoding information late in the stimulus period about the mouse’s upcoming response. Left, The second- to fifth-largest CCA modes lie in dimensions encoding stimulus-type. Results are from a CCA analysis of V1, LV, MV, PPC, A and S in which the cell ensembles significantly encoded stimulus-type or the mouse’s upcoming response (P<0.01; permutation test across trials of different types, using equal trials of each type (52–854 trials per type per mouse). We analyzed the 15 area pairs, projected activity in each area onto the dimensions identified, and computed how accurately ( )2 this activity subset encoded the stimulus-type (on Lick and No-Lick trials) or upcoming response (on Go trials). Plots show time-varying ( )2 values, averaged over both projections for each of 15 area pairs in 6 mice, for the 10 largest CCA modes. See also Extended Data Fig. 8.
(f) To determine the proportion of stimulus information shared via CCA modes, we plotted the total information encoded in CCA modes between a source (colored traces) and the other 7 areas, relative to the total information encoded within the source. Visual areas had a preponderance of their stimulus information encoded within CCA modes, especially early during stimulus presentation; ratios for non-visual areas peaked later in the trial. Shading: s.e.m. over 6 mice. See also Extended Data Fig. 9a.
We examined whether co-fluctuation modes carried signals relating to the discrimination task (Fig. 5d,e). About 0.5 s after stimulus onset, activity in the second and higher CCA modes accurately encoded stimulus identity. Up to ~80% of the total information encoded in cortex about stimuli identity was shared between areas in these modes, which conveyed almost nothing about the mouse’s upcoming response (Fig. 5e–f; Extended Data Fig. 9a). Later, ~1 s into stimulus presentation, on GO trials the global co-fluctuation mode encoded the upcoming response but no stimulus information, consistent with our ability to decode upcoming responses on GO but not NO-GO trials. Overall, neocortex uses non-interfering communication channels, viz. orthogonal co-fluctuation modes, to convey stimulus- and response-related signals to distinct sets of areas, in a targeted and global manner, respectively.
Discussion
By tracking neurons across all visual cortical areas, our study reveals information processing mechanisms that likely underlie reliable sensory performance. Historically, neuroscientists viewed correlated neuronal fluctuations as imposing limits on coding accuracy5,12–14, which our study supports. However, our data also show that accounting for correlated fluctuations facilitates the long-term reliability of neural population activity decoders, because day-to-day variations in population coding strongly correlate with the faster coding variations occurring within individual days. This similarity across time-scales arises even in simple network models and enables decoding strategies that are intrinsically robust to both forms of variability (Appendix). Decoders that neglect correlated fluctuations lack this dual robustness.
Beginning <100 ms and reaching an apex ~200 ms after stimulus onset, task-related neurons across cortex momentarily increase their correlated fluctuations for ~300 ms. Importantly, these rapid dynamics in no way conflict with reports that variability in individual cells’ activity declines after stimulus onset38, a pattern that our data confirm (Extended Data Fig. 5e–g). Moreover, the modulation of shared fluctuations seen here in mice performing a visual task contrasts with findings in untrained mice passively viewing stimuli, during which modulations of shared fluctuations were unapparent in V13. Thus, task performance, long-term training, or both might alter the dynamics of correlated fluctuations19,39.
The stimulus-evoked increase in shared fluctuations among task-related cells boosts the redundancy of cortical representations several-fold within a ~300-ms-interval. The transient, shared fluctuation modes convey a majority (~80%) of sensory information across cortical areas within signaling streams orthogonal to that conveying the animal’s response. Here, information about the mouse’s upcoming response arose in a unique, global mode of fluctuations starting ~0.6 s and peaking ~1 s after stimulus onset. In visual tasks without a delay period, choice-related fluctuations arose sooner after stimulus onset40,41.
In our experiments, the time-interval following the redundancy peak, namely ~0.5–2 s after stimulus onset, was when our stimulus decoders attained a stable form (Fig. 3b). Our analyses of long-term decoder stability used data from this 0.5–2 s interval and showed that common decoders can succeed across days without need for daily adjustments. However, these results carry no implications regarding the long-term stability of stimulus decoders trained on time bins within the 0–0.5 s interval, during which decoder forms were changing too rapidly for us to draw conclusions about long-term stability.
The rise and decay of shared fluctuations seen here after stimulus onset may reflect successive feedforward and feedback phases of information flow across sensory cortical areas42–44. In this view, early sensory cortex uses redundant, inbound sensory data to represent a stimulus’s basic features within the first few hundred milliseconds of its appearance; during later sensory processing, likely involving feedback from higher-order areas, the representations become less redundant and more efficient. This transition, which likely occurs more quickly in primates than mice, may reflect a shift in spiking patterns from those driven initially mainly by incoming sensory signals, arriving via overlapping connections, to those reflecting a rising influence of top-down or recurrent signals propagating through distinct circuitry. This processing shift may help relate local visual features to their global context or task demands42–44.
The time-varying, anatomic patterns of shared fluctuations likely support inter-area communication within distinct sub-networks. Human neuroimaging studies describe a ‘default-mode’ network of areas, whose co-fluctuations typify the brain’s resting state7, and other sets of functionally connected areas that co-fluctuate during performance of specific tasks21. Here, inter-area co-fluctuations during a visual task differed from those during inter-trial intervals, providing cellular-level evidence of task-dependent changes in the brain’s functional connectivity. Bolstering the idea that shared fluctuations sub-serve specific components of animal behavior, information about sensory stimuli and upcoming responses were communicated to distinct groups of areas, in orthogonal fluctuation modes, and with distinct timing. Future work should quantify the extent to which fluctuation modes are task-specific or generalize across tasks with similar components.
It is striking that response-related data was transmitted within a global fluctuation mode that engaged every area examined. Past observations of widespread fluctuations came from animals with no active task to perform10,11 or in which fluctuations reflected spontaneous movements or arousal23. Notably, widespread dissemination of perceptual decisions across brain areas distinguishes some models of conscious perception45, and, when related to reward expectation, is a key element in some models of reinforcement learning46. As past reports suggest brain connectivity might resemble ‘small-world’ networks47,48, we simulated small-world networks with varying connectivity and linear dynamical fluctuations, but they all lacked a global fluctuation mode; however, networks in which a single source broadcasted common signals to multiple areas did exhibit a global mode (Extended Data Fig. 9). Future work should determine whether such a broadcast exists in the mammalian brain, and, if so, in which area or areas it originates.
Methods
Mice
The Stanford University Administrative Panel on Laboratory Animal Care approved all procedures using animals. For imaging studies of layer 2/3 neocortical pyramidal neurons in live mice, we used 4 male and 2 female triple transgenic GCaMP6f-tTA-dCre (Rasgrf2-2A-dCre; Camk2a-tTA; Ai93) developed by the Allen Institute. Mice were 10–16 weeks old at the time of surgery.
Surgical procedures
To prepare mice for in vivo imaging sessions, we performed surgeries while mice were mounted in a stereotaxic frame under isoflurane anesthesia (1.5–2% isoflurane in O2). To reduce post-operative inflammation and pain, we administered a preoperative dose of carprofen (5 mg/kg; subcutaneous injection into the mouse’s lower back), which we repeated once a day for 3 days following the surgery. We created a cranial window by removing a 5-mm-diameter skull flap (centered at AP −2.5, ML 2.7) over the right cortical area V1 and surrounding cortical tissue. We covered the exposed cortical surface with a 5-mm-diameter glass coverslip (#1 thickness, 64–0700, CS-5R, Warner Instruments) that was attached within a circular steel annulus (1 mm thick, 5 mm outer diameter, 4.5 mm inner diameter, 50415K22, McMaster) and secured to the cranium using ultraviolet-light curable cyanoacrylate glue (Loctite 4305). Using dental acrylic, we cemented a metal head plate to the skull for head-fixation during imaging. In vivo brain imaging studies commenced at least 7 days after surgery.
Retinotopic Mapping
To locate the boundaries of the visual cortical areas, we performed retinotopic mapping of the visual cortex in awake mice using wide-field Ca2+ imaging by adopting a protocol that was used previously for retinotopic mapping by intrinsic signal imaging49–52. As in all subsequent imaging experiments, we held mice atop a 11.4-mm-diameter Styrofoam ball (Plasteel Corp.) using a two-point head holder positioned under the objective lens of our custom-built epi-fluorescence macroscope (see below, Fluorescence Macroscope; Fig. 1a). The styrofoam ball floated on a thin layer of water within a plastic bowl of nearly identical diameter (Critter-Cages), as previously described53.
Mice viewed a visual stimulus comprising a drifting bar (10 deg wide) displayed on a video monitor positioned 13 cm from the left eye. The bar swept across the entire monitor in 14 s at a speed of 7 deg · s−1 and was filled internally with a contrast-reversing checkerboard pattern (0.035 deg−1 spatial frequency; 1.25 Hz temporal frequency of checkerboard reversal). The bar drifted either left, right, up or down on the monitor; each mouse viewed 100 repetitions of this stimulus for each direction of motion. The monitor remained gray for a 2-s-interval between successive stimulus repetitions49,51. Throughout the mapping session, we imaged baseline and evoked neocortical Ca2+ activity using the fluorescence macroscope.
The visual stimulus used for mapping generally evoked retinotopic neural Ca2+ activity across the visual cortex, followed by a strong decline in Ca2+ activity below baseline levels. For each direction of stimulus motion, we computed the trial-averaged video of evoked Ca2+ activity, (a three-dimensional matrix with spatial indices and , and a temporal index ), across all 100 stimulus repetitions, temporally aligned to the moment of stimulus onset. To map positions of the moving bar within the visual field to the corresponding anatomic coordinates within the visual cortical retinotopic maps, we calculated the phase of Ca2+ excitation within the i, jth pixel at each time by approximating with a factorized model of a moving wave for each stimulus direction, so as to minimize the reconstruction error:
Through this factorization we approximated the average movie using a single waveform, , with amplitude, , and phase, , at the i, j th pixel. We determined the values for the matrices, and , and the function, , by using gradient descent to minimize the squared reconstruction error, summed over all pixels and time bins. We spatially smoothed the resulting phase maps using a Gaussian low pass filter (Extended Data Fig. 1).
Based on the smoothed phase maps determined for the vertical and horizontal directions of stimulus motion, we located the boundaries between V1 and the secondary visual areas (the medial visual (MV) and lateral visual (LV) cortical areas)49. We inferred the locations of other cortical areas by aligning the Allen Brain Atlas cortical map54 to the V1 boundaries determined in each mouse. Throughout the paper, for simplicity we refer to the union of the Lateromedial (LM) and Anterolateral (AL) cortical areas as the Lateral Visual (LV), to the union of the Anteromedial (AM) and Posteromedial (PM) areas as the Medial Visual (MV) areas, and to the union of the Rostrolateral (RL) and Anterior (A) areas as Posterior Parietal Cortex (PPC). This grouping of the smaller secondary visual areas reduced to 8 the number of areas used in our subsequent analyses.
Training Procedure and behavior
We trained mice to perform the GO/NO-GO task through successive stages of training (detailed below) that allowed us to gradually increase the complexity of the task performed by the mice while also ensuring that the association between visual stimuli and rewards remained stable. All mice in this study associated a GO stimulus with a horizontal grating orientation. To prevent light from the visual stimuli from entering the fluorescence collection pathway of the microscope, the stimuli used only the blue component of the RGB color model, which was blocked by the fluorescence emission filter. We also placed a color filter (Rosco, 382 Congo Blue) on the monitor screen. The mean luminance from the stimulus at the mouse eye was approximately 5 × 1010 photons mm−2 · s−1, which is more than two orders of magnitude higher than the transition threshold to photopic vision in mice.
In the first stage, we trained water-deprived mice (target weight: 80% of initial body weight) to respond to a 100% contrast single drifting grating stimulus (2 s in duration; 2 Hz temporal frequency; 0.04 deg−1 spatial frequency; located within a 40-deg-wide circle at the center of a video monitor positioned 13 cm from the eye throughout all stages). In the first stage, mice learned that by licking a spout during presentation of the GO stimulus they would immediately receive a drop of 5% sucrose in water (~5 μL per drop). After a few days of training, mice that consistently licked only during GO trials progressed to the next stage of training.
In the second training stage, in addition to the GO stimulus, mice also viewed an orthogonal drifting grating stimulus or NO-GO stimulus. Similarly to the first stage, mice were trained to respond during the grating presentation, but we also included a grace period (1 s) at the onset of the grating stimuli that did not count towards a response. This allowed for some level of compulsive licking. After the grace period, if mice responded during NO-GO stimuli, they received two aversive stimuli: (1) a small air puff (100 ms long) delivered to one eye of the mouse (contralateral eye to the stimulus); (2) simultaneously with the delivery of the air puff, the trial aborted and an 8-s-timeout period occurred, during which the video monitor was held entirely gray at its mean luminance value. During this timeout, any additional lick(s) by the mouse resulted in the delivery of additional air puff(s). Once mice learned to perform the visual discrimination correctly on >75% of trials by licking in response to the GO stimulus and not licking in response to the NO-GO stimulus, training progressed to its next stage.
In the third training stage, we sought to create a separate response window so that rewards would not be provided at the same time as presentation of the visual stimuli. In this stage, mice learned to withhold their licks during stimulus presentation and to wait for a response period that was cued by an auditory tone (3.4 kHz; 100 ms duration). As in the second training stage, if mice licked during the visual stimulus they automatically received an air puff and a timeout (timeout duration was 3 s in the third training stage). Because this training stage was the most challenging for the mice, we gradually increased the duration of the delay period either from session to session, or in 3 sub-blocks within one session, such that each mouse eventually performed the task with a delay of 0.5 s between the stimulus period (2 s duration) and the response period (3 s duration).
On a final day of training, we decreased the contrast of the moving gratings on both the GO and NO-GO trials to between 50 and 12% to increase the proportion of error trials. Mice received only a single day of training on which the visual discrimination task was presented with this reduced level of visual contrast. By the end of training, all mice used for neural Ca2+ imaging studies performed the task with an accuracy of >75% with the low-contrast stimuli, for both GO and NO-GO trials (Extended Data Fig. 1g,h; 83 ± 3% correct trials; mean ± s.e.m.; N = 6 mice). Mice took 21–29 days of training (mean: 25 days; N = 6 mice) to reach the end of the training protocol.
Fluorescence Macroscope
To image neural Ca2+ activity across 11 mouse cortical areas, we designed and built a custom wide-field fluorescence macroscope with a field-of-view spanning 4 mm in diameter (Fig. 1a). For epi-fluorescence illumination we used a light-emitting diode (LED) (Thorlabs M470L2) with an emission spectrum centered in the 440–480 nm range. The imaging pathway comprised an objective lens (Leica, 5.0× Planapo 0.5 NA; 19 mm working distance; anti-reflection coated for 400–1000 nm light; transmission >90% at 520 nm), a tube lens (75 mm focal length; Thorlabs AC508–075-A-ML), a custom fluorescence filter cube (excitation filter: Semrock FF01–466/40–25; dichroic mirror: Semrock FF495-Di03, custom-sized to 35 mm × 50 mm; emission filter: Semrock FF02–525/40, custom-sized to 30 mm × 30 mm), and a scientific-grade CMOS camera (Hamamatsu ORCA-Flash4.0 V2 sCMOS). To control image acquisition, we used HCImage software (Hamamatsu), which communicated with the camera via an Active Silicon Firebird Camera Link Board.
To collect light from the LED, we used a 75-mm-focal length focusing lens (Thorlabs LA1680, Thorlabs) to project convergent rays of excitation light at the back aperture of the microscope objective. We aligned the focusing lens to provide approximately uniform illumination across the field-of-view (5 mm diameter), i.e. close to the regime of Kohler illumination, while also ensuring that the illumination rays were divergent as they entered the brain. The purpose of this illumination strategy was to create more intense illumination within neocortical layer 2/3 and to reduce fluorescence excitation within out-of-focus, deeper cortical layers. To improve the optical resolution at the periphery of the field-of-view, beyond the nominal ~2-mm-diameter field-of-view of the objective lens, we reduced the effective numerical aperture (NA) by placing a 10-mm-diameter iris at the back aperture of the objective lens.
We built the opto-mechanical assembly using a combination of commercially available components (Thorlabs) and custom-designed mechanical parts machined in high-strength 7075 aluminum. The entire macroscope was mounted on a manual vertical translation stage that allowed the user to conveniently adjust the image focus by moving the entire optical pathway of the macroscope while the specimen was held immobile on the vibration-isolation table upon which the macroscope was built.
Image acquisition and preprocessing
We acquired Ca2+ videos of neural activity (20 fps; 2048 × 2048 pixels) on the fluorescence macroscope using 40–160 μW/mm−2 illumination. Custom software written in Matlab (version 2013b) controlled the presentation of the visual stimuli to the mouse, ran the behavioral apparatus via a NI-USB 6008 card, and triggered the start of video capture on the fluorescence macroscope.
After video acquisition, we downsampled each video to 1024 × 1024 pixels and 10 fps. Next, we corrected videos for lateral movements of the brain by using the Turboreg software package for image alignment55. To remove scattered fluorescence and background fluorescence signals from neuropil or neural elements outside the focal plane, we applied a gaussian spatial high-pass filter (σ = 80 μm) and calculated the movie of relative fluorescence changes, , for each imaging session, where F0 is the mean activity of each pixel over the entire session and is the mean subtracted activity of each pixel at time t.
To quantify the slight lateral spatial displacements of the field-of-view between different imaging sessions, we computed the maximum projection image of each session’s , movie over its entire duration (~1 h per session). We used the Matlab ‘imregtform’ function to find the optimal ‘similarity’ transformations (translation, rotation and scaling) between the maximum projection image determined for the first imaging session and each of the other individual sessions. We aligned all Ca2+ movies to the movie from the first session using this same set of transformations. Finally, we concatenated the aligned videos from all sessions and proceeded to extract individual cells and their Ca2+ activity traces (see below; Extended Data Fig. 1).
Cell sorting
We extracted the activity of individual neurons from the concatenated movies via the successive application of principal and independent analyses (PCA/ICA)56. We divided the concatenated, preprocessed Ca2+ video from each mouse (about 1 TB in size) into 16 tiles; each tile comprised 256 × 256 pixels collectively covering about 1 mm × 1 mm in the specimen plane. We ran PCA/ICA in parallel for all 16 tiles on 16 separate computing nodes (20 cores per node; 320 total cores; about 4 TB of RAM (random access memory) for each movie) and thereby identified Ca2+ activity traces and spatial filters for individual neurons. To isolate each cell soma, we thresholded each cell’s spatial filter at 4 s.d. of its noise fluctuations (determined by fitting a gaussian distribution to the negative values of each cell’s spatial filter) and replaced all filter weights below this threshold with zeros. To attain a final set of Ca2+ activity traces, we re-applied the truncated spatial filters to the movie (Extended Data Fig. 1).
To separate the sources of Ca2+ activity that represented individual cells from those that did not, for each mouse we took 3 of the 16 image tiles and we manually identified individual neurons based on both their morphologies and the temporal waveforms of their Ca2+ transients. To identify cells located within the other 13 tiles, we trained 3 different types of binary classifiers (Support Vector Machine (SVM), Linear Generalized Model (LGM) and Neural Network) to perform the classification based on the set of manually identified cells as training data and a set of 12 pre-defined cellular features that characterized a candidate neuron’s morphology (spatial features: eccentricity; diameter; area; orientation; perimeter; and solidity) and Ca2+ activity trace (mean peak amplitude of Ca2+ transients; signal-to-noise ratio between Ca2+ transients and baseline fluctuations; number of Ca2+ transients peaks that were 3 s.d. above baseline fluctuations; number of Ca2+ transients peaks that were 1 s.d. above baseline fluctuations; the difference of the mean decay and mean rise times of the Ca2+ transients, normalized by the sum of these two values; and the FWHM of the average Ca2+ transient) to perform this classification. We used the trained classifiers to identify cells in the 13 remaining tiles based on a majority vote of the 3 classifier outputs. We manually checked that every cell determined by this algorithm indeed met our visual inspection criteria to qualify as a neuron.
Event detection and definition of active cells
Using the fluorescence activity traces for the sources identified as neurons, we created binarized Ca2+ event traces for each cell (100 ms per time bin). To do this, we first subtracted the median level of fluorescence from each trace; we then calculated the s.d. of each cell’s fluorescence fluctuations about baseline by fitting the statistical distribution of the activity trace’s negative values to a gaussian function constrained to have zero mean. To identify individual Ca2+ events, we looked for individual Ca2+ transients with peak amplitudes >4 s.d. above baseline fluctuations. The resulting binarized event traces had entries of ‘1’ between the time at which the fluorescence amplitude of a Ca2+ transient surpassed 4 s.d. and the time at which the fluorescence amplitude started its decline back to baseline levels (Extended Data Fig. 1b). Entries were ‘0’ for all other time bins. To account for slight day-to-day variations in the illumination, optical focal plane, or amplitude of fluorescence fluctuations, we performed these computations separately for each imaging session.
To determine if a cell was active during an individual imaging session, we counted the number of time bins in the session in which the cell’s fluorescence emission was >3 s.d. above baseline fluctuations. We considered the cell to be ‘active’ if this number was >2 times greater than what would be predicted based on a null hypothesis that the fluorescence variations simply reflected gaussian-distributed noise (i.e., the prediction that 0.27% of the time bins per session should have trace values >3 s.d. above baseline fluctuations), (Fig. 2a; Extended Data Fig. 1d).
Assessments of spatial alignment quality
To evaluate the quality of spatial registration between datasets from different imaging sessions, we computed the spatial cross correlation functions between corresponding image patches, (256 μm × 256 μm in size) within the maximum projection images determined from the Ca2+ videos from the first imaging session and one of the subsequent sessions. We determined the slight day-to-day shifts in each patch’s location by finding for each session the displacement value corresponding to the peak amplitude in the cross-correlation function (Extended Data Fig. 2a). By sliding the location of the 256 μm × 256 μm patch used in this computation across the field-of-view, and computing the spatial cross-correlations for each location of the patch, we constructed maps of spatial displacement across the imaging field. These displacement maps revealed that our spatial alignments were almost perfect near the center of the field-of-view (mean displacements <1 pixel), and slightly deteriorated near the corners of the field-of-view (mean displacements ≈1 pixel).
To evaluate how these small imperfections in spatial registration might have affected alignments of cells and their identities across imaging sessions, we determined the displacement of each cell across sessions by examining 256 μm × 256 μm image patches centered on each cell on each day of the experiment and then computing spatial cross-correlation functions as above. We determined each cell’s day-to-day displacements in the datasets by identifying the maxima of these cross-correlations. This analysis showed that 98.5% of cells exhibit ≤ 1 pixel displacement across days (Extended Data Fig. 2b). We calculated each cell’s mean displacement across all imaging sessions and plotted the cumulative distribution of cells’ displacements by pooling the data from all mice (Extended Data Fig. 2c). For each cell, we also measured the distance to the nearest neighboring cell and plotted the cumulative distribution of these values for all mice (Extended Data Fig. 2d). A comparison of these two cumulative distributions revealed only a small overlap (~2%) between them, indicating that slight imperfections in image alignment did not affect registrations of cells’ identities across days.
Analyses of single cell coding
To characterize the extent to which individual neurons responded differentially to the two visual stimuli, we calculated the fidelity, , with which the two stimuli could be distinguished based on a cell’s stimulus-evoked dynamics:
where and are mean values and and are variances of the cell’s evoked Ca2+ dynamics (based on the binarized Ca2+ event traces) in response to GO and NO-GO stimuli. We computed these quantities as trial-averages across either the stimulus, delay or response periods of the correctly performed trials, as specified in the figure captions. To allow evenhanded comparisons between single cell and neural population coding properties, for analyses of single cell stimulus-evoked responses we used the same time interval within the stimulus presentation period, [0.5 s, 2 s] after stimulus onset, that we used to train consensus decoders (see below). We also computed a distribution of values for a set of trial-shuffled datasets, denoted . We created the set of trial-shuffled datasets by performing 1000 random permutations of the GO and NO-GO trial labels. We determined that an individual neuron coded significantly for stimulus identity during the stimulus, delay or response periods if the cell’s value for that period was significantly greater than its values for the same interval (P < 0.01; permutation test; N = 710–1340 trials). All analyses of single cell coding, as well as those of neural ensemble coding and CCA modes were done using only those trials on which the mouse’s locomotor speed remained <1 cm · s−1 throughout the trial.
Decoding neural population activity with optimal linear Fisher decoders
To quantify the information conveyed by neural ensemble dynamics about either the visual stimulus or the mouse’s response, we used partial least squares analysis (PLS) as a supervised method for performing a dimensionality reduction, followed by optimal linear decoding in the space of reduced dimensionality, to determine , the fidelity with which the two stimuli or two responses could be distinguished based on the activity patterns of the neural ensemble. The quantity ( )2 is a discrete analog of the Fisher information conveyed by the neural ensemble about the binary classification57. Recent theoretical and computational work has shown that this approach for determining ( )2 can yield accurate estimates even in the regime in which the number of experimental trials is far less than the number of neurons3.
For all decoding studies, we started by dividing all trials performed by each mouse into two distinct subsets, one used for decoder training and the other for decoder testing, and we represented the neural ensemble activity data in each subset using a three-dimensional tensor. The tensor elements, , denoted the binarized activity of cell on trial at time bin (Extended Data Fig. 3c). To train decoders, we used two different ways to convert these tensors into two-dimensional matrices.
In the first approach, we fixed the value of in the tensor and trained a separate decoder based on the two-dimensional data matrix, , created for each time bin, . We termed these decoders ‘instantaneous decoders’, because they allowed us to study the time-dependent dynamics of neural ensemble representations (Fig. 3a,b; Extended Data Fig. 3f,g). Notably, however, the instantaneous decoders of stimulus identity were largely stationary across the interval [0.5 s, 2 s] after stimulus onset. Based on this finding, we also pursued a second decoding approach that involved what we termed a single ‘consensus decoder’, which was designed to capture the non-dynamical aspects of the neural ensemble stimulus representations across all time bins in the [0.5 s, 2 s] interval.
In this second approach involving the consensus decoder, we took all 15 time bins of 100 ms each within the [0.5 s, 2 s] interval and concatenated the data from these time bins along the trial index dimension, yielding a two-dimensional data matrix, . This matrix contained the data from the same number of cells as used for instantaneous decoding, but the effective number of trials was 15 times larger (Fig. 3c–j; Extended Data Fig. 3g). We used these matrices to train the consensus decoders of either stimulus identity or the mouse’s response.
An important consideration when training optimal linear Fisher decoders of either the instantaneous or consensus type was the fact that Fisher decoders require an estimate of the inverse of the noise covariance matrix of the neural ensemble activity patterns. When the number of recorded neurons surpasses the number of experimental trials, one cannot accurately estimate the individual elements of the noise covariance matrix. However, the principal eigenmodes and eigenvalues of this matrix can be determined accurately with a much smaller number of trials than neurons, which in turn enables accurate decoding and estimation of ( )2 values3.
To achieve these estimates, as in our prior work we first used PLS analysis to perform a supervised linear dimensionality reduction3 by identifying dimensions of the neural population activity in which the amplitude is correlated with the outcome of the binary classification task58,59. The decoding strategy involved retaining a moderate number of these activity dimensions—while discarding the others—and then computing the optimal linear Fisher decoder and its associated value in this space of reduced dimensionality.
To train the optimal linear Fisher decoder for one of the binary classifications (i.e. of either the stimulus identity or the mouse’s response) we split the two-dimensional data matrix, , as determined above, into two subsets, and , corresponding to the pair of conditions to be decoded. Specifically, the conditions and referred either to the two different visual stimuli or the two different possible responses by the mouse. Each row of the matrices and represented the neural activity data on a trial of type or , and each column represented the activity data from an individual neuron across all trials of this type. We randomly sub-sampled (with no replacement) the rows of and to create three distinct equally-sized smaller data matrices, denoted and , which we respectively used for dimensionality reduction, decoder training and decoder testing, such that all the data from any given trial was only used in one of these three matrices. Specifically, we used to find the set of PLS basis vectors, which comprised the columns of a coordinate transformation matrix, . We transformed the training and testing datasets into the coordinate system defined by these PLS basis vectors:
We systematically varied from 1–50 the number of PLS dimensions retained for the decoding analysis; the symbol indicates the vector space of reduced dimensionality. To determine the number of retained dimensions that yielded the highest decoding performance, we evaluated and optimized decoder performances through a cross-validation procedure (Extended Data Fig. 3c). Specifically, in the space of reduced dimensionality, we computed the optimal linear Fisher decoder, , from the training datasets, using the formula
| (1) |
where is the average noise covariance matrix and is the vector difference between the trial-averaged responses under conditions and is also termed the ‘diagonal decoder’, namely a linear decoder that accounts for the mean responses under conditions and but not the covariances in these responses. We determined the binary decision boundary for the optimal linear decoder as the hyperplane normal to that bisected . To attain a decoder output or ‘score’ for an individual trial in the experiment, we projected the neural population dynamics from that trial onto and then subtracted where is the mean of and , so the decoder score would have zero mean when averaged across a set of trials with equal numbers of and trials. We determined the binary classification using the sign of the score. Using the testing dataset, we estimated the discriminability of the two trial types, :
| (2) |
We repeated this process 100 times using 100 different random sub-samplings of the trials for the construction of the dimensionality reduction dataset, the training dataset and the testing dataset.
To examine the extent to which visual stimulus encoding remained stationary over the course of the experiment, we trained an optimal ‘common decoder’ on the data recorded across all imaging sessions. To create the common decoder, we pooled all the data from each mouse and divided this aggregate set of data as described above into three subsets, to be used for dimensionality reduction, decoder training and decoder testing. Given this division and using the procedures described above, we trained a consensus decoder for the interval [0.5 s, 2 s] after stimulus onset, yielding an across-day common decoder. We additionally assessed the values of ( )2 for this common decoder on the testing datasets from the individual imaging sessions. This analysis revealed that the performance of the common decoder generally slightly surpassed that of decoders trained and tested on data exclusively from one imaging session (Fig. 3c; Extended Data Fig. 3i).
Analysis of error trials to distinguish neural coding of visual stimuli and mouse responses.
On trials on which mice performed the GO/NO-GO task correctly, the visual stimulus and the mouse’s response are perfectly correlated, precluding determinations of whether neural activity during the stimulus presentation is primarily evoked by the stimulus or also influenced by the mouse’s visual decision or information processing related to its upcoming response. To address this issue, we analyzed error trials and trained decoders of neural ensemble activity that were sensitive to only the stimulus or only the animal’s decision, while keeping the other factor fixed.
For example, on GO trials the mouse could either lick (Hit) or not lick (Miss) (Fig. 1b). By training a ‘response decoder’ to discriminate between Hit and Miss trials based on the neural activity during the stimulus presentation period, we estimated the encoded information about the mouse’s upcoming response while it observed the GO stimulus. Because Hit trials were far more common than Miss trials, we randomly subsampled the set of Hit trials to construct unbiased datasets with equal numbers of Miss and Hit trials. Using these datasets, we trained consensus common decoders of neural population activity following the procedures discussed in the prior section above, as there were insufficient numbers of incorrectly performed trials to accurately train instantaneous decoders. Analyses of the visual stimulus period were based on the same interval, [0.5 s, 2 s] after stimulus onset, as that used to construct trial-type decoders. Because the timing of the mouse’s responses differed from trial-to-trial and across trial-types, we sought to retain sensitivity to the time-dependence of coding by evaluating the response decoders’ ( )2 values across the individual time bins of the trial structure. To construct the plots of Extended Data Fig. 3k,4b–g, we identified the time bin of each trial with the maximum ( )2 value and used that ( )2 value when tabulating the results across trials and mice. Our decoding results revealed distinct patterns of neural activity during GO stimulus presentations that were predictive of the mouse’s upcoming response. We also executed an identical decoding analysis using equally sized datasets constructed from the neural activity recorded on NO-GO trials (i.e., Correct Rejection and False Alarm trials). However, in this case we did not find neural activity patterns during stimulus presentation that predicted the mouse’s response (Extended Data Fig. 3k, 4e). Because the response decoders trained on GO and NO-GO trials were constructed using equally sized datasets, the differences in their performances cannot be readily explained as due to a discrepancy in statistical power.
To determine if visual stimulus coding during stimulus presentation might have been affected by the mouse’s upcoming response, we trained and evaluated separate common consensus stimulus decoders for Lick trials (False Alarm and Hit) and No-Lick trials (Correct Rejection and Miss), using the same methods as for response decoders and with equally sized datasets that were constructed via sub-sampling. This analysis yielded no evidence that the quality of stimulus representations was impacted by the mouse’s upcoming response (Extended Data Figs. 3k,4b).
Calculations of information redundancy across cortical areas
To assess the extent to which Fisher information about the stimulus was represented independently across different cortical areas, we examined inter-area correlations in the output scores of the instantaneous neural activity decoders (see above). We quantified these correlations separately for the two types of correctly performed trials and then averaged the resulting correlation coefficients.
The results revealed that fluctuations in neural ensemble activity along the stimulus coding direction were strongly correlated between the different sensory areas just after stimulus onset and then progressively decayed (Fig. 4a–c; Extended Data Fig. 6). If information were represented independently in the different cortical areas, the sum of the information encoded in each of the individual brain areas would equal that encoded in the aggregate of all the brain areas25. Positive correlations in the decoder scores from different brain areas can reflect redundancy (Fig. 4d) such that this equality is not met and there are shared copies of the same information25:
| (3) |
Determination of noise correlations among neuron pairs
To measure noise correlations between pairs of similarly tuned neurons, we trained instantaneous population decoders of the stimulus based on the neural activity recorded in each mouse on all trials performed correctly (see above). We selected cells that significantly contributed to each decoder by identifying those cells with decoder weights that deviated >2 s.d. from the mean value across the entire set of cells considered (Fig. 3g–j). We divided the resulting set of cells into 2 groups, based on the sign of the individual cells’ mean-subtracted decoder weights as an indicator of similarity in the cells’ tuning to the visual stimulus. We then computed the noise correlation coefficients characterizing the joint activity fluctuations of pairs of cells around their mean responses. We averaged the values of these coefficients over the two types of correctly performed trials. The time dependence of these correlations closely resembled that of the noise correlations in decoder scores across brain areas (see above).
In our analysis, we did not find substantial noise correlations between cells with dissimilar stimulus tuning or between cells without stimulus tuning. This is in accord with our past findings in untrained mice viewing moving grating stimuli that differed by 60 deg in orientation3, but here, with trained mice actively performing a task involving an orthogonal pair of moving grating stimuli, the differences between the distributions of noise correlation coefficients between cell pairs with similar and dissimilar stimulus tuning were more substantial (Fig. 3m)43,60.
To estimate the time-dependent mean variability, , of individual neuronal responses in each mouse, we computed the variance in the activity level of each cell at time, , relative to stimulus onset, across the set of all correctly performed GO and NO-GO trials. We averaged the results across all cells and both trial types. To compute the time-dependent Fano factor across the set of all neurons (Extended Data Fig. 5e), we divided by , the cells’ mean response at time , averaged over all cells and correctly performed trials. Both and the Fano factor declined after stimulus onset, consistent with previous studies (Extended Data Fig. 5e)38.
Determinations of information saturation in large neural ensembles
Prior theoretical and recent experimental work has shown that the Fisher information encoded in the dynamics of a cortical neural ensemble saturates at large ensemble sizes, due to the existence of eigenvectors of the noise covariance matrix with eigenvalues that grow linearly in the limit of large ensemble size (Extended Data Fig. 5a)3,5,14,25. To characterize this information saturation at each time bin after stimulus onset, we trained instantaneous decoders of the visual stimulus based on the activity of a subset of the neurons recorded in each brain area. We systematically varied the size of this subset and measured the encoded information using the decoder ( )2 values for each ensemble size, as averaged over 100 random selections of neurons for each time bin during which the entire cell population significantly encoded information about the stimulus (P < 0.01; permutation test; N = 710–1340 trials). We normalized the ( )2 values from each time bin to the total information encoded by all neurons during this same time bin.
In accord with recent studies of V13,25, in all the cortical areas examined here the information encoded by a cell ensemble saturated at large ensemble sizes (Extended Data Fig. 5a). Further, just after stimulus onset this saturation occurred at much smaller neural ensembles as compared to later on in the trial. As stimulus presentation proceeded, the functional dependence of ( )2 on ensemble size became more similar to the form observed in trial-shuffled datasets (Fig. 3k; Extended Data Fig. 5b,c).
To estimate the sensitivity of the ensemble neural code to the hypothetical loss of one neuron, we determined the number of neurons whose loss would result in a 10% decrement in the total information encoded by the cell population. We re-scaled the result to express the information loss per cell removed (Extended Data Fig 5h).
Determinations of the similarity between pairs of vector subspaces
To assess the similarity between two -dimensional subspaces (Extended Data Figs. 3e, 5j), we first calculated the matrix , where and are matrices whose orthonormal columns form a basis for each subspace. We then performed a singular value decomposition of and determined the subspace similarity as the mean of the singular values. This calculation yields zero for orthogonal subspaces and one for identical subspaces. Since each singular value is the cosine of a canonical angle between the two subspaces, this measure is equivalent to the mean of the cosines of the canonical angles.
Assessments of how day-to-day drifts in neural encoding relate to trial-to-trial activity fluctuations.
To assess how the day-to-day variations in stimulus-evoked neural responses related to the trial-to-trial variations in these responses within individual imaging sessions, we first rescaled each neuron’s activity trace to have zero mean and unit variance on each day of the experiment. Using these traces, we calculated the noise covariance matrix of the stimulus-evoked neural responses on each day, and we averaged these matrices across the two trial-types. To identify the principle directions of the trial-to-trial activity fluctuations on each day, we performed an eigenvector decomposition of each of the averaged covariance matrices.
To examine how the day-to-day variations in the neural representations related to the trial-to-trial activity fluctuations, we projected the changes between successive days in the mean neural ensemble response on each trial-type onto the eigenvectors of the noise covariance matrix for the first day in each pair of consecutive days. (We obtained similar results if we alternatively chose the eigenvectors from the second day of each pair). We averaged the results over both stimuli and all pairs of consecutive days. As control, we performed the same analysis with trial-shuffled datasets, in which the noise covariance matrix was rendered isotropic by permuting the activity traces of each cell across trials of the same stimulus-type. The results showed that day-to-day drifts in the neural ensemble representations of the stimuli were significantly aligned with the principal directions of the trial-to-trial variations within individual days (Fig. 3f, Extended Data Fig. 4a). We obtained similar results when we projected the day-to-day changes in the visual stimulus tuning curve onto the eigenvectors of the within-day, noise covariance matrix. Please see the Mathematical appendix for a theoretical explanation for how this observation can enable optimal decoders to be robust across days, and also for an explanation of how this alignment between within-day fluctuations and across-day changes in mean neural ensemble responses can arise mechanistically in a simple network model without any fine-tuning.
Effects of correlated noise in a two-layer feedforward network model of visual cortex
To examine how redundant information coding across different neural ensembles is related to correlated fluctuations in activity that reflect neuronal connectivity patterns, we analyzed a two-layer feedforward network model, also discussed in Ref. (3). This network comprises an input layer of ‘sensory neurons’ and an output layer of ‘cortical neurons’, whose activity levels are respectively denoted by the vectors r and s and related by the expression
Here and are zero-mean gaussian-distributed additive noise vectors that represent the stochastic components of the input and output activity levels, denotes the connection matrix between the two layers, and is a non-linear transfer function relating the net input and output levels of activity. We approximate the response to a specific stimulus via a Taylor expansion:
where the prime symbol denotes the first-derivative. Since both and have zero means, the mean output response to this specific stimulus is where is the mean activity evoked in the sensory layer by stimulus . Under these assumptions, the noise covariance matrix between neurons in the cortical layer is:
where is a diagonal matrix whose elements denote the linear gain of each neuron around stimulus , as determined from the function . If all neurons operate at similar gains (assumed to be 1 here for simplicity), and if the noise terms and are uncorrelated between neurons, independent of the stimulus, and have variances, and , that are uniform for all cells in each layer, then:
| (4) |
where is the identity matrix. To compute the value for distinguishing between two distinct stimuli using an optimal linear decoder of activity in the output layer, the application of equation (1) above leads to:
| (5) |
Our prior analysis of this model3 shows that if we replace in equation (5) by its singular value decomposition (SVD), the minimum number of neurons, , needed on average to extract of the encoded information along each left-singular vector, , of is determined by:
| (6) |
where is the square of the th largest singular value of , divided by the total number of cortical neurons. From (4) we can also estimate the average value of the diagonal and non-diagonal elements of the noise covariance matrix:
| (7) |
| (8) |
where is a mean amplification factor, averaged over the singular vectors of (where is the number of cells in the output layer) and is the mean similarity between the receptive fields of cells in the output layer. Dividing (7) by (8) yields:
| (9) |
Finally, substituting (9) into (6) yields:
| (10) |
Equation (10) shows how the number of cells in the output layer needed to extract half-maximal information is related to the basic structure of the connectivity matrix, .
Empirical analyses of redundancy and noise covariance in cortical ensembles
To study whether equation (10) held empirically in our datasets, we computed the ratio, , from our recordings of cortical neurons and studied its relationship to . In equation (10), is related to an individual eigenvector of the connectivity matrix, . The value of for an entire neural ensemble will be primarily determined by those eigenvectors of the connectivity matrix that make significant contributions to stimulus coding. Since we do not have direct access to , the connectivity matrix of the mammalian brain, to test equation (10) we estimated the noise properties of neurons that contributed significantly to stimulus coding.
To estimate we computed the noise covariance for each stimulus separately and then averaged the results for both stimuli (GO and NO-GO). We estimated during the stimulus interval separately for each time bin (Fig. 3l; see above for detailed methods). In our experiment, the values and noise correlation coefficients varied over time during the stimulus presentation period. Equation (10) suggests that this time-dependence should be constrained such that there is a linear relationship between and at all time points. To test this, for each time bin we plotted the empirically determined values of (Fig. 3l) against the ratio, , computed across the set of all cells that significantly encoded the stimulus type (see above for how we identified these neurons). The results were strikingly consistent with the linear relationship predicted by equation (10) (Fig. 3o). The slope of the linear relationship was similar for all mice in the experiment, which presumably reflects conserved properties of the anatomical neural connectivity within the murine visual pathways, such as the degree of overlap in nearby cells’ receptive fields and the amplification factors across different stages of visual processing.
Analysis of canonical noise correlations
To examine the structure of correlated activity fluctuations across different cortical areas and their relationships to the representation of information, we used canonical correlation analysis (CCA)61 to study the co-variations of activity fluctuations within pairs of brain areas. For each trial type, we computed the trial-by-trial fluctuations in stimulus-evoked activity by subtracting from each fluorescence Ca2+ trace the mean Ca2+ activity trace, averaged over all trials. We concatenated the traces representing these fluctuations across trials that the mouse performed correctly. For a given pair of brain areas, we represented the dynamics in the two areas with matrices, and . These matrices were and in size, where was the total number of time points after the concatenation, and and were the numbers of cells detected in each brain area. We standardized these zero-mean matrices of fluctuations and by scaling each matrix column to have unit variance.
Following the standard approach in CCA, we identified two sets of loading vectors, and , termed here as CCA modes, each of which was an activity mode within one of the two neural ensembles (i.e. with and elements, respectively). The index denoted the individual modes, which we determined such that the projections of the neural activity fluctuations, and , onto and , were maximally correlated between the two ensembles,
| (11) |
subject to the normalization constraint, . Given this normalization condition, the quantity equals the correlation coefficient of the activity modes, and , in the two different brain areas. After finding the first CCA mode , we identified successive modes in an iterative manner. Specifically, for all previously identified CCA modes we removed the CCA fluctuations, and , respectively, from and . We applied equation (11) to the residuals and thereby identified a set of orthonormal fluctuation modes with correlation coefficient values that progressively declined with the index, . To identify the maxima specified by (11), we first randomly initialized the vectors and while constraining them to have unity length. We then found values of and that maximized the objective function in (11) by performing an alternating optimization62.
To create training and validation datasets, we randomly divided the full datasets into two subsets with equal numbers of trials, with all the data from each trial used only in one of the two subsets. We used the first subset to find the top 20 CCA modes for all pairs of cortical areas. We used the second subset of trials to determine the inter-area correlation coefficients of the fluctuations in each of the CCA modes; this revealed significant correlated fluctuations in the test dataset with no signs of overfitting (Extended Data Fig. 7d). We also performed a CCA of trialshuffled datasets. By comparing the correlation coefficients for CCA fluctuations in the real data with those observed across 100 different trial-shuffled datasets, we determined that the correlation coefficients in the real data were significantly larger than expected by chance (P < 0.01; permutation test; N = 710–1340 trials; 525 cells per brain area on average, range: 31–2297 cells; Extended Data Fig. 7a).
We also measured the amplitude of canonical correlations separately for GO and NO-GO trials and found out that, on average, the correlation coefficients had similar values for the two stimulus types (Extended Data Fig. 7d). Thus, for most of our analysis, to simplify visualization of the data we combined the sets of mean-subtracted activity traces for the two stimuli and identified a single set of CCA modes between each pair of brain areas, independent of the stimulus type.
As a control analysis to ensure that the inter-area activity fluctuations we had identified had not artifactually arisen from slight errors in determining the boundaries between brain areas, we performed CCA analysis on a control dataset in which we excluded all cells located <60 μm to the other brain area under consideration. These exclusions did not notably modify the amplitudes of correlated fluctuations or other aspects of our findings (Extended Data Fig. 7e).
To assess how the CCA correlation coefficients varied as a function of time relative to stimulus onset, for each pair of brain areas we projected the neural activity at different time bins onto the CCA modes and computed the correlation coefficient using the validation dataset; this yielded different values of the correlation coefficients for each time bin (Extended Data Fig. 8a). Across most of the visual stimulation period, the CCA fluctuations exhibited significantly greater correlation coefficients in the real than in trial-shuffled datasets (P <0.01, permutation test, N = 710–1340 trials 525 cells per brain area on average, range: 31–2297 cells).
To examine how the brain’s fluctuations modes might change at the onset of visual stimulation, we first used CCA to identify a distinct set of CCA modes of the neural ensemble dynamics during inter-trial intervals (ITI), within the period [−2 s, 0 s] relative to stimulus onset. We then compared these CCA modes to those found within the visual stimulus period, [0 s, 2 s]. To do this, once we had identified CCA modes during visual stimulus presentation using training datasets, we extended the temporal range of the validation datasets to include the [−0.5 s, 0 s] interval. Conversely, once we had identified CCA modes during the ITIs, we extended the temporal range of the validation datasets to include the [0 s, 0.5 s] interval. We found that the correlation coefficient values of the ITI CCA modes declined upon stimulus presentation, whereas those for the stimulus period CCA modes sharply increased shortly after stimulus onset (Extended Data Fig. 8a). For each CCA mode index, i, we also compared the directions of the mode vectors within the neural population activity vector space for the two different sets of CCA results, by determining the cosines of the angles between the i’th CCA mode vectors from before versus after visual stimulus onset (Extended Data Fig. 8b).
For comparison, we trained CCA modes using the data from the entire [−2 s, 2 s] interval, subsampled so that the training datasets were equally sized to those used to train the ITI and stimulus CCA modes from the [−2 s, 0 s] and [0 s, 2 s] intervals, respectively. At stimulus onset, many of these CCA modes exhibited either a rise or a decline in their canonical correlation coefficients, consistent with the results obtained when we trained CCA modes separately for the [−2 s, 0 s] and [0 s, 2 s] intervals. However, the values of the canonical correlation coefficients for the modes trained for the [−2 s, 2 s] interval were generally less than those of the CCA modes trained separately for the stimulus presentation and ITI presentations, suggesting that the implicit assumption in CCA of statistical stationarity does not hold at stimulus onset and that there is a bona fide transition in the noise correlation structure of cortical activity at stimulus onset.
Simulations of multi-area neural fluctuations
To study how neural connectivity can give rise to CCA modes that share information between brain areas, we modeled the linear network schematized in Extended Data Fig. 9f with Nc = 500 cells in each of one ‘early visual area’ and three ‘cortical areas’ (termed and ). Neural activity in the early visual area, , were set by
where and were 500-dimensional unit vectors (with fixed values in each simulation) representing input patterns of neural ensemble activity encoding the stimulus and the mouse’s response, respectively, and and were binary variables with values of either −1 or 1 that represented the two stimulus and response conditions. was a linear low-rank projection matrix from the space of the decision variable to that of the neural activity levels; we systematically varied the rank, , of this matrix from 1–10 across multiple runs of the simulation. Specifically, was the outer product of two matrices in which all the elements were randomly and independently chosen from a zero-mean unit variance gaussian distribution, and each column of these two matrices was normalized to have an L2-norm of 1. was an additive noise vector in which the individual elements were independently drawn from identical zero-mean gaussian distributions with variance . The neural dynamics in areas and differed in that, instead of directly receiving stimulus information, they received it indirectly via a low-rank linear projection from area . For example, activity levels in area were set by
where and are linear low-rank projection matrices; analogous equations governed the dynamics for areas and . As with , the elements of the additive noise terms, and were independently drawn from identical zero-mean gaussian distributions with variance . We systematically varied the ranks of the matrices and to have values between ; for each of the 10 different values of , we repeated the simulations 25 times with different sets of randomly chosen matrix elements and different randomly chosen values for and . We simulated each of the 250 models for 20,000 trials; on each trial, we chose the stimulus and decision variables, and , randomly and independently of each other. We used the methods described above to find the CCA modes of each model (Extended Data Fig. 9g–i).
Simulations of small-world networks
As shown in Extended Data Fig. 9f,g, global transmission of a common decision signal to multiple cortical areas can produce a global CCA mode that is shared among all pairs of cortical areas, similar to what we found in the real neural recordings. To explore whether a global CCA mode can also arise in the absence of a globally transmitted signal, we modeled networks with 11 brain areas that were interconnected according to a small-world connectivity rule63, with unidirectional connections30,64,65 (Extended Data Fig. 9b).
We simulated 30 different networks with varying degrees of interconnectivity and varying levels of randomness and regularity in the pattern of connections. For each network, we set the graph of connections by arranging the 11 brain areas in a ring formation. We then created unidirectional projections to each brain area from its nearest neighbors on the ring (i.e., from neighboring areas on both sides of each brain area). To introduce randomness into the connectivity pattern, the brain areas sending each of these unidirectional projections were then randomly re-assigned with probability, , to a different brain area that was randomly selected with uniform probability from among those areas that had originally lacked such a projection.
Within each area there were 500 neurons, whose activity levels were a linear function of the neural activity in the brain areas from which they received inputs:
Here is a vector of 500 elements that represent the activity of the 500 cells in the ‘th brain area at time is an additive noise term for the th area, in which the individual elements at time were independently drawn from identical zero-mean gaussian distributions with a variance of is a 500 -rank projection matrix from area to area , in which all the elements were chosen randomly and independently from a zero-mean unit variance gaussian distribution; all the columns of were normalized to have an L2 norm of if and only if there was an edge from node to node in the small-world graph; otherwise . The parameters and were gain factors; their relative amplitudes determined the degree of coupling between areas.
In general, , because increasing the value of too close to 1 can cause the whole network to enter a global oscillation mode with a period of 2 cycles. With further increases of 1, the network becomes unstable. Therefore, we selected so as to provide strong coupling between brain areas while avoiding the fast global oscillatory mode. We simulated this linear system for all possible combinations of and . To reproduce CCA modes with similar correlation coefficients to those we had observed in the real cortical recordings, we set and . For each set of and values, we initialized the neural activity levels, , in the model with zero-mean gaussian noise with variance and ran the simulation for 50,000 time points. To avoid effects arising from initial transients, we omitted from all analyses the data from the first 500 time steps.
Data and statistical analyses
We performed all data and statistical analyses using MATLAB (version R2019a; Mathworks). All statistical tests were two-sided, except for permutation tests, which were one-sided. All signed-rank tests were Wilcoxon signed-rank tests.
Computational simulations
We performed all simulations using MATLAB (version R2019a; Mathworks).
Extended Data
Extended Data Fig. 1. Long-term imaging and computational analysis of neural Ca2+ dynamics across multiple cortical areas during a visual discrimination task.
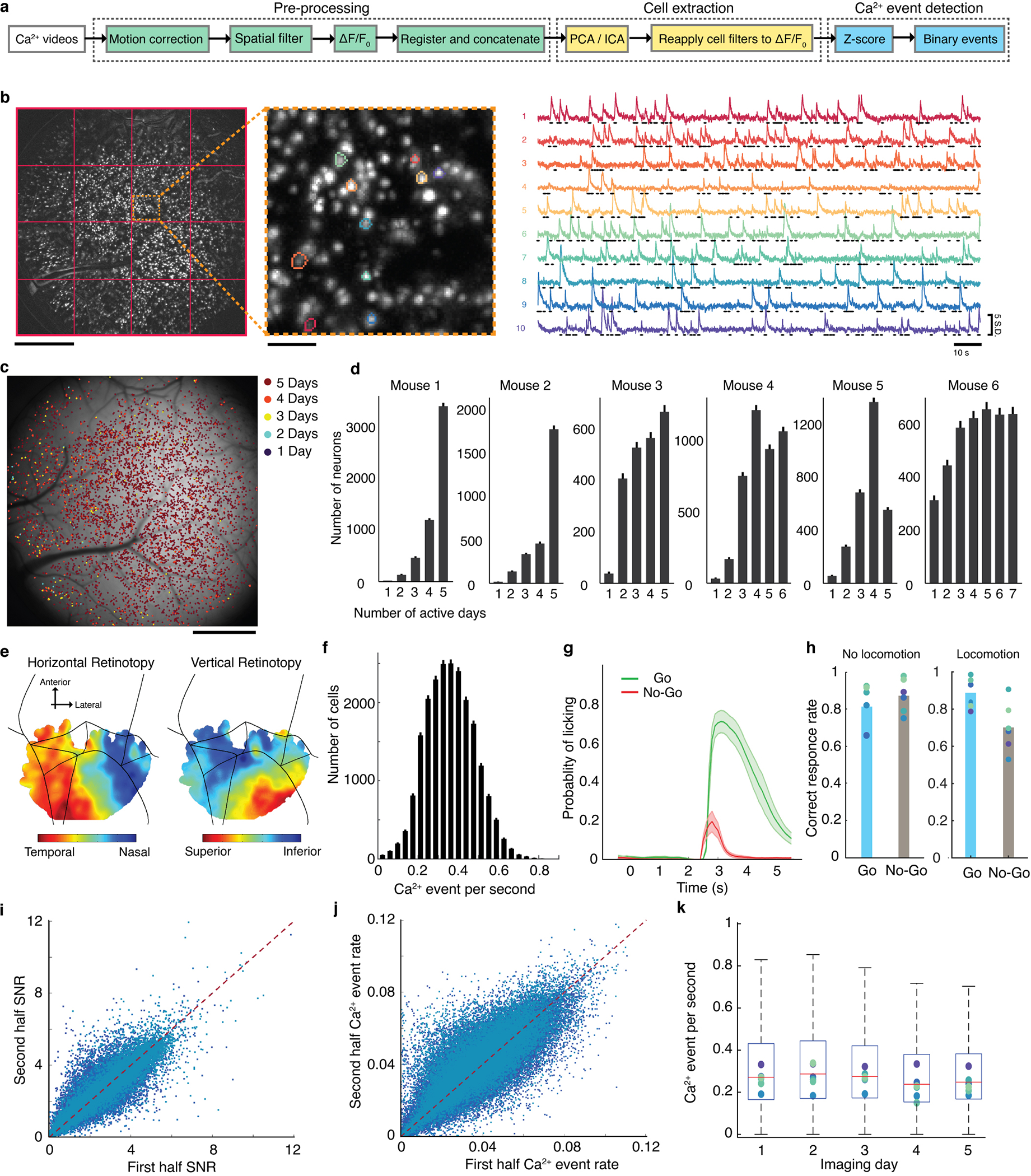
(a) Schematic of the algorithmic pipeline used for video preprocessing and cell extraction, as implemented using cluster computing.
Pre-processing (steps shown in green): For each movie of Ca2+ activity, we performed an image registration across all frames of the movie to correct for small displacements of the brain. We removed background noise and neuropil Ca2+ activity by applying a spatial Gaussian high-pass filter , and computed a movie of the relative changes in fluorescence . We then aligned and concatenated all the ) movies for each individual mouse, across all imaging sessions.
Cell extraction (steps shown in yellow): We divided each concatenated movie into 16 spatial tiles and then extracted individual cells within each tile by successively applying principal components and independent components analyses (PCA/ICA algorithm) to all tiles in parallel using the Stanford Sherlock computing cluster (using up to 320 cores and ~2 TB of memory for each concatenated movie).
Ca2+ event detection (steps shown in cyan): We converted the ) traces for each neuron to traces expressing the time-dependent fluorescence changes as a z-score, , relative to the s.d. of the baseline fluctuations in each cell’s fluorescence trace (computed separately for each imaging session). We detected Ca2+ events by identifying Ca2+ transients that attained a peak fluorescence value of s.d., and we assigned the cell as being ‘active’ within the interval between the initial threshold crossing and the time at which the Ca2+ event attained its peak fluorescence (Methods).
(b) Left: A maximum projection image over an entire concatenated set of Ca2+ movies from an example mouse. Red lines mark the 4 × 4 set of tiles that we processed in parallel during cell extraction. Scale bar: 1 mm. Middle: Magnified view of the area enclosed in orange in the left panel. Scale bar: 0.1 mm. Right: Z-scored traces (colored traces) of fluorescence Ca2+ activity for 10 example neurons in the middle panel marked with color-corresponding boundaries. Raster traces show the binarized patterns of activity for each cell.
(c) Most detected cells were active in all recording sessions, as illustrated via a map, computed for one example mouse, in which each detected cell is marked with a color-code indicating the number of days in which it was detected as active (Methods).
(d) Histograms of the number of days that each cell was detected as active for 6 different mice. Error bars are s.d. estimated as counting errors.
(e) Vertical and horizontal retinotopic maps of visual cortex in an example mouse (Methods). After identifying borders of area V1 determined by retinotopic mapping studies in each mouse, we aligned these borders with those in the Allen Brain Observatory map of the mouse cortex and thereby inferred the locations of other brain areas.
(f) Histogram of the mean Ca2+ event rate for each of 21,570 cortical neurons (N = 6 mice). Error bars are s.d. estimated as counting errors.
(g) Mean probability of licking over the time course of a trial, averaged over all trials and trained mice, for Go (green) and No-Go (red) trials. Shaded areas denote s.e.m. over N = 6 mice. After mice learned to discriminate between Go and No-Go visual stimuli, we trained them to withhold licking behavior during the stimulus presentation, [0 s, 2 s], and delay, [2 s, 2.5 s], intervals and to respond only during the response interval, [2.5 s, 5.5 s] (Fig. 1; Methods). Trained mice occasionally licked before the response interval; we discarded these trials from our analyses to allow inferences regarding stimulus encoding, decision-making, and motor preparation in the absence of overt licking responses.
(h) The mean behavioral performance of all mice on Go (cyan) and No-Go (gray) trials in which the mouse did (right) or did not exhibit locomotor behavior (left) (Methods). Individual data points denote values from individual mice.
(i, j) For every individual cell (blue data points), the plots show the mean signal-to-noise ratio (SNR) of Ca2+ activity, i, or the mean rate of Ca2+ transient events, j, in the first half of each imaging session versus that in the second half of the same session. From linear regression, the mean SNR and Ca2+ event rate in the second half of each session were 96 ± 2 % (N = 6 mice) and 99 ± 3 % (N = 6 mice), respectively, of their values in the first half.
(k) A box and whisker plot of the Ca2+ event rate across all cells imaged for 5 days in each mouse (N = 2236–5292 cells). Horizontal lines indicate median values, boxes cover the second and third quartiles, and whiskers extend to 1.5 times the interquartile distance. Dots show median values for individual mice.
Extended Data Fig. 2. Individual cortical neurons exhibit variable coding properties across time-scales from minutes to days.
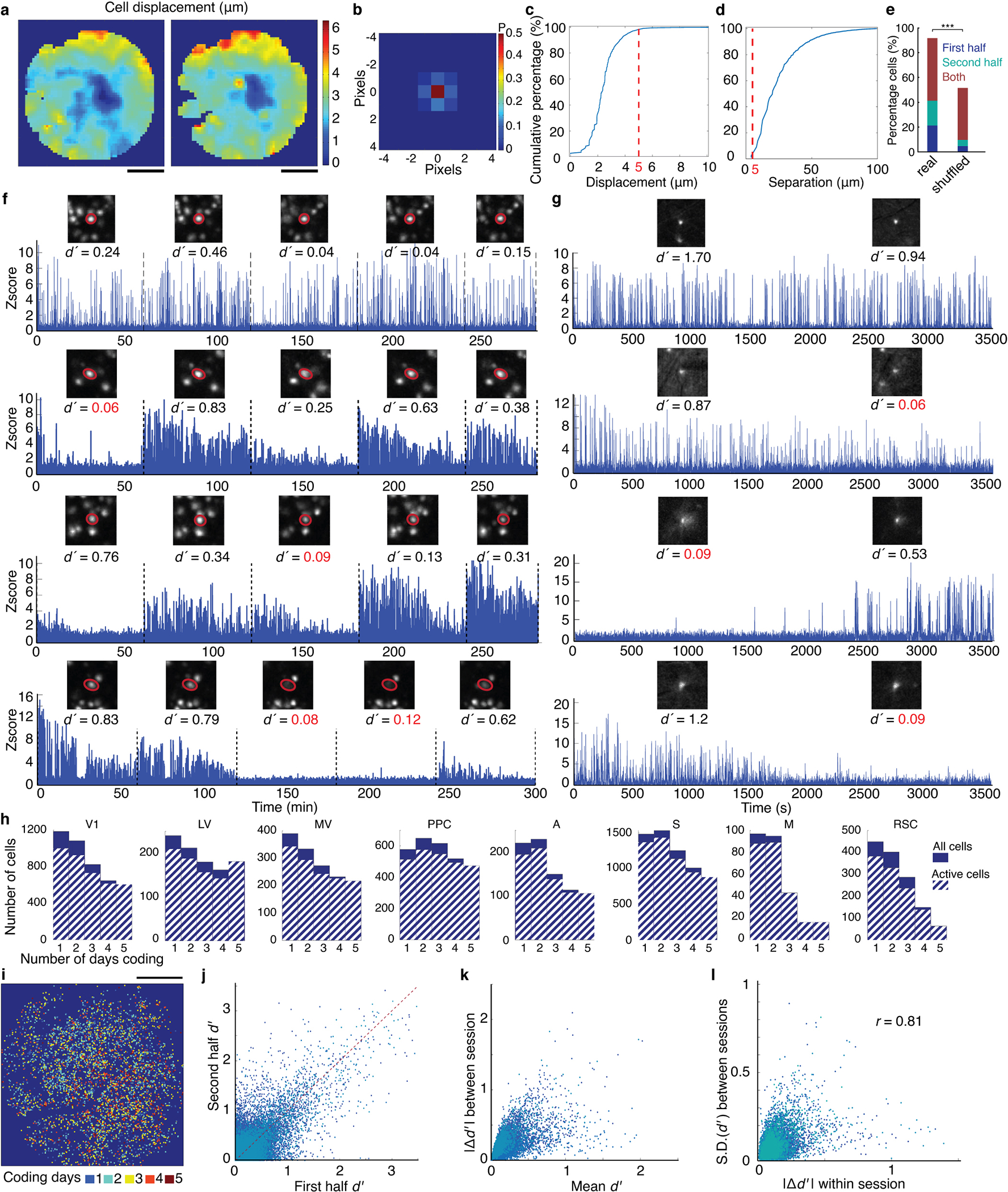
(a) Maps for each of two example mice, showing how the mean lateral displacement in individual cells’ centroid positions across multiple imaging sessions depended on the cells’ locations in the field-of-view. Across most of the field-of-view, this mean displacement was <1 pixel, corresponding to < 4 μm. To determine these displacements, we first computed the maximum projection image (MPI) of the Ca2+ video acquired in each imaging session. Using the MPI from the first imaging session as a reference, we computationally aligned it to the MPI from each of the other sessions. We then computed the spatial cross-correlation function between patches of the MPI containing ≥10 cells from the first session (patch size: 256 μm × 256 μm) and MPIs from each of the other sessions. For each session other than the first, we determined the displacement of an image patch to be the argument of the spatial cross-correlation function that yielded its maximum value. We then averaged these displacements across all imaging sessions subsequent to the first session. By examining all possible MPI patches (spaced 64 μm apart) in this way, we created the map shown. Scale bars: 1 mm.
(b) Two-dimensional probability distribution of cells’ daily lateral displacements from their mean position, averaged across all days of imaging and all imaged neurons (21,570 cells) from N = 6 mice (Methods). About 50% of the time, cells had a displacement of zero pixels from their mean position, and 98.5% of the time these displacements were ≤1 pixel (4 μm).
(c) Cumulative distribution of cells’ mean displacements (averaged over all days of imaging) from their mean positions as determined across the experiment. Red dashed line indicates that 95.4% of cells had a mean displacement of ≤5 μm.
(d) Cumulative distribution of the lateral separations between nearest neighbor pairs of cells. Red dashed line indicates that only 2% of nearest neighbor cell pairs were within 5 μm of each other.
(e) Among 18,528 cells with significant values on one or more sessions for encoding the trial-type in the stimulus period (P < 0.01; permutation test; N = 94–354 trials), 41% of these cells had significant values in only one half-session, split nearly evenly between the first (21%) and second (20%) half-sessions. Whereas in trial-shuffled data, only 10% of the cells had this variable coding, a highly significant difference from the real data (P < 0.001) indicating that trial-shuffling diluted the temporal concentration of trials in which cells had coding responses. Consistent with this, in the real data 91% of the 18,528 cells retained significant coding in one or both halves of the full sessions in which they displayed significant coding (P < 0.01; permutation test; 40–175 trials). But in trial-shuffled data, only 51% of the cells retained this coding in one or both half-sessions, a highly significant difference from real data (***P < 0.001; permutation test; 94–354 trials), again showing that in real data the cells had temporally concentrated coding epochs far more than expected by chance. These results are indicative of bona fide intra-session coding fluctuations. All s.d. values on the above percentages of cells were estimated as counting errors and were 0.1–0.4%.
(f) Some cortical neurons had visual coding properties that varied across days. Shown are data from 4 example cells, for which the plot shows traces of the neuron’s fluorescence intensity (z-scored values of ) as a function of time across 5 imaging sessions. Vertical dashed lines mark transitions between successive imaging sessions. Insets show maximum projection images of the example neurons, as determined over each individual imaging session. Values of denote the fidelity with which one can distinguish the two visual stimuli based on the binarized event train of the cell’s Ca2+ activity (Methods). In panels f and g, values of colored red are those for which the two stimuli cannot be significantly distinguished, as determined using a permutation test over the set of stimulus trials and requiring P < 0.01 for significance. The four example cells in this panel are from cortical areas PPC, MV, V1 and PPC, as arranged from top to bottom.
(g) Some cortical cells had visual coding properties that varied within the 1-h recording sessions. Shown are fluorescence intensity traces for 4 example cells (z-scored values of ) as a function of time across an individual imaging session. We measured d’ values of single neurons for the two different visual stimuli (gratings) separately during the first and second halves of each session based on their binary event traces computed from their Ca2+ activity. Cortical neurons that actively fired across the session exhibited variability in their visual coding, as well as cells that were not active throughout the session. The four example cells are from cortical areas LV, V1, MV and LV, as arranged from top to bottom. Insets: Example Ca2+ event images show that the same cells were imaged in the first and second halves of each session.
(h) Histograms of the number of days that neurons from each cortical area significantly encoded the visual stimulus type (permutation test over the set of stimulus trials; requiring P < 0.01 for significance), for all cells that did so in at least one session (solid bars) and for the subset of these cells with statistically significant levels of Ca2+ activity in every imaging session (hashed bars).
(i) A map of neurons from an example mouse, with the color of each cell denoting the number of days that the cell significantly encoded the visual stimulus type. Cells with different day-to-day reliabilities of stimulus-encoding were interspersed across the field-of-view. Scale bar: 1 mm.
(j) A scatter plot in which, for every individual cell (blue data points), the d’ value for stimulus discrimination during the first half of each imaging session is plotted against the d’ value determined for the second half of the same session.
(k) A scatter plot in which, for every individual cell (blue data points), the mean d’ value for stimulus discrimination (averaged over all imaging sessions) is plotted against the range of d’ values determined for the same cell across all imaging sessions.
(l) A scatter plot in which, for every individual cell (blue data points), the mean difference between the d’ values for stimulus discrimination determined for the first and second halves of each imaging session is plotted against the s.d. of the d’ values determined for the same cell across all imaging sessions. Variability in d’ values within a session was highly correlated (r = 0.81) with variability across sessions, suggesting that some neurons have greater intrinsic variability in the fidelity of stimulus encoding than others.
Extended Data Fig. 3. Neural ensemble representations of the visual stimuli were invariant over most of the stimulation period.
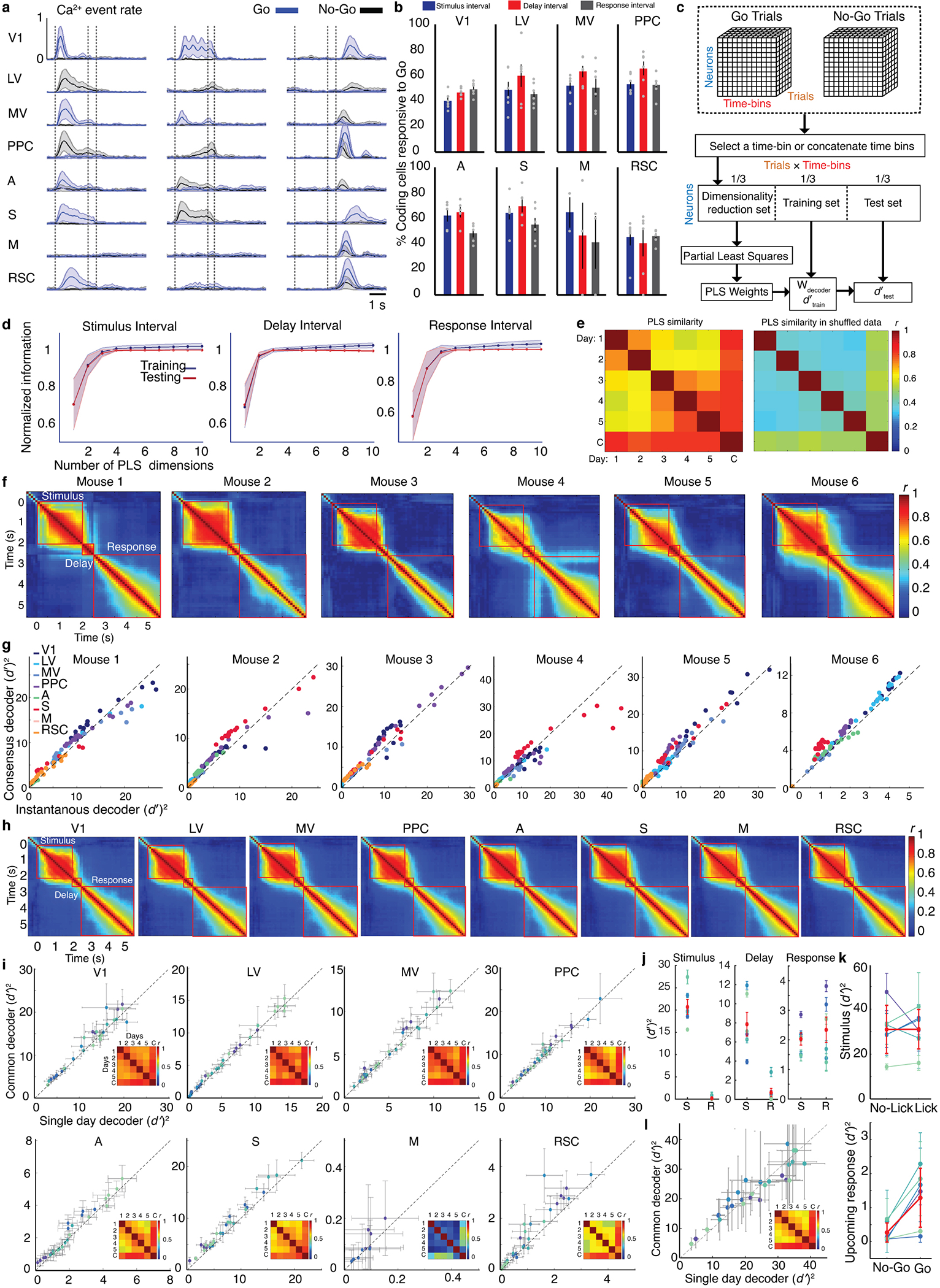
(a) Mean time-dependent rates of task-evoked Ca2+ events for 24 example neurons, 3 in each of 8 different cortical areas, as averaged across 5 days of imaging sessions in one example mouse on Go (blue traces) and No-Go (black traces) trials. Shading: s.d. across 415 trials of each type.
(b) For the subset of cells that responded significantly to one of the two visual stimuli (see Fig. 2c), the plot shows the mean percentages of coding cells that responded to the Go stimulus in each of 8 different brain areas. The remainder of the coding cells responded to the No-Go stimulus. Error bars: s.d. across N = 6 mice.
(c) Schematic of the computational pipeline used to train cross-validated instantaneous or consensus linear Fisher decoders. After constructing an unbiased dataset with equal numbers of Go and No-Go trials, we divided the set of trials into 3 equal portions, one used for dimensionality reduction, another used for decoder training, and the third for decoder testing. Using the first subset of trials, we applied a partial least squares (PLS) analysis to identify a low-dimensional subspace of the population neural activity with informative information for discriminating the two visual stimuli. Within this low-dimensional subspace, we used the second subset of trials to train a Fisher linear decoder (indicated by the vector Wdecoder) to discriminate the two stimuli. We used the third subset of trials to test the decoder’s performance. For both the training and testing datasets, we computed the fidelity, dʹ, with which the stimuli could be distinguished based on the evoked neural population activity. Similarly, to train decoders intended to identify the mouse’s decision from the neural activity, we followed the same computational procedures as for stimulus decoders, except we started with equal numbers of correctly and incorrectly performed trials with a given stimulus.
(d) Only a few of the dimensions identified by PLS analysis were required for optimal linear discrimination of the two stimuli. We trained consensus decoders based on the neural activity arising during the stimulus presentation, delay, and response intervals of the trials in which each mouse performed correctly. Plots show mean values of (dʹ)2 determined for decoder training (blue) and testing (red) datasets, versus the number of PLS dimensions used. When constructing each individual decoder, we used the number of PLS dimensions that maximized (dʹ)2 values for the testing datasets. All plotted values of (dʹ)2 are separately normalized for each mouse to the maximum (dʹ)2 value determined using the testing data. On average, with >5 PLS dimensions the decoders overfit the training data, as evidenced by (dʹ)2 values greater than those attained from the testing data. For shuffled datasets, the maximal (dʹ)2 values were achieved with 1 or 2 PLS dimensions (data not shown). Shading: s.d. across N = 6 mice.
(e) To assess the similarity between the PLS dimensions as computed for the data from different days, we computed the similarity of the subspaces defined by the top 3 PLS dimensions found for each mouse on different individual days (1–5) or for its across-day, common decoder (C) (Methods). We used the top 3 PLS dimensions, since these contain most of the information (panel d). The two matrices show the mean similarity values for all pairs of these subspaces, averaged over N = 6 mice, for real (left) and shuffled (right) datasets. Notably, for the real datasets the PLS dimensions for the common decoders were highly similar to those for the single-day decoders.
(f) Optimal linear decoders of stimulus type retained a constant form across the period of visual stimulus presentation. The 6 plots show the Pearson correlation coefficients, r, between all possible pairs of instantaneous decoders (constructed using all imaged neurons in each of 6 different mice), as computed for each time bin within the stimulus, delay or response intervals.
(g) Due to the stationarity of the optimal linear decoders across the period of stimulus presentation, f, consensus and instantaneous decoders of stimulus type performed nearly equivalently. To illustrate, the plots show mean values of (dʹ)2 for consensus decoders of stimulus type versus those for instantaneous decoders, for trials in which the mouse performed correctly. Each data point shows the testing results attained by applying the two types of decoders to the data from an individual time bin within the stimulus presentation interval. In some mice, e.g. Mice 5 and 6, the consensus decoder achieved slightly superior decoding performance, presumably due to the larger set of training data used to construct consensus decoders.
(h) Similar results to those of panel f, computed separately for different cortical areas and averaged over 6 mice.
(i) Similar results to those of Fig. 3c, computed separately for different cortical areas.
(j) To measure the extent to which the trial-type decoders captured information relating to the stimulus (S) or the mouse’s response (R) in the stimulus (left plot), delay (middle) or response (right) periods, we projected the neural ensemble activity on all 4 types of trials (Hit, Miss, Correct Rejection, and False Alarm) onto the common trial-type decoders that we had trained for each period using only the correctly performed trials (Methods). We then computed the (dʹ)2 values plotted using sets of trials in which either the stimulus or the response was held constant but the other factor varied. Information (dʹ)2 about the stimulus did not vary significantly between Lick and No-Lick trials, so we averaged the (dʹ)2 values for the two types of stimuli in the left columns of each plot. However, response coding was much stronger on Go than No-Go trials (see panel k), so the right columns only show the (dʹ)2 values from Go trials. Each blue point shows data from one mouse (mean ± s.d. , N =100 different subsets of trials, each with equal numbers of trials of the two types). Red points denote averages across all mice (mean ± s.e.m. , N = 6). These results show that during the stimulus period the common decoders nearly exclusively captured stimulus information, which was 691 ± 315 times greater (mean ± s.e.m.; N = 6 mice) than the information captured about the mouse’s response. In the delay period, the relative proportion of response information rose, and during the response period the common decoders captured response information that was comparable or greater to the levels of information about the stimulus.
(k) The mean Fisher information encoded by the neural ensemble activity about the stimulus type is independent of the mouse’s upcoming response (top), as shown by comparing the ( )2 values computed for consensus common stimulus decoders trained and tested on ‘No-Lick’ trials to those for ‘Lick’ trials (P <0.7; Wilcoxon signed-rank test; N = 6 mice). However, on ‘Go’ but not ‘No-Go’ trials, the mouse’s response can be predicted (P < 0.01; permutation test; N = 40–754 trials) from the neural activity during the stimulus presentation period (bottom), as shown by comparing decoders trained and tested on No-Go trials to those for Go trials (P <0.03; Wilcoxon signed-rank test; N = 6 mice). For each comparison, we constructed training datasets for the two decoders to have equal numbers of trials, 50% of each type. Blue-shaded points are from individual mice; error bars are s.d. (N = 100 different randomly chosen sets of trials. Red points are means; error bars are s.d. (N = 6 mice).
(l) A control analysis to accompany Fig. 3c, showing that across-day common consensus decoders performed equivalently to single-day consensus decoders, even when the two decoder-types were trained with datasets of equal size. Here we trained common decoders by sub-sampling trials from the datasets acquired in each session such that the training dataset had the same of number of trials as that of the day with the smallest number of trials. We also trained the single-day decoders using this same number of trials.
Extended Data Fig. 4. Neural ensemble representations of both the visual stimuli and the mouse’s response were widespread across multiple neocortical areas.
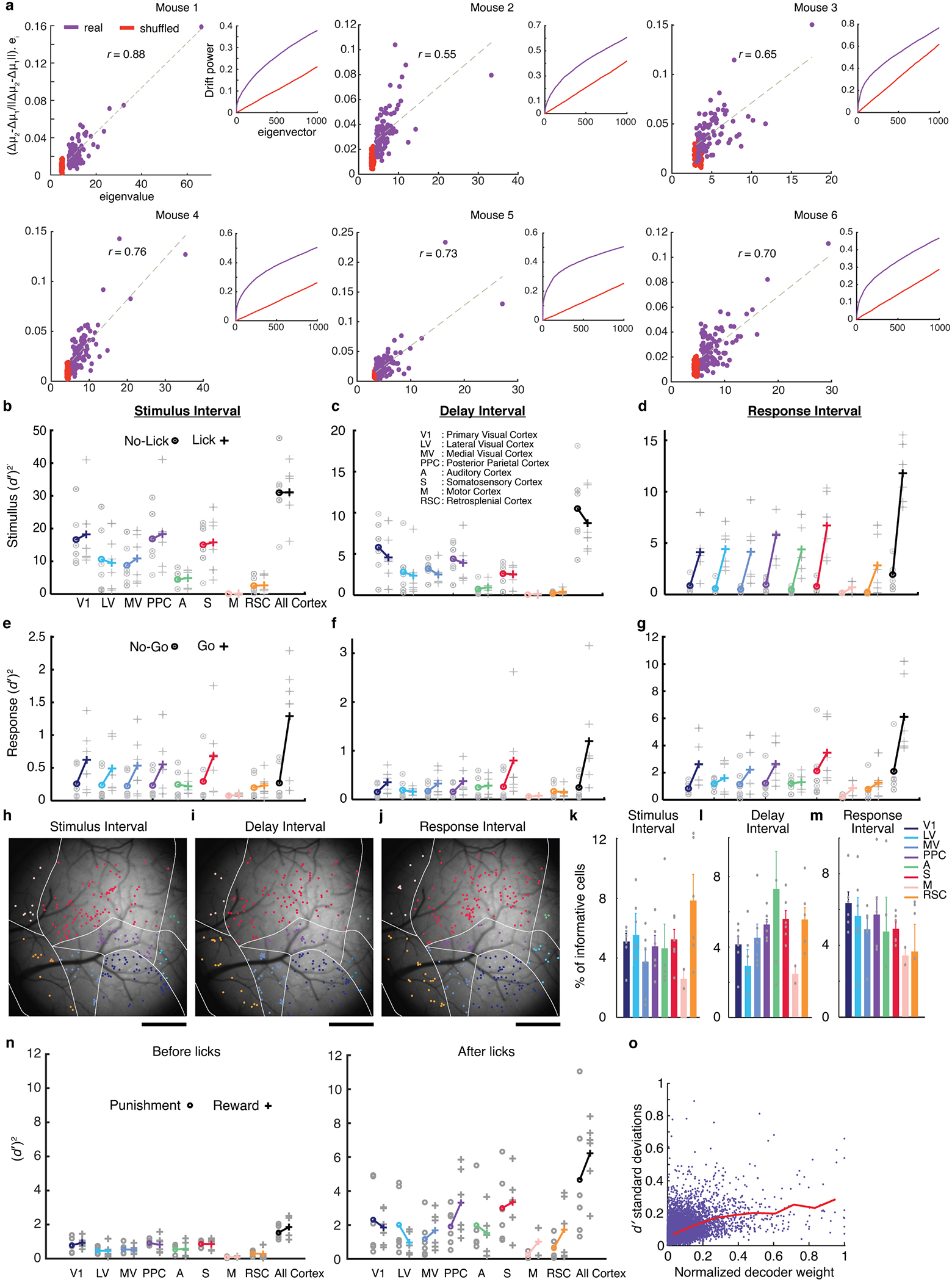
(a) Plots analogous to those of Fig. 3f, except that the data are from individual mice. In all 6 mice, the day-to-day changes in coding were significantly correlated with the within-day, trial-to-trial fluctuations (r = 0.85, 0.66, 0.79, 0.76, 0.83, 0.76 and P was between 5·10−14 – 5·10−29 for mice 1–6 for the real datasets, but 0.1 ≤ r ≤ 0.15 and 0.12 ≤ P ≤ 0.92 for trial-shuffled datasets).
(b) We trained consensus common decoders to discriminate the two visual stimuli based on the neural activity evoked either in individual cortical areas or across the visible cortical regions, during the stimulus presentation period on ‘No-Lick’ trials (defined as those trials on which the mouse withheld a licking response) and on Lick trials (on which the mouse made a licking response). Thus, decoders for ‘No-Lick’ trials discriminated ‘Correct Rejection’ from ‘Miss’ trials, and decoders for ‘Lick’ trials discriminated ‘Hit’ from ‘False Alarm’ trials. Both types of decoders were trained on equally sized datasets, with equal numbers of trials of each type. We evaluated decoder performance for each mouse across the individual time bins of the trial structure and constructed the plot using the maximum (dʹ)2 values attained for each mouse across all time bins during stimulus presentation (0.5–2 s after stimulus onset). (dʹ)2 values for stimulus decoding were statistically independent of the mouse’s upcoming ‘Lick’ or ‘No-Lick’ response (P < 0.7; Wilcoxon signed-rank test, N = 6 mice). Across b–g, gray and colored symbols respectively denote (dʹ)2 values for individual mice and mean values averaged over N = 6 mice; note that the y-axis scales vary substantially across the graphs.
(c, d) Using the same methods as in b, we trained consensus common decoders to discriminate the two visual stimuli based on the evoked neural activity in different cortical areas during the delay (c) and response (d) periods of the trial. Similarly to b, we evaluated decoder performance for each mouse across the individual time bins of the trial structure and constructed the plots using the maximum (dʹ)2 values attained for each mouse across all time bins during either the delay period, c, or the response period, d. Whereas values of (dʹ)2 for stimulus decoding during the delay period were independent of the mouse’s upcoming motor response (P <0.3; Wilcoxon signed-rank test; N = 6 mice), during the response period (dʹ)2 values were significantly greater for ‘Lick’ trials (P <0.03). The latter, higher values of (dʹ)2 could stem from the divergent neural signals evoked by receipt of a reward or air puff on ‘Hit’ and ‘False Alarm’ trials, respectively.
(e–g) Using methods analogous to those in b, we trained consensus decoders of the mouse’s response on ‘Go’ and ‘No-Go’ trials based on the neural activity in different cortical areas during the stimulus presentation (e), delay (f), and response (g) intervals. As in b–d, we evaluated decoder performance for each mouse across the individual time bins of the trial structure and constructed the plots using the maximum (dʹ)2 values attained for each mouse across all time bins during either the stimulus period (0.5–2 s after stimulus onset), e, delay period, f, or response period, g. To determine the neural representations of the mouse’s response during the response interval, g, we used data from across the full 3-s response interval. Within this interval, the mouse received liquid rewards and aversive air puffs at variable time points. Thus, a distinct analysis would be needed to separate the coding relating to the receipt of the rewarding and aversive stimuli from that relating to the mouse’s actions. (dʹ)2 values for response decoding were significantly greater for ‘Go’ trials during the stimulus presentation (P <0.03; Wilcoxon signed-rank test; N = 6 mice), delay (P < 0.06), and response (P < 0.06) intervals. These higher values of (dʹ)2 could reflect neural signals associated with reward prediction, motor planning and action arising on correctly performed ‘Go’ trials.
(h–j) Map of the cortex for the same mouse as in Fig. 3g–j. Colored dots mark locations of cells that made the greatest contributions to the response decoder score (defined as cells with decoder weights deviating >2 s.d. from mean values) during the stimulus presentation (h), delay (i), and response (j) intervals. Because the mouse’s response was only weakly encoded in the neural dynamics observed on ‘No-Go’ trials (as shown in e–g), we created h–m based on the response decoders found by analysis of the ‘Go’ trials. Cells are colored according to the same scheme as in a. Scale bars: 1 mm.
(k–m) Mean ± s.e.m. (N = 6 mice) fractions of neurons in each brain area that had response decoder weights deviating >2 s.d. from mean values, during the stimulus presentation (k), delay (l), and response (m) intervals.
(n) Right, We measured the information (dʹ)2 conveyed about reward and punishment in each brain area by studying the neural activity evoked when the mouse licked. To evaluate the encoding of punishment, we compared the mean neural ensemble activity in the first 0.5 s after licks that were punished with air puffs versus after licks that occurred during timeout periods and that elicited neither punishment nor reward. To evaluate the encoding of reward, we compared the mean neural ensemble activity in the first 0.5 s after licks that occurred during timeouts versus after licks triggered a reward. Both punishment and reward were represented to varying extents across the different brain areas. It is important to note that these representations could relate to any aspect of the rewarding or aversive experience, such as the experience of receiving or blinking in response to an aversive air puff or of receiving or tasting a reward. Left, As a control analysis, we performed the same calculations as for the right panel but using the neural activity that occurred within the 0.5 s intervals just before licks. As expected, during these periods there was notably less information encoded about upcoming rewards or punishments than about rewards or punishment that the mouse has just received.
(o) A graph of the s.d. of ( )2 values for each cell (individual data points) across all days of the study, for every cell with a significant (p<0.01) value for trial-type encoding on at least one day, as a function of the cell’s weight in the across-day common decoder. Decoder weights are normalized by the maximum weight found in each mouse. The results show that cells can have stable or variable coding properties, irrespective of their decoder weights. Nevertheless, coding variability generally increases for cells with larger weights, as shown by the red line, which is a plot of the mean s.d. in ( )2 values, averaged over all cells within x-axis bins of 0.1.
Extended Data Fig. 5. Information-limiting noise correlations and coding redundancy peaked just after stimulus onset and then declined for the rest of stimulus presentation.
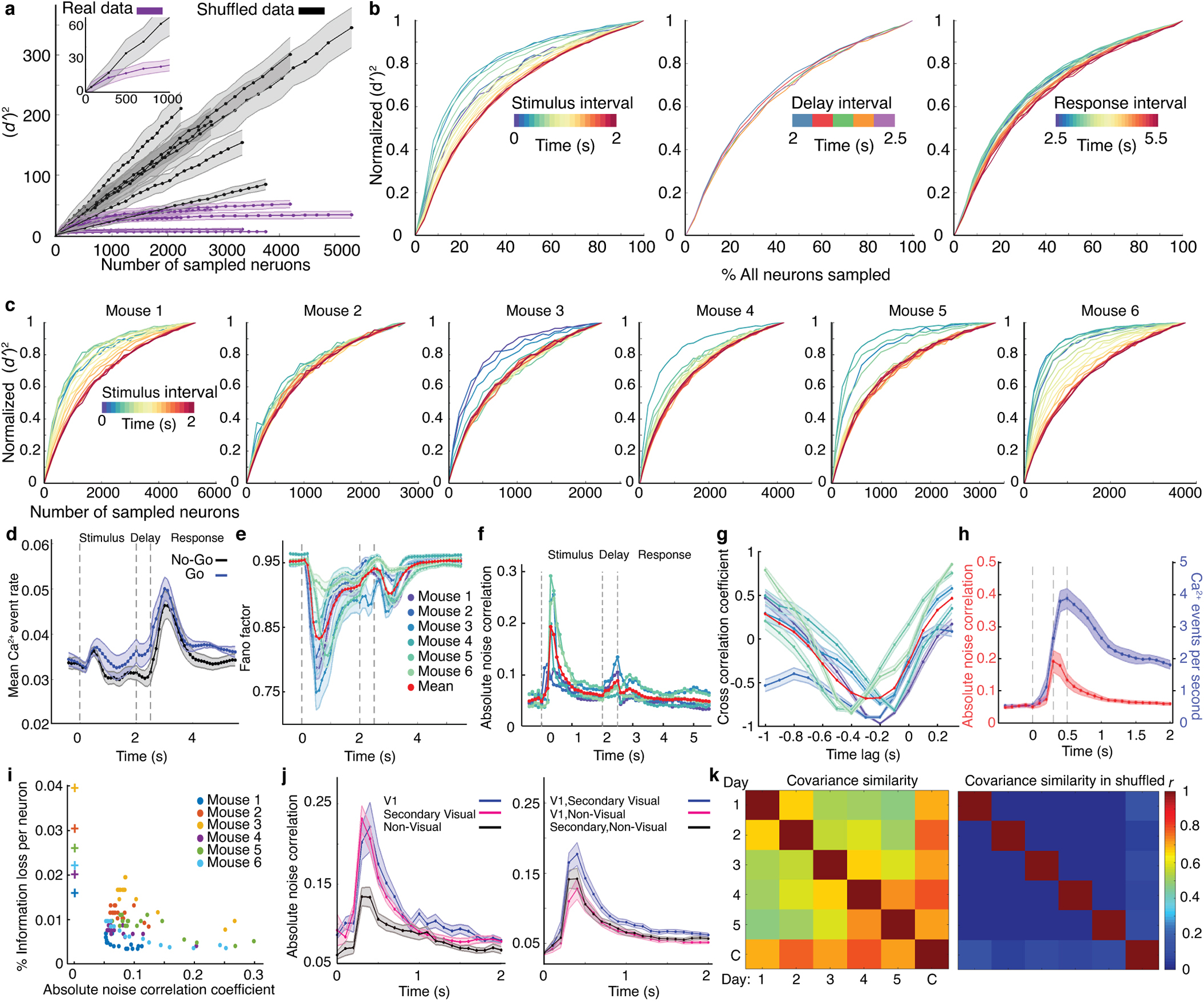
(a) The fidelity with which the stimulus identity could be decoded from neural ensemble activity saturated for large (>2000) populations of cells, for real (purple curves) but not trial-shuffled (black curves) datasets. To study ensembles of each size denoted on the x-axis, we randomly chose 100 different subsets of cells from the entire pool of neurons imaged across all brain areas. We then trained and tested optimal linear Fisher decoders using the neural activity during the interval [0.4 s, 0.5 s] after stimulus onset on trials that the mouse performed correctly. We quantified decoding performance using the (dʹ)2 value, which is related to the Fisher information the neural dynamics conveyed about the trial-type. Each curve shows data from one mouse. Whereas (dʹ)2 values saturated for large neural populations in the real data, this did not occur for trial-shuffled datasets in which cells’ correlated noise fluctuations were scrambled. Shading: s.d. across all 100 subsets of cells chosen for each ensemble size. Inset: A magnified view near the origin of the graphs for one example mouse.
(b) Using the same methods as in a, we assessed how well optimal linear decoders could discriminate Go and No-Go trials. Plots show mean (dʹ)2 values for this discrimination as a function of neural ensemble size and for different time bins within the trial structure, averaged over N = 6 mice. The size of the cell ensemble at which (dʹ)2 values saturated rose substantially with time during stimulus presentation, but stayed relatively constant during the delay and response periods. (dʹ)2 values are normalized relative to their maximum (saturating) value at each time bin. Ensemble size values are normalized relative to the total number of cells recorded in each mouse.
(c) Plots of the same kind as in b, for each of 6 mice during the stimulus interval. Data are shown only for time bins in which ( )2 values were significantly greater than for control datasets in which the trial-type labels were randomly shuffled (P < 0.01; permutation test; N = 710–1340 trials).
(d) Mean ± s.e.m. (N = 6 mice) Ca2+ event rates for all neurons on Go and No-Go trials in which the mouse performed correctly. These mean event rates had near identical time-dependencies on the trials of the two types, but the temporal variations were distinct from those of the decoder score fluctuations (Fig. 4b) or the correlated fluctuations in cells’ activity rates shown in f. Dashed vertical lines in d–f demarcate the stimulus, delay and response periods of the trial structure.
(e) The time-dependence of the mean Fano factor, determined for each mouse by computing for each cell the ratio of the variance in the cell’s Ca2+ event rate to its mean Ca2+ event rate, on trials in which the mouse performed correctly. Shading indicates s.e.m. values (N = 2236–5292 cells). The legend also applies to panels f and g.
(f) Noise correlations between pairs of cells with similar tuning to the stimulus rose sharply after stimulus onset, peaked ~0.2 s after stimulus onset, and then decayed to baseline values. Each colored trace shows the mean absolute value of noise correlation coefficients for all pairs of similarly tuned cells across all imaged brain areas in each mouse. Red trace is a mean over 6 mice.
(g) Plots of the cross-correlation functions between the dynamics of absolute noise correlations across pairs of cells, shown in f, and the Fano-factor, shown above in e, as determined for each mouse over the 2-s-stimulus period to characterize individual cells’ dynamical fluctuations. The graph shows that changes in pairwise noise correlation coefficients were negatively correlated with and most predictive of upcoming variations in the Fano factor with a lead time of ~200 ms. Shading indicates s.e.m. values (N = 10–20 time bins for each value of the abscissa).
(h) A plot of the mean time-dependent rate (blue trace) of Ca2+ events in GO-stimulus-tuned neurons on GO trials and NO-GO-stimulus-tuned neurons on NO-GO trials, averaged over both cell-types and across all mice (N=6 mice). Shown for comparison is a plot of the mean absolute noise correlation coefficient (red trace) for pairs of similarly tuned neurons, computed as in panel f for the same 6 mice. Notably, the changes in noise correlation coefficient levels peaked sooner after stimulus onset than the Ca2+ activity rates of tuned cells. Moreover, after reaching their peak values, noise correlation coefficients declined back to baseline values by the end of stimulus presentation, whereas the Ca2+ activity rates did not. These differences make it hard to explain the dynamics of noise correlation coefficients as resulting simply from changes in neural activity rates. Shading: s.e.m. across 6 mice.
(i) A scatter plot showing the change in information encoded by the neural ensemble if one cell were to become silent, assessed using instantaneous decoders (Methods). Each dot denotes the result from an individual time bin. (As shown in c and f, noise correlation coefficients vary with time following stimulus onset). Results for trial-shuffled data, in which correlated fluctuations have been scrambled, are denoted with crosses and reveal a greater sensitivity to the loss of one neuron.
(j) Left, Traces of the mean absolute noise correlation coefficients as a function of time during the stimulus presentation period, determined as in f for pairs of cells in primary visual cortex (V1; blue trace), secondary cortical visual areas (areas LV, MV and PPC; red trace) or non-visual cortical areas (areas A, S, M and RSC; black trace). Right, Traces of the mean absolute noise correlation coefficients between pairs of coding neurons located in different brain areas. The rise in noise correlations for similarly tuned cells in the visual cortex is greater than that for cells outside visual cortex (P < 0.03; Wilcoxon signed-rank test; N = 6 mice). Shading: s.e.m. across N = 6 mice.
(k) We calculated the covariance in the neurons’ responses on each trial-type and on each day. We then averaged the covariance matrices for the two trial-types and computed the top 3 eigenvectors for each day. Left, A plot showing the similarity between the pairs of different subspaces (Methods), each defined by the top 3 eigenvectors of the noise covariance matrix on each day of experimentation. The matrix row and columns labelled ‘C’ is for the noise covariance matrix computed for the set of all trials across all days. Right, As control, we computed the subspace similarities for trial-shuffled datasets in which each neuron’s responses were permuted across trials with the same stimulus. Overall, the results show that the noise covariance structure in the real data is significantly similar across days, to a degree much beyond that in shuffled datasets.
Extended Data Fig. 6. The discriminability of the two stimuli based on their evoked neural dynamics fluctuated trial-by-trial in a way that was highly correlated between cortical areas.
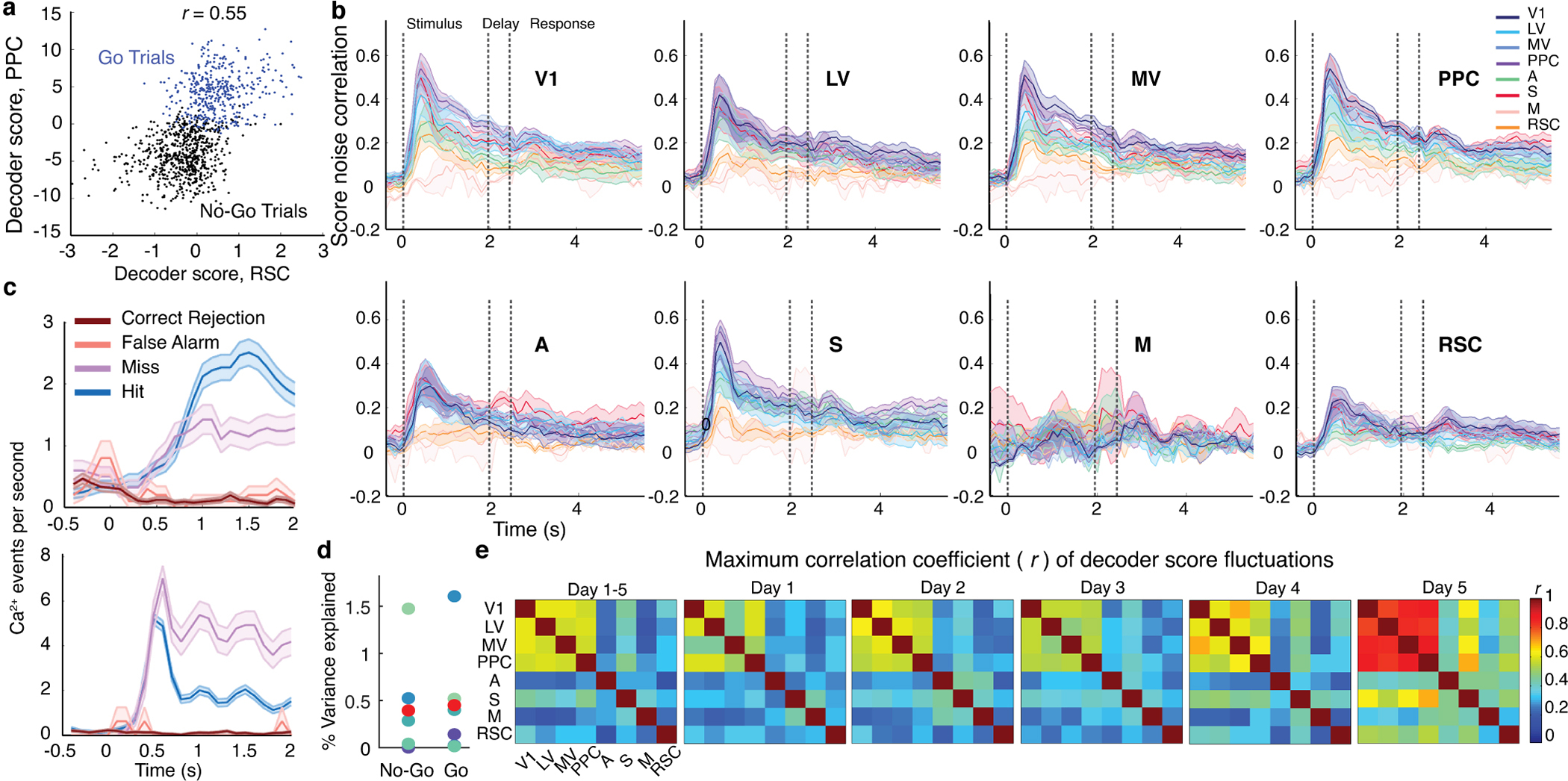
(a) Example scatter plot for an individual mouse in which the instantaneous stimulus decoder scores based on the activity patterns of cortical area PPC are plotted against those for cortical area RSC. Each data point shows results for an individual trial, at 0.5 s after stimulus onset, for Go trials (blue data points) or No-Go trials (black data points). Stimulus decoder scores for the two brain areas exhibit positively correlated trial-to-trial fluctuations.
(b) Traces showing the mean time-dependent correlations of the fluctuations in instantaneous stimulus decoder scores for 8 different cortical areas and each of the other 7 brain areas within the imaging field-of-view. For most pairs of brain areas, these correlated noise fluctuations in decoder scores attained their maximum shortly after stimulus onset and then gradually decayed. Decoder training and testing was limited in this analysis to trials that the mice performed correctly. Shading: s.e.m. over N = 6 mice. Vertical dashed lines demarcate the stimulus presentation, delay and response intervals.
(c) Two plots showing examples of stimulus-coding cells whose responses were modulated by the mouse’s response. Each plot shows the mean rate of Ca2+ events in an individual neuron, as a function of time relative to stimulus onset at t = 0, for the 4 different trial-types. The cell of the top plot is from area MV, and the cell of the bottom plot is from PPC. Both cells had P-values of <0.01 for stimulus-coding on Lick and No-Lick trials, and also had P<0.01 for response-coding on Go-trials). We determined P-values through comparisons to trial-shuffled datasets (1000 different sub-samplings and random permutations of trials using equal numbers of trials of both stimulus- or response-types). The separation between the traces for Hit and Miss trials shows the extent of response-related modulation on trials with a Go stimulus. Shading: s.e.m. over trials (410 Hit trials, 218 Miss trials, 665 Correct Rejection trials, 100 False Alarm trials).
(d) To determine if the elevated correlated noise fluctuations along the stimulus-coding direction within the interval [0.2 s, 0.5 s] after stimulus onset, when correlations were at their peak, reflects choice information relating to the formation of a motor response plan, we computed for each stimulus-type the proportion of the neural activity variance along the stimulus-coding direction that co-varied with the mouse’s upcoming motor response. The results show that only a tiny percentage (0.5% on average) of the variations in stimulus-coding can be explained as reflecting the mouse’s decision or response. Blue-shaded points denote data from individual mice. Red points are averages across mice. See also Fig. 5e.
(e) Peak values of the time-dependent decoder score noise correlations (r), determined as in b, for all pairs of imaged brain areas for an example mouse, using either the data from each of five different imaging sessions, or the aggregated set of data from all imaging sessions. Fluctuations of decoder scores were correlated between sensory cortical areas during all recording sessions. The same general pattern of correlations between brain areas was visible in every session.
Extended Data Fig. 7. Canonical correlation noise modes during the visual stimulation period for 28 different pairs of cortical areas.
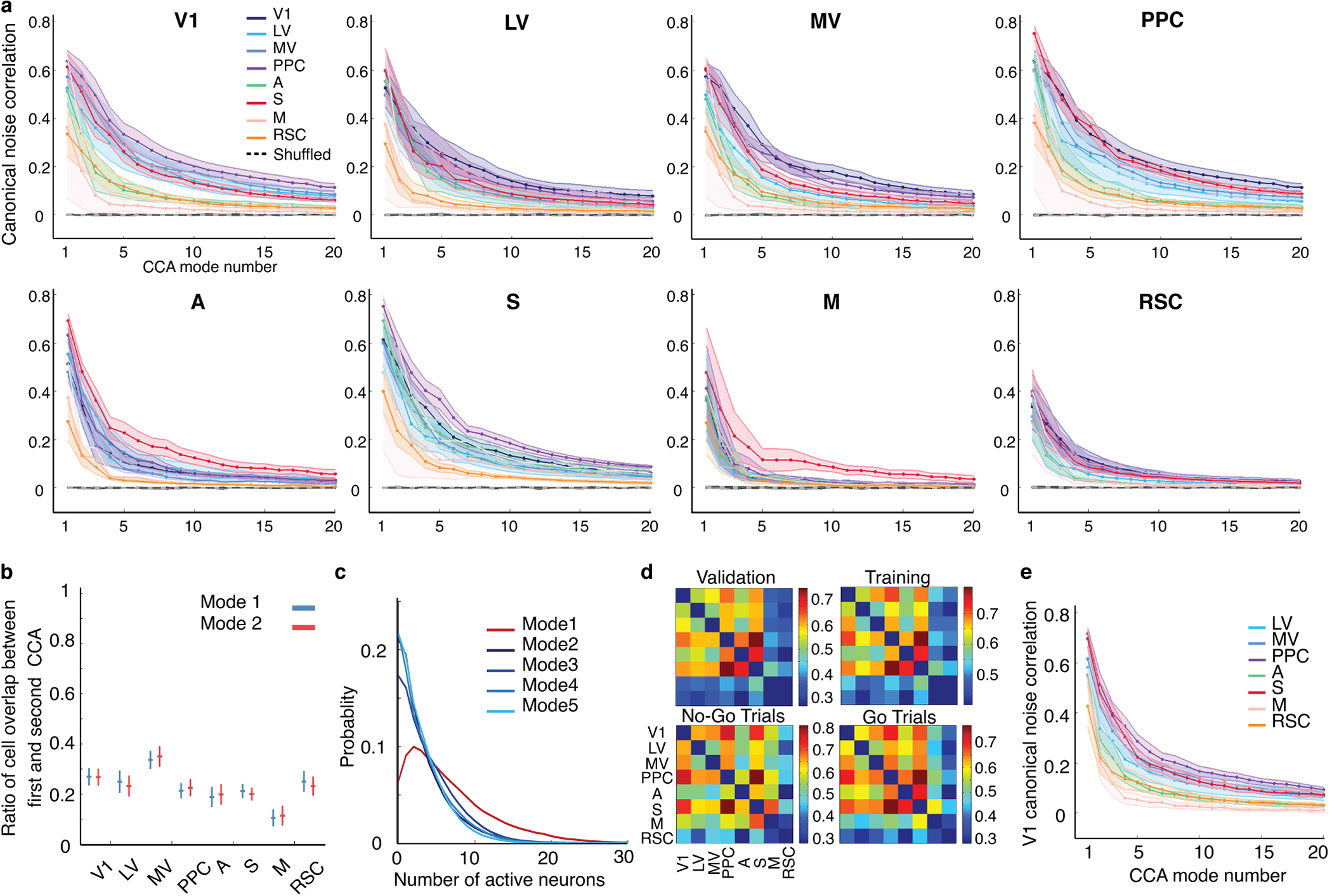
(a) Multiple ensembles of neurons from different cortical areas had strongly correlated noise fluctuations during visual stimulus presentation. By performing a canonical correlation analysis (CCA) on cells’ mean-subtracted activity traces for each trial type, we identified multiple modes of significantly correlated noise modes (P < 0.01; comparisons of real vs. trial-shuffled data using the permutation test; N = 710–1340 trials) that were shared across 28 different pairs of cortical areas (abbreviated as in Fig. 1). Plots show mean ± s.e.m. (N = 6 mice) correlation coefficients between the first 20 CCA noise modes for all pairs of brain areas, as determined from validation datasets that were held out from the training datasets used to identify the CCA noise modes (Methods).
(b, c) In each cortical area, ~70–90% of the neurons that contributed substantially to the largest CCA noise mode were distinct from the cells that contributed to the second-largest mode. A cell was considered to contribute substantially to a CCA noise mode if its weight in the CCA mode population vector was >2 s.d. above or below the ensemble mean. (b) The mean ± s.e.m. (N = 6 mice) number of cells that contributed substantially to both the first and second CCA noise modes in each brain area, normalized by the total number of cells that contributed substantially to either of these two modes and averaged over all pairings with the other 7 brain areas. (c) Distributions of the number of simultaneously active neurons in each time bin of the stimulus presentation period for the largest five CCA noise modes shared between V1 and the other 7 cortical areas.
(d) Mean correlation coefficients (N = 6) for neural activity in the first CCA noise mode shared between the 28 different pairs of cortical areas, for validation (top left) and training (top right) datasets, and on the set of No-Go (bottom left) and Go (bottom right) trials. The similarity of the noise correlation coefficients for all 4 subsets of trials suggests that correlated activity exists in these modes irrespective of the trial-type and that the results are not due to overfitting.
(e) Highly correlated noise fluctuations between cortical areas cannot simply be explained as resulting from the activity patterns of cells on the borders between pairs of cortical areas. We repeated the analysis in (a) for all pairs of areas, while discarding the activity traces of cells in each area closer than 60 μm to the boundary of the other area identified by retinotopic mapping. The plot shows the resulting mean ± s.e.m. (N = 6 mice) correlation coefficients for the CCA noise mode fluctuations between V1 and other cortical areas.
Extended Data Fig. 8. The canonical correlation noise modes before stimulus onset were distinct from those after stimulus onset, which were task-related.
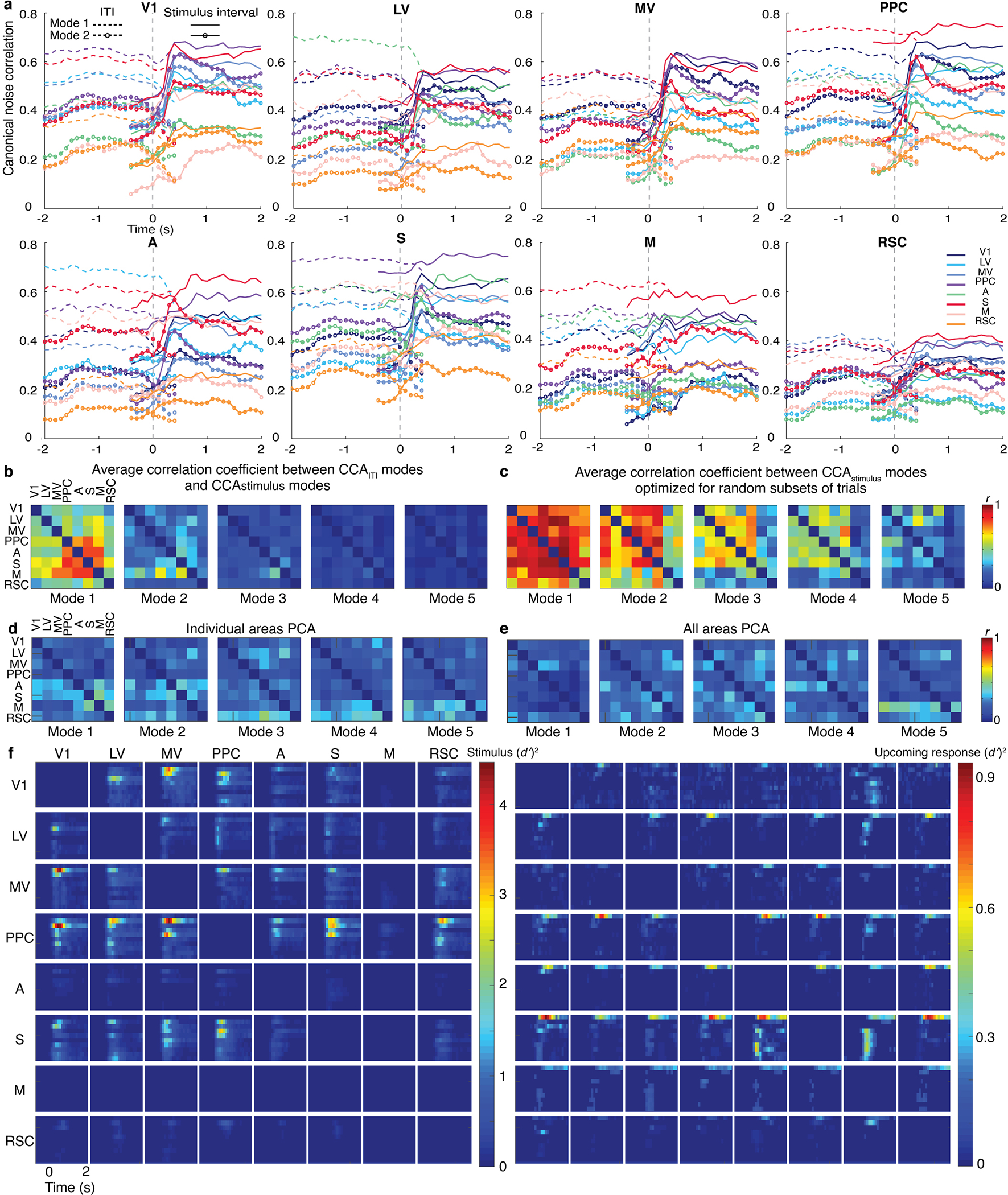
(a) During the inter-trial interval (ITI), there were significantly correlated noise fluctuation modes that were shared between cortical areas. However, these modes were not the same as the shared noise fluctuations that arose at stimulus onset. The plots show the mean (N = 6 mice) time courses of the correlation coefficients for the first- and second-largest noise modes shared between 28 different pairs of brain areas (pairs denoted via the graph titles and the color legend at far right), as found by applying canonical correlation analysis (CCA) separately to ITI periods (−2 < t < 0) and visual stimulation periods (2 > t > 0). Dashed traces, with and without open circles, respectively show the correlation coefficients for the first and second shared noise modes as identified during ITI periods. Solid traces, with and without open circles, respectively show the correlation coefficients for the first and second share noise modes as identified during stimulus periods. At stimulus onset (t = 0), correlated fluctuations declined within the CCA noise modes identified during ITI periods, whereas correlated fluctuations within the modes identified during the task substantially increased.
(b) CCA noise modes found during stimulus periods differ from those found during ITI periods, as shown by the cross-correlation coefficients between the CCA noise modes found for each pair of brain areas before vs. after stimulus onset. The plots show these cross-correlation coefficient values for the largest 5 modes for each pair of brain areas. To compute these coefficients, for each mouse we created 200 different random assignments of half of the trials into a training set and half of the trials into a validation set. Using 100 of these random assignments, we determined CCA noise modes for the ITI period. Using the other 100 assignments, we determined CCA noise modes for the task period. For each entry in the plots, we plotted the mean value of the cross-correlation coefficient, averaged across all 10,000 pairings of one mode from the ITI period and one from the stimulus period, and across 6 different mice. Within each plot, row labels designate the brain area for which we computed the cross-correlation coefficient; column labels designate the area with which the row area was paired in the CCA.
(c) As a control analysis for the results of (b), we examined the variability in our estimates of the largest 5 CCA noise modes during the stimulus period. To do this, we computed for each mouse the correlation coefficients between the CCA modes determined from 100 different random assignments of trials into training and validation sets. This showed that most CCA modes are stable during the stimulus presentation period. For each entry in the plots, we plotted the mean value of the cross-correlation coefficient, averaged across all 9,900 pairings of two different mode determinations from the stimulus period, and across 6 different mice. Within each plot, row labels designate the brain area for which we computed the cross-correlation coefficient; column labels designate the area with which the row area was paired in the CCA. The results show that the relative lack of stability exhibited in (b) between CCA noise modes before versus after stimulus onset is not simply due to the statistical variability in the determination of CCA noise modes.
(d) In each imaged brain area, we performed a principal component analysis (PCA) of the noise fluctuations around the mean stimulus-evoked responses, averaged over both stimuli. For each brain area, we then computed correlation coefficient between the modes identified by PCA and those identified by CCA with each of the other 7 brain areas. The results show that fluctuation modes identified by PCA are highly distinct from those found by CCA, indicating that PCA can be incapable of detecting correlated fluctuations between brain areas.
(e) Analogous plots to those in (d), except that we performed the PCA over the aggregated set of all brain areas.
(f) Plots analogous to those in Fig. 5e, except that results are shown for all pairs of brain areas, rather than averaged across all pairs of sensory areas.
Extended Data Fig. 9. Computational simulations of network dynamics show that the global CCA mode likely reflects a common signal that is broadcast to all the imaged cortical areas.
(a) For the real experimental data, the graphs show the time-dependence of the information, ( )2, encoded about stimulus identity within CCA modes 2–10 in each brain area, plotted as a function of time relative to stimulus onset. (We omitted the first CCA mode, which does not convey stimulus information, Fig. 5d,e). To compute ( )2 we trained consensus decoders based on the neural activity in each brain area during the stimulus presentation period of correctly performed trials. We then projected the neural dynamics onto each of the CCA modes and used the resulting 9-dimensional activity data to train and test instantaneous decoders of the stimulus identity. The vertical dashed lines indicate the stimulus onset.
(b) To explore the patterns of interconnectivity that can give rise to a global CCA noise mode, we simulated neural activity within a range of small world networks and systematically varied the extent and randomness of the inter-connections between pairs of brain areas (Methods). The schematic shows 3 example small world model networks with unidirectional connections between 11 brain areas. Each node denotes one brain area with 500 neurons. The parameter K is the ‘in-degree’, i.e. the number of projections received by each brain area. The parameter P determines the probability that the brain area sending a projection is randomly reassigned to a node outside the K nearest neighbors of the recipient brain area. The distribution of connection weights between areas was set so as to approximately match the canonical correlation coefficients observed in the real cortical recordings (Methods). A wide range of these models exhibited CCA modes among all pairs of brain areas that resembled the patterns of correlated activity fluctuations in our in vivo recordings of neural activity (panel c). However, no model had a global CCA mode, as each pair of brain areas generally had a unique set of co-fluctuations distinct from those in other pairs of brain areas (panel d).
(c) Canonical correlation coefficients for the strongest CCA modes between all pairs of 11 areas, plotted for different values of K and P. Strongly correlated CCA fluctuations were observed between all pairs of areas in most of the simulations.
(d) Correlation coefficients for the first CCA modes between one simulated brain area and each of the other 10 brain areas, plotted as in Fig. 5a. Even when strongly correlated CCA modes exist between all pairs of areas, as shown in (c), the neural ensembles comprising these modes are largely unique and do not establish a global mode—unlike in our actual recordings (Fig. 5a) in which the first CCA mode was global and independent of the pair of brain areas chosen for CCA. These results suggest that global CCA modes may be inconsistent with information transmission through a small-world architecture.
(e) The number of cells in each simulated brain area that had their first PCA weights >2 s.d. away from the mean value. Even though the simulated small world networks lacked a global CCA mode, the first mode identified by principal components analysis (PCA) was widely distributed across brain areas. Thus, the existence of distributed PCA modes does not imply the existence of a global CCA mode.
(f, g) Schematic, f, of a simulated neural network (Methods) in which information about the visual stimulus is transmitted via separate channels to different higher-order cortical areas, whereas information about the sensory decision is broadcasted in parallel to these higher-order areas. The strengths of neural connections from the early visual area and each of the two higher-order areas were chosen randomly from a Gaussian distribution. The matrix of neural connections between each pair of brain areas had a rank between 1–10. g, correlation coefficients between CCA modes in simulated cortical areas. In contrast to small-world connectivity, networks in which a single source broadcasted a common signal to multiple brain areas did have a global CCA mode, as in cortex (Fig. 5a). These results suggest the global CCA mode in cortex reflects the widespread distribution of a common signal conveying information about the mouse’s upcoming response to all imaged brain areas, rather than via separate inter-area connections.
(h, i) Normalized values of ( )2 determined for the simulated network of (f) for distinguishing between the two different stimuli, (h), or decisions, (i), plotted for each of the 10 largest CCA modes between all pairs of areas receiving input from the Early Visual Area. Results are shown separately for networks with neural connection matrices of different ranks. Results are averaged across 25 different networks with similar architecture. Shading: s.e.m. across the 3 different simulated areas, Areas A, B and C. Fig. 5e shows similar results for the real experimental data.
Supplementary Material
Acknowledgements
We gratefully acknowledge research support from HHMI (M.J.S.), the Stanford CNC Program (M.J.S.), DARPA (M.J.S.), NIH BRAIN Initiative grant 1UF1NS107610–01 (M.J.S.), the NSF NeuroNex Program (M.J.S.), an NSF CAREER Award (S.G.), and the Burroughs-Wellcome (S.G.), McKnight (S.G.), James S. McDonnell (S.G.) and Simons (S.G.; MJS) foundations, and a Stanford Graduate Fellowship (O.R.). We thank B. Ahanonu, A. Christensen, H. Kim, T. Rogerson, A. Shai, and A. Tsao, for helpful conversations, and H. Zeng for providing transgenic mice.
Footnotes
Competing financial interests. M.J.S. is a scientific co-founder of Inscopix Inc., which produces the Mosaic software used to identify individual neurons in the Ca2+ videos. J.A.L. is also an Inscopix stockholder.
Code availability. We used open source software routines for image registration55 (http://bigwww.epfl.ch/thevenaz/turboreg/) and partial least squares analysis (https://www.mathworks.com/matlabcentral/fileexchange/18760-partial-least-squares-and-discriminant-analysis). Software code for extracting individual neurons and their calcium activity traces from calcium videos by using principal component and then independent component analyses56 is freely available (https://www.mathworks.com/matlabcentral/fileexchange/25405-emukamel-cellsort), although for convenience we used a commercial version of these routines (Mosaic software, version 0.99.17; Inscopix Inc.). We used Matlab (version 2019a) to write all other analytic routines. The primary software code used to support the findings of the study is available at Zenodo.org (https://doi.org/10.5281/zenodo.6314932).
Reprints and permissions information is available at www.nature.com/reprints.
Data availability.
The data that support the findings of this study are available from the corresponding authors upon reasonable request.
References
- 1.Faisal AA, Selen LP & Wolpert DM Noise in the nervous system. Nat Rev Neurosci 9, 292–303, doi: 10.1038/nrn2258 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Lutcke H, Margolis DJ & Helmchen F Steady or changing? Long-term monitoring of neuronal population activity. Trends Neurosci 36, 375–384, doi: 10.1016/j.tins.2013.03.008 (2013). [DOI] [PubMed] [Google Scholar]
- 3.Rumyantsev OI et al. Fundamental bounds on the fidelity of sensory cortical coding. Nature 580, 100–105, doi: 10.1038/s41586-020-2130-2 (2020). [DOI] [PubMed] [Google Scholar]
- 4.Stein RB, Gossen ER & Jones KE Neuronal variability: noise or part of the signal? Nat Rev Neurosci 6, 389–397, doi: 10.1038/nrn1668 (2005). [DOI] [PubMed] [Google Scholar]
- 5.Zohary E, Shadlen MN & Newsome WT Correlated neuronal discharge rate and its implications for psychophysical performance. Nature 370, 140–143, doi: 10.1038/370140a0 (1994). [DOI] [PubMed] [Google Scholar]
- 6.Driscoll LN, Pettit NL, Minderer M, Chettih SN & Harvey CD Dynamic Reorganization of Neuronal Activity Patterns in Parietal Cortex. Cell 170, 986–999 e916, doi: 10.1016/j.cell.2017.07.021 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Greicius MD, Supekar K, Menon V & Dougherty RF Resting-state functional connectivity reflects structural connectivity in the default mode network. Cereb Cortex 19, 72–78, doi: 10.1093/cercor/bhn059 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Rosenberg MD et al. A neuromarker of sustained attention from whole-brain functional connectivity. Nat Neurosci 19, 165–171, doi: 10.1038/nn.4179 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Montijn JS, Meijer GT, Lansink CS & Pennartz CM Population-Level Neural Codes Are Robust to Single-Neuron Variability from a Multidimensional Coding Perspective. Cell Rep 16, 2486–2498, doi: 10.1016/j.celrep.2016.07.065 (2016). [DOI] [PubMed] [Google Scholar]
- 10.Semedo JD, Zandvakili A, Machens CK, Byron MY & Kohn A Cortical areas interact through a communication subspace. Neuron 102, 249–259. e244 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Stringer C et al. Spontaneous behaviors drive multidimensional, brainwide activity. Science 364, 255, doi: 10.1126/science.aav7893 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Abbott LF & Dayan P The effect of correlated variability on the accuracy of a population code. Neural computation 11, 91–101 (1999). [DOI] [PubMed] [Google Scholar]
- 13.Averbeck BB & Lee D Effects of noise correlations on information encoding and decoding. J Neurophysiol 95, 3633–3644, doi: 10.1152/jn.00919.2005 (2006). [DOI] [PubMed] [Google Scholar]
- 14.Moreno-Bote R et al. Information-limiting correlations. Nat Neurosci 17, 1410–1417, doi: 10.1038/nn.3807 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Carrillo-Reid L, Han S, Yang W, Akrouh A & Yuste R Controlling Visually Guided Behavior by Holographic Recalling of Cortical Ensembles. Cell 178, 447–457 e445, doi: 10.1016/j.cell.2019.05.045 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Graf AB, Kohn A, Jazayeri M & Movshon JA Decoding the activity of neuronal populations in macaque primary visual cortex. Nat Neurosci 14, 239–245, doi: 10.1038/nn.2733 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Ziv Y et al. Long-term dynamics of CA1 hippocampal place codes. Nat Neurosci 16, 264–266, doi: 10.1038/nn.3329 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Xia J, Marks TD, Goard MJ & Wessel R Stable representation of a naturalistic movie emerges from episodic activity with gain variability. Nat Commun 12, 5170, doi: 10.1038/s41467-021-25437-2 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Gonzalez WG, Zhang H, Harutyunyan A & Lois C Persistence of neuronal representations through time and damage in the hippocampus. Science 365, 821–825 (2019). [DOI] [PubMed] [Google Scholar]
- 20.Deitch D, Rubin A & Ziv Y Representational drift in the mouse visual cortex. Curr Biol 31, 4327–4339 e4326, doi: 10.1016/j.cub.2021.07.062 (2021). [DOI] [PubMed] [Google Scholar]
- 21.Sridharan D, Levitin DJ & Menon V A critical role for the right fronto-insular cortex in switching between central-executive and default-mode networks. Proceedings of the National Academy of Sciences 105, 12569–12574 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Allen WE et al. Thirst regulates motivated behavior through modulation of brainwide neural population dynamics. Science 364, 253, doi: 10.1126/science.aav3932 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Musall S, Kaufman MT, Juavinett AL, Gluf S & Churchland AK Single-trial neural dynamics are dominated by richly varied movements. Nat Neurosci 22, 1677–1686, doi: 10.1038/s41593-019-0502-4 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Niell CM & Stryker MP Modulation of Visual Responses by Behavioral State in Mouse Visual Cortex. Neuron 65, 472–479, doi: 10.1016/j.neuron.2010.01.033 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Montani F, Kohn A, Smith MA & Schultz SR The role of correlations in direction and contrast coding in the primary visual cortex. J Neurosci 27, 2338–2348, doi: 10.1523/JNEUROSCI.3417-06.2007 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Goard MJ, Pho GN, Woodson J & Sur M Distinct roles of visual, parietal, and frontal motor cortices in memory-guided sensorimotor decisions. Elife 5, doi: 10.7554/eLife.13764 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Poort J et al. Learning Enhances Sensory and Multiple Non-sensory Representations in Primary Visual Cortex. Neuron 86, 1478–1490, doi: 10.1016/j.neuron.2015.05.037 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Britten KH, Shadlen MN, Newsome WT & Movshon JA The analysis of visual motion: a comparison of neuronal and psychophysical performance. Journal of Neuroscience 12, 4745–4765 (1992). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Kanitscheider I, Coen-Cagli R & Pouget A Origin of information-limiting noise correlations. Proceedings of the National Academy of Sciences 112, E6973–E6982 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Bullmore E & Sporns O Complex brain networks: graph theoretical analysis of structural and functional systems. Nat Rev Neurosci 10, 186–198, doi: 10.1038/nrn2575 (2009). [DOI] [PubMed] [Google Scholar]
- 31.Yu Y, Stirman JN, Dorsett CR & Smith SL Mesoscale correlation structure with single cell resolution during visual coding. bioRxiv, 469114 (2018). [Google Scholar]
- 32.Gregoriou GG, Gotts SJ & Desimone R Cell-type-specific synchronization of neural activity in FEF with V4 during attention. Neuron 73, 581–594, doi: 10.1016/j.neuron.2011.12.019 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Gregoriou GG, Gotts SJ, Zhou H & Desimone R High-frequency, long-range coupling between prefrontal and visual cortex during attention. Science 324, 1207–1210, doi: 10.1126/science.1171402 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Ruff DA & Cohen MR Attention Increases Spike Count Correlations between Visual Cortical Areas. J Neurosci 36, 7523–7534, doi: 10.1523/JNEUROSCI.0610-16.2016 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.van Kempen J et al. Top-down coordination of local cortical state during selective attention. Neuron 109, 894–904 e898, doi: 10.1016/j.neuron.2020.12.013 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Chen JL, Voigt FF, Javadzadeh M, Krueppel R & Helmchen F Long-range population dynamics of anatomically defined neocortical networks. Elife 5, doi: 10.7554/eLife.14679 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Doiron B, Litwin-Kumar A, Rosenbaum R, Ocker GK & Josic K The mechanics of state-dependent neural correlations. Nat Neurosci 19, 383–393, doi: 10.1038/nn.4242 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Churchland MM et al. Stimulus onset quenches neural variability: a widespread cortical phenomenon. Nat Neurosci 13, 369–378, doi: 10.1038/nn.2501 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Wagner MJ et al. Shared Cortex-Cerebellum Dynamics in the Execution and Learning of a Motor Task. Cell 177, 669–682 e624, doi: 10.1016/j.cell.2019.02.019 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Steinmetz NA, Zatka-Haas P, Carandini M & Harris KD Distributed coding of choice, action and engagement across the mouse brain. Nature 576, 266–273, doi: 10.1038/s41586-019-1787-x (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Britten KH, Newsome WT, Shadlen MN, Celebrini S & Movshon JA A relationship between behavioral choice and the visual responses of neurons in macaque MT. Vis Neurosci 13, 87–100, doi: 10.1017/s095252380000715x (1996). [DOI] [PubMed] [Google Scholar]
- 42.Keller AJ, Roth MM & Scanziani M Feedback generates a second receptive field in neurons of the visual cortex. Nature 582, 545–549, doi: 10.1038/s41586-020-2319-4 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Bondy AG, Haefner RM & Cumming BG Feedback determines the structure of correlated variability in primary visual cortex. Nat Neurosci 21, 598–606, doi: 10.1038/s41593-018-0089-1 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Zipser K, Lamme VA & Schiller PH Contextual modulation in primary visual cortex. J Neurosci 16, 7376–7389 (1996). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Mashour GA, Roelfsema P, Changeux JP & Dehaene S Conscious Processing and the Global Neuronal Workspace Hypothesis. Neuron 105, 776–798, doi: 10.1016/j.neuron.2020.01.026 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Cohen MX & Ranganath C Reinforcement learning signals predict future decisions. J Neurosci 27, 371–378, doi: 10.1523/JNEUROSCI.4421-06.2007 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Bassett DS & Bullmore E Small-world brain networks. Neuroscientist 12, 512–523, doi: 10.1177/1073858406293182 (2006). [DOI] [PubMed] [Google Scholar]
- 48.Oh SW et al. A mesoscale connectome of the mouse brain. Nature 508, 207–214, doi: 10.1038/nature13186 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
Additional References for Methods and Extended Data Figures.
- 49.Garrett ME, Nauhaus I, Marshel JH & Callaway EM Topography and areal organization of mouse visual cortex. J Neurosci 34, 12587–12600, doi: 10.1523/JNEUROSCI.1124-14.2014 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Kalatsky VA & Stryker MP New paradigm for optical imaging: temporally encoded maps of intrinsic signal. Neuron 38, 529–545, doi: 10.1016/s0896-6273(03)00286-1 (2003). [DOI] [PubMed] [Google Scholar]
- 51.Marshel JH, Garrett ME, Nauhaus I & Callaway EM Functional specialization of seven mouse visual cortical areas. Neuron 72, 1040–1054 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Zhuang J et al. An extended retinotopic map of mouse cortex. Elife 6, e18372 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Lecoq J et al. Visualizing mammalian brain area interactions by dual-axis two-photon calcium imaging. Nat Neurosci 17, 1825–1829, doi: 10.1038/nn.3867 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Lein ES et al. Genome-wide atlas of gene expression in the adult mouse brain. Nature 445, 168–176, doi: 10.1038/nature05453 (2007). [DOI] [PubMed] [Google Scholar]
- 55.Thevenaz P, Ruttimann UE & Unser M A pyramid approach to subpixel registration based on intensity. IEEE Trans Image Process 7, 27–41, doi: 10.1109/83.650848 (1998). [DOI] [PubMed] [Google Scholar]
- 56.Mukamel EA, Nimmerjahn A & Schnitzer MJ Automated analysis of cellular signals from large-scale calcium imaging data. Neuron 63, 747–760 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Kanitscheider I, Coen-Cagli R, Kohn A & Pouget A Measuring Fisher information accurately in correlated neural populations. PLoS Comput Biol 11, e1004218, doi: 10.1371/journal.pcbi.1004218 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Barker M & Rayens W Partial least squares for discrimination. Journal of Chemometrics: A Journal of the Chemometrics Society 17, 166–173 (2003). [Google Scholar]
- 59.Wold H Estimation of principal components and related models by iterative least squares. Multivariate analysis, 391–420 (1966). [Google Scholar]
- 60.Kohn A & Smith MA Stimulus dependence of neuronal correlation in primary visual cortex of the macaque. J Neurosci 25, 3661–3673, doi: 10.1523/JNEUROSCI.5106-04.2005 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Hotelling H in Breakthroughs in statistics Vol. 2 Perspectives in Statistics (eds Kotz S & Johnson NL) 162–190 (Springer-Verlag, 1992). [Google Scholar]
- 62.Witten DM & Tibshirani RJ Extensions of sparse canonical correlation analysis with applications to genomic data. Stat Appl Genet Mol Biol 8, Article28, doi: 10.2202/1544-6115.1470 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Watts DJ & Strogatz SH Collective dynamics of ‘small-world’networks. Nature 393, 440–442 (1998). [DOI] [PubMed] [Google Scholar]
- 64.Honey CJ, Kotter R, Breakspear M & Sporns O Network structure of cerebral cortex shapes functional connectivity on multiple time scales. Proc Natl Acad Sci U S A 104, 10240–10245, doi: 10.1073/pnas.0701519104 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Lu J, Yu X, Chen G & Cheng D Characterizing the synchronizability of small-world dynamical networks. IEEE Transactions on Circuits and Systems I: Regular Papers 51, 787–796 (2004). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The data that support the findings of this study are available from the corresponding authors upon reasonable request.


