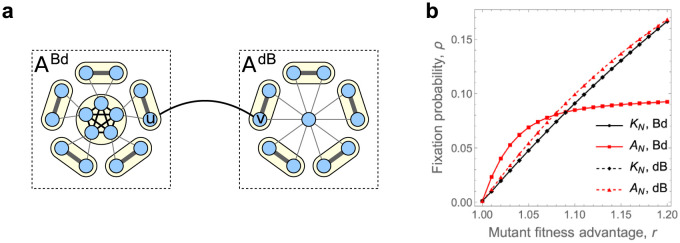
Fig 3. Simultaneous Bd- and dB-amplifier A_N.

a, The graph A_N is composed of two large chunks A^Bd and A^dB that are connected by a single edge. The chunk A^dB is a Fan graph with f nodes. The chunk A^Bd is a fan-like graph with a vertices in a central hub and b blades of two nodes each. The total population size is N = a + 2b + f (here a = b = 5, f = 11, and N = 26). The edge weights are defined such that different circled units within the chunks interact only rarely, and the chunks themselves interact even more rarely. b, Here we consider graph A_N with population size N = 1001 and (a, b, f) = (30, 85, 801). The fixation probabilities under Bd- and dB-updating are computed by numerically solving the underlying Markov chain. We find that the inequality ${\rho }_r^{\text{Bd}}\left(A_N\right)>{\rho }_r^{\text{Bd}}\left(K_N\right)$ is satisfied for r ∈ (1, 1.09) and the inequality ${\rho }_r^{\text{dB}}\left(A_N\right)>{\rho }_r^{\text{dB}}\left(K_N\right)$ is satisfied for r ∈ (1, 1.2). In particular, at r = 1.05 the ratios satisfy ${\rho }_r^{\text{Bd}}\left(A_N\right)/{\rho }_r^{\text{Bd}}\left(K_N\right)>1.44$ and ${\rho }_r^{\text{dB}}\left(A_N\right)/{\rho }_r^{\text{dB}}\left(K_N\right)>1.14$.