Quantum corrections in vibrational and electronic condensed phase spectroscopy: Line shapes and echoes

Abstract

Various linear and nonlinear vibrational and electronic spectroscopy experiments in liquids are usually analyzed within the second-cumulant approximation, and therefore the fundamental quantity of interest is the equilibrium time-correlation function of the fluctuating transition frequency. In the usual approach the “bath” variables responsible for the fluctuating frequency are treated classically, leading to a classical time-correlation function. Alternatively, sometimes a quantum correction appropriate for relatively high temperatures is included, which adds an imaginary part to the classical time-correlation function. This approach, although appealing, does not satisfy detailed balance. One can consider a similar correction, but where detailed balance is satisfied, by using the harmonic quantum correction factor. In this article, we compare these approaches for a model system and two realistic examples. Our conclusion is that for linear spectroscopy the classical result is usually adequate, whereas for nonlinear spectroscopy it can be more important to include quantum corrections.

Spectroscopy is a powerful experimental tool for obtaining information about molecular dynamics in condensed phases, since the frequency at which a molecule absorbs light (be it an electronic or vibrational transition) is perturbed by its local environment, and as this environment changes in time the frequency of the molecule fluctuates accordingly. In the limit that these fluctuations are relatively fast (the homogeneous limit), then one can extract some information about their dynamics by simply measuring the width of the absorption line shape (1, 2). On the other hand, when these frequency fluctuations occur slowly (the inhomogeneous limit), then the line shape contains no dynamical information, and in fact is simply proportional to the distribution of frequencies (2). In this limit experiments such as the three-pulse echo are particularly useful, as they allow one to recover dynamical information absent in the line shape (3).

Even within the two-level approximation (the molecule is considered to have only a ground state and a single vibrational or electronic excited state), the interpretation of experiments such as the three-pulse echo is difficult. The theoretical expression that describes the echo response is quite complicated and involves averages of exponentials of integrals of the fluctuating frequency operator (3, 4). To make progress, one typically uses a truncated cumulant expansion (3–5). Although this approximation is uncontrolled [which is sometimes accurate and sometimes not (6–9)], it allows one to express the echo response as a function only of the equilibrium frequency time-correlation function (FTCF). One of the main goals of echo experiments, then, is to extract this FTCF.

In general, the FTCF should be calculated quantum mechanically, and as such it is, of course, complex (10). To simplify matters, one often assumes that the system is classical enough that the real part of the quantum FTCF can be replaced by the classical FTCF, and the imaginary part can simply be neglected (8, 11–21). Alternatively, one can include the imaginary part of the quantum FTCF approximately (3, 4, 22–26) since in the high-temperature limit it is proportional to the time derivative of the classical FTCF (27, 28). The important point is that in either case the echo response depends on a single real function of time. One can assume a functional form with several adjustable parameters for this classical FTCF, and then obtain the parameters by fitting the measured spectroscopic observables (4, 12, 14, 18–21, 24, 26).

If the system is sufficiently classical (that is, the temperature is high enough compared with the relevant characteristic frequencies), then either neglecting the imaginary part of the quantum FTCF, or using its high-temperature approximation, will be adequate. On the other hand, if the system is not sufficiently classical, then these approximations may be quite inaccurate. Recently, several approaches to calculating quantum time-correlation functions have appeared in the literature and for certain problems and applications are very promising (29–32). In general, however, it is still not possible to perform accurate calculations of general quantum time-correlation functions, especially those involving operators that are nonlinear in coordinates or momenta. Nevertheless, simple (but ad hoc) prescriptions for obtaining approximate quantum time-correlation functions from their classical counterparts do exist and involve what are known as quantum correction factors (QCFs) (10, 28, 33–38). These QCFs are somewhat similar in spirit to the high-temperature approximation discussed above, but would appear to be superior in that they obey detailed balance (whereas the high-temperature approximation obeys detailed balance only to first order in ℏ).

Many different QCFs have appeared in the literature (10, 28, 33–37), and these different QCFs can lead to quite different approximations for quantum time-correlation functions. These differences become especially apparent in the frequency domain at high frequency (28, 39). By comparing to exact model problems (28) or approximate but presumably quite accurate semiclassical calculations (40) one can obtain some intuition and experience about which QCFs are most appropriate for a given type of problem. For example, for the problem of vibrational energy relaxation, where the rate constant is proportional to the Fourier transform of a certain quantum time-correlation function, for large vibrational energy gaps between initial and final states we have found the harmonic-Schofield QCF to be useful (28, 34). For vibration–vibration energy transfer in liquids we have suggested some QCFs that involve products of the harmonic and harmonic-Schofield forms (34). For certain problems in the time domain, such as the velocity time-correlation function for a neat fluid, the harmonic QCF can be quite accurate (30, 40).

So the question remains, for vibrational and electronic spectroscopy in condensed phases, and especially in liquids, are the usual classical or high-temperature approximations to the FTCFs adequate, or is the situation typically quantal enough so that one should instead pursue other approaches such as those involving QCFs? To get a rough answer to this question, consider that from both simulation and experiment it appears that at room temperature aqueous solution produces the fastest FTCF decays, which are on the order of 40 fs (6, 26, 41–43). Thus, the characteristic (angular) frequency ω_c is the inverse of this time or 2.5 × 10¹³ s^–1, which is 133 cm^–1, or somewhat less than kT at room temperature (205 cm^–1). Since in this instance ℏω_c ≃ kT, it suggests that quantum effects, although possibly significant, will not be enormous.

The primary goal of this article is to answer the above question more quantitatively; that is, to determine whether and when it is necessary to include quantum effects related to the FTCF in the calculation of line shapes and the three-pulse echo response. We are aware of only one calculation along these lines in the literature, by Kwac and Cho (44), in which the amide I line shape for N-methylacetamide in water was calculated with and without the standard and harmonic QCFs. We will begin by considering a simple analytic model for the classical FTCF and calculate the line shape and integrated three-pulse echo peak shift (3PEPS) in the classical limit, the high-temperature approximation, and using the harmonic QCF, for different values of the two relevant dimensionless parameters (see below). The results allow us to understand, in a quite general sense, when quantum effects are important. Even though the harmonic QCF represents an uncontrolled approximation, and therefore the conclusions we reach based on this approximation cannot be quantitatively accurate, we believe they are still qualitatively useful.

We will then consider two specific examples: the vibrational FTCF for the OH stretch of HOD in liquid D₂O, which comes from simulation (42), and the electronic FTCF for coumarin 343 in water from time-resolved Stokes shift experiments (43). In both cases we find that quantum effects for the line shape are really very modest. For the integrated 3PEPS, we find that for the vibrational problem quantum effects again are quite small, whereas for the electronic case they are more significant.

Theoretical Preliminaries

We begin by considering a two-level electronic or vibrational problem, with Hamiltonian

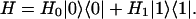[1]

|0〉 and |1〉 are the ground state and relevant excited state, respectively, and H₀ and H₁ are the associated quantum-mechanical Hamiltonians for all other (“bath”) degrees of freedom. Within the condon (the transition dipole operator is independent of these bath coordinates), semiclassical, and cumulant approximations, the absorption line shape is given by (1, 3, 45–47)

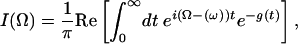[2]

where ω is defined by ω = (H₁ – H₀)/ℏ, ω(t) = eⁱH^{0t/ℏωe–iH0t/ℏ}, 〈A〉= Tr[e^–βH0A]/Tr[e^–βH0] for any operator A, β = 1/kT, δω(t) = ω(t) – 〈ω〉,

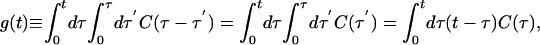[3]

and C(t) is the quantum FTCF C(t) ≡ 〈δω(t)δω(0)〉. Since C(t) is complex, so is g(t).

In general, the three-pulse echo response for a two-level system is given by a sum of four terms, commonly denoted R_i(t₃, t₂, t₁) for i = 1 – 4 (3). In the limit of infinitely short excitation pulses, only the so-called rephasing terms R₂ and R₃ contribute (3, 4). Performing the cumulant expansion for each of these terms, truncating at second order, and adding, yields (3, 4)

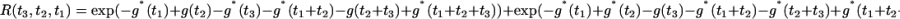[4]

In this work we will consider one particular echo observable, the integrated 3PEPS (7, 25, 48, 49). In this experiment one measures the time-integrated intensity

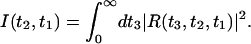[5]

The peak shift, 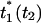, is defined as the value of t₁ that maximizes I(t₂, t₁) for a particular value of t₂.

First, consider the classical limit of the above. In this case the quantum FTCF is replaced by its classical analogue C_c(t), which is real, leading to a real line-shape function g(t). Thus, for example, (unlike in the general quantum-mechanical case) the line shape is symmetric. Also, in the third-order response function the two terms in Eq. 4 are identical and real.

One can easily include the effects of quantum mechanics as a high-temperature correction to this (infinite-temperature) classical limit (3). One can derive this correction very simply by considering the symmetry relation between the real and imaginary parts of the quantum FTCF (27, 28):

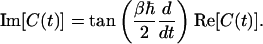[6]

At high temperature, the argument of the tangent is small, and so the function can be expanded in a Taylor series:

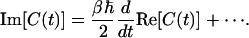[7]

Re[C(t)] can then be expanded in powers of ℏ: the zeroth-order term gives the classical FTCF C_c(t), and the first correction is of order ℏ² (50). Therefore, to first order in ℏ we have

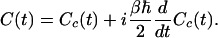[8]

In this case, the line-shape function, from the second equality in Eq. 3, is given by the familiar expression (3)

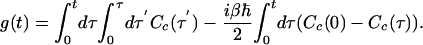[9]

Note that the symmetry relation between the real and imaginary parts of the quantum FTCF in Eq. 6 is very closely related to the detailed balance property Ĉ(–ω)=e^–βℏωĈ(ω), which must be satisfied by any quantum time-correlation function (10, 28). In the above, Ĉ(ω) is the Fourier transform of the quantum FTCF: 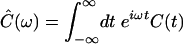. Since the high-temperature result of Eq. 8 comes from the first-order (in ℏ) expansion of Eq. 6, it follows that this high-temperature expression for the quantum FTCF satisfies detailed balance only to first order in ℏ.

In a similar spirit one can consider other useful approximations, which are also simple to apply, but satisfy detailed balance exactly (that is, to all orders in ℏ). These approaches involve so-called QCFs (10, 28, 33–37). In most cases, the QCF, Q(ω), is defined by Ĉ(ω) = Q(ω)Ĉ_c(ω), where the Fourier transform of the classical FTCF, Ĉ_c(ω), is defined as above. In other words, within this simple approach, to obtain the quantum FTCF C(t) from the classical FTCF C_c(t), one Fourier transforms the latter, multiplies by the QCF, and then inverse Fourier transforms. By construction Q(ω) is chosen so that Ĉ(ω) satisfies detailed balance. Still, there are many different possible choices for the QCF. One interesting choice, introduced >40 years ago by Schofield (51) is Q(ω) = e^βℏω/2. This result follows from the approximation C(t) = C_c(t + iβℏ/2), which when expanded to first order in ℏ gives precisely Eq. 8. It turns out, however, that the Schofield QCF does not generally provide an accurate approximation to quantum time-correlation functions (28). On the other hand, one that does appear to be generally more useful (28, 34, 40) is the harmonic QCF, given by (28, 35, 36, 39) Q(ω) = βℏω/(1 – e^–βℏω). This QCF is exact when the relevant operator (in this case δω) is a linear combination of harmonic (hence the name) coordinates. In this situation Im[C(t)] = (βℏ/2) dC_e^(t)/dt holds exactly (28). Therefore, in the harmonic QCF approach the imaginary part of the FTCF is the same as in the high-temperature approximation of Eq. 8. But since the harmonic QCF approach in general gives Re[C(t)] ≠ C_c(t) (which, of course, is correct), the harmonic QCF approximation to g(t) is not the same as the high-temperature approximation in Eq. 9. In fact, presumably this harmonic QCF leads to a better approximation, since detailed balance is satisfied exactly.

Results for a Model Classical FTCF

Despite the widespread use of the classical approximation, with or without the high-temperature correction, we have not found any discussion in the literature of whether or not these approximations are generally valid. Nor, with the single exception of the work of Kwac and Cho (44), have we found any attempt to apply QCFs to this problem. To address these two issues, we first focus on a simple analytical model for the classical FTCF: C_c(t) = Δ² sech(π t/2τ). This model has the attractive features that it gives the correct quadratic behavior at short times and decays exponentially at long times. It is characterized by the rms frequency fluctuation Δ, and correlation time τ [defined by τ = 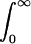dt C_c(t)/C_c(0)]. Thus, the model FTCF is determined by two “frequencies,” Δ and 1/τ. In the classical (infinite-temperature) limit only these two parameters are relevant, and in fact their dimensionless ratio Δτ determines whether the line shape is in either of the homogeneous (Δτ ≪ 1) or inhomogeneous (Δτ ≫ 1) limits (2). At finite temperature a third frequency 1/ℏβ enters the problem, and thus there are now two relevant dimensionless ratios. Since the general problem of quantum effects is motivated by considering the ratio of temperature to the characteristic frequencies associated with the bath dynamics, a natural choice for the second dimensionless ratio is therefore βℏ/τ (rather than βℏΔ). For a given Δτ, then, as βℏ/τ tends to zero we recover the classical result.

For the analytic model described above we evaluated both the line shape and the 3PEPS for a range of values of the two dimensionless ratios Δτ and βℏ/τ. The line shape was calculated from Eq. 2, and the peak shift was calculated from Eqs. 4 and 5. In both cases in the classical limit g(t) is obtained from the first term in Eq. 9. In this section our goal is to assess when the classical limit ceases to be accurate. To this end, since the harmonic QCF result is presumably more accurate than the high-temperature approximation, we compare the classical result with the former. For the harmonic QCF approach g(t) is obtained from Eq. 3.

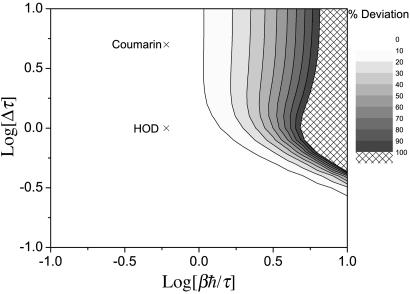
For the line shape we first focus on the full width at half maximum line width, and in particular on deviations between the classical line width Γ_c, and the harmonic QCF line width Γ. The normalized deviation (Γ–Γ_c)/Γ_c is shown in Fig. 1, as a function of Δτ and βℏ/τ. The contours show percent deviation. One first sees that when βℏ/τ is <1, the deviation is <10% (that is, the classical approximation is quite good), for any value of Δτ. One also sees that as Δτ gets small, the classical approximation works well even for larger values of βℏ/τ (lower temperatures).

Fig. 1.

Contour plot showing the percent deviation for the normalized line width (Γ–Γ_c)/Γ_c as a function of the two dimensionless ratios, βℏ/τ and Δτ. The Xs mark the estimated locations in this phase diagram of the two systems discussed in Two Examples.

Certainly it is to be expected that as βℏ/τ gets small this deviation disappears. What is a little surprising is that when βℏ/τ is as large as 1, the deviation is still <10%. In contrast, consider a different but related application of the harmonic QCF: the Fourier transform of the quantum velocity time-correlation function for neat neon at 30 K (40). In this case, the characteristic frequency can be determined from the peak in the Fourier transform of the classical velocity time-correlation function, which is at ≈17 cm^–1 and gives βℏ/τ ≃ 0.8. Except for at zero frequency, where the harmonic QCF approach is constrained to give the classical answer, for this neon system in general the deviations between the harmonic QCF and classical results are a factor of two or more. Thus for the current line-shape problem, it must be that the line width is dominated by the low-frequency behavior of Ĉ(ω) and hence is similar to the classical result. In fact, this observation also explains the surprising (at first glance) result that for small Δτ there is little deviation between the harmonic QCF and classical results even when βℏ/τ > 1. This agreement occurs because when Δτ ≪ 1 one is in the homogeneous limit (2), in which case one can take the long-time limit of Eq. 3, which gives 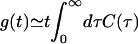. The imaginary part of the quantum FTCF produces a frequency shift (which does not affect the line width), whereas the real part gives tĈ(0)/2, which, since it is the zero-frequency Fourier transform, is the same as the classical result.

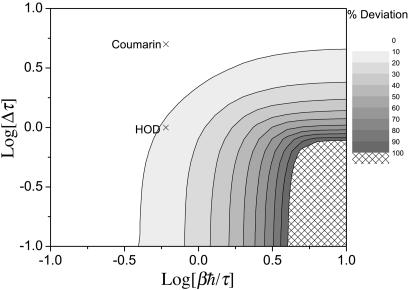
We next consider the line shift. To do so we first set 〈ω〉 = 0. In the classical limit the line shape is symmetric, and so the maximum occurs at Ω= 0. For the harmonic QCF approach the line shape is in general asymmetric, with a maximum at some frequency Ω_p. As a measure of the deviation between the classical and harmonic QCF peak frequencies, we consider the dimensionless ratio Ω_p/Γ_c, which is plotted in Fig. 2. Again, we find that at higher temperatures (in this case when βℏ/τ < 0.4), there is little difference between the classical and harmonic QCF approaches. And in contrast to the line width, here we see that for large Δτ the classical result is accurate even for lower temperatures. This result is also relatively easy to understand, since for Δτ ≫ 1 (the inhomogeneous limit) (2), one can take the short-time limit of Eq. 3, which gives g(t) ≃ t²C(0)/2, and since the initial value of the quantum FTCF is real, there is no line shift.

Fig. 2.

Contour plot showing the percent deviation for the normalized (peak) line shift Ω_p/Γ_c as a function of the two dimensionless ratios, βℏ/τ and Δτ. The Xs mark the estimated locations in this phase diagram of the two systems discussed in Two Examples.

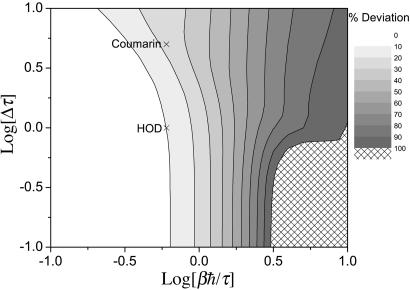
Finally, we compare classical and harmonic QCF results for the integrated 3PEPS. This peak shift is a function of the delay time t₂, and so to quantify the deviations between these two results we consider

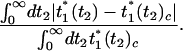[10]

The results are shown in Fig. 3. Here again we find that as long as βℏ/τ < 0.6 (and also in this case as long as Δτ is not too much larger than 1), we find that the classical result is accurate. For lower temperatures the classical result is a uniformly poor approximation regardless of the value of Δτ.

Fig. 3.

Contour plot showing the percent deviation for the normalized integrated 3PEPS (see text) as a function of the two dimensionless ratios, βℏ/τ and Δτ. The Xs mark the estimated locations in this phase diagram of the two systems discussed in Two Examples.

Our general conclusion, then, is that for high enough temperatures such that ℏω_c/kT < 0.4, 0.6, and 1, for the line shift, the echo peak shift, and the line width, respectively, the classical result is adequate.

Two Examples

Armed with these general results, we now consider the application of these ideas to real systems. There are two questions: (i) For room-temperature liquids where does one typically fall in the above 2D phase diagrams? (ii) For real systems where the FTCF decays on multiple time scales, are these general conclusions still valid?

To answer these questions we will consider two examples: the OH stretch vibrational transition of HOD in liquid D₂O and the lowest singlet-singlet electronic transition of coumarin 343 in water. The results that we will use for the classical FTCFs come from simulation (42) and time-resolved fluorescence experiments (43), respectively. The FTCFs for both of these systems have a relatively fast initial decay of ≈40 fs, which (as discussed in the Introduction) would lead one to believe that quantum-mechanical effects could be important, and which is the rationale for choosing these systems. The HOD/D₂O simulation of the SPC/E water model gives Δ = 141 cm^–1 (42), and considering only the short-time decay with τ = 40 fs, leads to Δτ ≃ 1. The electronic transition of the coumarin system has a much larger value of Δ ≃ 615 cm^–1 [which we obtain from the computer simulation estimate of 1,850 cm^–1 for the Stokes shift (43), ω_S, and using the linear response result (3, 47) that kTω_S = ℏΔ²]. Again taking τ = 40 fs gives in this case Δτ ≃ 5. Both systems are at room temperature, giving a value of βℏ/τ ≈ 0.6. The values of βℏ/τ and Δτ for these two systems are indicated in the phase diagrams of Figs. 1, 2, 3. From Figs. 1, 2, 3 our conclusion is that for HOD/D₂O the classical approximation should be good for the line width and fair for the line shift and the echo peak shift, whereas for coumarin the classical approximation should be good for both the line width and line shift, but show substantial error for the echo peak shift.

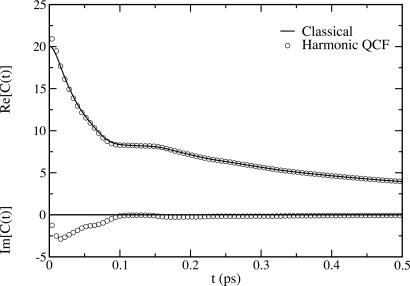
We next consider the HOD/D₂O system quantitatively. In Fig. 4 we show the classical FTCF obtained from computer simulation using the SPC/E model (42). Note, of course, that the classical FTCF has no imaginary part. We also show the real and imaginary parts of the approximate quantum FTCF obtained by using the harmonic QCF approach. We see that the real part of the quantum FTCF is almost identical to the classical result, whereas the imaginary part is demonstrably nonzero up to ≈100 fs. Also note that in the high-temperature approximation discussed above, the real part is given by the classical FTCF, whereas the imaginary part is identical to that in the harmonic QCF approximation. Thus in this case one can anticipate that the high-temperature and harmonic QCF results for the spectroscopic observables will be very similar.

Fig. 4.

Real and imaginary parts of the classical and harmonic QCF FTCFs for HOD in D₂O at 300 K. The units of the FTCF are 10⁴ (cm^–1)².

We next calculated line shapes (data not shown), from the classical, harmonic QCF, and high-temperature approximations [for the latter we use Eq. 9 for g(t)]. As anticipated, the harmonic and high-temperature approximations are nearly identical and give the same line width as the classical result, but have a small line shift of ≈14 cm^–1 or ≈5% of the classical width. We also performed analogous calculations for the echo peak shift. We found that the high-temperature approximation agrees well with the classical result, whereas the harmonic QCF approach is slightly different (≈8% deviation as defined above). Even the small difference between the high-temperature approximation and the harmonic QCF result is somewhat surprising in light of the above.

Looking at Figs. 1, 2, 3, we find that these results are more or less consistent with the predictions of the analytic model. For the HOD/D₂O values of Δτ and βℏ/τ, the model predicts that the classical result would make no significant error in the line width, but a ≈12% deviation from the harmonic QCF approach for the line shift and a 10% deviation for the 3PEPS. As the simulation FTCF for water is more complicated than the simple analytic function, this qualitative agreement with the above is about as accurate as one could anticipate.

Next, we turn to the electronic transition of coumarin in water. In this case the classical FTCT can be represented as a sum of a Gaussian and two exponential components (43). Comparison of the classical and harmonic QCF result for the FTCF (data not shown) indicates that the situation is qualitatively very similar to that in Fig. 4. Comparing the classical, high-temperature, and harmonic QCF line shapes (data not shown), we found that these three results are very similar; the deviation of the classical result from the harmonic QCF approach for the width is ≈2%, and the harmonic QCF line shift is ≈38 cm^–1, which normalized by the classical width results in a deviation of <3%. In Fig. 5 we show the corresponding results for the echo peak shift. Here, the high-temperature and harmonic QCF approaches are similar, but differ from the classical result by ≈32%. Once again, the qualitative predictions of the simple analytical model that the deviations for both the width and shift are quite small (≈4% and 2%, respectively), but that the deviation in the peak shift is >20%, are borne out by these more detailed calculations.

Fig. 5.

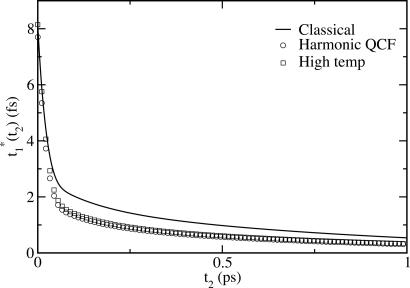
Classical, harmonic QCF, and high-temperature 3PEPS for coumarin in water at 300 K.

Conclusion

In this article we have addressed the question of if and when quantum corrections are necessary in the calculation of linear and nonlinear vibrational and electronic liquid-state spectroscopy. Naive frequency- and time-scale estimates suggest that they will indeed be important. Our conclusions are based on the use of the harmonic QCF to approximate quantum effects. As this approximation is uncontrolled it will never have quantitative accuracy. Nonetheless, given that the harmonic QCF is at least correct to first order in βℏω (28), it seems likely that our conclusions about when quantum effects are important will have general qualitative validity.

Consideration of a simple model problem shows that quantum effects for real systems should actually be quite modest. This suggestion is bolstered by detailed calculations on two specific systems. We find that quantum effects are most important for nonlinear spectroscopy, such as the integrated 3PEPS. In the case of strongly inhomogeneously broadened systems like the electronic spectroscopy of coumarin in water, for example, quantum effects lead to an ≈30% correction to the simple classical result. Much of this correction is captured by the commonly used high-temperature approximation. However, for a presumably more accurate approach (and one that at least obeys detailed balance), we suggest the use of the harmonic QCF.