Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2024 Mar 30;63(15):6898–6908. doi: 10.1021/acs.inorgchem.4c00345

Electronic, Vibrational, and Structural Properties of the Natural Mineral Ferberite (FeWO4): A High-Pressure Study

Daniel Diaz-Anichtchenko †, Jesus E Aviles-Coronado ‡, Sinhué López-Moreno §,∥,*, Robin Turnbull †, Francisco J Manjón ⊥, Catalin Popescu #, Daniel Errandonea †,*
PMCID: PMC11022173  PMID: 38554090

Abstract

graphic file with name ic4c00345_0012.jpg

This paper reports an experimental high-pressure study of natural mineral ferberite (FeWO4) up to 20 GPa using diamond-anvil cells. First-principles calculations have been used to support and complement the results of the experimental techniques. X-ray diffraction patterns show that FeWO4 crystallizes in the wolframite structure at ambient pressure and is stable over a wide pressure range, as is the case for other wolframite AWO4 (A = Mg, Mn, Co, Ni, Zn, or Cd) compounds. No structural phase transitions were observed for FeWO4, in the pressure range investigated. The bulk modulus (B0 = 136(3) GPa) obtained from the equation of state is very close to the recently reported value for CoWO4 (131(3) GPa). According to our optical absorption measurements, FeWO4 has an indirect band gap that decreases from 2.00(5) eV at ambient pressure to 1.56(5) eV at 16 GPa. First-principles simulations yield three infrared-active phonons, which soften with pressure, in contrast to the Raman-active phonons. These results agree with Raman spectroscopy experiments on FeWO4 and are similar to those previously reported for MgWO4. Our results on FeWO4 are also compared to previous results on other wolframite-type compounds.

Short abstract

A systematic study of the high-pressure behavior of iron tungstate is reported. A combination of density functional theory calculations, X-ray diffraction, Raman spectroscopy, and optical absorption experiments has been used to determine the effect of pressure on the structural, vibrational, and electronic properties of iron tungstate. A comparison between present results and previous results from related tungstates is also made.

1. Introduction

Wolframite-type AWO4 compounds (A = Mg, Mn, Fe, Co, Ni, Zn, Cd) form an interesting class of bimetallic oxides because of their properties,1,2 including the magnetic properties for A = Fe, Co, and Ni,3 and even multiferroic properties in the case of MnWO4.44 The magnetism is dominated by partially filled 3d orbitals of the divalent A cations.5 In addition to interesting magnetic properties, wolframites, such as FeWO4, have been used to develop supercapacitors and photocatalytic and photoluminescent materials.6−8 FeWO4 can be used for the cheap and environmentally friendly production of ammonia9 and for applications in phase-change optical recording devices.10 Therefore, accurate knowledge of the physical properties of this material is essential for its technological applications.

FeWO4 is one of the less studied AWO4 wolframites.1 Curiously, most studies on this material have focused on nanoparticles,11,12 with single crystals mainly synthesized to characterize their magnetic properties.10 FeWO4 showed an antiferromagnetic behavior at low temperatures with a Néel temperature of 75 K.10 In particular, the characterization of the band gap energy at ambient conditions has been conducted on compacted powders using diffuse reflectance10,12−14 rather than accurate optical absorption measurements on single crystals.15 As a consequence, the reported values of the band gap energy range from 1.8 to 2.2 eV. Additionally, there are previous Raman studies at ambient pressure, but not all of the expected Raman-active modes have been measured in these studies.2,11,16 On the other hand, nothing is known about the compressibility and structural stability of FeWO4 under high-pressure (HP) conditions.

The crystal structure of FeWO4 is monoclinic (space group P2/c) and contains two formula units per unit cell.17 The structure is shown in Figure 1a. The metal ions (Fe2+ and W6+) occupy half of the octahedral holes in a slightly deformed hexagonal close-packed lattice of oxygen atoms. The crystal structure can be described as two zigzag chains of edge-sharing FeO6 or WO6 octahedral units running along [001]. The high-spin d6 electronic configuration of Fe2+ distorts the FeO6 octahedron due to the Jahn–Teller effect.18

Figure 1.

Figure 1

Open in a new tab

(a) Crystal structure of the mineral ferberite (FeWO4). FeO6 octahedra are shown in brown, and WO6 octahedra are shown in gray. The oxygen atoms are shown in red. The black solid lines represent the unit cell. The arrows indicate the crystal axes. (b) Photograph of the ferberite crystal used for experiments.

It is well known that pressure can drastically change the interatomic distances in solids, which in turn can lead to a variety of fascinating phenomena such as metallization,19 superconductivity,20 changes in chemical bonding,21 and the formation of new compounds.22 Wolframites have been studied under compression over the past decade by several research groups.1 Due to their bulk modulus, an external pressure of 10 GPa causes a 10% change in the unit-cell volume. Consequently, the electronic, magnetic, vibrational, and elastic properties can be dramatically altered.23,24 However, it is known that several AWO4 wolframite-type compounds do not undergo phase transitions up to pressures of around 20 GPa.1,2,7,23−25

In the stability range of the wolframite structure, compression is anisotropic, with the symmetry of the structure decreasing with increasing pressure.23,24 The structural changes cause a decrease in the electronic band gap energy of NiWO4, MnWO4, and CoWO4,5,23,26 which has been attributed to an increase in hybridization between the 3d electrons of the divalent A cation and the 2p electrons of the oxygen atoms. However, the influence of the pressure on the properties of FeWO4 has not been investigated. The influence of the pressure on the crystal structure of FeWO4 has also not been studied experimentally. Therefore, we considered it timely to conduct a study of the HP behavior of FeWO4 and to investigate the Raman spectrum and optical absorption of single crystals of FeWO4 in detail. Here, we report optical absorption, Raman, and X-ray diffraction (XRD) measurements at ambient pressure and HP in a natural crystal of the mineral ferberite (FeWO4). The experimental results are complemented by first-principles calculations.

2. Experimental Details

The experiments were performed on samples obtained from natural ferberite crystals provided by Fabre Minerals from the Monte Cambillaya mining district, La Paz, Bolivia. An image of the original crystal is shown in Figure 1b. The dimensions of the natural crystal were 2.9 cm × 2.4 cm × 1.3 cm. Electron microprobe analysis was performed to determine the impurities present in the natural crystal. Nb (0.06%) and Ta (0.02%) were the only detected impurities. Such a minimal concentration of impurities is not expected to affect the properties studied in this work. Optical absorption and Raman experiments were performed on 40 μm × 40 μm × 10 μm platelets oriented perpendicular to the cleavage plane (010).10 The color of the crystals was dark brown in transmitted light. Powder XRD measurements were performed on a finely ground powder from a fragment of the original single crystal. All experiments at HP were performed using a membrane-driven diamond-anvil cell with diamond culets of 500 μm in diameter. Stainless steel gaskets preindented to a thickness of 55 μm were used. The pressure-transmitting medium was a 4:1 methanol–ethanol mixture, which provides quasi-hydrostatic conditions up to 10 GPa.27 Pressure was measured using ruby fluorescence with an error of less than 0.05 GPa.28

Synchrotron powder XRD experiments were performed at the BL04-MSPD beamline of ALBA synchrotron29 using a monochromatic X-ray beam with a wavelength of 0.4642 Å. The X-ray beam was focused down to a 20 μm × 20 μm spot. XRD was collected with a Rayonix SX165 charge-coupled device (CCD) image plate. The two-dimensional (2D) patterns were integrated using FIT2D,30 and FullProf was used to analyze (Rietveld refinement) the integrated 1D XRD patterns.31 Raman experiments were performed using an inVia Renishaw Raman spectrometer system with a 5× magnification objective. A laser wavelength of 682 nm with an output of less than 10 mW was used to avoid sample heating. The spectral resolution was greater than 2 cm–1. The optical absorption experiments were carried out in visible (Vis)–near-infrared (NIR) range using an optical setup consisting of a halogen lamp, reflecting optical objectives, and a Vis–NIR Ocean Optics spectrometer.32 The optical absorption was calculated by dividing the transmittance spectrum of the sample in normal incidence by the spectrum of the reference source.

3. Computational Details

First-principles calculations were performed within the framework of the density functional theory (DFT)33 and the projector-augmented wave (PAW)34,35 method as implemented in the Vienna Ab initio Simulation Package (VASP).36 A plane-wave energy cutoff of 520 eV was used to ensure high precision in calculations. The exchange-correlation energy was described within the generalized gradient approximation (GGA) in the GGA + U method with the Perdew–Burke–Ernzerhof for solids (PBEsol) functional37 to account for the strong correlation between the electrons in the d shell based on the method developed by Dudarev.38 In this method, Coulomb Interaction U and onsite exchange interaction JH are treated together as Ueff = U – JH. For our GGA + U calculations, we chose U = 6 eV and JH = 0.95 eV. Similar values were previously used with success in the study of other iron and ABO4 compounds.39−42 All properties computed in this study were calculated under the GGA + U approach. For the calculations, we considered nonmagnetic, ferromagnetic, and antiferromagnetic configurations. We found that for the pressures covered by this study, the configuration with the lowest energy is the antiferromagnetic one. All physical properties simulated in this work were calculated for this configuration.

The Monkhorst–Pack scheme43 was employed to discretize the Brillouin zone (BZ) integrations with a mesh 4 × 4 × 4, which corresponds to a set of 16 special k-points in the irreducible BZ for the wolframite structure. In the relaxed equilibrium configuration, the forces are less than 1 meV/Å per atom in each Cartesian direction. The highly converged results on forces are required to calculate the dynamical matrix using the direct force constant approach.44 This allows us to identify the irreducible representation and the character of the phonon modes at the zone center (Γ point). The electronic structure was obtained by using the primitive cell with a larger set of k-points.

4. Results and Discussion

4.1. XRD Measurements

Figure 2 shows powder XRD patterns of mineral ferberite (FeWO4) measured at selected pressures. The bottom trace of the figure shows the results at ambient pressure together with the results from the Rietveld refinement performed using the structural model reported in the literature.17 All measured peaks can be explained by the wolframite-type structure (space group P2/c).17 The goodness-of-fit parameters of the refinement are RWP = 4.16%, RP = 2.82%, and χ2 = 1.39, supporting a good agreement of the model with the experimental data. In Table 1, we can observe the good agreement between our structural parameters obtained at ambient pressure, those reported in the literature17 and those obtained from our DFT calculations.

Figure 2.

Figure 2

Open in a new tab

XRD patterns measured in natural mineral ferberite (FeWO4) at selected pressures. At ambient pressure (bottom, 10–4 GPa) and the highest pressure (top, 20.0 GPa), experimental data are shown with black symbols, Rietveld refinements with black lines, and residuals with green lines. Vertical ticks are the calculated positions for reflections. The Miller indices of the low-angle peaks are indicated.

Table 1. Unit-Cell Parameters (a, b, c, and β), Volume (V), and Atomic Positions of Natural Mineral Ferberite (FeWO4) Obtained from the Rietveld Refinements at Ambient Pressurea.

  exp. theo. ref (17)
a (Å) 4.742(2) 4.7142 4.730(3)
b (Å) 5.722(2) 5.7369 5.703(2)
c (Å) 4.971(2) 4.9512 4.952(2)
β (deg) 90.14(6) 90.513 90.0(2)
V (Å3) 134.9(2) 133.9 133.6(4)
atom site exp. theo. ref (17)
Fe 2f (0.5, 0.3234(5), 0.25) (0.5, 0.32182, 0.25) (0.5, 0.3256, 0.25)
W 2e (0, 0.1854(3), 0.25) (0, 0.16597, 0.25) (0, 0.1799, 0.25)
O1 4g (0.2158(9), 0.1049(9), 0.5775(9)) (0.21576, 0.10476, 0.56913) (0.2159, 0.1050, 0.5660)
O2 4g (0.2584(9), 0.3836(9), 0.0958(9)) (0.25518, 0.37562, 0.10428) (0.2538, 0.3744, 0.1096)
Open in a new tab
a

They are compared with results from present calculations and previous experiments.17

Figure 2 shows that the only change induced by pressure in the powder XRD pattern is the shift of peaks toward higher angles due to the contraction of the lattice parameters. We did not detect the emergence of any extra peaks up to 20 GPa. In fact, all XRD patterns up to this pressure can be properly refined assuming the same structural model used for the ambient pressure results. This is illustrated in Figure 2 by the Rietveld refinement of the XRD pattern measured at 20 GPa, which is the highest pressure measured. At this pressure, we obtained RWP = 6.33%, RP = 3.98%, and χ2 = 1.98, thereby confirming the assignment of the wolframite-type structure. Therefore, we can conclude that, as in other wolframites,11 there is no phase transition in FeWO4 up to 20 GPa.

Two important additional observations can be made from the XRD patterns. The first one is that we did not observe any significant peak broadening beyond the quasi-hydrostatic limit of the pressure medium (10 GPa).31 This suggests that the influence of nonhydrostatic stresses is negligible in our experiments. The second one is the splitting of several peaks as the pressure increases, which can be seen in Figure 2 by following the evolution of the 002/021 peaks and 1̅02/102/1̅21/121 peaks, which are close to 8 and 11°, respectively. This fact indicates that the compression is not isotropic, as we show next.

From the XRD results, the pressure dependence of the unit-cell parameters is obtained and compared with the results from the calculations (see Figure 3). Both experiments and calculations show a similar pressure dependence for the lattice parameters of the crystal structure. The only slight difference between calculations and experiments is that according to calculations the unit-cell parameters are slightly less compressible than in experiments. Such discrepancies are within the typical discrepancies between experiments and computational results in other wolframites.23 It might be possible to overcome them using different exchange-correlation functionals in calculations, but a systematic study of the optimum functional for FeWO4 is beyond the scope of this study. Our results confirm that the compression of FeWO4 is slightly anisotropic. In particular, the b parameter is the most compressible lattice parameter, and the c parameter is the least compressible, as is the case for CdWO4, MgWO4, and MnWO4 according to single-crystal XRD measurements.45 This result is confirmed by the fact that the Miller indices with k ≠ 0 move faster with pressure than those with k = 0.

Figure 3.

Figure 3

Open in a new tab

Pressure dependence of (a) lattice parameters a, b, and c, (b) unit-cell volume V, and (c) angle β of FeWO4. Solid (empty) symbols are results obtained from experiments (calculations). (b) Equations of state obtained from experiments (black line) and calculations (red line).

In Figure 3, it can be seen that according to the XRD data, there is an increase in the β angle with pressure, which also favors the aforementioned peak splitting described above. In experiments, two different trends are observed below and above 5 GPa. However, the slope change in the behavior of β at 5 GPa is within the experimental uncertainties, which suggests that the two different trends in the behavior of the β angle can be an experimental artifact. In fact, such a slope change is not observed in calculations (see the inset of Figure 3). Calculations predict a smooth behavior for the β angle, with a steeper increase than in experiments. A similar difference is observed when comparing the behavior of the β angle obtained from DFT calculations and XRD experiments in NiWO4.23

As shown in Figure 4a, the computed polyhedral volume of the distorted FeO6 octahedra compresses faster than that of the WO6 octahedra. This result is due to the stronger compression of the Fe–O distances (dFe–O) than the W–O distances (dW–O) (see Figure 4b). Note that W–O bonds are stronger (more ionic) than Fe–O bonds in terms of the Laplacian of the charge density at the respective bond critical point (∇2ρ).46,47 This is the reason behind the stiffness of W–O bonds in comparison to that of Fe–O bonds. On the other hand, Figure 4c shows that the polyhedral distortion index Δd, calculated using the definition established by Baur,48 decreases with pressure for the WO6 octahedra, but remains almost constant for FeO6. In Figure 4c, it can be seen that up to 20 GPa, the Jahn–Teller distortion is not suppressed by pressure effects. The fact that FeO6 octahedra are more compressible than WO6 octahedra can be correlated with the slightly anisotropic compressibility of FeWO4. The wolframite structure is formed by chains of FeO6 and WO6 octahedra, which alternate along the b-axis, and thus the change in volume of the FeO6 octahedra favors the compressibility along the b-axis rather than along the other axes.45 On the other hand, the fact that zigzag chains of WO6 octahedra run along the c-axis makes it the least compressible one.

Figure 4.

Figure 4

Open in a new tab

Pressure dependence of the computed (a) polyhedral volume, (b) interatomic distances dFe–O and dW–O, and (c) distortion index Δd in FeWO4.

Since the crystal structure of FeWO4 is monoclinic, the compressibility tensor is not diagonal, and a proper description of the compressibility of the material is obtained from the eigenvalues and eigenvectors of the compressibility tensor.49 We obtained these from our experiments using PASCal.50 The results are reported in Table 2. Among the principal axes of compressibility, the most compressible one is parallel to the b-axis, in agreement with our previous conclusions on axial compressibility.

Table 2. Eigenvalues, λi, and Eigenvectors, eνi, of the Isothermal Compressibility Tensor of FeWO4.

λ1 = 2.33(5) × 10–3 Gpa–1 eν1 = (0,1,0)
λ2 = 1.92(2) × 10–3 Gpa–1 eν2 = (10,0,1)
λ3 = 1.09(1) 10–3 Gpa–1 eν3 = (1,0,–10)
Open in a new tab

The results for the pressure dependence of the volume were fitted with a third-order Birch–Murnaghan equation of state51 using the program EoSFit.52 The obtained bulk modulus (B0), its pressure derivative (B0), and the volume (V0) at zero pressure are given in Table 3. The bulk modulus determined from our experiments, B0 = 136(2) GPa, agrees within two standard deviations with the bulk modulus previously reported for the rest of the AWO4 wolframites.1 The calculated bulk modulus is 10% larger than that determined from experiments. Such a difference is within the typical range of discrepancies between DFT calculations and experiments. A detailed discussion of the reason for this discrepancy can be found in ref (53).

Table 3. Unit-Cell Volume (V0), Bulk Modulus (B0), and Bulk Modulus Pressure Derivative (B0′) at Zero Pressure of FeWO4 Determined Using a Third-Order Birch–Murnaghan EOSa.

  V0 (Å3) B0 (GPa) B′0
experiment 134.9(5) 136(2) 5.0(4)
theoretical 133.9(1) 150(1) 4.8(2)
Open in a new tab
a

We present results from experiments and calculations.

4.2. Raman Measurements

According to group-theory analysis, FeWO4 has 36 vibrational modes at the Γ point of the Brillouin zone: Γ = 8Ag + 10Bg + 8Au + 10Bu. Three vibrations correspond to acoustic modes (Au + 2Bu); the rest are optical modes. This means that 18 Raman-active modes (8Ag + 10Bg) and 15 infrared (IR)-active modes (7Au + 8Bu) are expected. To the best of our knowledge, no IR experiments have been reported on FeWO4. Regarding the Raman-active modes, only seven modes were reported for FeWO4 in refs (11) and (16). In contrast, 15 were reported for FeWO4 in ref (2). The nondetection of all Raman modes in previous studies was due to mainly single-crystal orientation or overlapped peaks.

In Figure 5, we show the Raman spectrum of the natural ferberite mineral (FeWO4) at ambient pressure together with the fit we made, assuming peaks with a Lorentzian shape. The symmetry assignment of each Raman mode has been done with the theoretical results. Note that our Raman spectrum is similar to that reported for the mineral ferberite in the RRUFF database.54 In our measurements, we detected the 18 Raman-active modes predicted for FeWO4. Eleven modes can be directly visualized in Figure 5. The other seven modes are indicated by arrows in the figure. To clearly show the other, we have included a zoom of the 50–750 cm–1 region of the Raman spectrum. In this zoom, the seven weakest modes are also identified by arrows.55

Figure 5.

Figure 5

Open in a new tab

Raman spectrum of the natural mineral ferberite (FeWO4) measured at ambient conditions in a sample before loading it into the diamond-anvil cell. The black line corresponds to the experimental spectrum. The red line represents the overall fit. The contribution of each phonon to the fit is shown in different colors in the lower part of the figure. The 18 phonons are identified by asterisks (*). The arrows identify the weakest modes. The inset shows a zoom of the 50–750 cm–1 region to facilitate the identification of these peaks.

The values obtained for all Raman modes of FeWO4 are summarized in Table 4. They compare well to those previously reported.2 The good match obtained with the Lorentzian multipeak fitting analysis used for the deconvolution of the different modes and the comparison with previous studies make us confident in our mode identification. The modes at 192, 300, and 350 cm–1 were never reported before. The difference in wavenumber between this work and ref (2) is within 5 cm–1 (the accuracy of both setups is 2 cm–1). This could be due to an offset in the calibrations between the two setups and/or to the fact that the present study was carried out in a natural mineral and the previous study was performed in a synthetic sample.

Table 4. Wavenumbers of Raman-Active Modes in FeWO4 at Ambient Pressurea.

mode ωexp (cm–1), this work ωDFT (cm–1), this work ωexp (cm–1), ref (2) ωDFT (cm–1), ref (2)
Bg 91 97.8 86 92
Ag 129 130.9 124 132
Bg 155 159 154 162
Bg 178 183.7 174 179
Bg 192 194.9   184
Ag 206 222.9 208 213
Bg 271 275.5 266 263
Ag 284 279.1 299 278
Bg 300 301.1   295
Ag 328 333.1 330 330
Bg 350 350.2   350
Ag 398 393.7 401 406
Bg 502 502.1 500 483
Ag 539 536.3 534 530
Bg 648 644.1 653 637
Ag 688 686.8 692 676
Bg 775 764.4 777 754
Ag 875 869.2 878 866
Open in a new tab
a

Results from the present work are compared with those reported in the literature.2

Regarding calculations, the present results agree slightly better with our experiments than those of previous investigations.2 This difference could be mainly due to the exchange-correlation functional and the slight difference in the Ueff parameter. The relative difference between the present calculations and experiments is within 5%, which can be considered quite good.54Figure 4 shows that the strongest modes are in the highest-frequency region, corresponding to two Ag modes that can be assigned to internal symmetric vibrations of the WO6 octahedron. Not surprisingly, the strongest mode, which is assigned to the symmetric stretching vibration, in FeWO4 has nearly the same frequency (875 cm–1) as in MnWO4 (887.5 cm–1), NiWO4 (881 cm–1), and CoWO4 (887 cm–1).2 This is because the W–O distances and, hence, the force constants are nearly identical in the four compounds.

A selection of Raman spectra measured at different pressures is shown in Figure 6. The only changes observed in the spectra are a shift in the position of the modes and a decrease in their intensity. All spectra up to the highest pressure are compatible with the wolframite-type structure. We have observed the 18 modes only up to 2 GPa. The two weakest high-frequency modes cannot be distinguished from the background at this pressure. There are other modes that also cannot be detected up to the highest pressure (19.8 GPa), where only 12 Raman modes are observed.

Figure 6.

Figure 6

Open in a new tab

Raman spectra of natural mineral ferberite (FeWO4) at selected pressures. (a) The 50–600 cm–1 region. The spectra have been magnified five times to facilitate the identification of weak peaks. (b) The 600–1000 cm–1 region without magnification.

The pressure dependence of the Raman-active modes of ferberite is plotted in Figure 7a. A few low-frequency modes follow a quadratic pressure dependence, and the rest follow a linear trend. All modes harden under compression. In Figure 7a, we also plot the results of the DFT calculations, which are in very good agreement with the experimental results. In Table 5, we summarize the wavenumber (ω), the pressure coefficients at zero pressure (dω/dP), and the Grüneisen parameter (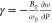Inline graphic, where ω0 is the wavenumber at zero pressure). The mode with the larger γ, i.e., the mode whose frequency varies more with the volume, is the Bg mode with wavenumber 350 cm–1. This is the internal bending mode of the WO6 octahedron. This is in agreement with the results reported for MgWO4 and MnWO4.2,7Figure 7a also shows that there are two phonon crossings between the Ag and Bg modes. One occurs at 5 GPa and the other at 15 GPa.

Figure 7.

Figure 7

Open in a new tab

(a) Pressure dependence of the Raman-active modes in FeWO4. Black (empty) symbols represent the experimental Bg (Ag) modes. Red (blue) solid lines are quadratic or linear fits to the experimental Bg (Ag) modes. The dashed lines represent the results of calculations (the color code is the same as for experiments). (b) Calculated pressure dependence of IR-active modes. Red (blue) lines represent the Bu (Au) modes. Solid lines have been used to identify the modes which soften under compression.

Table 5. Wavenumber (ω), Pressure Coefficient (dω/dP), and Grüneisen Parameter (γ) for Raman-Active and IR-Active Modes in FeWO4.

mode ωexp (cm–1) dω/dP (cm–1/Gpa) γ ωDFT (cm–1) dω/dP (cm–1/Gpa) γ mode ωDFT (cm–1) dω/dP (cm–1/Gpa) γ
Bg 91 0.66 0.99 97.8 0.38 0.73 Bu 163.0 0.07 0.10
Ag 129 0.59 0.62 130.9 0.22 0.32 Bu 206.3 –0.19 –0.17
Bg 155 0.89 0.78 159.0 0.69 0.82 Au 209.2 1.68 1.45
Bg 178 0.46 0.35 183.7 0.21 0.22 Bu 241.9 –1.20 –0.99
Bg 192 0.22 0.16 194.9 0.44 0.41 Bu 261.2 1.82 1.27
Ag 206 1.64 1.08 222.9 1.61 1.31 Bu 276.1 4.03 2.48
Bg 271 2.67 1.34 275.5 2.18 1.44 Au 319.2 –0.53 –0.32
Ag 284 0.53 0.25 279.1 0.37 0.25 Au 326.8 1.14 0.66
Bg 300 1.95 0.88 301.1 1.95 1.18 Au 415.6 2.83 1.23
Ag 328 2.53 1.05 333.1 2.34 1.27 Bu 446.9 4.35 1.71
Bg 350 4.36 1.69 3502 4.38 2.18 Au 496.9 4.16 1.50
Ag 398 0.59 0.20 393.7 1.41 0.67 Bu 526.0 2.12 0.75
Bg 502 3.13 0.85 502.1 3.11 1.13 Au 660.0 2.77 0.79
Ag 539 1.95 0.49 536.3 2.59 0.90 Bu 746.0 3.28 0.82
Bg 648 3.33 0.69 644.1 3.59 1.02 Au 838.1 2.37 0.54
Ag 688 2.87 0.57 686.8 2.92 0.79        
Bg 775 3.91 0.69 764.4 3.87 0.94        
Ag 875 1.95 0.30 869.2 2.28 0.50        
Open in a new tab

From the DFT calculations, we have obtained the frequency and symmetry assignment of the IR-active modes of FeWO4 as well as their pressure dependences. The results are summarized in Figure 7b and Table 5. They are presented for the sake of completeness and to help in mode assignment and identification in future IR absorption experiments. It can be observed that IR-active modes have a similar frequency distribution to Raman-active modes. In contrast to Raman-active modes, three IR-active modes soften with increasing pressure according to our calculations. The pressure dependence of IR modes has not yet been studied for other wolframites, so we do not know if the pressure-induced IR softening observed in FeWO4 is a fingerprint of this material or a common feature of the wolframite family. The IR mode with the largest Grüneisen parameter is the Bu mode with a wavenumber of 276.1 cm–1. Regarding phonon crossings and anticrossings, there are five phonon crossings and no phonon anticrossing predicted to occur up to 20 GPa, as shown in Figure 7a,b.

4.3. Optical Absorption Measurements

To study the electronic properties of FeWO4 at ambient pressure and under compression, we performed optical absorption experiments as well as DFT simulations of the electronic band structure and density of states. The optical absorption spectrum of the natural mineral ferberite at different pressures is shown in Figure 8. The shape of the absorption edge supports an indirect band gap. We have also observed a typical Urbach-type56 exponential sub-band gap absorption, which is normally observed in tungstates and related ternary oxides.57 According to our simulations, the band gap of FeWO4 is indirect, in agreement with our experiments. The band structure is shown in Figure 9. The top of the valence band is at the Y point of the BZ and the bottom of the conduction band is at the Γ point of the BZ. DFT calculations give a band gap energy (Eg) of 1.79 eV. Experimentally, we have determined the band gap energy by means of a Tauc analysis58 (see the inset of Figure 8); therefore, the reported value should be assumed as the lower limit value of Eg.59 We obtained Eg = 2.00(5) eV, which is between the previously reported values.10,12−14 This means that the calculated band gap energy is slightly underestimated, but the underestimation, 0.2 eV, is within typical differences between DFT and experiments.23,60 However, this does not affect the determination of the pressure dependence of Eg.60 In Figure 10, we present the electronic density of states, which shows that Fe states are the main contributors to the top of the valence band and hybridized W and O orbitals dominate the bottom of the conduction band.

Figure 8.

Figure 8

Open in a new tab

Optical absorption spectra of the natural mineral ferberite (FeWO4) measured at different pressures are indicated in the legend. The inset shows the Tauc plot used to determine the band gap energy at ambient pressure.

Figure 9.

Figure 9

Open in a new tab

Calculated band structure of FeWO4 at (a) ambient pressure and (b) 13.4 GPa. The dashed blue line is the Fermi level, which has been set at 0 eV.

Figure 10.

Figure 10

Open in a new tab

Electronic density of states of FeWO4 at (a) ambient pressure and (b) 13.4 GPa. The blue line is the Fermi level, which has been set at 0 eV.

The pressure dependence of the band gap energy from experiments and calculations is shown in Figure 11. Both methods give a qualitatively similar behavior, with the band gap closing at a rate of 25 and 20 meV/GPa according to experiments and calculations, respectively. This phenomenon is similar to the HP band gap closure reported for NiWO4,19 CoWO4,22 and MnWO4,61 and different from that found in CdWO4, ZnWO4, and MgWO4.59 The main reason for the band gap closure in FeWO4 at HP is the contribution of Fe orbitals to the top of the valence band. They move more quickly to higher energies under compression than the states at the bottom of the conduction band, causing the narrowing observed in Eg. This can be seen in Figures 9 and 10 where the band structure and electronic density of states at different pressures are compared. In addition to reducing the band gap, the main change induced by pressure in the band structure is in the topology of the conduction band, which becomes more dispersive at high pressure. On the other hand, in the figure of the density of states, it can be seen that the orbital composition of the bands near the Fermi level is not modified under compression, but the Fe orbitals in the top of the valence band get closer to the bottom of the conduction band.

Figure 11.

Figure 11

Open in a new tab

Pressure dependence of the band gap energy of FeWO4. Solid (empty) symbols are results from experiments (calculations).

5. Conclusions

We report an experimental and theoretical study of the natural mineral ferberite (FeWO4). The crystal structure, Raman-active phonons, and band gap energy have been accurately characterized both experimentally and computationally at ambient pressure and under compression up to 20 GPa, and we have found them to be in good agreement. We found that the ambient pressure wolframite-type structure of FeWO4 does not undergo any phase transition up to 20 GPa. FeWO4 exhibits an indirect band gap of 2.00(5) eV at ambient pressure, which decreases at a rate of 25 meV/GPa similar to other magnetic AWO4 (A = Mn, Ni, and Co) wolframites. The pressure dependence of Raman-active and IR-active modes has been reported, with all Raman-active modes hardening with pressure, as it is characteristic of the AWO4 wolframite compounds, and several IR-active modes showing pressure-induced softening. In general, we have found that FeWO4 follows a similar trend to other wolframites, with the behavior of the electronic structure being particularly different from the nonmagnetic AWO4 (A = Mg, Zn, Cd) wolframites due to the valence band electrons from Fe.

Acknowledgments

D.E. and F.J.M. gratefully acknowledge the financial support from the Spanish Research Agency (AEI) and Spanish Ministry of Science and Investigation (MCIN) under Projects PID2019-106383GB-41/42, PID2022-138076NB-C41/42, and RED2022-134388-T (DOI: 10.13039/501100011033). D.E. and F.J.M also thank the financial support of Generalitat Valenciana under grants PROMETEO CIPROM/2021/075 (GREENMAT), MFA/2022/007, and MFA/2022/025 (ARCANGEL). This study forms part of the Advanced Materials program and is supported by MCIN with funding from European Union Next Generation EU (PRTR-C17.I1) and by the Generalitat Valenciana. C.P. acknowledges the grant Proyectos de Generación de Conocimiento PID2021-125927NB-C21. R.T. and D.E. thank the Generalitat Valenciana for the Postdoctoral Fellowship No. CIAPOS/2021/20. The authors thank ALBA synchrotron for providing beam time for the HP XRD experiments (Proposal 2014071024). S.L.-M. thanks CONAHCYT of Mexico for financial support through the program “Programa de Investigadoras e Investigadores por México”. The authors gratefully acknowledge the computing time granted by LANCAD and CONAHCYT on the supercomputer Miztli at LSVP DGTIC UNAM, and also the IPICYT Supercomputing National Center for Education & Research, grant TKII-R2024-SLM/-JEAC.

Data Availability Statement

The data that support the findings of this study are available from the corresponding author upon reasonable request.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.inorgchem.4c00345.

  • Crystallographic data (PDF)

Author Contributions

D.E. conceived the project. D.D.-A., R.T., F.J.M., C.P., and D.E. performed experiments. D.D.-A. and D.E. performed data analysis. J.E.A.-C. and S.L.-M. performed density functional theory calculations. All authors participated in discussions and writing and editing of the manuscript. All authors have approved the final version of the manuscript.

The authors declare no competing financial interest.

Supplementary Material

ic4c00345_si_001.pdf (190.6KB, pdf)

References

  1. Errandonea D.; Ruiz-Fuertes J. A Brief Review of the Effects of Pressure on Wolframite-type Oxides. Crystals 2018, 8 (2), 71 10.3390/cryst8020071. [DOI] [Google Scholar]
  2. Ruiz-Fuertes J.; Errandonea D.; López-Moreno S.; González J.; Gomis O.; Vilaplana R.; Manjón F. J.; Muñoz A.; Rodríguez-Hernández P.; Friedrich A.; Tupitsyna I. A.; Nagornaya L. L. High-Pressure Raman Spectroscopy and Lattice-Dynamics Calculations on Scintillating MgWO4: Comparison with Isomorphic Compounds. Phys. Rev. B 2011, 83 (21), 214112 10.1103/PhysRevB.83.214112. [DOI] [Google Scholar]
  3. Liu C. B.; He Z. Z.; Liu Y. J.; Chen R.; Shi M. M.; Zhu H. P.; Dong C.; Wang J. F. Magnetic Anisotropy and Spin-flop, Transition of NiWO4 Single Crystals. J. Magn. Magn. Mater. 2017, 444, 190–192. 10.1016/j.jmmm.2017.08.032. [DOI] [Google Scholar]
  4. Heyer O.; Hollmann N.; Klassen I.; Jodlauk S.; Bohaty L.; Becker P.; Mydosh J. A.; Lorenz T.; Khomskii D. A new Multiferroic Material: MnWO4. J. Phys.: Condens. Matter 2006, 18 (39), L471–L475. 10.1088/0953-8984/18/39/L01. [DOI] [Google Scholar]
  5. Guillen R.; Regnard J. R. Magnetic Properties of Natural and Synthetic Wolframites FexMn1-xWO4. Phys. Chem. Miner. 1985, 12 (4), 246–254. 10.1007/BF00311294. [DOI] [Google Scholar]
  6. Almeida M. A. P.; Cavalcante L. S.; Morilla-Santos C.; Dalmaschio C. J.; Rajogopal S.; Li M. S.; Longo E. Effect of Partial Preferential Orientation and Distortions in Octahedral Clusters on the Photoluminescence Properties of FeWO4 Nanocrystals. CrystEngComm 2012, 14 (21), 7127–7132. 10.1039/c2ce25771h. [DOI] [Google Scholar]
  7. Ruiz-Fuertes J.; Friedrich A.; Gomis O.; Errandonea D.; Morgenroth W.; Sans J. A.; Santamaría-Pérez D. High-Pressure Structural Phase Transition in MnWO4. Phys. Rev. B 2015, 91 (10), 104109 10.1103/PhysRevB.91.104109. [DOI] [Google Scholar]
  8. Hoang K. Polaron Formation, Native Defects, and Electronic Conduction in Metal Tungstates. Phys. Rev. Mater. 2017, 1 (2), 024603 10.1103/PhysRevMaterials.1.024603. [DOI] [Google Scholar]
  9. Zhao Y.; Li F.; Li W.; Li Y.; Liu C.; Zhao Z.; Shan Y.; Ji Y.; Sun L. Identification of M-NH2-NH2 Intermediate and Rate Determining Step for Nitrogen Reduction with Bioinspired Sulfur-Bonded FeW Catalyst. Angew. Chem., Int. Ed. 2021, 60, 20331–20341. 10.1002/anie.202104918. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Maignan A.; Schmidt M.; Prots Y.; Lebedev O. I.; Daou R.; Chang C.-F.; Kuo C.-Y.; Hu Z.; Chen C.-T.; Weng S.-C.; Altendorf S.-G.; Tjeng L. H.; Grin Y. FeWO4 Single Crystals: Structure, Oxidation States, and Magnetic and Transport Properties. Chem. Mater. 2022, 34 (2), 789–797. 10.1021/acs.chemmater.1c03640. [DOI] [Google Scholar]
  11. Gao Q.; Liu Z. FeWO4 Nanorods with Excellent UV-Visible Light Photocatalysis. Prog. Nat. Sci.: Mater. Int. 2017, 27 (5), 556–560. 10.1016/j.pnsc.2017.08.016. [DOI] [Google Scholar]
  12. Chidambaram S.; Ramachandran K.; Gaidi M.; Daoudi K.; Natarajamoorthy M. Solution Combustion Synthesis of Iron Tungstate Nanoparticles for Photoelectrochemical Water Splitting Towards Oxygen Evolution. J. Mater. Sci.: Mater. Electron. 2022, 33 (12), 9134–9143. 10.1007/s10854-021-07146-0. [DOI] [Google Scholar]
  13. Ojha D. P.; Karki H. P.; Song J. H.; Kim H. J. Amine-assisted Synthesis of FeWO4 Nanorod g-C3N4 for Enhanced Visible Light-driven Z-scheme Photocatalysis. Composites, Part B 2019, 160 (1), 277–284. 10.1016/j.compositesb.2018.10.039. [DOI] [Google Scholar]
  14. Deng X.; Xie G.; Liu X.; Wu Y.; Qin L.; Li Q. Convenient Synthesis of Peony-like FeWO4 with Super Adsorbent Properties for Efficient Degradation of Organic Dye. Mater. Res. Express 2017, 4 (7), 075008 10.1088/2053-1591/aa7614. [DOI] [Google Scholar]
  15. Errandonea D.; Bandiello E.; Segura A.; Hamlin J. J.; Maple M. B.; Rodriguez-Hernandez P.; Muñoz A. Tuning the Band Gap of PbCrO4 through High-Pressure: Evidence of Wide-to-narrow Semiconductor Transitions. J. Alloys Compd. 2014, 587 (1), 14–20. 10.1016/j.jallcom.2013.10.179. [DOI] [Google Scholar]
  16. Qian J.; Peng Z.; Wu D.; Fu X. FeWO4/Fe Score/shell Nanorods Fabricated by Thermal Evaporation. Mater. Lett. 2014, 122 (1), 86–89. 10.1016/j.matlet.2014.02.001. [DOI] [Google Scholar]
  17. ÜlkÜ D. Untersuchungen zur Kristallstruktur und Magnetischen Struktur des Ferberits FeWO4. Z. Krist. 1967, 124 (1–6), 192–219. 10.1524/zkri.1967.124.3.192. [DOI] [Google Scholar]
  18. García-Matres E.; Stüßer N.; Hofmann M.; Reehuis M. Magnetic Phases in Mn1-xFexWO4 Studied by Neutron Powder Diffraction. Eur. Phys. J. B 2003, 32 (1), 35–42. 10.1140/epjb/e2003-00071-1. [DOI] [Google Scholar]
  19. Rahman S.; Saqib H.; Liang X.; Errandonea D.; Resta A. S.; Molina-Sanchez A.; Gao G.; Wang L.; Tian Y.; Mao H.-K. Pressure-induced metallization and robust superconductivity in pristine 1T-HfSe2. Mater. Today Phys. 2022, 25, 100698 10.1016/j.mtphys.2022.100698. [DOI] [Google Scholar]
  20. Torikachvili M. S.; Bud’ko S. L.; Ni N.; Canfield P. C. Pressure induced superconductivity in CaFe2As2. Phys. Rev. Lett. 2008, 101, 057006 10.1103/PhysRevLett.101.057006. [DOI] [PubMed] [Google Scholar]
  21. Liang A.; Turnbull R.; Errandonea D. A review on the advancements in the characterization of the high-pressure properties of iodates. Prog. Mater. Sci. 2023, 136, 101092 10.1016/j.pmatsci.2023.101092. [DOI] [Google Scholar]
  22. Zhang L.; Wang Y.; Lv J.; Ma Y. Materials discovery at high pressures. Nat. Rev. Mater. 2017, 2, 17005 10.1038/natrevmats.2017.5. [DOI] [Google Scholar]
  23. Errandonea D.; Rodriguez F.; Vilaplana R.; Vie D.; Garg S.; Nayak B.; Garg N.; Singh J.; Kanchana V.; Vaitheeswaran G. Band-Gap Energy and Electronic d-d Transitions of NiWO4 Studied under High-Pressure Conditions. J. Phys. Chem. C 2023, 127 (31), 15630–15640. 10.1021/acs.jpcc.3c03512. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Errandonea D.; Manjón F. J.; Garro N.; Rodríguez-Hernández P.; Radescu S.; Mujica A.; Muñoz A.; Tu C. Y. Combined Raman Scattering and ab initio Investigation of Pressure-Induced Structural Phase Transitions in the Scintillator ZnWO4. Phys. Rev. B 2008, 78 (5), 054116 10.1103/PhysRevB.78.054116. [DOI] [Google Scholar]
  25. Lacomba-Perales R.; Errandonea D.; Martínez-Garcia D.; Rodríguez-Hernández P.; Radescu S.; Mujica A.; Muñoz A.; Chervin J. C.; Polian A. Phase Transitions in Wolframite-type CdWO4 at High Pressure Studied by Raman Spectroscopy and Density-Functional Theory. Phys. Rev. B 2009, 79 (9), 094105 10.1103/PhysRevB.79.094105. [DOI] [Google Scholar]
  26. Bandiello E.; Rodríguez-Hernández P.; Muñoz A.; Buenestado M. B.; Popescu C.; Errandonea D. Electronic Properties and High-Pressure Behavior of Wolframite-type CoWO4. Mater. Adv. 2021, 2 (18), 5955–5966. 10.1039/D1MA00510C. [DOI] [Google Scholar]
  27. Klotz S.; Chervin J.-C.; Munsch P.; Marchand G. L. Hydrostatic Limits of 11 Pressure Transmitting Media. J. Phys. D: Appl. Phys. 2009, 42 (7), 075413 10.1088/0022-3727/42/7/075413. [DOI] [Google Scholar]
  28. Mao H. K.; Bell P. M.; Shaner J. W.; Steinberg D. J. Specific Volume Measurements of Cu, Mo, Pd, and Ag and Calibration of the Ruby R, Fluorescence Pressure Gauge from 0.06 to 1 Mbar. J. Appl. Phys. 1978, 49 (6), 3276–3283. 10.1063/1.325277. [DOI] [Google Scholar]
  29. Fauth F.; Peral I.; Popescu C.; Knapp M. The New Material Science Powder Diffraction Beamline at ALBA Synchrotron. Powder Diffr. 2013, 28 (S2), S360–S370. 10.1017/S0885715613000900. [DOI] [Google Scholar]
  30. Hammersley A. P.; Svensson S. O.; Hanfland M.; Fitch A. N.; Häusermann D. Two-Dimensional Detector Software: From Real Detector to Idealised Image or Two-Theta Scan. High Pressure Res. 1996, 14 (4–6), 235–248. 10.1080/08957959608201408. [DOI] [Google Scholar]
  31. Rodríguez-Carvajal J. Recent Advances in Magnetic Structure Determination by Neutron Powder Diffraction. Phys. B Condens. Matter 1993, 192 (1–2), 55–69. 10.1016/0921-4526(93)90108-I. [DOI] [Google Scholar]
  32. Panchal V.; Errandonea D.; Segura A.; Rodríguez-Hernandez P.; Muñoz A.; Lopez-Moreno S.; Bettinelli M. The Electronic Structure of Zircon-type Orthovanadates: Effects of High-Pressure and Cation Substitution. J. Appl. Phys. 2011, 110 (4), 043723 10.1063/1.3626060. [DOI] [Google Scholar]
  33. Jones R. O. Density Functional Theory: Its Origins, Rise to Prominence, and Future. Rev. Mod. Phys. 2015, 87 (3), 897 10.1103/RevModPhys.87.897. [DOI] [Google Scholar]
  34. Blöchl P. E. Projector Augmented-Wave Method. Phys. Rev. B 1994, 50 (24), 17953–17979. 10.1103/PhysRevB.50.17953. [DOI] [PubMed] [Google Scholar]
  35. Kresse G.; Joubert D. From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method. Phys. Rev. B 1999, 59 (3), 1758–1775. 10.1103/PhysRevB.59.1758. [DOI] [Google Scholar]
  36. Kresse G.; Hafner J. Ab Initio Molecular Dynamics for Liquid Metals. Phys. Rev. B 1993, 47 (1), 558–561. 10.1103/PhysRevB.47.558. [DOI] [PubMed] [Google Scholar]
  37. Perdew J. P.; Ruzsinsky A.; Csonka G. I.; Vydrov O. A.; Scuseria G. E.; Constantin L. A.; Zhou X.; Burke K. Restoring the Density-Gradient Expansion for Exchange in Solids and Surfaces. Phys. Rev. Lett. 2008, 100 (13), 136406 10.1103/PhysRevLett.100.136406. [DOI] [PubMed] [Google Scholar]
  38. Dudarev S. L.; Botton G. A.; Savrasov S. Y.; Humphreys C. J.; Sutton A. P. Electron-Energy-Loss Spectra and the Structural Stability of Nickel Oxide: An LSDA+U Study. Phys. Rev. B 1998, 57 (3), 1505 10.1103/PhysRevB.57.1505. [DOI] [Google Scholar]
  39. López-Moreno S.; Errandonea D.; Pellicer-Porres J.; Martínez-García D.; Patwe S. J.; Achary S. N.; Tyagi A. K.; Rodríguez-Hernández P.; Muñoz A.; Popescu C. Stability of FeVO4 under Pressure: An X-ray Diffraction and First-Principles Study. Inorg. Chem. 2018, 57 (13), 7860–7876. 10.1021/acs.inorgchem.8b00984. [DOI] [PubMed] [Google Scholar]
  40. Gonzalez-Platas J.; López-Moreno S.; Bandiello E.; Bettinelli M.; Errandonea D. Precise Characterization of the Rich Structural Landscape Induced by Pressure in Multifunctional FeVO4. Inorg. Chem. 2020, 59 (9), 6623–6630. 10.1021/acs.inorgchem.0c00772. [DOI] [PubMed] [Google Scholar]
  41. Romero-Vázquez P. B.; López-Moreno S.; Errandonea D. Stability of FeVO4-II under Pressure: A First-Principles Study. Crystals 2022, 12 (12), 1835 10.3390/cryst12121835. [DOI] [Google Scholar]
  42. López-Moreno S.; Sánchez-Martín J.; Bandiello E.; Bettinelli E.; Bull C. L.; Ridley C. J.; Errandonea D. The Effect of Pressure on the Band-Gap Energy in FePO4 and FeVO4. J. Phys. Chem. Solids 2023, 183, 111604 10.1016/j.jpcs.2023.111604. [DOI] [Google Scholar]
  43. Monkhorst H. J.; Pack J. D. Special Points for Brillouin-Zone Integrations. Phys. Rev. B 1976, 13 (12), 5188–5192. 10.1103/PhysRevB.13.5188. [DOI] [Google Scholar]
  44. Parlinski K.Computer Code PHONON, 2008. http://wolf.ifj.edu.pl/phonon.
  45. Macavei J.; Schulz H. The Crystal Structure of Wolframite type Tungstates at High Pressure. Z. Kristallogr. 1993, 207 (1–2), 193–208. 10.1524/zkri.1993.207.12.193. [DOI] [Google Scholar]
  46. Romero-Vázquez P. B.; López-Moreno S.; Errandonea D. Stability of FeVO4-II under Pressure: A First-Principles Study. Crystals 2022, 12, 1835 10.3390/cryst12121835. [DOI] [Google Scholar]
  47. Romero-Vázquez P. B.; López-Moreno S. Ab initio Study of RaWO4: Comparison with Isoelectronic Tungstates. J. Solid State Chem. 2023, 317, 123709 10.1016/j.jssc.2022.123709. [DOI] [Google Scholar]
  48. Baur W. H. The geometry of polyhedral distortions. Predictive relationships for the phosphate group. Acta Crystallogr. 1974, 30, 1195–1215. 10.1107/S0567740874004560. [DOI] [Google Scholar]
  49. Yuan H.; Rodriguez-Hernandez P.; Muñoz A.; Errandonea D. Putting the Squeeze on Lead Chromate Nanorods. J. Phys. Chem. Lett. 2019, 10 (16), 4744–4751. 10.1021/acs.jpclett.9b01978. [DOI] [PubMed] [Google Scholar]
  50. Cliffe M. J.; Goodwin A. L. PASCal: A Principal Axis Strain Calculator for Thermal Expansion and Compressibility Determination. J. Appl. Crystallogr. 2012, 45 (6), 1321–1329. 10.1107/S0021889812043026. [DOI] [Google Scholar]
  51. Birch F. Finite Elastic Strain of Cubic Crystals. Phys. Rev. 1947, 71 (11), 809–824. 10.1103/PhysRev.71.809. [DOI] [Google Scholar]
  52. Gonzalez-Platas J.; Alvaro M.; Nestola F.; Angel R. EosFit7-GUI: A New Graphical User Interface for Equation of State Calculations, Analyses and Teaching. J. Appl. Crystallogr. 2016, 49 (4), 1377–1382. 10.1107/S1600576716008050. [DOI] [Google Scholar]
  53. Zhang G.-X.; Reilly A. M.; Tkatchenko A.; Scheffler M. Performance of Various Density-Functional Approximations of Cohesive Properties of 64 Bulk Solids. New J. Phys. 2018, 20, 063020 10.1088/1367-2630/aac7f0. [DOI] [Google Scholar]
  54. https://rruff.info/all/chemistry/asc/R050632.
  55. Errandonea D.; Muñoz A.; Rodríguez-Hernández P.; Gomis O.; Achary S. N.; Popescu C.; Patwe S. J.; Tyagi A. K. High-Pressure Crystal Structure, Lattice Vibrations, and Band Structure of BiSbO4. Inorg. Chem. 2016, 55 (10), 4958–4969. 10.1021/acs.inorgchem.6b00503. [DOI] [PubMed] [Google Scholar]
  56. Urbach F. The Long-Wavelength Edge of Photographic Sensitivity and of the Electronic Absorption of Solids. Phys. Rev. 1953, 92 (5), 1324 10.1103/PhysRev.92.1324. [DOI] [Google Scholar]
  57. Errandonea D.; Bandiello E.; Segura A.; Hamlin J. J.; Maple M. B.; Rodriguez-Hernandez P.; Muñoz A. Tuning the Band Gap of PbCrO4 through High-Pressure: Evidence of Wide-to-Narrow Semiconductor Transitions. J. Alloys Compd. 2014, 587, 14–20. 10.1016/j.jallcom.2013.10.179. [DOI] [Google Scholar]
  58. Tauc J. Optical properties and electronic structure of amorphous Ge and Si. Mater. Res. Bull. 1968, 3, 37–46. 10.1016/0025-5408(68)90023-8. [DOI] [Google Scholar]
  59. Garg A. B.; Vie D.; Rodriguez-Hernandez P.; Muñoz A.; Segura A.; Errandonea D. Accurate Determination of the Bandgap Energy of the Rare-Earth Niobate Series. J. Phys. Chem. Lett. 2023, 14 (7), 1762–1768. 10.1021/acs.jpclett.3c00020. [DOI] [PMC free article] [PubMed] [Google Scholar]
  60. Botella P.; Errandonea D.; Garg A. B.; et al. High-pressure characterization of the optical and electronic properties of InVO4, InNbO4, and InTaO4. SN Appl. Sci. 2019, 1, 389 10.1007/s42452-019-0406-7. [DOI] [Google Scholar]
  61. Ruiz-Fuertes J.; López-Moreno S.; López-Solano J.; Errandonea D.; Segura A.; Lacomba-Perales R.; Muñoz A.; Radescu S.; Rodríguez-Hernández P.; Gospodinov M.; Nagornaya L. L.; Tu C. Y. Pressure Effects on the Electronic and Optical Properties of AWO4 Wolframites (A = Cd, Mg, Mn, and Zn): The Distinctive Behavior of Multiferroic MnWO4. Phys. Rev. B 2012, 86 (12), 125202 10.1103/PhysRevB.86.125202. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ic4c00345_si_001.pdf (190.6KB, pdf)

Data Availability Statement

The data that support the findings of this study are available from the corresponding author upon reasonable request.

Articles from Inorganic Chemistry are provided here courtesy of American Chemical Society

RESOURCES