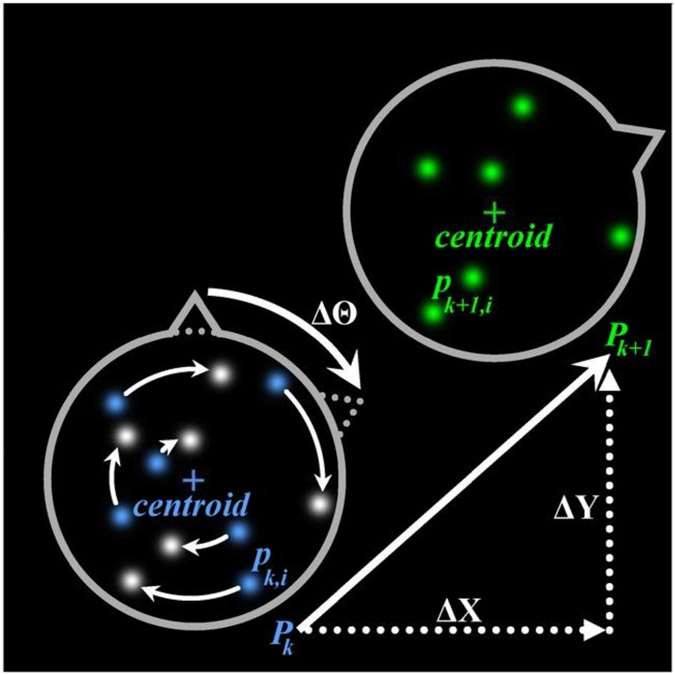
Fig. 1.

Schematic illustrating the measurement concept, in which a sparse constellation of point sources in an invariant constellation indicates the planarmotion of a microscopic rigid body. Planar motion of the body (gray) can be expressed by a rotation ($\Delta \Theta$) followed by a translation, ($\Delta X$, $\Delta Y$). The initial positions of the point sources (blue) are $P_k=\{p_{k,1},\dots ,p_{k,\eta }\}$, where $k$ is the index of a series of images, $\eta$ is the number of point sources, and $p_{i,j}$ is the position of the $j^{\text{th}}$ point source in the $i^{\text{th}}$ frame of an image sequence. After the body has moved, the final positions of the point sources (green) are $P_{k+1}=\{p_{k+1,1},\dots ,p_{k+1,\eta }\}$. Uncertainties of each of the three motion parameters are derived from the uncertainties of the positions of the point sources. The fundamental limits of uncertainty of position and orientation measurements are termed centroid precision and orientation precision, respectively. These limits are derived from the localization precision and radial position of the individual point sources in the constellation.