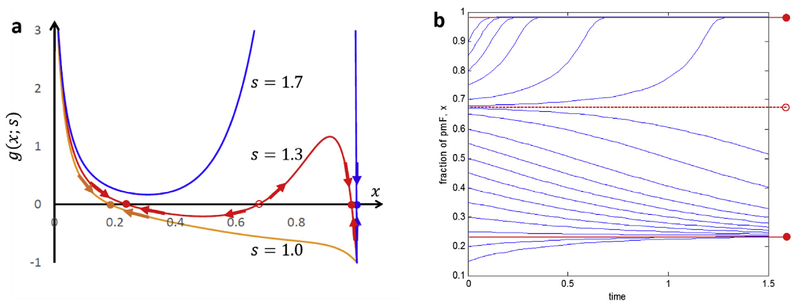
Fig. 2. Stability analysis of profibrotic tissue using bifurcation theory.

(a) Plots of g(x; s) with different values of tension, s (1:0–1:7). With increasing tension, s, by pmF in an ROI, the nF-to-pmF transformation switches from monostability with a single steady state at low x (≅0.20; s = 1) to bistability with two coexisting steady states (x≅0.23 and 0.98;s = 1.3). With a higher value of s (s = 1.7) the system becomes more stable with a single steady state at x ≅1.0 (~all pmF). Other parameters n = 10 and k_f/k_b = 5. Solid circle: stable fixed point and open circle: unstable fixed point. (b) Bistable behavior of the pmF fraction, x, of proto-myofibroblasts in an ROI predicted by the nonlinear model (s = 1.3) in (a). For an initial value of x below the unstable fixed point (x≅0.67) the system relaxes to the steady state with a low concentration of pmF (x≅0.23). When x > 0.67, x advances to the steady state with high pmF concentration (x≅0.98).