Origin, evolution, and maintenance of gene-strand bias in bacteria

Abstract

Gene-strand bias is a characteristic feature of bacterial genome organization wherein genes are preferentially encoded on the leading strand of replication, promoting co-orientation of replication and transcription. This co-orientation bias has evolved to protect gene essentiality, expression, and genomic stability from the harmful effects of head-on replication-transcription collisions. However, the origin, variation, and maintenance of gene-strand bias remain elusive. Here, we reveal that the frequency of inversions that alter gene orientation exhibits large variation across bacterial populations and negatively correlates with gene-strand bias. The density, distance, and distribution of inverted repeats show a similar negative relationship with gene-strand bias explaining the heterogeneity in inversions. Importantly, these observations are broadly evident across the entire bacterial kingdom uncovering inversions and inverted repeats as primary factors underlying the variation in gene-strand bias and its maintenance. The distinct catalytic subunits of replicative DNA polymerase have co-evolved with gene-strand bias, suggesting a close link between replication and the origin of gene-strand bias. Congruently, inversion frequencies and inverted repeats vary among bacteria with different DNA polymerases. In summary, we propose that the nature of replication determines the fitness cost of replication-transcription collisions, establishing a selection gradient on gene-strand bias by fine-tuning DNA sequence repeats and, thereby, gene inversions.

Graphical Abstract

Graphical Abstract.

Introduction

Typically, bacterial genomes consist of a single circular chromosome, with the replication proceeding bidirectionally across two replichores from the origin to the terminus. Replication shares the same DNA template with the transcription, and the two processes lack spatiotemporal separation leading to collisions between their machinery (1,2). Replication-transcription collisions can be either co-directional when the genes are encoded on the leading strand (in the same direction of replication) or head-on when genes are encoded on the lagging strand (opposite to the direction of replication). Replication stress, interrupted gene expression, increased mutagenesis, and genomic instability are the consequences of replication–transcription collisions, which are shown to be more detrimental during head-on collisions (1–8). It has been proposed that to avoid these potentially severe head-on collisions, genes are preferentially transcribed co-directionally with the replication by being on the leading strand, a phenomenon known as the gene-strand bias (GSB) (9). This bias is strongly evident for ribosomal operons, essential and highly expressed genes (1,9,10) and broadly at the whole-genome level (11,12). To date, the prevalence of GSB is wide-ranging across bacteria and is also noticeable in higher eukaryotes (13–18).

Studies have implicated gene expression levels, essentiality, and functionality as the factors driving GSB (9,19,20). Besides, the existence of GSB has been attributed to horizontal gene transfer, selection for energy efficiency, minimizing mutagenesis and genome instability (5,14,15,21). Further, a distinctive feature associated with GSB in bacteria is the composition of the replisome. Bacterial species that employ two different replicative DNA polymerases (PolC and DnaE) exhibit high GSB, while species that utilize two copies of a single replicative DNA polymerase (DnaE) show low GSB (22), highlighting a link between chromosomal replication and strand-biased gene distribution. Cumulatively, the aforementioned factors strongly imply selection for co-orientation of replication and transcription through strand-biased distribution of genes. Nevertheless, there exists a vast difference in the extent of GSB across the bacterial kingdom exhibiting a notable bimodal distribution (16). Yet, the mechanistic and evolutionary forces underlying the kingdom-wide variation in GSB and its maintenance remain elusive.

The variation in GSB can arise when genes switch from one replication strand to another (leading to lagging and vice-versa) due to gene inversions. Two types of inversions are seen in bacteria that differentially affect the fitness and genomic stability (23–25). Symmetric gene inversions around the origin and terminus of replication (inter-replichore) do not affect fitness and are tolerated in bacterial populations (25–27), as they do not change the replication strand and transcription orientation. Inversions within a replichore (intra-replichore) cause a strand switch, reversing the gene orientation, consequently the nature of replication-transcription collisions. Particularly, the genes inverted to lagging strand experience higher mutation rates, partly due to head-on replication-transcription collisions and thus such inversions are less prevalent in natural populations (5,28–31). Inversions generally occur through homologous recombination acting on a pair of inverted repeats (IRs) (32,33). Interestingly, the abundance and inversion potential of IRs has been shown to be negatively correlated with genomic stability (24). Overall, it is apparent that selection acts against strand-switching inversions that affect fitness and genomic stability. Hence, it is conceivable that selection may differentially control the levels of gene inversions across bacteria, which may account for the variation in GSB. Since, inverted repeats potentiate strand-switching inversions, selection may act on the evolution of IRs to regulate gene inversions.

In this study, we examined whether gene inversions account for the variation in gene-strand bias and how the variation is maintained across the bacterial kingdom. We employed a comparative phylogenomics approach to detect and quantify gene inversions that alter the direction of transcription of genes (henceforth referred to as gene inversions) in bacterial species representing varying degrees of gene-strand bias. Our results uncover a striking negative correlation between the frequency of gene inversions and gene-strand bias. We find that the density and chromosomal distribution of inverted repeats underlie the variation in gene-strand bias, and its maintenance. Furthermore, these observations are broadly evident at a kingdom-wide level highlighting the ubiquitous nature of this mechanism. Finally, we reveal that the distinct mode of replication across bacteria is associated with gene inversions and IR density. Overall, we present a model of replication-dependent selection on inverted repeats, which controls the frequency of gene inversions explaining the variation and preservation of strand-biased genome organization in bacteria.

Materials and methods

Species selection and data source

Genomes used for kingdom-wide analysis were selected from NCBI microbial genomes database (https://www.ncbi.nlm.nih.gov/genome/microbes/; as on April 2021) with the following filters: Kingdom—‘Bacteria’, Assembly level—‘complete’ and RefSeq category ‘reference/representative’. These filters were used to avoid oversampling of highly similar genomes from species that have been sequenced in abundance. Genomes were grouped into different clades following the NCBI microbial genomes taxonomic annotation (https://www.ncbi.nlm.nih.gov/genome/microbes/). Clades with fewer than two representative species were excluded. Finally, the dataset included 2369 genomes (Supplementary File 1) after filtering for replichore imbalance (described later) and the associated genomic FASTA and feature table files were downloaded. Species for population-level gene inversion analysis were selected to represent almost the entire range of gene-strand bias (GSB) (∼50 to 90%) observed across the bacterial kingdom. At least 10 or more completely sequenced genomes (except Mesoplasma florum, where only 9 genomes were available) were considered as representative population for each species. Genomes for the selected species were obtained from the NCBI Assembly database (https://www.ncbi.nlm.nih.gov/assembly/) using the species name as query and the following filters: Assembly level—‘Complete genome assembly’ and status—‘latest RefSeq’. The genomic, CDS nucleotide (.fna) and protein sequence (.faa), and general feature format files (.gff) for the selected genomes were downloaded with the source set as RefSeq. The reference genome for each species was selected either as assigned in the NCBI Assembly database or selected at random when the reference genome was unassigned or was absent from the dataset. Throughout the study, only primary chromosomes were analyzed. In the end, 18 species were included and the species-wise list of analyzed genomes is given in Supplementary File 2.

Kingdom-wide analysis of gene-strand bias

The origin and terminus of replication were determined by the GC-skew based method, as described previously (34,35). Briefly, GC-skew for each chromosome was calculated as (G + C)/(G – C), using a sliding window of 50 bp with a jump size of 25 bp. Cumulative GC skews were calculated and their minima and maxima were considered as the origin and terminus of replication, respectively (35). As the origin and terminus of replication in the kingdom-wide dataset were solely determined by the GC-skew method, the dataset was filtered to avoid replichore imbalance potentially resulting from erroneous detection of replichore boundaries. As most of the bacterial genomes have equal replichore sizes (36), the dataset was filtered to retain only the genomes where the difference between replichore sizes was less than 20% of the genome size. Gene start and end coordinates and strand information (plus/minus) were extracted from the feature table. Genes located on the plus strand of replichore 1 (between the origin and terminus of replication) and the minus strand of replichore 2 (between the terminus and origin of replication) were determined to be on the leading strand. Genes located on the minus strand of replichore 1 and plus strand of replichore 2 were assigned to the lagging strand (15). GSB for each genome was calculated as the percentage of genes on the leading strand of replication (22).

Detection of inversions in bacterial populations

An in-house bioinformatic pipeline as outlined in Supplementary Figure S1 was developed for detecting gene inversions in bacterial populations. The pipeline consists of a series of modules implemented in python (v3.6 and above) as elaborated below.

Detection of origin and terminus of replication

For the population-level dataset, the origin and terminus of replication were determined using two independent methods. First, we employed the GC-skew-based method as described above (34,35). The minima and maxima of cumulative GC-skew may not precisely overlap with the exact origin and terminus of replication. To avoid inaccurate determination of gene directionality due to uncertain replichore boundaries, we utilized a secondary approach to detect the replication origin and terminus. We selected 200 kb sequence around the origin predicted by the GC-skew method and performed a string search for the presence of dnaA recognition sequences (DnaA boxes) with the Escherichia coli dnaA box sequence (TTATCCACA) (37) in 500 bp windows. Hits with a maximum of one mismatch were permitted, and the window with maximum hits was considered as the origin of replication. Similarly, a 200 kb window around the terminus was used to search for dif sites (E. coli—GGTGCGCATAATGTATATTATGTTAAAT used for gram-negative species; S. aureus—ACTTCCTATAATATATATTATGTAAACT used for gram-positive species) (38) by BLASTN program of BLAST (v2.12.0+) (39). The hit with the highest BLAST score was considered to be the best match and used as the terminus of replication. As origin of replication was identified independently by GC-skew minima and enrichment of dnaA boxes, predictions with both methods did not exactly coincide. The genes located in the region flanked by two predictions could not be assigned to a replichore without ambiguity and hence were excluded to avoid erroneous determination of gene directionality. Similarly, genes located in the region between GC-skew maxima and dif site were also excluded from the analysis. If dnaA box or dif site was not found, genes located in 200 kb region around the origin or terminus as detected by the GC-skew method were excluded from the analysis. The proportion of excluded genes were calculated (Supplementary Figure S2A).

Identification of core genome

To identify the core genome of each species we used the all-vs-all reciprocal BLASTP approach (40). BLASTP hits with identity ≥75%, query coverage ≥80% and e-value ≤1e-05, were considered as reciprocal best hits. Single copy genes detected in all the genomes were considered core genes. Further, to determine the presence of these core genes in the outgroup species, a similar bidirectional best hit BLASTP approach (identity ≥ 65%, query coverage ≥ 80%, e-value ≤ 1e-05) was used with the reference genome proteins of the ingroup species as query.

Detection of gene inversions

Gene directionality for all the genes in the core genome was determined as described above. In the absence of inversion, the replication strand status of a core gene will be either leading or lagging in all the genomes within the population. However, due to inversion, the strand status can be altered in one or more genomes (Figure 2A). The core genes that have not maintained the same strand in the entire population were determined to have undergone inversion. In parallel, an alternate GC-skew-based approach was used to determine inversions. The average GC-skew ((G + C)/(G – C)) was calculated for each gene. The sign of GC-skew (positive or negative) for a gene was compared with the sign of the average GC-skew of the replichore containing the gene. A change in the sign, indicating local disparity in GC-skew was considered as an inversion as previously described (27,29). Only the gene inversions commonly detected by both methods were included for analysis. The inversion frequency (IF) was calculated as the number of inverted core genes over the total number of core genes for each species. IF to leading strand was calculated as the ratio of number of core genes switching from lagging to leading strand by the number of core genes on the lagging strand and the converse was used to calculate the IF to the lagging strand.

Figure 2.

Variable gene inversion frequencies in bacterial populations. (A) Schematic describing GC-skew and phylogeny-based methodology to determine inversions (details in Materials and methods). Arrows on a representative genome-wide GC-skew map (left) indicate regions with local GC-skew disparity and gray shades highlight inversions based on gene synteny (right). The rows (alphabets) represent genomes while columns (numbers) indicate core gene clusters. (B) The inversion frequency for species with low (<70%; left Y-axis) and high (>70%; right Y-axis) gene-strand bias. Species analyzed (X-axis): Pae, Pseudomonas aeruginosa; Ngo, Neiserria gonorrhoeae; Bma, Burkholderia mallei; Yps, Yersinia pseudotuberculosis; Eal, Escherichia albertii; Sma, Serratia marsescens; Eco, Escherichia coli; Cul, Corynebacterium ulcerans; Cje, Campylobacter jejuni; Bbr, Bifidobacterium breve; Ban, Bacillus anthracis; Bsu, Bacillus subtilis; Ppo, Paenibacillus polymyxa; Sor, Streptococcus oralis; Efa, Enterococcus faecium; Cbu, Clostridium butyricum; Cpe, Clostridium perfringens; Mfl, Mesoplasma florum. (C) Inversion frequency (Y-axis) plotted against the gene-strand bias estimated by parsimony (X-axis). Linear model fit between the two variables is represented as blue trendline (here and in all following figures where applicable). Spearman's rank correlation coefficient (ρ) and the P-value (P) are presented on the plot.

Reconstruction of species phylogeny and estimation of divergence time

To reconstruct the phylogeny of a species, we performed multiple sequence alignment of the protein sequence of the core genes of each species using the MAFFT G-INS-i (v7.487) (41) algorithm with the default parameters. The alignment quality was revalidated using the GUIDANCE2 tool (42). Codon-based nucleotide alignments were generated using the PAL2NAL program (v14) (43). Nucleotide alignments of all the core genes were then concatenated and species phylogeny was reconstructed using the maximum likelihood method implemented in IQ-TREE (v2.1.14) (44) program with nucleotide substitution model GTR + I + R and 1500 ultrafast bootstraps. The tree was rooted at the outgroup species. The mean branch length of the reconstructed species tree was calculated as the sum of branch lengths (obtained from MEGAX v10.2.6) (45) divided by the number of branches after excluding the outgroup branch.

Ancestral gene-directionality reconstruction and resolution of root inversions

In order to calculate the GSB for each species, the ancestral strand status (leading or lagging) of all the core genes was reconstructed using parsimony-based approach implemented in PAUP (v4.0a build 168) and the maximum likelihood method implemented in PastML (1.9.42) (46,47). These approaches enabled us to determine the original strand status of the core genes prior to inversions within the population. The reconstructed ancestral state was used to calculate GSB (% leading strand). For the scenario where all the genomes in a population had identical gene orientation for a core gene, but the orientation of the outgroup differed, presumably an inversion had occurred either in the outgroup species or the common ancestor of all ingroup genomes. To resolve whether an inversion occurred in the root of ingroup or the outgroup species, we determined the gene orientation in the common ancestor of both (ingroup and outgroup) species, called as ‘super-outgroup’. Using the representative genomes of three species (ingroup, outgroup, and the super-outgroup), the inversion detection pipeline was rerun and gene directionality was reconstructed using PAUP. If the gene orientation had changed in the ingroup species relative to the ancestor, the core gene was deemed to be inverted (Supplementary Figure S2B).

Calculation of inversion size

The size of the inversion was calculated as the total size of all the core genes inverted per inversion event (in bp) and the median size of all inversion events was normalized by the size of core genome of the species (in bp). The normalized median size was used in the correlations against GSB. The events were inferred based on the principle of parsimony as reconstructed by PAUP. Where contiguous genes were detected to have undergone inversion, they were assumed to be the result of a single recombination event and hence counted as one (Supplementary Figure S5D). Phylogenetically, when the same core gene was inverted in multiple branches on the species tree and mapped back to a common internal node, they were also considered as a single event. In cases where the inversions occurred at multiple parallel branches/nodes and could not be mapped to a common internal node, they were counted to be independent events (Supplementary Figure S5E).

Detection of inversions in kingdom-wide dataset

Inversions in the kingdom-wide dataset were detected solely based on the GC-skew disparity method (27,29). The average GC-skew for each gene was compared to the replichore average. Genes with a different sign of GC-skew (positive or negative) as compared to the replichore average were determined to be inverted. This approach enabled rapid detection of inversions in single genomes as population-level sequence data was not available for the entire dataset. IF was calculated as the number of genes inverted over the number of total genes.

Determination of recombination rate

The recombination rate was calculated using ClonalFrameML (v1.12) (48). ClonalFrameML estimates R/θ, where R is the rate of recombination and θ is the rate of mutations. As a single recombination event is more likely to introduce a higher number of nucleotide changes than independent point mutations, the R/θ ratio can be used to infer the relative recombination rate. In other words, a high R/θ ratio would indicate higher recombination rates and vice-versa. To estimate the R/θ ratio, we realigned the core genes without the outgroup sequence to minimize the effect of divergence. Concatenated alignments of the realigned core genes were then used to estimate the transition/transversion ratio (kappa parameter) for each species using the phyML tool (v3.3.20190909–1, default parameters) (49). ClonalFrameML was used to estimate the R/θ ratio for each aligned core gene with the estimated kappa parameter as the input and the rest of the parameters as default. The median R/θ value of all genes for each species was used in correlations.

Detection and analysis of inverted repeats

Inverted repeats (IRs) were detected for the reference genomes of all the analyzed species. Various properties of IRs including the IR density, length, replichore dependent positioning, the distance between the two repeat sequences of intra-replichore IR pairs and inversion potential were analyzed as described below.

The DNA sequence repeats were detected from the reference genome sequences for each species with the repeat-match algorithm of the MUMMER package (v3.0, all parameters - default) (50) and were used as the observed value. To control for species-specific differences in genome composition and size, we shuffled the reference genome sequence of each species 500 times and detected repeats from each of the shuffled genomes, and the median value of IRs of the 500 shuffled replicates was considered as the expected value as used before (51,52). IR density was then calculated as the ratio of the observed over the expected value. As an alternative measure of IR abundance, we detected inverted repeat sequences from the reference genome sequence for each species with the palindrome tool of EMBOSS suite (v6.6.0.0, parameters: -minpallen 20 -maxpallen 100 -gaplimit (length of genome) -nooverlap) (53). IR density was then calculated as the ratio of intra-replichore inverted repeats over the genome size (in bp).

IR length

The length of the IRs was obtained from the output of the repeat-match algorithm (all parameters default) for the reference genome of each species.

IR chromosomal distribution

The two copies of IRs were segregated into inter- and intra-replichore repeats based on their chromosomal coordinates.

IR distance

The distance between two repeat sequences of an intra-replichore IR (spacer length) was calculated end-to-end inclusive of the IR (in bp). Using the reference genome, the repeat distance for each IR was normalized by the genome size (in bp) and the median of all IRs was considered for analysis.

Inversion potential

The strand-switching inversions induced by IRs depend on the frequency and length of repeats, the repeat distance, and genome size. We calculated this cumulative effect of IR characteristics, termed as inversion potential as described previously (24). Repeat characteristics as determined by the repeat-match algorithm were used after filtering out the palindromic sequences. Briefly, for each genome, the summation of the product of repeat length (Lr_i) and spacer distance (Lsp_i) for each intra-replichore repeat pair was calculated and normalized by the product of total length of intra-replichore repeats (Lr_T) and the size of the genome (G_L) (equation below).

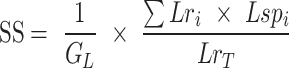The metric (SS or strand switch potential of an IR) was multiplied by the number of intra-replichore IRs to obtain the total inversion potential (SSxNi). For the kingdom-wide analysis, we limited our dataset to genomes with at least 500 total repeats. Further, we considered only the intra-replichore IR pairs with spacer lengths greater than 1 kb (equivalent to an average gene size) as smaller spacers may not accommodate the inversion of an entire gene.

Detection of PolC

To study the prevalence of DNA polymerase PolC in the 18 species used for inversion analysis, we constructed a consensus amino acid sequence of PolC from five different species in which PolC is either experimentally validated or well annotated. The amino acid sequences of PolC were downloaded from UniProt database (https://www.uniprot.org/) (54) for the following species - Clostridium butyricum (A0A512TRX6), Streptococcus pneumoniae (Q8DRA5), Bacillus subtilis (P13267), Staphylococcus aureus (P68852), and Bacillus anthracis (A0A640MZ74). A multiple sequence alignment of these sequences was performed using the Clustal Omega web tool (default parameters) (55) and a consensus sequence was generated using EMBOSS Cons web tool (default parameters) (53). The PolC consensus sequence was used as a query for BLASTP search against the database of protein sequences from the reference genomes of each species. Species with BLAST hits with identity ≥ 40%, query coverage ≥ 80%, and e-value ≤ 1e-05, were considered to have the PolC ortholog.

For the detection of PolC across the bacterial kingdom (2369 species, Supplementary File 1), we used a similar approach. Since this dataset is vastly diverse, we selected five phylogenetically diverse species Bacillus subtilis, Fusobacterium varium, Listeria monocytogenes, Spiroplasma mirium, and Thermotoga maritama, which resulted from the initial BLASTP hits. The PolC sequences from these five diverse species were then independently used as queries for another round of BLASTP. Species with best bidirectional best hits with identity ≥40%, query coverage ≥70% and e-value ≤1e-03, from at least one of the query sequences were considered to have PolC present.

Reconstruction and visualization of bacterial phylogeny

Bacterial kingdom-wide phylogeny was reconstructed using the maximum likelihood approach implemented in the whole-genome marker gene analysis tool PhyloPhlAn (v3.0, diversity= ‘high’, set to ‘fast’) (56,57), which included at least 100 marker genes. 10 archaeal genomes (listed in Supplementary File 1) were included as outgroup species to root the tree and were removed from further phylogenetic analysis. The phylogeny was visualized using ggTree package in R (58), as a dendrogram with clade information, absence/presence of PolC, % GSB and inversion frequencies displayed concentrically.

Phylogenetic analysis of the prevalence of PolC and gene-strand bias

The presence/absence of PolC was mapped on the reconstructed bacterial phylogeny with a stochastic character mapping approach using the simmap function (model = ‘ARD’, nsim = 100) of phytools package (59) in R. GSB and IF were mapped on the bacterial kingdom phylogeny using a continuous character mapping approach implemented in the contMap function of phytools package of R. The GSB for all species was categorized into low/high bias (based on a 70% threshold) as binary states. The low/high GSB was correlated with absence/presence of PolC by Pagel's binary character correlation test using the fitPagel function of phytools package in R. The method uses maximum likelihood estimation of character state change rates, with an independent rate assumed for every possible state change (All rates different (ARD) character model). A likelihood ratio test was used to statistically compare the two models, where the binary traits either evolve independent or in a dependent fashion.

To control for the effect of phylogenetic relatedness on the various correlations (the presence and absence of PolC, GSB, IF and inversion potential), phylogenetic analysis of variance was tested using aov.phylo function of geiger package implemented in R (60). PolC and non-PolC groups were tested for differences in GSB and IF with phylogenetic ANOVA, whereas a cumulative effect of both the factors was tested with phylogenetic MANOVA. Similarly, low and high GSB groups were tested for differences in IF and inversion potential using phylogenetic ANOVA and a cumulative effect of both with phylogenetic MANOVA.

Code, data visualization and statistical analysis

Codes used for the gene inversion detection pipeline were written in Python (v3.6 and above). The scripts for repeat analysis were coded in Python and R (v4.1.0 and above). The plots were generated using the ggplot2 package (61) of the R software or Graphpad Prism 10 (v10.0.0). The pipeline was integrated in workflows created using Snakemake (v 7.31.0) (62). Figures and schematics were presented using the Adobe Illustrator software (v27.7). All the statistical analyses were carried out using R.

Results

Extensive variation in gene-strand bias across the bacterial kingdom

To assess the extent of variation in GSB, we curated a non-redundant dataset for kingdom-wide systematic analysis by selecting a representative/reference genome from available sequenced bacterial species. For each genome, we determined the origin and terminus of replication by the cumulative GC-skew approach (34,35). As both the replichores of the majority of bacterial chromosomes have roughly equal lengths (36), only the genomes in which the larger replichore was not longer than 60% of the chromosome size were considered. The final dataset consisted of 2369 bacterial species distributed across 23 clades (see Materials and methods). Next, we determined if a gene is encoded on the leading or lagging strand of replication. GSB was calculated as the percentage of genes encoded on the leading strand of replication (22). If the genome organization is evolving neutrally, we would expect 50% of the genes to be encoded on each strand. We noticed a clear deviation from the neutral expectation for a large number of clades (Figure 1), consistent with previous observations (11,15,16,18). The overall distribution of all analyzed species showed a preferential leading strand bias (median = 57.9%) (Supplementary File S1). Nevertheless, GSB was heterogeneous across the bacterial kingdom ranging from less than 50% to a maximum of ∼90%. The bias showed a bimodal distribution consistent with the previous observation (16), with modes at ∼57% and ∼78% leading strand genes (Supplementary Figure S3A). The lowest GSB was observed in the clade Verrucomicrobia, while the highest was noted in Tenericutes (median = 49.9% and 82.0% respectively) (Figure 1). This variation is consistent with previous reports of GSB in the bacterial kingdom with limited datasets (16,18). Clades including Verrucomicrobia, Planctomycetes, and Cyanobacteria surprisingly showed a median GSB value close to the neutral expectation of 50% (Figure 1). Most bacterial clades including Proteobacteria, Bacteroidetes, Thermotogae, and Spirochaetes, displayed a modest GSB (54%–64%), whereas clades Fusobacteria, Synergistia, Firmicutes, and Tenericutes had a strong GSB (>70%) (Figure 1). We also noted a minor third group of predominantly Actinobacterial species exhibiting moderately opposite bias with a mode at 43% GSB. Thus, our analysis highlights the wide variation of gene-strand bias, despite the advantages of preferential co-orientation of replication and transcription. This kingdom-wide heterogeneity in GSB hints at the presence of intrinsic differences in the processes and factors underlying the bacterial genome organization.

Figure 1.

Gene-strand bias in bacteria. Distribution of gene-strand bias (calculated as the percentage of genes encoded on the leading strand) across bacterial clades. The X-axis denotes the clades, and the Y-axis represents the gene-strand bias (GSB) expressed as a percentage. The red horizontal line indicates a neutral scenario with no strand bias (50%). The median % GSB for each clade is shown on top and the number of species per clade is indicated at the bottom.

Integrated approach to detect gene inversions

We hypothesized that gene inversions may be one of the critical factors underlying the variation in GSB. To test this, we identified gene inversions within the population of a given species. Specifically, we focused on those gene inversions that switch the orientation of the transcription relative to replication upon inversion, as it would alter the nature of replication-transcription collisions, consequently influencing strand-biased gene distribution. The existing methods of determining inversions either use a phylogenetic approach or a local disparity in the direction of GC-skew on a single representative genome of a species (27,29,31,63). The local GC-skew disparity can detect inversions rapidly without requiring an outgroup species. However, this approach is indiscriminate to the genes under different selective pressures and horizontally acquired genes, which generally exhibit altered base compositions and evolutionary rates (64–66). Hence, the GC-skew method may overestimate gene inversions. Alternatively, the phylogeny-based comparative genomic approach is more reliable but studies have limited the analysis to a single representative genome, which may cause a sampling bias. Hence, we used an integrated and conservative approach to consider only the overlap of inversions detected by both GC-skew and phylogeny-based methods (Figure 2A). To circumvent the sampling bias, we estimated the inversion frequency (IF) within the population of a species. Further, we restricted our analysis to the core genome, the set of genes shared by all the strains in a population, to avoid genes affected by gene gain and loss events. Besides, core genes are phylogenetically more ubiquitous and characterize the species identity (67–70). Thus, it is imperative to focus on inversions in the core genome.

Inversion frequency negatively correlates with gene-strand bias

We constructed the core genomes of 18 species representing a GSB range of ∼50–90% and identified gene inversions within each population (Figure 2A, see Materials and methods). Inversion frequency (IF) was calculated as the ratio of the number of genes inverted over the total number of core genes in each species (Figure 2A), thus reflecting the proportion of gene inversions in a population and not their rates. We observed an extensive variation in IFs, ranging from no genes with inversion (B. subtilis and M. forum) to nearly 40% of the core genes inverted (B. mallei) (Figure 2B). Further, we calculated GSB by reconstructing the ancestral gene-strand status using parsimony and maximum likelihood approaches (see Materials and methods). Both methods yielded nearly identical values (Supplementary Figure S3B). We grouped the dataset into low GSB (<70%) and high GSB (>70%) groups, based on the observed bimodal distribution of GSB (Supplementary Figure S3A) (16,22). Although IFs exhibited a large variation across species, we observed a ∼26-fold higher median IF (median = 0.0667) in species with low GSB compared to those with high GSB (median = 0.0026). The observed heterogeneity in gene inversion frequency may explain the variation in GSB. To test this, we derived a correlation between the IF and GSB and found a strong negative correlation (Figure 2C; Supplementary Figure S3C; ρ = −0.7878, P = 0.0001), supporting our hypothesis. Thus, higher inversion frequencies are evident in bacteria with low gene-strand bias and the converse in species with high gene-strand bias. Next, we explored possible evolutionary, genomic and mechanistic features that may account for the negative relationship.

Divergence time and recombination potential do not underlie the variation in inversion frequencies

Our dataset encompasses species that are phylogenetically diverse with wide-ranging divergence times. Presumably, IF could be proportional to divergence times, explaining its variation. To examine this possibility, we calculated the evolutionary distance (patristic distance) from the species phylogenetic tree, which serves as a proxy for divergence times. If divergence time were to account for the inverse relationship, we would expect the IF to be positively correlated with distance. In contrast, we observed a statistically non-significant negative correlation between evolutionary distance and IF (Figure 3A), suggesting that species divergence time does not account for the difference in IFs. We further validated this by computing the mean branch lengths and confirmed that the correlation of IF normalized by the mean branch length against GSB remained significantly strong (Supplementary Figure S4A and B).

Figure 3.

Neither divergence times nor recombination potential underlie the inversion heterogeneity. (A) Inversion frequency plotted (Y-axis) against the evolutionary distance (X-axis) calculated as the median patristic distance from the phylogenetic tree of each species. Spearman's rank correlation coefficient (ρ) and the P-value (P) are displayed on the plot. (B) Distribution of IR lengths across the 18 analyzed species. The X-axis represents the species (labeled as in Figure 2) and the Y-axis denotes IR length (in bp) on a log scale.

The predominant mechanism underlying gene inversion is homologous recombination acting on inverted repeats (IRs) (24,71). The variation in IFs could arise from either the differences in recombination rate or IRs and their features. To investigate the first possibility, we estimated the rate of recombination (see Materials and methods). The recombination rate did not show a correlation with GSB (Supplementary Figure S4C, D and Supplementary Table S1). However, it was noted that the method used to measure the recombination rate relies on estimating inter-genomic recombination. Therefore, to ascertain the role of recombination, we calculated the length of target homologous sequences (IRs), which influences recombination efficiency (72). We found the median IR lengths to be comparable between species with low and high GSB (Mann–Whitney U-test, P = 0.8207) (Figure 3B). Together, these observations confirm that the variation in inversion frequency and its association with gene-strand bias may not be caused by the differences in recombination efficiency between species.

The density and distribution of inverted repeats negatively correlate with gene-strand bias

Having ruled out the contribution of IR length, we investigated whether other IR properties underlie the observed heterogeneity in inversions. We hypothesized that the differential density of IRs across species could drive the negative correlation between IF and GSB. A high density of IRs would indicate a greater chance for inversions, and vice versa. To this end, we estimated the observed-over-expected density of IRs for each species (see Materials and methods) and obtained a negative correlation with GSB (Figure 4A, Supplementary Table S2—outlier removed). As expected, the potential for inversions is likely dependent on the density of IRs, explaining the higher IF in species with low GSB and the converse for high GSB species.

Figure 4.

The abundance and distribution of inverted repeats (IRs) are correlated with gene-strand bias. (A) Inverted repeat density (Y-axis) was calculated as the ratio of the median observed over the expected density. The expected IR density was calculated by shuffling the representative genome (500 iterations) for each species and the median was considered. (B) Schematic illustrating the inter-replichore IRs that can mediate inversions causing no strand-switch, and intra-replichore IRs that potentiate strand-switching inversions. Blue and red lines represent leading and lagging strands of replication, respectively. Gray boxes indicate the location of two copies of an IR. (C) Intra-replichore IR density (Y-axis) was calculated as the ratio of the median observed over the expected density. Expected value was obtained similar to (A). (D) The ratio of inter-replichore to intra-replichore IRs (Y-axis). The gray line denotes the neutral scenario. In (A), (C) and (D), X-axis represents the gene-strand bias. Spearman's rank correlation coefficient (ρ) and the P-value (P) are displayed on the plots.

As we specifically focused on the inversions that switch the orientation of transcription relative to replication, we investigated the positional distribution of IRs. IRs can be classified into two types based on the relative location of the two copies of a repeat pair. When the two copies are present in different replichores (inter-replichore IRs), the IR pair leads to gene inversions that do not switch strands (Figure 4B). Alternatively, when both the sequences are present within a replichore (intra-replichore), IRs enable strand-switching inversions (Figure 4B) (23,24). We restricted our analysis of IR density to intra-replichore IRs and observed a stronger correlation with GSB (Figure 4C, Supplementary Table S2 – outlier removed), highlighting the role of intra-replichore IRs in the maintenance of GSB. In parallel, we detected IRs for each species with an alternative approach using the palindrome tool of EMBOSS suite (53), and calculated the density of intra-replichore IRs by dividing the number of IRs by the genome length. We observed that this alternative measure of IR density also negatively correlated with GSB (Supplementary Figure S5A), strongly supporting our hypothesis.

Further, we calculated the ratio of inter-replichore over intra-replichore IRs. A ratio close to 1 would indicate a similar potential for inversions that switch or do not switch the strand. A lower or higher ratio would indicate an increased or decreased strand-switching potential, respectively. We predicted that an altered inter-/intra-replichore IR ratio could account for the observed variation in IFs and in agreement found that the ratio was positively correlated with GSB (Figure 4D). The ratio was nearly 1 for low GSB species and increased in species with higher GSB. Hence, the relative distribution of the two copies of IR pairs influences the heterogenous inversion frequencies. Besides, the positive trend of the ratio may also indicate differential selection on the chromosomal distribution of IRs to modulate gene inversions.

Inverted repeat distance determines the inversion frequency

The distance between the two copies of an IR (repeat distance) would determine the number of genes inverted per inversion event (Figure 5A). Hence, repeat distance could control the IF, consequently the degree of GSB. To examine this possibility, we calculated the intra-replichore repeat distance (normalized by the chromosome lengths; see Materials and methods). The distributions of IR distances broadly exhibited large variance with a higher median in low GSB species, whereas the distributions were relatively narrow with a lower median for species with high GSB (Figure 5B). Moreover, we obtained a significant negative correlation between the median repeat distance and the GSB (Supplementary Figure S5B). The negative correlation suggested that larger repeat distances facilitate the higher IFs in species with low gene-strand bias. In contrast, shorter repeat distances account for the reduced IFs in high gene-strand bias species.

Figure 5.

Selection modulates inversion sizes through repeat distance. (A) Schematic explaining the scenario in which species with low gene-strand bias remain relatively unaffected by the size of inversion. Whereas, the species with high gene-strand bias can greatly be impacted by the larger inversions. Ratios indicate the percentage of genes on the leading (blue) and lagging (red) strand of replication. (B) Ridgeline plots of the distribution of the normalized repeat distances (X-axis) of intra-replichore IRs. The vertical line on each distribution represents median. Species denotations (Y-axis) are identical to Figure 2. (C) Inversion size (Y-axis) calculated as the median size of inversions normalized by the core genome size. (D) Inversion potential (Y-axis), calculated with the density, distribution, and size of intra-replichore IRs for every genome. In (C) and (D), X-axis represents the gene-strand bias. Spearman's rank correlation coefficient (ρ) and the P-value (P) are presented on the plots.

As the repeat distance negatively correlated with GSB, consequently, we expected that the size of inversions would follow the same trend. Species with low GSB have a nearly equal distribution of genes on leading and lagging strands. As a result, inversions would lead to an approximately equal number of genes switching between leading and lagging strands, unless there is a strong strand-biased selective pressure. Therefore, irrespective of the inversion size, GSB in extant genomes would not be significantly altered (Figure 5A). In contrast, in high GSB species, as the greater fraction of the genome is encoded on the leading strand, there is a higher probability for genes to switch to the lagging strand. Thus, larger inversions would cause a sudden and drastic decrease in the existing GSB (Figure 5A), which may be counter-selected. Consistent with this prediction, we obtained a strong negative correlation between the size of inversion (median inversion size/core genome size) and GSB (Figure 5C, Supplementary Table S2 – outlier removed). Thus, our results suggest that repeat distance could control the size of inversions and, consequently, the strand-biased distribution of genes.

Strand-switching potential dictates inversion frequency

Next, we analyzed whether the different properties of IRs including density, length, and distance contribute to the inversions in a cumulative manner. To factor in the combined effects, we quantified a measure called strand-switch potential (inversion potential) as previously described (see Materials and methods) (24). We observed a negative correlation between the measure for inversion potential and GSB (Figure 5D). Together, the results suggest that a cooperative effect of inverted repeat properties regulates inversion frequency (Supplementary Figure S5C), thereby impacting gene-strand bias.

Kingdom-wide negative correlation between inversion frequency and gene-strand bias

The population-based approach using representative species has implicated gene inversions as a major factor underlying the variation and maintenance of GSB. To further strengthen this finding, we verified our observations at a kingdom-wide scale. We calculated IFs in 2369 species analyzed in Figure 1. As the local GC-skew disparity-based method can rapidly detect gene inversions across large datasets, we utilized this approach for the kingdom-wide analysis. We observed a strong negative correlation between the IF (ratio of the number of inverted genes over the total number of genes) and GSB (Figure 6; ρ = −0.6246, P < 2.2e-16), reaffirming our findings. Further, we found that the inversion potential showed a statistically significant negative correlation with GSB at the kingdom-wide level (Supplementary Figure S6; ρ = −0.3594, P < 2.2e-16). These results assert the critical role of inversions and inverted repeats in the variation and preservation of gene-strand bias across the bacterial kingdom.

Figure 6.

Inversion heterogeneity in bacterial kingdom. Inversion frequency plotted against the gene-strand bias across bacterial kingdom. Color of the data points on the scatter denotes the clade as presented in Figure 1. Spearman's rank correlation coefficient (ρ) and the P-value (P) are displayed on the plot.

The nature of replication underlies the heterogeneity in gene inversions

Previously, it was shown that the nature of replisome is related to GSB and it was proposed that replication asymmetry could be a determinant of bacterial genome organization (22). Bacterial species can be classified into two groups based on the alpha subunit of the replicative DNA polymerase III. In the first group, two copies of the same DNA polymerase DnaE replicates both leading and lagging strands. In the second group, two different essential DNA polymerases DnaE and PolC are part of the replisome. PolC is responsible for the processive elongation of both DNA strands. DnaE extends the RNA primers during the lagging strand replication, followed by PolC-mediated elongation, analogous to the eukaryotic replication (73,74). Interestingly, the species that possess PolC exhibit high GSB (78%), while the species without PolC show moderate bias (58%) (22), congruent with the bimodal distribution of GSB (Supplementary Figure S3). This replication-dependent association suggested the possibility that the contrast in GSB between the two groups could be driven by differential IFs and maintained by the variation in IRs. To test this possibility, we categorized our dataset into PolC/non-PolC groups and found that the PolC group exhibited a striking ∼22-fold reduction in IFs compared to the non-PolC group (Figure 7A). Similar to our earlier observation (Supplementary Figure S4C), we did not see any difference in the recombination rates between the two groups (Figure 7B). Further, we found that the striking contrast in IFs amongst PolC/non-PolC species is corroborated by a greater than 6-fold difference in the IR density (Figure 7C). Together, these observations suggest that the maintenance of gene-strand bias may depend on the DNA polymerase composition of the replication fork, which is likely achieved by the differential regulation of IRs and associated inversions.

Figure 7.

Association of gene-strand bias and DNA polymerases. (A) Median inversion frequency (Y-axis), (B) Median recombination rate (Y-axis), and (C) Median inverted repeat density (Y-axis) were compared between species without (non-PolC) or with the polC gene (PolC), and their distributions are plotted. The central mark denotes the median, and the top and bottom edges indicate the first and third quartiles. The whiskers represent 1.5 times the interquartile range. Significance was calculated using Mann–Whitney U-test. (D) The ratio of the frequency of inversion to lagging strand over inversion to leading strand (Y-axis) plotted against the gene-strand bias (X-axis). Spearman's rank correlation coefficient (ρ) and the P-value (P) are indicated in the plot. The gray line indicates the neutral scenario. (E) Bacterial kingdom phylogeny and associated characters are represented as concentric circles. The phylogenetic clades are color-coded on the inner circle. In the middle circle presence (brown) or absence (light blue) of PolC is indicated. On the outermost circle, GSB is represented scaled from low (green) to high (blue) percentage. The height of the bar (gray) on the circumference corresponds to inversion frequency (same as Figure 6).

The distinct mode of lagging strand replication between PolC/non-PolC species may alter the outcomes of head-on replication-transcription collisions, resulting in a disparity in fitness costs and possibly the strength of selection. Therefore, in species with low GSB, unbiased switching of genes between leading and lagging strands may be tolerated, while in species with high GSB, switching to lagging strand may be strongly avoided. To test this possibility, we calculated the ratio of inversions to lagging over leading strand and obtained a strong negative correlation with GSB. The ratio was less than one in the PolC group, indicating that inversions to lagging strand are strongly avoided, whereas in the non-PolC group the ratio was ≥1 suggestive of weak or no selective constraint on inversions (Figure 7D). This result was further substantiated by a significant ∼4-fold difference in the ratio of inversions to lagging over the leading strand between the two groups (Mann–Whitney U-test, P = 0.0007). Hence, the differential outcomes of head-on replication-transcription collisions, presumably due to the distinct replicative DNA polymerases, could underlie the strand-biased variability in gene inversions between the species with and without PolC.

Concurrent evolution of DNA polymerases with gene-strand bias

DNA polymerase PolC has been suggested to have evolved from a common ancestor along with DnaE and is restricted to the phylogenetic clades - Firmicutes, Fusobacteria, Tenericutes, and Thermotogae (75). Interestingly, we found that all of these clades except Thermotogae exhibited high GSB (Figure 1). Considering the relationship between replicase-based groups and GSB as well as IFs, we wondered if the evolution of DNA polymerases and GSB were coupled. To examine this possibility, we reconstructed the bacterial kingdom-wide phylogeny of 2369 species using the previously reported 400 universal phylogenetic marker genes (57) and examined the phylogenetic prevalence of PolC. To classify species into PolC and non-PolC groups, the presence/absence of PolC orthologs were detected by protein homology based on the bidirectional best hit BLAST approach (22). Consistent with the previous study, we found that PolC was present in Firmicutes, Fusobacteria, Tenericutes and Thermotogae (Figure 7E) (75). We mapped the presence and absence of PolC on the kingdom-wide phylogeny using stochastic character mapping (see Materials and methods). Interestingly, we noticed that PolC had originated at the last common ancestral node of phyla Firmicutes, Fusobacteria, and Tenericutes. Additionally, PolC was also mapped to the last common ancestor of Thermotogae, indicating an independent origin possibly through horizontal gene transfer (Supplementary Figure S7A). Similarly, we mapped the GSB on the same phylogenetic tree as a continuous character (Figure 7E, Supplementary Figure S7B). Strikingly, we found that the clades with increased GSB (>70%) shared the same ancestral node as PolC (Supplementary Figure S7A and B), suggesting a congruent evolutionary origin. Species that exhibited low GSB spanned the rest of the bacterial phylogeny, where PolC was absent. We further tested if the differences in GSB were associated with presence/absence of PolC after controlling for phylogenetic relatedness. We carried out a phylogenetic analysis of variance between these two traits, implemented in geiger package of R. We observed that the difference in GSB is statistically significant (Table 1; P = 0.0010) among the PolC and non-PolC groups, indicating that the variation in GSB is associated with the nature of replisome (Table 1). To statistically validate the co-evolution of these traits, we classified the species as low (<70%) and high (>70%) GSB and carried out Pagel's binary character correlation test (76). The test compared the independent and inter-dependent evolutionary models for the absence/presence of PolC and low/high GSB, treated as the binary characters. The model defining the inter-dependent evolution of PolC and GSB performed significantly better than the independent evolution model (Table 1; likelihood ratio test, P = 1.61511e-09). This strongly signifies that the DNA polymerases and gene-strand bias have likely evolved in a concurrent manner.

Table 1.

Phylogenetic statistical analysis of the relationship between the nature of replisome, gene-strand bias, inversion frequency and strand-switch potential of inverted repeats

Groups	Genomic trait	Phylogenetic test		F-statistic	P-value
PolC (Present/Absent)	GSB	ANOVA		4733.2	0.0010
	IF			1138.5	0.0040
	GSB + IF	MANOVA		2366.8	0.0010
GSB (Low/High)	IF	ANOVA		1688.5	0.0010
	IF + SSxNi	MANOVA		843.9	0.0019
PolC (Present/Absent) & GSB (Low/High)	NA	Pagel's binary character correlation test	Independent model	Log likelihood = −231.0989 AIC = 470.1978	LRT = 1.61511e-09
	NA		Interdependent model	Log likelihood = −207.6588 AIC = 431.3176

GSB, gene-strand bias; IF, inversion frequency; ANOVA, analysis of variance; MANOVA, multivariate analysis of variance; SSxNi, inversion potential; AIC, Akaike information criterion; NA, not applicable; LRT, likelihood-ratio test.

Inversions and inverted repeats maintain gene-strand bias across bacterial kingdom

Our results highlighted the crucial role of IF and IRs in maintaining GSB both at the population level and in the entire bacterial kingdom. To examine if gene inversions phylogenetically co-varied with DNA polymerase groups and GSB, we mapped IF on the phylogeny of bacterial kingdom. We observed lower IFs in the clades that have PolC and a high GSB (i.e. Firmicutes, Fusobacteria, and Tenericutes) (Figure 7E, Supplementary Figure S7C), while the low GSB species without PolC spanned the rest of the phylogeny exhibited higher IFs. To statistically test if the combined effects of inversion potential and frequency could explain the differences in GSB after accounting for phylogenetic relatedness, we performed a phylogenetic multivariate analysis of variance (MANOVA). We found that the low (<70%) and high (>70%) GSB groups significantly differed in the IF and strand-switch potential of IRs (Table 1; P = 0.0019). These results suggested that a combinatorial effect of IF and IRs contributed to the maintenance of GSB among PolC and non-PolC species. Thus, the phylogenetic analyses suggest a close link between the evolution of the DNA replication machinery, gene inversions, and inverted repeats implicating a replication-dependent origin as well as maintenance of gene-strand bias.

Discussion

The existence of gene-strand bias (GSB) in bacteria is explained by selection primarily acting on essential, highly expressed, and functionally important genes (14–16,19–21). However, the evolution, variation and maintenance of GSB has remained elusive. We discover that strand-switching gene inversions underlie this variation, substantiated by the inverse relationship between GSB and inversion frequency (IF) across the bacterial kingdom. The properties of inverted repeats (IRs) are coordinately regulated by selection, elucidating the extensive heterogeneity in GSB and its preservation. The co-evolution of DNA polymerases with GSB suggests a causal effect of replication on the origin of GSB. Concordantly, IF and IR characteristics differ between the two bacterial groups classified by the DNA polymerase composition of the replisome. We propose that the distinct modes of replication may underlie the origin and evolution of gene-strand bias. Variation in GSB is likely driven by gene inversions primarily through IRs and presumably maintained via a selection gradient established by the differential outcomes of head-on collisions (Figure 8).

Figure 8.

Proposed model describing the role of the nature of replication in evolution and preservation of gene-strand bias. The nature of replication underlined by the employment of the DNA polymerase at the replication fork determines the differential fitness cost of head-on collisions. This differential fitness cost presumably led to the evolution of high gene-strand bias in species with high fitness cost, whereas in species with lower fitness cost the evolution of low-to-moderate gene-strand bias is favored. This fitness cost disparity also enforces a gradient strength of selection on the inverted repeat characteristics (density, distance, and distribution) leading to modulation of inversion frequency and size promoting the maintenance of the evolved gene-strand bias.

The strand-switching inversions within bacterial populations spanning gene-strand biases remain underexplored. Earlier reports on preferential inversions to leading strand only explain the occurrence of high GSB (31,63). We reveal that the IFs are heterogeneous, yet non-randomly associate with GSB, apparent from the strong negative correlation in representative populations (Figure 2C), and across the bacterial kingdom (Figure 6). Species with low/moderate GSB experience high/intermediate IFs that minimally alter the bias. The persistent switch between leading and lagging strands is evident from the marginal difference in strand-specific gene inversions. In contrast, high GSB species exhibit lower IFs with a skew towards leading strand. Previously, horizontal gene transfer and/or gene loss was proposed to contribute to GSB (14,77), however, their small fraction is insufficient to explain the GSB variation. Moreover, genomic flux affects the variable genome, rather than the core genome, which exhibits phylogenetic conservation in gene order and orientation (70,78,79). Therefore, the population-level analysis of core genome proved vital to demonstrate that the differential IF elucidates the variation and maintenance of gene-strand bias. Though this approach restricted species sampling, we believe an increased sequence availability will strengthen our findings considering our GC-skew based kingdom-wide analysis. The GC-skew approach may overestimate inversions, yet the IF negatively correlates with GSB reaffirming the population-level observation.

The inversion heterogeneity can result from the differences either in rate of occurrence or selection pressure. Having ruled out the contribution of species divergence time and recombination (Figure 3, Supplementary Figure S4), it is plausible that selection may regulate gene inversions by fine-tuning the IR density, distance, and distribution. The IR characteristics associate similarly with GSB as IF (Figures 4 and 5), rendering them as targets of selection. We propose that selection acts in a gradient manner allowing relatively unconstrained inversions in low GSB while minimizing/purging them in high GSB bacteria. Higher IR density implies a greater inversion potential, while repeat distance determines IF by controlling inversion size. It was hypothesized that selection minimizes the IR abundance and distance to avoid the adverse effects on genome stability and gene-dosage (23,80). Peculiarly, IRs are also enriched in species like N. gonorrhoeae as part of DNA uptake sequences (81), which may explain the observed overabundance in our study. Our results indicate that selection controls IR density and distance, consistent with the differential repeat distributions in species with contrasting GSB (82). The replichore-dependent IR distribution influences GSB with a bias toward inter-replichore inversions (23,25), while intra-replichore inversions appear restricted (24). We show that replichore-based positioning of IRs suitably explains the heterogeneity in strand-switching inversions among low and high GSB species. Together, we suggest that selection regulates the IR properties in a gradient fashion conditioned by species-specific gene-strand bias. Our results surprisingly implicate IRs in preserving genome organization via maintaining GSB, thus augmenting their contrasting roles in genomic instability and evolvability (33,83).

Although the strand-switching potential of IRs negatively correlates with GSB in representative species, the correlation is modest at the kingdom-wide scale, suggesting the involvement of alternative factors/mechanisms in generating inversions. For instance, mechanisms like non-homologous end joining, template switch, and microhomology-mediated break-induced replication also can create inversions (84,85). Besides, mobile genetic elements may also contribute to inversions either directly or by increasing the repeat density (33,83). Such a scenario possibly explains the high frequency of inversions seen in B. mallei, which is shown to experience extensive genomic rearrangements through IS elements (86). Thus, these alternative mechanisms of generating inversions warrant further investigation.

Recent studies suggested that genes inverted to lagging strand may experience faster evolution due to the increased mutagenesis caused by head-on replication-transcription collisions (7,29). However, this evolutionary advantage is too small to explain the wide-ranging GSB (63). Alternatively, the mutation-selection balance theory proposes that lagging strand genes exist through the interplay of inversions and negative selection on inverted genes (63,87–89) and modulation of this balance may account for the variation in GSB. Although selection purges inversions, we propose an intriguing possibility that it may also critically control the mutation supply, conceivably, through IR characteristics. In agreement, our data shows that the mutability (IR density, distance, and distribution), consequently the generation of mutations (inversions) is relatively unconstrained in low GSB species. In contrast, selection has minimized the mutability to invert genes, thereby constraining inversions in the high GSB species. Though the selection pressure is minimized genome-wide in low GSB species, strong selective constraints still exist on essential genes and rRNA operons, maintaining their co-orientation with replication (9,10,90). Thus, we believe that selection preserves genome organization by regulating the generation of mutations beyond purging them.

Replication underlies the selection on genome organization influencing gene order, gene dosage, strand compositional bias, and GSB (18,22,23,91–95). Though these are mutually nonexclusive, GSB could strongly influence genome stability and fitness. Therefore, maintenance of the evolved GSB is imperative emphasizing our model of gradient selection strength, which invokes the question about the factors driving the differential selection. The replication fork asymmetry defined by distinct DNA polymerases is linked to GSB and genomic rearrangements (21,22,79,96). We identify that the replicase-based groups (PolC/non-PolC) are distinctly associated with IFs and IR characteristics (Figure 7A–C). Thus, examining the link between the mode of replication and GSB becomes crucial. Genes experience strand-dependent mutational pressures due to differences in DNA replication fidelity, transcription, and DNA repair (97–101). The limited evidence linking GSB to the variability in these processes (14,102) indicates that they cannot sufficiently explain the selection gradient. Rather, the nature and severity of collisions could drive this selection gradient. Studies have demonstrated mutagenic and fitness costs of head-on collisions (3,5,8,31,89). Based on our observed strand-specific differences in inversions (Figure 7D), we propose that collision cost may differ between species with varying GSB. The inversion of highly expressed rRNA operon to lagging strand is tolerated in E. coli (low GSB), but detrimental in B. subtilis and L. lactis (high GSB) (5,103,104), providing empirical evidence to the GSB-associated differences in the fitness costs of head-on collisions. The fitness cost disparity may result from distinct prevalence of collision-mitigating factors (105,106). Alternatively, the disparate nature of replication between the PolC/non-PolC species may arise from the mode of lagging strand synthesis, potentially altering the severity of head-on collisions. The frequent switching between PolC and DnaE during lagging strand replication may cause a delay or alter the accessibility for collision-mitigating factors upon head-on collisions. Hence, the differential fitness cost could directly arise from the mode of replication, leading to a selection gradient orchestrating the genesis and maintenance of GSB. The co-evolution of replicases with distinct GSB across the bacterial kingdom strongly signifies this notion (Figure 7E, Supplementary Figure S7). Quantification of collision costs from diverse species would further strengthen our model.

Overall, we conclude that the origin of gene-strand bias and its variation are tightly linked to the evolution of DNA replication machinery and the bias is maintained by selection on inverted repeats that regulates gene inversions across bacteria. Selection appears to control the generation of inversions in a gradient fashion by governing inverted repeat density, distance, and distribution beyond purging inversions. The selection gradient is likely optimized by the differential fitness cost of head-on collisions across species. Essentially, the nature of replication may dominantly modulate gene inversions by enforcing gradient selection pressures, intrinsically on the evolution of DNA repeat sequences to preserve bacterial genome organization and stability.

Data availability

All the genomes used in the study are publicly available and the database accession numbers are provided in the Supplementary Data. The data and code underlying this article are available at: https://zenodo.org/doi/10.5281/zenodo.10455762.

Supplementary data

Supplementary Data are available at NAR Online.

Funding

Wellcome Trust-DBT India Alliance [IA/I/18/2/504037 to T.S.S.]; Prime Minister's Research Fellowship [0 800 295 to M.A.]. Funding for open access charge: PMRF Fellowship/Cumulative Professional Development Allowance.

Conflict of interest statement. None declared.