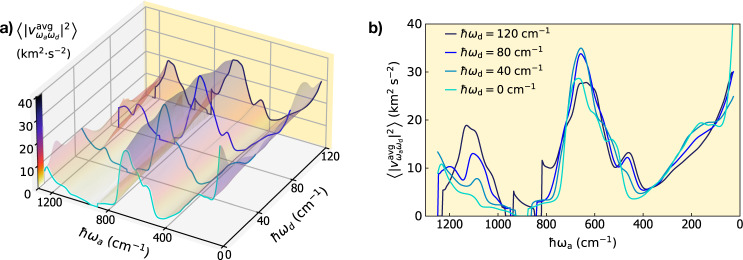
Fig. 7. Velocity operator of vitreous silica and conductivity saturation with temperature.

a Average square modulus of the velocity-operator elements $⟨\mid {\mathsf{v}}_{{\omega }_{\mathrm{a}}{\omega }_{\mathrm{d}}}^{\mathrm{avg}}{\mid }^2⟩$ for the 192(D) model of v-SiO₂, computed from first principles and represented as a function of the energy differences ($\hslash {\omega }_{\mathrm{d}}=\hslash \left(\omega {\left(\mathbf{q}\right)}_s-\omega {\left(\mathbf{q}\right)}_{s^{\prime }}\right)$) and averages ($\hslash {\omega }_{\mathrm{a}}=\hslash \frac{\omega {\left(\mathbf{q}\right)}_s+\omega {\left(\mathbf{q}\right)}_{s^{\prime }}}{2}$) of the two coupled eigenstates (having wavevector q and modes $s,s^{\prime }$; see text for details). The one-dimensional projections in (b) show that the elements $⟨\mid {\mathsf{v}}_{{\omega }_{\mathrm{a}}{\omega }_{\mathrm{d}}}^{\mathrm{avg}}{\mid }^2⟩$ are almost unchanged at a given average frequency for increasingly large energy differences. For increasingly larger temperatures, these almost-constant elements drive the saturation the rWTE conductivity (Eq. (1) with the Voigt distribution), yielding results very close to the Allen-Feldman conductivity curve (Fig. 5), which is determined exclusively by velocity-operator elements with ℏω_d → 0.