How Trustworthy Is Your Tree? Bayesian Phylogenetic Effective Sample Size Through the Lens of Monte Carlo Error

Abstract

Bayesian inference is a popular and widely-used approach to infer phylogenies (evolutionary trees). However, despite decades of widespread application, it remains difficult to judge how well a given Bayesian Markov chain Monte Carlo (MCMC) run explores the space of phylogenetic trees. In this paper, we investigate the Monte Carlo error of phylogenies, focusing on high-dimensional summaries of the posterior distribution, including variability in estimated edge/branch (known in phylogenetics as “split”) probabilities and tree probabilities, and variability in the estimated summary tree. Specifically, we ask if there is any measure of effective sample size (ESS) applicable to phylogenetic trees which is capable of capturing the Monte Carlo error of these three summary measures. We find that there are some ESS measures capable of capturing the error inherent in using MCMC samples to approximate the posterior distributions on phylogenies. We term these tree ESS measures, and identify a set of three which are useful in practice for assessing the Monte Carlo error. Lastly, we present visualization tools that can improve comparisons between multiple independent MCMC runs by accounting for the Monte Carlo error present in each chain. Our results indicate that common post-MCMC workflows are insufficient to capture the inherent Monte Carlo error of the tree, and highlight the need for both within-chain mixing and between-chain convergence assessments.

Introduction

Bayesian inference via Markov chain Monte Carlo (MCMC) is widely used in phylogenetic estimation (Nascimento et al., 2017). MCMC enables the generation of samples according to arbitrary distributions, such as the posterior distribution of a phylogenetic model, though it must draw autocorrelated samples (Geyer, 2011). In fact, it is only in the limit of running the analysis infinitely that we are guaranteed the summaries of our MCMC samples will converge to the true values of the corresponding posterior summaries. Users are thus left with the task of determining whether inference from their MCMC samples are trustworthy. In practice, this entails assessing whether any given chain appears to be stationary and assessing how well it is mixing (Kass et al., 1998). In this paper, we focus on the issue of mixing as embodied in the notion of the effective sample size (ESS). The effective sample size is closely related to the notion of Monte Carlo error, which describes the error in parameter estimation due to using sampling-based approaches (Geyer, 2011; Vats and Knudson, 2021; Vehtari et al., 2021).

A phylogenetic model describes the evolutionary history of a set of samples for which we have character data (such as DNA sequence data) (Felsenstein, 2004; Lemey et al., 2009; Chen et al., 2014). The core of a phylogenetic model is a discrete tree topology, which specifies how the samples are related to each other via a series of nested relationships (Thompson, 1975; Felsenstein, 1981). Describing the process of evolution along the tree also requires branch lengths, which specify the amount of evolutionary change, and a substitution model, which specifies the relative rates of change between character states (Felsenstein, 1981).

Phylogenetic posterior distributions are complex objects, and it is known that sampling from them via MCMC can be quite difficult (Lakner et al., 2008; Höhna and Drummond, 2012; Whidden and Matsen IV, 2015; Zhang et al., 2020; Meyer, 2021). Overall performance of the MCMC chain is often diagnosed by looking at the trace (collection of samples through time) of the log-likelihood or the log-posterior density, though this should only be the first step in a more rigorous pipeline (Lemey et al., 2009). Tracer is a popular tool for summarizing and visualizing MCMC samples from phylogenetic software, which will automatically compute the ESS for all values a program records, including continuous model parameters and the densities of the log-likelihood and log-posterior (Rambaut et al., 2018). Tracer flags parameters if the ESS is below 200, commonly taken as a rule-of-thumb minimum (Lanfear et al., 2016). This can be useful for determining whether continuous model parameters have been sampled appropriately, though Fabreti and Höhna (2021) argue for a more stringent cutoff of 625.

These tools and guidelines do not address a central question: how well did a given MCMC run sample from the posterior distribution of tree topologies, defined as unweighted tree graphs or, more informally, as branching structures of phylogenetic trees? Tree sampling is challenging, and previous theoretical (Mossel and Vigoda, 2005) and empirical (Harrington et al., 2021) work has demonstrated decoupling between the mixing of the log-likelihood and the sampling of the tree. For assessing MCMC convergence of trees, standard practice involves running multiple chains and comparing the estimated “split” probabilities (Lemey et al., 2009). Splits are bipartitions of taxa (tips of the tree), correspond to edges in an unrooted phylogeny, and can be useful for comparing tree distributions even when there are many sampled tree topologies (Lemey et al., 2009). Each split corresponds to a particular evolutionary grouping of taxa, and so the posterior probability of a particular split measures the strength of support for a hypothesized evolutionary relationship. Comparing split probabilities between runs addresses whether multiple chains are sampling from similar distributions, but it does not address how well those chains are mixing.

Ideally, a phylogenetic workflow should rigorously assess the quality of MCMC samples by examining both between-chain and within-chain diagnostics for all model parameters. Here and in the rest of this paper we set aside the related issue of determining the “burn-in” (the point at which the chain has reached the stationary distribution); for work on this see (Kelly et al., 2021) and (Fabreti and Höhna, 2021). For continuous model parameters, between-chain convergence can be assessed with the potential scale reduction factor (PSRF). This is reported for each variable by the Bayesian phylogenetic inference package MrBayes (Ronquist et al., 2012), and both univariate and multivariate versions are available in R packages like coda (R Core Team, 2018; Plummer et al., 2006). Mixing of continuous model parameters is easily addressed by examining the ESS of all variables in Tracer, or by computing a multivariate ESS (Vats et al., 2019) in the R package mcmcse. For the tree, split-based comparisons such as the average (or maximum) standard deviation of split frequencies (ASDSF) are a common approach to examine between-chain convergence. However, approaches for examining the mixing of the tree remain under-studied, and form the focus of this paper.

One promising approach to understanding MCMC mixing performance for the tree is to extend the notion of effective sample size to trees. Lanfear et al. (2016) present two approaches for computing a single ESS for tree topologies which they term the approximate ESS and the pseudo-ESS (both available in the RWTY package (Warren et al., 2017)). They additionally present several simulation-based validations of their ESS measures, but do not address how those ESS measures capture Monte Carlo error. Gaya et al. (2011) and Fabreti and Höhna (2021) alternatively consider taking the ESS individually for each split by representing it as a 0/1 random variable, which allows for standard ESS computations. However, this approach does not account for correlation in the presence or absence of splits due to the shared tree topology. Further, samples of trees can be summarized in many ways, and there is no obvious way to link a vector of persplit-probability ESS values to the Monte Carlo error of other key summary measures, like the probabilities of different tree topologies or the summary tree (a single tree taken to be representative of a sample of trees).

In this paper, we seek to understand the relationship between an ESS for phylogenies and phylogenetic Monte Carlo error. This requires special consideration because trees are complex and high-dimensional objects. Thus, classical means of linking ESS to Monte Carlo error are not directly applicable, and a considerable amount of the paper will be dedicated to making this link. We note that we will often use “tree” as synonymous with the topology of the phylogenetic tree, as we focus on the challenges posed by the discrete tree structure, and we will refer to ESS measures for phylogenies interchangeably as either tree or topological ESS measures. The goal of such measures is to adequately describe the mixing and autocorrelation of the MCMC samples of phylogenies such that the Monte Carlo error of phylogenetic quantities can be addressed.

Classically, the ESS is defined using the variance of the sample mean. Imagine we wish to estimate the mean, $\mu$, of some distribution with known (true) variance ${\sigma }^2$ given $n$ samples from this distribution. If the $n$ samples were independent, we would have a direct link between the variance of our sample mean and the number of samples, given by $\mathrm{V}\mathrm{a}\mathrm{r}\left(\hat{\mu }\right)={\sigma }^2/n$, where $\hat{\mu }$ is the sample mean. However, when samples are dependent this will underestimate the true variance of the sample mean. The ESS is a hypothetical number of independent samples which corrects for this and yields the correct variance (or standard error) of our estimator of the mean (Vats and Knudson, 2021), which can be defined by $\mathrm{V}\mathrm{a}\mathrm{r}\left(\hat{\mu }\right)={\sigma }^2/\mathrm{ESS}$. The ESS is important to MCMC-based Bayesian inference because we must use correlated samples to estimate quantiles of the posterior distribution. Run infinitely long, it is guaranteed that the posterior mean of a parameter calculated from MCMC samples will be infinitesimally close to the true posterior mean. Given finite run lengths we must account for the resultant error to understand how precise our estimates are (Neal, 1993; Kass et al., 1998). The Markov chain central limit theorem establishes that the sampling distribution of a mean converges asymptotically to a normal distribution (Jones, 2004). Thus, if we know the ESS of a (real-valued) model parameter, we can construct confidence intervals for it, making the ESS a key quantity for Bayesian inference.

In this paper, we focus on two questions: for what aspects of estimated phylogenies might a tree ESS capture Monte Carlo error, and how might we compute an ESS of phylogenies? Specifically, we consider whether an ESS of phylogenies is informative about the sampling variability of three summary measures (Figure 1): (1) the probabilities of splits in the tree, (2) the probabilities of tree topologies, and (3) a summary tree. Then, we describe several different ways to compute putative measures of tree ESS, including approaches of Lanfear et al. (2016) and newly-derived approaches. These methods can be broken down into three categories: (A) generalizing continuous variable ESS identities to trees, (B) computing the ESS on a reduced-dimensional representation of the trees, and (C) ad-hoc methods. We test these putative definitions and approaches to a tree ESS via simulations. In these simulations, we take probability distributions on phylogenetic trees inferred from real data and run an MCMC sampler targeting this known posterior. This allows us to compute brute-force estimates of sampling variability to which to compare the estimates based on our ESS measures.

Figure 1:

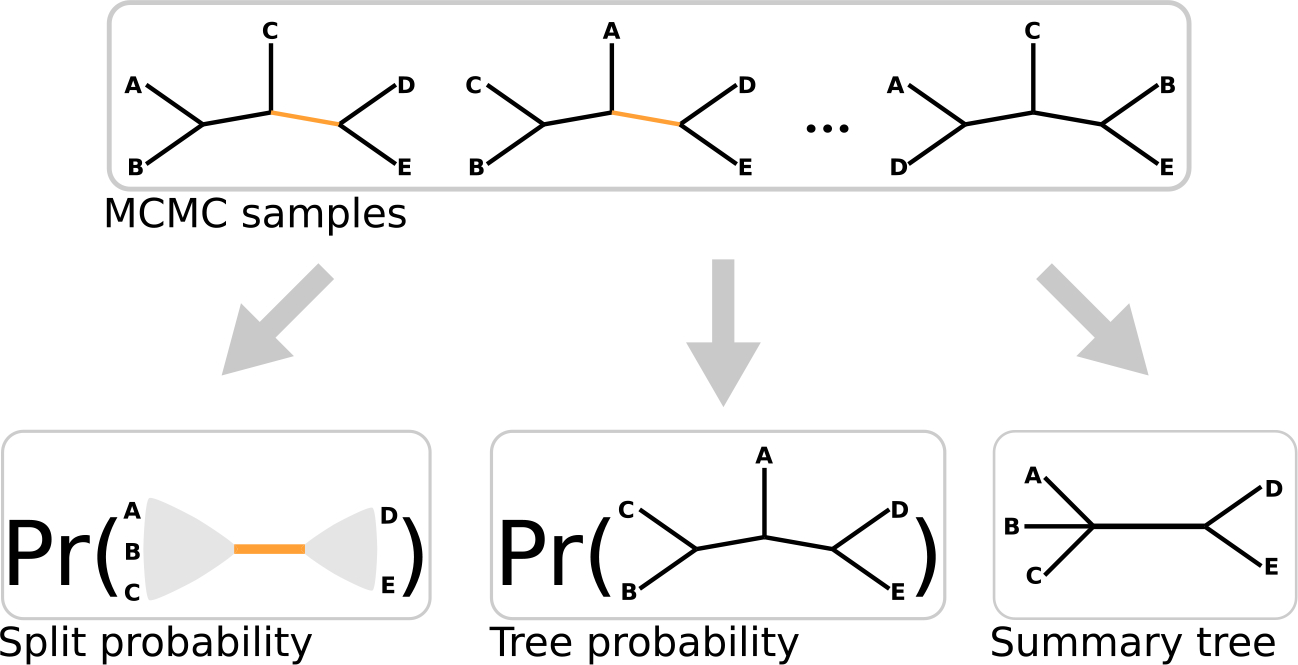
A cartoon depiction of a set of MCMC samples of a phylogenetic tree topology on five tips and the three summaries of the posterior distribution on trees we consider in this study. Split probabilities (left) are estimated by the fraction of MCMC samples which have a given bipartition of taxa, marginalizing out the rest of the tree topology. The depicted split partitions the tips into the tip-sets $\{A,B,C\}$ and $\{D,E\}$ (the edge corresponding to this split is colored orange in the MCMC samples). Tree probabilities (center) are estimated by the fraction of MCMC samples which have a given tree topology. Summary trees (right) are single trees which serve as a point estimate for all trees. Some, like the MRC tree, may not be fully resolved. The depicted MRC tree is unresolved (does not establish the particular topology with respect to) for the tip-set $\{A,B,C\}$.

We conclude with a case study, applying all ESS measures to six datasets of frogs and geckos from Madagascar (Scantlebury, 2013). Time-calibrated phylogenies of these groups were originally used to test hypotheses about adaptive radiations, and the datasets were revisited by Lanfear et al. (2016) as benchmarks for their ESS measures. Using these datasets, we demonstrate how tree ESS can be used to construct confidence intervals on split probabilities. When combined with a common visual multi-chain convergence diagnostic, the split probability plot, this allows us to decompose between-chain disagreement into disagreements that can be attributed to low sample size, and disagreements that cannot. This highlights both the importance of within-chain measures of Monte Carlo error, but also how they form only a part of the larger picture of MCMC convergence. Indeed, our results show that multiple chains are always necessary to be confident in phylogenetic MCMC convergence. Furthermore, these multiple-chain runs show that even with confidence intervals derived using our best ESS estimates, pairs of runs can have distinctly different estimates of split probabilities. Taken together, our empirical and simulated results make clear the importance of directly assessing how well the tree topology mixes using a tree-specific ESS.

Methods

We first offer a brief overview of this section before proceeding into the methods. In the first subsection, we present a brief summary of Bayesian phylogenetic inference as a point of reference. Next, we review background information on the ESS of one-dimensional Euclidean random variables, including how it is linked to the estimator variance of the sample mean (defined above) and how it is computed. Then, we detail three Markov chain Monte Carlo standard error (MCMCSE) measures which we will use to assess the performance of tree ESS measures. Specifically, we investigate Monte Carlo variability in estimated split probabilities, estimated tree probabilities, and the estimated summary tree. Lastly, we consider four tree ESS measures in several different families of approaches, including two methods from Lanfear et al. (2016).

Phylogenetic inference

Phylogenetic inference is centrally concerned with the estimation of a phylogenetic tree topology, $\tau$, from character data $y$ such as DNA sequences (Lemey et al., 2009). Standard inference approaches require a number of continuous parameters, $\mathit{\xi }$, and compute the likelihood, $\mathrm{P}\mathrm{r}(y\mid \tau ,\mathit{\xi })$ using the Felsenstein pruning algorithm (Felsenstein, 1981). The continuous parameters, $\mathit{\xi }$, define the branch lengths (the time parameter of a continuous-time Markov chain process of evolution), the relative rates of change between different character states (the transition rate matrix), and possibly heterogeneity among sites in the relative rate of change (the among-site rate variation model). In Bayesian phylogenetic inference, we use MCMC to sample from the $\mathrm{P}\mathrm{r}(\tau ,\mathit{\xi }\mid y)$ and marginalize out $\mathit{\xi }$ to obtain the distribution of interest, $\mathrm{P}\mathrm{r}(\tau \mid y)$. In this article, we consider unrooted tree topologies, where the topology depicts a set of nested evolutionary relationships without directionality (Figure 1). Unrooted trees can be defined by their collection of edges, which are often referred to as splits or bipartitions of taxa. Every fully resolved tree with $n_{\text{taxa}}$ tips contains $n_{\text{taxa}}-3$ non-trivial splits (internal edges) and $n_{\text{taxa}}$ trivial splits (pendant edges which exist in all trees). One common summary of the posterior distributions on trees is the majority-rule consensus (MRC) tree. The (strict) MRC tree includes every split estimated to posterior probability greater than 0.5, and only those splits (Margush and McMorris, 1981; Lemey et al., 2009), and is widely implemented in software for both Bayesian and maximum likelihood inference (where it summarizes bootstrap support). The set of all these splits correctly defines a tree (Semple and Steel, 2003), though it may not be completely resolved (see Figure 1 for an example of an unresolved MRC tree). The posterior probabilities of splits (henceforth simply split probabilities) themselves are useful as measures of posterior support for particular evolutionary relationships.

Classical definitions of ESS

Before we dive into the classical definition of ESS, we briefly review the Markov chain central limit theorem. Assume we have a set of MCMC samples (with any burn-in period previously removed as needed) $X_1,\dots ,X_n$, a function $g$, and use ${\bar{g}}_n$ to denote the sample mean using $n$ samples:

$${\overline{g}}_n=\frac{1}{n}\sum _{i=1}^{n}g\left(X_i\right).$$ (1)

Let $\pi$ denote the posterior distribution and ${\mathbb{E}}_{\pi }\left[g\right]={\int }_X g\left(x\right)\pi \left(dx\right)$ the true posterior expectation. Using the notation of Flegal et al. (2008), the Markov chain central limit theorem tells us that the asymptotic distribution of ${\bar{g}}_n$ is,

$${\bar{g}}_n~\mathrm{N}\mathrm{o}\mathrm{r}\mathrm{m}\mathrm{a}\mathrm{l}\left({\mathbb{E}}_{\pi }\left[g\right],{\sigma }_g^2/n\right).$$ (2)

Following Flegal et al. (2008), we can write ${\sigma }_g^2$ as the sum of a series of autocovariances at increasing time lags,

$${\sigma }_g^2={\mathrm{Var}}_{\pi }\left(g\left(X_1\right)\right)+2\sum _{i=2}^{\infty }{\mathrm{Cov}}_{\pi }\left(g\left(X_1\right),g\left(X_i\right)\right),$$ (3)

where we assume $X_1~\pi$ and use $\pi$ as a subscript to denote this. For the rest of this section, we will assume that $g$ is the identity function, such that $g\left(x\right):=x$ and ${\bar{g}}_n$ becomes the average of the MCMC samples, ${\bar{g}}_n=\bar{X}$. For clarity of terminology, we will distinguish between the two variance quantities of interest. We will use ${\sigma }_{\pi }^2$ to represent the variance of the posterior distribution,

$${\sigma }_{\tau }^2={\mathrm{Var}}_{\pi }\left(X_1\right).$$

We will refer to ${\sigma }_g^2$ as the limiting variance and represent it as ${\sigma }_{\mathrm{l}\mathrm{i}\mathrm{m}}^2$. In this simpler case, where we only care about the sample mean, (2) tells us that

$$\frac{{\sigma }_{\mathrm{l}\mathrm{i}\mathrm{m}}^2}{n}=\mathrm{Var}\left(\bar{X}\right).$$ (4)

This reveals why ${\sigma }_{\text{lim}}^2$ is an important value: it is tied directly to the variance of our estimate of the mean. Thus, it allows us to construct confidence intervals for the posterior mean computed from MCMC samples.

The effective sample size (ESS) of a set of MCMC samples is the (hypothetical) number of independent samples which would have the same variance of the sample mean (Liu, 2008). Written as an equation, this yields ${\sigma }_{\pi }^2/\mathrm{E}\mathrm{S}\mathrm{S}={\sigma }_{\mathrm{l}\mathrm{i}\mathrm{m}}^2/n$, which we can rearrange as

$$\mathrm{E}\mathrm{S}\mathrm{S}=n\frac{{\sigma }_{\pi }^2}{{\sigma }_{\mathrm{l}\mathrm{i}\mathrm{m}}^2}.$$ (5)

While in practice we only know $n$, we can easily estimate ${\sigma }_{\pi }^2$ from the MCMC samples as $(1/n){\sum }_{j=1}^n {\left(X_i-\bar{X}\right)}^2$. The difficulty in estimating the ESS lies in estimating either ${\sigma }_{\text{lim}}^2$ or ${\sigma }_{\pi }^2/{\sigma }_{\mathrm{l}\mathrm{i}\mathrm{m}}^2$. In practice, there are a number of different approaches to estimating these quantities, which do not always yield the same answers (Fabreti and Höhna, 2021).

Assessing performance of candidate ESS measures

In this paper, we deal with situations where there is no clear theoretical basis for deriving an ESS measure. To determine whether a putative ESS measure works, we turn to the definition of the effective sample size as the number of independent samples with the same standard deviation of the empirical mean as the standard deviation of the empirical mean obtained using MCMC samples. Briefly, the idea of our testing setup is that we draw two sets of samples from a known target distribution. First this is done with MCMC, producing many sets of autocorrelated samples. Second, we estimate the ESS values from the MCMC chains using a given ESS measure, then draw that number of samples iid from the target to obtain a Monte Carlo error for that ESS measure. We then estimate the standard error of both sets of samples. (There will be Monte Carlo error in our estimated Monte Carlo error, but for a sufficiently large number of sets of samples it will be negligible.) If a putative ESS measure works, then, by the definition of the effective sample size, the standard errors computed based on both sets of samples should be nearly the same. A graphical depiction of this setup is shown in Figure 2. We now explain this idea in more detail, starting with the mean of a Euclidean random variable and then moving on to summaries of phylogenetic posterior distributions.

Figure 2:

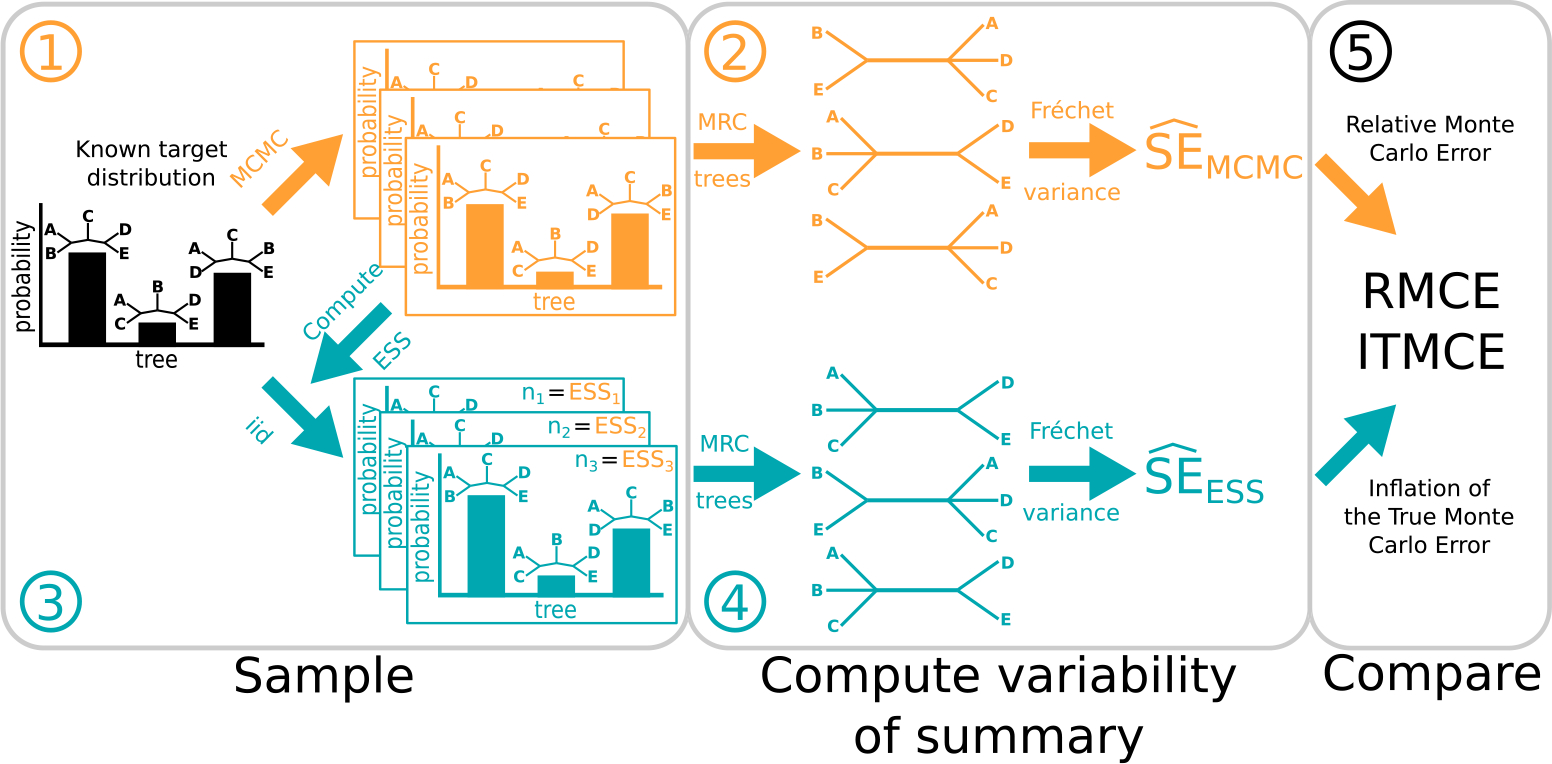
A graphical depiction of steps 1–5 of our approach to testing tree ESS measures, highlighting the case where we examine the Fréchet standard error of the MRC tree. The general workflow is the same for the other cases, which calculate the standard error of split and tree probabilities. Steps involving MCMC are shown on top in orange, while steps involving iid samples are shown on bottom in teal. We begin with a (known) target distribution. Before we can consider Monte Carlo errors, we must sample from this distribution. We do this first using an MCMC algorithm (Step 1), and then by simply drawing iid samples (Step 3). The key is that we draw iid samples according to the effective sample size of each of the MCMC chains from Step 1. Here we have $m=3$ MCMC chains, so we draw $m=3$ sets of ESS-equivalent samples. We must then summarize each of these sets of samples. In this paper, we consider three distinct summaries, as depicted in Figure 1. Here we show the MRC tree as the summary, yielding $m$ MRC trees from MCMC chains (Step 2, left) and $m$ MRC trees from the ESS-equivalent samples (Step 4, left). The variability of these summaries is a brute-force estimate of the Monte Carlo error. The Fréchet standard deviation of the $m$ MRC trees right). The Fréchet standard deviation of the $m$ MRC trees from the ESS-equivalent iid samples gives us the ${\widehat{\mathrm{S}\mathrm{E}}}_{\mathrm{M}\mathrm{C}\mathrm{E}\mathrm{S}\mathrm{S}}$ (Step 4, right). (For split and tree probabilities, the ${\widehat{\mathrm{S}\mathrm{E}}}_{\mathrm{M}\mathrm{C}\mathrm{M}\mathrm{C}}$ and ${\widehat{\mathrm{S}\mathrm{E}}}_{\mathrm{M}\mathrm{C}\mathrm{E}\mathrm{S}\mathrm{S}}$ are the usual standard error rather than a Fréchet standard error.) If an ESS measure works, then it is informative about the number of independent samples which would have the same Monte Carlo error as a given set of MCMC samples. Thus, we should expect the ${\widehat{\mathrm{S}\mathrm{E}}}_{\mathrm{M}\mathrm{C}\mathrm{M}\mathrm{C}}$ and ${\widehat{\mathrm{S}\mathrm{E}}}_{\mathrm{M}\mathrm{C}\mathrm{E}\mathrm{S}\mathrm{S}}$ to be similar, and the last step is to compare them. We use the RMCE and ITMCE, which are measures of relative difference.

Assessing the ESS for continuous parameters

Classical ESS measures “work” in the sense that they allow us to correctly compute the standard error of our estimate of the posterior mean $\hat{\theta }$. Let us review the Monte Carlo standard error of a Euclidean variable in the context of Bayesian inference via MCMC. We want to estimate the true posterior mean with the mean of our $n$ MCMC samples, $\hat{\theta }$. The standard deviation of our estimator $\hat{\theta }$ is $\mathrm{S}\mathrm{D}(\hat{\theta })=\sqrt{\mathbb{E}[(\hat{\theta }-\mathbb{E}[\hat{\theta }]{)}^2]}$. This is the standard deviation of the sampling distribution, also called the standard error (SE). In general, there is not a known closed form solution for the actual sampling distribution of $\hat{\theta }$, and thus for $\mathrm{S}\mathrm{E}(\hat{\theta })$. But if we were to run $m$ independent replicate analyses, we could use a brute-force approach to estimate the true Markov chain Monte Carlo SE (MCMCSE) as,

$${\widehat{\mathrm{S}\mathrm{E}}}_{\mathrm{M}\mathrm{C}\mathrm{M}\mathrm{C}}(\hat{\theta })=\sqrt{\frac{1}{m}\sum _{i=1}^m {({\hat{\theta }}_i-\widehat{\mathrm{E}}[\hat{\theta }])}^2},$$

where ${\hat{\theta }}_i$ is the estimate of $\theta$ using the ith set of MCMC samples and $\widehat{\mathrm{E}}[\hat{\theta }]$ is estimated using all $m\times n$ MCMC samples drawn. This is an estimate of the true standard error of the mean given $n$ MCMC samples. Imagine that we had the ability to draw samples in an identically and independently distributed (iid) manner from the true posterior. Then, as a comparison, for each run $i=1,\dots ,m$, we could compute the effective sample size, ${\mathrm{E}\mathrm{S}\mathrm{S}}_i$, and draw ${\mathrm{E}\mathrm{S}\mathrm{S}}_i$ samples iid according to the posterior distribution $\mathrm{P}\mathrm{r}(\theta \mid y)$. This gives us a second set of samples, for which we can repeat our above brute-force calculation of the Monte Carlo error. These $m$ sets of “ESS-equivalent” iid samples allow us to estimate ${\widehat{\mathrm{S}\mathrm{E}}}_{\mathrm{M}\mathrm{C}\mathrm{E}\mathrm{S}\mathrm{S}}(\hat{\theta })$, the Monte Carlo estimate of the standard error when drawing samples iid from the true posterior distribution according to the computed ESS. We should expect to find that ${\widehat{\mathrm{S}\mathrm{E}}}_{\mathrm{M}\mathrm{C}\mathrm{E}\mathrm{S}\mathrm{S}}(\hat{\theta })\approx {\widehat{\mathrm{S}\mathrm{E}}}_{\mathrm{M}\mathrm{C}\mathrm{M}\mathrm{C}}(\hat{\theta })$, because the classical ESS is derived to give us the hypothetical number of independent samples such that we will use the discrepancy between ${\widehat{\mathrm{S}\mathrm{E}}}_{\mathrm{M}\mathrm{C}\mathrm{E}\mathrm{S}\mathrm{S}}(\hat{\theta })$ and ${\widehat{\mathrm{S}\mathrm{E}}}_{\mathrm{M}\mathrm{C}\mathrm{M}\mathrm{C}}(\hat{\theta })$ to judge the quality of various ESS measures.

Assessing the ESS for trees

When running MCMC targeting multivariate distributions, the usual approach in high dimensions is to compute the ESS separately for each univariate variable. However, posterior distributions on phylogenetic trees are more complex than typical high-dimensional vector-valued distributions, which precludes this approach. Instead, we will consider several different summaries of posterior distributions of trees, and the Monte Carlo SE in the estimates of those summaries. We now write out more concretely our testing approach, which is a generalization of the above idea of how ESS measures should work.

We will assume that we have $m$ phylogenetic MCMC runs, and that each has $n$ samples. We will assume for the moment that we have both a topological ESS measure and a way to draw tree topologies iid from the posterior distribution, $\mathrm{P}\mathrm{r}(\tau \mid y)$. Let ${\widehat{𝒮}}_n$ be a summary of $n$ tree samples (possibly obtained via MCMC) from posterior distribution $\mathrm{P}\mathrm{r}(\tau \mid y)$. For example, ${\widehat{𝒮}}_n$ could be the probability of a particular split or tree topology, or a summary tree such as the MRC tree. Our approach to testing topological effective sample sizes can then be written out as follows (Figure 2):

1. Run $m$ independent MCMC chains.

2. Using the chains from step 1, compute the brute-force estimate of the true Markov chain Monte Carlo SE, ${\widehat{\mathrm{S}\mathrm{E}}}_{\mathrm{M}\mathrm{C}\mathrm{M}\mathrm{C}}({\widehat{𝒮}}_n)$.

3. For each chain $i=1,\dots ,m$, compute that chain’s ESS, ${\mathrm{E}\mathrm{S}\mathrm{S}}_i$, and draw ESS trees independently from the true posterior distribution $\mathrm{P}\mathrm{r}(\tau \mid y)$. Round ${\mathrm{E}\mathrm{S}\mathrm{S}}_i$ to the nearest integer such that we draw an integer number of trees.

4. Using the set of ESS-equivalent trees drawn in step 3, compute the ESS-equivalent estimate of the MCMCSE, ${\widehat{\mathrm{S}\mathrm{E}}}_{\mathrm{M}\mathrm{C}\mathrm{E}\mathrm{S}\mathrm{S}}({\widehat{𝒮}}_n)$.

5. Compare ${\widehat{\mathrm{S}\mathrm{E}}}_{\mathrm{M}\mathrm{C}\mathrm{E}\mathrm{S}\mathrm{S}}\left({𝒮}_n\right)$ and ${\widehat{\mathrm{S}\mathrm{E}}}_{\mathrm{M}\mathrm{C}\mathrm{M}\mathrm{C}}\left({𝒮}_n\right)$.

Generally speaking, if a putative measure of the topological ESS works with respect to an MCMCSE measure, then ${\widehat{\mathrm{S}\mathrm{E}}}_{\mathrm{M}\mathrm{C}\mathrm{E}\mathrm{S}\mathrm{S}}({\widehat{𝒮}}_n)\approx {\widehat{\mathrm{S}\mathrm{E}}}_{\mathrm{M}\mathrm{C}\mathrm{M}\mathrm{C}}({\widehat{𝒮}}_n)$, and the closer the ESS-based estimate of the SE is, the better that ESS estimator works. If we have overestimated the ESS, we will find ${\widehat{\mathrm{S}\mathrm{E}}}_{\mathrm{M}\mathrm{C}\mathrm{E}\mathrm{S}\mathrm{S}}<{\widehat{\mathrm{S}\mathrm{E}}}_{\mathrm{M}\mathrm{C}\mathrm{M}\mathrm{C}}$ (as we have drawn too many independent samples and thus the SE of the estimate from them will be too small). On the other hand, if we have underestimated the ESS, we will find ${\widehat{\mathrm{S}\mathrm{E}}}_{\mathrm{M}\mathrm{C}\mathrm{E}\mathrm{S}\mathrm{S}}>{\widehat{\mathrm{S}\mathrm{E}}}_{\mathrm{M}\mathrm{C}\mathrm{M}\mathrm{C}}$ (as we have drawn too few independent samples and thus the SE of the estimate from them will be too large). As the scales of the Monte Carlo SEs are not inherently meaningful, we instead measure the relative error in the estimated Monte Carlo error (the relative Monte Carlo error, RMCE),

$$\mathrm{R}\mathrm{M}\mathrm{C}\mathrm{E}=\frac{{\widehat{\mathrm{S}\mathrm{E}}}_{\mathrm{M}\mathrm{C}\mathrm{M}\mathrm{C}}-{\widehat{\mathrm{S}\mathrm{E}}}_{\mathrm{M}\mathrm{C}\mathrm{E}\mathrm{S}\mathrm{S}}}{{\widehat{\mathrm{S}\mathrm{E}}}_{\mathrm{M}\mathrm{C}\mathrm{M}\mathrm{C}}}.$$ (6)

This quantity is negative when we have underestimated the ESS, positive when we have overestimated the ESS, and tells us the relative proportion by which we have misestimated the MCMCSE using our ESS measure. In some cases, however, a more useful measure is given by the inflation (or deflation) of the true Monte Carlo error (ITMCE), which is defined by the relation,

$$\mathrm{I}\mathrm{T}\mathrm{M}\mathrm{C}\mathrm{E}=\frac{{\widehat{\mathrm{S}\mathrm{E}}}_{\mathrm{M}\mathrm{C}\mathrm{M}\mathrm{C}}}{{\widehat{\mathrm{S}\mathrm{E}}}_{\text{MCESS}}}.$$ (7)

This value measures how inflated the true Monte Carlo error is relative to the estimated Monte Carlo error, which can be seen by rewriting the above as ${\widehat{\mathrm{S}\mathrm{E}}}_{\mathrm{M}\mathrm{C}\mathrm{M}\mathrm{C}}={\widehat{\mathrm{S}\mathrm{E}}}_{\mathrm{M}\mathrm{C}\mathrm{E}\mathrm{S}\mathrm{S}}\times \mathrm{I}\mathrm{T}\mathrm{M}\mathrm{C}\mathrm{E}$. In essence, the ITMCE measures how much wider the true confidence intervals should be relative to our estimated intervals. The ITMCE is greater than one when we have overestimated the ESS, and less than one when we have underestimated it.

The RMCE and ITMCE are complementary; the RMCE is useful to quantify when ESS is underestimated, while the ITMCE clearly shows when ESS is overestimated. To see this, start by noting that by definition ${\widehat{SE}}_{\text{MCMC}}$ and ${\widehat{\mathrm{S}\mathrm{E}}}_{\mathrm{M}\mathrm{C}\mathrm{E}\mathrm{S}\mathrm{S}}$ are non-negative. Thus, $-\mathrm{\infty }<\mathrm{R}\mathrm{M}\mathrm{C}\mathrm{E}\le 1$ and $0\le \mathrm{I}\mathrm{T}\mathrm{M}\mathrm{C}\mathrm{E}<\mathrm{\infty }$ Underestimation of the ESS is represented by $\mathrm{R}\mathrm{M}\mathrm{C}\mathrm{E}<0$ and $\mathrm{I}\mathrm{T}\mathrm{M}\mathrm{C}\mathrm{E}<1$. In this underestimation case the RMCE may take any value in $(-\mathrm{\infty },0]$, while the ITMCE compresses this regime into the range [0, 1]. Overestimation of the ESS is represented by $\mathrm{R}\mathrm{M}\mathrm{C}\mathrm{E}>0$ and $\mathrm{I}\mathrm{T}\mathrm{M}\mathrm{C}\mathrm{E}>1$. In the overestimation case the RMCE is compressed, stuck in [0, 1], while the ITMCE may take any value in $[0,\mathrm{\infty })$. Thus, the RMCE has more effective resolution when the ESS is underestimated, while the ITMCE has more resolution when the ESS is overestimated.

In the introduction, we outlined three quantities a tree ESS might reflect; now we will more rigorously define three MCMCSE measures based on these, noting that they are all measures of the Monte Carlo standard error (MCMCSE). Broadly, we contemplate whether a tree ESS measure might reflect the standard deviations of our estimates of split probabilities, tree probabilities, or a summary tree.

ESS and split probabilities

We may wish for ESS of trees to reflect the quality of our estimates of the split probabilities. Let us denote the probability of this a particular split $p$, the estimate of the split probability from the ith MCMC run as ${\hat{p}}_{\mathrm{M}\mathrm{C}\mathrm{M}\mathrm{C}}^i$ (Step 1). Then, we can estimate the true MCMCSE of the split probability as (Step 2),

$${\widehat{\mathrm{S}\mathrm{E}}}_{\mathrm{M}\mathrm{C}\mathrm{M}\mathrm{C}}\left({\hat{p}}^i\right)=\sqrt{\frac{1}{m}\sum _{i=1}^m {({\hat{p}}_{\mathrm{M}\mathrm{C}\mathrm{M}\mathrm{C}}^i-\widehat{\mathbb{E}}\left[{\hat{p}}_{\mathrm{M}\mathrm{C}\mathrm{M}\mathrm{C}}\right])}^2},$$

where $\widehat{\mathbb{E}}\left[{\hat{p}}_{\mathrm{M}\mathrm{C}\mathrm{M}\mathrm{C}}\right]$ is the average probability of the split across all $m$ chains. Let us denote the estimate of the split probability computed from ESSi tree topologies drawn iid from the posterior distribution as ${\hat{p}}_{\mathrm{M}\mathrm{C}\mathrm{E}\mathrm{S}\mathrm{S}}^i$ (Step 3, we discuss how to do this in the section “Faking phylogenetic MCMC”). Then, using the ESS-equivalent tree samples, we can compute ${\widehat{\mathrm{SE}}}_{\text{MCESS}}$ (Step 4),

$${\widehat{\mathrm{S}\mathrm{E}}}_{\mathrm{M}\mathrm{C}\mathrm{E}\mathrm{S}\mathrm{S}}\left({\hat{p}}^i\right)=\sqrt{\frac{1}{m}\sum _{i=1}^m {({\hat{p}}_{\mathrm{M}\mathrm{C}\mathrm{E}\mathrm{S}\mathrm{S}}^i-\widehat{\mathbb{E}}\left[{\hat{p}}_{\mathrm{M}\mathrm{C}\mathrm{E}\mathrm{S}\mathrm{S}}\right])}^2},$$

and then we can compare ${\widehat{\mathrm{S}\mathrm{E}}}_{\mathrm{M}\mathrm{C}\mathrm{M}\mathrm{C}}\left({\hat{p}}^i\right)$ and ${\widehat{\mathrm{S}\mathrm{E}}}_{\mathrm{M}\mathrm{C}\mathrm{E}\mathrm{S}\mathrm{S}}\left({\hat{p}}^i\right)$ (Step 5).

We note two places that ${\widehat{\mathrm{S}\mathrm{E}}}_{\mathrm{M}\mathrm{C}\mathrm{M}\mathrm{C}}\left({\hat{p}}^i\right)$ appears in existing phylogenetic practice. The standard error of the probability of a split is better known as the standard deviation of the split probability (SDSF). The average across all splits is called the ASDSF and is commonly used to diagnose the convergence of multiple MCMC chains. MrBayes also uses the ${\widehat{\mathrm{S}\mathrm{E}}}_{\mathrm{M}\mathrm{C}\mathrm{M}\mathrm{C}}\left({\hat{p}}^i\right)$ from the (usually 2–4) independent chains run to quantify the Monte Carlo error in the consensus trees.

ESS and tree probabilities

We may wish for ESS of trees to reflect the quality of our estimates of the tree topology probabilities. As these are probabilities, we can compute ${\widehat{\mathrm{S}\mathrm{E}}}_{\mathrm{M}\mathrm{C}\mathrm{M}\mathrm{C}}\left({\hat{p}}^i\right)$ and ${\widehat{\mathrm{S}\mathrm{E}}}_{\mathrm{M}\mathrm{C}\mathrm{E}\mathrm{S}\mathrm{S}}\left({\hat{p}}^i\right)$ exactly as for split probabilities.

ESS and the summary tree

We may wish for the ESS of trees to reflect the quality of our estimates of the summary tree. This is less straightforward than with the probabilities of splits or tree probabilities, as trees are non-Euclidean objects. Hence, we turn to a Fréchet generalization of MCMCSE (we discuss Fréchet generalizations more thoroughly in the section Calculating the ESS by generalizing previous definitions). In this paper, we focus on the majority rule consensus (MRC) tree as the summary tree. As our measure of variability between topologies, we consider the squared Robinson-Foulds (RF) distance (Robinson and Foulds, 1981) (which we describe in more detail below). Thus, our MCMCSE measure here is a given by,

$${\widehat{\mathrm{S}\mathrm{E}}}_{\mathrm{M}\mathrm{C}\mathrm{M}\mathrm{C}}\left(\widehat{\tau }\right)=\sqrt{\frac{1}{m}\sum _{i=1}^m d{({\widehat{\tau }}_{\mathrm{M}\mathrm{C}\mathrm{M}\mathrm{C}}^i,\widehat{\mathbb{E}}\left[{\widehat{\tau }}_{\mathrm{M}\mathrm{C}\mathrm{M}\mathrm{C}}\right])}^2},$$

where $d(\cdot ,\cdot )$ is the RF distance. Here, we define ${\widehat{\tau }}_{\mathrm{M}\mathrm{C}\mathrm{M}\mathrm{C}}^i$ to be the MRC tree for the ith MCMC run, and $\widehat{\mathbb{E}}\left[{\widehat{\tau }}_{\mathrm{M}\mathrm{C}\mathrm{M}\mathrm{C}}\right]$ to be the MRC tree obtained by pooling all $m$ runs to estimate split frequencies. Then, using the ESS-equivalent tree samples (Step 3), we can compute ${\widehat{\mathrm{S}\mathrm{E}}}_{\mathrm{M}\mathrm{C}\mathrm{E}\mathrm{S}\mathrm{S}}$ (Step 4) analogously,

$${\widehat{\mathrm{S}\mathrm{E}}}_{\mathrm{M}\mathrm{C}\mathrm{E}\mathrm{S}\mathrm{S}}\left(\widehat{\tau }\right)=\sqrt{\frac{1}{m}\sum _{i=1}^m d{({\widehat{\tau }}_{\mathrm{E}\mathrm{S}\mathrm{S}}^i,\widehat{\mathbb{E}}\left[{\widehat{\tau }}_{\mathrm{E}\mathrm{S}\mathrm{S}}\right])}^2}.$$

Faking phylogenetic MCMC

Our goal is to use the testing procedure outlined in the section “Assessing performance of candidate ESS measures” to test whether tree ESS measures work appropriately. This requires that we have a distribution from which we can both draw MCMC samples (Step 1), to compute ${\widehat{\mathrm{S}\mathrm{E}}}_{\mathrm{M}\mathrm{C}\mathrm{M}\mathrm{C}}$ (Step 2), and draw iid samples (Step 3), to compute ${\widehat{\mathrm{S}\mathrm{E}}}_{\mathrm{M}\mathrm{C}\mathrm{E}\mathrm{S}\mathrm{S}}$ (Step 4). Because it is impossible to draw iid samples from a Bayesian phylogenetic posterior distribution—else we would not need MCMC in the first place—we set up a simulated (or “fake”) phylogenetic MCMC. In brief, our setup first uses MCMC samples from real-data phylogenetic analyses to define a categorical distribution on phylogenetic tree topologies. We can then use phylogenetic MCMC moves to draw MCMC samples from this distribution (Step 1), and using those we can estimate ${\widehat{\mathrm{S}\mathrm{E}}}_{\mathrm{M}\mathrm{C}\mathrm{M}\mathrm{C}}$ (Step 2). Because our target distribution is based on real-data phylogenetic posterior distributions, the resulting Monte Carlo error should be representative of the Monte Carlo error of real-data phylogenetic posterior distributions. Importantly, because we have a known, categorical, target distribution, we can draw iid samples from the categorical distribution (Step 3), and using those can estimate ${\widehat{\mathrm{S}\mathrm{E}}}_{\mathrm{M}\mathrm{C}\mathrm{E}\mathrm{S}\mathrm{S}}$ (Step 4). By comparing ${\widehat{\mathrm{S}\mathrm{E}}}_{\mathrm{M}\mathrm{C}\mathrm{M}\mathrm{C}}$ and ${\widehat{\mathrm{S}\mathrm{E}}}_{\mathrm{M}\mathrm{C}\mathrm{E}\mathrm{S}\mathrm{S}}$ (Step 5), we can assess whether the tree ESS measures work on target distributions that are known exactly yet which share key features of real phylogenetic posterior distributions. We now outline in more detail how we obtain this categorical distribution and run phylogenetic MCMC to approximate it.

We start with an estimate of tree probabilities based on MCMC samples from a real phylogenetic posterior distribution. In this paper we re-use posterior distributions inferred by Whidden et al. (2020) on a set of standard benchmark datasets, though any phylogenetic MCMC run could be used. This gives us a vector of trees $\tau$ and an associated estimate of the probability mass function $\widehat{\mathrm{P}\mathrm{r}}(\tau )$. As the number of trees in $\tau$ may be prohibitively large, one may wish to take only the top 95% highest posterior density (HPD) set of trees, or other such subset. Depending on the real-data MCMC algorithm which produced $\tau$, and depending on the truncation, these trees may not be connected with respect to the MCMC proposal used for the fake phylogenetic MCMC. Thus, we keep only the largest connected subset of $\tau$. We then take this set of trees and their estimated probabilities to be the true probabilities for our fake MCMC (we re-normalize the probabilities if trees are removed, though this is not strictly necessary). We define any tree $\mathrm{\Psi }\notin \tau$ to have zero probability.

To run a fake phylogenetic MCMC sampler on this known target distribution, we use nearest neighbor interchange (NNI, the interchanging of two subtrees across an edge in the tree) proposals. We first construct a list of all NNI neighbors for each tree, such that $N\left(\mathrm{\Psi }\right)$ is the set of all neighbors of $\mathrm{\Psi }$. Then, to initialize the MCMC run, we randomly draw a starting state according to $\widehat{\mathrm{P}\mathrm{r}}(\mathit{\tau })$. At each step thereafter, if the current state for the MCMC is $\mathrm{\Psi }$, we propose a tree ${\psi }^{\mathrm{*}}$ uniformly at random from $N\left(\mathrm{\Psi }\right)$ (excluding $\mathrm{\Psi }$), and the acceptance probability for the move is $\mathrm{m}\mathrm{i}\mathrm{n}(1,\widehat{\mathrm{P}\mathrm{r}}({\mathrm{\Psi }}^{\mathrm{*}})/\widehat{\mathrm{P}\mathrm{r}}(\mathrm{\Psi }))$. This move is symmetric and has a Hastings ratio of 1 (Lakner et al., 2008).

Although this is by necessity an artificial setup, we believe that it is an improvement over previous benchmarking exercises. The simulation approach of Lanfear et al. (2016) is based on accepting all proposed MCMC moves and assuming all trees were uniformly probable. They consider bimodal distributions by mixing sets of trees based on a small number of MCMC moves from distant starting points. In contrast, our approach is based on real-data posterior distributions of trees. This allows for multimodality, as well as uneven connectivity of trees, such that some trees have many neighbors (with notable posterior probability) and others have few, which can make exploration difficult as some trees may be hard to reach. Additionally, using real posterior probabilities replicates unevenness, such that some datasets may be particularly rugged and others relatively flat (Höhna and Drummond, 2012). Importantly, our approach includes rejected proposals, an important feature given that acceptance rates for phylogenetic MCMC proposals are notoriously low. Our setup allows for complete exploration of the target distribution with chains of sufficient length, whereas with a uniform distribution on all trees this is a practical impossibility. As we can initialize the chain from the target distribution, we can ignore burn-in and focus on mixing while accommodating these realistic features. We can improve the speed and memory requirements by tweaking the proposal step and neighbor tracking, which we discuss in the Supplemental Materials (Magee et al., 2022). We implement the functions needed to run fake phylogenetic MCMC on arbitrary phylogenetic posterior distributions in the R package treess.

Computing a tree ESS

In this paper, we consider four different tree ESS measures, which fall into the following three categories:

• ESS measures based on Fréchet generalizations of (5) to trees (we discuss Fréchet generalizations in the next section)

  • 1
    The Fréchet Correlation ESS (frechetCorrelationESS)
• ESS measures based on projecting the tree to a single dimension and computing the ESS of that using standard univariate approaches

  • 2
    The median pseudo-ESS (medianPseudoESS)
  • 3
    The minimum pseudo-ESS (minPseudoESS)
• Ad-hoc ESS measures

  • 4
    The approximate ESS (approximateESS)

In the next sections, we present short sketches of our new approaches and the medianPseudoESS of Lanfear et al. (2016). We refer readers to Lanfear et al. (2016) for explanation of the approximateESS. In the supplement, we describe six additional measures, as well as a more detailed derivation of the frechetCorrelationESS. We will use the notation $\mathit{\tau }$ for a vector of phylogenies, $d\left({\tau }_i,{\tau }_j\right)$ to denote the distance between trees $i$ and $j$, and $\mathit{D}=\left\{D_{ij}\right\}=\left\{d\left({\tau }_i,{\tau }_j\right)\right\}$ for the distance matrix of all trees in $\mathit{\tau }$.

All tree ESS measures presented depend on the distance matrix between all samples in the posterior. While in general any tree distance can be used, in this paper we focus on the Robinson-Foulds (RF) distance (Robinson and Foulds, 1981). The RF distance considers an unrooted tree as a collection of splits, and measures the number of splits by which two trees differ. For trees ${\tau }_A$ and ${\tau }_B$, let $𝒜$ be the set of splits in ${\tau }_A$ and $ℬ$ the set of splits in ${\tau }_B$, and further denote by ${𝒜}^c$ the set of splits not in ${\tau }_A$ and by ${ℬ}^c$ the set of splits not in ${\tau }_B$. The RF distance is $d_{\mathrm{R}\mathrm{F}}=\left|𝒜\cap {ℬ}^c\right|+\left|ℬ\cap {𝒜}^c\right|$. That is, the RF distance is the number of splits in ${\tau }_A$ but not ${\tau }_B$ plus the number of splits in ${\tau }_B$ but not ${\tau }_A$. If both trees are fully resolved, then any split which is in ${\tau }_A$ but not in ${\tau }_B$ must correspond to a split which is in ${\tau }_B$ but not in ${\tau }_A$, so $\left|𝒜\cap {ℬ}^c\right|=\left|ℬ\cap {𝒜}^c\right|$, and $d_{\mathrm{R}\mathrm{F}}=2\times \left|𝒜\cap {ℬ}^c\right|$. If one or both trees are unresolved, which may be the case with consensus trees, a split present in ${\tau }_A$ may simply be absent in ${\tau }_B$ without implying the presence of a split which is in ${\tau }_B$ but not in ${\tau }_A$. For two resolved trees on $n_{\text{taxa}}$ taxa, the maximum RF distance is twice the number of internal edges, or $2n_{\text{taxa}}-6$. When one or both trees are unresolved, the maximum distance is lowered. While there are some limitations of RF distance, it has many benefits, primarily that it is interpretable and easily computable in a wide variety of software. Additionally, RF distance is related to tree space exploration via NNI moves, as two (fully resolved) trees separated by one NNI are separated by an RF distance of 2.

Calculating the ESS by generalizing previous definitions

In this section, we will attempt to generalize the definition of ESS in (5) using concepts borrowed from the notions of Fréchet mean and Fréchet variance (see for example Dubey and Müller, 2019, and references therein). For this and all other measures presented in this paper, we provide detailed derivations in the supplement.

The Fréchet mean and variance generalize the concepts of means and variances to other complete metric spaces. Where the variance is the average squared deviation from the mean, the Fréchet variance is the average squared distance from the Fréchet mean. In the case where $X$ is continuous and one-dimensional and the Euclidean distance is chosen, the Fréchet mean is the classical mean and the Fréchet variance is the classical variance. We note that the Fréchet mean and variance of unrooted phylogenies with branch lengths have been studied previously (see Brown and Owen, 2020, and references therein) using Billera-Holmes-Vogtmann (BHV) space (Billera et al., 2001). However, in this paper we are purely interested in topological features and so use the purely topological RF distance metric. RF distances reflect the most challenging part of phylogenetic MCMC, the tree topology itself, and are thus linked directly to topological quantities of interest, like summary trees and split probabilities. BHV distances are somewhat less interpretable (they summarize both branch length and topological differences, thus small distances can reflect large topological changes) and are computationally burdensome.

The Fréchet correlation ESS, or frechetCorrelationESS, is a generalization of what we will call the sum-of-correlations ESS, which we will now review in the case of a single continuous random variable $X$. The autocorrelation function defines the correlation between samples at times separated by lag $s$, and can be related to the autocovariance (Von Storch and Zwiers, 2001),

$${\rho }_s=\mathrm{C}\mathrm{o}\mathrm{r}\left(X_t,X_{t+s}\right)=\frac{\mathrm{C}\mathrm{o}\mathrm{v}\left(X_t,X_{t+s}\right)}{{\sigma }_{\pi }^2}.$$

This means we can re-write (3) as,

$${\sigma }_{\mathrm{l}\mathrm{i}\mathrm{m}}^2={\sigma }_{\pi }^2\times \left(1+2\sum _{s=1}^{\mathrm{\infty }} \mathrm{C}\mathrm{o}\mathrm{r}(X_0,X_s)\right)={\sigma }_{\pi }^2\times \left(1+2\sum _{s=1}^{\mathrm{\infty }} {\rho }_s\right).$$

Re-arranged, this can be combined with (5) to get,

$$\mathrm{E}\mathrm{S}\mathrm{S}=\frac{n}{1+2\sum _{s=1}^{\mathrm{\infty }} {\rho }_s}.$$

In practice, we run into difficulties if we apply this definition naively. As there are fewer MCMC samples separated by large time lags, as $s$ gets larger our estimates ${\hat{\rho }}_s$ get noisier, and for odd time lags it is possible to have ${\rho }_s<0$, meaning we cannot smooth the estimates without care. Following Vehtari et al. (2021), we can overcome these limitations in several steps. First, they suggest summing adjacent correlations, defining ${\hat{P}}_{s^{\prime }}={\hat{\rho }}_{2s^{\prime }}+{\hat{\rho }}_{2s^{\prime }+1}$, which guarantees that ${\hat{P}}_{s^{\prime }}>0$. The estimated ${\hat{P}}_{s^{\prime }}$ may not be monotonically decreasing, but the actual curve $P_{s^{\prime }}$ should be, so Vehtari et al. (2021) smooth the curve by setting ${\hat{P}}_{s^{\prime }}$ to the minimum of all preceding values. We then find the largest time lag $k$ such that ${\hat{P}}_{s^{\prime }}>0$ for all $s^{\prime }=1,\dots ,k$, and sum the series only up to this time, yielding the final estimator (note the −1 appears because we start indexing at 0 and ${\hat{\rho }}_0=1$),

$$\widehat{\mathrm{E}\mathrm{S}\mathrm{S}}=\frac{n}{-1+2\sum _{s^{\prime }=0}^k {\hat{P}}_{s^{\prime }}}.$$ (8)

We will refer to this as the sum-of-correlations ESS.

Employing (8) to estimate an effective sample size for trees requires us to define a correlation between vectors of trees. It can be shown that, for Euclidean variables $X$ and $Y$, the covariance is related to Euclidean distances. If we denote the Euclidean distance between $X$ and $Y$ with $\mathrm{\Delta }=d(X,Y)$, one can derive $\mathrm{C}\mathrm{o}\mathrm{v}(X,Y)=1/2\times (\mathrm{V}\mathrm{a}\mathrm{r}(X)+\mathrm{V}\mathrm{a}\mathrm{r}(Y)-\mathbb{E}[{\mathrm{\Delta }}^2]+(\mathbb{E}[X]-\mathbb{E}[Y]{)}^2)$ (see supplement). In a setting where $X$ and $Y$ represent samples from the same MCMC run at some time lag $t$, we might expect $(\mathbb{E}[X]-\mathbb{E}[Y]{)}^2$ to be negligible so long as sufficient burn-in has been discarded. In this case, we can instead approximate the covariance as $\mathrm{C}\mathrm{o}\mathrm{v}(X,Y)\approx \frac{1}{2}\left(\mathrm{V}\mathrm{a}\mathrm{r}(X)+\mathrm{V}\mathrm{a}\mathrm{r}(Y)-\mathbb{E}\left[{\mathrm{\Delta }}^2\right]\right)$. By replacing Euclidean distances with arbitrary distance metrics and means/variances with Fréchet means/variances, we can use these relationships to define a generalization of the covariance and thus of the (auto)correlation. We propose to estimate the autocorrelation between MCMC samples of trees at time lag s as:

$${\hat{\rho }}_s=\frac{\frac{1}{2}(\widehat{\mathrm{V}\mathrm{a}\mathrm{r}}\left({\mathit{\tau }}_t\right)+\widehat{\mathrm{V}\mathrm{a}\mathrm{r}}\left({\mathit{\tau }}_{t+s}\right)-\widehat{\mathbb{E}}[{\mathrm{\Delta }}^2])}{\sqrt{\widehat{\mathrm{V}\mathrm{a}\mathrm{r}}\left({\mathit{\tau }}_t\right)\widehat{\mathrm{V}\mathrm{a}\mathrm{r}}\left({\mathit{\tau }}_{t+s}\right)}}.$$ (9)

Here, ${\mathit{\tau }}_t$ and ${\mathit{\tau }}_{t+s}$ represent vectors of MCMC samples of trees separated by a time lag of $s,$ $\widehat{\mathrm{V}\mathrm{a}\mathrm{r}}$ is the estimated Fréchet variance based on RF distance, and $\widehat{\mathbb{E}}\left[{\mathrm{\Delta }}^2\right]$ is the average squared RF distance between tree vectors ${\mathit{\tau }}_t$ and ${\mathit{\tau }}_{t+s}$. Once we obtain our estimates ${\hat{\rho }}_s$, we use the sum-of-correlations approach to estimate the ESS (8). A more thorough derivation of (9), including how to compute $\widehat{\mathrm{V}\mathrm{a}\mathrm{r}}(\mathit{\tau })$, is available in the Supplementary Materials.

Approaches to calculating the ESS by projecting the tree to a single dimension

The pseudo-ESS of Lanfear et al. (2016) projects trees to a single dimension and computes the ESS of this transformed variable. It is computed in several steps. First, $r$ “reference” trees are selected uniformly from among all $n$ posterior trees. For the ith reference tree, we turn the sequence of trees sampled by the MCMC into a real-valued sequence by computing the distance between each such tree and the reference. We can then compute the ESS of this real-valued sequence to obtain an ${\mathrm{E}\mathrm{S}\mathrm{S}}_i$. Lastly, we must summarize the vector of estimates, ESS₁,...,ESS_r. Lanfear et al. (2016) use the median as a point estimate and suggest reporting the 95 percentile range as well. We depart slightly from the original approach by using all $n$ samples in the posterior as reference trees rather than choosing a subset. As the ESS is a single number (the hypothetical size of an equivalent set of iid samples), we do not examine ranges but rather focus on point estimates. What Lanfear et al. (2016) refer to as the pseudo-ESS (the median of the $n$ distinct ESS values), we will refer as the medianPseudoESS. In addition to the median, as a potentially conservative estimator we also investigate the performance of the minimum of the ESS over reference trees, which we call the minPseudoESS. For both of these approaches, we first compute the dimension-reduced representation and then use the R package coda to compute the ESS. In the Supplemental Materials, we present three additional approaches to computing the tree ESS using projection, and a discussion of the coda approch to computing the ESS.

Results

Tree ESS measures reflect Monte Carlo variability in split probabilities, tree probabilities, and the summary tree

Now that we have several possible summaries of how an ESS measure could work and a number of potential ESS measures, we can determine whether any of the potential tree ESS measures perform well with respect to any of the summaries. We use a suite of common test datasets in phylogenetics (e.g. Lakner et al., 2008; Höhna and Drummond, 2012; Larget, 2013; Whidden and Matsen IV, 2015), commonly referred to as DS1-DS8 and DS10. We re-use previous MCMC analyses of these datasets consisting of 10 independent MCMC chains of 1 billion iterations, sampled every 100 iterations and pooled into a set of 100 million tree samples (Whidden et al., 2020). As the full set of trees is too large to work with efficiently, we consider a subset of these trees which we term the “best connected trees.” To obtain this subset, we start with either the 95% HPD set or the first 4096 trees in the 95% HPD set, whichever is smaller. Then, we ensure that every tree can be reached from every other tree using only NNI moves, and keep the largest connected subset. In our setting this required us to drop at most 20% of the trees and lose a maximum posterior probability mass of 0.065. For each of these 9 real-data posterior distributions, we run simulated MCMC analyses (as described in the section “Faking phylogenetic MCMC”) for run lengths of {10³, 10⁴, 10⁵, 10⁶, 10⁷}, in each case thinning in order to retain 1000 tree samples. Acceptance rates for the NNI moves are typical of those observed in real-data MCMC analyses, ranging from ≈ 3% (DS3) to ≈ 11% (DS6). Since we do not need to integrate out any of the continuous parameters such as branch lengths, and since we start each chain in the stationary distribution (avoiding burn-in), these shorter run lengths should be equivalent to longer runs on real datasets. For each dataset and run-length combination (of which there are 45), we run 100 replicate MCMC chains and use steps (1)–(5) to assess performance of the ESS measures for all summaries.

In the introduction, we mentioned that standard practice for phylogenetics often either ignores the mixing of the tree itself or uses the ESS of the log-posterior density as a proxy. Based on these approaches, we define two baseline ESS measures as points of comparison to more sophisticated approaches. One of these baselines, which we call fixedN, is to simply declare that the effective sample size is the sample size. This is akin to ignoring the mixing of the tree, in which case one essentially assumes that the n tree samples are worth n independent samples. Secondly, we consider using the univariate ESS (as implemented in coda) of the trace of the log-posterior-density, which we call the logPosteriorESS.

As an additional reference for our simulation results, we also run our testing setup in a non-phylogenetic context: estimating the mean of a Normal(0, 1) variable. We use 200 chain lengths between 1,000 and 100,000 and keep 1000 samples each time and use the coda univariate ESS. The proposal is a Normal distribution, centered on the current value, with a standard deviation of 0.3. This procedure produces ESS values from nearly 0 to nearly 1000, a range comparable to the observed tree ESS values computed. The median RMCE is 0.01, with 50% quantiles spanning [−0.073,0.057], and 80% quantiles spanning [−0.13,0.12]. The median ITMCE is 1.01, with 50% quantiles spanning [0.93,1.06] and 80% quantiles spanning [0.88,1.13]. This establishes a reference for how well we might expect our tree ESS measures to work, and provides a simulation-based confirmation of our procedure for testing ESS measures.

Overall, performance of the tree ESS methods is variable across both simulated conditions and MCMCSE measures. We account for variable performance across simulated conditions by binning our simulations based on the estimated ESS where possible. For each of the 45 simulated data analyses, and for each ESS measure, we compute the average ESS across all 100 replicate MCMC runs, and then bin results for split and tree probabilities into the ESS < 500 and ESS ≥ 500 regimes. In the ESS < 500 regime, the RMCE and ITMCE are quite variable, and often far from the optimal values of 0 and 1 (Figures 3, 4). This is not ideal, as it means that the performance is quite variable across different splits, trees, and datasets. In the ESS ≥ 500 regime, however, performance is much better for all methods. For split probabilities, in both ESS regimes the tree ESS measures readily outperform the baseline measures (fixedN and logPosteriorESS), and in the ESS ≥ 500 regime perform comparably to the univariate ESS of a Gaussian. For the MRC tree (Figure 5), performance is not as good as the univariate ESS of a Gaussian, but the tree ESS measures readily outperform the baseline measures. For tree probabilities (Figure 4), performance is somewhat worse. In the ESS ≥ 500 regime, the tree ESS measures do not present as clear an improvement over the baselines as they do for split probabilities. Further, none of them perform particularly well when compared to standard univariate ESS of a Gaussian (Figure 4). However, in aggregate the tree ESS measures do capture the Monte Carlo error of the estimated tree probabilities, with the median RMCE ≈ 0 and the median ITMCE ≈ 1 in the ESS ≥ 500 regime for most measures. It seems the tree ESS measures perform most usefully for split probabilities and the summary tree in the ESS ≥ 500 regime. In the supplement, we present analogous figures for an ESS cutoff of 250, where the performance is poor both below and above the cutoff.

Figure 3:

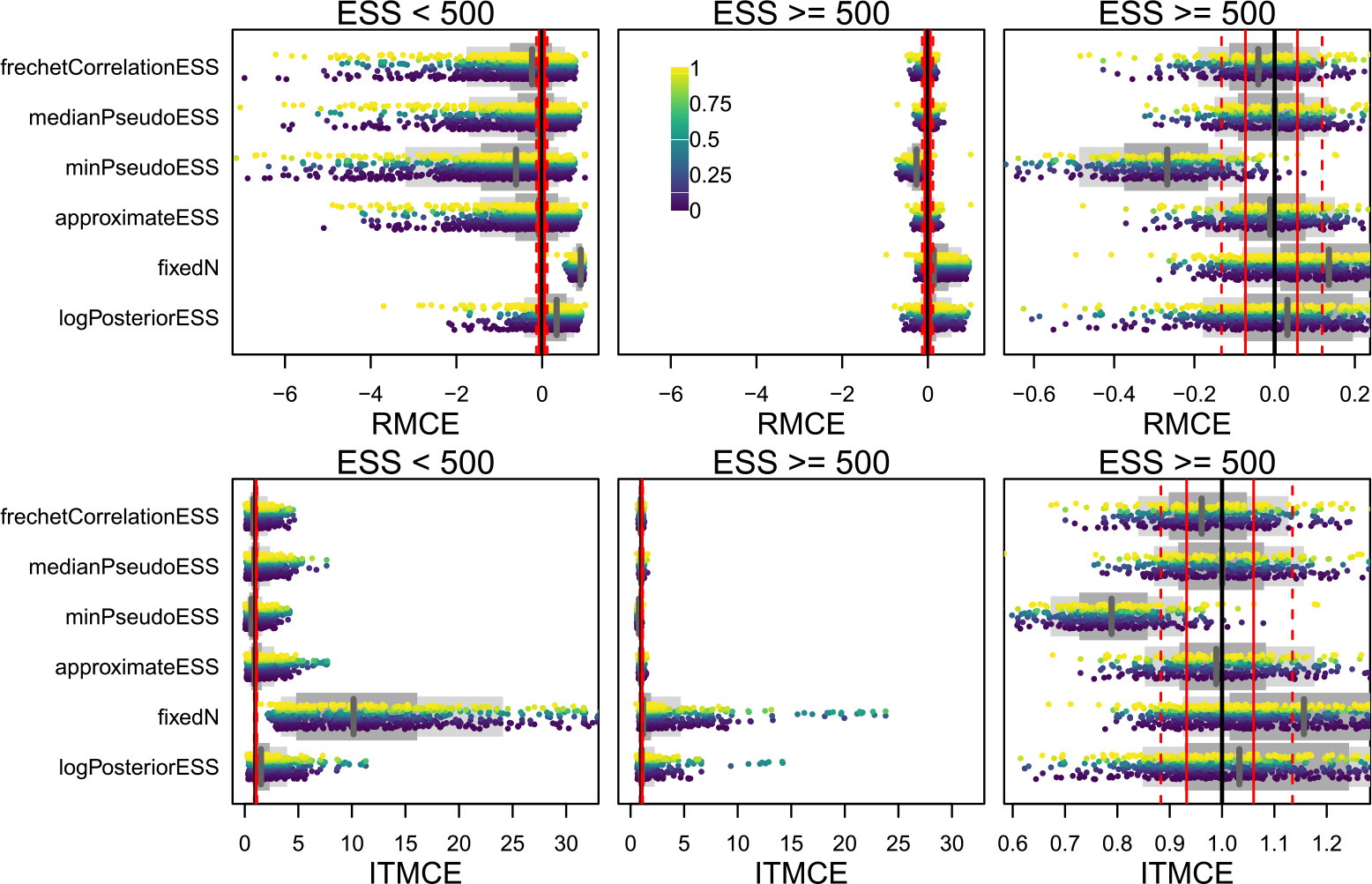
The RMCE $(({\widehat{\mathrm{S}\mathrm{E}}}_{\mathrm{M}\mathrm{C}\mathrm{M}\mathrm{C}}-{\widehat{\mathrm{S}\mathrm{E}}}_{\mathrm{M}\mathrm{C}\mathrm{E}\mathrm{S}\mathrm{S}})/{\widehat{\mathrm{S}\mathrm{E}}}_{\mathrm{M}\mathrm{C}\mathrm{M}\mathrm{C}})$ and ITMCE $({\widehat{\mathrm{S}\mathrm{E}}}_{\mathrm{M}\mathrm{C}\mathrm{M}\mathrm{C}}/{\widehat{\mathrm{S}\mathrm{E}}}_{\mathrm{M}\mathrm{C}\mathrm{E}\mathrm{S}\mathrm{S}})$ for split probabilities for all topological ESS measures and all 45 combinations of 9 datasets and 5 run lengths. Each point is the RMCE or ITMCE for a single split from one of the 45 simulations, colored by their estimated probabilities (see scale bar in top middle panel). Only splits with a posterior probability of at least 0.01 are shown. The two right panels are the same except for the scale of the x-axis. Whether a simulation appears in the left or right panels is determined by the estimated average ESS of each of the 45 simulations (the “ESS” in the column label), such that all splits from a simulation with average frechetCorrelationESS of 100 would appear in the left panel, while all splits from a simulation with an average Fréchet correlation ESS of 600 would appear in the right two panels. As fixedN always assumes ESS = 1000, for this row we split by the number of MCMC iterations run, with the left panel including 10³ and 10⁴, and the right panel 10⁵, 10⁶, and 10⁷. The thinner light grey bar below the points shows the 80% quantile range, the thicker dark grey bar the 50% quantile range, and the vertical grey line is the median. Ideal performance is $\mathrm{R}\mathrm{M}\mathrm{C}\mathrm{E}=0$ and $\mathrm{I}\mathrm{T}\mathrm{M}\mathrm{C}\mathrm{E}=1$ (perfect estimation of the Monte Carlo SE). As references we have plotted a solid black line for perfect performance, while the dashed (solid) red lines represent the 80% quantile range (50% quantile range) from the univariate Normal(0, 1) experiment. The best performance that might reasonably be expected of a tree ESS measure would match the Normal(0, 1) experiment, and thus have the grey line on the solid black line, the thinner light grey bar align with the dashed red lines, and the thicker dark grey bar align with the solid red lines. $\mathrm{R}\mathrm{M}\mathrm{C}\mathrm{E}<0$ $(\mathrm{I}\mathrm{T}\mathrm{M}\mathrm{C}\mathrm{E}<1)$ implies underestimating the ESS, while $\mathrm{R}\mathrm{M}\mathrm{C}\mathrm{E}>0$ $(\mathrm{I}\mathrm{T}\mathrm{M}\mathrm{C}\mathrm{E}>1)$ implies overestimating the ESS. The log-posterior ESS and assuming $\mathrm{E}\mathrm{S}\mathrm{S}=n$ tend to overestimate the ESS for splits, often substantially, while most tree ESS measures are much closer to the truth.

Figure 4:

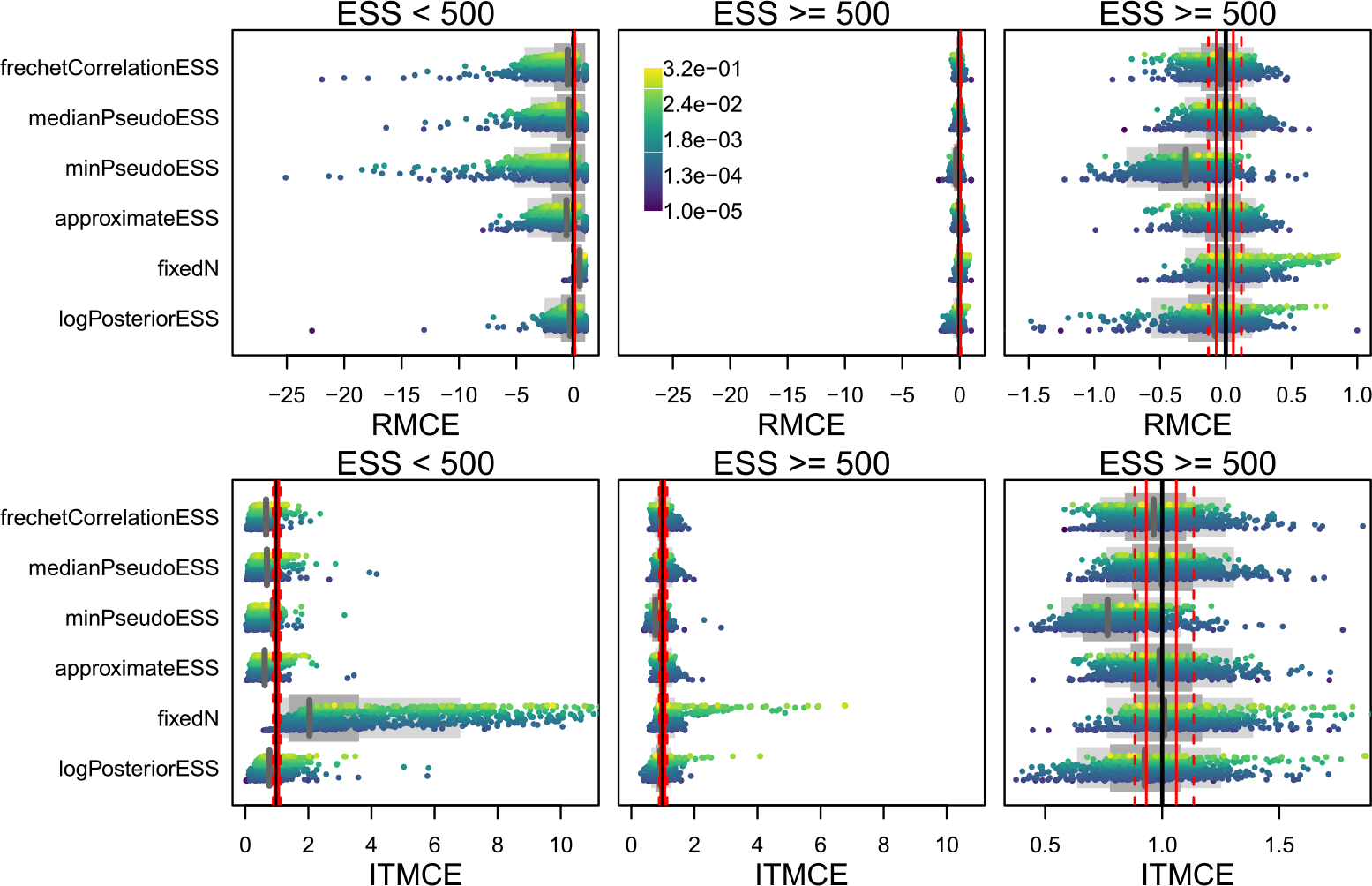
The RMCE $(({\widehat{\mathrm{S}\mathrm{E}}}_{\mathrm{M}\mathrm{C}\mathrm{M}\mathrm{C}}-{\widehat{\mathrm{S}\mathrm{E}}}_{\mathrm{M}\mathrm{C}\mathrm{E}\mathrm{S}\mathrm{S}})/{\widehat{\mathrm{S}\mathrm{E}}}_{\mathrm{M}\mathrm{C}\mathrm{M}\mathrm{C}})$ and ITMCE $({\widehat{\mathrm{S}\mathrm{E}}}_{\mathrm{M}\mathrm{C}\mathrm{M}\mathrm{C}}/{\widehat{\mathrm{S}\mathrm{E}}}_{\mathrm{M}\mathrm{C}\mathrm{E}\mathrm{S}\mathrm{S}})$ for topology probabilities for all topological ESS measures and all 45 dataset by run length combinations. Each point is the RMCE or ITMCE for a single tree topology from one of the 45 simulations, colored by their estimated probabilities (see scale bar in top middle panel). As there are too many distinct topology probabilities (nearly 100,000 across all 45 simulations), we plot only 1000 per row, preferentially keeping the highest-probability trees as these are the ones that contribute most to summary trees. For more explanation, see Figure 3 caption.

Figure 5:

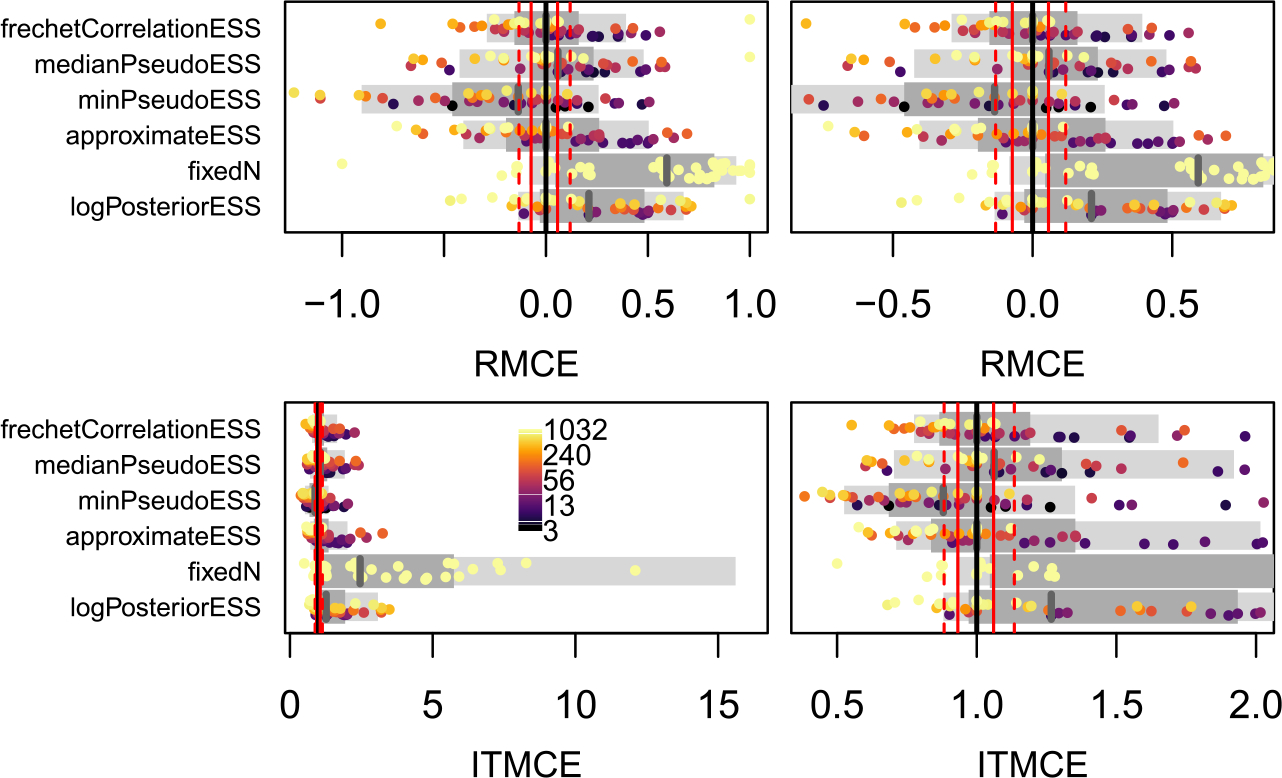
The RMCE $(({\widehat{\mathrm{S}\mathrm{E}}}_{\mathrm{M}\mathrm{C}\mathrm{M}\mathrm{C}}-{\widehat{\mathrm{S}\mathrm{E}}}_{\mathrm{M}\mathrm{C}\mathrm{E}\mathrm{S}\mathrm{S}})/{\widehat{\mathrm{S}\mathrm{E}}}_{\mathrm{M}\mathrm{C}\mathrm{M}\mathrm{C}})$ and ITMCE $({\widehat{\mathrm{S}\mathrm{E}}}_{\mathrm{M}\mathrm{C}\mathrm{M}\mathrm{C}}/{\widehat{\mathrm{S}\mathrm{E}}}_{\mathrm{M}\mathrm{C}\mathrm{E}\mathrm{S}\mathrm{S}})$ for the majority-rule consensus (MRC) tree for all topological ESS measures and all 45 dataset by run length combinations. Each point represents the RMCE or ITMCE for the summary tree from one of the 45 simulations. The standard error for the MRC tree is a Fréchet Monte Carlo SE, rather than a classical Euclidean Monte Carlo SE. The right and left panels are the same except for the scale of the x-axis. As there are only 45 MRC trees, points are colored by the estimated average ESS (see scale bar in bottom left panel), and all 45 are plotted together rather than separated according to an ESS threshold as in Figures 3 and 4. For more explanation, see Figure 3 caption.

The frechetCorrelationESS and medianPseudoESS are the best-performing tree ESS measures. Generally, the frechetCorrelationESS is a bit more conservative. For both split and tree probabilities, it avoids some of the overestimation of the ESS evident in the medianPseudoESS in the ESS ≥ 500 regime. For the MRC tree, the frechetCorrelationESS has the appropriate median RMCE and ITMCE, while the median of medianPseudoESS is slightly inflated (though there are fewer MRC trees to compare than splits). The approximateESS is at best no better than the frechetCorrelationESS or the medianPseudoESS, is in general more likely to overestimate the ESS, and for the MRC tree appears to overestimate the ESS when it is small and underestimate the ESS when it is large. The minPseudoESS is overly conservative, and even in the ESS ≥ 500 regime almost exclusively underestimates the ESS. In practice we recommend that practitioners consider multiple ESS measures, and note that any accurate quantification of Monte Carlo error requires an ESS of at least 500 for the ESS measure being used. Using the minPseudoESS alone would be a conservative choice, though the cost is longer MCMC runs than strictly necessary to achieve a desired level of accuracy. Using the minPseudoESS and either the frechetCorrelationESS or the medianPseudoESS (or both) allows for the best estimation of error in split probabilities, tree probabilities, and the MRC tree, while also providing an upper bound on the error.

Tree ESS measures reveal difficulties in MCMC sampling in real-world datasets

Now that we have some understanding of how tree ESS measures work (and do not work), we turn our attention to applying them to real-world datasets. Following Lanfear et al. (2016), we apply our ESS measures to datasets from Scantlebury (2013) spanning six taxonomic groups of Malagasy herpetofauna: Brookesia, Cophylinae, Gephyromantis, Heterixalus, Paroedura, Phelsuma, and Uroplatus. These datasets are convenient because the same well-documented analysis methodology was applied to each, and because 4 independent replicate MCMC analyses for each dataset have been deposited at Dryad (https://doi.org/10.5061/dryad.r1hk5).

In Figure 6, we show ESS measures computed for 1001 samples from each of the 4 replicate chains for all 6 datasets. While individual methods may often disagree, they all clearly agree that the Gephyromantis and Phelsuma datasets have low topological ESS across all chains, and other than the approximateESS they agree that the 3rd Paroedura chain has a low ESS. On these datasets, the performance of the baseline approaches (fixedN and logPosteriorESS) is completely inadequate for assessing the mixing of the phylogeny. Unlike in the simulations, though, here the logPosteriorESS says the ESS is much smaller than any of the actual tree ESS measures. That it is so low here, while the tree ESS measures are much larger, suggests that there were mixing problems with other model parameters than the tree, and highlights the need to address all parameters in the phylogenetic model, including the tree, on their own merits. That is, the logPosteriorESS is at best only loosely linked to the sampling of the tree topology, and its performance in our simulated scenarios is likely more closely linked to the actual Monte Carlo error in the tree than it ever will be in practice.

Figure 6:

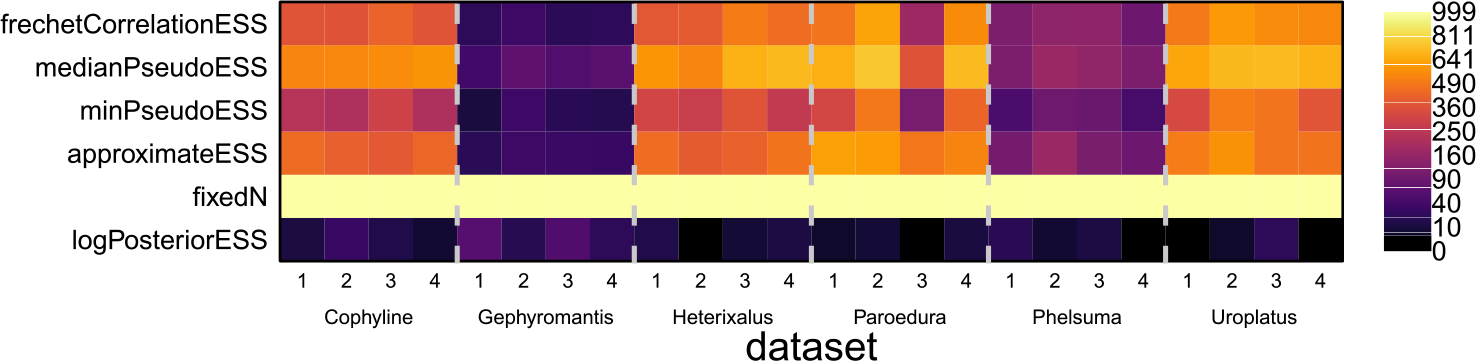
Tree ESS measures computed on 4 replicate chains for the 6 datasets from Scantlebury (2013) as a heat map. To make differences clearer when ESS is low, the heatmap is spaced on the square-root scale. The ESS of the log-posterior and the fixedN approaches are included as baselines, though neither captures the meaningful between-dataset differences in topological ESS.

In Figure 7, we use the tree ESS to construct confidence intervals for split probabilities, and update a standard MCMC convergence plot, the plot of split frequencies for two chains. Specifically, the confidence intervals are useful for determining whether the disagreement in split probabilities between two chains can be ascribed to a low sample size (CIs overlap), or whether it may be indicative of a convergence problem (CIs do not overlap). By plotting thresholds, we can also examine whether a given split can be confidently assumed to be above a specific cutoff, such as 0.5 for inclusion in the MRC tree. In this case we find that, even accounting for the topological ESS, only chains 2 and 4 for the Paroedura dataset have complete agreement for all split probabilities. This highlights the importance of performing multiple independent MCMC runs and using between-chain convergence diagnostics to assess between-chain differences, in addition to assessing the ESS of parameters. On every dataset other than the Uroplatus dataset, regardless of ESS, at least two chains disagree about the probability of at least one split (Supplemental Figures S8–S12). Topological ESS measures flag the Gephyromantis and Phelsuma datasets as having relatively low ESS, but despite the low ESS, all four Gephyromantis chains, and all Phelsuma chains except one, show levels of conflict in line with the other datasets. This further highlights the difference between low ESS (large uncertainty about parameter means) and between-chain convergence (two chains producing discordant estimates).

Figure 7:

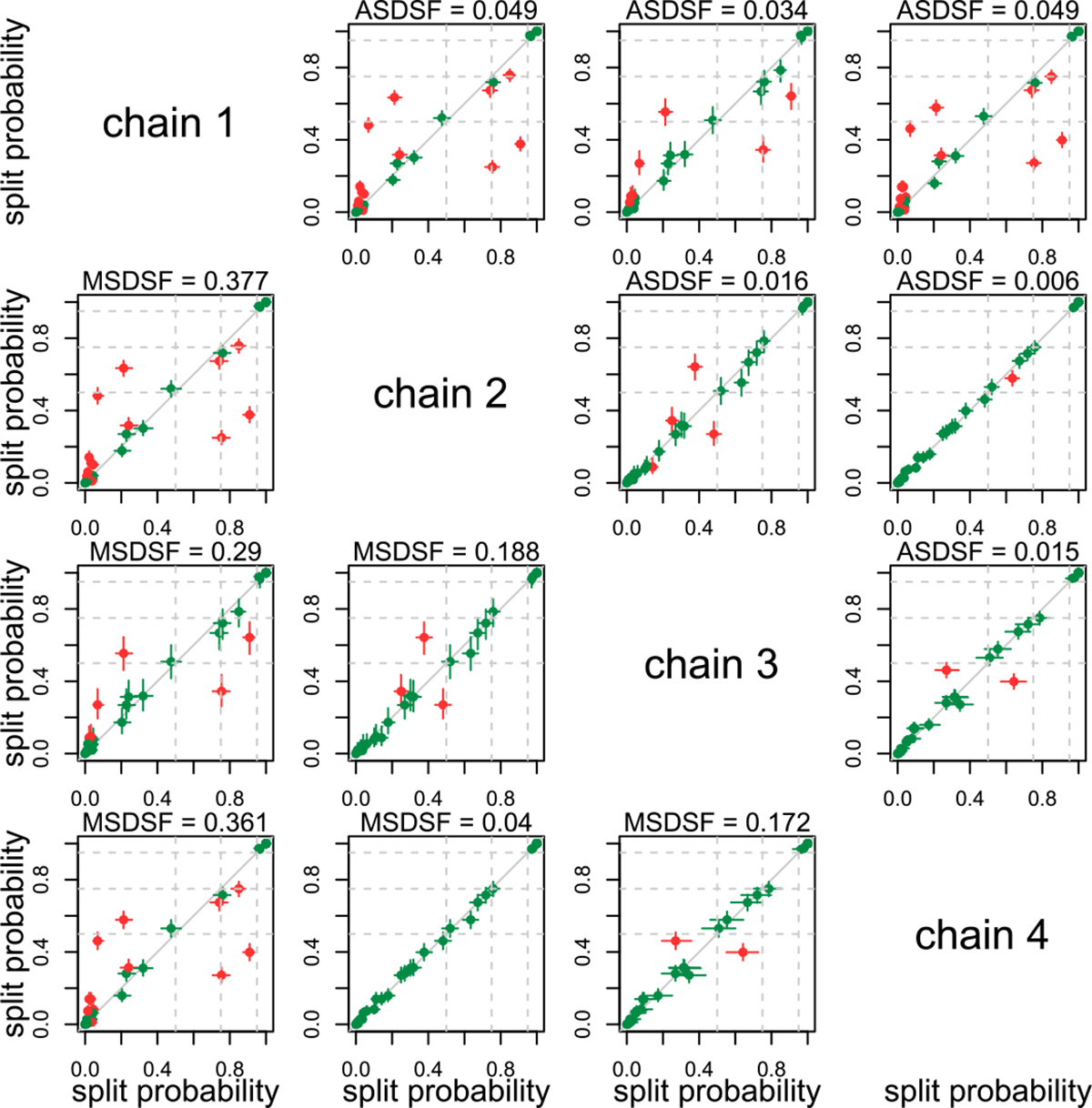
Split probabilities computed for all chains of the Paroedura dataset of Scantlebury (2013), plotted against the probabilities computed for all other chains, with confidence intervals. Comparisons above the diagonal use the frechetCorrelationESS to compute confidence intervals, while comparisons below the diagonal use the minPseudoESS, which is generally smaller and thus leads to larger confidence intervals. Each confidence interval is colored by whether or not the 95% CI for the difference in split probability between chains i and j includes 0 (green for including 0, red for excluding 0). CIs for differences in probability that exclude 0 (or non-overlapping confidence intervals) are more likely to be indicative of convergence issues between chains. Narrower confidence intervals from larger tree ESS estimates will flag more splits as problematic (as in chains 1 and 4). Dashed grey lines indicate posterior probabilities of 0.5 (threshold for inclusion in the MRC tree), 0.75 (moderate support for a split), and 0.95 (strong support for a split). For comparison, we include the average standard deviation of split frequencies (ASDSF, above the diagonal) and maximum standard deviation of split frequencies (MSDSF, below the diagonal).

Data and code availability

All necessary functions for computing the ESS of phylogenetic trees have been implemented in an R package named treess available at github.com/afmagee/treess. This package also includes functions for creating our new split-split probability plots and running fake phylogenetic MCMC on arbitrary phylogenetic posterior distributions. Code for the simulation study and real-data analyses is available at available at bitbucket.org/afmagee/tree_convergence_code.

Discussion

In this paper, we have investigated Monte Carlo error for phylogenetic trees. We present three summaries of Monte Carlo error that a topological ESS measure might capture: the MCMCSEs of split probabilities, tree probabilities, and summary trees. With simulations leveraging real-data posterior distributions, we use these MCMCSE summaries to assess four putative tree ESS measures (as well as two additional baselines based on standard practice). We find that the performance of these measures varies across summary measures and within summaries based on the ESS. At their best, the frechetCorrelationESS and medianPseudoESS can capture the Monte Carlo error inherent in MCMC estimates of split probabilities and MRC trees about as well as the univariate ESS captures the Monte Carlo error of the mean of a Normal(0, 1) variable. That is, these measures capture the Monte Carlo error of split probabilities and MRC trees about as well as could be hoped. When the estimated ESS is less than 500, however, performance is notably less than ideal, severely overestimating the ESS for some split probabilities and underestimating it for others (similar patterns hold for tree probabilities and the summary tree). Thus, if one wants to use ESS to accurately quantify the Monte Carlo error in their phylogeny, a larger cutoff, such as the 625 advocated for by Fabreti and Höhna (2021) would be more appropriate. For split probabilities and MRC trees, the frechetCorrelationESS and medianPseudoESS clearly outperform the standard practices of ignoring Monte Carlo error or using the ESS of the log-posterior density as a proxy. The tree ESS measures also capture Monte Carlo error in the estimated tree probabilities, though they do not clearly outperform the baselines. When assessing the ESS of tree topologies, we recommend that practitioners consider the minPseudoESS, frechetCorrelationESS, and the medianPseudoESS. If the estimated ESS is at least 500, then this combination provides an upper bound on the error (the minPseudoESS), and the best estimation of split probability error (the frechetCorrelationESS) and MRC tree error (the medianPseudoESS). If the estimated ESS is less than 500, then all three approaches may overestimate the ESS quite severely.

The medianPseudoESS and the frechetCorrelationESS perform very similarly, which we found surprising given their quite distinct derivations. The frechetCorrelationESS is derived as a generalization of the classical univariate ESS, and does not require a reference tree. The medianPseudoESS is the ESS of a reduced-dimensional representation of the MCMC samples and requires fixing a reference tree. We know of no obvious reason that they should work similarly.

While the simplicity of the purely topological measures we have considered are important as starting places for understanding MCMC for trees, extending this work to branch lengths via BHV space (Billera et al., 2001) is an interesting possibility. This would have the advantage of additionally assessing the mixing of the branch lengths, which is often unaddressed in phylogenetic workflows (we note, however, that MrBayes reports the potential scale reduction factors of branch lengths as a between-chain diagnostic). By comparing purely topological and BHV-based measures, one could also understand how differences in branch lengths contribute to the tree-to-tree distances relative to the topological distances. It is possible that most of the distance comes from differences in branch lengths, and thus the BHV-based tree ESS measures miss key differences in topology. Alternately, BHV-based tree ESS measures could adequately capture both branch length and topological dynamics. It is also possible that these two regimes co-exist in different regions of parameter space. In either case, reducing the mixing of a very complex structure (a tree with branch lengths) to one or even two ESS measures would be a useful simplification. In BHV space, it may also be possible to extend the work in Willis (2019) on confidence sets for phylogenetic trees to better describe the uncertainty in summary trees.

Recently, Harrington et al. (2021) performed an in-depth exploration of MCMC across thousands of empirical datasets. They computed the approximate ESS of Lanfear et al. (2016) for all runs. This represents the largest use to date of tree ESS measures, though until now the properties and performance of these ESS estimators have been somewhat ambiguous. Our results show that effective sample sizes of at least 500 are generally capable of capturing the true mixing behavior of the tree, while smaller effective sample sizes are not. The MCMC settings used by Harrington et al. (2021) led to most topological ESS on the order of 750, meaning that in their usage the tree ESS is likely to adequately capture Monte Carlo error in the phylogeny. We note, however, that a large within-chain ESS is not indicative of good between-chain convergence. While 97% of the analyses run by Harrington et al. (2021) achieved a topological ESS of at least 200, only 37% achieved an ASDSF below the standard cutoff of 0.01.

Fabreti and Höhna (2021) have recently published a paper on convergence diagnostics for phylogenetic MCMC, and an accompanying R package convenience. We agree with Fabreti and Höhna (2021) (and Rambaut et al. (2018)) that ESS > 200 is an arbitrary cutoff, and appreciate the approach Fabreti and Höhna (2021) take to deriving an ESS threshold which centers on Monte Carlo error. Our work departs from theirs, though, in considering the entire tree, where the tree-based diagnostics in convenience consider each split separately. As trees are inherently multivariate objects, we think it is important to attempt to consider them in their entirety. Consider, for example, that the fixedN approach estimates the Monte Carlo error for tree probabilities as well as the tree-based measures for longer runs (Figure 4), but severely underestimates the Monte Carlo error for split probabilities (Figure 3). In the supplement we also show that while the split probabilities may appear to have converged over the course of an MCMC run, there can still be notable uncertainty in the MRC tree (see section on “Visualizing convergence of a single chain” and Figure S1).

The tree ESS methods we have considered are applicable out-of-the-box to any data structure where one can compute a distance. As distance measures exist for a wide range of objects, we hope that this work may prove useful for understanding Monte Carlo error in other non-Euclidean cases. In phylogenetic applications, one might seek to understand the Monte Carlo error in estimates of phylogenetic networks, sequence alignments (for joint models of tree and alignment as in BAli-Phy (Redelings, 2021)) ancestral state estimates, or migration matrices.

We have identified tree ESS measures that can sufficiently describe the Monte Carlo error of both split probabilities and the summary tree. Further, we have implemented these measures and approaches for constructing confidence intervals for split probabilities (as in Figure 3) in the R package treess. Focusing on Monte Carlo error as we have in this paper stands in contrast to the widespread use of ESS in phylogenetics, which is commonly treated as a “box that should be checked” by having ESS above a threshold before proceeding on to interpreting results. We hope that this work motivates phylogenetic community to take more seriously the quality of MCMC estimation of its focal parameter, and more broadly that it helps de-mystify the matter of how long to run phylogenetic MCMC. An analysis should be run long enough that the Monte Carlo error of the important quantities is small enough that conclusions are robust.

Most Bayesian phylogenetic MCMC run lengths are fixed in advance. This can lead to runs which are too short to achieve good inference, or runs which are longer than needed and waste CPU time. The problem of too-short runs is addressed by checkpointing, allowing post-hoc longer runs. The problem of too-long runs is addressed by dynamic stopping criteria. In non-phylogenetic contexts, dynamic stopping criteria have been considered based on between-chain and within-chain comparisons. Among phylogenetic software, MrBayes enables auto-termination based on between-chain comparisons of split probabilities using the ASDSF. While between-chain comparisons can capture Monte Carlo error, it appears that the number of chains required for accurate estimation of the Monte Carlo error is prohibitive (Figures S14, S15, and S16). Future work may enable auto-termination when sufficient precision is achieved in split probabilities or the summary tree, leveraging the work done in this paper on phylogenetic effective sample sizes and methods developed for MCMC in Euclidean spaces (Gong and Flegal, 2016; Vats et al., 2019).