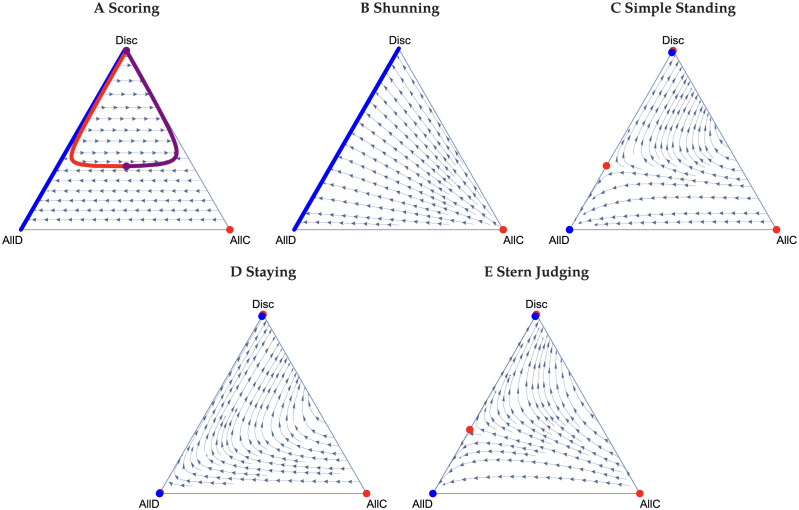
Fig 1. Ternary plots for the leading five norms under public assessment of reputations.

Stable, semi-stable, and unstable equilibria are plotted in blue, purple, and red, respectively. Circles are singular equilibria, and lines sets of them. A: For Scoring, if z is sufficiently low, then the system can only evolve to the AllD-Disc boundary of the simplex where Discriminators always defect. If z is higher, then we observe bistability, which includes a set of equilibria through the interior of the simplex. Note that the red curve representing a set of unstable equilibria is interior to the simplex and only intersects with the blue curve at z = 1. The purple curve in turn is semistable since all points along it are attractors except at the end of the curve where Discriminators at their lowest frequency, which is unstable. B: Under Shunning, the AllD-Disc boundary is a stable set of equilibria (note that this also applies to private assessment). C-E: Simple Standing, Staying, and Stern Judging give qualitatively similar results. The system either evolves to AllD or to a position on the AllD-Disc boundary. Note that the stable equilibria on the AllD-Disc boundary are very near z = 1. In all figures, the benefit to cost ratio is r = 3 and the error rates are e₁ = e₂ = 0.01.