MRBEE: A bias-corrected multivariable Mendelian randomization method

Summary

Mendelian randomization (MR) is an instrumental variable approach used to infer causal relationships between exposures and outcomes, which is becoming increasingly popular because of its ability to handle summary statistics from genome-wide association studies. However, existing MR approaches often suffer the bias from weak instrumental variables, horizontal pleiotropy and sample overlap. We introduce MRBEE (MR using bias-corrected estimating equation), a multivariable MR method capable of simultaneously removing weak instrument and sample overlap bias and identifying horizontal pleiotropy. Our extensive simulations and real data analyses reveal that MRBEE provides nearly unbiased estimates of causal effects, well-controlled type I error rates and higher power than comparably robust methods and is computationally efficient. Our real data analyses result in consistent causal effect estimates and offer valuable guidance for conducting multivariable MR studies, elucidating the roles of pleiotropy, and identifying total 42 horizontal pleiotropic loci missed previously that are associated with myopia, schizophrenia, and coronary artery disease.

We introduce a multivariable MR method MRBEE that is capable of simultaneously removing weak instrument and sample overlap bias and identifying horizontal pleiotropy. The real data analyses offer valuable guidance for conducting MR studies, and identifying 42 horizontal pleiotropic loci associated with myopia, schizophrenia, and coronary artery disease.

Introduction

Mendelian randomization (MR) is an instrumental variable (IV) approach used to infer causal relationships between exposures and outcomes and can apply to summary statistics from genome-wide association studies (GWASs), providing a cost-effective and generalizable alternative to randomized controlled trials.¹ Inverse-variance weighting (IVW)² is the fundamental approach to perform MR with GWAS summary statistics, and the validity of which relies heavily on three so-called valid IV assumptions: the genetic IVs are (IV1) strongly associated with the exposures; (IV2) not directly associated with the outcome conditional on the exposures; and (IV3) not associated with any confounders of the exposure-outcome relationships. Violations of the (IV1)–(IV3) assumptions will introduce weak instrument,³ unbalanced uncorrelated horizontal pleiotropy (UHP),⁴ and correlated horizontal pleiotropy (CHP)⁵ biases into the casual effect estimation, respectively. As for balanced UHP, which aligns with the instrument strength independent of direct effect (InSIDE) assumption,⁴ the causal effect estimation remains unbiased.

From a statistical perspective, both unbalanced UHP and CHP in an MR model exhibit characteristics similar to outliers in traditional regression analyses. Therefore, these issues can be addressed using robust statistical tools. In the literature, MR-PRESSO⁶ and IMRP⁷ identify and remove horizontal pleiotropic variants through hypothesis tests, while the MR-Lasso⁸ and MRcML⁹ methods detect horizontal pleiotropy through variable selection tools. On the other hand, approaches like MR-Median¹⁰ and MR-Robust¹¹ employ robust loss functions to mitigate the horizontally pleiotropic effects. Furthermore, Gaussian mixture models are implemented in methods such as MRMix,¹² MR-Conmix,¹³ CAUSE,⁵ MRAID,¹⁴ and MR-CUE.¹⁵ These models offer an advantage over traditional robust tools by utilizing fewer degrees of freedom to describe unbalanced UHP and CHP, thereby increasing efficiency when the mixture models are correctly specified.

While univariable MR (UVMR) methods allow some IVs to have horizontally pleiotropic effects, they generally assume that most IVs influence the outcome solely through the mediation of the exposure. However, this assumption can be problematic when traits share more than 50% causal variants. For instance, both systolic and diastolic blood pressure (SBP and DBP)¹⁶ are revealed to share substantial causal variants. When analyzing the causal effect of SBP on cardiovascular disease, it is often challenging to remove the effect through DBP. A more effective way to address this issue is multivariable MR (MVMR), which accounts for the majority of horizontally pleiotropic variants that are shared by multiple exposures.¹⁷ To date, the multivariable versions of IVW,¹⁸ MR-Egger,¹⁹ MR-Median,¹⁰ and MRcML²⁰ have been developed. As demonstrated by Sanderson et al.,¹⁷ MVMR is reliable in estimating the direct causal effects of one or more exposures.

The issue of weak instrument bias, stemming from the violation of the (IV1) assumption, poses even more challenging to resolve in MVMR than in UVMR. Specifically, it is usually difficult to find a set of IVs that are strongly associated with all exposures under consideration. In contrast, IVs are generally selected if they are associated with at least one exposure.²¹ With the growing identification of causal variants for complex traits, the pool of IVs used in MVMR can easily reach the thousands due to this IV selection procedure, therefore worsen weak instrument bias. Traditional approaches to mitigate this bias involve discarding weak IVs whose F-statistic or conditional F-statistic is less than 10. This threshold is believed to keep the relative bias in causal effect estimates below 10%.^3,22 However, the exclusion of IVs can lead to reduced statistical power and introduce a “winner’s curse,” thereby compromising the validity of the causal inference.²³

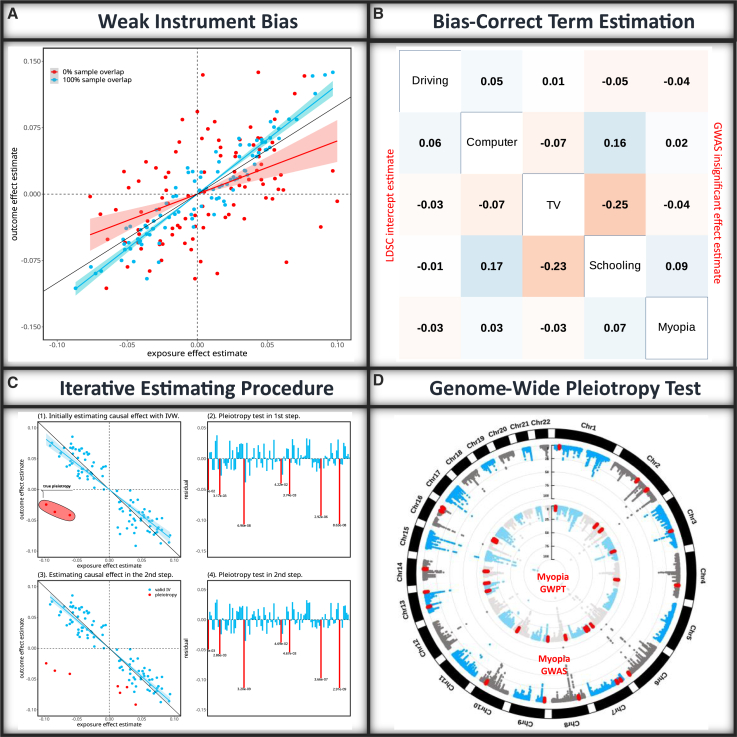
We propose to resolve the weak instrument bias by using tools in measurement error analysis.²⁴ Specifically, measurement error bias occurs when explanatory variables are measured with random error, leading to biased estimates of model parameters. Since current MR approaches are performed with GWAS summary statistics that always contain estimation errors, the causal effect estimates inevitably suffer from measurement error bias.^25,26 Therefore, we view a weak instrument as a relatively large measurement error in effect size estimate based on finite sample size and is the primary reason for violating assumption (IV1) in IVW and other MR approaches. Furthermore, unlike traditional measurement error analyses that assume uncorrelated estimation errors in exposures and outcomes, overlapping individuals in exposure and outcome GWAS can result in correlated measurement errors, leading the direction of measurement error bias either toward or away from zero. As we observed in Figure 1, IVW estimates²⁷ exhibit negative bias with small numbers of overlapping samples and positive bias with large numbers of overlapping samples, respectively.

Figure 1.

Principle of MRBEE

(A) Traditional MR methods are vulnerable to weak instrument bias arising from the estimation errors in GWAS associations for the exposure(s) and outcome. The direction of the bias is influenced by the degree of sample overlap between the studies where the red and blue points refer to two simulated data with 0% and 100% sample overlap. The shadow regions represent the 95% confidence interval regions.

(B) MRBEE corrects for weak instrument bias using bias-correction terms which are calculated from the matrix of correlations between measurement errors for all exposures and the outcome. In this example with myopia and its four exposures, the numbers in the lower triangle of the table are the correlations estimated using LD score regression and that in the upper triangle of the table are the correlations estimated using non-significant SNPs.

(C) MRBEE uses an iterative estimation procedure, where horizontally pleiotropic IVs are removed at each iteration until convergence. The y axis in panels (2) and (4) reflect the SNP association with the outcome not mediated by the exposures. The numbers under the red vertical lines represent p values.

(D) After estimating causal effects, MRBEE performs genome-wide horizontal pleiotropy testing to find loci associated with the outcome (e.g., myopia) that were not detected in the original GWAS.

We develop a computationally efficient MVMR method, MR using bias-corrected estimating equations (MRBEE), to eliminate weak instrument bias while simultaneously accounting for horizontal pleiotropy in the presence of weak IVs or sample overlap. In contrast, existing methods only address weak instrument bias in specific cases such as no sample overlap (debiased IVW)²⁶ or no horizontal pleiotropy (MRlap).²⁸ Although the multivariable MRcML methods²⁰ generally provide unbiased causal estimates, they may be vulnerable to horizontal pleiotropy and computationally intensive. To underscore its practical significance, we apply MRBEE to three datasets, each targeting a unique disease, namely, myopia, schizophrenia (SCZ), and coronary artery disease (CAD), with the aim to unravel the distinct causal exposures associated with each. In addition, we extend the pleiotropy test to a genome-wide pleiotropy test (GWPT) for detecting novel loci. These empirical analyses offer valuable guides for conducting MVMR studies, elucidating the roles of pleiotropy and weak instrument bias, and illustrating how to identify novel loci through pleiotropy tests. The study was approved by the institutional review board (IRB number: STUDY20180592) at Case Western Reserve University.

Results

Overview of method

The detailed MRBEE is described in the material and methods section. Briefly, suppose that there are p exposures having causal effects on an outcome and m genetic variants as IVs. Let $\mathit{\alpha }={\left({\alpha }_1,\dots ,{\alpha }_m\right)}^T$ be a vector of length $m$, representing the genetic effect sizes of IVs on the outcome, $\mathbf{B}={\left({\beta }_1,\dots ,{\beta }_m\right)}^{\top }$ be an $\left(m\times p\right)$ matrix with ${\mathit{\beta }}_j={\left({\beta }_{j1},\dots ,{\beta }_{jp}\right)}^{\top }$ representing the genetic effect sizes of the $j$ th IV on the p exposures, $\mathit{\theta }={\left({\theta }_1,\dots ,{\theta }_p\right)}^{\top }$ be a vector of length $p$ representing the causal effects of the $p$ exposures on the outcome, and $\mathit{\gamma }={\left({\gamma }_1,\dots ,{\gamma }_m\right)}^{\top }$ be a vector of length $m$ representing horizontal pleiotropy. We model the causal effects of the exposures on the outcome by

$$\begin{array}{r}{\alpha }_{\mathrm{j}}={\beta }_{\mathbf{j}}^{\top }\theta +{\gamma }_{\mathrm{j}}\text{.}\end{array}$$

The goal in MR analysis is to estimate the causal effects $\theta$ unbiasedly. In the above equation, the true genetic effect sizes $\mathit{\alpha }$ and $\mathbf{B}$ are not observed but can be estimated through the GWAS of exposures and outcome and the pleiotropy effect $\gamma$ is simply unknown. Let ${\hat{\alpha }}_j$ and ${\hat{\beta }}_j$ be the effect size estimates of the $j$ th IV from the outcome and exposure GWASs. We have

$$\begin{array}{rr}{\hat{\alpha }}_j& ={\alpha }_j+w_{{\alpha }_j}\text{,}\\ {\hat{\beta }}_j& ={\beta }_j+{\mathbf{w}}_{{\beta }_j}\text{,}\end{array}$$

where $w_{{\alpha }_j}$ and ${\mathbf{w}}_{{\beta }_j}$ represent the measurement errors because of finite sample sizes of the GWASs.

In general, an MVMR analysis is performed by the following linear regression:

$$\begin{array}{r}{\hat{\alpha }}_j={\hat{\beta }}_j^{\top }\theta +{\gamma }_j+{\epsilon }_j\text{,}\end{array}$$

where ${\epsilon }_j$ represents the residual. When we standardize ${\hat{\alpha }}_j$ and ${\hat{\beta }}_j$ by their corresponding standard errors obtained from GWASs, the multivariable IVW (MV-IVW) estimates $\theta$ is

$$\begin{array}{c}{\hat{\theta }}_{\text{IVW}}=\arg \underset{\theta }{\min }\left\{{\Vert \hat{\alpha }-\hat{\mathit{B}}\theta \Vert }_2^2\right\}={\left({\hat{\mathbf{B}}}^{\top }\hat{\mathbf{B}}\right)}^{-1}{\hat{\mathbf{B}}}^{\top }\hat{\alpha },\end{array}$$

which is equivalent to solve the score equation ${\mathbf{S}}_{\text{IVW}}\left(\theta \right)={\hat{\mathbf{B}}}^{\top }\left(\hat{\mathbf{B}}\theta -\hat{\alpha }\right)$ = 0. However, the MV-IVW fails to consider the weak IVs and the correlations among $w_{{\alpha }_j}$ and ${\mathbf{w}}_{{\beta }_j}$ induced by sample overlap and assumes pleiotropy ${\gamma }_j$ = 0 for all IVs. Thus, the MV-IVW is biased. To solve this problem, we propose MRBEE by solving the following estimating equation,

$$\begin{array}{c}{\mathbf{S}}_{\text{BEE}}\left(\theta \right)={\mathbf{S}}_{\text{IVW}}\left(\theta \right)-m\left({\mathrm{\Sigma }}_{W_{\beta }{W}_{\beta }}\theta -{\sigma }_{W_{\beta }{w}_{\alpha }}\right)=0,\end{array}$$

where ${\mathrm{\Sigma }}_{W_{\beta }{W}_{\beta }}$ and ${\sigma }_{W_{\beta }{w}_{\alpha }}$ represent the covariance matrix among ${\mathbf{w}}_{{\beta }_j}$ and between ${\mathbf{w}}_{{\beta }_j}$ and $w_{{\alpha }_j}$ (material and methods) in the set of the $m$ IVs. The score function in ${\mathbf{S}}_{\text{BEE}}\left(\theta \right)$ adds a corrected term, which corrects the bias because of weak IVs and sample overlap, meanwhile assumes there are no pleiotropic IVs (${\gamma }_j=0)\text{.}$ The solution of the equation ${\mathbf{S}}_{\text{BEE}}\left(\theta \right)$ is

$$\begin{array}{c}{\hat{\theta }}_{\text{BEE}}={\left({\hat{\mathbf{B}}}^{\top }\hat{\mathbf{B}}-m{\mathrm{\Sigma }}_{W_{\beta }{W}_{\beta }}\right)}^{-1}\left({\hat{\mathbf{B}}}^{\top }\hat{\alpha }-m{\sigma }_{W_{\beta }{w}_{\alpha }}\right).\end{array}$$

With the presence of pleiotropic IVs, we apply an iterative procedure⁷ with the pleiotropy test $S_{\text{pleio}}$ for multiple exposures and an outcome, which uses the following statistic $S_{\text{pleio}}$ for the $j$ th IV,

$$\begin{array}{r}{S}_{{\text{pleio}}_j}\left(\hat{\theta }\right)=\frac{{\left({\hat{\alpha }}_j-{\hat{\beta }}_j^{\top }\hat{\theta }\right)}^2}{\text{var}\left({\hat{\alpha }}_j-{\hat{\beta }}_j^{\top }\hat{\theta }\right)}\text{.}\end{array}$$

Thus, MRBEE estimates the causal effect $\theta$, and identifies pleiotropic IVs with the current estimated causal effect $\theta$ iteratively. The entire pipeline from inputting summary statistics, estimating causal effects, and identifying pleiotropic IVs is illustrated in Figure 1. Note that after estimating the causal effect $\theta$, we can further search pleiotropic variants across the entire genome.

Simulation

We compared MRBEE with the multivariable MR of IVW, MR-Egger, MR-Median, MR-Lasso, MRcML-DP, and MRcML-BIC. MRBEE is implemented with the R package MRBEE and the other methods are implemented through the R package MendelianRandomization.²⁹ We call IVW, MR-Egger, MR-Median, and MR-Lasso the traditional MVMR methods, as they either do not account for estimation error of effect size or the sample overlap. Our simulation setting was adapted from the ones considered by Lin et al.,²⁰ but with specific adjustments to better reflect real-world situations. Specifically, we set the heritability of both exposures and confounders at 0.1, introduced moderate genetic correlations among the exposures, and added correlations among random errors of exposure and outcome GWAS cohorts. In our analysis, we consider three scenarios: no pleiotropy, 30% unbalanced UHP, and 30% CHP. All exposures are assumed to come from the same GWAS sample, while the outcome may overlap completely (100% sample overlap), partially (50% and 77% overlap), or be entirely independent (0% sample overlap). In addition, the sample size was set at 50,000, the number of IVs was set at 50, 100, and 200, representing the increasing of weak IVs, the number of exposures was 4, and the causal effect was $\theta ={\left(0,0.2,-0.2,0.4\right)}^{\top }$, which represents no causal effect, and positive, negative, and large causal effects, respectively. Simulation settings are fully presented in supplement 1 and the R code used to generate simulated data is available at the GitHub repository of this paper. The number of simulation replicates was 500, and additional simulations can be found in supplement 1.

Bias of causal effect estimates

Figures 2A, 2D, 2G, and 2J demonstrate that the bias in traditional MVMR methods (IVW, MR-Egger, MR-Median, MR-Lasso) is proportional to the number of IVs used, especially in the absence of horizontal pleiotropy. The direction of this bias is influenced by sample overlap: no overlap results in bias toward the null, while sample overlap leads to bias away from the null. On the contrary, MRBEE, MRcML-BIC, and MRcML-DP are unbiased under these conditions. The unbiasedness for MRcML methods is likely attributed to the fact that the objective function of MRcML methods²⁰ accounts for the covariance of estimation errors. Our results suggest that incorporating the estimation error covariance matrix mitigates measurement error bias.

Figure 2.

Comparison of the causal effect estimates by the 7 MVMR methods

(A–L) Boxplots display the causal effect estimates from seven methods in the MVMR simulation. The four rows represent the four causal effects ${\theta }_j$, $j=1,2,3,4$. Each column corresponds to one of the three pleiotropy scenarios for IVs (i.e., No pleiotropy; 30% unbalanced UHP IVs; 30% CHP IVs). The x axis indicates the value of the causal effect estimate, while the y axis lists the seven methods. The true values of causal effects are denoted by dashed lines. Plots in (A), (D), (G), and (J) when the sample overlap proportion is 0% can be used to infer the magnitude of weak instrument bias since differences between MRBEE and IVW causal estimates in these scenarios are proportional to the degree of weak IV bias. The left and right vertical edges of each box plot represent the 25^th and 75^th percentiles of causal effect estimate, and the vertical middle line represent the 50th percentile.

Figures 2B, 2E, 2H, and 2K demonstrate that when there was 30% unbalanced UHP, IVW, and MR-Egger generally incurred substantial bias. Moreover, there were inflated standard errors in the causal estimates due to the horizontal pleiotropy. MR-Median and MR-Lasso also incurred substantial bias, but the standard errors of their causal estimates were smaller than that from IVW and MR-Egger. These methods apply robust tools to estimate the causal effects in the presence of horizontal pleiotropy but are not able to remove the bias by weak instrument or sample overlap. MRcML-BIC and MRcML-DP generally provided unbiased causal estimates when there was no sample overlap. When the sample overlap percentage was 100%, both MRcML-BIC and MRcML-DP incurred biases in different directions. The magnitude of this bias was proportional to the number of IVs used. For example, for exposure 1 with true ${\theta }_1=0$, MRcML-BIC and MRcML-DP had bias away from the null; for exposure 3 where ${\theta }_3=-0.2$, the two methods had bias toward, and even past, the null. In comparison, MRBEE was unbiased in all scenarios except when there were 200 IVs and 100% overlap. In this case, MRBEE still had a smaller upward bias for exposure 3 with ${\theta }_3=-0.2$ than other methods.

Figures 2C, 2F, 2I, and 2L demonstrate that when there was 30% CHP, IVW, and MR-Egger had larger bias and standard errors in their causal estimates than the rest of methods. Both had bias away from the null for exposure 1, and the magnitude of which depended on the number of IVs used. MR-Median and MR-Lasso generally were less biased than IVW and MR-Egger, as they are more robust in handling of CHP IVs. The weak instrument bias of MR-Median and MR-Lasso followed the same bias patterns as no pleiotropy. MRcML-BIC and MRcML-DP were both biased when the sample overlapping percentage was 100% or 0%, potentially due to the instability of algorithm when horizontal pleiotropy is present. MRBEE was unbiased in all cases and generally had standard errors comparable to other methods excluding IVW and MR-Egger. Finally, when the number of IVs increased from 50 to 200, representing the increasing of weak IVs, MRBEE was always performing better than the comparing methods (Figure 2).

Type I error and power

Figures 3A–3C present the type I error rates for all the methods when the true causal effect ${\theta }_1=0$, which corresponds to the first exposure in our simulations. When there was no sample overlap between exposures and the outcome, the type I error was well controlled for MRBEE in all three scenarios, i.e., no pleiotropy, 30% unbalanced UHP, and 30% unbalanced CHP. In comparison, MRcML-DP, MR-Median, MR-Egger, and IVW was generally conservative, while MRcML-BIC and MR-LASSO usually had inflated type I error rates. When 100% overlap between exposures and the outcome, MRBEE still controlled type I error rate well. The rest of the methods either had inflated or extremely conservative type I error rate.

Figure 3.

Comparisons of type I error and power of the seven MVMR methods

(A–C) Type I error of the seven methods (MRBEE, MRcML-BIC, MRcML-DP, MR-LASSO, MR-Median, MR-Egger and IVW). (D–L) Power of the seven methods. The three columns corespond to no pleiotropy, 30% unbalanced UHP IVs and 30% CHP IVs, respectively. In each figure, the top and bottom panels represent 0% and 100% sample overlap between exposures and outcome, respectively. Each row represents different causal effects. Simulation settings are described in the simulation section in the main text, supplement 1, and at our GitHub repository. Displayed are bar plots of rejection frequency estimations across 500 simulations for each scenario, which represents the type I error or power depending on the true causal effect is zero or not. The two dotted vertical lines in (A)–(C) represent the 95% confidence interval.

Figures 3D–3L present power for different causal effects in the three scenarios. Overall, MRBEE has comparable power with the best of the other methods but maintains a type I error rate. We specifically compared MRBEE and MRcML-DP, where the latter controlled type I error rate well under all the simulation scenarios. We observed that MRBEE either had similar or better power than MRcML-DP. The power pattern across the seven methods does not align well with the type I error pattern, that is, high type I error rate corresponds to high power and vice visa. We observed that the reason is the bias direction in causal effect estimates as illuminated in Figure 2, i.e., the bias direction could be in opposite to the true causal effect.

Again, when the number of IVs increased from 50 to 200, the performance of type I error and power of MRBEE was either equal well or better than the comparing methods. We further evaluated these approaches in terms of the root-mean-square error (RMSE), standard error (SE) estimation, and coverage frequency of causal effects. MRBEE was again the best among the methods evaluated (Figures S1–S3, and Tables S1–S24 in supplement 1).

We have performed additional simulations in which the overlapping proportion takes values 0, 0.5, 0.77, and 1. In these scenarios MRBEE still performs well. The results are presented in supplement 1.

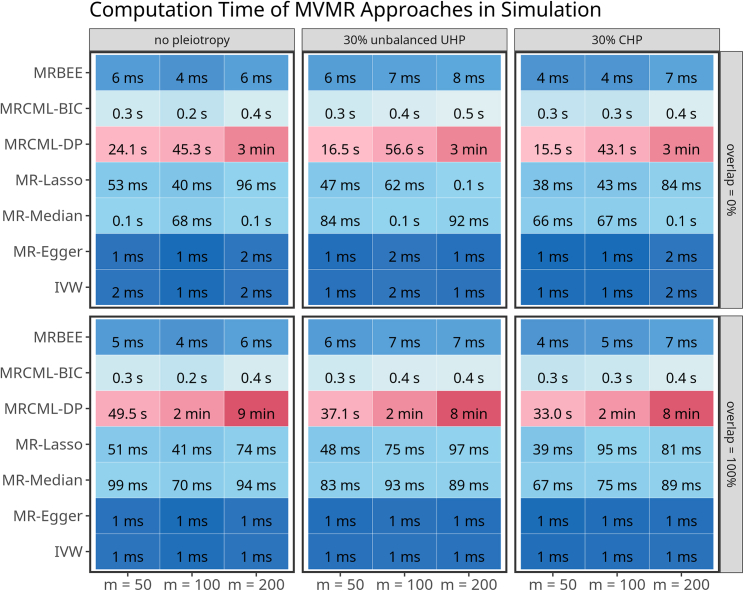
Computational efficiency

Figure 4 illuminates the computation efficient across seven methods. We observed that MRBEE is computationally as efficient as MR-Median, MR-Lasso, MR-Egger, and MR-IVW. We attribute the computational requirements of MRcML to two potential factors. First, MRcML methods utilize an algorithm similar to the best subset selection to identify the optimal subset of pleiotropic variants. This involves performing MVMR iteratively by considering numbers of pleiotropic variants ranging from 1 to $K$ (defaulting to $m/2$), and determining the optimal number based on the BIC criteria. In contrast, MRBEE automatically detects pleiotropic variants using a hypothesis test, and MR-Lasso utilizes lasso for pleiotropic variant selection, both of which are computationally efficient. Second, MRcML-DP relies on permutations to derive the SE, which further increases computational burden. Conversely, MRBEE uses the sandwich formula to estimate its SE, which appears to be accurate in our simulations (Equation 19 in material and methods).

Figure 4.

Comparison of computation efficiency of the seven MVMR methods

This figure depicts the average computation time of the seven methods over 500 simulations.

Real data analysis

Data sources

To demonstrate the MRBEE performance in real data analysis, we analyzed three outcomes, including myopia, SCZ, and CAD. Myopia is known to be influenced by a combination of genetic and environmental factors, including educational attainment (EDU), near-work activity, and outdoor activities³⁰ but their direct causality to myopia is not clear. In this MVMR analysis, we considered refractive error, the measure of myopia degree, as the outcome. The exposures include EDU, near-work activity measured by time spent watching TV and playing on the computer (TV and Computer), and outdoor activity measured by time spent driving (Driving).

Attention-deficit/hyperactivity disorder (ADHD), cannabis use disorder (CAN), EDU, intelligence (INT), left-handedness (LH), intelligence (INT), neuroticism (SESA), and sleep duration (SLP) have been reported as risk factors for SCZ. Of these risk factors, CAN arguably has the strongest evidence of causality with respect to SCZ, with studies reporting dose-response³¹ and strong temporal³² relationships for at-risk individuals. The direct causality of the risk factors on SCZ is also not clear.

Many studies have been published to understand the causal effects of risk factors on CAD. However, the findings in these studies have been inconsistent. For instance, Holmes et al. and Lin et al.^20,33 found that HDL-C is not significant, while Zhu et al.,⁷ using the GWAS summary data with a much larger sample size (1.3M vs. 90K), found it to be significant. Besides, Wang et al.²¹ found that low-density lipoprotein cholesterol (LDL-C) is not significant in European populations, which seems unreasonable. In this data analysis, we investigated the causal relationships of these risk factors on CAD using the GWAS summary data with the largest sample sizes to date. We focus on the same eight factors studied in Lin et al.,²⁰ i.e., body mass index (BMI), DBP, fasting plasma glucose (FPG), height, HDL-C, LDL-C, triglycerides (TG), and SBP.

Data preprocessing

For UVMR, we applied the C + T procedure with the linkage disequilibrium (LD) parameter $r^2<0.01$ in $\pm 500$ Kb window to SNPs with association p value at least as small as 5E−5. We performed this operation for each exposure separately and used the 1000 Genomes project (phase 3) data as the LD reference panel.³⁴ For MVMR, we initially considered the union set of all exposure-specific IV sets from UVMR, then restricted this set to only include SNPs with a joint ${\chi }^2$-test p value reaching genome-wide significance and again passing C + T using the same parameters as before. The joint ${\chi }^2$-test for the exposures is presented in Equation 22 in material and methods and is used to assess the null hypothesis that an SNP is not associated with any exposure. We additionally standardized the GWAS effect size estimates so that their SEs were the inverse of the sample sizes. This procedure leads to comparable causal effect estimates across different exposures. We used false discovery rate (FDR) correction in MRBEE to identify and remove SNPs with evidence of horizontal pleiotropy (see Algorithm 1).

Algorithm 1. Pseudo-code of MRBEE + pleiotropy test.

• 1. Input: Initial estimates ${\hat{\theta }}^{\left(0\right)}$, Bias-correction terms ${\hat{\mathrm{\Sigma }}}_{W_{\beta }{W}_{\beta }}$ and ${\hat{\sigma }}_{W_{\beta }{w}_{\alpha }}$, $S_{\text{pleio}}$, FDR q-value threshold $\kappa$, Tolerance $ϵ$, Full set of $m^{\ast }$ IVs

• 2. Output: Causal effect estimates ${\hat{\theta }}_{\text{BEE}}$, Set of $m$ non-UHP/CHP IVs ${\mathcal{F}}_{\Theta }$

• 3. Pseudo-code:

  • Initialize ${\mathcal{F}}_{\Theta }^{\left(0\right)}=\left\{j:j=1,...,m^{\ast }\right\}$
  • While${\Vert {\hat{\theta }}^{\left(t+1\right)}-{\hat{\theta }}^{\left(t\right)}\Vert }_2>ϵ$

    • 1. Calculate $S_{{\text{pleio}}_j}^{\left(t\right)}\left({\hat{\theta }}^{\left(t\right)}\right)$ for all $j=1,...,m^{\ast }$,
    • 2. Update ${\mathcal{F}}_{\Theta }^{\left(t+1\right)}=\left\{j:S_{{\text{pleio}}_j}^{\left(t\right)}\left({\hat{\theta }}^{\left(t\right)}\right)<F_{{\chi }_1^2}^{-1}\left(1-\kappa \right)\right\}$,
    • 3. Update ${\hat{\theta }}^{\left(t+1\right)}$ using Equation 14 and IVs in ${\mathcal{F}}_{\Theta }^{\left(t+1\right)}$
  • End While

Table 1 summarizes the information of GWAS data in this study. In Table 1, the last three columns present the SNP heritability estimated by the LD score regression (LDSC),³⁵ the variances explained by the IVs in UVMR, and the variances explained by the IVs in MVMR. It is evident that for the trait with lower heritability and small sample sizes, the UVMR IVs account for about 1% of its SNP heritability, which may reduce power to detect causal effects using UVMR. However, for most traits, IVs in MVMR analyses explain a substantial portion of the variance, which will provide good power to detect causal effects. This is because the standard error of causal estimate(s) is inversely proportional to the variance(s) explained by the IVs. The last column of Table 1 shows the reliability ratios, a measure of IV strength, for exposures used in real data analysis. The estimation errors averagely account for ∼20% variance of the GWAS effect estimates.

Table 1.

Summary of GWAS data used in real data analyses

	Trait	Source	Sample size	Significant IVs	LDSC heritability	UVMR variancea	MVMR varianceb	Reliability ratioc
Myopia	Driving	van De Vegte etal. 54	422K	4	0.0365	0.00034	0.00400	0.705
	Playing computer	Arns et al. 55	422K	46	0.0719	0.00408	0.01154	0.873
	Watching TV	Rustad et al. 56	422K	189	0.1321	0.01788	0.02775	0.943
	EDU	Okbay et al. 57	765K	656	0.1352	0.03954	0.03683	0.976
	Joint 4 test			707
	Refractive error	Hysi et al. 58	246K	420	0.2702	0.11079	0.01433	0.838
Schizophrenia	ADHD	Demontis et al. 59	55K	12	0.0956	0.00279	0.01871	0.832
	CAN	Johnson et al. 60	384K	5	0.0174	0.00033	0.00272	0.552
	EDU	Okbay et al.57	765K	656	0.1222	0.03954	0.03728	0.973
	Intelligence	Neale’s Lab	430K	48	0.2326	0.01527	0.06023	0.900
	Left handedness	Cuellar-Partida et al. 61	205K	4	0.0338	0.00086	0.00533	0.576
	Neuroticism (SESA)	Nagel et al. 62	450K	42	0.0800	0.00476	0.01056	0.825
	Sleep duration	Dashti et al. 63	493K	66	0.0649	0.00589	0.00998	0.850
	Joint 7 test			1,227
	SCZ	Trubetskoy et al.64	320K	287	0.3380	0.06378	0.03570	0.855
Coronary artery disease	BMI	Loh et al. 65	458K	882	0.2076	0.09494	0.10612	0.918
	DBP	Evangelou et al. 66+MVP	1.00M	942	0.1095	0.06022	0.04525	0.823
	FPG	Neale’s Lab	361K	115	0.0848	0.03729	0.05156	0.789
	Height	Loh et al. 65	458K	2,728	0.6023	0.48986	0.49156	0.981
	HDL-C	Graham et al. 67	1.32M	1,031	0.1779	0.09207	0.09745	0.965
	LDL-C	Graham et al. 67	1.32M	754	0.1293	0.08435	0.08713	0.961
	TG	Graham et al. 67	1.32M	900	0.1251	0.07298	0.08105	0.959
	SBP	Evangelou et al. 66+MVP	1.00M	895	0.1152	0.05626	0.04550	0.829
	Joint 8 test			4,336
	CAD	Aragam et al.68+MVP	1.45M	343	0.0500	0.01610	0.01712	0.850

^aVariance explained by the IVs in UVMR analysis.

^bVariance explained by the IVs in MVMR analysis.

^cReliability ratios of exposures in MVMR analysis.

Myopia

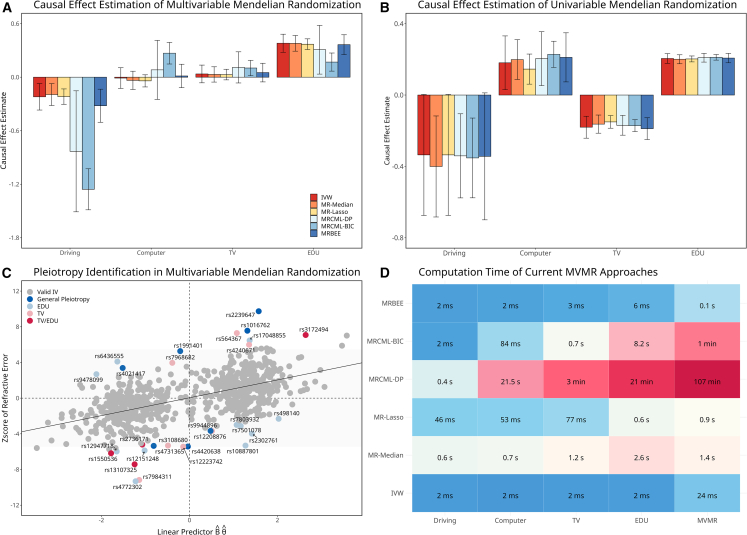
All the MVMR methods consistently showed that EDU (MRBEE p = 9.3E−21) and Driving (p = 3.8E−11) are directly causal on myopia, but not TV (p = 0.136) or Computer (p = 0.972) (Figure 5A). The no direct causal effect of TV or Computer on myopia risk although all exposures were observed to have significant causal effects on myopia in the UVMR analysis (Figure 5B). The insignificance of both TV and Computer in MVMR analysis suggests their correlations with myopia could be attributed to the confounding with EDU and Driving time. MRBEE provided larger protective causal estimate of driving time than that by IVW (i.e., MRBEE odds ratio [OR] = 0.71 vs. IVW OR = 0.84), likely due to a correction for weak instrument bias given that the driving time variance explained by the IVs was less than 1%. The causal effect of driving time estimated by MRcML-BIC and MRcML-DP was 3–5 times larger in magnitude than those from other methods. (MRcML-BIC OR = 0.38 and MRcML-DP OR = 0.58, respectively). In the iterative pleiotropy test, we detected 31 IVs demonstrating pleiotropy of the exposures and myopia (Figure 5C). Figure 5D compares the computational efficiency of the MR methods. We observed that IVW was the fastest (<0.1 s), followed by MRBEE (0.1 s), MR-Lasso (0.9 s), MR-Median (1.4 s), MRcML-BIC (1 min), and MRcML-DP (107 min), which were consistent with the simulations.

Figure 5.

Myopia data analysis

(A) Causal effect estimates by the six MVMR methods. The corresponding 95% confidence interval shown as vertical error bars.

(B) Corresponding causal effect estimates by UVMR approaches. The corresponding 95% confidence interval shown as vertical error bars. The radius of the confidence interval equals $\sqrt{a}\times$ SE, where $a=F_{{\chi }^2}^{-1}\left(1-0.05/4,1\right)$, $F_{{\chi }^2}^{-1}\left(x,\text{df}\right)$ is the inverse cumulative distribution function of a ${\chi }^2$ distribution.

(C) Pleiotropy test where the x axis represents the linear predictor $\hat{B}{\hat{\theta }}_{\text{BEE}}$ and the y axis represents the corresponding standardized association with myopia from GWAS. The annotation of a pleiotropic variant is made if its pleiotropic test p value is < 5E−8. Only IVs are present in the figure.

(D) Computation times of the six comparing methods. Columns 1–4 represent computation time for UVMR of four exposures and the last column represents computation time for MVMR.

Schizophrenia

All MVMR methods consistently estimated that CAN (MRBEE p = 3.7E−8), EDU (p = 3.6E−15), INT (p = 7.7E−12), and SESA (p = 1.8E−7) have direct causal contributions on schizophrenia (Figure 6A). MRBEE, MR-Lasso, and MR-Median suggested that SLP (p = 3.4E−4) has direct causal contribution on schizophrenia but not MRcML-BIC or MRcML-DP. It is not clear why both MRcML-DP and MRcML-BIC failed to detect this causal contribution given our simulations suggest MRcML-BIC could be more powerful although with inflated type I error. A potential reason could be the instability of MRcML, which may converge to local maximum. However, this requires additional investigation. MRBEE suggested no direct causal effect of ADHD (p = 0.510) or LH (p = 0.096), possibly due to the relatively low exposure variance explained by the IV set (i.e., 0.018 for ADHD and 0.005 for LH). We observed relatively larger odds ratios of EDU and CAN for MRBEE than MR-Median, MR-Lasso, and IVW, but less than MRcML-DP and MRcML-BIC. In comparison, UVMR analyses by all methods suggested evidence of total causal effects of CAN (MRBEE p = 1.6E−4), INT (p = 3.2E−7), SESA (p = 2.0E−10), ADHD (p = 0.017), and SLP (p = 1.4E−4), but not EDU (p = 0.542) or LH (p = 0.716) (Figure 6B). We did not observe any IVs with evidence of horizontal pleiotropy at the Bonferroni-corrected p = 0.05 level (Figure 6C), suggesting that the genetic association of the IVs with SCZ are strictly mediated by the five significant exposures. Again, we observed similar computational efficient for these methods as before (Figure 6D).

Figure 6.

Data analysis of schizophrenia

(A) Causal effect estimates by the six MVMR methods. The corresponding 95% confidence interval shown as vertical error bars.

(B) Causal effect estimates by UVMR approaches. The corresponding 95% confidence interval shown as vertical error bars. The radius of the confidence interval equals $\sqrt{a}\times SE$ where $a=F_{{\chi }^2}^{-1}\left(1-0.05/7,1\right)$.

(C) Pleiotropy test where the x axis represents the linear predictor $\hat{B}{\hat{\theta }}_{\text{BEE}}$ and the y axis represents the standardized association of the IV with SCZ from GWAS.

(D) Computation times of the comparing methods. Columns 1–7 represent computation time for UVMR of seven exposures and the last column represents computation time for MVMR.

Coronary artery disease

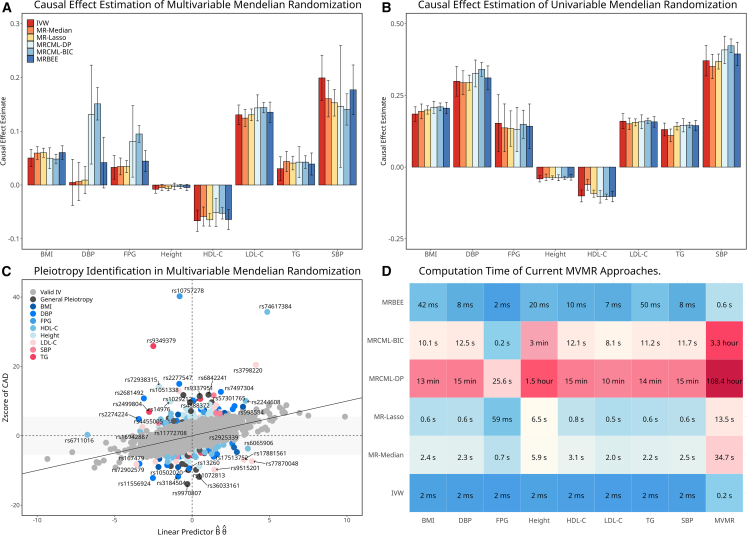
Figure 7A presents MVMR causal estimates for the effects of BMI, DBP, SBP, FPG, height, HDL-C, LDL-C, TG, and SBP on CAD. Using MRBEE, we identified the following significant direct causal effects on CAD, including BMI (MRBEE p = 3.8E−39), FPG (p = 6.7E−10), HDL-C (p = 8.4E−21), LDL-C (p = 1.5E−87), TG (p = 1.9E−7), and SBP (p = 1.1E−25). We observed that MRBEE estimates were generally consistent with estimates from IVW, MR-Median, and MR-Lasso. Conversely, MRcML-BIC and MRcML-DP estimates diverged from all other methods for DBP and FPG. For example, MRcML-DP/BIC were the only methods that simultaneously produced significant causal effects for SBP (p = 1.6E−39) and DBP (p = 1.8E−45) on CAD, two traits that are highly genetically correlated. In comparison, UVMR analyses by all methods consistently suggested that all the exposures have causal contributions on CAD (Figure 7B). We also observed 173 IVs demonstrating horizontal pleiotropy by the horizontal pleiotropy test in MVMR (Figure 7C). Again, our proposed MRBEE is computationally efficient (Figure 7D).

Figure 7.

Data analysis of coronary artery disease

(A) Causal effect estimates by the six MVMR methods. The corresponding 95% confidence interval shown as vertical error bars.

(B) Causal effect estimates by UVMR approaches. The corresponding 95% confidence interval shown as vertical error bars. The radius of the confidence interval equals $\sqrt{a}\times$ SE where $a=F_{{\chi }^2}^{-1}\left(1-0.05/8,1\right)$.

(C) Pleiotropy test where the x axis represents the linear predictor $\hat{B}{\hat{\theta }}_{\text{BEE}}$ and the y axis represents the standardized association between the IV and CAD from GWAS. The annotation of this pleiotropic variant is made if it is associated with the most significant exposures with p < 5E−8.

(D) Computation times of the comparing methods. Columns 1–8 represent computation time for UVMR of eight exposures and the last column represents computation time for MVMR.

Pleiotropic variants detected by GWPT

GWPT uses the $S_{\text{pleio}}$ statistic (Equation 21 in materials and methods) to test whether a genetic variant is associated with the outcome phenotype strictly through the mediation of a select group of exposures. In our GWPT analyses, these groups of exposures are those that were used in each MVMR. This test can be used to find these outcome-associated loci¹⁶ that do not reach the level of genome-wide significance in the original outcome phenotype GWAS but are genome-wide significant in GWPT. In these regions, it is possible that the local genetic correlations between the exposures and outcome are of different sign or magnitude than the genome-wide genetic correlations.³⁶ To ensure that the loci identified in GWPT were not primarily influenced by other exposures, we excluded any loci that showed even a marginal association with any of the exposures at a genome-wide significance level (i.e., p < 5E−8). We also compared GWPT with cross-phenotype association analysis (CPASSOC),³⁷ multi-trait analysis of GWAS (MTAG),³⁸ which are joint tests of association between all exposures in the outcome.

Table 2 lists the variants detected by GWPT for myopia, SCZ, and CAD but missed in the original GWAS. For comparison, we listed the p values for association from the original outcome GWAS, cross-phenotype tests by CPASSOC and MTAG, and by GWPT, respectively. The GWPT identified 18 genome-wide significant loci for myopia, four for SCZ, and 20 for CAD, respectively. All these loci did not reach genome-wide significance level in the outcome GWASs, suggesting GWPT captures pleiotropic evidence and the standard GWAS does not. We also performed expression quantitative trait loci (eQTL) mapping for the identified loci using functional mapping of GWAS (FUMA GWAS).³⁹ Each SNP that tagged a locus had marginal evidence of association with the expression of a gene in that locus in at least one tissue, where association p values ranged from 3.3E−310 to 6.7E−5. This suggests that these loci may have functionally relevant consequences in their conferred risk for myopia, SCZ, or CAD.

Table 2.

Loci detection of GWPT and eQTL mapping of leading variant

	SNP information		Association test				eQTL mapping
	SNP	CHR:BP	GWAS	MTAG	CPASSOC	GWPT	Symbol	Tissue	Database	p
Myopia	rs55761633	1:20757820	9.9e−07	3.1e−05	5.6e−07	9.6e−09	CAMK2N1	Muscle Skeletal	GTEx/v8	3.9e−06
	rs2419964	2:124252256	1.3e−07	1.2e−05	2.6e−10	6.0e−10	NA	NA	NA	NA
	rs7602460	2:182261869	4.9e−07	9.2e−06	6.6e−07	3.2e−08	ITGA4	Blood	eQTLgen	2.0e−19
	rs61548163	2:184349492	9.2e−07	1.3e−05	3.3e−06	2.7e−08	NA	NA	NA	NA
	rs6764842	3:123106287	1.6e−06	NA	2.0e−07	3.1e−08	ADCY5	Artery Tibial	GTEx/v8	3.0e−17
	rs9761983	4:138482973	1.5e−07	NA	9.0e−06	4.4e−08	RP11-714L20.1	Cortex	GTEx/v8	2.2e−06
	rs2461726	6:166316838	5.1e−07	1.7e−05	1.2e−06	1.1e−08	SDIM1	Pituitary	GTEx/v7	2.8e−07
	rs12699288	7:11975557	3.8e−06	1.4e−04	3.4e−08	1.4e−08	THSD7A	Nerve Tibial	GTEx/v8	6.7e−05
	rs2970498	7:30478056	1.1e−07	1.8e−06	7.0e−06	3.1e−08	NOD1	Blood	eQTLgen	1.0e−07
	rs1532278	8:27466315	3.4e−07	1.1e−05	9.6e−07	6.7e−09	CLU	Eye	EyeGEx	1.1e−26
	rs7048915	9:4206388	1.0e−07	2.0e−06	6.2e−06	1.3e−08	NA	NA	NA	NA
	rs902997	10:105384262	1.9e−07	9.2e−07	1.2e−08	3.2e−09	USMG5	Blood	eQTLgen	3.0e−37
	rs17065719	13:44925021	4.3e−07	1.1e−05	2.6e−05	3.7e−08	SERP2	Blood	eQTLgen	7.7e−48
	rs1926715	13:111538590	8.6e−08	1.4e−05	2.4e−12	2.0e−09	ANKRD10	Eye	EyeGEx	3.0e−48
	rs7141076	14:67922172	9.2e−08	1.8e−05	5.7e−06	1.7e−08	TMEM229B	Pituitary	GTEx/v8	1.1e−08
	rs12889206	14:68769182	8.8e−08	1.5e−06	1.2e−06	3.9e−08	NA	NA	NA	NA
	rs7198357	16:67884619	2.5e−07	4.2e−06	2.1e−09	4.3e−09	DUS2	Blood	eQTLgen	3.3e−310
	rs35594082	16:84796864	8.5e−07	1.8e−05	1.8e−06	3.1e−08	USP10	Eye	EyeGEx	2.9e−09
Schizophrenia	rs17672204	5:74946518	1.1e−06	8.2e−06	1.9e−06	2.4e−08	COL4A3BP	Muscle Skeletal	GTEx/v8	5.8e−15
	rs79650876	3:187997616	1.7e−07	4.3e−08	4.5e−07	3.2e−08	AC022498.1	Blood	eQTLGen	5.7e−06
	rs2300921	3:185651001	8.0e−06	8.9e−06	4.9e−06	3.2e−08	TRA2B	Breast	GTEx/v8	1.8e−06
	rs7225476	17:78561603	8.2e−07	2.1e−06	7.0e−05	3.3e−08	RPTOR	Blood	eQTLGen	4.0e−89
Coronary artery disease	rs2045886	2:29010517	3.6e−07	4.6e−05	2.7e−21	7.7e−11	PPP1CB	Blood	eQTLGen	3.3e−310
	rs6727524	2:238570309	8.9e−07	6.3e−05	4.4e−09	2.8e−08	LRRFIP1	Blood	eQTLGen	3.4e−76
	rs1868217	3:98445534	2.1e−05	4.5e−04	1.3e−10	3.6e−08	ST3GAL6	Blood	eQTLGen	2.0e−30
	rs73070809	3:186885760	1.1e−07	NA	3.7e−07	1.0e−08	RPL39L	Adipose	GTEx/v8	4.0e−05
	rs12523133	5:86297919	8.5e−08	2.3e−05	3.2e−19	2.5e−10	RP11-72L22.1	Spinal Cord	GTEx/v8	6.6e−08
	rs6899197	5:111250597	8.8e−06	NA	1.2e−20	2.2e−09	EPB41L4A	Esophagus	GTEx/v8	5.0e−05
	rs13202921	6:41687366	3.3e−07	2.9e−06	1.8e−08	3.8e−08	CCDC77	Artery Coronary	GTEx/v7	4.9e−11
	rs2073533	7:14029739	1.1e−07	2.6e−05	5.2e−14	3.2e−11	NA	NA	NA	NA
	rs7822979	8:106468592	6.0e−08	NA	1.5e−08	1.6e−10	NA	NA	NA	NA
	rs4734881	8:106587829	7.8e−08	3.1e−05	5.3e−06	1.3e−10	ZFPM2	Esophagus	GTEx/v8	3.8e−08
	rs12375254	8:125054365	3.2e−07	4.0e−06	2.5e−04	1.0e−08	TRMT12	Blood	eQTLGen	4.3e−15
	rs12412313	10:134456762	2.4e−06	6.8e−03	2.7e−19	2.3e−10	INPP5A	Blood	eQTLGen	6.6e−13
	rs7113595	11:70236819	7.8e−07	2.2e−05	2.7e−08	2.4e−08	PPFIA1	Blood	eQTLGen	5.3e−305
	rs7315852	12:417633	3.0e−07	NA	7.7e−19	2.1e−11	CCDC77	Blood	eQTLGen	3.3e−310
	rs55893521	15:83955536	2.2e−07	1.7e−04	3.4e−20	2.9e−09	BTBD1	Brain	xQTLServer	3.4e−75
	rs12918327	16:30626616	6.8e−06	9.7e−04	2.8e−32	5.2e−10	STX4	Blood	eQTLgen	1.1e−85
	rs9958798	18:52769637	4.0e−06	NA	9.9e−10	4.2e−08	RP11-99A1.2	Testis	GTEx/v8	6.3e−08
	rs35496634	22:39147235	8.5e−06	1.2e−03	4.6e−17	3.4e−08	SUN2	Blood	eQTLGen	7.0e−79
	rs5757949	22:40820151	2.9e−06	9.3e−06	5.2e−15	3.8e−08	MKL1	Eye	EyeGEx	1.6e−07

Discussion

We proposed MRBEE to overcome the weak instrument, pleiotropy and sample overlap bias in MVMR analysis. We pointed out that weak instrument bias is essentially driven by measurement error of GWAS effect estimates, whose scale and bias direction are influenced by the degree of weakness of IVs and the GWAS sample overlap, respectively. An IV is not considered weak when the estimation error is negligible, which can be achieved with a sufficiently large GWAS sample size, no matter how large or small the effect size is. In genetics, Burgess et al.³ suggested using the F-statistics to define the strength of an IV, whereas we recommend the reliability ratio (material and methods, Equation 11), a commonly used statistic in measurement error analysis. Both metrics are equivalent and will be influenced by the GWAS sample size and the number of IVs, highlighting that the definition of a weak instrument is dynamic. MRBEE removes the measurement error bias by using an unbiased estimating function. Although this estimating function has a long history in the literature of measurement error analysis,⁴⁰ it has not been utilized to modify the current MVMR approaches.

Our simulations suggested that MRBEE in general leads to equal or less bias of causal effect estimate than the comparing methods when weak IVs, pleiotropy, and sample overlap are present (Figure 2). Similarly, MRBEE also has equal or better type I error control and statistical power than robust comparing methods (Figure 3). MRcML-DP and MRcML-BIC were robust to weak IVs and consistently yield unbiased causal effect estimates under the “no pleiotropy” case. However, in the presence of horizontal pleiotropy, our simulations suggested that MRcML methods may produce local minimizers in some specific scenarios in which horizontal pleiotropy was not completely removed. MRcML employs the best subset selection for detecting pleiotropy and the algorithm’s stability and time consumption could be a challenge,⁴¹ as we observed in our simulations. MRBEE uses an iterative pleiotropy test, whose reliability has been validated in MR-PRESSO and IMRP.

In the myopia analysis, our detected causal effects for outdoor activities are consistent with the literature. For example, spending more time outdoors reducing incident myopia was confirmed by a randomized clinical trial.⁴² On the other hand, near-work activities such as time spent watching TV or using the computer have not been found to be associated with myopia risk.⁴³ The potential biological mechanism is that outdoor activities increase the exposure time to natural light, which induces the release of dopamine and thereby inhibits axial elongation, thus suppressing the development of myopia.³⁰ Moreover, MRBEE yields a relatively large causal estimate for time spent driving, likely correcting for weak instrument bias given the small variation of driving time explained by the IVs. Although MRcML-DP and MRcML-BIC can effectively reduce weak instrument bias in simulations, their estimates for the effects of driving time were 3–5 times larger than those from other methods.

We observed that cannabis use disorder and education have substantially larger causal effects on SCZ than other exposures we examined. For LH, the current GWAS has identified four genome-wide significant IVs together explaining its 0.086% variation. As a result, we did not have sufficient power to confirm their causal effect due to its relatively smaller variance of LH explained by IVs. MRBEE did not identify pleiotropic variants in these data, suggesting that our study may already include most of the direct causal risk factors for SCZ.

Our MVMR analysis seems to suggest that HDL-C is likely a protective factor against CAD but with a weaker effect size than that from UVMR analysis, aligning with recent pharmaceutical trial outcomes.⁴⁴ The previously observed negative results^20,33 are likely because they did not utilize the lipid GWAS summary data with the largest available sample sizes. When using the largest GWAS summary statistics of CAD as in this study, all methods including IVW, MRcML-DP, and MRBEE resulted in significant protective causal effect of HDL-C on CAD (Figure 7A). We noted that the estimated equal contributions of DBP and SBP on CAD risk by MRcML-BIC and MRcML-DP, which is in direct conflict with all other MR methods we tested and the literature.⁴⁵ In addition, MRBEE identified 173 pleiotropic IVs, one of which (rs10757278) is strongly associated with CAD (p < 5E−300) but whose biological mechanism warrants for further investigation.

We introduced the GWPT using the statistic $S_{\text{pleio}}$, which can be applied in UVMR or MVMR to identify specific IVs with evidence of horizontal pleiotropy. When $S_{\text{pleio}}$ was applied to the whole genome, we identified genetic loci associated with myopia, SCZ, and CAD that were missed in their original GWAS. These loci also reflect their direct association with the outcomes or through exposures not included in this study. Genes in these loci had genome-wide significant eQTLs across a range of tissues, suggesting that these genes might be functionally relevant in modifying disease risk. For example, we identified the RPTOR gene for SCZ, which has previously been found to be associated with BMI⁴⁶ and blood pressure.⁴⁷ This gene also has significant eQTLs (smallest p = 4E−89) in blood tissue. This and other examples highlight the potential utility of $S_{\text{pleio}}$ in identifying trait-associated loci and functionally relevant genes.

In our theoretical study (supplement 2), we consider the effect size of IVs to follow a normal distribution, representing a genomic random effect model.⁴⁸ We observed that increasing the sample size of GWAS often yields more novel loci, hence more IVs with non-zero effects can be used in a corresponding MR analysis. Therefore, in our theoretical investigation, we allow the number of IVs $m$ to increase with the sample size $n$ and examine the outcomes of MRBEE and MV-IVW under different rates of $m$ and $n$. Our conclusion can be summarized as follows: for scenarios like those in our myopia and CAD data, where GWAS sample sizes for exposures are approximately half a million or more, MRBEE and MV-IVW are equally efficient (supplement 2, Theorem 1.3 (i)). In this case, MRBEE’s inference is asymptotically valid, whereas MV-IVW may lead to incorrect inferences. For the SCZ data involving CUD, with GWAS sample sizes in the tens of thousands, MRBEE is less efficient than MV-IVW, but the inference made by MRBEE remains valid (supplement 2, Theorem 1.3 (ii)-(iii)). In these cases, the confidence intervals of MRBEE will be wider than MV-IVW but ensure the 95% coverage frequency. Although MRBEE can remove the weak instrument bias in general, we still recommend including the IVs with the association p values below a significance threshold. The reason is that weak IVs still require to be truly associated with an exposure although their effect sizes can be extremely small. Variants with the association p values above the threshold are likely to be false positive and including false positive IVs will lead to bias for MRBEE because of the violation of assumption (IV1). The purpose of developing MRBEE is to enhance existing methods, making causal effect estimation and inference more robust to weak IVs.

The comparison between MRBEE and MRcML in terms of statistical principle is as follows. MRBEE employs the unbiased estimating function method which constructs its unbiased score function from the score function of the MV-IVW method. In contrast, the MRcML method is a conditional score function method, characterized by first estimating the sufficient statistic containing parameters to be estimated and then estimating the parameter based on this sufficient statistic through an iterative method.⁴⁰ Although Stefanski and Carroll²⁴ demonstrated that the conditional score function possesses statistical efficiency, whether this conclusion can be directly applied to the MRcML method requires further investigation. In contrast, our investigation shows that MRBEE reaches statistical efficiency if $m/n_{\mathit{min}}\to 0$ where $n_{\mathit{min}}$ is the minimum GWAS sample size (supplement 2, Theorem 1.3 (i)). Furthermore, our simulations in Section S1.3 of supplement 1 suggest that MRcML-DP tends to overestimate its SD (i.e., SE > SD), MRcML-BIC underestimates its SD (i.e., SE < SD), and MRBEE estimates its SD well in most cases, suggesting MRBEE can achieve more efficiency than MRcML. The exact reason that MRcML does not estimate SD well warrants further investigation.

MRBEE also has some limitations. MRBEE is ineffective in handling exposures associated with significantly weaker IVs, such as CUD and LH in the SCZ data. This is also a challenge inherited from the field of measurement error analysis. In this case, MRBEE and analogous methods such as MRcML tend to produce causal effect estimates with relatively large SE. MRBEE is effective when the proportion of pleiotropic variants is relatively low (e.g., below 30%). Incorporating a Gaussian mixture model with MRBEE might improve the robustness for scenarios with a high proportion of pleiotropic variants. Finally, MRBEE is designed to handle a fixed number of exposures. Expanding its capability to a high-dimensional MR model is warranted in future research.⁴⁹

Last, it is worth offering guidance on how to perform MVMR analysis from our perspective. First, rather than selecting the optimal number of IVs such that the F-statistics and conditional F-statistics are larger than 10,^3,22 we suggest including all independent IVs that are genome-wide significantly associated with at least one exposure. The main purpose of doing this is to reduce the winner’s curse. Our simulations found that all methods, including MRBEE, were affected by the winner’s curse, and the only way to alleviate the winner’s curse was to include as many causal variants as possible (supplement 1, and Figure S10). Besides, our theory (supplement 2, Theorem 1.2 and 1.3) illustrates that the asymptotic variance of a causal effect estimate is related to the cumulative variance explained by all specified IVs instead of the average variance explained by each IV. Hence, including more IVs in the MR model can reduce the variance of the related causal effect estimate. Second, when performing MVMR analysis, it is not necessary to remove variants that are pleiotropic between the exposures. The reason why Wang et al.²¹ found that LDL-C was not significant in European populations is likely caused by this procedure. In contrast, simultaneously including all the relevant exposures and their IVs is recommended because the multivariable regression can automatically account for the pleiotropic variants shared by the specified exposures. Third, we suggest conducting a GWPT after performing the MR analysis, which represents an effective multi-trait approach for discovering loci with pleiotropy effect, beyond current methods such as CPASSOC and MTAG. In statistical principle, GWPT is likely to identify new loci associated with the outcome if the effect directions of pleiotropy and exposure mediation are opposite in these genome regions.

During the revision of this manuscript, we noted that a recent preprint⁵³ claimed that MRBEE was biased with extremely large SD and SE for some of simulation scenarios. We observed that the reason was that the authors of the preprint did not perform the standardization for the instrument effects of both exposures and outcome, which was documented in in the MRBEE software. We present the reproduction of Table 1 in the preprint before and after the standardization in Table S25 in supplement 1. The result indicates MRBEE has reasonable SD and SE. We have updated MRBEE software on GitHub and it does not need the standardization now.

Material and methods

MR model

We describe MRBEE with details here. As in the main text, let ${\mathbf{g}}_i={\left(g_{i1},\dots ,g_{im}\right)}^{\top }$ be a vector of $m$ independent genetic variants where each variant is standardized with mean zero and variance one, ${\mathbf{x}}_i={\left(x_{i1},\dots ,x_{ip}\right)}^{\top }$ be a vector of $p$ exposures, and $y_i$ be an outcome. Consider the following linear structural model:

$${\mathbf{x}}_i={\mathbf{B}}^{\top }{\mathbf{g}}_i+{\mathbf{u}}_i\text{,}$$ (Equation 1)

$$y_i={\theta }^{\top }{\mathbf{x}}_i+{\gamma }^{\top }{\mathbf{g}}_i+v_i\text{,}$$ (Equation 2)

where $\mathbf{B}={\left({\beta }_1,\dots ,{\beta }_m\right)}^{\top }$ is an $\left(m\times p\right)$ matrix of genetic effects on exposures with ${\beta }_j={\left({\beta }_{j1},\dots ,{\beta }_{jp}\right)}^{\top }$ being a vector of length $p$, $\theta ={\left({\theta }_1,\dots ,{\theta }_p\right)}^{\top }$ is a vector of length $p$ representing the causal effects of the $p$ exposures on the outcome, $\gamma ={\left({\gamma }_1,\dots ,{\gamma }_m\right)}^{\top }$ is a vector of length $m$ representing horizontal pleiotropy, which may violate the (IV2) or (IV3) conditions, and ${\mathbf{u}}_i$ and $v_i$ are noise terms. Substituting for ${\mathbf{x}}_i$ in (2), we obtain the reduced-form model:

$$\begin{array}{r}{y}_i={\mathbf{g}}_i^{\top }\alpha +{\mathbf{u}}_i^{\top }\theta +v_i\text{,}\end{array}$$ (Equation 3)

where

$$\begin{array}{r}\alpha =\mathbf{B}\mathbf{\theta }+\gamma \text{.}\end{array}$$ (Equation 4)

In practice, ${\mathbf{u}}_i$ and $v_i$ are usually correlated, and hence traditional linear regression between ${\mathbf{x}}_i$ and $y_i$ cannot obtain a consistent estimate of $\theta$. In contrast, the genetic variant vector ${\mathbf{g}}_i$ is assumed to be independent of the noise terms ${\mathbf{u}}_i$ and $v_i$ because the genotypes of individuals are randomly inherited from their parents and do not change during their lifetime.⁵⁰ Hence, ${\mathbf{g}}_i$ can be used as IVs to remove the confounding effect of ${\mathbf{u}}_i$ and $v_i$.

We assume that the genetic effect ${\beta }_j$ ($j=1,\dots ,m$) is a $p$-dimensional random vector with zero-mean, covariance matrix ${\mathrm{\Sigma }}_{\beta \beta }$, and cumulative covariance matrix ${\mathrm{\Psi }}_{\beta \beta }$:

$$\begin{array}{r}{\mathrm{\Sigma }}_{\beta \beta }=\mathrm{E}\left({\beta }_j{\beta }_j^{\top }\right),{\mathrm{\Psi }}_{\beta \beta }=m{\mathrm{\Sigma }}_{\beta \beta }\text{.}\end{array}$$

The covariance matrix ${\mathrm{\Sigma }}_{\beta \beta }$ will vanish as $m\to \infty$, but the cumulative covariance matrix ${\mathrm{\Psi }}_{\beta \beta }$ is still a constant matrix, representing the total genetic covariance contributed from the $m$ IVs. The genetic variant $g_{ij}$ ($i=1,\dots ,n$, $j=1,\dots ,m$) is standardized so that $\mathrm{E}\left(g_{ij}\right)=0$ and $\text{var}\left(g_{ij}\right)=1$, and all IVs are assumed to be in linkage equilibrium (LE), i.e., cov $\left(g_{ij},g_{ik}\right)=0$ for $j\ne k$. Next, the noise terms ${\mathbf{u}}_i$ and $v_j$ have zero-means and joint covariance matrix:

$$\begin{array}{r}{\mathrm{\Sigma }}_{u\times v}=\text{cov}\left({\left({\mathbf{u}}_i^{\top },v_j\right)}^{\top }\right)=\left(\begin{array}{cc}{\mathrm{\Sigma }}_{uu}& {\sigma }_{uv}\\ {\sigma }_{uv}^{\top }& {\sigma }_{vv}\end{array}\right)\text{.}\end{array}$$

Thus, the exposure ${\mathbf{x}}_i$ and outcome $y_i$ have zero-means and joint covariance matrix:

$$\begin{array}{r}{\mathrm{\Sigma }}_{x\times y}=\text{cov}\left({\left({\mathbf{x}}_i^{\top },y_j\right)}^{\top }\right)=\left(\begin{array}{cc}{\mathrm{\Sigma }}_{xx}& {\sigma }_{xy}\\ {\sigma }_{xy}^{\top }& {\sigma }_{\text{yy}}\end{array}\right)\text{,}\end{array}$$

${\mathrm{\Sigma }}_{xx}={\mathrm{\Psi }}_{\beta \beta }+{\mathrm{\Sigma }}_{uu}$, ${\sigma }_{xy}={\mathrm{\Psi }}_{\beta \beta }\theta +{\mathrm{\Sigma }}_{uu}\theta +{\sigma }_{uv}$, and ${\sigma }_{yy}={\theta }^{\top }{\mathrm{\Psi }}_{\beta \beta }\theta +{\theta }^{\top }{\mathrm{\Sigma }}_{uu}\theta +2{\theta }^{\top }{\sigma }_{uv}+{\sigma }_{vv}$. Note that ${\sigma }_{uv}\ne \mathbf{0}$ means the confounders affect both ${\mathbf{x}}_i$ and $y_i$.

Bias of multivariable IVW estimate

Since large individual-level data from GWAS are less publicly available, most of the current MR analyses are performed with summary statistics of IVs through the following linear regression:

$$\begin{array}{r}{\hat{\alpha }}_j={\hat{\beta }}_j^{\top }\theta +{\gamma }_j+{\epsilon }_j\text{,}\end{array}$$ (Equation 5)

where ${\hat{\alpha }}_j$ and ${\hat{\beta }}_j$ are respectively estimated from the outcome and exposure GWASs, ${\gamma }_j$ is the horizontal pleiotropy, ${\epsilon }_j$ represents the residual of this regression model, and $j=1,\dots ,m$ referring to the $m$ IVs. MV-IVW, which is the foundation of most existing MR methods, estimates $\theta$ by

$$\begin{array}{r}{\hat{\theta }}_{\text{IVW}}=\arg \underset{\theta }{\min }\left\{{\left(\hat{\alpha }-\hat{\mathbf{B}}\theta \right)}^{\top }{\mathbf{V}}^{-1}\left(\hat{\alpha }-\hat{\mathbf{B}}\theta \right)\right\}={\left({\hat{\mathbf{B}}}^{\top }{\mathbf{V}}^{-1}\hat{\mathbf{B}}\right)}^{-1}{\hat{\mathbf{B}}}^{\top }{\mathbf{V}}^{-1}\hat{\alpha }\end{array}\text{,}$$ (Equation 6)

where $\mathbf{V}$ is a diagonal matrix consisting of the variance of estimation errors of $\hat{\alpha }$. In practice, it is routine to standardize ${\hat{\alpha }}_j$ and ${\hat{\beta }}_{jk}$ by ${\hat{\alpha }}_j/\text{se}\left({\hat{\alpha }}_j\right)$ and ${\hat{\beta }}_{js}/\text{se}\left({\hat{\beta }}_{jk}\right)$ to remove the minor allele frequency effect.¹⁶ With this standardization, the MV-IVW estimates $\theta$ by

$$\begin{array}{c}{\hat{\theta }}_{\text{IVW}}=\arg \underset{\theta }{\min }\left\{{\Vert \hat{\alpha }-\hat{\mathit{B}}\theta \Vert }_2^2\right\}={\left({\hat{\mathbf{B}}}^{\top }\hat{\mathbf{B}}\right)}^{-1}{\hat{\mathbf{B}}}^{\top }\hat{\alpha }\text{.}\end{array}$$ (Equation 7)

However, the MV-IVW estimate ${\hat{\theta }}_{\text{IVW}}$ is biased due to the estimation errors of ${\hat{\alpha }}_j$ and ${\hat{\beta }}_j$:

$${\hat{\alpha }}_j={\alpha }_j+w_{{\alpha }_j}\text{,}$$ (Equation 8)

$${\hat{\beta }}_j={\beta }_j+{\mathbf{w}}_{{\beta }_j}\text{.}$$ (Equation 9)

To see this, observe the estimating equation and Hessian matrix of ${\hat{\theta }}_{\text{IVW}}$:

$$\begin{array}{r}{\mathbf{S}}_{\text{IVW}}\left(\theta \right)={\hat{\mathbf{B}}}^{\top }\left(\hat{\mathbf{B}}\theta -\hat{\alpha }\right),{\mathbf{H}}_{\text{IVW}}={\hat{\mathbf{B}}}^{\top }\hat{\mathbf{B}}\text{.}\end{array}$$

That is, ${\mathbf{S}}_{\text{IVW}}\left(\theta \right)$ is the score function of Equation 7 and ${\hat{\theta }}_{\text{IVW}}$ is estimated by solving ${\mathbf{S}}_{\text{IVW}}\left({\theta }_{\text{IVW}}\right)=\mathbf{0}$, and ${\mathrm{H}}_{\text{IVW}}$ is the 2nd derivative matrix of Equation 7. As shown in supplement 2, since ${\hat{\theta }}_{\text{IVW}}-\theta =-{\mathbf{H}}_{\text{IVW}}^{-1}{\mathbf{S}}_{\text{IVW}}\left(\theta \right)$ , the bias of ${\hat{\theta }}_{\text{IVW}}$ is approximately:

$$\begin{array}{c}\mathrm{E}\left({\hat{\theta }}_{\text{IVW}}-\theta \right)\approx -\mathrm{E}{\left({\mathbf{H}}_{\text{IVW}}\right)}^{-1}\mathrm{E}\left({\mathbf{S}}_{\text{IVW}}\left(\theta \right)\right)=-{\left\{{\Sigma }_{\beta \beta }+{\Sigma }_{W_{\beta }{W}_{\beta }}\right\}}^{-1}\left\{{\Sigma }_{W_{\beta }{W}_{\beta }}\theta -{\sigma }_{W_{\beta }{w}_{\alpha }}+{\sigma }_{\beta \gamma }\right\}\text{,}\end{array}$$ (Equation 10)

where

$$\text{cov}\left({\left({\mathbf{w}}_{{\beta }_j}^{\top },w_{{\alpha }_j}\right)}^{\top }\right)={\mathrm{\Sigma }}_{W_{\beta }\times w_{\alpha }}=\left(\begin{array}{cc}{\mathrm{\Sigma }}_{W_{\beta }{W}_{\beta }}& {\sigma }_{W_{\beta }{w}_{\alpha }}\\ {\sigma }_{W_{\beta }{w}_{\alpha }}^{\top }& {\sigma }_{w_{\alpha }{w}_{\alpha }}\end{array}\right),\text{cov}\left({\beta }_j,{\gamma }_j\right)={\sigma }_{\beta \gamma }\text{.}$$

Interpretation of weak instrument bias

Here, ${\mathrm{\Sigma }}_{\beta \beta }$ can be regarded as the average information carried by each IV, while ${\mathrm{\Sigma }}_{W_{\beta }{W}_{\beta }}$ can be regarded as the information carried by each estimation error. If ${\mathrm{\Sigma }}_{\beta \beta }$ is not substantially larger than ${\mathrm{\Sigma }}_{W_{\beta }{W}_{\beta }}$, then the weak instrument will inflate the measurement error bias by the multiplier ${\left({\mathrm{\Sigma }}_{\beta \beta }+{\mathrm{\Sigma }}_{W_{\beta }{W}_{\beta }}\right)}^{-1}$. This is the primary reason why violating assumption (IV1) introduces bias into causal effect estimates in IVW and other MR approaches.²⁶

The covariance between the estimation errors of SNP-exposure and SNP-outcome associations ${\sigma }_{W_{\beta }{w}_{\alpha }}$ can be affected by the fraction of overlapping samples of the exposures and outcome GWAS. If the exposures and outcome GWAS are independent of each other, then ${\sigma }_{W_{\beta }{w}_{\alpha }}=\mathbf{0}$ and hence the measurement error bias always shrinks ${\hat{\theta }}_{\text{IVW}}$ toward the null. In contrast, if the exposures GWAS and outcome GWAS are estimated from the same cohorts, ${\sigma }_{W_{\beta }{w}_{\alpha }}$ usually introduces bias toward the direction of ${\sigma }_{uv}$, reflecting the degree of sample overlap between exposures and outcome. This is the reason why in some empirical studies,^23,27 IVW cannot completely remove the confounding bias if the overlapping sample fraction is large.

If ${\sigma }_{\beta \gamma }\ne \mathbf{0}$, there is additional pleiotropy bias due to the horizontal pleiotropy that violates the InSIDE assumption. In UVMR, it is challenging to guarantee ${\gamma }_j=0$ or $\text{cov}\left({\gamma }_j,{\beta }_j\right)=\mathbf{0}$ for all $1\le j\le m$, resulting in a potentially biased IVW estimate. Traditional solutions to horizontal pleiotropy bias require that only a small proportion of IVs exhibit horizontally pleiotropic effects.^5,7,12 However, for complex traits, it is plausible that a large portion of IVs (even possibly $>50\%$) possess horizontally pleiotropic effects, leading to the failure of UVMR methods. MVMR can balance these pleiotropic effects shared by multiple exposures, significantly reducing the number of IVs with horizontal pleiotropy evidence when conditioned on specified exposures. In other words, it is more likely to guarantee that only few IVs violate the InSIDE assumption ${\sigma }_{\beta \gamma }=\mathbf{0}$ after accounting for multiple exposures, which can be then detected and removed using the robust tools such as a pleiotropy hypothesis test.

Reliability ratio

In practice, we suggest using the reliability ratio⁴⁰:

$$\begin{array}{c}{\omega }_k=\frac{\text{var}\left({\beta }_{jk}\right)}{\text{var}\left({\hat{\beta }}_{jk}\right)}\end{array}$$ (Equation 11)

to measure the degree of bias in ${\hat{\theta }}_{k,\text{IVW}}$, which can be empirically estimated by

$${\hat{\omega }}_k=\frac{\sum _{j=1}^m\left({\hat{\beta }}_{jk}^2-\text{var}\left(w_{{\beta }_{jk}}\right)\right)}{\sum _{j=1}^m{\hat{\beta }}_{jk}^2}\text{.}$$ (Equation 12)

${\hat{\omega }}_k$ reflects the proportion of variability in the estimated effects attributable to the underlying true genetic effects. For example, a reliability ratio of 0.6 indicates that 60% of the variance of the estimated effects is attributable to the true effects and the rest is attributable to their estimation errors. From the perspective of measurement error theory, the IVW estimate ${\hat{\theta }}_{\text{IVW}}$ converges to $\omega \theta$ in a univariable MR analysis when there is no sample overlap, where $\omega$ is equal to $\text{var}\left({\beta }_j\right)/\text{var}\left({\hat{\beta }}_j\right)\text{.}$⁴⁰ Here $\omega$ is less than 1 and is viewed as a shrinkage coefficient for ${\hat{\theta }}_{\text{IVW}}$ relative to the true effect $\theta$. We adopt this reliability ratio to much broader contexts, such as multivariable MR and sample overlap. In our real data analysis, we found this reliability ratio works reasonably well although additional investigation is warranted. While the reliability ratio and the F-statistics³ are similar, the former has a simpler calculation and can more clearly reflect the proportion of weak IV bias than the latter.

MR using bias-corrected estimating equation

We propose MRBEE, which estimates causal effects by solving a new unbiased estimating equation of causal effects. The unbiased estimating equation of $\theta$ is

$$\begin{array}{r}{\mathbf{S}}_{\text{BEE}}\left(\theta \right)={\mathbf{S}}_{\text{IVW}}\left(\theta \right)-m\left({\mathrm{\Sigma }}_{W_{\beta }{W}_{\beta }}\theta -{\sigma }_{W_{\beta }{w}_{\alpha }}\right),\end{array}$$ (Equation 13)

where ${\mathbf{S}}_{\text{IVW}}\left(\theta \right)=-{\hat{\mathbf{B}}}^{\top }\left(\hat{\alpha }-\hat{\mathbf{B}}\theta \right)$. Equation 13 states that the MRBEE estimating function is equal to the IVW estimating equation minus its bias. Unbiasedness of the MRBEE estimating equation implies unbiasedness of the MRBEE estimator. The solution ${\hat{\theta }}_{\text{BEE}}$ such that ${\mathbf{S}}_{\text{BEE}}\left({\hat{\theta }}_{\text{BEE}}\right)=\mathbf{0}$ is

$$\begin{array}{c}{\hat{\theta }}_{\text{BEE}}={\left({\hat{\mathbf{B}}}^{\top }\hat{\mathbf{B}}-m{\mathrm{\Sigma }}_{W_{\beta }{W}_{\beta }}\right)}^{-1}\left({\hat{\mathbf{B}}}^{\top }\hat{\alpha }-m{\sigma }_{W_{\beta }{w}_{\alpha }}\right).\end{array}$$ (Equation 14)

Note that unlike other optimizations such as generalized linear model in measurement error,⁴⁰ the Hessian matrix ${\mathbf{H}}_{\text{IVW}}={\hat{\mathbf{B}}}^{\top }\hat{\mathbf{B}}$ does not involve $\theta$ and hence ${\mathbf{S}}_{\text{BEE}}\left(\theta \right)$ can be directly obtained from ${\mathbf{S}}_{\text{IVW}}\left(\theta \right)$ without any iterative approximation.

Bias-correction terms estimation

We estimate the bias-correction terms ${\mathrm{\Sigma }}_{W_{\beta }{W}_{\beta }}$ and ${\sigma }_{W_{\beta }{w}_{\alpha }}$ from the insignificant and independent GWAS summary statistics.³⁷ Let ${\hat{\alpha }}_j^{\ast },{\hat{\beta }}_{j1}^{\ast },\dots ,{\hat{\beta }}_{jp}^{\ast }$ ($j=1,\dots ,M$) be $M$ insignificant GWAS effect size estimates of outcome and exposures, where the insignificance means that the $p$ value of the genetic variants are larger than 0.05 for all exposures and outcome, and the independence means that they are not in LD. Because ${\hat{\alpha }}_j^{\ast }$ and ${\hat{\beta }}_{jk}^{\ast }$ follow the same distributions of $w_{{\alpha }_j}$ and $w_{{\beta }_{jk}}$, ${\mathrm{\Sigma }}_{W_{\beta }\times w_{\alpha }}$ can be estimated by

$$\begin{array}{r}{\hat{\mathrm{\Sigma }}}_{W_{\beta }\times w_{\alpha }}=\frac{1}{M}\sum _{j=1}^M{\left({\hat{\beta }}_{j1}^{\ast },\dots ,{\hat{\beta }}_{jp}^{\ast },{\hat{\alpha }}_j^{\ast }\right)}^{\top }\left({\hat{\beta }}_{j1}^{\ast },\dots ,{\hat{\beta }}_{jp}^{\ast },{\hat{\alpha }}_j^{\ast }\right)\text{.}\end{array}$$ (Equation 15)

Here, ${\hat{\mathrm{\Sigma }}}_{W_{\beta }{W}_{\beta }}$ is the first $\left(p\times p\right)$ sub-matrix of ${\hat{\mathrm{\Sigma }}}_{W_{\beta }\times w_{\alpha }}$ and ${\hat{\sigma }}_{W_{\beta }{w}_{\alpha }}$ consists of the first $p$ elements of the last column of ${\hat{\mathrm{\Sigma }}}_{W_{\beta }\times w_{\alpha }}$. The intercept provided by LDSC³⁵ is also a consistent estimate of $\text{cov}\left(w_{{\alpha }_j},w_{{\beta }_{jk}}\right)$. Each of these two estimators may be used by MRBEE and experience with real data suggests that they generally produce similar results. LDSC requires specification of an LD reference panel that is from an ancestrally similar population to that under study in MR. Differences in genetic architecture between the LD reference panel and the MR study population could introduce bias. Use of Equation 15 does not require an LD reference panel and so will not be biased for this reason. Additionally, use of Equation 15 is computationally simpler.

SE estimation

The covariance matrix of ${\hat{\theta }}_{\text{BEE}}$ is yielded through the sandwich formula:

$$\begin{array}{r}\text{cov}\left({\hat{\theta }}_{\text{BEE}}\right)≔{\mathrm{\Sigma }}_{\text{BEE}}\left(\theta \right)={\mathrm{F}}_{\text{BEE}}^{-1}{\mathrm{V}}_{\text{BEE}}\left(\theta \right){\mathrm{F}}_{\text{BEE}}^{-1},\end{array}$$ (Equation 16)

where the outer matrix ${\mathrm{F}}_{\text{BEE}}$ is the Fisher information matrix, i.e., the expectation of the Hessian matrix of ${\mathbf{S}}_{\text{BEE}}\left(\theta \right)$, and the inner matrix ${\mathrm{V}}_{\text{BEE}}\left(\theta \right)$ is the covariance matrix of ${\mathbf{S}}_{\text{BEE}}\left(\theta \right)$. A consistent estimate of ${\mathrm{\Sigma }}_{\text{BEE}}\left(\theta \right)$ is

$$\begin{array}{r}{\hat{\mathrm{\Sigma }}}_{\text{BEE}}\left(\theta \right)={\hat{\mathrm{F}}}_{\text{BEE}}^{-1}{\hat{\mathrm{V}}}_{\text{BEE}}\left({\hat{\theta }}_{\text{BEE}}\right){\hat{\mathrm{F}}}_{\text{BEE}}^{-1}\text{,}\end{array}$$ (Equation 17)

where ${\hat{\mathrm{F}}}_{\text{BEE}}={\hat{\mathbf{B}}}^{\top }\hat{\mathbf{B}}-{\hat{\mathrm{\Sigma }}}_{W_{\beta }{W}_{\beta }},{\hat{\mathrm{V}}}_{\text{BEE}}\left({\hat{\theta }}_{\text{BEE}}\right)=\sum _{j=1}^m{\hat{\mathbf{S}}}_j\left({\hat{\theta }}_{\text{BEE}}\right){\hat{\mathbf{S}}}_j{\left({\hat{\theta }}_{\text{BEE}}\right)}^{\top }\text{,}$ and ${\hat{\mathbf{S}}}_j\left({\hat{\theta }}_{\text{BEE}}\right)=-\left({\hat{\alpha }}_j-{\hat{\theta }}_{\text{BEE}}^{\top }{\hat{\beta }}_j\right){\hat{\beta }}_j-{\hat{\mathrm{\Sigma }}}_{W_{\beta }{W}_{\beta }}{\hat{\theta }}_{\text{BEE}}+{\hat{\sigma }}_{W_{\beta }{w}_{\alpha }}\text{.}$

When the number of IVs $m$ is small, the standard sandwich formula has been observed to underestimate the SE.⁵¹ We apply the MD correction⁵² to solve this problem. Consider the so-called hat matrix:

$$\mathbf{H}=\hat{\mathbf{B}}{\left({\hat{\mathbf{B}}}^{\top }\hat{\mathbf{B}}-m{\hat{\mathrm{\Sigma }}}_{W_{\beta }{W}_{\beta }}\right)}^{-1}{\hat{\mathbf{B}}}^{\top }$$

and $H_{jj}$ is its $j$ th diagonal entries. The MD correction adjusts the inner matrix as

$${\hat{\mathrm{V}}}_{\text{BEE}}^{\text{MD}}\left({\hat{\theta }}_{\text{BEE}}\right)=\sum _{j=1}^m{\left(1-H_{jj}\right)}^{-2}{\hat{\mathbf{S}}}_j\left({\hat{\theta }}_{\text{BEE}}\right){\hat{\mathbf{S}}}_j{\left({\hat{\theta }}_{\text{BEE}}\right)}^{\top }\text{.}$$ (Equation 18)

Their theory shows that

$$\mathrm{E}\left({\hat{\mathbf{S}}}_j\left({\hat{\theta }}_{\text{BEE}}\right){\hat{\mathbf{S}}}_j{\left({\hat{\theta }}_{\text{BEE}}\right)}^{\top }\right)\approx {\left(1-H_{jj}\right)}^2{\mathrm{V}}_{\text{BEE}}\left(\theta \right)\text{,}$$

and hence it can obtain a more reliable covariance matrix by adjusting ${\left(1-H_{jj}\right)}^{-2}$ when estimating ${\mathrm{V}}_{\text{BEE}}\left(\theta \right)$ with the moment method. When there is horizontal pleiotropy, we adjust Equation 18 as

$${\hat{\mathrm{V}}}_{\text{BEE}}^{\text{MD}}\left({\hat{\theta }}_{\text{BEE}}\right)=\frac{m+m_{pleiotropy}}{m}\sum _{j=1}^m{\left(1-H_{jj}\right)}^{-2}{\hat{\mathbf{S}}}_j\left({\hat{\theta }}_{\text{BEE}}\right){\hat{\mathbf{S}}}_j{\left({\hat{\theta }}_{\text{BEE}}\right)}^{\top },$$ (Equation 19)

where $m$ is number of valid IVs and $m_{pleiotropy}$ is the number of detected pleiotropies. Section S1.3 of supplement 1 compares the estimated and true standard errors of causal effect estimates for MRBEE and other MVMR estimators. These results demonstrate that the MD correction described above controls the Type I error rate well. It is also worth noting that the standard errors of the MRBEE causal estimates will generally become smaller as the degree of weak instrument bias becomes smaller.

Horizontal pleiotropy detection

We illustrate how to remove specific IVs with evidence of UHP or CHP effects with the pleiotropy test $S_{\text{pleio}}$ which tests the same null hypothesis for each SNP as MR-PRESSO and IMRP. The null hypothesis for the $j$ th IV not having any horizontally pleiotropic effects on the outcome is

$$\begin{array}{r}{\mathbf{H}}_{\mathbf{0}\mathit{j}}:{\gamma }_j=0v.s.{\mathbf{H}}_{\mathbf{1}\mathit{j}}:{\gamma }_j\ne 0\text{.}\end{array}$$ (Equation 20)

The statistic $S_{\text{pleio}}$ for the $j$ th IV is defined as

$$\begin{array}{r}{S}_{{\text{pleio}}_j}\left(\hat{\theta }\right)=\frac{{\left({\hat{\alpha }}_j-{\hat{\beta }}_j^{\top }\hat{\theta }\right)}^2}{\text{var}\left({\hat{\alpha }}_j-{\hat{\beta }}_j^{\top }\hat{\theta }\right)}\text{,}\end{array}$$ (Equation 21)

which follows a ${\chi }_1^2$ distribution under ${\mathbf{H}}_{\mathbf{0}\mathit{j}}$. The only assumption here is that ${\hat{\alpha }}_j-{\hat{\beta }}_j^{\top }\hat{\theta }$ is asymptotically normal distributed. In fact, this test examines whether the outcome effect can be explained by the mediation effects through all exposures. In practice, we estimate $\mathrm{v}\text{ar}\left({\hat{\alpha }}_j-{\hat{\beta }}_j^{\top }\hat{\theta }\right)$ using the delta method:

$$\begin{array}{r}\widehat{\mathrm{v}\text{ar}}({\hat{\alpha }}_j-{\hat{\beta }}_j^{\top }\widehat{\theta )}={\sigma }_{w_{\alpha }}^2+{\hat{\theta }}^{\top }{\hat{\mathrm{\Sigma }}}_{W_{\beta }{W}_{\beta }}\hat{\theta }+{\hat{\beta }}_j^{\top }{\hat{\mathrm{\Sigma }}}_{\text{BEE}}{\hat{\beta }}_j-2{\hat{\theta }}^{\top }{\hat{\sigma }}_{W_{\beta }{w}_{\alpha }}\text{.}\end{array}$$

Other methods such as empirical variance and robust variance estimates of the residual can also be used here. We calculate $S_{\text{pleio}}$ for all candidate IVs and remove IVs with large $S_{\text{pleio}}$ values in an iterative manner. Algorithm 1 uses an FDR Q-value threshold to exclude IVs showing potential pleiotropy evidence. We suggest a threshold Q-value <0.05 in general. Additional simulation results presented in Section S2.5 of supplement 1 show that FDR correction generally performs well.

GWPT

Since $S_{\text{pleio}}$ tests a very general null hypothesis, we can also calculate $S_{\text{pleio}}$ for all SNPs across the genome after obtaining the causal effect estimates of $p$ exposures on the outcome. Results from these tests can be used to (1) find novel loci associated with the MR outcome and (2) draw inferences about pathways of genetic association with the MR outcome. Specifically, when an SNP has a negative effect on the exposure ${\mathit{\beta }}_{\mathit{j}}$ and a positive pleiotropic effect on the outcome ${\gamma }_j$, and simultaneously the causal effect $\mathit{\theta }$ is positive, then the total effect of this variant on the outcome ${\alpha }_j$ is canceled and hence cannot be detected in the outcome GWAS. In contrast, the pleiotropy test directly tests the effect ${\gamma }_j$ and therefore can detect novel loci. For example, Zhu et al.¹⁶ successfully detected many blood pressure loci missed previously by using this GWPT with IMRP as the estimator of the causal effect. The results indicated that most detected pleiotropic variants influenced SBP and DBP in opposite directions, providing support for the principle of the GWPT.

Joint ${\chi }^2$-test for IVs selection

We applied the joint ${\chi }^2$-test to select a set of IVs that are strongly associated with multiple exposures. Let ${\mathit{\beta }}_j={\left({\beta }_{j1},\dots ,{\beta }_{jp}\right)}^{\top }$ be the p-length vector of standardized associations between the jth SNP and the p exposures. We performed the following hypothesis test:

$${\mathbf{H}}_{0j}:{\beta }_{j1}=\cdots ={\beta }_{jp}=0,v.s.{\mathbf{H}}_{1j}:{\beta }_{j1}\ne 0,\text{or}\cdots \text{or}{\beta }_{jp}\ne 0\text{.}$$ (Equation 22)

The test statistic is

$$t_j={\hat{\beta }}_j^{\top }{\hat{\mathrm{\Sigma }}}_{W_{\beta }{W}_{\beta }}^{-1}{\hat{\beta }}_j\text{,}$$ (Equation 23)

which follows a ${\chi }_p^2$ distribution when the null hypothesis holds, where ${\hat{\mathrm{\Sigma }}}_{W_{\beta }{W}_{\beta }}$ is the estimated matrix of covariances between estimation errors. We only considered variants as IVs if they are genome-wide significant in the joint ${\chi }^2$-test.

Estimation of variance explained by instrument variables

Assume that we intend to estimate the SNP heritability of a trait $Y$ using a set of m IVs in the m-length vector $\mathbf{g}={\left(G_1,\dots ,G_m\right)}^{\top }$ with corresponding associations with $Y$ in the vector $\beta ={\left({\beta }_1,\dots ,{\beta }_m\right)}^{\top }$. If the variance of $Y$ is 1 and $E\left(G_j\right)=0$, we can estimate the variance in $Y$ explained by the m IVs using the following equation:

$$\begin{array}{c}{R}^2=\sum _{j=1}^{m}2{\hat{\beta }}_j^2{p}_j\left(1-p_j\right)\end{array}$$ (Equation 24)

where $p_j$ is the minor allele frequency of $G_j$. We used Equation 24 to produce the heritability estimates in Table 1.

Asymptotic results

We assume that both total number of IVs $m$ and the minimum sample size among the exposure and outcome GWAS $n_{\min }$ can approach infinity, while the number of exposures $p$ and the $p$-dimensional causal effect vector $\theta$ are fixed and bounded. Our goal is to identify the scenarios when MV-IVW outperforms MRBEE, when they perform equally well, and when MRBEE outperforms MV-IVW in terms of unbiased estimation of causal effects and the asymptotic validity of causal inference. We demonstrate the related theorems and the related regularity conditions and lemmas in supplement 2.

Data and code availability

The data referenced in this study can be accessed through the GWAS Catalog (https://www.ebi.ac.uk/gwas/home), with the corresponding GWAS summary data available for download in the “data availability” section of the respective papers. Some of the GWAS summary data are exclusive of the Million Veteran Program (MVP) summary results, which are available through dbGAP under the accession number phs001672.v3.p1.

The MRBEE R package generated during this study is available at https://github.com/noahlorinczcomi/MRBEE. Simulation codes generated during this study are available at https://github.com/harryyiheyang/MRBEE.Simulation.