Protocol to identify biomarkers in patients with post-COVID condition using multi-omics and machine learning analysis of human plasma

Summary

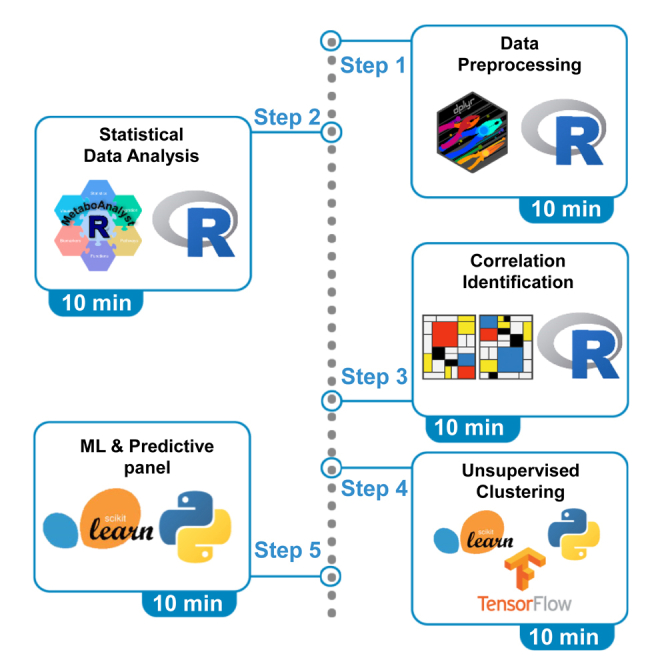
Here, we present a workflow for analyzing multi-omics data of plasma samples in patients with post-COVID condition (PCC). Applicable to various diseases, we outline steps for data preprocessing and integrating diverse assay datasets. Then, we detail statistical analysis to unveil plasma profile changes and identify biomarker-clinical variable associations. The last two steps discuss machine learning techniques for unsupervised clustering of patients based on their inherent molecular similarities and feature selection to identify predictive biomarkers.

For complete details on the use and execution of this protocol, please refer to Wang et al.¹

Graphical abstract

Highlights

• •Integrate and analyze multi-omics data
• •Statistical analysis of sequential data to identify diagnostic biomarkers
• •Identify inherent molecular similarities in study groups using unsupervised clustering
• •Employ linear classifier and feature selection to detect predictive biomarkers

Publisher’s note: Undertaking any experimental protocol requires adherence to local institutional guidelines for laboratory safety and ethics.

Here, we present a workflow for analyzing multi-omics data of plasma samples in patients with post-COVID condition (PCC). Applicable to various diseases, we outline steps for data preprocessing and integrating diverse assay datasets. Then, we detail statistical analysis to unveil plasma profile changes and identify biomarker-clinical variable associations. The last two steps discuss machine learning techniques for unsupervised clustering of patients based on their inherent molecular similarities and feature selection to identify predictive biomarkers.

Before you begin

Institutional permissions

This study was conducted under the ethical principles of the Declaration of Helsinki with approval from the University of Alberta Health Research Ethics Board (Pro00100319 and Pro00100207). Written and informed consent was obtained from all participants. We also remind the users of this protocol that they need to acquire permissions from relevant institutions to collect plasma samples and clinical information of their patients.

Hardware preparation

A computer with a MacOS or Windows operating system and network connection is required. The RAM requirement depends on the size of the datasets, the complexity of machine learning models, and the analysis pipeline. Since the machine learning models and analysis pipeline are moderate in this protocol, 16 GB RAM would be sufficient for small-to-moderate-size datasets. For larger datasets containing over 1000 samples and several thousands of features, 32 GB RAM may be required.

Software preparation

The applications described in this section are required to analyze multi-omics data.

• 1.
  Install R programming language.

  • a.
    Access R webpage (https://www.r-project.org) and install the latest version.
• 2.
  Install R studio.

  • a.
    Download the latest version of R Studio (https://posit.co/downloads) and install it.
• 3.
  Install Python programming language.

  • a.
    Access Python webpage (https://www.python.org) and install the latest version.
• 4.
  Install Visual Studio code (VS code).

  • a.
    Access VS code webpage (https://code.visualstudio.com) and install the latest version.

Note: Instead of installing the mentioned programming language, one can use web-based interactive computing platforms, such as Jupyter notebook or Google Colaboratory (Google Colab).

Dataset preparation

Prior to implementing the detailed protocol, it is necessary to convert raw output from omics platforms into concentration tables. These tables should have samples arranged in rows and may contain categorical features (such as study group, disease severity, clinical outcome) and numerical features (molecular concentrations) stored in columns in Excel or .csv files.

Note: The example datasets used in this protocol follow this arrangement and are provided in supplemental files.² (Data S1, S2, and S3).

Note: Raw output from omics platforms have also been deposited to online repositories (PeptideAtlas: PASS03810, MetaboLights: MTBLS7337).

Key resources table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Deposited data
Raw proteomics dataset	PeptideAtlas: PASS03810	https://peptideatlas.org/
Raw metabolomics dataset	MetaboLights: MTBLS7337	https://www.ebi.ac.uk/metabolights/
Supplemental files	Khoramjoo et al.2	https://data.mendeley.com/datasets/zyzt62gbrw/1
GitHub repository	Khoramjoo et al.3	https://github.com/MobinKhoramjoo/Biomarker-identification-by-multi-omics-analysis
Software and algorithms
R (v4.2.3)	The R Project for Statistical Computing4	https://www.r-project.org/
Python (v3.8.16)	Jupyter Notebook	https://www.python.org/doc/versions/
dplyr (v1.1.4)	Wickham et al.5	https://dplyr.tidyverse.org
ggplot2 (v3.4.4)	Wickham et al.6	https://ggplot2.tidyverse.org
MetaboAnalystR (v4.0)	Pang et al.7	https://github.com/xia-lab/MetaboAnalystR
ComplexHeatmap (v2.18.0)	Gu et al.8	https://doi.org/10.18129/B9.bioc.ComplexHeatmap
Circlize (v 4.1.2)	Gu et al.9	https://doi.org/10.1093/bioinformatics/btu393
Numpy	Harris et al.10	https://doi.org/10.1038/s41586-020-2649-2.
Pandas	The pandas development team11	https://doi.org/10.5281/zenodo.3509134
Matplotlib	Hunter et al.12	https://doi.org/10.1109/MCSE.2007.55
Scikit learn	Buitinck et al.13	https://doi.org/10.48550/arXiv.1309.0238
TensorFlow	TensorFlow Developers14	https://doi.org/10.5281/zenodo.10126399
Others
Computer with an operating system that can run software as listed above	https://code.visualstudio.com, https://posit.co/downloads	https://code.visualstudio.com, https://posit.co/downloads

Step-by-step method details

Herein, we describe essential steps to analyze the integrated omics datasets, from data binding to machine learning analysis. Python performs the last two steps: unsupervised clustering and feature selection.

Part 1: Data preprocessing

Timing: 10 min

Note: Missing values in omics data often arise because concentrations fall below the limit of detection for the molecule in the assay for a particular sample. Therefore, we adopt the approach of replacing remaining missing values with the minimum observed value for each corresponding molecule.

• 1.Load packages in R (troubleshooting 1).

>library(readxl)

>library(MetaboAnalystR)

>library(ComplexHeatmap)

>library(circlize)

>library(dplyr)

>library(ggplot2)

• 2.Import the datasets as data frames.

> cytokines <- read_excel(‘Data.xlsx', sheet = 'Cytokines')

> Proteins <- read_excel(‘Data.xlsx', sheet = 'Proteins')

> Metabolites <- read_excel(‘Data.xlsx', sheet = 'Metabolites')

Note: The file Data.xlsx contains all three raw concentration tables generated from omics platforms along with patients’ categories in three separate sheets (Data S1).

Note: If you are using your own dataset, you need to import them to RStudio environment as data frames.

• 3.Bind the datasets.

>n_protein = 5 #number of the first protein column in your data

>n_metabolite = 5 #number of the first metabolite column in your data

>Data <- cbind(cytokines,

        Proteins[n_protein:length(Proteins)],

        Metabolites[n_metabolite:length(Metabolites)])

Note: In all datasets, samples should be in rows and features (molecules) should be in columns.

Note: Make sure the order of samples in the datasets is identical.

• 4.Change the type of features (molecules) to numeric in the merged dataset.

>desc_cols = c(1:4) #number of the descriptive columns in the merged data

>n_first_mol = 5 #number of the first molecule column in the merged data

> Data <- cbind(Data[,desc_cols],

        as.data.frame(sapply(Data[,n_first_mol:length(Data)],

                    function (x) as.numeric(as.character(x)))))

Note: In this step, all the missing values which were annotated by texts or characters turn into “NA”s.

• 5.Change the zero values to “NA”s, as they are considered as missing values.

>sum(Data == 0, na.rm = TRUE)

>Data <- replace(Data, Data == 0, NA)

>sum(Data == 0, na.rm = TRUE) #Should return 0

• 6.Data cleaning: filtering the features based on percentage of their missing values.

>Transposed_Data <- as.data.frame(t(Data))

## missing value vector:

>p <-c()

>for (i in 1:nrow(Transposed_Data)) {

p[i] <- sum(is.na(Transposed_Data[i,]))/ncol(Transposed_Data)

}

#input the vector to the data

>Transposed_Data <- Transposed_Data %>%

    mutate(percent_of_missing_Values= p) %>%

    select(percent_of_missing_Values, everything())

#filter the data based on the generated column (percent of #missing values)

>missing_value_cut_off = 0.5

>filtered_Transposed_Data <- Transposed_Data %>%

    filter(percent_of_missing_Values < missing_value_cut_off)

##re-transpose the data:

>cleaned_data <- as.data.frame(t(filtered_Transposed_Data))

>cleaned_data <- cleaned_data[-1,]

>row.names(cleaned_data) <- row.names(data)

Note: Features (molecules) with over 50% of the values missing are eliminated. To know what features got deleted, run the following code:

# features containing more missing values than cut off

>eliminated_data <- Transposed_Data %>%

    filter(percent_of_missing_Values > missing_value_cut_off)

• 7.Data Imputation: replacing the remaining missing values by corresponding minimum value of each feature (molecule).

## imputation of remaining missing values

>sum(is.na(cleaned_data))

>for (i in n_first_mol:ncol(cleaned_data)){

  for(j in 1:nrow(cleaned_data)){

    if (is.na(cleaned_data[j,i]) == "TRUE"){

      cleaned_data[j,i] = min(cleaned_data[,i], na.rm = TRUE)

    }

  }

}

##check NAs and zero values to be removed

>sum(is.na(cleaned_data))

>sum(cleaned_data[,n_first_mol:ncol(cleaned_data)]== 0, na.rm = TRUE)

Part 2: Statistical data analysis

Timing: 10 min

Here, we detail the steps to analyze the processed data, from normalization to exploratory analysis. xpro_103041_gr2_3c.tif - These steps are pivotal in gaining valuable insights into the omics profile of different study groups. To accomplish this, we leverage the MetaboAnalyst library.

• 8.Create a dataset object to store the processed data via the MetaboAnalystR library.

>mSet<-InitDataObjects("conc", "stat", FALSE)

>mSet<-Read.TextData(mSet, cleaned_data, "rowu", "disc")

>mSet<-SanityCheckData(mSet)

• 9.Normalize and scale the data. Here, we perform log transformation and mean centering.

>mSet<-PreparePrenormData(mSet)

>mSet<-Normalization(mSet, "NULL", "LogNorm", "MeanCenter", "NULL", ratio=FALSE, ratioNum=20)

• 10.Perform and visualize the principal component analysis (PCA) (Figure 1A) (troubleshooting 2).

>mSet<-PCA.Anal(mSet) #Perform PCA

>mSet<-PlotPCAPairSummary(mSet, "pca_pair_0_", format = "png", dpi = 72, width=NA, 5) # Create PCA overview

>mSet<-PlotPCAScree(mSet, "pca_scree_0_", "png", dpi = 72, width=NA, 5) # Create PCA scree plot

>mSet<-PlotPCA2DScore(mSet, "pca_score2d_0_", format = "png", dpi=300, width=NA, 1, 2, 0.95, 0, 0) # Create a 2D PCA score plot

• 11.Perform pairwise fold change analysis (troubleshooting 3).

>Fold_change_cut_off= 1.5 #set your cut off for fold change

>P_Value_cut_off = 0.05 #set your cut off for adjusted p value

>mSet<-Volcano.Anal(mSet, FALSE, Fold_change_cut_off, 0, F, P_Value_cut_off, TRUE, "fdr")

Note: The criteria set for this step should be tailored based on each specific study. Higher fold change thresholds will result in the identification of fewer differentially changed molecules and vice versa.

• 12.Visualizing the pairwise fold change analysis by a volcano plot (Figure 1B)

>mSet<-PlotVolcano(mSet, "volcano_0_", 1, 0, format ="png", dpi=300, width=NA)

• 13.Visualizing molecules with the greatest change across all study groups through heatmap (Figure 1C).

>top_mol = 100 #number of the top molecules to be shown in the heatmap

>mSet<-PlotSubHeatMap(mSet, "heatmap_1_", "png", 300, width=NA,"norm", "row", "euclidean", "ward.D","bwm", 8, "tanova", top_mol, "overview", F, T, T, F, T, T, T)

Note: Depending on the number of features (molecules) after data preprocessing, we can decide on the number of molecules to be shown by the heatmap. This decision can be made considering the heatmap’s readability and interpretability. Displaying too many molecules may result in a cluttered and difficult-to-interpret visualization, while showcasing too few may overlook potentially relevant information. Thus, it is advisable to strike a balance by selecting a suitable number of molecules that adequately represent the dataset's characteristics while ensuring clarity in the heatmap presentation.

Optional: We can highlight the changes in meaningful molecules across study groups by box plots to emphasize their role in disease of interest.

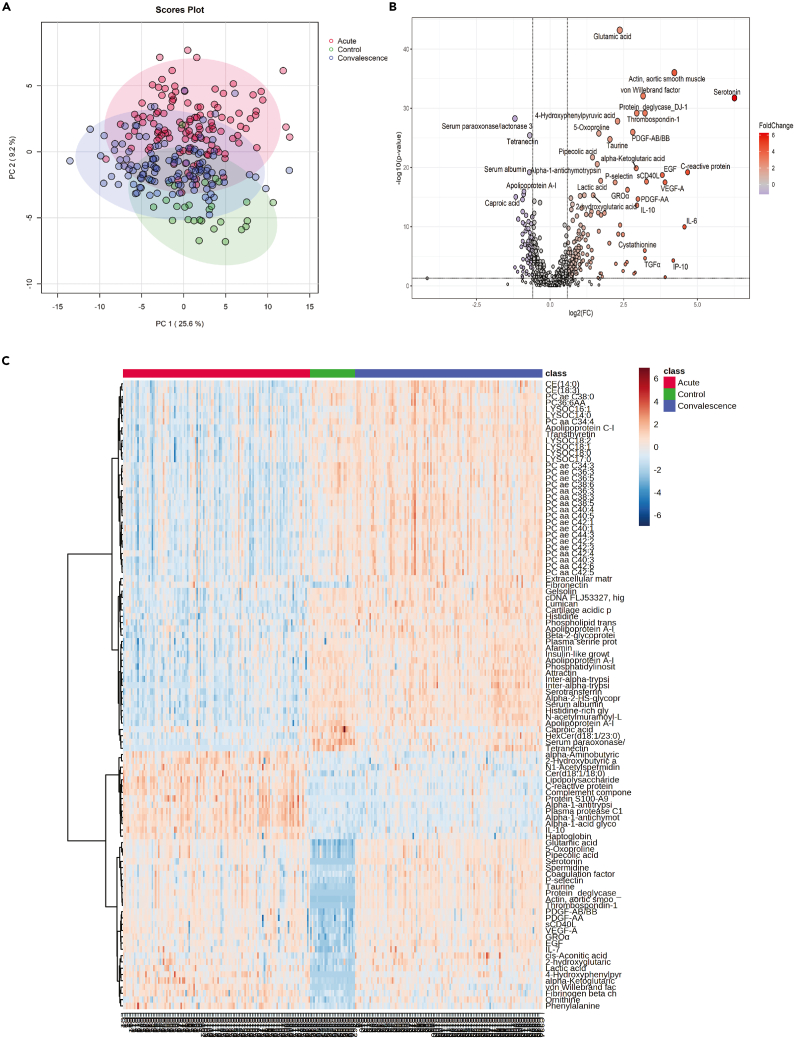
Figure 1.

Statistical analysis of multi-omics datasets

(A) Principal component analysis utilizing proteomics, metabolomics, and cytokines illustrating the different plasma profiles among healthy controls, acute, and convalescence phases of patients infected by SARS-CoV-2. Reprinted and Adapted from Wang et al.¹ (B) Volcano plot comparing convalescence samples and healthy controls. Adapted from Wang et al.¹ with modifications.

(C) Heatmap showing the top 100 molecules with the most significant p values comparing healthy control with acute and convalescence phases using ANOVA test on log10 transformed data. Reprinted and Adapted from Wang et al.¹

Part 3: Identifying the correlation between DEMs and clinical variables

Timing: 10 min

Identifying associations between differentially expressed molecules and clinical variables such as symptoms can facilitate the discovery of diagnostic biomarkers. By employing generalized linear models, we can identify those associations while adjusting them to other variables that may influence a disease state. We utilize a loop to iterate through all the molecules and clinical variables.

• 14.Importing the clinical dataset.

>clinical_variables<-read.csv("Data.csv")

Note: For this part, the dataset should have differentially expressed molecules (DEMs) and clinical variables in the same file in columns. (Data S2).

• 15.Import the values based on your data.

>n_o_clinical_variables = 20

>n_of_differentially_changed_molecules = 219

>A = n_o_clinical_variables + n_of_differentially_changed_molecules

>ncol_adjustment_var = 240

>n__adjustment_var = 7

>B= c(ncol_adjustment_var:(ncol_adjustment_var+n__adjustment_var))

• 16.Make two empty data frames for the coefficients and p values.

#empty data frame for odds ratios

>Coefficients<-data.frame(matrix(nrow = n_o_clinical_variables,

         ncol = n_of_differentially_changed_molecules))

>row.names(Coefficients)<-colnames(clinical_variables [(n_of_differentially_changed_molecules+1):A])

>colnames(Coefficients)<-colnames(clinical_variables [1:n_of_differentially_changed_molecules])

#empty data frame for p values

> pvalue<-data.frame(matrix(nrow = n_o_clinical_variables,

          ncol = n_of_differentially_changed_molecules))

>row.names(pvalue)<- row.names(Coefficients)

>colnames(pvalue)<- colnames(Coefficients)

• 17.Perform the generalized linear model for all molecules and clinical variables by a loop.

>for(i in 1:n_of_differentially_changed_molecules){

 for(j in (n_of_differentially_changed_molecules+1):A){

  sym<-glm(unlist(clinical_variables [j])∼unlist(clinical_variables [i])+

     unlist(clinical_variables [B[1]])+ #list all your adjustment variables

     unlist(clinical_variables [B[2]])+

     unlist(clinical_variables [B[3]])+

     unlist(clinical_variables [B[4]])+

     unlist(clinical_variables [B[5]])+

     unlist(clinical_variables [B[6]])+

     unlist(clinical_variables [B[7]])+

     unlist(clinical_variables [B[8]]),

     family=binomial(),

     data= clinical_variables)

  pvalue [j-n_of_differentially_changed_molecules,i]<-coef(summary(sym))[2,4]

  Coefficients [j-n_of_differentially_changed_molecules,i]<-exp(coef(summary(sym))[2,1])

  }

}

• 18.After performing the adjusted regression, molecules with three or more significant p values were filtered for illustration.

# transposing the matrix

>n.pval <- as.data.frame(t(pvalue))

#Make a column for the number of significant p values in each row for transposed table

>v <- c()

>for (i in 1:nrow(n.pval)){

 v[i]<- sum(n.pval[i,] < 0.05)

}

>n.pval <- n.pval %>%

 mutate(n.of.sig = v)

# subset the molecules with >= 3 significant p values

>P_Value_cut_off = 3 #set your cut off for number of significant p vales

>n.pval.filtered<- n.pval %>%

 filter(n.of.sig >= P_Value_cut_off)

>n.pval.filtered$n.of.sig <- NULL

#subset of odds ratio values of molecules with >= 3 significant p values

>odds.filrtered <- Coefficients %>%

 select(rownames(n.pval.filtered))

>odds.filrtered <- as.data.frame(t(odds.filrtered))

Note: The threshold to filter out the molecules for illustration purposes should be determined based on results of the regression analysis. This threshold ensures that only molecules exhibiting a certain number of significant associations are included in the visualization.

• 19.Illustrating the associations by a heatmap (Figure 2).

Note: In this heatmap, significant associations are denoted by asterisks and the color of each cell shows the direction of the association, where blue indicates negative and red indicates positive associations.

>my_color_mapping <- colorRamp2(c(0, 1, 10), c("#2E2EFF", "white", "#FF2E2E"))

>Heatmap(

 as.matrix(odds.filrtered),

  width = ncol(odds.filrtered)∗unit(4.5, "mm"),

  height = nrow(odds.filrtered)∗unit(3, "mm"),

  cluster_rows = FALSE,

  cluster_columns = FALSE,

  show_row_dend = FALSE,

  show_column_dend = FALSE,

  clustering_method_rows = "ward.D2",

  heatmap_legend_param = list(

   title = "Odds Ratio",

   at = seq(0, 2, length.out = 3),

   labels = c( "10ˆ-5", "1", "10ˆ5")),

  cell_fun = function(j, i, x, y, w, h, fill) {

   if(n.pval.filtered [i, j] < 0.05) {

    grid.text("∗", x , y-(0.3∗h) ,gp=gpar(fontsize=18))

   }

    },

 col = my_color_mapping,

 column_names_gp = grid::gpar(fontfamily= "Arial", fontface= "bold", fontsize = 10),

 row_names_gp = grid::gpar(fontfamily= "Arial", fontface= "bold", fontsize = 9)

)

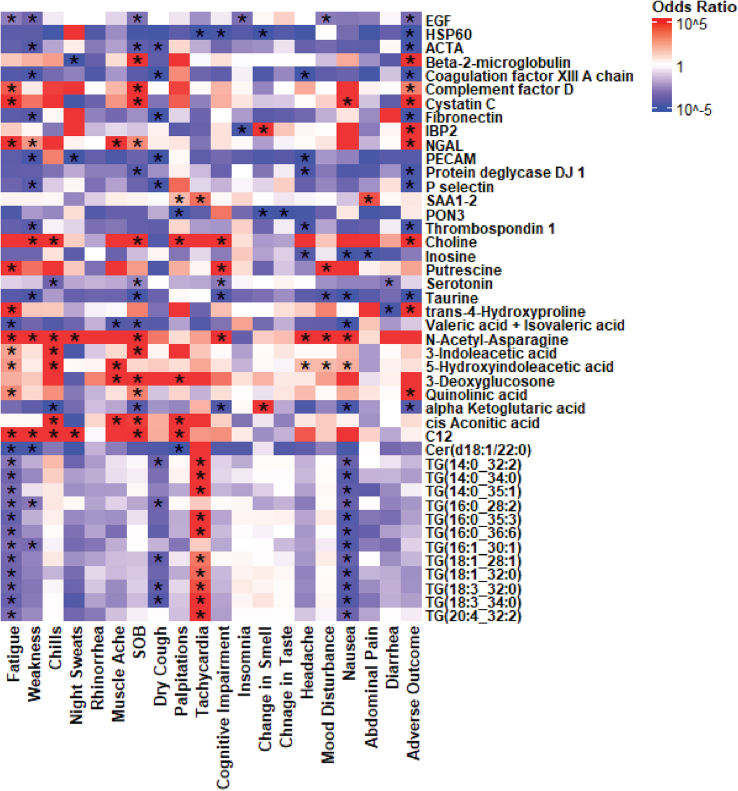
Figure 2.

Heatmap illustrating the association between biomarkers and self-reported PCC symptoms assessed by multivariable logistic regression analysis

Asterisks indicate statistical significance (p < 0.05).

Reprinted and Adapted from Wang et al.¹

Part 4: Unsupervised clustering of patients based on their multi-omics profile

Timing: 10 min

To capture significant similarities between patients on a biological scale, we cluster patients based on the degree of change in molecule levels from the acute to convalescence phase. We utilized autoencoder as a non-linear dimensionality reduction tool. A lower dimensional representation of the data is beneficial for clustering, and hence, the initial data with all the omics profiles is sent through an autoencoder to generate a lower dimensional representation and then clustered using the k-means algorithm.

Note: We will use Python to analyze the data from this step forward.

• 20.Import required libraries.

>import pandas as pd # To read data files

>import numpy as np # Process matrices

>from matplotlib import pyplot as plt # Plot figures

>from sklearn.decomposition import PCA # Perform PCA

>from sklearn.cluster import KMeans # Perform K-Means .layers

# Following packages are used to build the autoencoder

>import tensorflow as tf

>from tensorflow import keras

>from tensorflow.keras.layers import Dense

>from tensorflow.keras import models,Sequential

• 21.Read the split data files of the acute and convalescence values and calculate the delta values.

# Extract Long and Acute covid values

>X_acute_cyt=pd.read_csv(‘Acute_cytokine.csv’).iloc[:,:].values

>X_long_cyt= pd.read_csv(‘Long_cytokine.csv’).iloc[:,:].values

>X_acute_pro= pd.read_csv(‘Acute_proteins.csv’).iloc[:,:].values

>X_long_pro= pd.read_csv(‘Long_proteins.csv’).iloc[:,:].values

>X_acute_meta= pd.read_csv(‘Acute_metabolities.csv’).iloc[:,:].values

>X_long_meta= pd.read_csv(‘Long_metabolites.csv’).iloc[:,:].values

>X_acute = np.hstack((X_acute_cyt,X_acute_pro,X_acute_meta))

>X_long = np.hstack((X_long_cyt,X_long_pro,X_long_meta))

>patient_labels = pd.read_csv(‘Patient labels.csv).iloc[:,:].values

>X=X_long-X_acute

>scaler=StandardScaler()

>X=scaler.fit_transform(X) # Normalize the data

>print(X.shape)

Note: The data that should be used in this step is the log10 transformed version of data created in step 7 (Data S3), which is split into different datasets based on the type of molecules (cytokine, protein, and metabolite) and the sampling time (acute and long COVID).

• 22.Build autoencoder architecture.

Note: The number of neurons in each layer is [100, 70, 50, 30] for the encoder and [50, 70, 100, 782] for the decoder. The autoencoder reduces our data from 782 features (dimensions) to 30 features.

>model=Sequential()

>model.add(Dense(100,input_shape=(782,),activation='sigmoid'))

>model.add(Dense(70,activation='sigmoid'))

>model.add(Dense(50,activation='sigmoid'))

>model.add(Dense(30,activation='sigmoid'))

>model.add(Dense(50,activation='sigmoid'))

>model.add(Dense(70,activation='sigmoid'))

>model.add(Dense(100,activation='sigmoid'))

>model.add(Dense(782))

>model.summary()

>callback=tf.keras.callbacks.EarlyStopping(monitor ='loss', min_delta= 1E-7, patience= 1000, restore_best_weights= True) #Earlystopping

>model.compile(loss='mse',optimizer='adam') # Compile model with MSE loss

>model.fit(X,X,epochs=1000,verbose=1,callbacks =[callback]) # Fit model for 1000 epochs

>Encoder=keras.Model(model.inputs,model.layers[3].output) #Extract the bottleneck layer to give lower dimensional features

>Encoder.summary() # Print summary of model structure

>X_low=Encoder.predict(X) # Generate lower dimensional features

• 23.Create label vector and color vector for plotting.

>label_dict_comb={'recovered':'green','mild':'blue','severe':'red'}

>class_dict_comb={'recovered':0,'mild':1,'severe':2}

>cvec=[label_dict_comb[label] for label in patient_labels]

>org_label=[class_dict_comb[label] for label in patient_labels]

• 24.Perform K-means clustering. The number of clusters is chosen based on the silhouette coefficient of clustering.

>kmeans_comb=KMeans(n_clusters=3).fit(X_low) #3 clusters

>cluster_new =kmeans_comb.labels_ #Store cluster labels for each sample

• 25.Save AutoEncoder Model.

>keras.models.save_model(model,'AutoEnc_Allfeatures_Delta_Sigmoid.hp5',save_format='h5')

• 26.Save Clustered Data.

>dict={

>for i,key in enumerate(df.keys()[1:]):

  dict[key]=X[:,i]

>dict['Cluster Label']=kmeans_comb.labels_

>pd.DataFrame(dict).to_csv(‘Cluster labels.csv’)

• 27.Plotting clustering results (Figure 3A).

>s=np.ones(X.shape[0])∗200

>mpl.rcParams['figure.dpi']=1200

>mpl.rcParams.update({'font.size':22})

>colors=ListedColormap(['#69B0F8','#FEE0D2','#F2757B'])

>colors1=ListedColormap(['magenta','yellow','black'])

>fig,ax=plt.subplots(1,2,figsize=(20,20))

>scatter=ax[0].scatter(X_low[:,0],X_low[:,1],s=s,c=org_label,cmap=colors,edgecolors='black')

>ax[0].set_xlabel('Encoded Dim 1')

>ax[0].set_ylabel('Encoded Dim 2')

>ax[0].legend(handles=scatter.legend_elements()[0], >labels=["Recovered",'Mild','Severe'],fontsize=35,markerscale=5)

>scatter1=ax[1].scatter(X_low[:,0],X_low[:,1],s=s,c=cluster_new,cmap=colors1,edgecolors='black')

>ax[1].set_xlabel('Encoded Dim 1')

>ax[1].set_ylabel('Encoded Dim 2')

>ax[1].legend(handles=scatter1.legend_elements()[0], labels=["Cluster A",'Cluster B', "Cluster C"],fontsize=35,markerscale=5)

• 28.Find features with deviations above 65%.

# Function to find features with deviations above 65%

>def find_deviations(df_clustered,cutoff,name):

 means =df_clustered.abs().mean(numeric_only=True)

 cluster_means =df_clustered.abs().groupby(['ClusterLabels']).mean(numeric_only=True)

 deviation=cluster_means.sub(means[:-1]).div(means[:-1])

 features=deviation.copy()

 features[features.abs()>=cutoff]=1

 features[features.abs()<cutoff]=0

pd.concat([features,deviation.multiply(100)]).transpose().to_csv('Impute_Test_781/Features/Random_Impute_'+name+'.csv')

return features

#Find features in each cluster

> print('Finding features for',name)

> features = find_deviations(df_clustered,cutoff,name)

Note: Different thresholds should be examined for this step to find the proper number of deviated features. Higher thresholds will lead to fewer deviated features while lower thresholds may result in more.

Note: Following the generation of clusters, clinical variables and symptoms of the newly formed clusters can be examined. This analysis enables the identification of biomarkers that contribute significantly to the predominant symptoms or characteristics exhibited by each cluster. For further guidance, refer to the example provided in Figure 5 of our published paper.¹

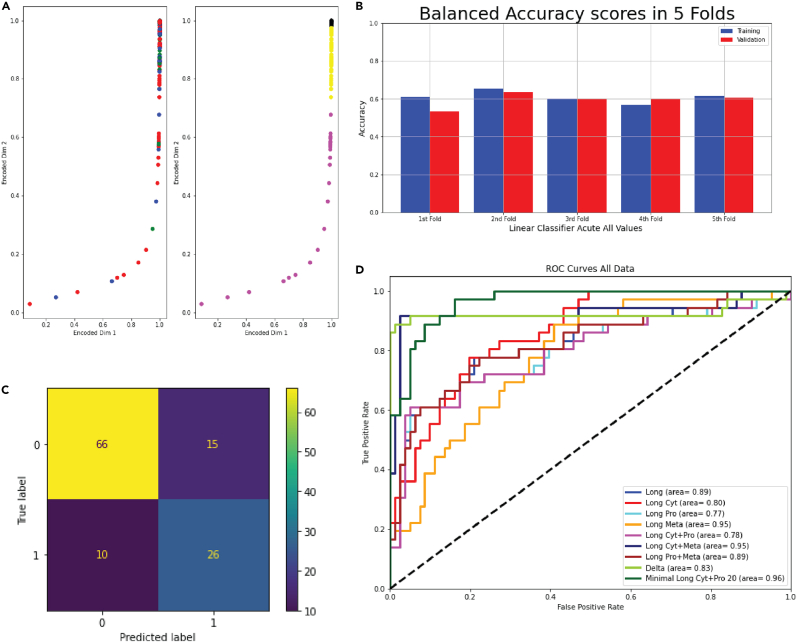
Figure 3.

Machine learning analysis

(A) Dot plot showing the k-means clustering on latent space generated by autoencoder. Reprinted and Adapted from Wang et al.¹

(B) Bar plot showing the accuracy of classification in all 5-fold validation groups.

(C) Confusion matrix illustrating the predicted labels and true labels of samples classified by logistic classification.

(D) Receiver operator characteristic curves of prediction models trained on each individual omics datasets, combined omics (cytokines, proteomics, and metabolomics), and the minimal panel using molecular profile. Reprinted and Adapted from Wang et al.¹

Part 5: Perform ML and feature selection to identify predictive biomarkers

Timing: 10 min

In this section, we make a classical machine learning model to predict the clinical outcomes of patients with PCC. We fit a linear classifier to the data to classify patients with and without clinical outcomes based on their omics profile in the convalescence phase. By doing that, we are able to assess the ability of each assay to predict the outcomes and subsequently perform feature selection to identify the most predictive biomarkers.

• 29.Import libraries.

>import pandas as pd # To read data files

>import numpy as np # To perform matrix operations

>import math # Mathematical operations (check if nan)

>import os # To access directories

>from sklearn.preprocessing import StandardScaler # Normalize data

>from sklearn.linear_model import LogisticRegression # Linear classifier

#Obtain metrics to test classifier

>from sklearn.metrics import >f1_score,confusion_matrix,roc_curve,ConfusionMatrixDisplay,auc,balanced_accuracy_score,roc_auc_score

>from sklearn.model_selection import train_test_split,cross_validate,GridSearchCV # Split data to train-test, perform Grid search

>from sklearn.feature_selection import SequentialFeatureSelector,RF # Feature elimination tools

>import matplotlib.pyplot as plt # To plot data

• 30.Open data file and split into different sets containing specific omics profiles.

>X_acute_cp=np.hstack((X_acute_cyt,X_acute_pro)) # stack cytokines and proteins together for acute data

>X_long_cp=np.hstack((X_long_cyt,X_long_pro)) #stack cytokines and proteins for long data

>X_acute_cm=np.hstack((X_acute_cyt,X_acute_meta)) # stack cytokines and metabolites for acute

>X_long_cm=np.hstack((X_long_cyt,X_long_meta)) # stack cytokines and metabolites for long

>X_acute_pm=np.hstack((X_acute_pro,X_acute_meta)) # stack protein and metabolites for acute

>X_long_pm=np.hstack((X_long_pro,X_long_meta)) # stack protein and metabolites for long

>X_acute = np.hstack((X_acute_cyt,X_acute_pro,X_acute_meta))

>X_long = np.hstack((X_long_cyt,X_long_pro,X_long_meta))

• 31.Generate color vector and label vector for classifier.

>label_dict_comb={0:'green',1:'red'}

>class_dict_comb={'Event-Free':0,'With Event':1}

>cvec=[label_dict_comb[label] for label in patient_labels]

>org_label=patient_labels.

• 32.Create Data Matrix combining all data to automate the procedure for different datasets.

>DATA=[]

>DATA.append(X_acute)

>DATA.append(X_acute_cyt)

>DATA.append(X_acute_pro)

>DATA.append(X_acute_meta)

>DATA.append(X_acute_cp)

>DATA.append(X_acute_cm)

>DATA.append(X_acute_pm)

>DATA.append(X_long)

>DATA.append(X_long_cyt)

>DATA.append(X_long_pro)

>DATA.append(X_long_meta)

>DATA.append(X_long_cp)

>DATA.append(X_long_cm)

>DATA.append(X_long_pm)

>DATA.append(X_long-X_acute)

>NAMES=['Acute','Acute_Cyt','Acute_Pro','Acute_Meta','Acute_CP','Acute_CM','Acute_PM','Long','Long_Cyt','Long_Pro','Long_Meta','Long_CP','Long_CM','Long_PM','Delta']

• 33.Function to perform 5-fold cross validation.

>def cross_validation(model, _X, _y, _cv=5):

  _scoring = ['balanced_accuracy', 'precision', 'recall', 'f1']

  results = cross_validate(estimator=model,

       X=_X,

       y=_y,

       cv=_cv,

       scoring=_scoring,

       return_train_score=True)

  return {"Training Accuracy scores": results['train_balanced_accuracy'],

    "Mean Training Accuracy":results['train_balanced_accuracy'].mean()∗100,

    "Training Precision scores": results['train_precision'],

    "Mean Training Precision": results['train_precision'].mean(),

    "Training Recall scores": results['train_recall'],

    "Mean Training Recall": results['train_recall'].mean(),

    "Training F1 scores": results['train_f1'],

    "Mean Training F1 Score": results['train_f1'].mean(),

    "Validation Accuracy scores": results['test_balanced_accuracy'],

    "Mean Validation Accuracy": >results['test_balanced_accuracy'].mean()∗100,

    "Validation Precision scores": results['test_precision'],

    "Mean Validation Precision": >results['test_precision'].mean(),

    "Validation Recall scores": results['test_recall'],

    "Mean Validation Recall": results['test_recall'].mean(),

    "Validation F1 scores": results['test_f1'],

    "Mean Validation F1 Score": results['test_f1'].mean()

    }

• 34.Function to plot 5-fold cross validation results (Figure 3B).

>def plot_result(x_label, y_label, plot_title, train_data, val_data,name):

   '''Function to plot a grouped bar chart showing the training and validation

   results of the ML model in each fold after applying K-fold cross-validation.

   Parameters

   ----------

   x_label: str,

    Name of the algorithm used for training e.g 'Decision Tree'

   y_label: str,

    Name of metric being visualized e.g 'Accuracy'

   plot_title: str,

    This is the title of the plot e.g 'Accuracy Plot'

   train_result: list, array

    This is the list containing either training precision, accuracy, or f1 score.

   val_result: list, array

    This is the list containing either validation precision, accuracy, or f1 score.

   Returns

   -------

   The function returns a Grouped Bar chart showing the training an validation result in each fold.

   '''

   '# Set size of plot

   'plt.figure(figsize=(12,6))

   'labels = ["1st Fold", "2nd Fold", "3rd Fold", "4th Fold", "5th >Fold"]

   'X_axis = np.arange(len(labels[:len(train_data)]))

   'ax = plt.gca()

   'plt.ylim(0.0, 1)

   'plt.bar(X_axis-0.2, train_data, 0.4, color='blue', label='Training')

   'plt.bar(X_axis+0.2, val_data, 0.4, color='red', label='Validation')

   'plt.title(plot_title, fontsize=30)

   'plt.xticks(X_axis, labels[:len(train_data)])

   'plt.xlabel(x_label, fontsize=14)

   'plt.ylabel(y_label, fontsize=14)

   'plt.legend()

   'plt.grid(True)

plt.savefig('MinimalPanel_New/RFE/FU_2023/Minimal/IMAGES/Cross_Val/'+str(name)+'_CV.png')

   'plt.show()

• 35.Perform grid search to tune in on hyper-parameters for the classifier.

Note: Since the number of samples for each class is unequal, we need to weigh the classes to ensure the classifier gives equal importance. A grid search allows us to find the optimum weight by computing all combinations of parameters.

>FPR=[]

>TPR=[]

>FPR_ALL=[]

>TPR_ALL=[]

>results_df=pd.DataFrame()

>for i in range(len(DATA)):

  X=DATA[i]

  results_dict={}

  #GRID SEARCH

  parameters={'class_weight':[{0:1,1:1},{0:1,1:2},{0:1,1:5},{0:1,1:10},{0:2,1:1},{0:10,1:1},'balanced'],'C':[1E-5, 1E-3, 0.1, 1, 10, 100,1000]}

  _scoring = ['balanced_accuracy', 'precision', 'recall', 'f1']

  clf = GridSearchCV(LogisticRegression(penalty='l2',max_iter=5000,), parameters,scoring=_scoring,refit='balanced_accuracy')

  clf.fit(X_train,y_train);

  results_dict = clf.best_params_

  if clf.best_params_['class_weight'] !='balanced':

   clf.best_params_['class_weight']

   dummy=str(clf.best_params_['class_weight'][0])+','+str((clf.best_params_['class_weight'][1]))

   results_dict['class_weight'] = dummy

• 36.Feature Elimination (troubleshooting 4).

Note: Features correspond to the different molecular profiles. They are eliminated based on whether they are important to the classification or not based on the weights of the classifier.

>Estimator=clf.best_estimator_

>n_features = 20 # number of features to be selected

>selector=RFE(estimator,step=1,n_features_to_select= n_features )

>selector.fit(X,org_label) >mask=selector.support_

• 37.Reduce input feature space.

>X_low=selector.transform(X) # reduces the dimensionality of the data based on step 36

>X_train,X_test,y_train,y_test,train_id,test_id = train_test_split(X_low,org_label,sample_num,test_size=0.1, random_state=42)

>Clf_result=cross_validation(Clf,X_train,y_train,5)

>plot_result('Linear Classifier '+ str(NAMES[i]),"Accuracy","Balanced Accuracy scores in 5 Folds", Clf_result["Training Accuracy scores"],Clf_result["Validation Accuracy scores"],NAMES[i])

• 38.Fit best regressor from grid search using reduced features.

>Estimator.fit(X_train,y_train) # Fit the classifier

>y_pred=Estimator.predict(X_test) # Predict the labels for unseen data

>y_score=Estimator.decision_function(X_test) # Probability of the sample being in a class

>y_train_pred = Estimator.predict(X_train)

>results_dict['Test Accuracy'] = balanced_accuracy_score(y_test,y_pred) # Test Accuracy

>results_dict['Test F1 Score']=f1_score(y_test,y_pred) # Test F1 Score

>results_dict['Train Accuracy'] = balanced_accuracy_score(y_train,y_train_pred) # Train accuracy

>results_dict['Train F1 Score']=f1_score(y_train,y_train_pred) # Train F1 score

>results_dict['Dataset'] = NAMES[i]

• 39.Print confusion matrix (Figure 3C). Generates a .csv file that contains Accuracy and F1 score.

>cm = confusion_matrix(y_test, y_pred, labels=Clf.classes_) # Confusion matrix

>disp = ConfusionMatrixDisplay(confusion_matrix=cm,display_labels=Clf.classes_

>disp.plot()

>plt.savefig('MinimalPanel_New/RFE/FU_2023/IMAGES/Confusion_Matrix/'+str(NAMES[i])+'_CM.png')

>print('Saving results for ',NAMES[i])

>results_df=pd.concat([results_df,pd.DataFrame(results_dict,index=[0])],ignore_index=True)

>results_df.to_csv('MinimalPanel_New/RFE/FU_2023/Summary_new.csv') # Change to the location to store results in

• 40.Compute and plot the ROC curve for test data (Figure 3D).

Note: ROC curve provides a means of visualizing the performance of the classification task. The larger the area under the ROC curve, the better the classification performance.

>fpr_all,tpr_all,_ =roc_curve(org_label,y_score)

>area=auc(fpr_all,tpr_all)

>plt.figure()

>lw=3

>label ='Linear '+NAMES[i]+' (area= %0.2f)'

>plt.plot(fpr_all,tpr_all,color='blue',lw=lw,label=label % area,)

>plt.plot([0,1],[0,1],color='black',lw=lw,linestyle="--")

>plt.xlim([0.0,1.0])

>plt.ylim([0.0,1.05])

>plt.xlabel('False Positive Rate')

>plt.ylabel('True Positive Rate')

>plt.title('ROC Curves All Data')

>plt.legend(loc='lower right')

>plt.savefig('MinimalPanel_New/RFE/FU_2023/IMAGES/ROC/'+str(NAMES[i])+'_ROC.png')

• 41.Save weights and bias for linear model.

>Weights_dict={}

>Weights_dict['Features']=np.array(mols_list[i])[mask] >Weights_dict['Weights']=Estimator.coef_[0] >Weights_df=pd.DataFrame(Weights_dict) >pd.concat([Weights_df,pd.DataFrame({'Features':'Bias','Weights':Estimator.intercept_[0] }, index=[0])],ignore_index=True).to_csv('MinimalPanel_New/RFE/FU_2023/Minimal/Weights/'+NAMES[i]+'.csv') #Change to desired location

Expected outcomes

This protocol serves as a resource for omics analysis of plasma samples from patients with PCC. These steps can be applied to similar studies that conducted omics assays on plasma samples of other diseases. The primary outcome of this protocol is a processed dataset (part 1: data preprocessing) containing no missing values prepared for any downstream statistical analysis.

A key part of this protocol is the statistical analysis section (part 2: statistical data analysis), which yields informative plots elucidating the characteristics of individual groups in an omics study. Firstly, principal component analysis (PCA) (step 10) generates a score plot which visualizes how distinct the omics profiles of the study groups are (Figure 1A). Then, pairwise fold change analysis (step 12) produces a volcano plot (Figure 1B) highlighting the molecules significantly altered in a comparison. These identified molecules can then undergo further downstream analyses, such as pathway analysis.¹ This provides insights into dysregulated pathways in a disease, offering potential diagnostic and therapeutic targets. At the end of this part, the heatmap (Figure 1C) shows the top changed molecules, which are identified based on the analysis of variance (ANOVA) (step 13). This heatmap showcases molecules with different trajectories during a disease, which is particularly valuable in study designs with paired samples across multiple time points.

Another important outcome of the protocol is the correlation heatmap (Figure 2) illustrating the association between differentially expressed molecules and symptoms, which is adjusted for other clinical variables, such as comorbidities, age, and sex that may play important roles in a disease. This analysis can identify important associations between symptoms with specific biomarkers to provide crucial insights into the pathophysiological processes and unveil novel therapeutic targets. For example, taurine and serotonin showed negative associations with several symptoms, including diarrhea, nausea, mood disturbance, and cognitive impairment in PCC, highlighting their potential role in modulating neurological and mitochondrial dysfunctions in patients with PCC.

We next performed unsupervised clustering (part 4: unsupervised clustering of patients based on their multi-omics profile) for individuals based on the changes in concentrations of molecules (cytokines, proteins, and metabolites) between acute and convalescence phases (step 21). A non-linear dimensionality reduction was performed using an autoencoder (step 22). Autoencoders (AE) are a class of artificial neural networks where the network architecture creates a bottleneck by encoding a layer of lower dimensions to generate a lower-dimensional data projection. Since the activation of each layer in the AE is non-linear, the lower dimensional projection of the data is a non-linear combination of the original variables. The autoencoder consisted of three encoding layers of 100, 70, and 50 neurons each. The bottleneck layer consisted of 30 neurons followed by three decoding layers, with all layers using the sigmoid activation on their outputs. Utilizing k-means (step 24) on autoencoders yielded three phenotypically distinct clusters (Figure 3A) based on their inherent molecular similarities (step 28). These new clusters can be further analyzed to identify the unique clinical features of each cluster.

In the last step of the protocol (part 5: perform ML and feature selection to identify predictive biomarkers), we utilized logistic regression to evaluate the ability of different omics platforms to predict adverse clinical outcomes. A 5-fold validation (step 33) is conducted (Figure 3A) to prevent over- or underfitting of the model output. Following this, optimal hyperparameters were identified through grid search (step 35), and recursive feature elimination (step 36) was performed for feature selection to identify the minimum number of molecules with the highest predictive ability. The best regressor was fitted to the data (step 38), and a confusion matrix (step 39) was generated (Figure 3C). Finally, the predictive ability of different omics platforms and the minimal panel was evaluated using ROC curves (Figure 3D).

Limitations

This protocol has some limitations. Users need to perform this protocol on relatively high-performance computers. The required computing power depends on the number of samples and molecules being analyzed. Therefore, it’s important to mention that this protocol may not accurately estimate the computing power needed for different scales of multi-omics studies.

Another inherent limitation arises from the fact that the accuracy of classification and unsupervised clustering is highly dependent on the characteristics of the input data. The efficacy of these tasks is not guaranteed to be uniform across different datasets. It is advisable to explore different unsupervised learning and classification algorithms to optimize the accuracy of this analysis.

Troubleshooting

Problem 1

You might encounter problems for installing and loading the MetaboAnalystR package (step 1).

Potential solution

• •Update the Rtools through https://cran.r-project.org/bin/windows/Rtools/
• •For more information, please refer to their GitHub (https://github.com/xia-lab/MetaboAnalystR).

Problem 2

Including data from two or more batches into one analysis could introduce technical variability, which potentially disrupts the biological signals in the downstream analyses. The initial step in detecting batch effects is in principal component analysis where samples of one study group (ex. treated) exhibit divergence (step 10).

Potential solution

The batch effect should first be remediated prior to statistical analysis. Various R libraries, including limma, Deseq2, sva, and ComBat, offer functions to remove the batch effect.^15,16

Problem 3

Performing differentially expressed analysis with these predefined criteria (FC > 1.5 and adjusted p-value < 0.05) may result in an excessively low or high number of molecules in other datasets (step 11).

Potential solution

Set the criteria for differential expression analysis (fold-change and p-value) based on the study’s unique characteristics. In multi-omics studies measuring numerous molecules, utilizing adjusted p-values is recommended for statistical rigor. Consider a lower fold-change threshold in cases where even small changes should be considered.

Problem 4

The feature extraction task is an iterative routine that fits multiple models of increasing complexity to determine a lower number of features best suited for the classification. When the initial number of features is large, it can lead to a long computational time (step 36).

Potential solution

To expedite the process, consider employing a less complicated unsupervised dimensionality reduction technique, such as PCA, for data preprocessing before integrating it into the routine.

>pca = PCA(0.95) >X_low = PCA.fit_transform(X) # X is the original data matrix with large number of features # Use X_low instead of X from Box 35

Resource availability

Lead contact

Further information and requests for resources and reagents should be directed to and will be fulfilled by the lead contact, Dr. Gavin Oudit (gavin.oudit@ualberta.ca).

Technical contact

Questions about the technical specifics of performing the protocol should be directed to and will be answered by the technical contact, Mobin Khoramjoo (khoramjo@ualberta.ca).

Materials availability

This study did not generate any reagents.

Data and code availability

Raw data of omics platforms in this study have been deposited to PeptideAtlas: PASS03810 and MetaboLights: MTBLS7337.

The datasets (Data S1, S2, and S3) used in this protocol have been deposited to Mendeley data (https://doi.org/10.17632/zyzt62gbrw.1).²

The codes generated during this study are available at a GitHub repository (https://github.com/MobinKhoramjoo/Biomarker-identification-by-multi-omics-analysis) and Zenodo (https://doi.org/10.5281/zenodo.10880873).³