Charge Transfer from Quantum-Confined 0D, 1D, and 2D Nanocrystals

Abstract

The properties of colloidal quantum-confined semiconductor nanocrystals (NCs), including zero-dimensional (0D) quantum dots, 1D nanorods, 2D nanoplatelets, and their heterostructures, can be tuned through their size, dimensionality, and material composition. In their photovoltaic and photocatalytic applications, a key step is to generate spatially separated and long-lived electrons and holes by interfacial charge transfer. These charge transfer properties have been extensively studied recently, which is the subject of this Review. The Review starts with a summary of the electronic structure and optical properties of 0D–2D nanocrystals, followed by the advances in wave function engineering, a novel way to control the spatial distribution of electrons and holes, through their size, dimension, and composition. It discusses the dependence of NC charge transfer on various parameters and the development of the Auger-assisted charge transfer model. Recent advances in understanding multiple exciton generation, decay, and dissociation are also discussed, with an emphasis on multiple carrier transfer. Finally, the applications of nanocrystal-based systems for photocatalysis are reviewed, focusing on the photodriven charge separation and recombination processes that dictate the function and performance of these materials. The Review ends with a summary and outlook of key remaining challenges and promising future directions in the field.

1. Introduction

The intrinsic electronic properties of bulk semiconductor crystals are determined by their chemical composition and lattice structure. When the crystal is small enough, its energy levels can also be tuned by its size through the quantum confinement effect.¹⁻⁴ The effect occurs when the crystal dimension is smaller than the exciton Bohr radius, which is usually in the scale of a few to tens of nanometers.⁵⁻⁷ These quantum-confined nanocrystals (NCs) can be classified as zero-dimensional (0D) quantum dots (QDs), one-dimensional (1D) nanorods (NRs), and two-dimensional (2D) nanoplatelets (NPLs), with their exciton motions confined in three, two, and one dimensions, respectively (Figure 1A).

Figure 1.

0D, 1D, and 2D nanocrystals. (A) Representative transmission electron microscopy (TEM) images of colloidal 0D, 1D, and 2D CdSe nanocrystals (NCs), which are also termed quantum dots (QDs), nanorods (NRs), and nanoplatelets (NPLs), respectively. (B) Schematic plots of density of states (DOS) as a function of energy for 3D (bulk), 2D, 1D, and 0D systems. (C–E) Static absorption spectra of (C) a series of CdSe QDs with various diameters from 1.2 to 11.5 nm, (D) CdSe NRs with three different diameters, and (E) CdSe NPLs with three different thicknesses. The thickness-dependent photoluminescence (PL) spectra of NPLs are also plotted in (E). (B) Adapted from ref (75). Copyright 1996 American Association for the Advancement of Science. (C) Adapted from ref (8). Copyright 1993 American Chemical Society.

Different from the bulk materials, the band gap absorption and emission energy of quantum-confined NCs can be tuned over a wide range by changing the size of the quantum-confined dimensions. Taking CdSe QDs as an example, their size-tunable band gap range from 1.8 to 3.0 eV.⁸ Semiconductor NCs also have a high surface area and a much larger absorption coefficient (typically in the range of ∼10⁵–10⁷ cm^–1 M^–1) than molecules.⁹⁻¹³ The spatial locations of the conduction band electron and valence band hole can also be controlled by forming NC heterostructures composed of two or more components to enable novel exciton and charge separation properties.¹⁴ Finally, quantum-confined NCs have also been shown to facilitate multiple exciton generation, in which one high-energy absorbed photon can lead to the generation of two or more lower energy excitons. These features combined to make quantum-confined NCs a unique class of emerging materials for solar energy conversion.¹⁵⁻²¹ Both the solar-to-current conversion efficiency of QD solar cells²² and the solar-to-hydrogen conversion efficiency of QD-based photoelectrochemical cells²³ have been reported to exceed 100%.

Since the initial discovery, various properties of quantum-confined nanocrystals and their applications have been extensively studied in the last 40 years, and the increasing recognition of the importance of these materials has led to the 2023 Nobel Prize in Chemistry to Moungi Bawendi, Louis Brus, and Alexei Ekimov for their pioneering contributions to the discovery and synthesis of quantum dots.^1−4,8 This Review focuses on the applications of quantum-confined nanocrystals in solar energy conversion and the key process essential to these applications, i.e., charge transfer to and from NCs. Optical excitation of NCs generates bound electron–hole pairs (or excitons) in semiconductor NCs, which can be dissociated to form separated electrons and holes to generate photocurrent and conduct redox reactions in photovoltaic and photosynthetic cells, respectively.²⁴ The studies of charge transfer from NCs trace back to the 1980s when Brus and co-workers measured electron transfer from CdS QDs to methyl viologen via transient Raman spectroscopy^25,26 and Kamat and co-workers studied electron transfer from CdS QDs to methylene blue using nanosecond laser flash photolysis and microwave absorption techniques.²⁷ Although much of the research in this field in the late 1980s and 1990s focused on synthesis, emission properties, spectroscopic characterization, and photophysics of quantum dots,^8,28−33 charge transfer from QDs was studied in the pioneering works by El-Sayed and co-workers³⁴ and Zhang and co-workers³⁵ using sub-picosecond transient absorption (TA) spectroscopy. Interest in the time-resolved study of charge transfer processes from QDs has grown considerably since then; Kamat and co-workers reported charge transfer from QDs to TiO₂ nanoparticles in QD solar cells,³⁶⁻⁴⁰ Nozik and co-workers studied electron and hole transfer from InP QDs and their heterostructures,⁴¹⁻⁴³ Klimov and co-workers demonstrated a new approach to the sensitization of Ru complexes via charge transfer from CdSe QDs,⁴⁴ Lian and co-workers reported ultrafast interfacial electron and hole transfer from QDs to molecular acceptors by TA and single-particle photoluminescence (PL) decay,⁴⁵⁻⁴⁸ and Alivisatos reported electron transfer from CdSe/CdS NRs to Pt tips and how it affects the light-driven H₂ generation performance of this semiconductor–metal heterostructure.⁴⁹ These early works are followed by an explosion of detailed studies of charge transfer from quantum-confined QDs, NRs, and NPLs and their applications of photocatalysis and solar energy conversion.

Advances of charge transfer to and from NCs have been covered in some review articles. Early reviews focus on photochemistry and redox reactions on the surface of non-quantum-confined colloidal nanocrystals and nanocrystalline thin films.^50,51 Interfacial charge transfer in donor–bridge–acceptor systems on nanoparticles and bulk metals⁵² and in solar energy conversion systems, including QD-sensitized solar cells,^16,53,54 has also been reviewed. Charge transfer dynamics from quantum-confined NCs to molecular acceptors,⁵⁵⁻⁵⁷ redox enzymes,⁵⁸ and 2D transition metal dichalcogenides⁵⁹ have been subjects of more recent review articles, including a comprehensive Review published in this journal.⁵⁵ Advances in the use of quantum-confined nanocrystals in photocatalytic reactions, including QDs,^60,61 NRs,^62,63 and NPLs,⁶⁴ have also been reviewed. Most of these review articles focus on charge transfer from one nanocrystal morphology or type of electron acceptors. In this Review, we aim to provide a comprehensive review of charge transfer processes from 0D, 1D, and 2D quantum-confined nanocrystals, focusing on their dependence on the nanocrystal dimensionality. This Review will not cover triplet energy transfer from QDs to molecules,^65,66 and charge transfer from perovskite NCs,⁶⁷⁻⁷⁰ which have received intense interest in recent years. Significant advances have also been made in the field of using microcrystals for photocatalysis,⁷¹⁻⁷³ which is not covered in this article.

In this Review, we first introduce the electronic structure and optical properties of 0D-2D NCs in section 2, which is followed by a discussion of the recent progresses in understanding wave function engineering and carrier dynamics of 0D–2D NC heterostructures in section 3, single carrier (electron and hole) transfer from NCs in section 4, and multiple exciton generation and dissociation in section 5. In section 6, we discuss the design and performance of NC-based photocatalytic systems, with a focus on charge transfer kinetics. At last, we conclude with a summary of key advances and an outlook for future directions.

2. Electronic and Optical Properties of 0D, 1D, and 2D Nanocrystals

2.1. Dimensionality and Size Effects in 0D, 1D, and 2D Nanocrystals

The electronic structure and associated optical spectra of low-dimensional nanocrystals (NCs) can be qualitatively understood by considering two important effects in nanoscience: the dimensionality effect⁷⁴ and the size effect.² Dimensionality affects the density of states (DOS) of semiconductors, as qualitatively illustrated in Figure 1B. For a 3D (i.e., bulk) semiconductor, the DOS increases as a function of the square root of excessive energy above the band edge.⁷⁵ In 2D materials, the DOS increases with energy in a step-like function form. In 1D materials, the DOS exhibits unique Van Hove singularities at the band edges and decreases as a function of the square root of excessive energy above the band edge. Finally, for 0D QDs, the DOS evolves into atomic-like discrete lines. The size effect is more specifically termed the quantum confinement effect. When the size of the NC is smaller than the characteristic length scale of excitons (the so-called exciton Bohr radius), the exciton energy is determined by the physical size of the nanocrystal.^28,76 This effect can be approximated by a quantum mechanical “particle-in-a-box” model, which predicts that the transition energy (or the bandgap) of the nanocrystal scales with 1/L², with L being the length of quantum-confined dimensions (diameter of the 0D QDs and 1D NRs and the thickness of 2D quantum wells).⁷⁷

The simple dimensionality and size effect considerations can capture some essences of the optical spectra of colloidal NCs. Figure 1C presents the size-dependent absorption spectra of colloidal CdSe QDs synthesized using a hot-injection method.⁸ The optical gap of the QDs, as determined from the energy of the first transition peak, increases by ∼1.1 eV when the diameter is reduced from 11.5 to 1.2 nm, which is a direct demonstration of the quantum confinement effect. For NRs and NPLs, quantum confinement only exists in two and one dimensions, respectively, along the diameter and thickness directions. As such, tuning the rod diameter and platelet thickness can change the optical gaps of NRs (Figure 1D)^20,78,79 and NPLs (Figure 1E),^80,81 respectively. However, the absorption spectra of QDs, NRs, and NPLs all deviate significantly from their respective DOS spectra. The deviation results from the effects of nonidealized shapes and heterogeneous distribution of sizes, as well as the oversimplification of the realistic band structure of semiconductors and, for NR and NPLs, the neglect of electron–hole Coulomb interactions and their self-interactions (image charge effect).^74,82,83 In the following, we review a higher-level theory that includes these factors and hence can almost quantitatively reproduce the optical spectra of low-dimensional NCs. Specifically, for QDs, because the confinement energy is much higher than electron–hole binding energy, the latter can be treated as a first-order perturbation;^4,77 additionally, because the charge distributions of electron and hole virtually compensate each other within the QD, the image charge effect can be ignored.⁸² For NRs and NPLs, however, the electron and hole are at a distance larger than the diameter of the NR or the thickness of the NPL and interact predominantly through the surrounding medium, which usually has a smaller dielectric constant than the semiconductor itself. This strongly enhances the electron–hole interaction as well as their self-interactions, leading to sizable bandgap renormalization and the formation of strongly bound excitons whose optical features dominate the absorption and PL spectra of NRs and NPLs (see the sharp features on Figure 1D and E).⁸¹⁻⁸³

2.2. Multiband Effective Mass Approximation

For quantum-confined NCs, multiband effective mass approximation (EMA) is often employed to obtain a quantitative picture of the electronic states,^77,84 although plane-wave semiempirical pseudopotential methods have also been used.⁸⁵⁻⁸⁷ Within the EMA framework, the wave functions of carriers comprise the envelope wave function part and the Bloch part, which describe carrier motions in the quantum confinement potential and in the rapidly oscillating lattice potential, respectively.⁸⁸ The applicability of various EMA models is determined by the complexity of band structures in various semiconductors.⁷⁷ One of the typical band structures for semiconductors having zinc blende lattice symmetry (such as CdS, CdSe, CdTe, GaAs, InAs, etc.) is shown in Figure 2A.⁷⁷ The conduction band (CB) shows a near-parabolic band at the band edge, whereas the valence band (VB) is much more complicated with a heavy-hole band, a light-hole band, and a spin–orbit split-off band.

Figure 2.

Multiband effective mass approximation (EMA) models. (A) A typical band structure for bulk semiconductors with a zinc blende lattice structure near the Γ-point of the Brillouin zone. The boxes indicate the applicability of various EMA models used for the calculation of electron and hole energy levels and wave functions. (B) Absorption spectrum of CdSe NCs with a mean radius of 4.1 nm. Some of the well-resolved optical transitions are marked by arrows. (C) Energy of the first excited state (1S_3/21S_e) absorption (black crosses) plotted as a function of 1/radius² for CdSe QDs and its comparison with EMA calculation results (black solid line). (D) Energy of higher-lying excited states (2S_3/21S_e and 1P_3/21P_e; black squares) with respect to that of the first excited state (1S_3/21S_e) plotted as a function of the first excited state transition energy. The black solid lines are EMA calculation results. (A) Adapted from ref (77). Copyright 2000 Annual Reviews. (B) Adapted from ref (92). Copyright 2007 Annual Review. (C and D) Adapted from ref (89). Copyright 1996 American Physical Society.

Efros and co-workers have shown that, for large band gap semiconductors such as CdSe, the CB is sufficiently separated from the VB in energy such that the calculation of electron levels and wave functions near the band edge can be approximated by a single parabolic band EMA model and the calculation for holes near the band edge can be performed under the so-called Luttinger–Kohn (LK) model, which accounts for the light- and heavy-hole bands only (Figure 2A). For holes of higher excitation energy, however, the spin–orbit split-off band must also be included using the so-called six-band model.^63,89 For narrow band gap semiconductors such as InAs, the mixture between CB and VB needs to be included, which is described by the eight-band Pidgeon–Brown (PB) model.^90,91 In the following, we briefly introduce the EMA models for CdSe NCs that treat electrons within the single parabolic band approximation and holes within the six-band approximation, as CdSe is arguably the most prototypical material for quantum-confined NCs. For the calculation of narrow band gap semiconductor nanocrystals such as InAs and PbSe, the readers are referred to other references.^71,72

2.2.1. EMA for QDs

Using the simple single parabolic band EMA approximation for electrons in CdSe QDs, the solved envelope wave function is the product of a spherical harmonic and a spherical Bessel function. The energy levels are labeled by their angular momentum L_e (with L_e = 0, 1, 2, 3... called S, P, D, F... respectively) and radial quantum number n_e.⁸⁹ The first excited state for the electron is the 1S_e level. Because the valence band of CdSe primarily arises from p atomic orbitals, it has an inherent sixfold degeneracy near the band edge (k = 0). The spin–orbit coupling splits this degeneracy into a fourfold degenerate J = 3/2 band and a twofold degenerate J = 1/2 band. J is the total unit-cell angular momentum J = l + s, with l and s being the orbit and spin angular momentums, respectively. The J = 3/2 band is further split into the J_m = ± 3/2 heavy-hole band and the J_m = ± 1/2 light-hole band at k > 0. Taking into consideration this complex band structure (Figure 2A) in the six-band EMA model, the solution to a spherical confinement potential shows significant mixing between the bulk valence band levels. As a result, neither the total unit-cell angular momentum J nor the envelop angular momentum L_h is a good quantum number. Rather, one needs to introduce the total angular momentum F, where F = J + L_h. QD hole states are commonly labeled as n_hL_F. Note that because of the mixing QD hole states nominally labeled as L_h have contributions from both L_h and L_h + 2 spherical harmonics (the so-called “S-D mixing”).^88,89 For example, the first excited hole state 1S_3/2 contains three hole components: (F = 3/2, J = 3/2, L_h= 0), (F = 3/2, J = 3/2, L_h= 2), and (F = 3/2, J = 1/2, L_h= 2). The total QD wave function is the product of the individual electron and hole components. The optical selection rules are calculated from the overlap integral between electron and hole envelop functions, which should be Δn = 0 and ΔL = 0 in the simplest case. In reality, however, this selection rule does not apply due to the hole state mixing; for example, transitions from both S and D hole states into S electron states are allowed.

This six-band EMA model captures almost all the important features in the electronic structure of QDs. The absorption spectrum of a R = 4.1 nm CdSe QD sample in Figure 2B clearly shows the features of optically allowed electron–hole pair states, with the three lowest energy states being 1S_e1S_3/2, 1S_e2S_3/2, and 1P_e1P_3/2, consistent with theoretical calculations.⁹²Figure 2C compares the experimentally measured and theoretically calculated size-dependent energy for the band edge 1S_e1S_3/2 transition, showing good agreement except for very small and large size QDs.⁸⁹ Note that in order to calculate optical transition energies the electron–hole Coulomb interaction needs to be accounted for. For QDs with strong quantum confinement, this binding energy can be treated as a first-order perturbation, and for spherical QDs it is calculated to E_b = −1.8e²/(εr), with ε and r being the high-frequency QD dielectric constant and radius, respectively. In addition to the band edge transition, the experimentally measured size-dependent energy difference between 1S_e2S_3/2 (or 1P_e1P_3/2) and 1S_e1S_3/2 transitions (Figure 2D) can also be reproduced from the theory.⁸⁹ Overall, results show that the six-band EMA model allows for a quantitative description of the electronic and optical properties of CdSe QDs.

2.2.2. EMA for NRs and NPLs

EMA models have also been applied to calculate the electronic structures of 1D NRs and 2D NPLs.^81,82,93,94 Here we briefly review the results on CdSe NRs and NPLs. The basic idea is to treat the dimensions with and without quantum confinement separately using the adiabatic approximation, as the carrier motions along the quantum-confined direction(s) are much faster than those along the unconfined direction(s).⁸² For the calculation of CdSe NRs, Efros and co-workers treat them as ellipsoids with major semiaxis length b (the NR axis) much larger than the minor semiaxis length a (the NR radius).⁸² The quantum-confined fast motion in the radial direction is first solved using the EMA models and then the axial motion is treated by averaging the position over the fast radial motion.⁸² Similar to QDs,^29,77,84,95 the excited states of electrons and holes in the radial direction are calculated using the single-band and six-band EMA models, respectively. A distinction from QDs is that, because of symmetry of NRs, electron states are characterized by the angular momentum projection (m) on the NR axis and labeled as nΣ_e, nΠ_e... for |m| = 0, 1... and n is the number of the level for the given symmetry. Due to the mixing effect in the valence band, hole states are characterized by the total angular momentum projection (j_z) on the NR axis: j_z = m + J_z, where J_z is the projection of the hole spin on the NR axis (J_z = ±1/2, ±3/2...). These states are labeled as nΣ_|jz|, nΠ_|jz|..., respectively.

Based on the optically allowed transitions between these quantum-confined electron and hole levels, Efros and co-workers first calculated the diameter-dependent “bare” gaps of CdSe NRs (Figure 3A), which are defined as the energy difference between the band edge electron and hole states (without the electron–hole binding energy) and should match the gap measured by STM tunneling current experiments. However, Figure 3A shows that the calculated diameter-dependent “bare” gaps for NRs deviate significantly from the tunneling data (by ∼100–200 meV). This is a consequence of bandgap renormalization due to the dielectric confinement effect that strongly enhances charge self-interactions in 1D NRs. As mentioned above, the dielectric confinement effect also strongly enhances the electron–hole binding energy. It is interesting to note that the increases in the charge self-interaction energy and the electron–hole binding energy almost exactly compensate each other. As a result, the exciton transition energy or the optical gap remains largely unaffected by the dielectric confinement effect. For example, Efros and co-workers calculated the electronic structure of 2D CdSe NPLs using an eight-band EMA model.⁸¹ The eight-band EMA model was used for improved accuracy, although six-band EMA should, in principle, be sufficient for CdSe NPLs. In their calculation, they ignored the contribution of the self-interaction terms as well as the increase of the binding energy and simply used a 2D limit for binding energy: E_b = 4E_ex, where E_ex is the exciton binding energy in bulk semiconductors. As shown in Figure 3B, this calculation reproduces the thickness-dependent optical gaps of CdSe NPLs. However, if one needs information on the bandgap renormalization effect and electron–hole binding energy in 1D and 2D nanocrystals, the dielectric confinement effect should be calculated, as we review below.

Figure 3.

Dielectric confinement effect in NRs and NPLs. (A) Diameter-dependence of the tunneling and optical energy gap in CdSe NRs. Dotted and dashed lines show bare and self-interaction-corrected energy gaps between the 1Σ_1/2 hole and the 1Σ_e electron sub-band. Two solid lines show the optical transition energy for the first two optically active 1D excitons. Experimental data for the tunneling and optical gap measured in CdSe NRs from ref (96) are shown by empty circles and filled squares. (B) Thickness-dependent energies of the electron/light-hole (green circles) and electron/heavy-hole (black circles) optical transitions and their comparison with EMA calculations (solid lines). (C) Schematic illustration of the “bare”, tunneling, and optical gaps and dielectric-confinement-induced electron (hole)–image charge-repulsive self-interaction and enhanced electron–hole attraction. (D) Single-particle self-interaction energies as a function of an external medium dielectric constant (ε_ext), with the CdSe dielectric constant fixed at 6, for CdSe NPLs with thicknesses of 3 (black squares), 5 (red circles), and 7 (blue triangles) monolayers calculated using an advanced tight-binding model. (E) Electron/heavy-hole transitions energies calculated for 1S (red circles), 2S (green triangles), 1P (blue triangles), and ∞S (approaching optical gap; black squares) as a function of the NPL thickness using ε_ext = 2. (A) Adapted with permission from ref (82). Copyright 2004 American Chemical Society. (B) Adapted with permission from ref (81). Copyright 2011 Springer Nature. (C) Adapted with permission from ref (20). Copyright 2016 Royal Society of Chemistry. (D and E) Adapted with permission from ref (83). Copyright 2014 American Physical Society.

2.3. Dielectric Confinement Effect in 1D NRs and 2D NPLs

The dielectric confinement effect arises from the difference between the dielectric constants of 1D and 2D semiconductors (ε_s) and their external medium (ε_ext).⁹⁷ First, it enhances the (repulsive) self-interactions of electrons and holes with their image charges, thus leading to a sizable increase in the quasi-particle gap (bandgap renormalization),⁹⁸ as illustrated in Figure 3C. On the other hand, it also strongly enhances the electron–hole attractive interactions, resulting in a large exciton binding energy that lowers the optical gap considerably from the quasi-particle gap. In their calculation for CdSe NRs, Efros and co-workers calculated Coulomb interactions enhanced by the dielectric contrast effect using U(r_e, r_h) = −e²/(ε_s|r_e – r_h |) – eV(r_e, r_h) + eV(r_e, r_e) + eV(r_h, r_h), where the first and second terms are electron–hole interaction potentials through inside and outside the NR, respectively, and the last two terms are electron and hole self-interaction potentials.⁸² By averaging U(r_e,r_h) over the electron and hole wave functions in the radial direction, they obtained a 1D potential profile of electron–hole (e-h) Coulomb interaction and electron (hole) self-interaction corrections to their quantum-confined energy levels. As shown in Figure 3A, after adding the self-interaction corrections to the energy difference between the band edge electron and hole states, the “bare” gaps increase by ∼100–200 meV and become consistent with the experimentally measured tunneling gaps. The two lowest optically allowed excitonic transitions obtained by solving the 1D e-h potential are shown in Figure 3A. The diameter-dependent energies for the ground excitonic states match the experimental optical gaps well. Also, it can be seen that the energy of the ground excitonic state is lower than the tunneling gap by ∼150 meV, which reflects the large exciton binding energy in CdSe NRs.

Similar calculations have been performed on 2D CdSe NPLs.^83,99Figure 3D shows the calculated electron and hole self-interaction energies as a function of the dielectric constant of the external medium ε_ext for NPLs with different thicknesses.⁸³ The self-interaction energies increase considerably as ε_ext decreases, and this effect is more obvious for thinner CdSe NPLs, indicating that the dielectric confinement effect is stronger for thinner NPLs and for the situation with a smaller ε_ext. For the 3 monolayer (ML) CdSe NPLs, when ε_ext is 1 (i.e., in the air), electron and hole self-interaction energies reach ∼300 meV and the total bandgap renormalization reaches ∼600 meV. Figure 3E shows the calculated thickness-dependent electron and hole binding energies for ε_ext = 2, which decrease from ∼100 meV for 3 ML NPLs to ∼50 meV for 7 ML NPLs.⁸³ Similar dielectric-contrast-enhanced strongly bound excitons have been observed in many other 1D and 2D material, such as carbon nanotubes, graphene, and monolayer transition metal dichalcogenides.^{74,98,100−104}

2.4. Exciton Fine Structure and Lifetime in 0D, 1D, and 2D Nanocrystals

Besides the spectral properties, it is also important to understand the dynamic properties of quantum-confined NCs, as they dictate the time window available for charge extractions from these NCs. The electron–hole recombination dynamics in NCs are determined by the trap states and the fine-structures. The trapping process is usually much faster than the radiative recombination process; for example, the hole trapping in CdSe QDs can be as fast as ∼10 fs.¹⁰⁵ Therefore, in QD ensembles, QDs with traps are dominated by the nonradiative recombination between the CB edge electron and trapped hole, while QDs without traps undergo radiative recombination between band edge carriers with their dynamic properties controlled by the fine structure of their band edge excitons. In 1D NRs and 2D NPLs, other factors such as giant oscillator strength transition effect further modify the band edge exciton radiative lifetime in addition to the fine structure.

The fine structure of the band edge 1S_e–1S_3/2 excitons of CdSe QDs, as developed by Efros, Bawendi, and co-workers,^28,29 is schematically shown in Figure 4A. The splitting of the fine structure is mainly induced by the combined effect of short- and long-range electron–hole exchange interactions and anisotropies associated with the crystal field and nanocrystal shape asymmetry.¹⁰⁶ The exchange interaction is typically weak (at most a few meVs) for bulk inorganic semiconductors and thus is often ignored, unlike the strong interaction that leads to large singlet–triplet splitting in organic materials. In NCs, however, the quantum-confinement-induced strong electron–hole wave function overlap enhances the exchange interaction energy up to tens of meVs. As a result, one should consider a correlated band edge exciton, rather than independent electron and hole, with a total angular momentum of N (N = 1 or 2). N = 1 corresponds to a high-energy optically active exciton (so-called “bright” exciton), whereas N = 2 is a lower-energy optically passive exciton (so-called “dark” exciton), as a photon can only carry a momentum of 1. Due to the asymmetric crystal field and NC shape, the good quantum number is the projection of the total angular momentum along the unique crystal axis (N_m) and hence the N = 1 and 2 states are further split into two manifolds of states (Figure 4A). The new lowest-energy state is still a “dark” exciton characterized by N_m = ±2, and the next higher-energy state is a “bright” exciton with N_m = ±1.

Figure 4.

Exciton fine structure and lifetime. (A) Scheme of the fine structure of the band edge 1S_e–1S_3/2 excitons of CdSe QDs. The fine structure splitting is mainly introduced by anisotropic effects and e-h exchange interactions. (B) Time-resolved PL decay curves measured for typical CdSe QDs at indicated temperatures. (C) Scheme of the fine structure of the band edge excitons of perovskite NCs. Here the fine structure splitting is mainly introduced by e-h exchange interactions and the Rashba effect under orthorhombic symmetry. (D) Time-resolved PL decay curves measured for single CsPbI₃, CsPbBr₃, and CsPbBr₂Cl perovskite NCs at cryogenic temperatures. (E) Bright–dark splitting of CdSe NPLs (ΔE_AF) as a function of the reciprocal of NPL thickness (1/L). Crosses and circles represent results measured by PL line narrowing and temperature-dependent time-resolved PL, respectively. (F) Time-dependent PL decay curves measured for typical CdSe NPLs at indicated temperatures. (A and B) Adapted with permission from ref (88). Copyright 2016 American Chemical Society. (C and D) Adapted with permission from ref (107). Copyright 2018 Springer Nature. (E) Adapted with permission from ref (108). Copyright 2018 Royal Society of Chemistry. (F) Adapted with permission from ref (81). Copyright 2011 Springer Nature.

The splitting between the “dark” and “bright” excitonic states is in the range of a few to 10 meV, with smaller QDs having larger splitting due to stronger electron–hole exchange interactions. This splitting controls the temperature-dependent radiative recombination dynamics of band edge excitons. As shown in Figure 4B, at very low temperatures excitons primarily occupy the “dark” state and thus recombine on a μs time scale. With increasing temperatures, excitons more and more occupy the “bright state”, resulting in faster radiative recombination. At room temperature, the thermal energy (∼26 meV) is sufficiently high as compared to the dark–bright splitting energy of a few meV. As a result, excitons are approximately distributed equally between the “dark” and “bright” states, leading to a lifetime of ∼20 ns for typical CdSe QDs. This intrinsic exciton lifetime is longer than the time constants for many interfacial charge transfer from QDs and hence is often not a limiting factor for efficient charge extraction from QDs.

The band edge exciton structures of most QDs can be explained by the picture depicted above. The recently introduced lead halide perovskite nanocrystals (NCs), however, likely feature a different type of fine structure. These NCs have large extinction coefficients and exceptional light-emitting properties; as-synthesized NCs can attain emission quantum yields in the range of 50–90% without any postsynthetic treatments.¹⁰⁹ To account for these properties, Efros and co-workers theoretically examined the fine structure of perovskite NCs and proposed a structure with a “bright” triplet state as the lowest-energy band edge state.^107,110 Specifically, because the top of the valence band is contributed by Pb 6s and Br 4p atomic orbitals with an overall s-like symmetry, the band edge hole state has J_h = 1/2, which is different from that of CdSe QDs. The electron–hole exchange interaction mixes the angular momentum of the electron and hole states to form a J = 0 singlet state and a threefold degenerate J = 1 triplet state, with the former being “dark” and the latter “bright” (Figure 4C). The singlet state would lie below the triplet state if only considering the electron–hole exchange interaction. These perovskite NCs, however, exhibit a strong Rashba effect due to strong spin–orbital coupling and breaking of inversion symmetry. The reasons for the inversion asymmetry remain unclear but are likely related to cation positional instabilities or surface effects. The Rashba effect inverts the energetic order between the singlet and triplet states, leading to a unique fine structure featuring a lowest-energy “bright” triplet state (Figure 4C). Because of the large oscillator strength of the “bright” triplet state, radiative recombination of band edge excitons in perovskite NCs is very fast (a few ns at room temperature) and accelerates with decreasing temperatures. As shown in Figure 4D, at cryogenic temperatures, the recombination time of band edge excitons can be as fast as 0.18 ns. The fast radiative recombination in perovskite NCs, along with the unique “defect-tolerance” in these materials, is responsible for their exceptional light-emitting performances, which, on the other hand, could also limit the efficiency of charge extraction from these NCs. Nonetheless, ultrafast measurements revealed that interfacial charge transfer from these NCs could be engineered to occur on a ps time scale, thus competing effectively with exciton recombination.¹¹¹

For fine-structures of CdSe NRs, Efros and co-workers found that the optically dark F_z = 0 state (the projection of the total angular momentum along the rod axis) is situated a few meV below the optically bright F_z = ±1 state, which is partially responsible for the linearly polarized emission from NRs in addition to the dielectric polarization effect, similar to QDs.⁸² On the other hand, different from the QDs, the order of fine structure states can depend on both the length and radius of the NR.^112,113 For fine-structures of CdSe NPLs, Biadala and co-workers measured the PL lifetime of CdSe NPLs as a function of temperatures and applied magnetic fields.¹¹⁴ They found that the PL lifetime increases with decreasing temperatures and that at a constant temperature of 4.2 K the PL lifetime decreases with increasing applied magnetic fields. Using similar PL measurements, Shornikova and co-workers reported the splitting between the bright and dark exciton states as ∼3–6 meV for 3–5 ML CdSe NPLs (Figure 4E).¹⁰⁸ All these observations are qualitatively consistent with those of 0D QDs, suggesting similar band edge fine structures. Moreover, due to the large exciton binding energy, Rydberg series of the band edge excitons in CdSe NPLs can be observed under optical measurements,¹¹⁵ similar to transition metal dichalcogenide.^100,116 In particular, Achtstein and co-workers observed the emission from the p-state of the band edge exciton in 4 ML CdSe NPLs at low temperature (4 K) with an s- and p-state splitting of ∼30 meV and found that the relaxation rate between p- and s-state of band edge exciton strongly depends on the lateral dimension of the NPL and shows a LO-phonon bottleneck.¹¹⁵ Unlike 0D QDs, the band edge exciton recombination dynamics 2D NPLs are strongly modified by a so-called giant oscillator strength transition effect, which is induced by a coherent extension of the exciton center-of-mass motion along the unconfined dimensions at low temperature due to the suppressed exciton–phonon scattering.^81,117−119 This effect leads to a fast radiative recombination of excitons; hence, intrinsic exciton half-lifetimes decrease to sub-ns at low temperatures (<150 K) (Figure 4F).^81,119 Because of the fast diffusion of excitons/carriers in NRs and NPLs and the fast interfacial charge transfer from them, this lifetime window is also sufficient to enable efficient exciton dissociation.

2.5. Effect of Exciton Fine Structure on Transient Absorption Spectral Signatures

Ultrafast pump–probe transient absorption (TA) spectroscopy has been widely used to study the excited charge carrier dynamics in quantum-confined nanocrystals.^120,121 The photogenerated exciton, or electron and hole, blocks the ground state excitonic transitions due to the state filling in the conduction band (CB) and valence band (VB), causing an exciton bleach (XB) signal in the TA spectrum. The bleach amplitude can be related to the exciton or electron and hole population according to the band edge exciton fine structures^29,122−125 and can be used as a convenient probe of exciton and carrier dynamics in QDs, such as hot carrier cooling,^126,127 electron–hole recombination,^128,129 Auger processes,^130−132 and charge transfer and recombination.^121,133,134 It has been reported that both CB electron and VB hole contribute to the band edge XB signal in PbS,^135−137 PbSe,^121,138,139 and CsPbX₃ (X = Cl, Br, I) QDs or nanocrystals^140−142 due to the band edge state filling effect. However, in cadmium chalcogenide QDs, such as CdSe,^{123,124,133,143−145} CdS,¹⁴⁶ and CdTe,^134,147 the XB is dominated by CB electron state filling effect with negligible VB hole contribution. For example, selectively removing electron from the CdSe or CdS QDs leads to complete XB recovery.^148,149 Same XB signal assignment was applied to their nanorods (NRs)^150−153 and nanoplatelets (NPLs)^154−156 counterparts, as well as InP^157,158 and Cd₃P₂ QDs.¹⁵⁹ The lack of a VB hole state filling effect was assumed to result from the high degeneracy of the hole states at VB top and/or the ultrafast hole trapping in these materials.^160,161 It is worth noting that, however, the XB decay corresponding to ultrafast hole trapping in CdSe QDs has not been observed even in transient measurements with 10 fs time resolution.¹⁰⁵

The VB hole-induced bleach signal in TA spectrum in cadmium chalcogenide QDs was not observed until recently when the hole traps were eliminated in core/shell heterostructures or surface passivation.^162−165 Grimaldi et al. showed that the VB hole contributes to 32 ± 2% of the 1S exciton [1S_3/2(h)–1S(e)] bleach in CdSe/CdS/ZnS core/shell/shell QDs with a photoluminescence quantum yield (PLQY) of 82%.¹⁶² This hole contribution was measured from the growth kinetics of the 1S XB when the hole relaxes from the 2S_3/2 state to the 1S_3/2 state. A fourfold degeneracy of the 1S_3/2 hole state at the top of the VB was assumed to account for the one-third hole contribution to the exciton bleach, while the band edge exciton fine structure was not considered. In similar CdSe/CdS core/shell QDs with a PLQY of 81%, He at al. reported a hole contribution of 22 ± 1% by fitting the TA spectrum of the single hole state in QDs after selective removal of the CB electron.¹⁶³ The authors proposed that, in the absence of hole traps, the low hole contribution to the XB signal is mainly due to the exciton fine structure, i.e., the thermal distribution of hole populations in bright and dark exciton states. The hole bleach signal was later reported by Huang et al.¹⁶⁶ in TA spectra of Cd-based core/shell QDs and by Brosseau et al.¹⁶⁷ in two-dimensional electronic spectroscopy with high energy and time resolutions. Identification of hole-induced absorption bleach implies possible optical gain in Cd-based QDs and helps to rationalize the design of QD lasers.^162,166 Moreover, hole-state-filling-induced TA spectra of Cd-based QDs may enable direct probing of the hole transfer process by TA spectroscopy.

3. Wave Function Engineering and Carrier Dynamics in 0D, 1D, and 2D Heteronanocrystals

3.1. Wave Function Engineering in Heteronanocrystals

The spectral and dynamic properties of NCs can be further engineered by building heterostructured NCs such as core/shell QDs. In these heterostructures, the spatial distribution of the wave functions of electrons and holes can be tailored by the sizes and compositions of the constituent materials.¹⁶⁸ This is the concept of “wavefunction engineering”. On the basis of the energy offsets of bulk conduction band (CB) and valence band (VB) edges of the constituent materials, the band alignment in semiconductor heterostructures can be classified as type I, quasi-type II, and type II, as depicted in Figure 5A. In a type I structure, both the CB and VB edges of one component are situated within the band gap of the other component, a typical example for which is CdSe/ZnS. As a result, both the lowest-energy electron and hole wave functions are primarily confined in the low band gap material. In contrast, a type II structure features a staggered band alignment with the lower energy CB and VB edges situated on different components, as exhibited in, e.g., CdSe/CdTe. This type of band alignment should lead to spatial separation of electron and hole wave functions into different domains. A quasi-type II structure is the intermediate case between type I and type II structures, with the two components share the same (or similar) CB or VB edge. For example, the VB edges are similar for CdSe and ZnSe, while their CB edges have an offset of ∼0.9 eV.¹⁶⁹

Figure 5.

Wave function engineering in heterostructured nanocrystals. (A) Schematic depictions of the band alignments (black lines) and electron (red) and hole (blue) wave function distributions in type I, quasi-type II, and type II core/shell QDs. (B) Schematic of the “giant” NC structure where R is the CdSe core radius and H is the CdS shell thickness (left). Spatial probability distribution of the hole (dark gray area) and electron (light gray area) for an R = 1.5 nm and H = 5.0 nm core/shell QD (right). The inset shows a contour plot of the calculated electron–hole overlap integral. White and black lines are boundaries between regions of (R, H)-space that correspond to different localization regimes. (A) Adapted with permission from ref (168). Copyright 2012 Royal Society of Chemistry. (B) Adapted with permission from ref (179). Copyright 2009 American Chemical Society.

However, because of the quantum confinement effect strongly modifying the band edges of semiconductor NCs, it is important to note that the electronic structure of a heterostructured NC can be different from that of its bulk counterpart. To avoid this confusion, we shall use the term “band alignment” only for bulk materials and the term “electronic structure” for NCs. For example, the VB offset between bulk wurtzite CdSe and CdS is large (≥0.45 V) and the CB offset is relatively smaller (≤0.3 V),^170,171 which is a type I band alignment. However, the electronic structure of CdSe@CdS NRs is tunable from type I (with both the electron and hole confined in CdSe) to quasi-type II (with the hole confined CdSe and the electron delocalized among CdSe and CdS) depending on the sizes of the CdSe and CdS domains.^171−178

Figure 5B (right) shows the spatial probability distributions (proportional to the square of wave function) of the lowest-energy CB electron and VB hole in CdSe/CdS core/shell QDs with a core radius (R) of 1.5 nm and a shell thickness (H) of 5.0 nm, as calculated using EMA methods.¹⁷⁹ The hole wave function is mostly confined in the core, while the electron wave function is delocalized over the whole core/shell, which is a typical signature of quasi-type II electronic structure. Calculations also show that the electron and hole wave function distributions indeed depend sensitively on the R and H parameters, as illustrated by the calculated electron–hole wave function overlap integral in Figure 5B (right inset). When the shell is very thin (small H), both the electron and hole can effectively tunnel into the shell regardless of the core size. As a result, the electron–hole overlap is large, corresponding to the type I regime. Alternatively, in the case of a diminishingly small core, both the electron and hole effectively spill into the shell regardless of the shell thickness, which is also a type I structure; however, this is not a practical case, as it would be very difficult to coat a shell on a diminishingly small core. For a normal core size (R > 1 nm), when the shell becomes thicker, a small core with strong electron confinement energy leads to a delocalized electron and a core-confined hole, which is a quasi-type II structure featuring a smaller electron–hole overlap, whereas a larger core with weaker electron confinement energy results in a core-confined electron and hole in the type I regime.

The concept of wave function engineering has also been extended to 1D hetero-NRs and 2D hetero-NPLs.^{170,180−184} For example, ZnSe@ZnS dot-in-rod hetero-NRs¹⁸⁵ have a type I electronic structure (Figure 6A), whereas ZnSe@CdS hetero-NRs¹⁸⁶ have a type II electronic structure (Figure 6B). Particularly interesting are the CdSe@CdS dot-in-rod hetero-NRs (Figure 6C), which can attain the same type of wave function engineering from type I to quasi-type II as CdSe@CdS core/shell QDs by simply tuning the core sizes and rod diameters (refs (49, 170−176, 181, 182, 187−206)). The absorption spectrum of CdSe@CdS NRs mainly consists of two features, B1 and B2, that are associated with the lowest-energy exciton states of the rod and the core, respectively (Figure 6C). For NRs with relatively small-size cores, the electron wave function is delocalized from the core to the rod, whereas the hole wave function is still confined in the core (i.e., B1 and B2 share the same electronic level but have different hole levels), forming a quasi-type II structure. For samples with larger cores, both the lowest electron and hole levels are located in the core, forming a type I structure. Experimentally, these electronic structures can be readily probed using TA measurements.^173,196,207 Specifically, one can selectively excite the B2 band of the core and monitor its influence on B1 band of the rod.¹⁷⁷Figure 6D shows the TA spectra averaged between 1 and 2 ps following B2 excitation for NRs of various lengths with both 2.7 and 3.8 nm diameter seeds. For NRs with a 2.7 nm seed (Figure 6D, top), excitation at B2 leads to instantaneous and simultaneous formation of strong bleaches of both B2 and B1 bands. Since these bleaches are dominated by the CB electron state filling contribution,²⁰⁷ this result indicates that B1 and B2 bands share the same CB electronic level, consistent with a quasi-type II electronic structure.^174,207 In contrast, for 3.8 nm seeded NRs (Figure 6D, bottom), excitation at B2 only generates a strong B2 bleach with negligible B1 bleach. The derivative-like feature near B1 bleach is also observed in CdSe core only QDs and can be attributed to a biexciton-interaction-induced shift of higher energy transitions in the core.²⁰⁸ Therefore, these 3.8 nm seeded NRs have a type I electronic structure.

Figure 6.

Wave function engineering in 1D hetero-NRs and 2D hetero-NPLs. (A–C) The absorption spectra (shaded regions) and PL spectra (colored lines) of (A) ZnSe@ZnS, (B) ZnSe@CdS, and (C) CdSe@CdS dot-in-rod hetero-NRs. B1 and B2 transition features on CdSe@CdS NRs are labeled. (D) Averaged transient absorption (TA) spectra of CdSe@CdS hetero-NRs with 2.7 nm (top) and 3.8 nm (bottom) diameter CdSe cores and varying rod lengths at 1–2 ps after ∼580 nm excitation. For comparison, TA spectra of corresponding CdSe QDs with similar confinement energies are also shown. (E) Absorption, PL, and PL-excitation (PLE) spectra of type II CdSe@CdTe core/crown hetero-NPLs. The inset shows the scheme of the hetero-NPL. (F) Absorption and PL spectra of type I CdSe@CdS core/crown hetero-NPLs. Inset shows the scheme of the htero-NPL. (A–C) are reproduced with permission from ref (180). Copyright 2013 Elsevier Ltd. (D) Adapted with permission from ref (177). Copyright 2015 American Chemical Society. (E) is reproduced with permission from ref (209). Copyright 2014 American Chemical Society. (F) is reproduced with permission from ref (210). Copyright 2014 American Chemical Society.

Wave function engineered 2D NPLs have also been reported. For example, growing a CdTe NPL laterally on the edge of a CdSe NPL, or vice versa, leads to core/crown hetero-NPLs with a type II electronic structure (Figure 6E).^{209,211−218} The strongest evidence for the type II heterostructure is the appearance of an absorption tail with lower energy than both CdSe and CdTe band edge absorptions and the emission associated with this tail (Figure 6E),²⁰⁹ which is the so-called charge-transfer (CT) transition from the top of the CdTe VB to the bottom of the CdSe CB formed due to strong electronic coupling between the two epitaxially attached domains.^209,211,218 It is also worth noting that Scholes and co-workers attributed the emission of CdSe/CdTe core/crown NPLs to trapped state emission instead of CT exciton emission, as the latter has a very weak transition strength.²¹⁹ Type I hetero-NPLs with a CdSe core embedded in a CdS crown have also been reported (Figure 6F).^{210,213,220,221} Due to the type I electronic structure, photoexcitation energy generated in the CdS crowns can be effectively funneled in to the CdSe cores where light can be emitted.^210,221 Owing to the exceptional light-harvesting capability of 2D structures, this funneling mechanism can leads to very high excitation densities at the CdSe cores for light-emitting or conversion applications.^{213,217,222,223}

An important difference between 1D hetero-NRs (2D hetero-NPLs) and 0D core/shell QDs is that the band alignment (or electronic structure) is not the only factor that dictates the wave function distributions of the electron and hole. The strong electron–hole binding in 1D and 2D systems also strongly modifies the wave function distributions. As a result, in (quasi-)type II NRs and NPLs, for example, the electron and hole are not completely delocalized over different domains but instead are localized near the charge separation interface.²¹¹

Mauser and co-workers reported the effect of electron–hole binding on electron and hole wave functions in quasi-type II CdSe@CdS tetrapods (Figure 7A-D).¹⁹⁸ They calculated the wave functions of the CB electron and VB hole using an EMA model that takes into account e-h Coulomb interactions. The Coulomb attraction energy used in the calculations is 75 meV, which is a lower limit but already significantly affects the electron and hole wave functions. The initially photogenerated electron and hole are delocalized along the CdS rod arms (Figure 7C). The hole wave function is then localized to the CdSe core region due to a large VB offset between the CdSe and CdS. As a consequence of the strong e-h interaction, the electron wave function is also localized in and near the CdSe core instead of delocalized over the CdS arms despite the quasi-type II electronic structure of the tetrapods (Figure 7B). Not only the band edge hole but also a trapped hole can bind strongly to the electron. As shown in Figure 7D, when the hole is localized to a defect state on the CdS arm, the electron wave function is also localized in and near the hole trapping site. In a more recent work, Beard and co-workers showed that even an electron transferred to an acceptor bound to the NR surfaces can strongly localize the hole to near the reduced acceptor.²²⁴ As schematically shown in Figure 7E, photoexcitation of CdSe NR–methylene blue (MB) complexes leads to electron transfer from the CdS to MB in ∼3.5 ps, as measured by transient absorption spectroscopy. Additional measurements using time-resolved terahertz spectroscopy indicate that the hole remained in the rod, localized around the reduced MB in ∼11.7 ps. Calculations performed by Efros and co-workers show that, because of the strong electron–hole binding energy that acts as a Coulomb potential well for the hole, the wave function of the lowest energy hole in the bound state is localized to a ∼ ±0.8 nm region near the reduced electron acceptor, and the activation energy to detrap the hole from the potential well can be as large as 235 meV.²²⁴

Figure 7.

(A–D) Calculated electron and hole wave functions in CdSe@CdS tetrapods. (A) Energy level plotted along the long axis of one of the tetrapod arms. The arrows indicate the real-space dynamics of the electron and hole transfer to the core (red) or to a trapping site (blue). (B) Electron and hole wave functions at the band edge of the structure with the hole confined in the CdSe. (C) Electron and hole at the band edge states of the CdS rod before relaxation of the hole to the CdSe core. (D) The hole wave function is localized in a low-energy trapping site in one of the CdS arms, resulting in the localization of the electron wave function to the same arm. (E) Schematic illustration of the hole localization after ET from a CdSe NR to adsorbed methylene blue. (F) Coulomb potential well (black line) and hole wave function density distribution, in the lowest two states, in charge-separated CdSe NR–MB. (A–D) Adapted with permission from ref (198). Copyright 2010 American Physical Society. (E and F) Adapted with permission from ref (224). Copyright 2016 American Chemical Society.

In some cases, the electron–hole binding energy is stronger than the energy level offset in heterostructures such that it does not simply modify the wave function but rather completely alters the localization behavior of carriers. As demonstrated by Wu and co-workers, the CB level offset in CdSe@CdS dot-in-rod NRs can be probed by doping an electron into the core and observing the localization behavior of the doped electron.²²⁵ They find that for NRs with relative small CB level offset the electronic structure of the NR probed by electron-doping is quasi-type II whereas transient absorption measurement reveal they are type I NRs. Thus, these NRs behave as a quasi-type II structure for a single CB electron but as a type I structure in the presence of an electron–hole pair. All these reports suggest that for 1D and 2D hetero-NCs the band alignment (electronic structure) and electron–hole coulomb interaction codictate the spatial distribution of the electron and hole wave functions. Furthermore, the interfacial strain, introduced by external force or additional growth of heterostructures, also provides strong impact on electronic structure and carrier dynamics of NCs.²²⁶ With a sub-100 nm dimension, NC heterostructures can withstand significant elastic deformations, with their equilibrium lattice constant differing from their bulk counterpart. It has been reported that strain can convert the band alignments of CdTe/ZnSe QDs from type I to a type II.²²⁷ Moreover, strain also strongly affect carrier relaxation and recombination in CdSe/CdTe^228−230 and CdSe/CdS NR heterostructures.²²⁶

3.2. Charge Transfer and Transport Dynamics Inside Hetero-NCs

From the standpoint of charge transfer from NCs, wave-function-engineered hetero-NCs are attractive because of their internal charge transfer/separation behaviors that can be used to tailor the rate and yield of charge transfer to external acceptors. As such, it is important to understand charge transfer/separation inside hetero-NCs. For hetero-QDs, we illustrate internal charge separation using CdTe/CdSe type II core/shells (Figure 8A–F).¹⁴⁷ The absorption spectra of these QDs shows B1, B2, B3, and C features (Figure 8B). According to EMA calculations, B1 and B2 can be assigned to the CT transitions from the CdTe VB to the CdSe CB, and B3 and C can be assigned to the transitions within CdSe and CdTe, respectively (Figure 8A). The TA spectra of core/shell QDs after 400 nm excitation show that the decay of the bleach of the C feature leads to the concomitant growth of the bleach at the B1, B2, and B3 features (Figure 8C), which can be assigned to interdomain electron transfer from the CdTe core to CdSe shell because the bleach of exciton bands is dominated by the contribution of the CB electron. Fitting the kinetics of these features (Figure 8D) reveals that this internal charge separation process occurred with a time constant of ∼0.77 ps. Similar sub-ps processes have been reported in other type II QDs.^231−233 After initial charge separation, all the TA features that correspond to the CdSe CB edge electrons are long-lived (Figure 8E). Fitting the TA features reveals an excited-state lifetime of 62 ns (half-life) for the CB electron, which is more than one order of magnitude longer than that in CdTe core QDs (Figure 8F). Thus, the wave function engineering approach not only effectively localizes the electron and the hole to the shell and the core, respectively, which facilitates electron transfer to external acceptors and suppresses ensuing charge recombination (illustrated in the next section), but also leads to a longer-lived excited state for more efficient charge extraction.

Figure 8.

Charge separation dynamics in type II heterostructured nanocrystals. (A) Band alignment diagram of bulk CdTe/CdSe (black solid lines) and calculated quantum-confined energy levels (colored dashed lines) of CdTe/CdSe QDs. B1, B2, B3, and C transitions are indicated by arrows. (B) Absorption (solid) and emission (dashed) spectra of CdTe seeds (black) and type II CdTe/CdSe core/shell QDs (red). Also shown is a TA spectrum of CdTe/CdSe QDs probed at 1 ps after 400 nm excitation, which clearly shows four bleach bands (B1, B2, B3, and C). (C and E) TA spectra of CdTe/CdSe QDs at selected delays in (C) 0–5 ps and (E) 5 ps to 1 μs following 400 nm excitation. (D) Formation and decay kinetics of the bleaches at the B1, B2, B3, and C bands from 0 to 5 ps. These signals have been scaled by factors indicated in the legend for better comparison. (F) Comparison of the bleach recovery kinetics of B1, B2, and B3 bands in CdTe/CdSe QDs with the exciton bleach recovery kinetics of CdTe seeds. (G) Absorption (red) and emission (blue) spectra of CdSe/CdTe NRs. The inset illustrates three absorption bands: lowest-energy exciton states of CdSe (a) and CdTe (b) and charge transfer (CT) transition (c). (H) TA spectra of CdSe/CdTe NRs (top) and mixed CdSe and CdTe NRs (bottom) at indicated time delays following 620 nm excitation (exciting CdTe). (A–F) Adapted with permission from ref²³⁴. Copyright 2011 American Chemical Society. (G and H) Adapted with permission from ref (235). Copyright 2008 American Chemical Society.

Internal charge separation was also reported for CdSe/CdTe type II hetero-NRs (Figure 8G and H).²³⁵ The absorption spectrum of CdSe/CdTe NRs contains a, b, and c bands that can be assigned to the 1Σ excitonic feature of the CdSe, the 1Σ excitonic feature of the CdTe, and the CT transition from the CdTe VB to the CdSe CB, respectively (Figure 8G). The PL spectrum of CdSe/CdTe consists of only the CT band emission (Figure 8G), indicating efficient charge separation between CdSe and CdTe domains. These static spectra features are similar to those of type II QDs. The internal charge separation dynamics was investigated using TA spectroscopy by applying a 620 nm excitation pulse that resonantly excites the CdTe 1Σ band (Figure 8H). The CdTe bleach feature forms instantaneously and then shows significant decay within 2 ps, which is accompanied by the growth of the CdSe and CT band bleach. Analysis of the TA kinetics reveals a CdTe-to-CdSe electron transfer time constant of ∼500 fs. In a related work, Zamkov and co-workers measured carrier dynamics in CdS/ZnSe type II nanobarbells and reported an electron transfer time of ∼0.35 ps from the ZnSe tips into the CdS NR.²³⁶ These time constants are similar to those reported in CdSe/CdTe core/shell QDs above (∼770 fs¹⁴⁷) and also 2D core/crown nanoplatelets (∼640 fs²¹¹).

In principle, the electron transfer time in core/shell QDs only contains interfacial electron transfer and that in hetero-NRs or core/crown nanoplatelets contains both interfacial electron transfer and carrier/exciton transport to the interface. The even faster time constant observed in NRs and nanoplatelets indicates that the carrier/exciton transport in these materials is fast and there likely exists charge transfer barrier in curved core/shell interface in QDs caused by interfacial lattice strain.²³⁷ These results show that interdomain electron transfer inside these 1D NRs and 2D NPLs are often fast due to fast carrier/exciton transport along the NRs and NPLs and strong electronic coupling between epitaxially grown semiconductor domains.

For 1D NRs and 2D NPLs, surface/interfacial carrier trapping and strong electron–hole binding also play critical roles in the carrier/exciton transport dynamics. These effects in 1D NRs were illustrated in our previous work by studying the length dependence of rod-to-seed exciton localization efficiency in CdSe@CdS NRs.¹⁷⁷ Transmission electron microscopy (TEM) images and energy dispersive X-ray spectroscopy (EDX) maps can be used to accurately determine the rod-to-seed exciton transport distances (Figure 9A).^181,195 In these NRs, photoluminescence is dominated by excitons localized in the CdSe seed. Through photoluminescence excitation (PLE) measurements, the rod-to-seed exciton localization efficiency can be determined by comparing the PLE spectra of these NRs to their absorptance spectra (Figure 9B). Specifically, by normalizing the PLE spectra to corresponding absorptance spectra at the B2 band (Figure 9B, inset), the efficiency of exciton localization from the CdS rod into the CdSe seed can be calculated from the ratio of normalized PLE over absorptance.²⁰⁷ The ratio is 1 at >520 nm, decreases gradually at 480–520 nm, and finally levels off at <480 nm, where the CdS rod absorption dominates, to ∼76%, 56%, and 30% for NRs with lengths of 29, 47, and 117 nm, respectively (Figure 9C).

Figure 9.

Competition between exciton transport and trapping in hetero-NRs and NPLs. (A) TEM images of CdSe@CdS NRs with 2.7 nm CdSe cores and different lengths (top, 29 nm; middle, 47 nm; bottom, 117 nm). Insets show the corresponding EDX elemental maps indicating the location of the CdSe core (green). (B) Absorptance (black solid line), PL (blue solid line), and PLE (red dashed line) spectra of NRs shown in (A). The PLE and absorptance spectra have been normalized at the lowest energy exciton peak in the core, as shown by the insets. (C) Wavelength-dependent relative PL QYs of the NRs shown in (A). The shaded areas show regions of gradual decrease of relative PL QYs. (D) Scheme showing the competition between exciton transport to the core through 1D diffusion and exciton localization on the rod through hole trapping (top). Measured (symbols) and simulated (dashed line) exciton localization efficiencies in CdSe@CdS NRs (middle). The efficiency is independent of core sizes: 2.5 nm (blue triangles), 2.7 nm (red circles), and 3.8 nm (green squares). CdS rod absorption cross-section (black solid line) and effective CdSe seed absorption cross section (red dashed line) as a function of rod length (bottom). (E) Schematics of crown-to-core exciton diffusive transport, EDX image, and band alignment in type I CdSe/CdS core/crown NPLs. (F) Schematics of crown-to-core exciton diffusive transport, EDX image, and band alignment in type II CdSe/CdTe core/crown NPLs. (A–D) Adapted with permission from ref (177). Copyright 2015 American Chemical Society. (E) Adapted with permission from ref (221). Copyright 2016 American Chemical Society. (F) Adapted with permission from ref (212). Copyright 2017 American Chemical Society.

The length-dependent exciton localization efficiencies are modeled by a 1D diffusion model that includes exciton surface trapping:²⁰⁷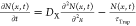, where D_X is the exciton diffusion constant, N(x, t) is the time- and position-dependent exciton concentration, and τ_Trap is the exciton trapping time (0.78 ps).¹⁷⁷ This model implicitly assumes that charge transfer at the CdSe–CdS interface is much faster than exciton diffusion along the rod. As shown in Figure 9D (middle), with D_X as the only fitting parameter, we can simultaneously fit the localization efficiency for all NRs. The best fit gives a diffusion constant D_X of 2.3 cm²/s, slightly smaller than the bulk value of 3.2 cm²/s.^238−242 According to this diffusion constant, exciton diffusion over 10 nm takes ∼0.5 ps (and further scales quadratically with diffusion length). Based on the length-dependent exciton localization efficiency in these CdSe@CdS NRs, we define an effective absorption cross section as a product of the rod absorption cross section and the localization efficiency, which represents the cross section for creating excitons in the seed through absorption at the rod.¹⁷⁷ As shown in Figure 9D (bottom), the effective seed absorption cross section first increases with the rod length and approaches saturation at a rod length of ∼100 nm, with an effective seed absorption cross section saturating at ∼3.5-fold of that of the short rod. This result suggests the existence of an optimal rod length for light harvesting applications. In addition to CdSe@CdS hetero-NRs, competition between exciton transport and interfacial trapping was also reported in CdSe tetrapods, which are homojunctions with a zinc blende CdSe core with four wurtzite CdSe rod arms.²⁴³ Upon exciting the wurtzite arms, 86% of the excitons are transported to the zinc blende core with a time constant of ∼1 ps, driven by the CB offset across the rod/core quasi-type II interface. The remaining 14% form a charge-separated state across the interface, with the electron in CdSe core and hole trapped at the CdSe rod.

The exciton transport behaviors in 2D hetero-NPLs are different from those in 1D NRs. In our previous work, we compared the PLE (monitored at core emission) and absorptance spectra of CdSe/CdS type I core/crown NPLs to quantify the crown-to-core exciton transport efficiency (Figure 9E).²²¹ Using CdSe/CdS core/crown NPLs with the same CdSe core and different CdS crown sizes, we found that the crown-to-core exciton localization efficiency does not depend on the crown size but instead depends on the excitation wavelength, which higher efficiency at higher excitation energy.²²¹ Unlike NRs, CdSe/CdS NPLs have negligible surface trap states on the well-passivated basal planes, and their trap states are concentrated at the core/crown interface, independent of the crown size.²⁴⁴ The wavelength-dependent transport efficiency is attributed to more efficient transport of “hot” excitons with excessive energy (the energy difference between excitation energy and CdS crown band gap) bypassing the interfacial trap.²²¹ Interestingly, for CdSe/CdTe type II core/crown NPLs, the PLE (monitored at CT-exciton emission) and absorptance spectra agree very well with each other, indicating a unity CT-exciton formation efficiency (Figure 9F).^211,212 The crown-to-core exciton transport efficiency in type II hetero-NPLs is excitation-wavelength-independent, which is likely because the CT-exciton (with the electron in the CdSe core and hole in the CdTe crown) is formed prior to trapping process and does not require the hole to move across the interface.^211,245 Recently, Rao and co-workers also observed emissions from the CdSe core and CdTe crown of CdSe/CdTe NPLs, indicating the CT exciton formation efficiency is not unity.²¹⁸ Although the emission property may change with the sample quality, all these results have shown that interface of hetero-NPLs is important for both exciton transport and emission.

Due to the uniform quantum confinement along the thickness direction and the giant oscillator strength transition effect, it is speculated that the wave function of the exciton center-of-mass can delocalize throughout the whole NPL, resulting in a ballistic exciton in-plane transport property.^246,247 Buhro and co-workers studied single CdSe quantum belts and showed that the spatial distribution of the PL intensity is independent of the excitation location.²⁴⁷ They attributed this result to the exciton center-of-mass motion delocalizing to the whole quantum belt at the room temperature. However, Ma and co-workers have shown recently that the exciton center-of-mass wave function extension at room temperature (∼160 nm²) can be smaller than the NPL lateral dimension.²⁴⁸ In our recent works, we showed that the exciton transports diffusively in both CdSe/CdS and CdSe/CdTe core/crown NPLs.^212,221 Take CdSe/CdS type I hetero-NPLs as an example, the exciton bleach of the CdS crown decays slower in larger CdS crowns, indicating slower exciton transport from the larger CdS crowns; correspondingly, the formation of exciton bleach of the CdSe core, which represents the exciton arrival at CdSe core, is slower at larger CdS crowns.²²¹ These size-dependent exciton transport kinetics show that the exciton does not transport ballistically and can be well fitted by 2D in-plane classical diffusion model with a diffusion constants as 2.2 cm²/s and 2.5 cm²/s for CdS and CdTe NPLs, respectively, close to the diffusion constant in bulk crystals.^212,221

4. Electron and Hole Transfer from Nanocrystals

4.1. Nonadiabatic Charge Transfer from QD in a Weak Coupling Regime

In the conventional two-states Marcus model describing electron transfer from a discrete reactant state to a discrete product state, the nonadiabatic electron transfer (ET) rate can be described by eq 4.1.^{134,249−251}

4.1

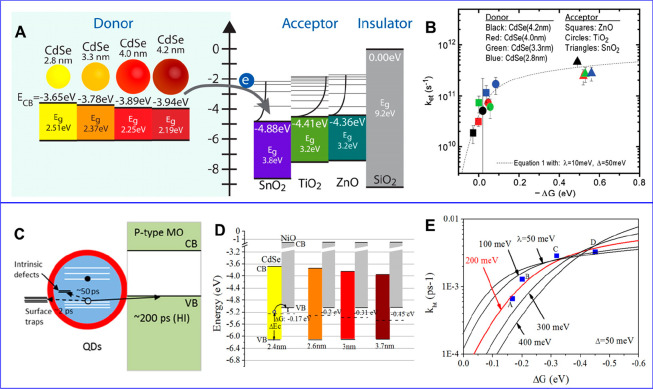
Here λ is the reorganization energy of the donor–acceptor system associated with the ET process due to electron–nuclear interaction, |H_DA|² is the electronic coupling strength between initial and final states, and ΔG₀ is the free energy difference between the initial state and final state (−ΔG₀ is the so-called driving force). Next we will discuss how these factors affect ET rates in QD–acceptor systems and how this model should be modified to count the unique excitonic properties of QDs.¹³⁴

4.1.1. Reorganization Energy

The total reorganization energy λ contains the inner-sphere contribution (λ_i) from the nuclear displacement of the donor–acceptor system and the outer-sphere contribution (λ_o) from the solvent dielectric response (λ = λ_i + λ_o). Typically, QD contributes negligibly (<10 meV) to λ_i because of its weak electron–phonon coupling,^252−254 and λ_i mostly comes from acceptor molecules, which is often in the range of a few hundred meV and can be computed theoretically.^251,255,256

The solvent molecules contribute to the charge transfer reorganization energy (λ_o) mostly through the orientation polarization, and λ_o can be estimated using dielectric continuum model²⁵⁷

4.2

where ε_op and ε_s are solvent high-frequency optical and static dielectric constants, respectively (therefore, the first bracket reflects the pure solvent orientation contribution); d_D and d_A are diameters of spherical donor and acceptor cavities, respectively; and r_DA is the center to center distance of the spherical donor and acceptor cavities. According to eq 4.2, a nonpolar solvent (such as hexane) contributes negligibly to the reorganization energy because of vanishing orientation contribution. Indeed, Ellis et al. observed similar ET kinetics of QD–methyl viologen (MV²⁺) complexes dispersed in hexane and under vacuum, consistent with negligible reorganization energy from a nonpolar solvent.²⁵⁰

Various experiments have been attempted to examine the dependence of the ET rate on solvent polarity and thus the effect of reorganization energy.^258−260 Cui et al. showed that ET rates between CdSe/ZnS QDs and pyromellitimide did not show a clear correlation with the solvent reorganization energy.²⁵⁸ Similarly, Hyun et al. reported that ET rates from a PbS QD to 10-dodecylanthracene-9-thiol did not correlate with solvent reorganization energy but increased with the static dielectric constant.²⁵⁹ Unfortunately, the acceptor molecules in these studies are soluble in solvents and the ratio between QD donor and molecular acceptors, which affects the apparent ET rate, is poorly controlled, hindering a careful study on solvent reorganization energy.

Charge transfer from QDs to semiconductor films (e.g., TiO₂) in principle can circumvent the problem of a poorly defined QD to adsorbed acceptor ratio. Hyun et al. reported that ET rates from a PbS QD to colloidal TiO₂ nanoparticles showed weak solvent dependence²⁶⁰ and attributed it to the small solvent contribution as a result of large TiO₂ nanoparticles. In principle, the solvent molecules around PbS QD (with much smaller size compared to TiO₂) should contribute to the ET reorganization energy. It appears that the solvent-dependent ET rates from QDs as predicted by eq 4.2 have not yet been observed. While better experiment designs may be needed, another possibility could be that the model in eq 4.1 does not adequately describe the ET from QDs,¹³⁴ as will be discussed later.

4.1.2. Electronic Coupling

Electronic coupling strength dependence can be most conveniently examined in donor–bridge–acceptor (D-B-A) complexes, in which the donor–acceptor coupling strength depends on the donor chemical nature and geometrical factors, acceptor, and bridge.²⁶¹ If ET occurs by tunneling through the bridge, the electronic coupling strength, and thus the ET rate, depends exponentially on the donor–acceptor distance.^261,262

An unique and precise way to tune the QD–acceptor distance and ET electronic coupling strength is through an inorganic barrier layer between the QD and acceptor with controlled thickness, e.g., using core/shell QDs.^{147,263−267} Using a CdSe/ZnS type I core/shell QD-anthraquinone (AQ) complex and by varying ZnS shell thickness (Figure 10A), Zhu et al. found both the electron transfer (or charge separation, k_CS) and back electron transfer (or charge recombination, k_R) rates decay exponentially with the shell thickness (d).

4.3

Here k₀ is the CT rate at d = 0 and the exponential decay constants β were reported to be 0.35 ± 0.03 Å^–1 and 0.91 ± 0.14 Å^–1 for the electron and hole transfers, respectively.²⁶³ More interestingly, the ET and HT rate decay constants agree well with the exponential decrease of 1S electron and hole surface density, respectively (Figure 10B). This result confirms that the ZnS shell serves as a tunneling barrier for the electron and hole transfer and slows down their rates by decreasing the electronic coupling with the adsorbate. Besides electron transfer, Ding et al. systematically investigated the hole transfer process from CdSe/CdS core/shell QDs to three different ferrocene hole-accepting molecules (Figure 10C) and found a general exponential dependence of hole transfer rates on the CdS shell thickness (Figure 10D).^264,265 Similar shell-thickness-dependent CT behavior has been also observed in ZnTe/CdSe core/shell QDs.²⁶⁷ The specific ET (HT) attenuation factor β varies for different systems and depends on the electron (hole) effective mass in shell materials and the core/shell band offset (potential barrier). This suggests exciting opportunities for independently controlling ET and HT (or BET) rates from QDs and leads to the idea of “wavefunction engineering” for controlling charge separation and recombination process in heterostructures.¹⁶⁸ For an in-depth discussion about wave function engineering and its application, reader can refer to the review paper in ref (168).

Figure 10.

(A) Scheme showing electron transfer (charge separation) and back electron transfer (charge recombination) processes in CdSe/ZnS core/shell QD–anthroquinone molecule complexes. (B) Plot of the logarithm of k_CS (red circles) and k_R (blue triangles) rates as a function of the ZnS shell thickness. Also shown are the calculated electron (red dashed line) and hole (blue dashed line) densities at the shell surface as a function of the shell thickness. (C) Scheme showing hole transfer from CdSe/CdS core/shell QD to surface adsorbed ferrocene molecules. (D) Plot of the logarithm of hole transfer rate as a function of CdS shell thickness for three different hole acceptor molecules. (A and B) Adapted with permission from ref (263). Copyright 2010 American Chemical Society. (C and D) Adapted with permission from ref (264). Copyright 2015 American Chemical Society.

Another way to change the donor–acceptor distance is to vary the length of the bridge molecule, which has been extensively applied in both QD-semiconductor film systems^269−272 and QD–molecule acceptor systems.^260,268,273 Wang et al. studied the ET process from CdSe QDs to TiO₂ films linked by n-methylene-based SH–[CH₂]_n–COOH (n = 1, 3, 5, 7) or n-phenylene-based SH–[C₆H₄]_n–COOH (n = 1, 2) as a function of n using optical pump-terahertz probe spectroscopy (Figure 11A).²⁶⁸ They observed a clear exponential decay of the ET rate as a function of the bridge length with an attenuation factor of β = 0.75 ± 0.06 Å^–1 for the n-methylene bridges, which agrees quantitatively with values from conductance measurements.²⁷⁴ On the other hand, the bridge geometry can also dramatically alter the influence of bridge length on the ET rate and leads to a much weaker dependence.^269−271 Tagliazucchi et al. measured photoinduced electron transfer from CdSe QDs with a HS–(CH₂)_n–COOH ligand (n = 1, 2, 5, and 7) to poly(viologen) as a function of n (Figure 11C) and observed that the attenuation of the ET rate constant with n is weaker than that expected from the decay of the electron tunneling probability across extended all-trans mercaptocarboxylic acids but can be well described by electron tunneling across a collapsed ligand shell (Figure 11D).²⁶⁹ Morris-Cohen et al. even found that ET rates from QD to alkylcarboxylate-functionalized viologens are independent of the number of methylene groups between the carboxylic acid and the bipyridinium core,²⁷⁰ suggesting that the dominant ET pathway is a through-space pathway from the QD to the bipyridinium core directly adsorbed on the QD surface, bypassing the bridging chain. These results indicate the importance of molecular-level morphology of the bridge ligands and suggest that ET studies could also provide a sensitive probe of the QD ligand shell structure and dynamics.

Figure 11.

(A) Schematic depiction of time-resolved THz photoconductivity measurements on a (CdSe)QD–bridge–(TiO₂) oxide system and relevant energetics of donor, bridge, and acceptor. (B) ET rate constants vs molecular bridge length for n-methylene-based bridges (HS–[CH₂]_n–COOH, with n = 1, 3, 5, 7; black dots) and n-phenylene-based bridges (HS–[C₆H₄]_n–COOH, with n = 1, 2; red squares). Solid lines are best fits to eq 4.3. (C) Scheme of mercaptocarboxylic acid-coated CdSe QDs with different bridge lengths, the polyviologen (PV) structure, and multilayer films of QDs coated by mercaptocarboxylic acids and PV on glass substrates. (D) Plot of the logarithm of the electron transfer time constant for PV/CdSe-C_n films as a function of n. The red dashed line shows the best-fit curve assuming electron tunneling across all-trans ligands. Solid lines show the predictions using collapsed-shell model. (A and B) Adapted with permission from ref (268). Copyright 2013 American Chemical Society. (C and D) Adapted with permission from ref (269). Copyright 2011 American Chemical Society.

In addition to the bridge length and geometry, the chemical nature of the bridge and anchor groups has also been shown to affect the ET rates.^{260,268,272,275−277} As shown in Figure 11B, the attenuation factor β decreases from 0.75 Å^–1 for a methylene bridge to 0.29 Å^–1 for a phenylene bridge due to stronger interunit coupling and the smaller barrier height in the latter.²⁶⁸ Hyun et al. compared the ET rate from a PbS QD to TiO₂ nanoparticles with four different anchor groups (carboxylic acid group, phosphonic acid, silane group, and sulfonic acid) binding to TiO₂ and observed that sulfonic acid yielded the highest ET rate.²⁶⁰

In principle, the electron transfer coupling matrix element, |H_DA|², can be computed using the effective one-electron model that has been successfully applied for inter- and intramolecular ET processes.²⁶¹ However, full ab initio electronic structure calculations of QDs of realistic sizes remain challenging. Computational studies of ET processes in QD–acceptor complexes have been carried out for smaller nanoclusters at the TD-DFT level²⁷⁸ or larger particles (comparable to experiments) at the empirical pseudopotential level.²⁷⁹ Motivated by the experimental observations that the ET and HT coupling matrix element depend on the electron (hole) density that extends outside the QDs (Figure 10B),²⁶³ a hybrid method was developed to compute |H_DA|² in QD–acceptor complexes.²⁵¹ The computed ET rates were found to be in reasonable agreement with the measured values, suggesting that such approximate methods may worth further investigation.²⁵¹

4.1.3. Driving Force

In QD–acceptor complexes, ΔG comes from three main contributions: (1) the potential energy difference between the donor (e.g., QD 1S electron, E_1Se) and acceptor orbitals (E_A/A^–), (2) the electron–hole Coulombic interaction in both the initial excited state (E_e-h) and the final charge-separated state (E_CS), and (3) the charging energy (E_c) from the initially neutral system to the charge-separated state. With all three contributions, the total free energy change is

4.4

The redox potential energy for 1S electron (or hole) level of the QD or acceptors (E_A/A^–) can be directly obtained from electrochemical method, i.e., cyclic voltammetry^280−284 (solution phase) or photoelectron spectroscopy²⁸⁵ (dry films). The 1S_e (1S_h) level of QDs of known sizes can also be estimated using effective mass approximation.^77,281 The latter three terms in eq 4.4, E_CS, E_e-h and E_C, cannot be measured directly from experiments but can be calculated using a simple model (see refs (134) and (253) for the detailed process). Because of a partial cancellation of E_CS and E_e-h, the overall e-h Coulombic interaction contribution to the free energy change is weakened.

4.1.4. Charge Transfer from QD to Molecular Acceptors with Discrete States

According to the classical Marcus ET model (eq 4.1), with increasing driving force (−ΔG), the ET rate increases in the normal regime (−ΔG < λ), reaches a maximum at the barrierless regime (at −ΔG = λ), and decreases in the inverted regime (−ΔG > λ). The prediction of the existence of the inverted regime has been the most prominent feature of Marcus ET theory and has been experimentally observed in molecular donor–acceptor systems.²⁸⁶ QDs with discrete and tunable electronic levels provide an ideal system to explore the driving force dependence and test theoretical models for describing ET from nanoscale excitonic systems. Changing QD size changes the ET driving force, and ET rates from the photoexcited QDs as a function of QD sizes to molecular acceptors^{134,287−292} and metal oxide semiconductor films^{37,253,254,293,294} have been extensively studied. Here, we focus on ET to molecular adsorbates; ET from QDs to metal oxide semiconductor will be discussed in the next section.

An increase of ET rates with decreasing QD sizes has been generally observed. Early studies of ET in QD–acceptor complexes have covered a relatively small driving force range (<0.6 eV), and a critical test of ET models, especially the presence of Marcus inverted regime, has not been possible.^287−290 Zhu et al. investigated ET processes from CdS, CdSe, and CdTe QDs of different sizes to three molecular acceptors, namely, methylene blue (MB⁺), methylviologen (MV²⁺), and anthraquinone (AQ), as shown in Figure 12A, to cover a wide driving force range (0–1.3 eV).¹³⁴ The observed ET rates increase monotonically with increasing driving force (or decreasing QD size) regardless of QD compositions and acceptor redox potentials (Figure 12B symbols). With the estimated total reorganization energy of ∼0.4 eV, this result is in marked contrast with the conventional two-state ET model (eq 4.1 and Figure 12B, green dashed line). Considering enhanced electron–hole Coulomb interaction in QDs, the authors proposed an Auger-assisted ET model to successfully account for the observed driving force dependence.

Figure 12.

(A) Schematic diagram of bulk conduction band edge positions of CdX (X = S, Se, Te) and reduction potentials of acceptor molecules (vs vacuum). (B) Measured (symbols) and predicted (lines) ET rates as a function of the driving force according to the conventional (green dashed line with λ of 0.4 eV) and Auger-assisted (red and black solid lines with λ of 0.4 and 0.5 eV, respectively) ET models. (C) Auger-assisted model for ET from QDs where ET can be coupled with a change in the hole energy level. (D) Marcus representation showing the energy of the reactant and product states as a function of the nuclear displacement along the ET coordinate. (E) Schematic of hole transfer from CdSe/CdS core/shell QDs to adsorbed ferrocenes. (F) Plot of the relative hole transfer rate constant as a function of the driving force. The dashed lines show behavior expected from a two-state Marcus model. The solid lines show behavior expected from the Auger-assisted model. Reorganization energies of 400 (black) and 500 meV (gray) were used. (A–D) Adapted with permission from ref (134). Copyright 2014 American Chemical Society. (E and F) Adapted with permission from ref (291). Copyright 2015 American Chemical Society.

In the Auger-assisted model, the excess energy of the transferred electron can be conserved by the excitation of 1S holes to a higher level (with energy E_h,i below the 1S hole), in addition to exciting vibrations of the lattice and acceptor molecules (Figure 12C). Because of the quasi-continuum nature of the hole states in these QDs, there is a manifold of product states (QD + [E_h,i] – A^–) with the excited hole at different levels (E_h,i). The total ET rate is the sum of Auger-assisted ET rates to these product states.

4.5

The electronic coupling strength in Auger-assisted ET model, H_AET(E_h), depends not only on the overlap of the 1S electron and acceptor orbitals (as in conventional ET) but also on the electron–hole Coulomb interaction.

According to the Auger-assisted ET model, the ET rates increase rapidly with the driving force at −ΔG < λ, which is similar to the conventional ET model (Figure 12B, left area). However, the ET rate continues to increase with driving force even when −ΔG > λ due to the presence of the continuum of product states, to which ET can occur with effective driving forces (−ΔG′= (−ΔG) – E_h) ranging from 0 (hole excitation takes all the free energy change) to −ΔG (hole is not excited) (as shown in Figure 12D). The regime where −ΔG > λ is denoted as the Auger-assisted regime (Figure 12B, right area) because ET occurs most effectively with the excitation of holes, overcoming the unfavorable Franck–Condon overlap in the conventional Marcus inverted regime. As shown in Figure 12B, the Auger-assisted ET model can satisfactorily explain the experimental data, confirming that it is the appropriate model for ET from QDs.

The driving force effect on the hole transfer process from QDs to molecular acceptors has also been examined.²⁹¹ Olshansky et al. measured hole transfer from photoexcited CdSe/CdS QDs to six ferrocene derivatives as hole acceptors, spanning a driving force range of 150–950 meV (Figure 12E). Similar to ET, the hole transfer rate increases with increasing driving force without an inverted regime. The authors explain their observation using an Auger-assisted mechanism in which the electron intraband excitation accompanies interfacial hole transfer process (Figure 12F). It should be noted that compared to the quasi-continuous hole states, the electron states in the conduction band are more sparsely spaced, which leads to the nonmonotonic dependence of the calculated hole transfer rate on the apparent driving force.

Auger-assisted charge transfer from QDs is fundamentally different from that in molecular donor–acceptor and bulk semiconductor–adsorbate complexes. In bulk semiconductors, the electron–hole interaction is weak and they behave as independent carriers. Although Coulomb interaction is strong in molecule, the density-of-electronic states is too sparse to enable an efficient Auger-assisted ET process. Furthermore, Auger-assisted ET only requires that electron–hole coupling is stronger than electron–phonon coupling and there is a large density of states, especially at high energy. Since these conditions can be readily met in excitonic nanomaterials (nanorods, nanosheets, and nanotubes), Auger-assisted ET should be a general model for charge transfer from these nanomaterials. It would be very interesting to experimentally verify the general applicability of this model beyond the observation in QDs discussed above.

Importantly, in a recent study, the conventional Marcus inverted region has been observed in charge transfer processes in nanocrystal-molecule complexes.²⁹⁵ The key to this observation is to measure charge transfer from the single-electron states of nanocrystals to surface-anchored molecules in the absence of strongly Coulomb-coupled holes. Specifically, through rational design of the energy level alignment in nanocrystal–molecule complexes, photoexcitation can create transient charge-separated states, for which the electrons are located in the conduction band of 0D QDs or 2D NPLs whereas the holes are in the surface-adsorbed molecules; the ensuing charge recombination processes were followed by transient absorption spectroscopy. By further tuning the electron transfer driving forces through the quantum confinement effect, this measurement unambiguously revealed a Marcus inverted region that had been hidden by the Auger-assisted mechanism. This result thus provides strong support to the Auger-assisted mechanism for charge transfer from excitonic states of these low-dimensional materials.

4.1.5. Charge Transfer from QD to Metal Oxide Semiconductors with Continuous States

ET from a QD to TiO₂, SnO₂, and ZnO metal oxide (MO) semiconductor films has been extensively studied,^{37,253,254,260,268,293,296} in part due to its important role in QD photovoltaic devices. Previous studies on dye-sensitized oxide films have already shown that, because of the continuous accepting states in MO conduction bands, the conventional two-state (single donating state and single accepting state) Marcus ET model (eq 4.1) has to be extended to a many-state Marcus ET model by integrating over all possible accepting states.^{252,297−299}

4.6

Here ρ(E) is the density of accepting states in the metal oxide CB, including both bulk and defect states,^253,298 and ΔG₀ is the driving force for electron transfer to the band edge of MO.

To test this many-state ET model in QD-MO systems, Tvrdy et al. examined ET from CdSe QDs of four different sizes to different metal oxide films (SnO₂, TiO₂, and ZnO) (Figure 13A).²⁵³ With increasing −ΔG₀, they found a sharp increase in ET rates at small driving forces, followed by a modest increase when the driving force significantly exceeds the reorganization energy. This trend can be well described by eq 4.6, as shown in Figure 13B. According to the many-state ET model, the ET rate is the sum of ET rates to all available states and is determined by the density of accepting states. When −ΔG₀ < λ, accepting states are below and near the band edge, where density of states increases rapidly with driving force. At −ΔG₀ > λ, the ET rate occurs to states above the band edge, the density of which varies slowly with increasing energy (scaling with). Similar ET behavior has been observed in CdSe QD-ZnO²⁹³ and PbS QD-SnO₂²⁵⁴ systems, which have also been successfully described by eq 4.6.

Figure 13.

(A) Diagram of the relative electronic energy differences between CdSe donating species and MO accepting species for all CdSe–MO combinations. (B) Global plot of all CdSe (donor) to MO (acceptor) electron transfer data and trace of eq 4.6 with λ = 10 meV and Δ = 50 meV. (C) Scheme showing the hole transfer process when QDs are attached to a p-type hole acceptor semiconductor. (D) Energy alignment of the CdSe QD–NiO system of different QD sizes (2.5, 2.6, 3.0, and 3.7 nm). (E) Hole injection rate vs driving force of QDs attached to NiO (blue squares) and fitting curves (black and red lines). (A and B) Adapted with permission from ref (253). Copyright 2011 National Academy of Sciences. (C and D) Adapted with permission from ref (294). Copyright 2014 American Chemical Society.

Besides the more extensively reported electron transfer process, its counterpart, hole transfer to MO, has also been investigated by Zheng and co-workers using a CdSe QD as the donor and p-type NiO film as the hole acceptor (Figure 13C).²⁹⁴ The hole transfer from CdSe QDs to NiO was observed to occur on the time scale of a few hundreds of picoseconds. This HT rate is more than an order of magnitude slower than the ET rate, which could be attributed to the larger effective mass of holes, giving rise to a smaller surface hole density and hence the HT coupling strength. The competition between hole transfer and hole trapping on similar time scale leads to low HT yield from CdSe QDs. The authors tuned the HT driving force by changing the size of CdSe QDs (Figure 13D). The HT rate increases with the driving force, which can also be well described by eq 4.6 with a relatively large reorganization energy of 200 meV (Figure 13E). Due to the complex electronic states and dynamics of holes in CdSe QDs, hole transfer process from a QD might deviate from simple direct transfer mechanism, as will be discussed in the next section.

It should be noted that eq 4.6 predicts a driving force dependence that is similar to the Auger-assisted ET, but the fundamental origins are quite different. For ET in QD-MO, the continuum of products states comes from a continuum of acceptor electronic levels (i.e., CB of MO), while in QD–molecule complexes it is caused by the quasi-continuum in the donor hole levels. As discussed above, the Auger-assisted ET pathway significantly enhances the ET rate in the inverted regime; since the inverted regime is not present in QD-MO, the effect of Auger-assisted pathways may not be significant.

4.1.6. Direct vs Trap-Mediated Hole Transfer

The discussions above on the QD CT process assumes electron (hole) transfers directly from well-defined lowest energy 1S state in conduction (valence) band, which is a reasonable assumption for electrons in cadmium chalcogenide QD and holes in high quality core/shell QDs. In reality, due to the presence of ill-defined and undercoordinated surface atoms, carriers, especially holes, in a cadmium chalcogenide QD are known to undergo reversible/irreversible traps,^300,301 which could affect the charge transfer pathways and dynamics. To differentiate the direct transfer vs trap-mediated transfer process, Olshansky et al. examined the HT process from CdSe/CdS core/shell QDs to different ferrocene hole-accepting molecules as a function of temperature (Figure 14A). Overall, the HT rate increases with temperature for all acceptors and all QDs. The Arrhenius plot of hole transfer rates exhibits an activated regime at higher temperatures and a weak temperature-dependent regime at low temperatures (Figure 14B). The extracted activation energies in the high-temperature regime are almost the same for a given QD, regardless of hole acceptors or driving force. This constant activation energy across all driving forces (100–900 meV) contradicts the activation energy in the Marcus model assuming direct hole transfer from the QD valence band to hole acceptors (Figure 14C). Based on the temperature-dependent results, the authors proposed a model where, besides direct hole transfer from valence band, an additional dominant hole transfer pathway is through a shallow and reversible trap (Figure 14A). The latter relies on thermal excitation of the hole into a trap state higher than the valence band edge and is therefore temperature-dependent. This model contrasts with simple direct transfer mechanism that is often assumed and necessitates a careful study on charge transfer process. It should be noted that only reversible traps that can contribute to fluorescence are investigated here, while irreversible traps, which lead to nonradiative recombination, are neglected in this study.

Figure 14.

(A) Schematic of the model that assumes the charge transfer rate is a sum of two pathways: direct transfer and trap-mediated transfer. (B) Arrhenius plots for the hole transfer rate from 6.3 nm QDs to five ferrocene molecules with fits to the trap-mediated model. (C) Driving force dependence of extracted effective activation energies (Arrhenius slopes from the high-temperature regime) for HT from 6.3 nm QDs to five ferrocene molecules and that of direct transfer models assuming two states (conventional Marcus model) or multiple final states (Auger-assisted mode). Adapted with permission from ref (292). Copyright 2017 American Chemical Society.

4.2. Adiabatic Charge Transfer from QD in the Strong Coupling Regime

For QDs with large exciton Bohr radii, such as PbS (∼20 nm) and PbSe (∼46 nm), a large portion of the wave functions of electrons and holes extends outside the QD due to the strong quantum confinement.³⁰² When these QDs are attached directly or through a short bridge to bulk semiconductors such as TiO₂, the electronic coupling can be strong and electron transfer from the QD to semiconductors can fall in the adiabatic regime.^137,296,303 One consequence of the strong electronic coupling is the broadening of the discrete electronic state in QDs resulting from mixing with the continuum states in semiconductors. The Newns–Anderson model for chemisorption can be used to describe this spectral broadening.^304,305 The density of states (ρ) of the broadened electron level in QDs as a function of energy E is given by

4.7

where E_QD is the energy of a discrete QD state prior to broadening and Δ is the half width of the broadened level and is related to the coupling strength. According to the Heisenberg uncertainty principle, a homogeneous spectral line with a full width at half-maximum of 2Δ corresponds to a lifetime of τ = ℏ/2Δ of the electron in this broadened level. This electron lifetime reflects the electron packet propagation time between the strongly coupled QD state and the TiO₂ CB, or the adiabatic electron transfer time.

Yang et al. reported the spectral broadening due to strong electronic coupling and ultrafast electron transfer from PbS QDs to a TiO₂ semiconductor film.¹³⁷ As shown in Figure 15A and B, the static absorption spectra of PbS QDs adsorbed directly on TiO₂ show a broadened 1S exciton band, and the extent of broadening decreases significantly in the presence of an insulating Al₂O₃ spacer layer between the QD and TiO₂. This spectral broadening can be more clearly seen from the transient absorption spectra (Figure 15C–E). Compared to QDs on a sapphire substrate, the 1S exciton peak for PbS QDs on TiO₂ films is significantly broadened. Inserting a relatively thick Al₂O₃ insulating layer between PbS QDs and TiO₂ mostly recovered the peak width, indicating decreased electronic coupling with the Al₂O₃ insulating layer. Fitting these spectra reveals homogeneous broadening (and electron transfer lifetime) for the QD on TiO₂ of ∼49 meV (∼6.5 fs). Time-resolved measurements showed that the ET time from QD to TiO₂ was faster than the instrument time resolution (∼150 fs), in line with the results obtained from the spectral broadening. The adiabatic electron transfer from PbSe QDs to TiO₂ (with ET time of ∼10 fs) has also been theoretically predicted.³⁰⁶ This ultrafast ET rate suggests the possibility of extracting hot electron before electron cooling, which will be discussed in the next section.

Figure 15.

(A and B) Static absorption spectra of PbS QD on TiO₂ (A) without and (B) with an insulating Al₂O₃ spacer. The inset shows a schematic depiction of the varying degrees of broadening of the 1S electron level as a result of interaction with the TiO₂ CB. (C–E) Simulated (black lines) and measured (red circle) 1S exciton bleach spectra for PbS QDs (C) on sapphire windows, (D) on 3Al₂O₃/TiO₂, and (E) on TiO₂. Adapted with permission from ref (137). Copyright 2010 American Chemical Society.

It should be noted there are a wide range of reported ET times from lead chalcogenide QDs to TiO₂. Wise and co-workers found that the ET from PbS QDs to TiO₂ colloidal particles was on the time scale of several to tens of ns.^260,281 The reason for the different coupling strength was unclear, which could be due to sensitive dependence of the coupling strength on the interfacial ligand structure.

4.3. Hot Electron Transfer from Nanocrystals

The discussions above mostly focus on electron/hole transfer from lowest-energy 1S state, as hot carrier cooling in typical QDs occurs usually on an ultrafast (<300 fs) time scale through Auger-type energy transfer between electrons and holes and/or to ligand vibrations and phonons.^308,309 Hot carrier cooling represents one of the major efficiency losses in solar energy conversion devices, leading to the so-called Shockley–Queisser limit. The ultrafast adiabatic electron transfer from QDs to semiconductor films in a strong coupling regime discussed above suggests the possibility of extracting hot carrier before thermalization (Figure 16B), which potentially can overcome the Shockley–Queisser limit and lead to hot carrier solar cell with 66% theoretical efficiency. Indeed, Tisdale et al. observed hot ET in PbSe QD-sensitized TiO₂ (with an ET time of ∼31 fs) using time-resolved second harmonic generation (SHG) spectroscopy at 80 K (Figure 16A).³⁰³ Negligible hot ET was observed at room temperature, presumably due to faster electron cooling at higher temperatures. Using CdSe QDs as electron acceptors, Grimaldi et al. also observed fast hot ET from PbSe QDs to CdSe QDs assembled in a quantum dot heterojunction solid.³¹⁰ The hot ET efficiency increases with excitation energy and reaches ∼4.5% when the excitation photon energy approaches the onset of CdSe absorption. Recently, Wang et al. directly nucleated PbS QDs onto SnO₂ films and performed a comprehensive study of hot ET from PbS QDs to SnO₂. They observed hot ET up to unity quantum efficiency from PbS QDs at room temperature.³⁰⁷ As shown in Figure 16C, both hot (<150 fs) and cold ET (∼10 ps) were observed, depending on excitation photon energy, giving rise to the nonsingle exponential kinetics. The hot ET amplitude (Figure 16D) and rate (Figure 16E) increase with the excitation photon energy, i.e., excess energies of hot electrons, due to the increased density of states of both the donor and acceptor at higher energies. The authors also reported enhanced hot ET efficiency by increasing the QD size or by lowering the temperature. The hot ET efficiency depends on the kinetic competition between the hot ET rate (k_ET) and the hot electron thermalization rate (γ_r) in QDs.

Figure 16.

(A) Time-resolved second harmonic response of the TiO₂ surface coated with 1.5 monolayers of hydrazine-treated 3.3 nm PbSe nanocrystals. The large increase in the SHG intensity is indicative of efficient electron transfer from PbSe to TiO₂. (B) Illustration of the competing pathways of interfacial electron transfer and intra-quantum dot relaxation. (C–E) Photon-energy-dependent hot electron transfer (HET) from PbS QDs to SnO₂ probed by time-resolved THz spectroscopy. (C) Excitation-wavelength-dependent electron transfer (ET) dynamics (from 400 to 1200 nm) for PbS QDs with ∼2.7 nm diameter. The solid lines are biexponential fits based on hot and cold electron transfer (HET on sub-ps time scales and CET on a ∼10 ps time scale; see arrows). (D) The weight of the fast HET component in the dynamics shown in panel C vs hot electron excess energy in the QDs. (E) HET rates vs the excess energies of hot electrons. The CET rate was found to be independent of the excess energy and fixed to 10.2 ps (gray dotted-dash line). In panels D and E, the dashed black lines are to guide the eye; the red dotted line represents the time resolution of our setup. (A and B) Adapted with permission from ref (303). Copyright 2010 American Association for the Advancement of Science. (C–E) Adapted with permission from ref (307). Copyright 2018 American Chemical Society.

Hot ET has also been observed in perovskite nanocrystal–molecular acceptor systems.^311,312 Li et al. investigated the hot electron cooling and extraction from colloidal MAPbBr₃ perovskite nanocrystals and observed room temperature hot electron extraction (with efficiency up to 83%) from a colloidal MAPbBr₃ nanocrystal film to a 4,7-diphenyl-1,10-phenanthroline hot-electron extraction layer within 0.2 ps.³¹¹ Using time-resolved terahertz spectroscopy, Sarkar et al. measured the electron and hole transfer process from a CsPbBr₃ nanocrystal to surface adsorbed benzoquinone and phenothiazine molecules as electron and hole acceptors, respectively.³¹² They observed a major ultrafast hot carrier transfer channel within their time resolution (<300 fs) and a secondary cooled carrier transfer process to molecular acceptors on the order of tens to hundreds of ps. These proof-of-concept studies on model systems suggest the possibility of employing colloidal nanocrystals to extract hot carriers and circumvent energy loss in solar energy conversion applications, but it still remains challenging to implement the hot carrier extractions in real devices, as the light harvesting layer, the energy selective contacts, and the interface have to be carefully designed and engineered.

4.4. Electron Transfer from 2D Nanocrystals: The Effect of Dimensionality

The ET mechanism in 2D nanocrystals, in particular, 2D CdSe NPLs, has also been studied. In 0D QDs, because of the quantum confinement in all three dimensions, the electron and hole are completely localized. 2D NPLs have unconfined lateral dimensions extending to tens to hundreds of nm. This increased lateral dimension brings the question of how dimensionality affects the ET rate from 2D NPLs. Schaller and co-workers reported a lateral-area-dependent ET from CdSe NPLs to MV²⁺.³¹³ They used time-resolved PL quenching of CdSe NPL-MV²⁺ complexes to characterize the ET time (Figure 17A), which is shown to scale with the square of the NPL lateral area (S²) (Figure 17B). They explained this experimental result by assuming that the ET rate is proportional to the square of the product of wave functions for the charge-separated state (Ψ^CT) and initial state (Ψ^S). The former (Ψ^CT) is independent to NPL lateral area considering the transferred electron is fully localized on MV⁺ radical, while the in-plane normalization factor in the latter results in an area dependence (Ψ^S ∝ 1/S). As a result, the ET time scales with the reciprocal of S². This mechanism has assumed that the exciton center-of-mass wave function extends throughout the whole NPLs. However, the exciton center-of-mass coherent area (∼160 nm²) may be smaller than the NPL lateral area²⁴⁸ as discussed in section 3.2, in which case the fast exciton in-plane diffusion may come into play, but the relevant studies are still lacking.

Figure 17.

(A) The time-resolved PL decay kinetics of CdSe NPLs with four different lateral areas (circles). The solid lines are the exponential fits to the kinetics. (B) The PL quenching lifetime (1/k_CT) as a function of the CdSe NPL lateral area. The inset shows the PL quenching rate (k_CT) as a function of the NPL lateral area (S). (C) The transient absorption kinetics of exciton bleach (red curve) and MV⁺ radical (blue curve). The inset shows the lateral size of the CdSe NPLs. (D) Scheme of surface-dependent MV²⁺ adsorption on CdSe NPLs. (A and B) Adapted with permission from ref (313). Copyright 2016 American Chemical Society. (C and D) Adapted with permission from ref (314). Copyright 2016 American Chemical Society.

Tamai and co-workers proposed a different mechanism for lateral-area-dependent ET from CdSe NPLs to MV²⁺ based on a transient absorption spectroscopic study.³¹⁴ They observed biexponential ET kinetics from both the exciton bleach and MV⁺ radical kinetics (Figure 17C) and found slower ET rates from larger NPLs. They attributed this size-dependent ET rate to the size-dependent electronic coupling between CdSe and MV²⁺. It is suggested that MV²⁺ molecules selectively adsorb on the edges of NPLs, while the basal plane of NPLs is well passivated with oleic acid (Figure 17D). In this case, the higher amount of adsorbed MV²⁺ on the longer edges give to a faster ET rate compared to that in the shorter edges. Although this proposed mechanism explains the fast and slow components of biexponential transient absorption kinetics, which represent the ET from long and short edges of NPLs, respectively, the direct evidence of how MV²⁺ adsorbed on NPL surfaces is still lacking.

These reports indicate that the dimension change of NCs affects the ET mechanism in two ways: (1) the exciton in-plane motion, which includes center-of-mass coherent delocalization and diffusion, and (2) anisotropic adsorption of acceptors on NC surfaces. Both aspects require more extensive studies for further understanding of ET mechanisms in 1D and 2D NCs.

5. Multiple Exciton Generation and Dissociation from Nanocrystals for Generation III Photovoltaics

5.1. Theoretical Interpretations of Multiple Exciton Generation

In the bulk semiconductors, a carrier with sufficiently high kinetic energy can lose its excess energy by promoting a bound electron from the valence band to the conduction band via multicarrier Coulomb interactions, and this process is rationalized by impact ionization (II). Analogous to their bulk counterparts, quantum-confined nanocrystalline semiconductors can also generate multiple excitons by absorbing a single high-energy photon, known as multiple exciton generation (MEG) or carrier multiplication (CM). Several mechanisms have been proposed to interpret this phenomenon,^315−318 and three of them will be highlighted here.

According to Franceschetti et al., II can be used to explain the MEG process,³¹⁵ predicting its rate and threshold. As shown in Figure 18A, the photogenerated high-energy single exciton can result in two biexciton states (with a hot electron or hot hole) via II. In this physical picture, II must compete with the high-energy single-exciton relaxation via phonon emission, which is on a time scale of few ps for lead chalcogenide QDs. According to the Fermi–Golden rule, the II rate is proportional to the transition probability between the initial (single exciton state) and final states (biexciton state), and this transition is induced by the carrier Coulomb interaction, which is treated as a perturbation. Taking into account the density of states (DOS) and selection rules, the computational results indicate that the II rate increase nearly drastically as the energy increases due to the steep growth of the DOS of the final states. When the energy reaches 2.1-fold of the band gap energy (2.1E_g), the II rate surpasses the biexciton Auger recombination rate that is nearly energy-independent, and when the energy is larger than 2.7E_g the former is approximately two orders of magnitude larger than the latter, which is also comparable to hot carrier cooling rate. Therefore, the II rate calculation suggests that II rate may account for the MEG rate at high energy. To satisfy energy conservation, the II process in QDs only requires either the electron or hole in the single exciton with excess energy (energy above the respective band edge) larger than E_g. As indicated in Figure 18A, the energy levels in conduction and valence bands for PbSe QDs were believed asymmetric rather than “mirror-like”, and the absorbed photon with energy in the range of 2–3E_g could distribute its energy primarily to the electron so that the electron gains excess energy larger than E_g. Thus, the threshold of MEG also falls in the range of 2–3E_g. Based on this model, the MEG threshold for PbSe QDs with a 3.1 nm diameter is predicted as 2.2E_g. Note that the II rate at the threshold energy may not compete with the carrier relaxation, resulting in a negligibly small MEG efficiency.

Figure 18.

Proposed multiple exciton generation mechanisms. (a) The impact ionization of carriers with high kinetic energy create an additional electron–hole pair. (b) The Coulomb interaction creates a coherent superposition between a single exciton state and multiple exciton states.

According to Shabaev et al., MEG in QDs can also be explained by the optical excitation of a coherent superposition between isoenergetic states, single and multiple exciton states, that are strongly coupled by Coulomb interactions.³¹⁶ Briefly, the Coulomb coupling among the single and multiple exciton states can no longer be treated as a perturbation when these states have the same energy and thus the eigenstates of the Hamiltonian including this Coulomb coupling will be mixed states of the single and various multiple exciton states or a superposition between these states. The coherence cannot be formed among nonresonant states due to the weak coupling. As shown in Figure 18B, a photon with energy in the range of 2–3E_g will only create superpositions between a single exciton state and biexciton states because of the energy conservation. The superposition is damped due to the thermalization of either the single or the biexciton components with thermalization rate of γ₁ and γ₂, respectively. In the case of strong coupling, the oscillation frequency (γ_c) between the two coherent states is much higher than both γ₁ and γ₂ and thus the MEG efficiency is determined by the competition of the two damping channels, with a larger ratio of γ₂/γ₁ resulting in a higher MEG efficiency. In the case of weak coupling, when γ_c ∼ γ₂, the MEG efficiency can still be high if γ₂/γ₁ ≫ 1. However, when γ_c ≪ γ₂, γ₁, optical excitation of a single exciton, instead of superposition, is dominant, and the MEG efficiency will be negligibly small. Assuming a mirror-like conduction and valence bands for lead chalcogenide QDs, the energy of the single exciton state has to be higher than that of the 2P exciton in order to find resonant biexciton states with the same energy. Thus, the threshold of MEG in these QDs has been predicted as ∼3E_g. It should be noted that if the valence band has a higher DOS than conduction band near band edge then the MEG threshold should be lower than 3E_g.

In addition, Klimov and co-workers have proposed a model of direct photogeneration of multiexcitons by a single photon absorption via virtual single-exciton states.³¹⁷ Similar to the indirect optical transitions in bulk semiconductors, photoexcitation of multiexciton states is also forbidden because of momentum conservation.³¹⁷ However, according to second-order perturbation theory, the Coulomb interaction between multiple exciton states and virtual single exciton states can give a nonvanishing oscillator strength for the direct multiple exciton state excitations with the assistance of virtual single exciton states. In contrast to the dephasing of coherent superposition model, this perturbation approach allows low or moderate coupling strength between the single and multiple exciton states.

5.2. Statistical Description of the Multiple Exciton Dynamic Behavior

To characterize MEG, understanding of multiple exciton dynamics in quantum-confined systems is required. Furthermore, this knowledge is also desirable for the development of QD-based optoelectronic applications such as LEDs and lasers. When a semiconductor nanocrystal has multiple electron–hole pairs (or excitons), one of the electron–hole pairs can recombine by promoting a third charge carrier to a higher energy level due to the Coulomb interaction, known as Auger recombination, which is usually more efficient than the radiative recombination (Figure 19A). In bulk and nanocrystalline semiconductors with low exciton binding energies, Auger recombination occurs via three-particle-involved Coulomb interactions, which are responsible for the third-order recombination channel.³¹⁹ In nanocrystals with strong exciton binding energies, Auger recombination occurs between two excitons.^151,320 Thus, the different Auger recombination mechanisms give different recombination rate scaling laws with the number of exciton or electron–hole pairs (n): k_n ∝ n²(n–1) and k_n ∝ n(n–1) for three-particle and two-particle (or bimolecular) mechanisms, respectively.^92,321−324

Figure 19.

(a) Illustration of biexciton Auger recombination. (b) Illustrative scheme of cascade Auger recombination in QDs.

After optical excitation, the initial distribution of exciton number per dot in a QD ensemble is governed by the Poisson equation:²⁰⁸

5.1

where P_n(0) is the probability of QDs with n photogenerated excitons per dot and w is the average exciton number per dot. As shown in Figure 19B, the multiexcitons in a QD decay sequentially via Auger recombination. As a consequence, the statistical distribution of excitons in QDs will vary as a function of time after optical excitation. The kinetics of P_n will be described by

5.2

where k_n+1 and k_n are the decay rate constant for n + 1 and n exciton states, respectively, which should obey the aforementioned Auger recombination rate scaling law. Therefore, the average multiple exciton annihilation (MEA) kinetics for a QD ensemble can then be simulated by combining a complete set of coupled eq 5.2 with an initial condition defined by eq 5.1.

Although the photon energy of visible light is below the threshold of MEG for CdSe QDs, multiple excitons can still be generated by the absorption of multiple photons per dot under high-intensity optical excitation. The average number of excitons per dot (w) is proportional to the excitation intensity. The dependence of the first exciton (1S) bleach recovery kinetics of CdSe QDs on excitation intensity is displayed in Figure 20A.³²⁵ The kinetics traces have been scaled by normalizing their amplitude at 1 ns in order to emphasize the MEA component. The larger magnitude of the fast component for higher pump intensity is due to the greater fraction of dots with multiple excitons. Before ∼200 ps, the kinetics show a fast decay component, attributed to MEA via Auger recombination. After ∼200 ps, all the kinetic traces show negligible decay, indicating the completion of MEA and the resultant long-lived single excitons. Since the 1S bleach in CdSe QD TA spectra mainly arises from the state filling of the two-fold degenerate 1S electron level, QDs with multiple excitons (n ≥ 2) all contribute equally to 1S exciton bleach amplitude, and the fast decay component only reflects the biexciton annihilation rate. Thus, these kinetic traces can be fitted by the following equation:

5.3

where the first and second terms on the right side represent the contributions from QDs with multiple excitons (n ≥ 2) and a single exciton. Because the biexciton recombination rate constant (k₂) is orders of magnitude larger than that for single excitons (k₁), the differential rate equation set (eq 5.2) for one and two excitons can be approximately decoupled, and eq 5.3 is then expressed as two isolated exponential components:

5.4

where the first and the second terms on the right side account for the decay caused by biexciton and single exciton recombinations, respectively. The prefactors consist of the initial Poisson distribution of QDs, which constrains the relative amplitudes of the two decay components. This equation suggests that the QDs with at least two excitons contribute to the biexciton decay and those with at least one exciton (also including those with multiple excitons) contribute to the single exciton decay. k₂ given by this fitting is consistent with reported values for CdSe QDs. k₂^–1 has also been shown to be size-dependent and increases nearly linearly with the QD volume. As mentioned before, the 1S bleach signal for CdSe QDs is not sensitive to the occupation of higher exciton states and thus the higher order MEA (n > 2) should have negligible contribution to the 1S bleach recovery kinetics. Nonetheless, Klimov et al. have reported the higher-order multiexciton state (n = 2, 3, 4) lifetimes by successive subtraction of carrier decay kinetics under different pump intensities.³⁰ The carrier kinetics was converted from 1S exciton bleach recovery kinetics through a phenomenological fitting equation. In principle, when n > 2, the electrons start to populate the 1P electron levels, leading to the bleach of the 1P exciton transition. Indeed, additional fast decay components have been observed in the 1P bleach recovery kinetics, as shown in Figure 20B, from which an averaged lifetime of n (n > 2) exciton states was estimated to be 2.6–4.5 ps.³²⁵ A more detailed analysis was hindered by the presence of other TA signals, such as the multicarrier interaction-induced spectral shift. Kanemitsu and co-workers reported that a photoinduced absorption (PA) signal for CdSe QDs in the near IR region of TA spectra is proportional to the pump intensity.³²⁶ This linear relationship holds even in a high intensity region where 1S bleach signal magnitude is saturated (Figure 20C), implying that the kinetics of PA may include the higher-order MEA information. The analysis the PA kinetics for different intensities based on the Poisson statistical model reveals the time constant of the MEA process in CdSe QDs, which is well described by the three-particle Auger recombination model (Figure 20D).

Figure 20.

Comparison of (A) 1S and (B) 1P exciton bleach recovery kinetics at different pump intensities obtained from TA measurement of CdSe QDs. The kinetic traces have been normalized to the same value at a 1 ns delay time. (C) Maximum amplitude of the photoinduced absorption signal (0.84 eV) and 1S exciton bleach signal (2.07 eV) as a function of pump intensity for CdSe QDs. (D) Auger decay time extracted by probing the kinetics of photoinduced absorption signal as a function of the excitation intensity. The red curve shows the calculated result using the quantized Auger recombination model with three-carrier collisions. (A and B) Adapted with permission from ref (325). Copyright 2010 American Chemical Society. (C and D) Adapted with permission from ref (326). Copyright 2009 The Physical Society of Japan.

The three-particle Auger recombination model works for free carriers (electron and hole) with small binding energies that are strongly confined in a small region as in QDs. In 1D NRs and 2D NPLs, where dielectric confinement effects enhance the exciton binding energy as discussed in section 2, excitons rather than free carriers dominate at the band edge. In this case, the recombination tends to happen between the bound electron–hole pairs following the bimolecular Auger recombination model. Using similar transient spectroscopic methods, bimolecular Auger recombination has been reported by Klimov and co-workers for PbSe NRs^324,327 and Siebbeles and co-workers for both CdSe only and CdSe/CdS/ZnS core/shell NPLs.²⁴⁶

There are mainly three ways to control the MEA rates: (1) NC size, (2) electron–hole wave function overlap, and (3) confinement potential abruptness. Klimov et al. first reported that the Auger constant (C_A) of CdSe QDs scales with the QD volume.³⁰ Following this pioneering work, the Auger constants of other QDs, with both direct and indirect band gap such as PbSe, InAs, and Ge QDs, have been reported to scale with QD volume, showing a “universal volume scaling law” (Figure 21A).^{328,330−332} The N-exciton Auger recombination lifetime (τ_N) follows , where V is the QD volume and R is the QD radius, so that the Auger lifetime of QDs also scales with QD volume.^30,328 Note that this assumes a continuous carrier density in QDs similar to bulk materials, which is not accurate because the recombination occurs as sequentially quantized steps in QDs with only several electron–hole pairs.³³³ Although the insight of this “universal volume scaling law” observed in QDs remains unclear, it shows that the Auger recombination in QDs is significantly different from that in bulk materials. Auger recombination in indirect band gap bulk semiconductors is orders of magnitude slower than that in their direct band gap counterparts due to the requirement of momentum conservation, while this momentum conservation is relaxed by strong quantum confinement in QDs.³²⁸ Biexciton lifetimes of 1D PbSe NRs have also been reported to scale with the NR volume following this “universal volume scaling law” (Figure 21B).^334,335

Figure 21.

(A) Auger constants of different QDs as a function of the QD radius. (B) The biexciton lifetimes of PbSe QDs (black squares) and NRs (red circles) as a function of the NC volume. (C) The biexciton lifetime of CdSe NPLs with different thicknesses and lateral areas as a function of the NPL area (A_NPL). The solid lines are the linear fits of NPLs with the same thickness. (D) Scheme of the classic 2D biexciton collision model. a is the exciton diameter, v̅ is the mean velocity of exciton in-plane motion, and Δt is the time spacing between collisions. (E) The biexciton lifetime of CdSe NPLs with different thicknesses and areas as a function of the product of the NPL area (A_NPL) and the quantum-confined energy of the electron (E_k(e)) to the order of −7/2. (A) Adapted with permission from ref (328). Copyright 2009 American Physical Society. (B) Adapted with permission from ref (327). Copyright 2013 American Chemical Society. (C–E) Adapted with permission from ref (329). Copyright 2017 American Chemical Society.

The volume-scaled Auger lifetime in 1D NRs is surprising because 1D NRs contain both quantum-confined and non-quantum-confined dimensions and the volume-scaled Auger lifetime indicates these two different dimensions contribute equally to Auger recombination in NRs. Heinz and co-workers reported an exciton-collision-based Auger recombination model for 1D carbon nanotubes and showed the Auger lifetime scales with nanotube length.³³⁶ Recently, using CdSe NPLs with well-controlled lateral area and thickness, Lian and co-workers studied the area- and thickness-dependent Auger recombination in CdSe NPLs and found that the biexciton Auger lifetime does not scale with NPL volume, breaking the “universal volume scaling law”.³²⁹ Instead, the biexciton Auger lifetime scales linearly with the NPL lateral area for NPLs with the same thickness and increases dramatically in thicker NPLs (Figure 21C). A new two-step Auger recombination model is proposed by Lian and co-workers for 2D NPLs: (1) excitons diffuse and collide to each other frequently within NPLs due to the fast exciton in-plane transport^212,221 and (2) each collision has a finite probability for Auger recombination.³³⁷ The lateral area dependence is due to the binary exciton collision (Figure 21D): the exciton in the middle of the effective collision line, within time interval Δt, can collide with any excitons whose center (black dots) are in the collisional square so that the collision frequency (F_C) scales with the reciprocal of the NPL lateral area. The Auger probability is considered similar to that reported in similar quantum wells and is determined by the quantum-confined energy of electrons in the conduction band (E_k(e)).³³⁸ This two-step Auger recombination model fits the biexciton Auger lifetime of CdSe NPLs excellently (Figure 21E) and may also work for other 1D and 2D nanomaterials. These size-dependent Auger recombination studies have clearly shown that the Auger rates of NCs can be tuned by their sizes and dimensions. For example, biexciton lifetime in CdSe NPLs (hundreds of ps)^329,339 is much longer than that in QDs (tens of ps);³⁰ in particular, the biexciton lifetime in 2D NPLs can be extended to several ns by increasing the thickness through shell coating.^340,341

The MEA rate can also be controlled by electron–hole wave function engineering such as constructing core–shell or interfacial alloy because the Auger recombination rate depends on electron–hole overlap.¹³³ As shown in Figure 22A, CdSe/CdS core/shell QDs with a 1.2 nm core radius and 2.2 nm shell thickness have a quasi-type II band alignment and thus the electron wave function spreads over both core and shell, while the hole wave function is confined in the core. The peak at 575 nm and shoulder at 475 nm in the linear absorption spectrum correspond to the lowest-energy CdSe core-based transition (T0) and CdS shell-based transition (T1), respectively. The TA spectra of CdSe/CdS QDs (Figure 22B) show three spectral signatures: two negative peaks at the T0 and T1 positions and a broad positive signature at a wavelength longer than 650 nm. The two negative peaks have been attributed to the bleach of T0 and T1 absorption due to the state-filling effect. The broad positive signal has been assigned to photoinduced absorption (PA), more specifically, hole-induced absorption, and this assignment is supported by selective charge removal experiments. As pump intensity increases, the T0 bleach band gradually increases and saturates when exciton per dot exceeds two because of the twofold degeneracy of the 1S electron state. The T1 bleach shows blue shifting of the peak position and broadening of bandwidth due to the dynamic Burstein–Moss shift, indicating the quasi-continuum nature of the T1 transition. Like the near-IR PA signal for CdSe QDs, the PA signal of these core–shell QDs is also proportional to exciton numbers in QDs, providing a convenient probe to follow the MEA process.

5.5

The T0 and PA kinetics are simultaneously fitted by eqs 5.3 and 5.5, respectively (Figure 22C and D), giving a biexciton lifetime of ∼440 ps that is much longer than that for CdSe QDs with similar confinement energy.

Figure 22.

MEA in quasi-type II CdSe/CdS core/shell QDs. (A) UV–vis absorption spectrum. The inset shows a schematic energy level diagram, lowest energy electron and hole wave functions, and T0 and T1 optical transitions. (B) TA spectra at 0.3 ps after 400 nm excitation at different intensities. The inset shows an expanded view of the TA spectra between 500 and 840 nm. (C and D) Normalized TA kinetics (symbols) at (C) T0 and (D) PA bands and fits (solid curves) to the independent carrier Auger recombination model. Adapted with permission from ref (133). Copyright 2012 American Chemical Society.

Moreover, it has been shown theoretically that the abrupt confinement potentials of NCs break the strict momentum conservation and enhance the Auger recombination rate, while smooth confinement potentials of NCs suppress Auger recombination.^342−346 As a result, alloyed interface in core/shell QDs are reported to suppress the QD blinking.^347−349 Klimov and co-workers used giant core/shell QDs with multiple shells to provide a smoothly changed confinement potential for the QDs, which extended the biexciton Auger lifetime to ∼1.3 ns, and achieved the optical gain by direct current electrical pumping.³⁵⁰ Compared to the size-tuning method, which is limited by the NC size within a quantum-confined size region, interfacial alloying is a more efficient way to suppress the Auger recombination.³⁵¹

5.3. Observations of Multiple Exciton Generation

Time resolved spectroscopies have been exploited to study the MEG in QDs because of the distinct lifetimes of single and multiple excitons. Under extremely low pump intensity, the probability of QDs with multiple excitons created by multiple photon absorption, according to the Poisson statistics, is negligibly small, and under such condition, MEG, if it occurs, will be the primary source for producing multiple excitons that lead to a fast decay component of exciton dynamics. Thus, the fast MEA can be employed as indicator of MEG under low-intensity excitation. In 2004, Schaller and Klimov noticed that when hν_pump > 3E_g, a fast component in the first exciton bleach kinetics of the PbSe QD solution persisted even when the pump intensity was attenuated to a condition with average number of excitons (w) of less than 0.25.³³¹ This fast component was not observed when hν_pump was reduced to less than 2E_g. The time constant of this fast decay for the high-energy and low-intensity pump was then shown to be consistent with that of the biexciton Auger recombination and thus this fast decay component was ascribed to the short lifetime of multiple excitons generated by MEG. In 2005, Nozik and co-workers reported MEG in both PbS and PbSe QDs.³⁵² They found that under similar pump intensity (w ∼ 0.25) the amplitude corresponding to the fast component increased with increasing hν_pump after exceeding a threshold (∼3E_g). Additional ultrafast spectroscopic studies report the observation of MEG occurring in PbS,³⁵³ PbSe,³⁵⁴ PbTe,³⁵⁵ InAs,^332,356 Si,³⁵⁷ InP,³⁵⁸ CdSe,^359,360 CdTe,³⁶¹ CdSe/CdTe core/shell QDs,³⁶², PbSe/PbS core/shell QDs,³⁶³ CuInSe₂ nanocrystals,³⁶⁴ and SWCNTs.³⁶⁵

However, during the same time controversy also arose about the reported occurrence or efficiency of MEG in some QDs. Nair and Bawendi reported that the quantitative analysis of biexciton and exciton signatures in time-resolved photoluminescence (TRPL) kinetics of CdSe and CdTe QDs shows no evidence of MEG when hν_pump > 3E_g.³⁶⁶ Furthermore, a report from Pijpers and co-workers regarding MEG in InAs NCs was withdrawn by the authors because they could not reproduce the results and conclusion.³⁵⁶ Ruhman and co-workers reported negligible MEG in InAs/CdSe/ZnSe core–shell QDs at hν_pump > 3.8E_g.³⁶⁷ Researchers also questioned that if the multiplication process in QDs was enhanced compared to bulk semiconductors. Bonn and co-workers indicated that for given hν_pump, the carrier multiplication process in PbS and PbSe QDs may occur less efficiently than their bulk counterparts, and the enhancement of the multiplication arising from quantum confinement may be offset by the reduced DOS in QDs.³⁶⁸ Contrary to this argument, Beard and co-workers found that the efficiency of this multiplication process was enhanced by at least two times in PbSe QDs compared to their bulk counterpart, and they also argued that the MEG yield should be plotted as a function of hν_pump/E_g because E_g is the fundamental unit of energy required to produce additional electron–hole pair in a given QD.³⁶⁹

Beside the aforementioned controversy, the large inconsistency of the reported MEG yields led to the re-examination of the MEG determination methods.^370,371 Several artifacts from the experimental design or data analysis have been uncovered to be responsible for the overestimation of the MEG yields reported in some of the earlier literatures. In principle, the number of excitons is proportional to TA amplitude under low pump intensity, and the MEG yield (η) can be extracted from the kinetics as the ratio between the initial and long delay amplitude (Figure 23A), ΔA_i/ΔA_f, where ΔA_i and ΔA_f represent the number of initially generated excitons and initially excited QDs, respectively. However, photocharging or photodegradation of QDs under high photon energy illumination can also cause similar fast exciton kinetics decay due to trion recombination or trapping, which leads to an overestimation of the MEG yield.^136,372,373 This artifact can be avoided by vigorously stirring or flowing the samples during the measurement.³⁷³ Furthermore, another source of overestimation might be subtle to notice, yet its influence can be significant. Because the QD absorption coefficient increases drastically with the photon energy, the assumption of a homogeneous optical excitation along the light path in a QD solution is not valid. For this reason, multiphoton absorption is not negligible under high hν_pump even when w (average exciton number per dot) is very small, giving rise to overestimation of the MEG yield.^371,374 This overestimation can also be reduced or eliminated by taking proper data analysis or experimental methods.

Figure 23.

(A) Schematic illustration of 1S exciton TA kinetics (black dash curve). The amplitudes at short (ΔA_i) and long (ΔA_f) delays are proportional to the initially generated exciton and initially excited QDs, respectively. (B) MEG yield extraction for a PbSe QD solution. The symbols are the ratio of ΔA_i/ΔA_f for different pump intensities. The curves represent eq 5.9 in the main text. (C) The plot of normalized TA signals (ΔS) of ΔA_i and ΔA_f (symbols) as a function of pump photon fluence. The scaling factor is defined in the main text. The lines and curve represent eqs 5.6 and 5.8, respectively, in the main text. (D) The ratio of ΔS at short and long delays at different pump photon fluences. The dashed curves represent the ratio of eq 5.6 to eq 5.8 in the main text. Adapted with permission from ref (136). Copyright 2012 American Chemical Society.

5.4. Quantification of Multiple Exciton Generation Yield

To avoid the overestimation stemming from multiple photon absorption, several methods have been developed to more accurately determine the MEG yield from TA measurements. In the first method, the samples were measured with different pump intensities. As the intensity decreases, the exciton kinetics approach to the same decay, indicative of the negligible contribution of multiphoton absorption events.³⁷¹ Under such circumstances, η (MEG yield) can be determined from ΔA_i/ΔA_f (Figure 23A).

Following this concept, the MEG yield at infinitely low pump intensity can be extrapolated from fitting of intensity-dependent TA signals. For lead chalcogenide QDs, the 1S exciton state is eightfold degenerate (including the spin degeneracy).³⁷⁵ According to the Poisson statistics, ΔA_i can be expressed as

5.6

where P_n(0, w) represents the Poisson probability of QDs absorbing n photons when the average exciton number per dot is w and c is the effective absorption cross section of the sample at the probe wavelength. When the pump intensity is low, the first term in the square bracket of eq 5.6 is dominant and thus ΔA_i is proportional to the pump intensity (Figure 23B). Thus, eq 5.6 can be simplified as

5.7

where J₀ is the pump photon flux, and σ_p is the effective absorption cross section of the samples at the pump wavelength. ΔA_f is recorded from the TA kinetics when MEA is completed, and its amplitude is proportional to the probability of optically excited QDs (including those with both single and multiphoton absorption events). ΔA_f is expressed as

5.8

Note that ΔA_i and ΔA_f are recorded from the normalized kinetics as shown in Figure 23A.¹³⁶ The ratio of ΔA_i/ΔA_f is now expressed as³⁵⁷

5.9

where δ accounts for the single-exciton loss during the MEA process. For well-passivated QDs, δ is approximated to 1 because the single-exciton recombination is orders of magnitude slower than multiple-exciton recombination. As shown in Figure 23C, the measured R_pop is plotted as a function of the pump photon flux and eq 5.9 is applied as a fitting function with σ_p and η as fitting parameters. To improve the accuracy of the fit, a set of control R_pop values of the same sample were collected well below the MEG threshold so that η is known as 1. Thus, the η given by the fitting is equivalent to extrapolating η at infinitely small pump intensity so that the influence of multiphoton absorption can be minimized. Given the large degeneracy of 1S state, ΔA_i fell in the low pump intensity region (linear region) in most MEG reports. Thus, the MEG yield has been determined accurately by using either eq 5.6 (Figure 23D) or eq 5.7 (Figure 23C).

Another approach was developed by Ruhman and co-workers.³⁷⁴ Briefly, the concentration of the QD samples as well as the pump intensities was carefully controlled so as to obtain an identical multiphoton absorption contribution between large hν_pump (above MEG threshold) and small hν_pump (control experiment) pumping conditions. Thus, any difference in the number of generated excitons can be attributed to the MEG process. The accuracy of this measurement depends critically on the ability to measure the relative pump intensity, which can be difficult because of the variations of beam profiles and pump/probe overlap.

5.5. Strategies to Enhance Multiple Exciton Generation

Cunningham and co-workers have reported that, compared with 0D QDs with similar E_g, the MEG yield in PbSe 1D NR is enhanced by a factor of 2 at hν_pump ∼3E_g, and the MEG threshold (determined as 2.23E_g) is also significantly reduced (Figure 24A).³⁷⁶ This enhancement has been attributed to the increased Coulombic interaction in NRs. Later, Klimov and co-workers further explored this MEG enhancement strategy by examining the influence of aspect ratio of the NRs.³²⁷ To quantitatively assess the MEG enhancement, a MEG enhancement factor is defined as the MEG yield in NRs divided by that in QDs with the same E_g, which exhibits a maximum at an aspect ratio (length/diameter) of 6–7 (Figure 24B). For NRs with larger (>10) or smaller (<4) aspect ratios, MEG is not enhanced compared to QDs. In addition to shape controlling of nanocrystals, Klimov and co-workers recently have demonstrated that thick-shell PbSe/CdSe nanostructures can enhance the MEG yield by a factor of 4 over conventional PbSe QDs, and the enhancement is also accompanied by a considerable reduction of the MEG threshold (Figure 24C).³⁷⁷ The nanostructure and the band alignment in these core–shell QDs enable the high-energy holes to reside in the CdSe shell for longer time, evidenced by the cross-band emission at the visible region, and thus increases the probability of MEG by retarding the competitive hot carrier cooling process. Recently, Mohammed and co-workers reported the colloidal Ag₂S QDs (band gap of 1.23 eV) as a new class of MEG materials due to their high photostability, low toxicity with a MEG threshold of 2.28E_g, and efficiency of 173% at 3.2E_g excitation.³²⁰ Furthermore, Parkinson and co-workers reported the synthesis of the single-layered Ag₂S nanoplatelets, which are expected to possess an enhanced Coulombic interaction due to the 2D morphology.³⁷⁸ Siebbeles and co-workers reported highly efficient MEG in 2D PbS nanosheets recently with MEG threshold about 3 eV (∼4E_g), similar to PbS QDs but with higher MEG efficiency than QDs at the same hv_pump/E_g ratio.³⁷⁹

Figure 24.

MEG enhancement. (A) Comparison of MEG in nanorods and nanocrystals. The MEG yield is plotted against hν_pump/E_g for NRs and QDs with different E_g. (B) The MEG enhancement factor for NRs as a function of the NR aspect ratio. (C) Comparison of the MEG yield in PbSe/CdSe QDs and PbSe NRs at various values of hν_pump/E_g. (A) Reprinted with permission from ref (376). Copyright 2011 American Chemical Society. (B) Reprinted with permission from ref (327). Copyright 2013 American Chemical Society. (C) Reprinted with permission from ref (377). Copyright 2014 Springer Nature.

Recently, the emerging perovskite nanocrystals have offered another platform for the study of MEG, and the highly efficient MEG yield in these weakly confined QDs has been attributed to the slow hot carrier relaxation.^380−386 Highly efficient MEG with low threshold energy has been observed in formamidinium lead iodide and cesium lead iodide perovskite nanocrystals.^380,381 Li and co-workers found that in the lead iodide perovskite nanocrystal the MEG efficiency could be tuned by partially substituting the lead ion by tin, and in this report the MEG threshold approached twice the bandgap.³⁸⁵

5.6. Multiple Exciton Generation in Electronically Coupled QD Solids

The aforementioned MEG measurements have been conducted on QDs dispersed in solution, which are electronically isolated from one another. Nonetheless, many QD photovoltaic applications, such as solar cells,^387−389 photoelectodes,²³ and photodetectors³⁹⁰ are based on the coupled and compact QD solids in which the charge carriers can diffuse from one dot to another. Thus, it is critical to understand and control the MEG in these electronically coupled QD solids for MEG-based devices.

Compared with QD solutions, the TA studies of PbSe QD films have indicated the decreased single exciton lifetime and increased biexciton lifetime, and these changes are escalated when the interdot distance is shortened after hydrazine treatment due to delocalization of the exciton wave function.³⁹¹ However, distinguishable changes of the MEG yield between the QD solution and the films was not observed (Figure 25A).³⁹¹ Further experiments revealed a particularly interesting result in that the MEG yield showed strong dependence upon the post-chemical treatments (Figure 25B), and several interpretations of this result were proposed, such as ligand-modified hot carrier cooling, relaxation of quantum confinement due to the coupling, and/or introduction of dopants.³⁹² These studies have inspired the development of MEG-enhanced solar cells based on chemically treated QD films.^22,23 It should be noted that to accurately extracted the MEG yield in the films, the value of both σ and δ in eq 5.9 were experimentally determined, which were different from those in QD solution.

Figure 25.

(A) The comparison of MEG yield for PbSe QD films and QD solutions. Note that the QYs for QDs in solution and untreated films are identical. (B) The comparison of MEG yield as for the indicated QD solids between QD solution and the ideal MEG yield (achieving n excitons at n times E_g). (A) Reprinted with permission from ref (391). Copyright 2007 American Chemical Society. (B) Reprinted with permission from ref (392). Copyright 2009 American Chemical Society.

For QD film photovoltaic devices, higher carrier mobility is always desirable to achieve a longer diffusion length and less carrier loss. The mobility can be controlled by tuning the interdot spacing of the films. Siebbeles and co-workers have demonstrated that the MEG yield varies with the carrier mobility in PbSe QD films.³⁹³ In this experiment, the carrier mobility in QD films was systematically tuned over more than two orders of magnitude by changing the cross-linking molecules (Figure 26A). As shown in Figure 26B, the determined MEG yield of the films progressively decreases as the carrier mobility increases. The film with the smallest mobility, treated with 1,2-ethanedithiol (purple diamonds), shows the least MEG yield, whereas the film with the largest mobility, treated with 1,2-ethanediamine (red squares), shows the highest MEG yield. This experiment further reveals that the threshold energy of the MEG in these films is 2E_g, much lower than the reported values for dispersed QDs. More recently, Siebbeles and co-workers showed that, compared with a QD solid, MEG is more efficient in a percolative network of directly connected PbSe QDs (Figure 26C).³⁹⁴ It was found in this study that the MEG yield in this percolative QD network increased in a step-like fashion with hν_pump and was higher than that for the QD solids with weaker interdot coupling (Figure 26D), implying the dependence of MEG on coupling strength.

Figure 26.

(A) Photoconductivity of the QD films as a function of the average number of absorbed photons per QD for QD films with various cross-linking molecules. The inset shows a typical photoconductance transient and the point that corresponds to the maximum value. (B) MEG yield as a function of hν_pump/E_g for all films. The lines are linear fits to the data assuming an energy threshold of 2E_g. (C) TEM image of a monolayer percolative PbSe network (scale bar represents 10 nm). (D) MEG yield as a function of hν_pump/E_g (bottom axis) and as a function hν_pump (top axis) for the percolative PbSe network and the PbSe NC solid. (A and B) Reprinted with permission from ref (393). Copyright 2013 Springer Nature. (C and D) Reprinted with permission from ref (394). Copyright 2018 American Chemical Society

5.7. Multiple Exciton Dissociation via Charge Transfer

QDs can generate and accumulate multiple excitons through MEG resulting from the absorbance of either one high-energy photon or multiple photons. For QD-based solar cells or photocatalysts, efficient photon-to-charge conversion requires a complete exciton dissociation. Owing to the strong quantum confinement, the electron and hole wave functions extends beyond the QD surfaces, which facilitates the exciton dissociation either via interdot charge transfer in coupled QD films or via interfacial charge transfer in QD–molecule complexes. Unfortunately, the spatial confinement of QDs also enhances the exciton Auger recombination process, leading to ultrafast multiple exciton decay via MEA. Thus, the quantum yield of multiple exciton dissociation (MED) depends on the competition between charge transfer and MEA. As illustrated in Figure 27A, the electron transfer (ET) from QDs to molecular adsorbates is exploited to dissociate the multiple excitons in QDs. The ET process occurs on time scales of sub-ps to tens of ps, and the dependence of ET rates (γ) on various factors have been discussed in section 4. In parallel to the ET process, the multiple excitons can also decay via MEA. The biexciton lifetime in QDs is on the time scale of tens of ps, and its decay rate constant is denoted as γ_A. As discussed previously, the MEA rate increases quickly with the number of excitons per dot, k_n = 1/2γ_An²(n – 1). Thus, as the exciton number increases, the MEA rate will eventually exceed the ET rate, giving rise to a maximum number of dissociated exciton (n_max). Assuming the average adsorbates per dot is much larger than the average exciton number per dot, Hilczer and Tachiya derived the analytical expression describing the MED yield based on the Poissonian exciton distribution model.³⁹⁵ According to this analysis, n_max is governed by the ratio of γ/γ_A and bounded between two limits (Figure 27B) under various pump intensities: 1 when γ/γ_A ∼ 0, corresponding to solely single exciton dissociation, and n when γ/γ_A ∼ ∞, corresponding to complete MED. To experimentally determine n_max, the molecular adsorbate TA signals are normally used as indicators. When the ET rate from QDs to the adsorbate is much faster than single exciton recombination, a complete exciton dissociation can be assumed under very low pump intensity when the single excitation event dominates. Then, the measured adsorbate TA signals is linearly scaled to match the average exciton number per dot determined from QD TA signal, and the same scaling factor is applied to the adsorbate TA signals for all different pump intensities. Thus, these scaled TA signals (ΔAM) represent the number of dissociated excitons, which can also be predicted from the Poisonian exciton distribution model:

5.10

where P_n(0, w) is the Poissonian exciton distribution term that is defined in eq 5.1.

Figure 27.

(A) Schematic illustration of MED via electron transfer to adsorbed molecular electron acceptors. (B) The calculated ultimate yield of dissociated excitons per dot as a function of the average initial exciton number per dot calculated for various values of the ratio of ET rate and biexciton decay rate (γ/γ_A). The calculation is based on the Poissonian initial exciton distribution model described in the main text. (B) Reprinted with permission from ref (395). Copyright 2009 American Chemical Society

It has been experimentally demonstrated that the multiple excitons generated by multiple photon absorption can be efficiently dissociated via ET to adsorbates in competition with MEA in nanocrystals. The complexes of CdSe QDs and efficient electron acceptors, methyl viologen (MV²⁺) and methylene blue (MB⁺), have been used as prototypes to study MED from QDs.^{133,151,325,396} As shown in Figure 28A, C, and E, the ET from QDs with a single exciton to MV²⁺ and MB⁺ are on the time scales of sub-ps and several ps, respectively, both of which are much faster than the single exciton lifetime. The ET-induced adsorbed TA signals, absorption of methyl viologen radical (MV^•+), or the bleach of methylene blue (MB⁺) in TA spectra have been used to measure n_max. As shown in Figure 28B, D, and F, the scaled MV^•+ absorption and MB⁺ bleach signals (symbols), representing the number of dissociated excitons, are compared with the predicted values given by eq 5.10 (curves) with different hypothetical n_max values. These comparisons imply that the experimental n_max values in CdSe-MV²⁺, CdSe-MB⁺, and CdSe@CdS-MV²⁺ are around 5, 3, and 19, respectively. Compared with MB⁺, the faster ET rate to MV²⁺ results in the larger n_max. Compared with CdSe QDs, the spatial distribution of electron and hole wave functions in the quasi-type II CdSe@CdS QDs retains the ultrafast ET rate while greatly reducing the MEA rate (biexciton lifetime 440 ps). In other words, this core/shell structure enables a large γ/γ_A ratio, which is believed to the reason for the large n_max. In Figure 28F, the consistence between the scaled exciton and MV^•+ signals suggests a unity MED yield at the corresponding pump intensity. In addition to wave function engineering, Lian and co-workers have also demonstrated another approach to enhance MED yield exploiting the scaling law for MEA.¹⁵¹ Compared to the spherical QDs, the exciton binding energy in a 1D quantum rod (QR) is significantly enhanced, arising from the dielectric confinement of the surrounding medium. As a result, the MEA in QRs is expected to proceed via exciton–exciton collision following the two-particle Auger recombination model. According to the scaling law, the MEA rate increases cubically with the exciton number in QDs because of three-particle Auger recombination, while it increases quadratically with exciton numbers in QRs because of two-particle Auger recombination. Thus, the MEA, especially for high-order multiple exciton states, is slowed in QRs. Consequently, the experimentally determined n_max in CdSe QR-MV²⁺ complexes is increased up to 21.

Figure 28.

(A) TA kinetics probed at the absorption band of the MV^•+ radical (411 nm) with (red triangle) and without (black circles) adsorbed MV²⁺. The time constant of ET from QD to MV²⁺ is extracted as 70 fs by fitting the kinetics traces (solid curves). (B) Comparison of the experimental (symbol) and predicted (curves) MV^•+ TA signal as a function of the average initial exciton number per dot. (C) The formation of ground-state bleach (GSB) of MB⁺ is consistent with the 1S exciton bleach decay, suggesting the ET from QD to MB⁺. The comparison of TA kinetics of 1S exciton between QDs and the QD-MB⁺ complex also suggests this fast ET process. The kinetics fitting gives the ET time constant as 2.2 ps. (D) Comparison of the experimental (blue triangle) and predicted (curves) MB⁺ GSB and 1S exciton bleach signal as a function of pump intensity. (E) TA kinetics probed at the absorption band (630 nm) of the MV^•+ radical with (blue circles) and without (red triangle) adsorbed MV²⁺. (F) Comparison of the experimental (green solid circle) and predicted (dash curves) MV^•+ TA signal and 1S exciton bleach signal (red triangle) as a function of the pump intensity. (A and B) Reprinted with permission from ref (396). Copyright 2009 American Chemical Society. (C and D) Reprinted with permission from ref (325). Copyright 2010 American Chemical Society. (E and F) Reprinted with permission from ref (133). Copyright 2012 American Chemical Society.

More recently, multiple exciton dissociation in CdS-Pt NRs has also been reported.³⁹⁷ In CdS NRs, rapid hole trapping leads to a long-lived biexciton lifetime (1/k^A₂) of 2.0 ± 0.2 ns and multiexciton Auger recombination processes that follow a Carrier-Collision model, k^A_n = n²(n – 1)/4k^A₂. In CdS-Pt nanorods, because of ultrafast electron transfer from CdS to Pt (with a half-life time of 5.6 ± 0.6 ps), multiple electrons can be transferred to the Pt from the multiple exciton states. The half-life of charge-separated state decreases from 10 μs in single charge-separated state to 42 ns in nine charge-separated states. This result suggests metal-tipped NCs can be a promising platform for exploiting the unique multiple exciton properties of NCs to drive multiple electron chemistry.

5.8. MEG Enhanced Multiple Carrier Extraction

The method of using ET to dissociate excitons has also been extended to dissociate the multiple excitons created by MEG in lead sulfide (PbS) QDs (Figure 29A).¹³⁶ The complex of PbS QD adsorbed by MB⁺ was used as a model to demonstrate this idea. The TA spectra of PbS-MB⁺ show two prominent features: the 1S exciton bleach at 1140 nm and the MB⁺ ground-state bleach (GSB) at 667 nm (Figure 29B). The former is due to the state filling of both the 1S electron and hole levels, and the latter indicates ET from the excited QDs to MB⁺ molecules. The analysis of kinetics of these two features reveals the time constant of ET from the QD single exciton state to MB⁺ to be around 2.3 ps. The MEG efficiency in free PbS QDs for hν_pump = 2.9E_g was quantified as 112% using the methods introduced previously. Then, PbS-MB⁺ complex solutions with the same concentration as free QDs were examined under the identical experimental condition to measure the MEG and the following MED in the QD–acceptor complexes. Using the similar MED analysis approach for CdSe QDs, the ET-induced MB⁺ GSB signal was scaled to determine the dissociated excitons. As shown in Figure 29C, the scaled MB⁺ GSB signals are consistent with the normalized 1S exciton bleach signals at different pump intensities, suggesting that all excitons are dissociated in PbS-MB⁺ complexes and the presence of efficient electron acceptors does not influence the MEG efficiency of PbS QDs. This study has demonstrated that ultrafast interfacial ET can be an efficient way for extracting multiple excitons generated by the MEG process.

Figure 29.

(A) Schematic illustration of MEG and the following MED in the PbS/MB⁺ complex. (B) The TA spectra at indicated delays. The fast recovery of 1S exciton bleach and formation of MB⁺ GSB suggest the ET from PbS to MB⁺. (C) Comparison of the experimental (blue square) and predicted (dash curves) MB⁺ GSB TA signals and the 1S exciton bleach signal (red circle) as a function of pump intensity. Reprinted with permission from ref (136). Copyright 2012 American Chemical Society.

Besides the dispersed QD–adsorbate systems, MEG-enhanced photocurrent and hydrogen generation have also been demonstrated in PbS QD-integrated photoelectrochemical systems. Parkinson and co-workers observed the MEG effect in a photoelectrochemical cell where light was captured by a PbS QD monolayer chemically bound to a TiO₂ single crystal electrode.³⁹⁸ The excitons generated in PbS were dissociated via electron injection into the TiO₂ electrode, and the remaining holes were shuttled to the counter electrode by the electrolyte to form photocurrent (Figure 30A). Taking into account the loss from uncaptured photons, the absorbed photon-to-current efficiency (APCE) was reported to reach as high as 180% at large hv_pump/E_g because of MEG (Figure 30B). The APCE measurements also indicated that the threshold of MEG in a PbS QD-sensitized TiO₂ electrode was QD-size-dependent, falling in a range of 2.4–3E_g. Recently, Beard and co-workers demonstrated that extra carriers produced via MEG in PbS QD-based photoelectrodes can be used for hydrogen generation with a quantum yield above unity.²³ The electrochemical device was composed of a PbS QD photoanode and a Pt cathode that were placed into two compartments connected by a salt bridge (Figure 30C). The PbS QD multilayer film in the photoanode captures photons. The resultant electrons are extracted by the TiO₂ substrate and flow to the Pt cathode for hydrogen evolution, while the holes in the QD film are filled by oxidizing the surrounding sulfide ions in the electrolyte. Since no external bias was applied, the driving force for the whole chemical reactions should be provided by the photovoltage arising from the illumination of the photoanode and the chemical potential difference in the two compartments. Thanks to the nearly unity Faraday efficiency, both the incident photon-to-current efficiency (IPCE) and the external quantum yield of the photon-to-hydrogen conversion exceed 100% due to MEG at hv_pump/E_g > 2.7 (Figure 30D).

Figure 30.

(A) Illustrative representation of a QD adsorbed on a TiO₂ single crystal and the expected charge transfer process. 1S_e and 1S_h refer to the lowest electron and hole states, respectively. (B) APCE values of a QD-sensitized TiO₂ electrode as a function of the illumination photon energy. (C) Schematic of the PEC apparatus. The QD layers serves as photon absorber of the photoanode. Photogenerated holes oxidize sulfide in one compartment while electrons reduce hydrogen in the other compartment at the dark Pt cathode. A salt bridge connects the two compartments and transports H⁺ and Na⁺. (D) EQE (filled symbols) for hydrogen generation induced by PbS QD photoelectrodes with various E_g in Na₂S aqueous electrolyte. IPCE (open symbols) at the range of 380–500 nm is also illustrated for comparison. (A and B) Reprinted from ref (398) with permission from AAAS. (C and D) Reprinted with permission from ref (23). Copyright 2017 Springer Nature.

To take advantage of MEG in QD solar cells, the MEG-resultant excitons should be efficiently dissociated and extracted from QD films. Klimov and co-workers has demonstrated that MEG can also contribute to the photocurrent extracted from a PbSe QD film.³⁹⁹ As shown in Figure 31A, a PbSe QD film with strong interdot coupling was sandwiched between a gold ground plane and gold top contact. One contact of the switch is biased with an adjustable d.c. voltage, while the other is connected to the input port of a fast sampling oscilloscope with a 20 GHz bandwidth. The switch is triggered with 100 fs laser pulses. The overall system response time is 40 ps. In analogy to the MEA kinetics in TA measurements, the detected transient photocurrents have also exhibit the fast decay component from Auger recombination, which is also exploited to uncover the multiple exciton contribution by applying the Poissonian exciton distribution model (Figure 31B). The low-fluence transient photocurrent traces measured with hν_pump above the MEG threshold can be reproduced by pumping the sample below the MEG threshold with a higher pump intensity (inset of Figure 31B). The consistent kinetic traces imply the presence of multiple excitons for both pump conditions despite different origins: MEG in the former case and multiple photon absorption in the latter case. At hν_pump = 4.5E_g, the MEG yield of the QD film could be extracted as 144% from the analysis of the pump-intensity-dependent transient photocurrents (inset of Figure 31C). The MEG yields have been determined for different hv_pump/E_g ratios using this optoelectronic measurement, which is in agreement with those obtained from the spectroscopic measurements.

Figure 31.

(A) Illustration of the transient photocurrent detection apparatus. A photoconductive switch comprises a thin film of PbSe QDs deposited on a glass substrate with top interdigitated Au contacts. Photocurrent is excited by short laser pulses and monitored with a 20 GHz sampling oscilloscope. (B) Tail-normalized transient photocurrent traces with excitation above the MEG threshold show the persistence of a fast Auger decay component in the limit of low pump fluences, indicating the presence of MEA. The inset shows that the low-fluence transient photocurrent kinetics measured with 3.1 eV photons can be reproduced using 1.5 eV excitation but with a much higher pump intensity. (C) Comparison of the MEG yields determined from the transient photocurrent measurements (red solid circles) of the QD films to those from TA measurements of the QD solutions. Reprinted with permission from ref (399). Copyright 2015 Springer Nature.

The MEG-induced photocurrent enhancement in a QD solar cell was first demonstrated by Beard and co-workers, and the external quantum efficiency (EQE) maximum of 114% was reported for the best device.²² In this report, the solar cells were fabricated in a planar multilayer heterojunction structure (Figure 32A, inset). The PbSe QD films were deposited on the substrate in a layer-by-layer fashion with a 1,2-ethanedithiol (EDT) and hydrazine treatment. Compared with the EDT-only treatment, this cotreatment method leads to significant improvement of the solar cell performance (Figure 32A). The EQE spectra of most tested devices (15 out of 18) with QD E_g ∼ 0.7 eV show peak values exceeding 100% near 3.2 eV, and the champion device gives a peak EQE of 107% (Figure 32B). To further assess the MEG efficiency and threshold, the internal quantum efficiency spectrum, obtained by only considering the absorbed photons, is plotted as a function of the normalized photon energy (hv/E_g). The internal quantum efficiency (IQE) curves for different devices exhibit nearly constant short-circuit collection yields (∼85%) until the photon energy surpasses the MEG threshold, after which the IQE increases to a peak efficiency (Figure 32C). Taking into account the 15% intrinsic carrier loss, these IQE curves are qualitatively consistent with the modeled MEG efficiency as a function of hv/E_g (eq 5.9), evidencing the MEG enhancement in these devices when hv is above the threshold. The IQE drops at higher photon energy (>3.3 eV) because of the absorption of ITO. The IQE spectrum also indicates that the MEG threshold for the device with a QD E_g of 0.72 eV is around ∼2.8E_g.

Figure 32.

(A) Comparison of current–voltage characteristics under simulated AM1.5G illumination of devices assembled from EDT- and EDT+hydrazine-treated QD films. The inset shows structure of the PbSe QD solar cells. (B) EQE peaks for different independent solar cells made with QD E_g ∼ 0.7 eV. (C) Collected IQE curves vs hv/E_g for three solar cells with different values of E_g. The dashed curve represents the predicted MEG yield based on eq 5.9 in main text. Reprinted from ref (22) with permission. Copyright 2011 AAAS.

6. Photocatalysis Using Nanocrystals

The efficiency of a photocatalytic reaction depends on the efficiencies of three important processes: light absorption, charge separation, and catalytic turnover.^{60,206,400−402} In this context, quantum-confined NCs are ideal light-harvesters to drive photocatalytic reactions. The quantum confinement effect leads to strong light–matter interaction that enhances the light absorption cross sections of these NCs. Artemyev and co-workers quantified the NC intrinsic absorption coefficient (absorption coefficient per unit NC volume) via inductively coupled plasma atomic emission spectroscopy and a continuum absorption Lorentz local field model.¹³ In particular, they showed that the intrinsic absorption coefficient of 2D NPLs is even further enhanced compared to that of 1D NRs and 0D QDs due to higher optical field penetration along the basal plane, where the local field factor along these directions approaches unity.¹³ Meanwhile, the charge separation properties of 0D, 1D, and 2D NCs can be precisely engineered via both the quantum confinement effect and wave function engineering approaches, as we review above. Compared to 0D QDs, 1D NRs and 2D NPLs provide an additional knob to tune the charge separation distances by tailoring the length or area of their unconfined dimensions. In addition, surface defects or atoms on NCs in some cases function as catalytic sites themselves,^403,404 although the efficiency of photocatalytic reactions using these “intrinsic” catalytic sites tends to be low. There are several ways to design efficient photocatalytic systems using NCs, such as NC–molecular catalyst hybrids, NC–enzyme hybrids, NC–redox mediator–catalyst triads, and NC–metal heterojunctions. It is important to emphasize that most of these studies focus on the photoreduction half-reaction, with the photogenerated holes removed by the use of sacrificial electron donors (or hole acceptors). In this section, we review the structure, charge separation mechanism, and efficiency-limiting factors in these systems, and we also introduce their applications in emerging photocatalytic schemes such as photoredox catalysis and photoreforming.

6.1. General Principle and System Design

6.1.1. Nanocrystal–Molecular Catalyst or Enzyme Hybrids

These hybrids combine the light-harvesting and charge-donating capabilities of NCs with the catalytic performance of artificial transition-metal-based molecular catalysts or natural enzymes. Cobaloxime-based molecules have long been known to catalyze the reduction of protons to molecular H₂.^405−408 Chen and co-workers demonstrate that photogenerated electrons in CdSe/ZnS core/shell QDs can be transferred to surface-attached cobaloxime molecules with high efficiency and can be subsequently used to reduce protons to H₂ (Figure 33A).⁴⁰⁹ In related studies, other Co-based⁴¹⁰ and Ni-based molecules^411,412 are also shown to be efficient electron acceptors for NCs and catalysts for H₂ generation. In addition to these specially designed molecular catalysts, it has been found that many transition metal complexes formed in situ by adding transitional metal salts into water-soluble NCs are efficient molecular catalysts for H₂ generation.^{409,410,413−415} The pioneering work by Krauss and co-workers reported that a Ni–dihydrolipoic acid (DHLA) complex formed on the surface of CdSe QDs catalyzed H₂ generation with a quantum efficiency of >36% (Figure 33B).⁴¹³ Similarly, Wu and co-workers reported several similar in situ formed catalysts by adding nickel or cobalt salts to aqueous solutions of QDs with mercaptopropionic acid (MPA) ligands.⁴¹⁶ For the rational design and improvement of these in situ catalysts, their structures and reaction mechanisms need to be elucidated. There have also been extensive efforts on photodriven H₂ generation using NCs coupled to natural enzymes^417−419 (such as [FeFe]- and [FeNi]-hydrogenases) or their artificial analogues typically containing Fe–S carbonyl assemblies to mimic the functional subsites of hydrogenase.^420−423 These works are mostly motivated by the fact that natural enzymes can efficiently catalyze the reduction of proton into H₂ with minimal overpotentials, which is typically unachievable with man-made metallic or organometallic catalysts. For example, King and co-workers have shown that complexes of MPA-capped CdS NRs with Clostridium acetobutylicum [FeFe]-hydrogenase I (CaI) can photocatalyze H₂ generation with an apparent quantum efficiency (AQE) of ∼20% under illumination at 405 nm (Figure 33C),⁴¹⁸ which is superior to the performance of Pt-tipped CdS NRs measured under similar conditions (with AQE < 10%).^49,424

Figure 33.

Design of various NC–molecular catalyst or enzyme systems. (A) CdSe/ZnS core/shell QDs coupled with a cobaloxime molecular catalyst for H₂ generation. (B) CdSe QDs coupled with an in situ formed Ni-DHLA catalyst for H₂ generation. (C) CdS NRs coupled with Clostridium acetobutylicum [FeFe]-hydrogenase I (CaI) for H₂ generation. (D) CdS-Pts coupled with a Ru(tpy)(bpy)Cl₂-based oxidation catalyst for overall water splitting. (E) CuInS₂ QDs coupled with a meso-tetraphenylporphyrin iron(III) chloride (FeTPP) catalyst for the reduction of CO₂ to CO. (F) CdS NRs coupled with a nitrogenase molybdenum–iron (MoFe) protein for the reduction of N₂ to NH₃. (A) Adapted with permission from ref (409). Copyright 2012 American Chemical Society. (B) Adapted with permission from ref (413). Copyright 2012 American Association for the Advancement of Science. (C) Adapted with permission from ref (418). Copyright 2012 American Chemical Society. (D) Adapted with permission from ref (425). Copyright 2014 Nature Publishing Group, Macmillan Publishers Limited. (E) Adapted with permission from ref (426). Copyright 2017 American Chemical Society. (F) Adapted with permission from ref (427). Copyright 2016 American Association for the Advancement of Science.

Among the various photocatalytic reactions, proton reduction to H₂ is a relatively simple one in terms of both thermodynamic and kinetic aspects. Indeed, by optimizing various charge separation and catalytic process in a system, near-unity efficiency H₂ generation has already been achieved.^428,429 In recent years, researchers have attempted to tackle more challenging reactions such as water oxidation, CO₂ reduction, and N₂ fixation. These reactions involve many more electrons and are kinetically more demanding than H₂ generation. In these efforts, many efficient catalysts have been developed and, in principle, quantum-confined NCs can be coupled with these catalysts to perform photodriven reactions. In a recent report, Stolarczyk and co-workers demonstrate that Pt-tipped CdS NRs can efficiently transfer photogenerated holes to Ru(tpy)(bpy)Cl₂-based water oxidation catalysts to generate O₂ (Figure 33D).⁴²⁵ As a result, this system, for the first time, can perform overall water-splitting using colloidal NCs, although the AQE is low (∼0.27%). As for CO₂ reduction, Weiss and co-workers report that CuInS₂/ZnS QDs with very energetic CB edges (∼ −2.5 V vs SCE) can transfer electrons to a meso-tetraphenylporphyrin iron(III) chloride (FeTPP) in <200 fs, which is leveraged to selectively reduce CO₂ to CO (Figure 33E).⁴²⁶ The AQE of the reaction remains low (∼0.01%), but is already many-fold better than similar systems using Ir(ppy)₃ (∼0.0013%) or 9-cyanoanthracene (0.0008%) sensitizers. N₂ fixation is challenging because the cleavage of the nitrogen-nitrogen triple bond has a very large activation barrier. To date, very few man-made catalysts for the reduction of N₂ to NH₃ under mild conditions have been reported,^430−433 while natural nitrogenase enzymes can perform N₂ fixation under ambient conditions using chemical energy released from the hydrolysis of adenosine 5′-triphosphate (ATP). King and co-workers show that it is possible to replace the chemical energy with the photoexcitation energy to reduce N₂ to NH₃ using CdS NRs coupled with molybdenum–iron (MoFe) nitrogenase (Figure 33F).⁴²⁷ The turnover rate of the photodriven reaction already reaches 63% of the ATP-coupled reaction rate, showing the great potential of this hybrid approach in N₂ fixation.

6.1.2. Nanocrystal–Redox Mediator–Catalyst Triads

This type of systems utilizes a redox mediator to transfer charge between NCs and catalysts, which is partially inspired by natural photosynthetic systems. Charge recombination between NCs and catalysts can in principle be suppressed in this design. Fundamentally, this design also enables more mechanistic insights into the photocatalytic systems as it allows for detailed spectroscopic studies by using the well-established spectroscopic feature of redox mediators as a handle. For example, photoreduction of methyl viologen (MV²⁺) is often used as a model reaction to examine the performance of photocatalytic systems because MV²⁺ is a well-known one-electron acceptor,^151,434 and redox mediator for H₂ evolution.^206,435,436

In a previous study, Lian and co-workers compared the performances of various NCs and also the benchmark Ru(bipy)₃²⁺ molecule for MV^•+ generation and H₂ generation.²⁰⁶ These NCs include CdSe core-only QDs, CdSe@CdS core/shell QDs, CdS NRs, and CdSe@CdS dot-in-rod NRs. The as-synthesized NCs were transferred to the aqueous phase by replacing native ligands with MPA ligands that also function as sacrificial electron donors. When measured under the same conditions, the radical generation QYs show the following trend (Figure 34A): CdSe@CdS NRs (∼98%) > CdS NRs (∼65%) > CdSe@CdS core/shell QDs (∼31%) > Ru(bipy)₃²⁺ (∼20%) > CdSe QD (∼11%).²⁰⁶ Pt nanoparticles were added as electron acceptors for MV^•+ radicals and as H₂ evolution catalysts. As expected, the H₂ generation efficiencies follow the trend of those for MV^•+ generation (Figure 34B). However, the absolute values for the former are much lower than those for the latter. In particular, the MV^•+ generation efficiency is essentially unity for CdSe@CdS NRs, but the internal quantum efficiency for H₂ generation is only ∼13%.

Figure 34.

NC–redox mediator systems for photocatalysis. (A) Steady-state MV^•+ radical photogeneration QYs using different light harvesters: Ru(bipy)₃²⁺, CdSe QD seed, CdS NR, CdSe@CdS dot-in-rod NRs, CdSe/CdS core/shell QDs of similar lowest exciton energy (CS-SE), and CdSe/CdS core/shell QDs of similar volume (CS-SV) as the CdSe@CdS NRs. Also plotted are the transient QYs (open triangles) at 10 μs obtained from TA measurements. For experimental conditions, see ref (206). (B) Internal (left axis) and external (right axis) QYs for H₂ generation from the systems in (A) coupled with Pt nanoparticles, as illustrated by the scheme in the inset. (C) Electron transfer kinetics from various NCs to MV²⁺ measured from the TA kinetics of exciton bleach features. The lines and circles are NCs without and with MV²⁺, respectively. (D) Formation and decay kinetics of MV^•+ radicals for various NCs. The color coding is the same as that in (C). (E) Charge separation mechanisms and MV^•+ radical generation QYs of ZnSe@CdS dot-in-rod NRs under 415 (bottom) and 550 nm (top) excitations. The partition ratios and MV^•+ generation QYs of different states are labeled. (F) The concentration of MV^•+ radicals generated by photoreduction using CdSe NRs and CdSe@CdS dot-in-rod NRs with different lengths (S, short, ∼25 nm; M, medium, ∼32 nm; L, long, ∼54 nm). (G) Radical generation QY for CdS QDs coupled with three different mediators, BV²⁺, MV²⁺, and PDQ²⁺. (H) Scheme of a H₂ generation system comprising CdSe@CdS rod-in-rod NRs, PDQ²⁺ redox mediators, and [NiFe] hydrogenase. The H₂ generation QYs for using MV²⁺ and PDQ²⁺ mediators are indicated. (A–D) Adapted with permission from ref (206). Copyright 2012 American Chemical Society. (E) Adapted with permission from ref (437). Copyright 2014 Royal Society of Chemistry. (F) Adapted with permission from ref (438). Copyright 2015 American Chemical Society. (G) Adapted with permission from ref (439). Copyright 2018 American Chemical Society. (H) Adapted with permission from ref (440). Copyright 2017 Royal Society of Chemistry.

In order to rationalize the different performances between these NCs, TA measurements were performed. Both the decay of exciton bleach features of NCs (Figure 34C) and the formation of a MV^•+ radical absorption band (Figure 34D) can be used to follow NC-to-MV²⁺ electron transfer kinetics. As the exciton bleach in NC-MV²⁺ complexes decays much faster than free NCs, the electron transfer yield is near 100% for all NCs. However, the lifetimes of MV^•+ radicals generated by these NCs are different (Figure 34D), reflecting the different recombination rates between MV^•+ and holes in NCs. Specifically, the recombination is negligible within 10 ps for CdSe@CdS NRs, accounting for their near-unity MV^•+ generation yield. Detailed measurements showed that the NR-to-MPA hole transfer process (0.31 ns) was much faster than charge recombination between MV^•+ radicals and holes in NRs (320 ns). In contrast, the fast recombination in core-only QDs leads to large recombination loss and a small steady-state QY.²⁰⁶ CdSe@CdS NRs show the best MV^•+ generation performance compared to both CdSe@CdS core/shell QDs with similar confinement energy and QDs with similar total NC volume because the former and the latter suffer from fast charge recombination and slow charge separation, respectively. This comparison highlights the importance of NC morphology in controlling charge separation and recombination for efficient photocatalysis.

A further demonstration of the role of the morphology of hetero-NRs in promoting charge separation and suppressing charge recombination was reported in our excitation wavelength dependence study of MV^•+ generation using type II ZnSe@CdS dot-in-rod NRs.⁴³⁷ The radical generation yield was ∼90% under 415 nm excitation but became much lower (∼34%) under 550 nm excitation. Detailed spectroscopic studies show that the excitation wavelength controls the charge separation and recombination pathways for NR-MV²⁺ complexes (Figure 34E). In the case of 550 nm excitation, excitons are generated near the ZnSe core and the NRs essentially function as ZnSe@CdS core/shell QDs. The excitons are dissociated by electron transfer to MV²⁺ to form charge-separated state A. Due to the relatively fast charge recombination rate of this state, the MV^•+ generation yield is only ∼34% for this state. In contrast, in the case of 415 nm excitation, a competition between exciton localization to near the core, exciton trapping along the rod, and exciton dissociation by electron transfer to MV²⁺ leads to the formation of three charge-separated states A, B, and C. State C, in particular, has a unity MV^•+ generation yield, as the charges are separated over a longer distance. The partition between states A, B, and C leads to an averaged MV^•+ generation yield of ∼90% under 415 nm excitation. This mechanism also explains the rod-length-dependent MV^•+ generation yield reported for CdSe@CdS dot-in-rod NRs by Kamat and co-workers (Figure 34F).⁴³⁸ Longer NRs presumably give a higher partition ratio for the charge-separated state C, as it becomes more difficult for exciton transport to the core to compete with direct exciton dissociation by electron transfer to MV²⁺. In a related study, Lian and co-workers also found this type of competition between exciton localization and dissociation for the homojunction CdSe tetrapods.²⁴³

In addition to NC morphologies, the type of redox mediator used in the reaction also strongly affects the yields of radical generation and subsequent H₂ generation. In a recent work, Lian and co-workers compared the photoreduction efficiency of three mediators, namely, propyl-bridged diquat (PDQ²⁺), MV²⁺, and benzyl viologen (BV²⁺), using CdS QDs.⁴³⁹ The steady-state radical generation yields follow the trend of BV²⁺ < MV²⁺ < PDQ²⁺, which appears to contradicts the reduction potentials of these mediators (−370, −448, and −550 meV vs NHE for BV²⁺, MV²⁺, and PDQ²⁺, respectively). TA measurements indicate the electron transfer yields are near unity for all three mediators; however, charge recombination rates between radicals and holes in CdS QDs follow the trend of BV²⁺ > MV²⁺ > PDQ²⁺, likely because charge recombination falls in the Marcus inverted region. Thus, the steady state radical generation yields are limited by charge recombination in this system. The redox potential of the mediator not only affects its own reduction efficiency but also controls the efficiency of the coupled H₂ generation reaction. Dyer and co-workers studied light-driven H₂ generation from a system consisting of CdSe@CdS NRs, MV²⁺, or PDQ²⁺ mediators and [NiFe]-hydrogenases.⁴⁴⁰ They found that although the electron transfer rate from NRs to MV²⁺ is much faster than that for PDQ²⁺ due to a larger electron transfer driving force for the former, the IQE of H₂ generation is ∼77% for PDQ²⁺ but is essentially zero for MV²⁺, as MV^•+ cannot donate electrons to the [NiFe]-hydrogenase. It is concluded that in these systems the redox potential of the mediators should be chosen to balance the electron transfer from NCs to mediators and the subsequent electron transfer from mediators to catalysts.

6.1.3. All-Inorganic Heteronanocrystals for Photocatalysis

All-inorganic hetero-NCs combine the light-harvesting and charge-donating capabilities of quantum-confined semiconductor NCs with the catalytic functions of another type of nanoparticles (often metal) to realize the goal of an “all-in-one” photocatalytic system. Banin and co-worker reported the synthesis of Au-tipped CdSe NRs as the first example for this type of heterostructure.⁴⁴¹ These Au-tipped NRs have been applied in photocatalysis reactions such as dye degradation and H₂ generation,^442,443 suggesting charge separation at the semiconductor–metal interfaces. Later, Habas and co-workers reported the synthesis of Pt-tipped CdS NRs by thermal reduction of Pt(II) salts.⁴⁴⁴ These NRs are more suited for solar-to-fuel conversion, as Pt is one of the best catalysts for the hydrogen evolution reaction.⁴⁴⁵ In a related work, Dukovic and co-workers achieved photodeposition of Pt on CdS NRs,⁴⁴⁶ where the electrons generated by photoexcitation of CdS NRs were used to reduce Pt salts and led to nucleation of multiple Pt nanoparticles on CdS NRs. Metal (including Au, Pt, and Ni) decorated NPLs have also been reported.^{154,223,447,448} These Pt-tipped NRs and NPLs have been intensely studied for solar-driven H₂ generation reactions.^{49,424,447−453} In particular, Alivisatos and co-workers demonstrate in their pioneering work that the photocatalytic H₂ generation efficiencies of Pt-tipped CdSe@CdS dot-in-rod NRs (CdSe@CdS-Pt NRs) can be systematically tuned using the CdSe core sizes and CdS rod lengths (Figure 35A).⁴⁹ Specifically, they find that for NRs with the same core size, the H₂ generation efficiency increases with the rod length, presumably because of increase charge separation distance in longer NRs; when rod lengths are comparable, NRs with a smaller CdSe core (2.3 nm) show higher activity than those with a larger core (3.1 nm), also presumably due to a better charge separation enabled by the more delocalized electrons for smaller cores. Kuno and co-workers first reported the light-driven H₂ generation performance of Ni-decorated CdS NPLs in aqueous solution with apparent quantum efficiencies of ∼64% for the first 2 h and ∼25% for 40 h, demonstrating a great potential of 2D NPLs in photosynthesis systems.⁴⁴⁸ Bigall and co-workers studied how the H₂ generation performances of CdSe/CdS core/crown NPL-Pt heterostructures change with core and crown size and found that the larger the core and crown, the better the performance.²²³

Figure 35.

All-inorganic NC systems for photocatalysis (A) Structural scheme (left), energy level scheme (middle), and TEM images (right) of the all-inorganic CdSe@CdS-Pt NRs (top). Relative quantum efficiency of H₂ generation for NRs with different core sizes and rod lengths (bottom). (B) Scheme of the CdS/ZnS core/shell QDs loaded with dual cocatalysts for H₂ generation. Amounts of generated H₂ for different system designs (bottom). (C) Scheme of a self-assembled framework for H₂ generation comprising cross-linked CdSe QDs and Pt nanoparticles (left). Amounts of generated H₂ for the assembly and an unassembled control (right). (A) Adapted with permission from ref (49). Copyright 2010 American Chemical Society. (B) Adapted with permission from ref (455). Copyright 2013 American Chemical Society. (C) Adapted with permission from ref (456). Copyright 2017 American Chemical Society.

Recently, Amirav and co-workers showed that the functionalities of CdSe@CdS-Pt NRs can be further expanded by adding an oxidation catalyst, as exemplified by the Ru-CdSe@CdS-Pt NRs.⁴⁵⁴ These NRs are good models for fully integrated all-inorganic artificial photosynthetic systems, but their photocatalytic performances have not been tested. In a related study, Li and co-workers reported CdS core and CdS@ZnS core/shell QDs coloaded with reduction catalyst Pt and oxidation catalyst PdS (Figure 35B).⁴⁵⁵ They found that the dual-catalysts-loaded QDs indeed have a better H₂ generation performance than QDs loaded with either Pt or PdS only, presumably because the best charge separation can be achieved in dual-catalysts-loaded samples. It is also interesting to note that for CdS core QDs Pt-loaded samples perform better than PdS-loaded ones, while for CdS/ZnS core/shell QDs PdS-loaded samples perform better. It suggests that hole extraction from core/shell QDs by sacrificial donors is difficult and an oxidation catalyst can improve the photocatalytic performance by accelerating hole transfer.

All-inorganic heterostructures are not limited to those with directly attached domains. They can be fabricated by cross-linking NCs with catalytic nanoparticles, as demonstrated by Wu and co-workers.⁴⁵⁶ This strategy is important, as the attachment of catalytic nanoparticles such as Pt onto small-size NCs such as strongly quantum-confined QDs is challenging. In addition, in the case of a 1:1 QD/Pt ratio, the absorbance of Pt will dominate over that of the QDs, diminishing the apparent QY of a photocatalytic system. Wu and co-workers effectively overcome these issues by designing a self-assembled architecture of QDs and Pt nanoparticles where these two are jointed together by molecular polyacrylate (Figure 35C, left). Many QDs can be attached with one Pt nanoparticle to ensure light absorption dominated by QDs; meanwhile, the distance between QDs and Pt can be tuned by the length of the polyacrylate chain such that electron transfer from QDs to Pt is still efficient. As a result of this unique design, the system achieved very fast H₂ generation (Figure 35C, right) with an internal quantum yield of ∼65%. This strategy can in principle be extended to various combinations of NCs and catalytic nanoparticles, greatly expanding the scope of all-inorganic photocatalysts.

6.2. Charge Separation in Photocatalytic Systems Using Nanocrystals

In all system designs described above, a critical step determining their photocatalytic efficiencies is the charge separation and recombination between the light-harvesting NCs and catalytic molecules or particles. In the redox mediator approach, charge separation and recombination between NCs and mediators are often relatively easy to measure due to the well-established spectral features of these mediators. As such, these have been discussed above along with the system descriptions. In comparison, such a spectroscopic handle is often not as straightforward to establish for molecular or nanoparticle catalysts. In this section, we review progress made toward understanding charge separation and recombination dynamics between NCs and molecular or nanoparticle catalysts.

6.2.1. Charge Separation in Nanocrystal–Molecular (Enzyme) Catalyst (Or Enzyme) Hybrids

Due to the large number of binding sites available on the surface of NCs, molecular or enzyme catalysts usually interact with NCs through the so-called static quenching mechanism, i.e., charge transfer from NCs to surface-adsorbed catalysts. This is important as the exciton lifetimes of NCs are typically much shorter than the triplet excited states of molecular light-harvesters such as Ru and Ir complexes. While the latter can achieve efficient charge separation via the diffusion controlled dynamic quenching mechanism,⁴⁵⁷ a short NC–catalyst distance is required for efficient charge separation for NCs.

Chen and co-workers studied charge separation between CdSe/ZnS core/shell QDs and surface-adsorbed cobaloxime hydrogen evolution catalysts using TA spectroscopy.⁴⁰⁹ The exciton bleach recovery in QD–cobaloximes is much faster than that of free QDs (Figure 36A and B). Energetic considerations indicate that electron transfer is the only exciton quenching mechanism by cobaloxime. Thus, the accelerated bleach recovery suggest fast electron transfer from the CB of QDs to the Co(III)/Co(II) redox level of cobaloxime. Fitting the bleach recovery kinetics reveals an electron transfer time constant of ∼105 ps (Figure 36C). In addition to following the exciton bleach feature, they find that the TA spectra of QD-cobaloximes at >100 ps exhibit a positive TA feature that is absent in free QDs (Figure 36B inset). This feature could arise from the absorption of Co(II) or charge-separation-induced absorption shifts of QDs via a transient stark effect. In either case, it confirms electron transfer from QDs to cobaloxime; fitting the kinetics at this feature gives a consistent electron transfer time constant (Figure 36D). The kinetics of this feature also suggests that the charge-separated state is long-lived, showing negligible decay within 3 ns.

Figure 36.

Charge separation dynamics in NC–catalyst hybrids. (A and B) TA spectra of QDs (A) without and (B) with the cobaloxime catalyst. (C and D) TA kinetics probed at (C) 525 nm and (D) 445 nm for QDs without (red) and with the cobaloxime catalyst (black). (E) TA kinetics of CdSe QDs with (red) and without (green) the Ni-DHLA catalyst. (F) TA decay kinetics (at 470 nm) of CdS–CaI samples with varying CaI/CdS ratios. (A–D) Adapted with permission from ref (409). Copyright 2012 American Chemical Society. (E) Adapted with permission from ref (459). Copyright 2015 American Chemical Society. (F) Adapted with permission from ref (419). Copyright 2014 American Chemical Society.

Hydrogen evolution requires the reduction of cobaloxime by two electrons. In the experiments performed under single exciton conditions (Figure 36A–D), the second electron transfer from QDs to the Co(II)/Co(I) redox level of cobaloxime is not observable. By exciting QDs with at least two excitons, one can, in principle, realize two electron reduction of cobaloxime. In reality, there exists an intrinsic challenge for this goal. Specifically, the ultrafast electron transfer observed by Chen and co-workers is enabled by the presence of 66 cobaloxime molecules on each QD. As the reduction potential of Co(II)/Co(I) is ∼0.3 V more negative than that of Co(III)/Co(II), the second electron should preferentially transfer to an unreduced cobaloxime, resulting in two catalysts in the Co(II) state instead of one catalyst in the desired Co(I) state. On the other hand, if there is only one cobaloxime molecule per QD, the electron transfer rate would be much slower due to the additive nature of electron transfer channels. Besides, as we review above, realizing a 1:1 QD/catalyst ratio is not easy due to the Poisson distribution for the adsorption events, where the probability of a QD to adsorb n catalyst is P_n (see eq 5.1 and details of the Poisson distribution in section 5.2). Thus, the ultimate goal should be to assemble QD–catalyst complexes in a 1:1 ratio while ensuring efficient charge separation at this ratio. Recently, Wasielewski and co-workers reported the simultaneous transfer of two electrons from one CdS QD to an attached extended-viologen cylophane.⁴⁵⁸ Such demonstration for realistic hydrogen evolution or other types of catalysts, however, is still lacking.

There have been extensive studies on the charge separation kinetics in many other NC–molecular catalyst or enzyme systems. For example, electron transfer from CdSe QDs to the in situ generated Ni-DHLA catalysts was studied using TA spectroscopy by Krauss and co-workers (Figure 36E).^459,460 It was reported that an electron transfer time constant of ∼69 ps and transfer yield of ∼90% can be realized in QD–Ni-DHLA complexes with a QD/Ni-DHLA ratio of ∼1:20⁴⁵⁹ by comparing the exciton bleach recovery kinetics of QDs with and without Ni-DHLA (Figure 36E). This efficient charge separation is a prerequisite for the efficient H₂ generation (AQE ∼ 36%). Dukovic and co-workers studied the charge separation dynamics in CdS NR-hydrogenase (CaI) hybrids using TA spectroscopy (Figure 36F), as well as by comparing the exciton bleach recovery kinetics of NRs with and without CaI.⁴¹⁹ They reported an electron transfer time of ∼100 ns and yield of ∼47% for a CaI/NR ratio of 1:1. The charge separation yield increases with the CaI:NR ratio (Figure 36F) and reaches ∼89% for a CaI/NR ratio of 10:1. Their previous work showed that the AQY of light-driven H₂ generation from NR–CaI hybrids with a CaI/NR ratio of 0.67:1 was ∼20%, for which the charge separation yield should be <47%. This H₂ generation performance is exceptional given that Pt-tipped CdS NRs with virtually 100% charge separation yields display AQYs of <10% (see more discussions in the following section). The authors speculate that the electron injected to the distal F-cluster of CaI diffuses inside the enzyme before being captured by the active site (H-cluster) that is several nm away from the F-cluster, effectively suppress charge recombination between the catalytic center and the hole located in the NR and/or oxidized sacrificial donors. This mechanism showcases the advantage of natural enzymes over man-made catalysts.

It is noteworthy that in the studies shown in Figure 36E and F and many related examples, electron transfer kinetics is derived solely from the exciton bleach feature of NCs. A more unambiguous demonstration should include the observation of signals from reduced products, which, on the other hand, also allows for measuring the lifetime of charge-separated states. However, these signals are often too weak to be resolved or simply absent in the commonly studied UV–vis–IR ranges. In recent years, X-ray TA spectroscopy has proven to be a unique tool to probe charge transfer dynamics, as X-ray absorption is sensitive to the oxidation state of the elements in catalytic centers. For example, Huang and co-workers reported direct evidence for the reduction of Co(III) to Co(II) upon electron transfer from QDs to cobaloxime catalysts using X-ray TA based on a synchrotron light source.⁴⁶¹ The time resolution of this type of X-ray TA is often limited to hundreds of ps. Recent developments in X-ray free electron lasers (FEL) offer a better solution for X-ray TA by use of femtosecond X-ray pulses. This technique is becoming a powerful tool to study charge transfer in catalysts in the years to come.

6.2.2. Electron and Energy Transfer from Photoexcited Nanocrystals to Attached Metals

The interaction mechanisms between semiconductor NCs and attached metallic catalysts are intrinsically more complex than those between NCs and molecular catalysts due to the continuous bands of metals as compared to the discrete levels of molecules. Based on a typical band alignment between metal and semiconductor using CdS and Pt as an example (Figure 37A, bottom), the metallic domain can quench the excitons in the semiconductor domain via electron, hole, and energy transfer channels. For photodriven H₂ generation, only electron transfer is the useful mechanism. Thus, it is fundamentally important to understand how electron transfer competes with energy and hole transfer channels and how long-lived charge separation can be achieved for the rational design of such integrated semiconductor–metal photocatalysts.

Figure 37.

Charge transfer in NR-Pt heterostructures. (A) Absorption (solid lines,) and emission (dashed lines) spectra of CdS NRs (black) and CdS-Pt NR heterostructures (red) (top). Schematic energy levels and possible exciton quenching pathways in CdS-Pt NR heterostructures (bottom). (B) TA spectra of CdS-Pt NRs at indicated time delays following 400 nm excitation. (C) TA kinetics of exciton bleach (XB, black solid line, top), photoinduced absorption (PA, red solid line, middle), and charge-separated state (CS, green solid line, bottom) spectral features for CdS-Pt NRs. Also shown for comparison are corresponding kinetics for free CdS NRs (gray dashed lines) at the same wavelengths. The inset shows a comparison of CS and PA kinetics in CdS-Pt after 1 ns. (D) Absorption (solid lines, left axis) and emission (dashed lines, right axis) spectra of CdS NRs (black) and CdS-Pt NR heterostructures (red). (E) TA kinetics probed at the exciton bleach (red circles) and charge-separated state (blue triangles) features of CdSe@CdS-Pt NRs following excitation of the CdSe core. (F) TA kinetics probed at three different exciton bleach features (X1, X2, and X3) and three corresponding charge-separated state features (CS1, CS2, and CS3) of CdSe@CdS-Pt NRs following excitation of the CdS rod. (A–C) Adapted with permission from ref (450). Copyright 2012 American Chemical Society. (D–F) Adapted with permission from ref (424). Copyright 2014 American Chemical Society.

In our previous study, Lian and co-workers investigated the effect of a metal tip on exciton dynamics in the semiconductor NR using CdS-Pt NRs as a model system.⁴⁵⁰ The absorption spectrum of CdS-Pt NRs contains both the excitonic absorption bands of CdS NRs and the broad absorption of Pt tips (Figure 37A, top).⁴⁶² Both band edge and trap state emissions of CdS NRs are strongly quenched by the Pt tips. To determine whether the quenching mechanism of excited CdS NRs by Pt is electron, hole, or energy transfer, TA spectroscopy was applied to investigate the detailed carrier dynamics.⁴⁵⁰ TA spectra of CdS-Pt NRs excited at 400 nm show the fast recovery of the exciton bleach (XB) feature of CdS NRs on a few ps time scale (Figure 37B, top) and the formation of a set of derivative-like spectral features (Figure 37B, bottom). Kinetics analysis shows that during the decay of XB (Figure 37C, top) the photoinduced absorption PA feature (from 500 nm to NIR; not shown in Figure 37B) that has been assigned to trapped holes remains unaffected (Figure 37C, middle). This comparison suggests that the decay of XB is a result of electron transfer rather than hole or energy transfer processes, as the latter should also remove the hole. This charge separation process is also responsible for the formation of the derivative-like spectral features via the stark effect in the CdS⁺-Pt^– charge-separated state (CS). It is proposed that the ultrafast (∼0.7 ps) hole trapping on CdS NRs suppresses both hole and energy transfer pathways, enabling a near-unity electron transfer yield.⁴⁵⁰ The ensuing back electron transfer process from the Pt to CdS, i.e., charge recombination, can be followed using both PA and CS features (Figure 37C, middle and bottom). Kinetics fitting reveals half-lives of ∼3.4 ps and ∼1.2 μs for charge separation and recombination processes, respectively. This large asymmetry in charge separation and recombination rates is also enabled by the hole trapping, as it sets up a long distance between the electron in Pt and the hole in the trap site, leading the long-lived charge-separated state. Based on this study, ultrafast hole trapping is the key to the photocatalytic H₂ production from CdS-Pt NRs.^49,453

Hole trapping facilitates charge separation in CdS-Pt NRs, but the nature of these hole trap sites remains unclear. A recent computational study using a semiperiodic density functional theory model for CdS NC surfaces supports the common assumption that hole trapping states are related to the nonbonding sp³ orbitals of sulfur atoms on the NC surfaces.⁴⁶³ Nonetheless, a way to control the spatial location and energetic depth of the trapping sites is lacking. In contrast, as we review above, in CdSe@CdS dot-in-rod NRs, the VB hole can be localized to the CdSe core with known and controllable location and depth by tuning the rod length and core size.^49,173 As shown Figure 37D, the absorption spectrum of CdSe@CdS-Pt NRs contains features from both domains, and the emission of CdSe@CdS NRs is efficiently quenched by the Pt tips. The quenching dynamics in CdSe@CdS-Pt NRs was also investigated by TA spectroscopy.⁴²⁴Figure 37E shows the TA dynamics of CdSe@CdS-Pt NRs excited by a 540 nm pulse, which selectively excites the CdSe core. Similar to CdS-Pt NRs, the core exciton bleach (XB) feature quickly recovers and a derivative-like charge-separated state (CS) signal grows concomitantly, suggesting electron transfer from the CdSe core to the Pt tip. Fitting the kinetics reveals charge separation and recombination half-lives of ∼43.5 ps and ∼211 ns, respectively.⁴²⁴ Thus, this system also shows near-unity yield and long-lived charge separation. Similarly efficient charge separation was found for ZnSe@CdS-Pt NRs⁴⁶⁴ and CdSe@CdS-Pt octapods.⁴⁶⁵ For all these seeded structures, hole transfer is suppressed by ultrafast localization of the hole to the seed, and energy transfer is suppressed by the long distance between seed exciton and the Pt tip. Figure 37F shows the TA dynamics of CdSe@CdS-Pt NRs excited by a 400 nm pulse, which is more complicated than the case of 540 nm excitation due to the competition between exciton trapping on the rod, exciton localization to the core and exciton localization to the bulb region surrounding the core. Detailed analysis shows that the three types of excitons (i.e., X1 trapped on the rod, X2 trapped on the bulb, and X3 localization to the core) have distinct electron transfer dynamics, generating three types of charge-separated states, namely, CS1, CS2 and CS3. Fitting the kinetics in Figure 37F reveals half-lives of 1.75, 30.1, and 43.5 ps for charge separation and 102, 211, and 211 ns for charge recombination for X1, X2, and X3 excitons, respectively. Thus, charge separation yields for all three types of exciton also approach unity in the case of 400 nm excitation. Note that the high charge separation yield and long-lived charge-separated states for X3 are enabled by ultrafast hole localization to the CdSe core, whereas those for X1 and X2 are enabled by ultrafast hole trapping on CdS surfaces.

The importance of hole trapping or localization for efficient charge separation in NC–metal heterostructures is further corroborated by our recent studies of exciton quenching dynamics in Pt-decorated CdSe¹⁵⁴ and CdS NPLs.⁴⁴⁷ These NPLs have an atomically precise thickness of only a few monolayers (MLs) and are strongly quantum-confined in the thickness direction.^{80,81,466−469}Figure 38A shows the absorption spectrum of 5 ML CdSe NPLs with the sharp and discrete excitonic band arising from the precise quantum confinement in their thickness. These CdSe NPLs are well passivated upon synthesis, as implied by their relatively high PLQY of ∼36% for core-only samples and the absence of a trap-related emission band in their PL spectrum (Figure 38A). TA and time-resolved PL measurements show no evidence for the sub-ps hole trapping observed in CdS NRs.¹⁵⁴ Upon Pt decoration, the PL of CdSe NPLs was quenched by 100% (Figure 38A). The TA measurements show that the exciton bleach (XB) of CdSe completely recovers within ∼100 ps for CdSe-Pt NPLs (Figure 38B, bottom), consistent with PL quenching. However, the analysis of the charge-separated state (CS) signatures indicates that the decay of CS and the formation of XB are not well correlated. Specifically, the decay of 86.6% of the XB amplitude within ∼1 ps does not lead to the formation of CS, whereas only the decay of the remaining 13.4% of XB is accompanied by the formation of CS. Based on this observation, we propose that the majority of excitons (∼86.6%) are quenched by ultrafast exciton transport to the CdSe/Pt interface, followed by rapid energy transfer (schematically shown in Figure 38B, top). 13.4% of excitons are dissociated to form the desired CdSe⁺-Pt^– charge-separated state in ∼9.4 ps, and the charge recombination half-life is ∼75 ns, both enabled by some CdSe NPLs in the ensemble exhibiting hole trapping. Note, however, that this hole trapping is not as fast and efficient as that in CdS NRs.

Figure 38.

Charge and energy transfer in NPL-Pt heterostructures. (A) Absorption and emission spectra of CdSe NPLs (black solid line and green dashed line, respectively) and CdSe-Pt NPLs (red solid line and blue dashed line, respectively). Inset is a TEM image of the CdSe-Pt NPLs. (B) TA kinetics probed at the exciton bleach (blue triangles) and charge-separated state (red circles) features of CdSe-Pt NPLs following 400 nm excitation (bottom). As indicated in the figure, ∼87% of excitons in CdSe NPLs are quenched by energy transfer (EnT) to Pt. Proposed mechanism for the ultrafast EnT quenching that comprises exciton diffusion inside the NPLs on the hundreds of fs time scale, followed by interfacial EnT on the tens of fs time scale (top). (C) Absorption and emission spectra of CdS NPLs (black solid line and blue dashed line, respectively) and CdS-Pt NPLs (red solid line and pink dashed line, respectively). (D) Comparison of exciton bleach (XB) kinetics at 416 nm of CdS NPLs (blue circles) and CdS-Pt NPLs (red squares) and the scaled charge-separated state (CS) kinetics (green triangles). (A and B) Adapted with permission from ref (154). Copyright 2014 American Chemical Society. (C and D) Adapted with permission from ref (447). Copyright 2013 American Chemical Society.

Our more recent study on CdS-Pt NPLs demonstrates very different hole trapping and exciton quenching mechanisms from CdSe-Pt NPLs.⁴⁴⁷ The absorption spectrum of CdS NPLs shows discrete excitonic bands, but their PL spectrum shows emission from both the lowest-energy excitonic band and two much broader trap-related bands (Figure 38C). Ultrafast PL measurements show a hole trapping time constant of ∼0.2 ps for CdS NPLs, which is even faster than that of CdS NRs. Both excitonic and trap-related emission bands are completely quenched by the decorated Pt nanoparticles (Figure 38C). TA measurements show that, because of the ultrafast and efficient hole trapping, the quenching mechanism of excitons in CdS NPLs by Pt is dominated by interfacial electron transfer to form charge separation states (CS). As shown in Figure 38D, the decay of XB and the formation of CS correlated well. Fitting these kinetics reveals charge separation and recombination half-lives of ∼8.8 ps and ∼96.2 ns, respectively. These time constants are similar to those reported for CdSe-Pt NPLs, but the charge separation yield is near unity for CdS-Pt NPLs. The comparison CdSe-Pt and CdS-Pt NPLs clearly demonstrates the essential role of hole trapping in enabling selective and efficient electron transfer in these semiconductor–metal heterostructures.

6.3. Determining and Improving the Efficiency Limiting Steps in Photocatalytic Systems Using Nanocrystals

6.3.1. Photocatalytic Efficiency-Limiting Steps

Based on the works we review in the previous section, electron transfer from quantum-confined NCs to attached catalysts including molecules, enzymes, and metals are fast and the charge separation efficiencies approaches unity in many systems. In contrast, their photocatalytic quantum efficiencies for multielectron reactions such as H₂ generation are often far from unity.^49,424,453 The complete light-driven H₂ generation process involves many forward and backward steps, and the competition of these processes determines the overall quantum efficiency. These competitive processes have been illustrated in recent studies of efficiency-limiting steps in the overall light-driven H₂ generation process in CdS-Pt NRs using l-cysteine as a the sacrificial electron donor and mercaptoundecanoic acid (MUA) as the NR surface capping ligand and the initial hole acceptor, where the sacrificial donor removes the hole from the NRs and undergoes the oxidation half-reaction.^470,471 As shown in Figure 39A, starting from an exciton state in the nanorod, the overall light to H₂ generation using CdS-Pt NRs involves multiple forward electron and hole transfer steps indicated by solid arrows: ET from the excited CdS to Pt, a two-electron/two proton water/proton reduction (WR) process on Pt, hole transfer (HT) from the CdS valence band or trap states to surface ligands (L = 11-MUA), hole transfer from the surface ligand to the sacrificial donor (l-cysteine) in solution, which is referred to as the hole scavenging (HS) step, and finally the oxidation reaction occurring on the hole scavenger or sacrificial donor (not shown). These forward steps compete with a series of backward e-h charge recombination steps (also known as the back electron transfer step), which are indicated by dashed arrows. It was proposed that because of the time separation of many of these electron and hole transfer processes the overall process can be described by a simplified kinetics model shown in Figure 39B, which involves four sequential kinetics stages with their own quantum efficiencies. The excitation of a L-CdS-Pt NR creates an exciton state (L-CdS*-Pt) that undergoes fast trapping of the VB hole on a sub-ps time scale. In the HT stage starting with L-CdS*-Pt, hole transfer to the MUA ligand to form L⁺-CdS^–-Pt (with a rate constant of k_HT) competes with the electron–hole recombination (k_CR1) within CdS* to determine the hole transfer QE (QE_HT). In the ET stage, starting with L⁺-CdS^–-Pt, ET from CdS^– to Pt (k_ET) to form the charge-separated state (L⁺-CdS-Pt^–) competes with charge recombination between CdS^– and L⁺(k_CR2), giving rise to the ET QE (QE_ET). In the hole scavenging stage, starting with L⁺-CdS-Pt^–, hole transfer from L⁺ to SD in solution (k_HS) to forms L-CdS-Pt^– competes with charge recombination between L⁺ and Pt^– (k_CR3) to determine the hole scavenging QE (QE_HS). The resulting L-CdS-Pt^– is a long-lived species that can continue on to the slow water or proton reduction steps with a quantum efficiency of QE_WR. Although the detailed mechanism of the two-electron/two-proton H₂ generation process on Pt is complex, it can be assumed that it has a rate limiting step and its competition with charge recombination, likely between Pt^– and oxidized SD, controls its QE. Within this simplified sequential kinetics model, the overall QE of the light-driven H₂ production process can be considered as the product of the four elementary stages: QE_H2 = QE_HT × QE_ET × QE_HS × QE_WR. Although the rates of individual steps likely change in different systems and the kinetics models should be modified, we believe that decomposing the overall light-to-H₂ conversion process into its elementary stages facilitates the determination of key efficiency-limiting factors. In the following, we review several studies of NC-based photocatalytic H₂ generation systems to illustrate how these steps affect the quantum yield of the overall reactions.

Figure 39.

Photodriven H₂ generation using CdS-Pt NRs. (A) Key energy levels and elementary processes and (B) simplified kinetic model with key intermediate states and processes for light-driven H₂ generation using L-CdS-Pt nanorods. L indicates the MUA capping ligands on the CdS surface. Forward processes (solid arrows): hole transfer from the trapped exciton state to surface ligand L (with a rate constant k_HT), electron transfer from the CdS to Pt (k_ET), hole transfer from the oxidized surface ligand L⁺ to sacrificial donor SD (k_HS), and water reduction on a reduced Pt particle (k_WR). Each process competes with a charge recombination process (k_CRi, i = 1–4, dashed arrows), which determines their quantum efficiency. The overall quantum efficiency of light-driven H₂ generation is the product of the quantum efficiencies of the elementary steps. Also shown in (A) is a schematic of overall light-driven H₂ generation. (A and B) Adapted with permission from ref (470). Copyright 2022 American Chemical Society.

For NC–molecular catalyst systems, Llobet and co-workers investigated all the involved reactions in a model system comprising CdTe QDs, a molecular cobalt catalyst, and ascorbic acid as sacrificial electron donor (Figure 40A); while the former accepts the electrons from QDs for the H₂ reduction half-reaction, the latter consumes the holes from CdTe QDs for the oxidation half-reaction.⁴¹⁰ The importance of hole transfer to sacrificial donors is illustrated by the donor-concentration-dependent H₂ generation behavior (Figure 40B). When the concentration of the donor increases from 0.1 to 0.6 M, the QY for H₂ generation is enhanced by 33-fold from 0.3% to 10%. A higher donor concentration improves the hole transfer rate for it compete with and suppress charge recombination between catalysts and holes in NCs. When the donor concentration further increases from 0.6 to 1.2 M, the QY slightly drops, likely due to saturation of the hole transfer rate. The authors have also measured all the charge transfer and recombination time constants in the reaction. The results of these time scales are summarized in the scheme in Figure 40C. They find that electron transfer from QDs to catalysts occurs fast enough and efficiently (nanosecond time scale) whereas the charge recombination and catalysis are much slower (microsecond to millisecond time scales). On the basis of these measurements, they conclude that for this system efficiency improvements should focus on the catalytic rate enhancement, which should be at least on the hundreds of ns time scale.

Figure 40.

Photocatalytic efficiency-limiting factors for NC-based systems. (A) A photocatalytic H₂ generation system using CdTe QDs as light-harvesters, Co(III)-1 as the H₂ evolution catalyst, and ascorbic acid (H₂A) as the sacrificial electron donor. (B) H₂ turnover number per Co catalyst (TON_Co) as a function of time for the system in (A) with varying concentrations of H₂A/NaHA donors. The inset shows the long-term performance. (C) Scheme summarizing the energetics and kinetics parameters for the system in (A). The time scales for the various charge separation and recombination processes in the system are labeled. (D) Comparison of H₂ production traces from MUA-capped ZnSe@CdS-Pt (blue) and ZnTe@CdS-Pt (red) NRs. (E) Comparison of H₂ generation quantum efficiencies for MPA- and cysteine-capped CdS-Pt NRs using SO₃^2–, TEA, EDTA^4–, and MeOH as sacrificial electron donors. The inset shows hydrogen evolution as a function of time. (F) H₂ generation quantum efficiencies for both MUA-capped CdSe@CdS-Pt and CdS-Pt NRs in an aqueous solution with SO₃^2– or MeOH as the added sacrificial electron donor. (A–C) Adapted with permission from ref (410). Copyright 2014 American Chemical Society. (D) Adapted with permission from ref (452). Copyright 2011 American Chemical Society. (E) Adapted with permission from ref (472). Copyright 2012 American Institute of Physics. (F) Adapted with permission from ref (424). Copyright 2014 American Chemical Society.

Many research groups including us have studied the efficiency-limiting factors for NC–metal heterostructures. As the electron transfer yields for these structures are generally high, hole removal by sacrificial electron donors is often a limiting step.^{424,452,472,473} Zamkov and co-workers show that the H₂ generation rate of MUA-capped ZnSe@CdS-Pt NRs is ∼300-fold faster than that of MUA-capped ZnTe@CdS-Pt NRs measured under the same conditions (Figure 40D), where methanol was used as the sacrificial donor for the hole removal from the ZnSe or ZnTe cores inside the NRs.⁴⁵² The difference is attributed to the fact that initial hole transfer from the ZnSe core to the surface hole acceptor ligand (MUA) is energetically allowed, while it is not favored for the ZnTe core, which is confirmed by their time-resolved PL decay measurements. The importance of hole removal is also confirmed by Berr and co-workers in their study of H₂ generation from CdS-Pt NRs in the presence of different sacrificial donors.⁴⁷² As shown in Figure 40E, various molecules were used as sacrificial donors for the hole removal from the NRs. The highest efficiency for cysteine-capped NRs is achieved using SO₃^2– as the donor (1.7%), and it drops to 0.7% for TEA, 0.1% for EDTA^4–, and below the detection limit for MeOH. The same trend is observed for MPA-capped NRs but with systematically higher efficiencies. This efficiency trend positively correlates the reducing power (i.e., more negative oxidation potentials) of sacrificial donors: SO₃^2– > TEA > EDTA^4– > MeOH. The authors further show that faster hole transfer not only improves H₂ generation QYs but also is essential for the stability of the photocatalytic systems. TEM images reveal obvious shortenings and aggregations of NRs with MeOH and EDTA^4– as the hole acceptors, suggesting that the holes in NRs, if not scavenged fast enough, oxidize and etch their own surfaces.

Our recent study also shows that the photocatalytic efficiency of H₂ generation from CdS-Pt and CdSe@CdS-Pt NRs depends sensitively on sacrificial electron donors.⁴²⁴ In particular, we find that the relative performance between these two types of NRs depends on the choice of sacrificial electron donors for removing the holes from the NRs (Figure 40F). With MeOH as the sacrificial electron donor, we observe higher efficiency for CdSe@CdS-Pt NRs (1.8%) than for CdS-Pt NRs (0.8%). The efficiencies of both NRs are improved with SO₃^2– as the electron donor, but CdS-Pt NRs have an efficiency (9.6%) higher than CdSe@CdS-Pt NRs (3.2%). These generation efficiencies correlate positively with the hole transfer rates measured with time-resolved PL decay.⁴²⁴ We suspect that because of their strong coupling with phonons,^474,475 trapped holes require a large reorganization energy and/or driving force for fast hole transfer.²⁵⁷ Therefore, the rates for hole transfer from CdS NRs to weakly reductive MeOH and MUA are slower than that for CdSe@CdS NRs. When using strongly reductive SO₃^2– as the donor, the driving force is not a limiting parameter and hence the trapped holes on CdS NR surfaces are more easily accessed by donors than the core-confined holes in CdSe@CdS NRs.

6.3.2. Approaches to Improving Photocatalytic Efficiency

Wu and co-workers reported that modifying CdSe QDs with hole-accepting ligands, such as phenothiazine (PTZ), strongly enhanced the photocatalytic H₂ generation efficiency of CdSe QDs in aqueous solution and also the photoelectrochemical H₂ generation efficiency of the CdSe QD-sensitized photocathode.⁴⁷⁶ The choice of the hole-accepting ligand is based on previous extensive studies showing that PTZ is a good acceptor for II–VI group NCs, capable of scavenging holes on the ps to ns time scale. As shown in Figure 41A, the rate of H₂ evolution from PTZ-modified CdSe QDs is ∼40-fold that of bare CdSe QDs when using ascorbic acid as the sacrificial donor. It is proposed that PTZ ligands extract holes rapidly and efficiently from CdSe QDs and the generated PTZ⁺ radicals react with ascorbic acids to transform the latter into diascorbic acid. As hole transfer from QDs to PTZ is faster than that from QDs directly to ascorbic acid, this shuttling mechanism suppresses charge recombination between electrons on catalytic sites and holes in QDs and thus improves the photocatalytic efficiency. A parallel approach to accelerate hole transfer is to engineer the morphology of NCs. For example, Zamkov and co-workers reported that CdSe@CdS-Pt NRs etched with peroxides display a H₂ generation rate that is ∼3–4-fold that of unetched ones (Figure 41B). They found that this simple chemical etching procedure led to partial dissolution of the CdS shell surrounding the CdSe core and thus facilitated physical contacts between CdSe core and electron donors for fast hole transfer.⁴⁵¹

Figure 41.

Approaches to suppress recombination and enhance photocatalytic efficiency. (A) Light-driven H₂ evolution of bare CdSe QDs, PTZ-modified CdSe QDs, and bare PTZ from 10.0 mL of ascorbic acid aqueous solution (0.2 M) at pH = 4.0. (B) CdSe@CdS-Pt NRs with an exposed CdSe core prepared via chemical etching (top). Representative TEM image of etched CdSe@CdS NRs (bottom left). Comparison of the H₂ generation efficiency of etched and nonetched CdSe@CdS-Pt NRs (bottom right). (C) H₂ generation rates from cysteine-capped CdS-Ni NRs as a function of pH. The inset shows a scheme of OH^– hole-shuttle-mediated photocatalytic generation of H₂. At high pH, i.e., high hydroxyl anion concentration, the photoexcited holes in CdS NRs oxidize hydroxyl anions to hydroxyl radicals, which carry away the positive charges and in turn oxidize ethanol to acetaldehyde. The electrons are transferred to the Ni nanoparticle and catalyze H₂ formation. (D) Light-driven H₂ generation internal quantum efficiency (IQE) for CdS-Pt (green column) and CdSe-Pt NPLs (red column) at varying pH levels. The black dots with dashed line is a fit to the pH-dependent IQE of CdS-Pt NPLs. (E) Scheme of charge recombination processes in 2D NPL-Pt and 1D NR-Pt heterostructures in aqueous solution at pH < 13 when the major electron donors are cysteine molecules. It is assumed that the holes transferred to cysteine (with a rate of k_HT) can be ionized back to the NPLs and NRs (with a rate of k_ion). The holes diffuse along the NPLs and NRs (with a rate of k_h) to the NC–Pt interface, where they recombine with electrons in Pt (with a rate of k_X). The 2D morphology can effectively slow down k_h and thus retard charge recombination. (A) Adapted with permission from ref (476). Copyright 2016 John Wiley & Sons. (B) Adapted with permission from ref (451). Copyright 2013 American Chemical Society. (C) Adapted with permission from ref (473). Copyright 2014 Springer Nature. (D and E) Adapted with permission from ref (447). Copyright 2018 American Chemical Society.

Faster hole transfer to sacrificial donors can suppress charge recombination between electrons on catalytic sites and holes in NCs, but it does not guarantee efficient photocatalysis. Indeed, many previous studies on Pt-tipped NRs, for example, show that the hole transfer to donors (ps to ns time scale) is much faster than the recombination between electrons on Pt and holes in NRs (tens of ns to μs time scale), while the H₂ generation efficiency of these systems is generally below 10%. This is likely because the chemical transformation of donors used in the reaction (such as alcohol and thiol molecules) is slow such that there is significant efficiency loss to recombination between electrons on Pt and holes in donors. Simon and co-workers recently reported a mechanism to effectively accelerate the oxidation of sacrificial donors and thus improve the H₂ generation efficiency of Ni decorated CdS NRs.⁴⁷³ They found that the H₂ generation rates increased significantly with pH (Figure 41C). In particular, at pH 14.7, an external QY of 53% (or internal QY up to 71%) has been achieved. They propose that, at high pH, the concentration of hydroxyl anions (OH^–) is high enough to shift their oxidation potential above the VB and hole-trapping levels of CdS NRs such that OH^– anions become hole scavengers. The small size of OH^– anions allows for their fast diffusion and facile permeation through the ligand shell to reach holes in CdS NRs for fast hole transfer. This is similar to the shuttling mechanism of PTZ-modified QDs introduced above. However, a more important role of OH^– anions is that their oxidized products, hydroxyl radicals (OH^•), are known to be a very reactive species that are able to oxidize ethanol molecules to acetaldehyde with a high rate. In this way, chemical transformation of ethanol donors is significantly accelerated, leading to a high photocatalytic efficiency. More recently, this strategy was applied by Amirav and co-workers to CdSe@CdS-Pt NRs, and a near perfect internal QY (100%) of light-driven H₂ generation has been achieved at pH ≥15.⁴²⁸

Besides the expected hole removal role, the potential undesired roles of the sacrificial donors also need to be carefully examined. For example, the sacrificial donor-involved oxidation half-reaction itself could generate H₂, in parallel with the H⁺ or H₂O reduction half-reaction.^477,478 For widely used sacrificial donors like methanol, ascorbic acid, S^2–, and triethanolamine (TEOA), it has been reported that oxidation of methanol and ascorbic acid can produce CO₂ and H₂, oxidation of S^2– leads to sulfur and H₂, and oxidation of TEOA generates nitride acid, CO₂, and H₂. With TEOA as the sacrificial donor, the oxidation half-reactions can contribute up to 34% of the total H₂ generated in some cases.⁴⁷⁷ In these cases, in addition to the photoreduction of water or proton, H₂ was also produced by consuming the holes from the NCs. Moreover, in some cases, sacrificial donor radicals (e.g., alkoxy radicals as the oxidized alcohol) generated by the oxidation process can react with electrons again before they get oxidized and reduce back to their original form.⁴⁷⁹ This process consumes the electrons that are supposed to be used for the H₂ reduction half-reaction. Therefore, the measurement of the H₂ generation quantum efficiency in systems using sacrificial donors should carefully account for the contributions of the oxidation of sacrificial donors in addition to the desired photoreduction half-reaction. Control experiments of the effects on the oxidation of sacrificial donors should be provided to fairly determine the true light-driven reduction efficiency of H⁺ or H₂O.

In addition to facilitating hole transfer to donors and the chemical transformation of oxidized donors, one can improve the photocatalytic efficiency by suppressing charge recombination between electrons on catalysts and holes in NCs and/or holes in donors via NC morphology control. For example, our recent study of light-driven H₂ generation from CdS-Pt NPLs reveals the key role of the 2D morphology in suppressing charge recombination as compared to the 1D morphology.⁴⁴⁷ We examined the pH-dependent internal QYs of CdS-Pt NPLs and found that they also displayed near-unity QYs at pH 14.7 (Figure 41D). An important difference between CdS-Pt NPLs and the CdS-Pt and CdSe@CdS-Pt NRs introduced above is that NPLs have QYs higher than 40% at pH <13, whereas QYs of NRs typically drop to <20%. We propose that, at pH <13, thiol ligands instead of OH^– anions are the dominant hole acceptors. In this case, charge recombination, especially recombination between electrons on Pt and holes in thiols (k_CR2), is the key efficiency-limiting factor. We numerically simulated this recombination process for CdS-Pt NPLs and NRs by assuming that charge recombination proceeds via ionization of the holes in thiol ligands back to NPLs or NRs, followed by diffusion along the hole trapping sites to CdS–Pt interface where recombination takes place (Figure 41E). The simulation shows that charge recombination in 2D NPLs is over five-fold slower than that in 1D NRs when the same rate constants for elementary steps and lateral size (same length for NRs and square NPLs) are used. The simple physical underpinning is that the 2D morphology requires many more random walk steps for the hole to reach the recombination interface than the 1D one.

The photocatalytic efficiency of NC–catalyst systems can also be improved by optimizing the catalysts, as fast catalytic turnover (large k_cat) favorably outcompetes various charge recombination processes. The importance of catalysts is illustrated in the work by Llobet and co-workers. They compared light-driven H₂ generation from CdTe QDs coupled with two different cobalt catalysts, Co(III)-1 and Co(III)-2, under the same conditions. Co(III)-1 and Co(III)-2 have the same active Co(III) center but different stabilizing ligands. As shown in Figure 42A and B, the H₂ generation rate of Co(III)-1 is almost two orders of magnitude faster than that of Co(III)-2. This comparison also highlights the essential role of ligand design in enhancing the efficiency of molecular catalysts. The fastest molecular catalysts reported to date are the so-called Dubois-type catalysts with a H₂ turnover frequency of >10⁵ s^–1.^480,481 Mechanistic studies on these catalysts point to a key role of pendant amines on the ligands that function as proton relays for the formation and cleavage of the H–H bond.⁴⁸⁰ This precisely controlled delivery of protons is proposed to be critical in natural hydrogenase enzymes.

Figure 42.

Other factors affecting photocatalytic efficiency. (A and B) H₂ turnover number per catalyst (TON_Co) as a function of time for a CdTe QD-based system using (A) Co(III)-1 and (B) Co(III)-2 catalysts. Experiments performed using different concentrations of H₂A/NaHA donors are shown as the indicated colored lines; experiments performed in the absence of catalysts are shown as gray lines. The structures of Co(III)-1 and Co(III)-2 are shown in the sets. (C) PL QYs (corrected for the metal absorption contribution) of CdSe@CdS-Ni NRs (blue triangles), TA signal difference at 471 nm between NRs with and with Ni tips (a measure of charge separation efficiency; green stars), corrected and simulated photon to H₂ efficiencies (red circles and orange squares, respectively), and exciton bleach recovery half-life time (green pentagons) displayed as a function of the metal domain size. The optimal charge separation efficiency and H₂ generation efficiency are achieved at a Ni tip size of ∼5 nm. (D) H₂ generation efficiency of CdSe@CdS NRs decorated with a single, double, or multiple Pt nanoparticles. (E) Photodriven H₂ production internal quantum efficiency QE_H2 of CdS-Pt NRs as a function of the average Pt tip size. Also shown is the ET quantum efficiency QE_ET determined from transient absorption kinetics and the water reduction quantum efficiency C*QE_WR calculated by the ratio of QE_H2 and QE_ET. (F) Quantum efficiencies of H₂ production (purple circles) and electron transfer (orange triangles) as a function of the CdS rod length. (A and B) Adapted with permission from ref (410). Copyright 2014 American Chemical Society. (C) Adapted with permission from ref (482). Copyright 2018 American Chemical Society. (D) Adapted with permission from ref (483). Copyright 2015 American Chemical Society. (E) Adapted with permission from ref (470). Copyright 2022 American Chemical Society. (F) Adapted with permission from ref (471). Copyright 2022 American Chemical Society.

For nanoparticle- or nanocluster-based catalysts, the importance of catalyst size is often noticed.⁴⁸⁴ Catalyst size affects the efficiency of a photocatalytic reaction through the size-dependent Coulomb blockade charging energy for charge transfer and/or the size-dependent activity of catalytic sites. For example, Amirav and co-workers studied Ni-tipped CdSe@CdS NRs with different tip sizes for light-driven H₂ generation (Figure 42C).⁴⁸² The internal QY for H₂ generation increases from ∼7% for the 2.3 nm tip to ∼14% for the 3.1 nm tip and ∼51% for the optimal 5.2 nm tip size, which is followed by a drop to ∼11% for the 8.9 nm tip and finally to ∼6% for the 10.1 nm tip size. This efficiency trend is found to correlate well with the charge separation efficiency determined from TA measurements (Figure 42C). The authors propose that the Coulomb blockade charging energy and a size-dependent Schottky barrier decreases and increases, respectively, with increasing Ni sizes. These two opposing trends result in an optimal Ni size for highest charge separation yield. Similarly, Banin and co-workers also reported an optimal size for the Au domain for light-driven H₂ generation from Au-tipped CdS NRs.⁴⁸⁵ In an earlier work, Schweinberger and co-workers examined the effect of Pt cluster size on light-driven H₂ generation in Pt-decorated CdS NRs.⁴⁸⁶ In their experiment, the size of Pt clusters deposited on CdS NR films can be controlled with an atomic level of precision by using a high-frequency laser ablation technique.⁴⁸⁷ They found that the H₂ generation rate initially increased with cluster size, peaked at Pt46 (a cluster with 46 Pt atoms), and then decreased with cluster size. They propose that the electron transfer rate from the NR to the cluster and that from the cluster to the proton increases and decreases, respectively, with the cluster size.

More recently, Lian and co-workers investigated the detailed mechanisms of light-driven H₂ generation in CdS-Pt nanorods through systematic variation of the Pt size and CdS rod length.^470,471 Using CdS-Pt with the same NR size and length but a different Pt tip size, it was reported that the QE_H2 of CdS-Pt increases from 0.5 ± 0.2% to 38.3 ± 5.1% by nearly two orders of magnitude when the Pt catalyst size increases from 0.7 ± 0.3 to 3.0 ± 0.8 nm, respectively (Figure 42E). This trend is consistent with the results of Amirav and co-workers (Figure 42C),⁴⁸² and Banin and co-workers,⁴⁸⁵ in the small size regime. Using transient absorption spectroscopy, they directly measure the electron transfer rate as a function of the Pt diameter (Figure 42E). The observed trend was understood by a simplified kinetic model shown in Figure 39 A and B, in which the overall efficiency for light-to-H₂ generation is assumed to be a product of the quantum efficiencies of sequential hole transfer (QE_ET), electron transfer (QE_HT), hole scavenging (QE_HS), and water reduction (QE_WR) steps. The quantum efficiencies of both the electron transfer and water reduction steps were shown to increase with the Pt sizes. This work suggests that catalyst size can affect both charge separation and catalysis efficiencies, and both should be considered in designing efficient semiconductor–metal hybrid photocatalysts. This work also reveals that the ET rate from the CdS NR to the Pt tip decreases at smaller Pt diameter following a scaling law of d^5.6, suggesting the challenge in designing nanorod–catalyst hybrid electrodes with small clusters, single-atom catalysts or molecular catalysts. In a related work, Lian and co-workers examine the rod length dependence of light-to-H₂ generation in CdS-Pt nanorods (Figure 42F).⁴⁷¹ In addition to the H₂ generation efficiency, the charge separation and recombination rates were also measured by transient absorption spectroscopy. They observed that QE_H2 increases from 0.2 ± 0.0% in quantum dots to 27.8 ± 0.4% at 28 nm NRs and changes negligibly at longer rod lengths, and QE_HT decreases from 92% at short rod lengths to 70% at long rod lengths (Figure 42F). Analyzing the results using the model shown in Figure 39A and B, Lian and co-workers concluded that the quantum efficiency for hole removal by the sacrificial electron donor (QE_HS) changes with the rod length and is the key factor for the observed rod-length-dependent QE_H2.

Yet another important but often overlooked factor influencing photocatalytic performances of multielectron photocatalytic reactions is the number of catalysts immobilized on each NC.⁴⁸³ Taking the H₂ evolution reaction as the example, generating one H₂ molecule requires sequential absorption of two photons. If there are multiple catalysts on one NC, the first and second photogenerated electrons might be transferred onto two different catalysts. Considering Coulomb repulsion between electrons, this is more likely to take place than the situation of two electrons being transferred to the same catalyst.⁴⁸⁸ As a result, it is difficult to accumulate two electrons on the same catalyst as required for the H₂ evolution reaction. Indeed, Amirav and co-workers compared light-driven H₂ generation performances using CdSe@CdS NRs decorated with a different number of Pt sites (Figure 42D) and found that the QY of NRs decorated with one Pt catalyst was 27%, higher than that of NRs having two Pt catalysts (18%) and that of NRs with multiple Pt catalysts (<1%).⁴⁸³ Similar trends were observed for Pt-decorated CdSe NRs by Bang and co-workers⁴⁸⁹ and for Pt-decorated CdS NRs by Stolarczyk and co-workers.⁴⁹⁰ Therefore, for many of the multielectron solar-to-chemical conversion reactions, such as O₂ evolution and CO₂ reduction,^491−494 one should control the number of catalysts on each NC to be approximately one for the successful accumulation of multiple redox equivalents on the catalyst. This, in turn, can minimize the amount of precious elements (such as Pt, Ru, Re...) used in photocatalysts for cost-effective solar-fuel generation.

6.4. Emerging Photocatalytic Applications Using NCs

The photocatalytic reactions reviewed above are primarily photoreduction reactions utilizing the photogenerated electrons for product formation. The photogenerated holes are often scavenged by sacrificial donors. The chemical transformation of donors induced by the hole is essentially a photooxidation reaction. Therefore, with appropriate choices of donors, it is possible to simultaneously perform photoreduction and photooxidation half reactions to fully utilize the potential energy stored in both photogenerated electrons and holes in NCs.^495−497 For example, thiols that are frequently used as sacrificial electron donors for light-driven H₂ generation can be transformed into disulfides by the holes.⁴⁹⁷ Given the importance of disulfide formation reactions in many systems, Wu and co-workers investigated photodriven disulfide formation using CdSe QDs (Figure 43A).⁴⁹⁷ They found that indeed disulfides formed quantitatively (i.e., with chemical yields approaching 100%) from a variety of thiol molecules and H₂ was generated with the same near unity chemical yield. The QYs of these reactions were not reported. More recently, Wu and co-workers further demonstrated that the thiyl radicals generated from hole oxidation of thiol ligands on CdSe QDs, before being homocoupled to disulfides, can be intercepted by alcohols to perform selective oxidation of alcohols to aldehydes or ketones (Figure 43B).⁴⁹⁸ These reactions can attain high chemical yields (>90%), high site-selectivity (>90%), and good functional group tolerance, suggesting that photocatalysis using NCs may find important applications in the industrial transformation of alcohols.

Figure 43.

Emerging photocatalytic applications of NCs. (A) Proposed mechanism for the photocatalytic conversion of thiol ligands on QD surfaces to simultaneously generate disulfides and H₂. (B) The thiyl radicals generated by the photooxidation of thiol ligands on QD surfaces can be intercepted to perform selective oxidation of alcohols into carbonyl compounds. (C) Photoredox synthesis using CdSe QDs. The photogenerated electron and hole in QDs can act as a one-electron reductant and oxidant, respectively, to perform organocatalysis. (D) Amount of C–C coupling product as a function of time for QDs with varying ligand shell permeabilities. (E) CdS QDs coated with CdO_x shells can perform photoreforming of lignocellulose from various crude sources into H₂. (F) Selective photocatalytic conversion of formic acid into either H₂ or CO using CdS QDs, with the product selectivity controlled by the solvent and particle capping ligand. (A) Adapted with permission from ref (497). Copyright 2014 John Wiley & Sons. (B) Adapted with permission from ref (498). Copyright 2017 John Wiley & Sons. (C) Adapted with permission from ref (499). Copyright 2017 American Chemical Society. (D) Adapted with permission from ref (500). Copyright 2017 American Chemical Society. (E) Adapted with permission from ref (501). Copyright 2017 Springer Nature. (F) Adapted with permission from ref (502). Copyright 2015 John Wiley & Sons.

Photoredox catalysis, sharing the same principle with common photocatalysis, has emerged as a very important research area in organic synthesis. In these reactions, Ru or Ir complexes are frequently used as photosensitizers. The triplet excited states of these complexes can perform one-electron reduction and oxidation reactions to induce important C–C formation schemes. It is thus a natural idea to replace the organometallic complexes with NCs considering the excellent light-harvesting and charge-donating capabilities of NCs. Krauss and co-workers reported that a single-sized CdSe QD (3.0 nm) was able to photocatalyze five different types of photoredox reactions, including β-alkylation, β-aminoalkylation, dehalogenation, amine arylation, and decarboxylative radical formation.⁴⁹⁹ Without optimizations, the efficiency of QDs is already on par with or superior to that of optimal organometallic catalysts reported in the literature, presumably due to the aforementioned advantages of QDs in terms of light-harvesting and charge-donating. In addition, the QD catalysts are effective at extremely low loadings that are 17 orders of magnitude lower than organometallic catalysts. While this work demonstrates the performance and scope of QDs in photoredox catalysis, the work reported almost at the same time by Weiss and co-workers provides mechanistic insights into photoredox catalysis using QDs.⁵⁰⁰ They studied the reaction of C–C coupling between 1-phenylpyrrolidine (PhPyr) and phenyl trans-styryl sulfone driven by photoexcited CdS QDs and found that photooxidation of PhPyr by QDs was the rate-limiting step, consistent with the more sluggish hole transfer compared to electron transfer typical for NCs. The rate of the reaction can be improved by ∼2.3-fold by using QDs with mixed oleate and octylphosphonate ligands, as it increases the ligand permeability and thus facilitates interfacial charge transfer between QDs and substrate molecules (Figure 43D). Photoredox catalysis using engineered core/shell QDs has been reported by the König group⁵⁰³ and Peng group.⁵⁰⁴

Photocatalysis using NCs also find broad applications in photoreforming substrates into high-added-value products. Reisner and co-workers reported light-driven photoreforming of lignocellulose (including cellulose, hemicellulose and lignin) to H₂ using CdS QDs (Figure 43E).⁵⁰¹ As lignocellulose is the most abundant form of biomass on earth, its photoreforming into H₂ may provide a cost-effective approach to large-scale clean production of H₂. The reaction takes place in basic aqueous solutions where CdS QDs form CdS/CdO_x core/shells in situ, which enables the long-term stability of the system. The external QY of the reaction under 430 nm monochromatic light is ∼1.2%, while the QY for photoreforming MeOH reaches 17.7% using the same system, suggesting that photooxidation of the polysaccharide chains is the rate-limiting step. In addition, the system was shown to even be able to reform unprocessed lignocellulose, such as wood and paper. The same group also reported selective photoreforming of formic acid, which is considered as a promising energy carrier and hydrogen storage material, into either H₂ or CO using photoexcited CdS QDs.⁵⁰² Using MPA-capped CdS QDs in combination with a cobalt cocatalyst, the system releases H₂ with >99% selectivity and the external QY under 460 nm monochromatic light reaches ∼21.2%. Using ligand-free charge-stabilized CdS QDs (QD-BF4), the same system releases CO with >95% selectivity and a 19.7% external QY.

NC crystals have been used for many more photocatalytic reactions than we can list here. To name some of them, Garcia-Garibay and co-workers reported the reduction of aromatic azides to amines using CdS and CdSe QDs back in 2004,⁵⁰⁵ Weiss and co-workers reported reduction of nitrobenzene to aniline using CdS QDs,⁵⁰⁶ Ford and co-workers reported the oxidation of 1,1-dithiooxalate to carbon disulfide using CdSe QDs,⁴⁹⁶ Pandey and co-workers reported the aerobic oxidation of boronic acids using CdSe QDs,⁵⁰⁷ and Egap and co-workers reported controlled light-mediated radical polymerization using CdSe QDs.⁵⁰⁸ These reactions involve very different chemicals and substrates, but the physical underpinnings are similar. In general, fast and efficient charge separation and suppressed charge recombination are desired for these reactions. As such, further improvements in their QYs should be achievable by using engineered 0D, 1D and 2D NCs and related heterostructures to facilitate charge separation and suppress recombination losses in these reactions.

While it is essential to suppress the recombination of charge-separated states for the photoredox reactions discussed above, in recent years it has been discovered that charge recombination in QD–molecule complexes can actually generate the triplet excited states of the molecules as long as the energies of the charge-separated states are higher than those of the molecular triplets.^509−523 Thus, sequential charge transfer in QD–molecule complexes opens a pathway to sensitizing the triplet states of the surface-anchored molecules. It turns out that these molecular triplets are also important species involved in many organic photochemical reactions, such as isomerization and [2 + 2] cycloaddition.^524−528 Therefore, QD–molecule complexes can find a broad scope of applications well beyond photoredox catalysis. In principle, they can be adopted in any demonstrated organic reactions driven by charge transfer or energy transfer using Ru- or Ir-based metal–organic complexes.

7. Summary and Outlook

In this Review, we review the progress in understanding charge transfer processes from quantum-confined nanocrystals in model NC–acceptor complexes and in photocatalytic systems. We first introduce the key size-dependent electronic and optical properties of 0D, 1D, and 2D nanocrystals according to the theoretical model of the multiband effective mass approximation. The ability to tune the energetics of conduction band electrons and valence band holes in quantum-confined NCs through their size, morphology, and composition has led to extensive effort in developing nano-heterostructures with desired spatial distributions of electrons and holes and significantly improved properties compared to single-component nanocrystals. We discuss representative time-resolved spectroscopic studies of charge transport and transfer dynamics within these nano-heterostructures.

Electron and hole transfer from quantum-confined nanocrystals and their heterostructures to acceptors have been extensively studied. Because of the strong e-h Coulomb interaction and relatively small energy spacing of the conduction and valence band levels, both electron and hole transfer from the excitonic states of quantum dots were found to follow the Auger-assisted electron transfer model. According to this model, for electron (hole) transfer with a large driving force, the excess energy can be used to excite the hole (electron) to higher energy levels, thus creating a manifold of product states and avoiding the unfavorable Franck–Condon overlap in the Marcus inverted regime. Although the Auger-assisted charge transfer model was only confirmed experimentally for ET and HT from quantum dots, it should be a general model for charge transfer from exciton states of many 0D, 1D, and 2D quantum-confined nanocrystals. Similar to molecular donor–acceptor systems, the ET coupling strength can be conveniently controlled by adding insulating spacers between the NCs and acceptors. A unique way to turn the electronic coupling strength from quantum-confined nanocrystals is to turn their size, which affects the amplitude of wave functions outside the crystal. Unlike molecular chromophores, carriers in nanocrystals can be trapped and can be transferred by a trap-mediated pathway. Most of the ET and HT processes reported so far have been described in the nonadiabatic charge transfer limit. In the presence of strong coupling between the NC and acceptor, ET can occur in the adiabatic limit, especially for strongly quantum-confined nanocrystals. In this limit, NCs show significantly broadened exciton bands due to strong coupling with the acceptor. When ET or HT rates become faster than hot carrier cooling rates within the nanocrystals, hot carriers can be extracted by charge transfer to acceptors. For charge transfer from 1D and 2D nanocrystals, the internal transport of excitons and carriers also plays a role in determining the charge transfer kinetics to acceptors.

The phenomenon of multiple exciton generation has been observed in nanocrystals of various semiconducting materials and has attracted intense research interest because it could be potentially utilized to boost the power conversion efficiency of NC-based photovoltaic devices. In contrast to single-exciton states, the multiple exciton states decay via the Auger process, a significantly faster decay channel, leading to drastically different exciton recombination kinetics. With an assumption of a Poissonian photon absorption in QD ensembles, the number of excitons per dot and their decay pattern can be quantitatively described, and the MEG yield can then be quantified based on this method. For isolated QD–molecular electron acceptor complexes, the multiple exciton states, created either from multiple photon absorption or MEG, can be completely dissociated through ultrafast electron transfer from the QD to the molecule. It has also been demonstrated that the photocurrent of photovoltaic and photoelectrochemical devices based on QD films can also be enhanced by MEG.

Photocatalysis using hybrid nanocrystal/catalysts has been successfully demonstrated, often focusing on the reduction half-reaction with the help of sacrificial electron donor to remove holes. We reviewed representative examples of three major types of NC systems for photocatalysis: NC–molecular catalyst (or enzyme) complexes, NC–mediator–catalyst complexes, and all-inorganic NC–metal particle heterostructures. The mechanisms of light-driven initial charge transfer from NCs to catalysts have been examined by time-resolved spectroscopy in these systems, often monitoring the distinct spectral signature of CB electrons in these NCs and/or PL quenching. While the initial charge transfer can be efficient in some systems, this process alone is not sufficient to guarantee efficient photocatalysis. The overall light-to-H₂ conversion efficiency depends on many forward and backward processes, and detailed mechanistic studies provide helpful guidance for improving the quantum efficiency. Key progresses in such mechanistic studies are also discussed in this Review. Finally, we discuss emerging applications of NCs in photoredox chemistry.

Through the extensive studies in the last 40 years, the field has made significant advances in understanding charge separation and recombination in quantum-confined nanocrystal–acceptor complexes and demonstrated their applications in photocatalysis. There are many opportunities for making further advances in the field. Compared to the light-driven reduction half reactions using quantum-confined NCs, the oxidation half-reactions of the photogenerated holes are less understood. Sacrificial hole acceptors (or electron donors) are often used to rapidly remove the photogenerated holes to suppress electron hole recombination and to improve the efficiency of slow photoreduction reactions. However, this also inevitably introduces the oxidized complexes/radicals and side reactions of the sacrificial donors in the system. For example, the oxidized sacrificial donor can participate in the reduction process and consume the electrons that are supposed to be used for H₂ generation, thus reducing the efficiency. Furthermore, the stability and activity of the sacrificial donors directly determine the oxidation half-reaction and thus the long-term stability and the overall efficiency of the photocatalytic system.

There are opportunities to utilize both the photogenerated electrons and holes for alternative desired photocatalytic reactions. This will require further advances in nano-heterostructure or system design that can produce much longer-lived charge-separated states. NC-based photocatalysis of organic transformations is an emerging field that is attracting intense recent interest.^529−533 These reactions are often conducted in organic solvents, which are more benign toward NCs than aqueous environments. Moreover, such reactions are targeted for high-added-value small molecules and therefore long-term stability might not be a necessity for a practical system. The combination of material composition and size tunability can in principle afford NC-based photosensitizers with desired reduction, oxidation, or sensitization capabilities required for many existing photodriven organic transformations. More specifically, they can be developed as viable replacements for the commonly used noble metal Ru- or Ir-based metal–organic complexes. Although the current mainstream NCs are based on Cd or Pb elements, which might eventually limit their widespread adoption as photosensitizers, NCs free of these elements (such as ZnSe,⁵²⁸ CuInSe₂⁵³⁴) are also being developed for efficient organic transformations.

So far, most studies focus on the performance of model systems and insights of detailed mechanisms, and there are no known reports of long-term stability tests and large-scale applications. The former is limited by the long-term stability of chemical components (e.g., QDs, sacrificial donors, molecular catalysts/enzymes...) involved in the photocatalytic systems. The latter brings more fundamental and technological challenges, including but not limited to materials production and photon collection on a large scale, transfer of charge carriers in a macroscopic QD-based system (e.g., QD films), and the diffusion of chemical components and reaction efficiency in a large-scaled solution. Significant progress has been made in the field of photocatalysis using microcrystals, as either a single entity or in a Z scheme, for unassisted photodriven complete water splitting (i.e., both water oxidation and proton reduction),⁷¹⁻⁷³ which may offer interesting design rules that are applicable to nanocrystal photocatalysis. In addition to band offsets, it would be interesting to explore the possibility to create build-in fields to drive charge separation in nano-heterostructures, similar to those in microcrystals and bulk semiconductors. There have been successful demonstrations of combining redox mediators with nanocrystals to drive light-driven H₂ generation, and further investigation of this approach will likely yield promising improvements, learning from the lessons of natural photosynthetic systems and the microcrystal photocatalysis. Impressive quantum efficiencies have been reported in NC-based systems for the light-driven H₂ evolution half-reaction, but light-driven CO₂ reduction is still relatively inefficient and is an important area for further research. In Pt tipped nanorods, the use of nano-heterostructures with designed electron and hole spatial distribution has led to the improvement of light-driven H₂ generation. It would be potentially beneficial to explore similar approaches in a nanocrystal/molecular catalyst hybrid if strategies for selectively binding molecular catalysts to a specific location of the heterostructure can be developed.

Another potentially promising direction is to use NC solid films instead of colloidal solutions. These films can be used as photoelectrodes for either reduction or oxidation reactions without the need for sacrificial agents. While these films have been used extensive in solar cells, they remain under-explored in photocatalysis or photoelectrochemistry. The fabrication of the films inevitably brings complexity or challenges, such as the stacking order, the ligand on the NCs, the uniformity of size and the energy levels, and the optimized NC spacing in the solids for efficient charge and energy transport. There have been reports of using nanocrystal assembly to improve light harvesting, but further research would be needed to fully exploit the power of this approach, drawing on lessons of natural light harvesting antenna systems. Moreover, the toxicity of the widely used NCs, such as chalcogenides and perovskites involving heavy metals (e.g., Cd, Pb...), is still a challenge for their industrial use. Therefore, the replacement of heavy metals and the synthesis of new NCs with similar or better optical and photocatalytic properties are still necessary.

In summary, with the advances in the synthetic and assembly methodologies, the understanding of charge separation and recombination properties, and the development of design rules, we are hopeful that more advanced nanocrystal-based photocatalytic systems will be developed in the near future.

Biographies

Qiuyang Li received his B.S. in materials physics from the University of Science and Technology of China and a Ph.D. in physical chemistry from Emory University. He is currently a research fellow at University of Michigan–Ann Arbor. His research focuses on ultrafast dynamics and photophysics in new and emerging semiconductors and quantum materials.

Kaifeng Wu obtained his B.S. degree in materials physics from USTC and a Ph.D. in chemistry from Emory University. He worked as a director’s postdoctoral fellow at Los Alamos National Laboratory and currently is a group leader at Dalian Institute of Chemical Physics. He investigates carrier and spin dynamics in low-dimensional materials using ultrafast spectroscopy and explores their relevant applications in energy conversion and quantum control.

Haiming Zhu got his B.S. degree from chemistry from the University of Science and Technology of China in 2008 and a Ph.D. in physical chemistry from Emory University in 2014. Afterwards, he worked as a postdoctoral scientist at Columbia University. He joined the Department of Chemistry in Zhejiang University as a tenure-track professor in July 2016. His research has mainly focused on using ultrafast laser spectroscopy to investigate excited-state dynamics in low-dimensional materials and at interfaces.

Ye Yang received a B.S degree in chemistry from University of Science and Technology of China in 2008 and a Ph.D. degree in physical chemistry from Emory University in 2013. He was a postdoctoral fellow and research scientist in National Renewable Energy Laboratory at Golden, Colorado, from 2014 to 2018. He joined the college of chemistry and chemical engineering at Xiamen University in China as a professor in 2018. His research focuses on photocarrier dynamics in semiconductors, polaron dynamics in transition metal compounds, and in situ detection of ultrafast photoconversion processes in working solar cells.

Sheng He graduated with B.S. degree in applied chemistry from Dalian University of Technology in 2017 and is currently a Ph.D. candidate in chemistry department at Emory University. His research focuses on charge transfer in semiconductor nanocrystals.

Tianquan Lian received his B.S. degree from Xiamen University in 1985, his M.S. degree from the Chinese Academy of Sciences in 1988, and his Ph.D. degree from the University of Pennsylvania in 1993. After postdoctoral training in the University of California at Berkeley, he joined the faculty of chemistry department at Emory University in 1996. He is currently the William Henry Emerson Professor in chemistry. Prof. Lian’s research interest is focused on ultrafast dynamics in photovoltaic and photocatalytic nanomaterials and at interfaces.

The authors declare no competing financial interest.