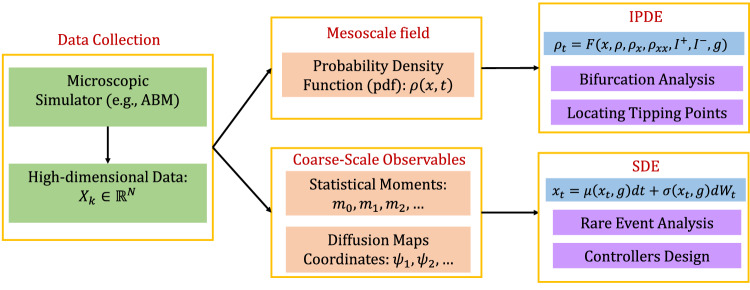
Fig. 4. Schematic of the machine learning-based approach for the multiscale modeling and analysis of tipping points.

At the first step, and depending on the scale of interest, we discover via Diffusion Maps latent spaces using, mesoscopic fields (probability density functions (pdf) and corresponding spatial derivatives) with the aid of Automatic Relevance Determination (ARD); or macroscopic mean-field quantities, such as statistical moments of the probability density function. At the second step, on the constructed latent spaces, we solve the inverse problem of identifying the evolutionary laws, as IPDEs for the mesosopic field scale, or mean-field SDEs for the macroscopic scale. Finally, at the third step, based on the constructed surrogate models, we perform system level analysis, such as numerical integration at a lower computational cost, numerical bifurcation analysis for the detection and characterization of tipping points, and rare event analysis (uncertainty quantification) for the catastrophic transitions occurring in the neighborhood of the tipping points.