Spatiotemporal positioning of multipotent modules in diverse biological networks

Abstract

A biological network exhibits a modular organization. The modular structure dependent on functional module is of great significance in understanding the organization and dynamics of network functions. A huge variety of module identification methods as well as approaches to analyze modularity and dynamics of the inter- and intra-module interactions have emerged recently, but they are facing unexpected challenges in further practical applications. Here, we discuss recent progress in understanding how such a modular network can be deconstructed spatiotemporally. We focus particularly on elucidating how various deciphering mechanisms operate to ensure precise module identification and assembly. In this case, a system-level understanding of the entire mechanism of module construction is within reach, with important implications for reasonable perspectives in both constructing a modular analysis framework and deconstructing different modular hierarchical structures.

Introduction

Modularity is a ubiquitous phenomenon in various network systems [1]. A functional module, composed of many types of interacting molecules, is a discrete entity whose function is separable from those of other modules [2]. Its members have more relations or interactions among themselves than with members of other modules [3], and many cellular functions are carried out by modules [2]. Modular organization has been observed in metabolic [4], transcriptional regulation [5], and protein–protein interaction (PPI) [6] networks. Moreover, the exploration of modular structure has been proposed as a key factor in understanding the complexity of biological systems [7]. Some disease-specific functional modules have been identified in the human disease network [8]. Causative genes for the same or phenotypically similar diseases may generally reside in the same biological module [9]. It is proposed that a disease is a result of the breakdown of a particular functional module [10], and it has been demonstrated that the modular structure is of great significance in aiding the diagnosis, prevention, and therapy of deadly diseases, especially in cancer research [11, 12]. In pharmacological research, a novel concept of modular pharmacology (MP) has emerged recently [13]. Therefore, it is extremely important and necessary to identify functional modules in networks. Furthermore, much of a cell’s activity is organized as a network of interacting modules [14], and altering the connections between different modules may affect changes in cellular properties and functions [2]. Thus, it is also essential to analyze the interactions between modules, and preferably, even to quantify the inter-modular interactions [15]. Additionally, increasing studies indicate that there is a profound interaction between network structure and dynamics, and the dynamic properties of network motifs contribute to biological network organization [16]. For this reason, understanding modularity in molecular networks requires dynamics [17].

Currently, researchers have proposed a wide variety of module identification or network decomposition methods, and on the basis of module identification, researchers have also presented some approaches for analyzing the inter-module relationships as well as the interactions between network modularity and dynamics. Analyses using these methods seem to have reported good results, but in light of the huge number of available methods and a lack of systematic, reasonable classification criteria, there are still many challenges that need to be addressed for practical application. Consequently, this review aims to summarize these methods (or algorithms) proposed in the existing literature, identify the difficulties and challenges we are facing, and thereby attempting to provide potential and reasonable perspectives on the development of more robust methods for deconstructing complex biological systems.

Classification of module identification methods

The first step in understanding the organization and dynamics of cell functions is to identify multiple modules in complex networks. Generally, identifying functional modules from high-throughput data can be formulated as an optimization problem. From an algorithmic viewpoint, the existing computational methods can be classified into two groups: heuristic approaches and exact approaches [18]. These methods rely on a scoring function for subnetworks/modules and an algorithm to find high-scoring subnetworks [19, 20]. Ideker et al. [21] proposed a scoring function (Z-score calculation) and simulated an annealing algorithm to search for high-scoring subnetworks. Dittrich et al. [22] presented a scoring function based on aggregated p values and identified optimal-scoring subnetwork and suboptimal solutions by integer-linear programming (ILP). The difference lies in the fact that exact approaches are able to find optimal and suboptimal subnetworks while heuristic algorithms can only identify high-scoring subnetworks [18], but cannot guarantee to identify the highest scoring subnetwork, that is, heuristic methods do not guarantee to find the optimal solution and are unable to assess the solution quality [22]. Moreover, exact approaches compute optimal solutions without computationally demanding parameter optimization, while this is usually necessary in heuristic approaches [22]. Currently, many different approaches proposed to identify modules can be broadly classified into six major categories as listed in Table 1. We describe the characteristics of these methods briefly below.

Table 1.

Six major categories of module identification methods

Classification of methods	Characteristics of methods	Data sources	Number of modules	Strengths and weaknesses	Network type(s)a	Software	References
Clustering algorithms	Hierarchical average-linkage clustering	Quantified proteomics data, 13 protein datasets	13 modules	The framework may be useful to reliable proteome analyses	Human mitochondrial protein functional network	OC software (cluster analysis program)	[101]
	Module map analysis: (bottom-up) hierarchical clustering to identify gene set clusters; leave-one-out cross-validation to derive modules from gene set clusters	Human DNA microarrays (expression data) + gene sets	456 modules	Advantage: to construct a module map from any collection of gene sets and expression data in any organism. The quality of current annotations and normalization procedures may limit the map’s accuracy	Module map	GeneXPress	[11]
	WGCNA identifies gene modules using unsupervised clustering, the default method is hierarchical clustering and branch cutting method (dynamic tree cut)	Liver expression data from female mice	18 modules	WGCNA implements methods for both weighted and unweighted correlation networks. This package is limited to undirected networks	Weighted and unweighted correlation networks	WGCNA	[102]
	A novel biclustering algorithm: local coherence detection (LCD)	E-MAP datasets for chromosome biology	298 modules	Advantages: grouping one gene into multiple clusters; revealing functional links between complexes or pathways	Epistatic or genetic interactions network	NA	[103]
	Molecular Complex Detection (MCODE)	Yeast protein interaction data set	209 complexes	The algorithm allows fine-tuning of clusters of interest without considering the rest of the network and allows examination of cluster interconnectivity	Protein interaction networks	Cytoscape/MCODE	[25]
	Markov clustering (MCL)	Yeast proteome	189 clusters	The method is suited to the rapid and accurate detection of protein families on a large scale. MCL is remarkably robust to graph alterations	Protein–protein interaction networks	Cytoscape/MCL	[104]
	Markov clustering algorithm (MCL)	Drosophila protein interaction map (DPiM)	556 clusters			Cytoscape/MCL	[105]
	CFinder, a fast program locating and visualizing overlapping, densely interconnected groups of nodes in undirected graphs	PPI of S. cerevisiae	82 communities	CFinder allows for any node to belong to more than one group. It is efficient for networks with millions of nodes	Networks with millions of nodes	CFinder	[56]
	DetMod algorithm	PPI + gene expression data	335 modules	It manages to capture inter-module cross-talk by allowing a controlled degree of overlap among modules	PPI network	NA	[58]
	(1) Hierarchical clustering to get a initial guess for hierarchical organization (2) Heuristic search can perform local improvements to find a much better one	Genetic interaction maps in Saccharomyces cerevisiae	ESP: 113 modules; CB: 242 modules	Advantages: be applied to various existing genetic interaction maps; to elucidate some of the mechanisms underlying the interactions between modules	Genetic interaction maps	NA	[66]
	Learning module networks: (1) PCluster, a hierarchical agglomerative clustering; (2) Expectation Maximization (EM) algorithm	Candidate regulators + DNA microarray data set of S. cerevisiae	50 modules	Generating detailed testable hypotheses concerning the role of specific regulators and the conditions under which this regulation takes place. Automatically select the number of modules for a given data set. Modules are non-overlapping	Gene expression data	GeneXPress	[14]
	Fuzzy c-mean (FCM) clustering and the relative entropy estimate method	Rat CNS gene expression data	5 modules	The method allows a data point to belong to two or more clusters	Gene regulatory network	NA	[67]
Network topology	MoNet: combining new module definition with the relative edge order generated by the G–N algorithm (edge betweenness)	The yeast core protein interaction network from the database of interacting proteins (DIP)	86 modules	MoNet output retains adjacent relationships between modules and allows constructing module interaction web. Limitations: some modules contain proteins related to different biological processes. MoNet is dependent on G–N algorithm	Protein interaction networks	MoNet	[72]
	Betweenness-based partitioning algorithm (extended G–N algorithm), quantitative definition of community	Protein–protein interaction network + microarray datasets	266 modules	/	Weighted graphs	NA	[41]
	(1) Shortest paths through the network are calculated using Dijkstra’s algorithm. (2) Edge-betweenness centrality (EBC) index is calculated for all edges based on the shortest paths in step 1	Rat liver model (consisting of many major pathways)	3 modules	/	Metabolic reaction networks	NA	[37]
	The decomposition method is based on the bow-tie structure and the shortest reaction path length	Metabolic network of Escherichia coli	11 modules	Advantage: combining both the local and global properties of the metabolic network	Metabolic network	NA	[106]
	To automatically decompose biochemical networks into modules using the absence of retroactivity among modules	EGF-signaling network	55 modules	The method can analyze large networks, especially when little a priori knowledge on the structure of the network is available	Signaling networks	MATLAB, ProMoT	[39]
	The approach is based on inherent topological features of hierarchical modular networks. It recognizes hubs and classifies them as independent elements, and reveals modules by removing the hubs	Transcriptional regulatory network of Escherichia coli	62 modules	This method enabled us to reveal natural organization of the TRN	Transcriptional regulatory networks	Cytoscape, mfinder program	[55]
	ModuLand: determination of influence functions; construction of a community landscape; determination of hills of community landscape; determination of a hierarchy of higher level networks	The modular assignment of cAMP-dependent protein kinase family in the yeast protein–protein interaction network	10 highly overlapping modules	Overlapping modules are determined based on node centrality/density values defined by limited network walks started from each edge	Protein structure and metabolic networks	Cytoscape/ModuLand	[64]
	ComCIPHER, a Bayesian partition method to identify drug-gene-disease co-modules underlying the gene closeness data	Drug and disease gene closeness profile data	86 co-modules	Advantages: to investigate drug-disease associations; provide evidence to reveal their mechanisms. Indicator variables provide a relatively clear structure of co-modules	Drug-gene-disease interactome network	comCIPHER	[69]
	Dense module enumeration (DME) algorithm: exhaustively enumerating all modules which satisfy a minimum density threshold	Human protein interaction network with tissue-specific expression data	460 distinct modules	Advantages: completeness guarantee; the possibility of transparent data integration	Weighted protein interaction network	NA	[71]
Modularity optimization	The objective is to find the partition p that maximizes network modularity Q. To identify modules that optimize the network modularity, we implement a greedy optimization algorithm	Human brain structural network construction using cortical thickness from MRI	6 modules	The advantage of this optimization approach is that it takes into account of the heterogeneity of module size observed in real networks	Human brain structural networks	NA	[107]
	Simulated annealing algorithm. We used a simulating annealing algorithm to find the set of modules (i.e., partition) that maximizes modularity	A bipartite network of protein complexes and drugs	23 modules in drug projection, 17 modules in protein complexes projection	It offers the highest accuracy in the detection of modularity in bipartite networks comprising up to a few thousands of nodes	Bipartite network	NA	[42]
	Spectral method: (1) construct modularity matrix and find its leading eigenvalue and eigenvector; (2) divide network into two parts, then repeat the process using generalized modularity matrix. If a split makes a zero or negative contribution to the total modularity, the algorithm ends	A network of books about politics, the vertices represent 105 recent books, and edges join pairs of books that are frequently purchased by the same buyer	4 communities	Spectral algorithm returns results of demonstrably higher quality than competing methods in shorter running times	Multiple networks, e.g., social networks, computer networks, and metabolic and regulatory networks, etc	NA	[45]
	Information-theoretic approach: network information bottleneck (NIB) algorithm	E. coli genetic regulatory network	23 modules	Advantages: correctly assigning nodes to modules; determining the optimal number of existing modules	A number of real world networks	NA	[108]
Seed expansion	Bayesian approach: each interaction is weighted by posterior probability. (1) identify all four-cliques as seeds; (2) these four-cliques are greedily expanded into modules	Probabilistic genetic interaction network obtained by EMAP dataset	27 modules	Bayesian approach outperforms others in efficiently recovering biologically significant modules	Genetic interaction networks	NA	[109]
	CEZANNE: (1) identification of high-scoring seeds; (2) greedy optimization, e.g., node additions and module merges; (3) significance filtering	PPI networks + gene expression data	14 modules	Advantages: it does not require the number of modules to be specified in advance; modules can incorporate genes that are not affected on the transcription level; it can handle not only expression profiles but also any type of data that can be represented as a similarity matrix	PPI network	MATISSE/CEZANNE	[48]
	MATISSE: (1) detection of relatively small, high-scoring gene sets, or seeds, (2) seed improvement, (3) significance-based filtering	Protein–protein/protein-DNA interaction network + gene expression profiles of S. cerevisiae	20 modules			MATISSE	[47]
	(1)Scoring subgraphs: Zm score; (2) Iterative greedy searching: a seed module is assigned; identify neighborhood interactors; module expanding process	GWAS + PPI (breast cancer GWAS and pancreatic cancer GWAS)	Breast cancer: 93 modules; Pancreatic cancer: 93 modules	It has the advantage of searching whole interactome and examining the combined effect of multiple genes in an exhaustive manner	Protein–protein interaction networks	dmGWAS	[70]
Matrix decomposition/factorization	Singular value decomposition (SVD)	Two time series microarray data sets of M. drosophila	8 modules	Advantages: the correlations among genes can be considered in the initial stage; the complicated patterns can be easily captured; the implementation is less subject to the restrictions on the number of time points of temporal microarray data	Gene expression data	svdPPCS	[49]
	Two-stage matrix decomposition: firstly by the non-linear independent component analysis (NICA), and then by the probabilistic sparse matrix factorization (PSMF) approach	Yeast microarray dataset	30 modules	Advantages: taking into account the non-linear structure existed in the data; identifying genes of the similar functions yet without similar expression profiles; assigning one gene into different modules; avoiding the singularity problem in matrix decomposition	Transcriptional regulatory networks	ModulePro	[110]
	Knowledge-driven matrix factorization (KMF): firstly using the gene expression data to estimate a correlation matrix, and then factorize the correlation matrix to recover the gene modules and the interactions between them	250 genes selected from hepatocellular carcinoma (HepG2) cells cultured in different free fatty acids (FFAs)	9 gene modules	Advantages: (1) derives both gene modules and their interactions from a combination of expression data and GO information; (2) incorporates the prior knowledge of co-regulation relationships into the network reconstruction using a regularization scheme	Phenotype-specific gene networks	NA	[74]
	Mutual exclusivity modules (MEMo): build binary event matrix of significantly altered genes; Identify all gene pairs likely to be involved in the same pathway; Build graph of gene pairs and extract cliques; Assess each clique for mutual exclusivity	Glioblastoma multiforme (GBM) data	8 modules	Advantages: integrating mutation and copy number data; automatically identifying new candidate driver networks in diverse cancer types Limitations: depends on prior biological knowledge to connect gene pairs	Oncogenic network	MEMo	[111]
Comparative network analysis (network comparison)	Functional similarity-based network alignment algorithms	Human network aligned to yeast network	94 modules	Disadvantage: it offers limited coverage compared to graph clustering methods. It highly depends on graph topology for correct results	Protein interaction networks	NA	[51]
	Multiple network alignment (three-way network comparisons)	Three-way alignment of protein–protein interaction networks of C. elegans, Drosophila, and Saccharomyces cerevisiae	183 protein clusters and 240 conserved paths	Advantages: to detect both paths and clusters; incorporates probabilistic model for protein interaction data; laying out and visualizing the resulting conserved subnetworks	Protein–protein interaction networks	NetworkBLAST	[112]
	Integrating genetic and physical interactions; between-pathway or within-pathway models are identified using a probabilistic scoring scheme	Combined genetic and physical networks in yeast	360 between-pathway and 91 within-pathway models	/	Genetic interaction network	NA	[89]
	MetaPathwayHunter: given a query pathway and a collection of pathways, finds and reports all approximate occurrences of the query in the collection, ranked by similarity and statistical significance	Genome-scale metabolic networks of the bacterium E.coli and the yeast S. cerevisiae	62 metabolic pathways	/	Metabolic pathways	MetaPathwayHunter	[113]

NA means no software available

"/" Denotes that the contents were not found in the literature

Denotes that overlapping modules were identified in the literature

Indicates that a module interaction network was constructed or the interactions between modules were analyzed in the literature

^aThe network type is the primary network where the method has been tested in the literature, but many methods are also applicable to other types of molecular networks

Traditional clustering algorithms, including hierarchical clustering [23] and partitional clustering, e.g., k-means clustering [24], are extensively used for identifying highly connected clusters or modules in biological networks. A large number of graph clustering-based methods have also been developed to identify functional modules, including Molecular Complex Detection (MCODE) [25], Markov clustering (MCL) [26], affinity propagation [27], ClusterONE [28], Super-paramagnetic clustering (SPC) [29], etc. Additionally, some researchers present a novel graph entropy-based clustering algorithm that tries to find a partition with low entropy and keeping in mind the modularity, and performs well in identifying functional modules/communities [30–32]. The strength of these clustering methods is that they uncover structures within biological networks, even when nothing is known about individual proteins; however, there are still some limitations for clustering methods; for example, they rely on the available functional annotation of identified modules to interpret biological roles, e.g., GO term enrichment analysis [33], and they depend on certain parameters or measurement criteria that, when modified, can generate different modules.

Network topological approaches decompose the interaction network into subnetworks mainly based on some topological properties, e.g., degree [34], edge betweenness in the G–N algorithm [35], or edge-clustering coefficient [36]. Such a method requires only the structure of the network, and it usually combines graph theory or clustering algorithms with certain topological properties to identify modules [37, 38]. Moreover, in consideration of directionality and retroactive connectivity (cyclical or retroactive interactions between network components) in signaling and metabolic networks, module detection based on “retroactivity” has also been proposed [39, 40]. However, one of the shortcomings is that it is very difficult to partition PPI networks using algorithms based solely on topology because of a very high degree of inter-module crosstalk [41].

Besides, modularity optimization is a popular method for module/community detection. By assumption, high values of modularity indicate good partitions [23], and thereby the principle of this method is to maximize the modularity. There have been several suggested algorithms, including simulated annealing [42], greedy algorithms [43], extremal optimization [44], and spectral methods [45]; the latter three are better suited to deal with very large networks (sizes of millions of nodes). The spectral method is usually combined with modularity optimization to find the community structure in complex networks, using the eigenvalues and eigenvectors of the modularity matrix [45, 46]. However, it requires constructing an ensemble of randomized networks to evaluate the statistical significance of the modularity of each network. Therefore, the modularity maximum of a network reveals a significant modular structure only if it is appreciably larger than the modularity maximum of randomized networks of the same size and expected degree sequence [23, 42].

In addition, the approaches of seed expansion usually propose a probabilistic model to assign a weight (probabilistic/confidence score) to each interaction or each pair of genes and extract q-connected seeds, then use a heuristic algorithm (e.g., greedy algorithm) to optimize the initial seeds while maintaining their q-connectivity. Finally, these seeds are expanded into modules by node addition, module merges, node removal or reassignment [47, 48].

Matrix decomposition/factorization has also been used to identify modules, such as singular value decomposition (SVD) [49]. SVD assumes that the data matrix is in the form with genes in rows and arrays in columns. Given a cutoff and a direction (positive or negative), a gene group (i.e., a functional module) that is naturally a co-expression cluster can be extracted. A main challenge in implementing SVD-based module identification algorithms is how to choose the cutoffs [49].

Given two or more networks, comparative network analysis is often used to identify modules across networks or species. There are three modes of comparison: network alignment is applied to two or more networks of the same type across species to detect conserved subnetworks; network integration combines several networks of different types for the same species to study their interrelations; and network querying is to identify subnetworks in a given network that are similar to the query of interest [50]. However, network comparison offers limited coverage compared to clustering methods, and they are highly dependent on the graph topology for correct results, thus error rates pose a special challenge [51].

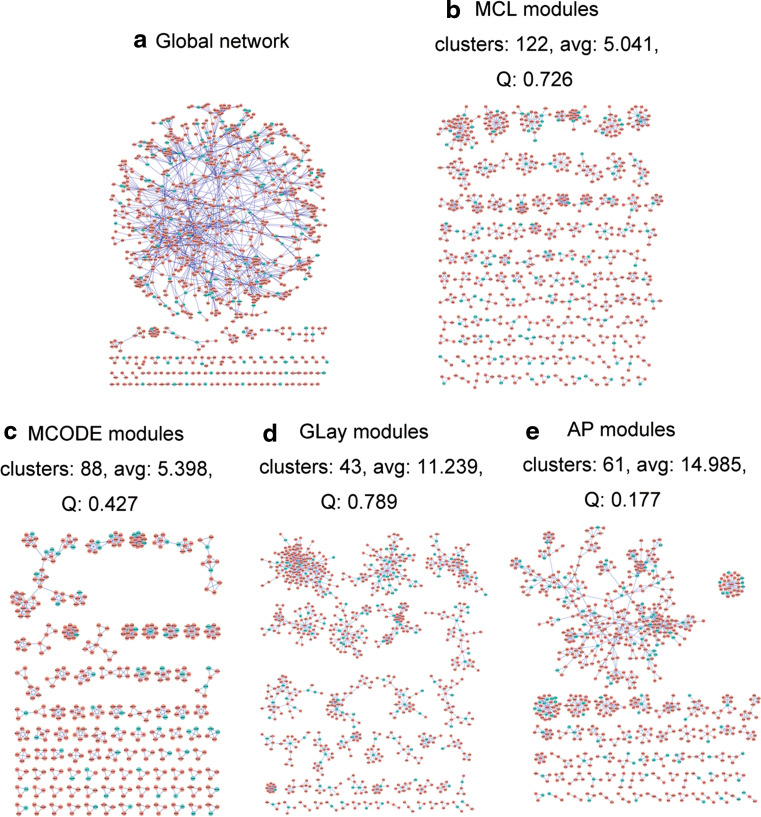
Next, we would like to give an example to evaluate the consistency of the results obtained from different identification methods. We used 258 stroke-associated genes downloaded from Online Mendelian Inheritance in Man (OMIM) [52] in February 2012 to construct a global network via the Agilent Literature Search plugin (version 2.77) in Cytoscape (version 2.8.2), which contained 989 nodes and 2,167 edges (Fig. 1a). We applied four different methods successively and independently to identify functional modules from this network, including MCL (inflation = 2), MCODE (degree cutoff = 3, haircut = true), Community Clustering (GLay) [53], and affinity propagation [27] (lambda = 0.5, preference = −1.0, iterations = 10). Finally, modules identified by the four methods were found to be inconsistent (Fig. 1b–e), and regression analysis of the four methods’ results showed that there were no significant correlations between the number of modules and modularity, average size of modules and modularity, or average size of modules and number of modules, indicating that the four methods are very different from each other depending on their basic principles.

Fig. 1.

Graphical representation of the global network and comparison of MCL, MCODE, GLay, and affinity propagation results. a The global network containing 258 stroke-associated genes downloaded from the OMIM. The blue-green nodes denote the 258 genes we entered. Average size (avg), modularity (Q), affinity propagation (AP). b 122 functional modules identified by MCL (size ≥3), average size: 5.041, maximum size: 45, minimum size: 3, modularity: 0.726. c 88 functional modules identified by MCODE, average size: 5.398, maximum size: 51, minimum size: 3, modularity: 0.427. d 43 functional modules identified by GLay (size ≥3), average size: 11.239, maximum size: 146, minimum size: 3, modularity: 0.789. e 61 functional modules identified by affinity propagation (size ≥3), average size: 14.985, maximum size: 681, minimum size: 3, modularity: 0.177

Overlapping and non-overlapping functional modules

From a structural point of view, there are two forms of identified modules, i.e., overlapping and non-overlapping modules. Some of the approaches mentioned above can produce both overlapping and non-overlapping modules (Table 1), while other methods tend to generate exclusive (non-overlapping) modules.

Generally speaking, modular overlaps show that nodes or links may belong to two or more modules [54, 55]. Several common clustering algorithms, including CFinder [56, 57], MCL [26], MCODE [25], DetMod [58], ClusterONE [28], and MINE [59], permit overlaps between the modules, or in other words nodes may be assigned to multiple clusters. CFinder is a fast program for locating and visualizing overlapping dense groups of nodes in networks, based on the clique percolation method (CPM), which is one of the most popular methods to identify overlapping communities [60] and locate the k-clique percolation clusters of the network. Farkas et al. [61] also introduced CPMw for weighted networks, an extension of CPM that includes an additional clique filtering step, and both of them allow modular overlaps. Additionally, Sameith et al. [62] applied iterated simulated annealing to discover potentially overlapping sub-networks in a large network of physical interactions. Bachman and Liu [63] presented a pattern-based network decomposition method by using sub-graph queries, and this method extracted “shared member” modules matching the topologies of query patterns. A recent study introduced an integrative method family for determining extensively overlapping network modules, called ModuLand, which is based on the novel concept of understanding the overlapping modules as hills of an influence function-based, centrality-type community landscape. The x–y plane of a community landscape is a conventional 2D visualization of the network, while the Z axis represents community centrality. Community centrality represents an integrated measure of the whole network’s influence to one of its edges or nodes. Hills of the community landscape correspond to network modules yielding extensive overlaps [64], and the authors showed the utility of the ModuLand method family to determine overlapping modules in a variety of model and real-world networks [64]. Besides, Nepusz et al. [65] proposed fuzzy community detection in networks, and their approach allowed each vertex of the graph to belong to multiple communities at the same time, determined by exact numerical membership degrees. Furthermore, researchers also analyzed the importance of detecting overlapping modules in complex networks. Modular overlaps are the primary transmitters of network perturbations and signal transduction and are key determinants of network cooperation [54]. Overlapping nodes are also the predominant sites of modulation during cellular adaptation. These properties of modular overlaps all suggest the importance of these proteins as potential drug targets, and imply the necessity of multi-target drugs. Thus, modular overlaps of PPI and signaling networks may be of key importance in future drug design [54].

On the contrary, some other methods are inclined to identify non-overlapping modules of genes, and by eliminating their overlap, generate a coherent network structure describing both the intra- and inter-modular interactions [66]. Zhang et al. [67] used a hybrid of particle swarm optimization and recurrent neural network (PSO-RNN) methods to infer the underlying network among the modules. Ariel et al. [66] introduced a computational approach based on the minimum description length principle to construct module hierarchy. Their method allowed to identify large parent modules with more general functions that contained sub-modules with more specific functions, and finally showed that revealing the intra- and inter-modular interactions enabled insights into the function of cellular machineries. In another study, the authors developed the Prism algorithm, which hierarchically clusters interacting genes into modules that have strictly monochromatic interconnections with each other (i.e., with purely aggravating or purely buffering epistatic links). These results suggest a new definition of biological modularity, which emphasizes interactions between, rather than within, functional modules [68]. Additionally, Zhao and Li [69] proposed a concept of “co-module”, which is characterized by closely related drugs, diseases and genes, and developed a novel co-module approach to discover drug–gene–disease relationships.

Ranked modules based on structures or functions

The importance or the weight of each module in complex networks should not be identical, and some modules may play vital roles and take a very central position in a network. Typically, there are two situations: one is that the identified modules are sorted by a ranking criterion, such as p value [14], module score [70], module size [48], cross-validated classification accuracy [62], etc. Georgii et al. [71] ranked modules by their probability values, and they claimed their ranking scheme was more principled than the ranking criterion used by Bader and Hogue [25], which was the product of size and density.

Considering the relationship between modules, the other is to reconstruct a module interaction network. In Fig. 2, we also constructed a module interaction network using modules identified by MCODE in the OMIM stroke-associated genes network, which concisely represented a complete view of the interconnections among the 88 modules with a size ≥3 nodes (Fig. 2). This may facilitate to visualize the high-level relationships among modules within larger interaction networks [62, 68, 72–74]. In addition, several important topological concepts involved in the interactions or interconnections among modules have been proposed, including bridges, inter-modular hubs, bottlenecks, etc. All of them connect different modules, occupy an inter-modular position, and they have been proposed as attractive drug targets [7]. Commonly, in the module interaction network, each module is shrunk into a node, i.e., each node represents a module, and each edge denotes the interaction between modules. Moreover, some approaches are able to analyze the importance of interacting modules quantitatively through assigning a weight to each node or edge in module networks. Luo et al. [72] constructed an interaction network of modules based on edge betweenness scores, and in the network the width and grayscale of edges reflected the order of edge deletion in the Girvan–Newman (G–N) algorithm, which also represented relative relationships among modules. Ulitsky et al. [73] developed four methods (‘Alleviating’, ‘Correlated’, ‘Alleviating Connected’, and ‘Correlated Connected’ models) to identify distinct functional modules, and constructed a map of modules. The edge width was inversely proportional to the average S-score between two modules: thicker edges corresponded to stronger aggravating genetic interactions, while dashed edges corresponded to weaker aggravating genetic interactions. Yang et al. [74] reconstructed a gene module network by knowledge-driven matrix factorization (KMF) algorithm, and each element C _i,j in the generated C matrix represented the strength of the interaction between modules. A higher C _i,j value, suggesting stronger interaction, was indicated by a thicker and darker edge line; whereas a higher ‘sum’ value in the C matrix, suggesting that the module was more highly correlated with the other modules and thereby took a more central position in the overall gene module network, was indicated by a larger and darker node.

Fig. 2.

The interaction network of modules. The module interaction network is constructed using modules identified by MCODE in the OMIM stroke-associated genes network mentioned in section Classification of module identification methods. It represents the interconnections among 88 modules with a size ≥3 nodes identified by MCODE. The blue-green nodes denote the 258 stroke-associated genes we entered. Each lilac square denotes a module. Blue edges denote the inter-module connections and intra-module connections

In addition, there are other methods based on functional categories to arrange modules. According to a functional classification of genes in modules, Singh et al. [75] determined specific functions which modules were enriched in, and then arranged modules using distinct functions. Chen et al. [76] identified different sub-networks representing key functional units in the co-expression network, and found that the contributions of each sub-network to complex disease traits were not equal. Only one in five sub-networks was very significantly enriched for expression traits supported as having a causal relationship with all metabolic traits tested, directly implicating this sub-network as a key mediator.

Dynamic features of functional modules

Although cellular behaviors are dynamic, most available biological data are static, or only correspond to snapshots of cellular activity [77], and thus the majority of approaches listed in Table 1 have only focused on static properties. However, it has been demonstrated that the dynamic molecular interactions play a central role in regulating the functioning of cells and organisms [78], and a dynamic perspective is essential to grouping molecules into modules and determining their collective function [17]. Therefore, modular analysis needs to incorporate network dynamics. The shift from static to dynamic network analysis is essential for further understanding of molecular systems. Many of these existing approaches have inferred and analyzed network dynamics by integrating static molecular interaction data sets, such as PPI network [77] and metabolites profiles [79], with other types of dynamic data, such as gene expression data, coexpression data, phenotypic responses to perturbations like gene knock-outs or knock-downs, and information about expression quantitative trait loci (QTL) [78]. Modules change and vary over ontogenetic and phylogenetic time [80], and studies have provided evidence for dynamic modularity in protein interaction networks [6, 81]. In dynamic functional modules, interactions are not realized at the same time or place, actually the corresponding physical interactions occur at different times and/or different spaces [6, 29]. Furthermore, phenotypic variation is often an outcome of modular change [80]. For example, it has been shown that changes in dynamic network modularity may provide a prognostic signature for patients with breast cancer [81].

A number of methods and models have been proposed to determine molecular network dynamics, such as Dynamic Bayesian Networks (DBNs) [82, 83], network component analysis (NCA) [84, 85], dynamic flux balance analysis [86], and state space model [87] (Table 2). Kholodenko et al. [15] proposed a framework of modular response analysis to determine molecular network dynamics. A series of different perturbations affected each module separately. The modular response analysis was able to quantify the strength of interaction between the modules, generating a dynamic modular network. Additionally, an analysis of hubs identified two types of hubs: ‘party’ hubs (i.e., intramodular hubs), which interact with most of their partners simultaneously (static hubs), and ‘date’ hubs (i.e., intermodular hubs), which bind their different partners at different times or locations (dynamic hubs). Arguably, hubs play important roles in network modularity and dynamics [6, 78, 81, 88].

Table 2.

Examples of dynamic network analysis methods

Classification of methods	Characteristics of methods	Data sources	Number of modules	Strengths and weaknesses	Network type(s)a	Software	References
Dynamic Bayesian Networks (DBNs)	DBN inference algorithm: searching for high-scoring networks that describe probabilistic relationships between discrete variables. (1) Bayesian scoring metrics; (2) search heuristics; (3) influence score	Gene expression data	/	Advantages: to infer cyclic phenomena such as feedback loops; infer direction of causality because they incorporate temporal information. Limitation: imprecision	/	/	[83]
Network component analysis (NCA)	NCA is an approach that can predict transcription factor activities over time as well as the relative regulatory influence of transcription factors on each target gene	Gene expression data + regulatory network	/	Limitations: difficult to predict the direction of transcription factor activity; inability to incorporate time course information from the data set	Transcriptional regulatory networks	/	[85]
State space model	State space model automatically identifies the temporal aggregations of the gene expression profiles and assembles them into large scale gene networks	Time-course microarray gene expression profiles	/	The state space model has the potential to infer large-scale gene networks, but its applicability is limited by when the length of time series is exceedingly short, e.g., <10	Gene networks	TRANS-MNET	[87]

"/" Denotes that the contents were not found in the literature

^aThe network type is the primary network where the method has been tested in the literature, but many methods are also applicable to other types of molecular networks

Conclusions

Modularity is a very important property in genomic complex networks, and modular research can help us better understand the functions and properties of those networks. Although researchers have proposed a variety of module identification approaches, due to the lack of a systematic and reasonable framework to guide the application of these methods, and in light of the fact that some methods do not have a clear scope of application, we still face many difficulties and challenges in practical applications in the future. For example, as the number of functional modules in a given network is unknown in advance, different results may be generated when different module identification methods are applied to the same network, like different numbers of modules, or different module sizes (Fig. 1). And even the same method with different parameter settings may also generate different modules; for example, Markov clustering is dependent on the inflation parameter used. The value of the inflation parameter strongly influences the number of clusters. Moreover, with regard to the overlapping functional modules, some methods are able to identify overlapping modules, while other methods are not. However, in reality, most real networks should involve overlapping modules. The noise and incompleteness of the available PPI data may increase difficulties in modularity research. Confronting these challenges, we propose two potential perspectives listed below.

A reasonable framework is required to guide modular analysis

Firstly, modular analysis mostly depends on high-throughput experimental data, especially that PPI data are usually utilized to construct a background network. The available PPI data, however, are often noisy and incomplete with high false-positive and false-negative rates. To address this problem, one effective solution is data integration. As shown in Table 1, gene expression data, protein-DNA regulation, genetic interactions [89], phenotypic profiles [90], and metabolic information [91] have been integrated with PPI data to identify functional modules. A lot of other information from multiple levels, such as protein complexes, pharmacological data, disease information, and drug targets, can also be incorporated together to construct background networks, e.g., bipartite networks [42]. Therefore, integrating diverse data from multiple levels may provide a reliable foundation for modular analysis.

Secondly, facing such a variety of methods, which one is more appropriate for identifying modules in a given network? And how does one assess the performance of different algorithms? In the published literature, researchers usually compare or evaluate the performance of various algorithms based on benchmark graphs, e.g., the benchmark used by Girvan and Newman [35], and the benchmark graphs provided by Lancichinetti et al. [92]. However, these benchmark graphs have been criticized recently due to their limited capacity to reflect the complexity of real-world networks [23]. Unlike benchmark networks, we do not know the “correct” modules of the network in advance. As a result, it is quite necessary to set up systematic and reasonable criteria to guide the application of these approaches and evaluate their performances in real-world settings. Since the existing methods are mainly based on network topology or mathematical relationships, we suggest assessing functional modular analysis by incorporating the notion of entropy. The entropy of a random variable quantifies the uncertainty or randomness of that variable [93]. We consider that the ultimate purpose of module identification is to find a stable modular state, which should have the minimum uncertainty. Since the number of modules in a given network is uncertain in advance, what we can do is to try to minimize the uncertainty. The minimum entropy means the minimum uncertainty, and thus we propose to evaluate the results of module identification in the light of minimum entropy criteria. As of now, only a few pertinent reports have been published. For example, in addition to the graph entropy-based clustering algorithm mentioned in the section Classification of module identification methods [30–32], Varadan et al. [94] presented an approach of entropy minimization to identify modules of genes directly from gene expression data. Due to the limited literature available, more research in this area is still required.

Deconstructing different modular hierarchical structures

Generally speaking, modular structures can be broadly classified into two categories, i.e., intramodular structure and intermodular structure. As reflected in network topology, the difference between the two is that there are dense connections within the module, but only sparse connections between different modules [45], and corresponding to these structures, two types of hubs are uncovered in the organized modularity model: “party” hubs (i.e., intramodular hubs), and “date” hubs (i.e., intermodular hubs). Date hubs represent a global, or “higher level”, connectors between modules, whereas party hubs function inside modules at a “lower level” [6, 81]. Moreover, Arenas et al. [95] defined the contribution matrix C of N nodes to M modules, the mathematical object containing all the information about the partition of interest. The rows of C correspond to nodes, and the columns to modules, and then they used truncated SVD to extract the best representation of this matrix in a plane. The analysis of this projection helped to scrutinize the skeleton of the modular structure, revealing the structure of individual modules and interrelations between modules. In previous sections, we introduced bridges and bottlenecks, which should belong to intermodular structure, and to some extent, modular overlaps, bridges, inter-modular hubs, and bottlenecks may reflect the interrelations between different modules.

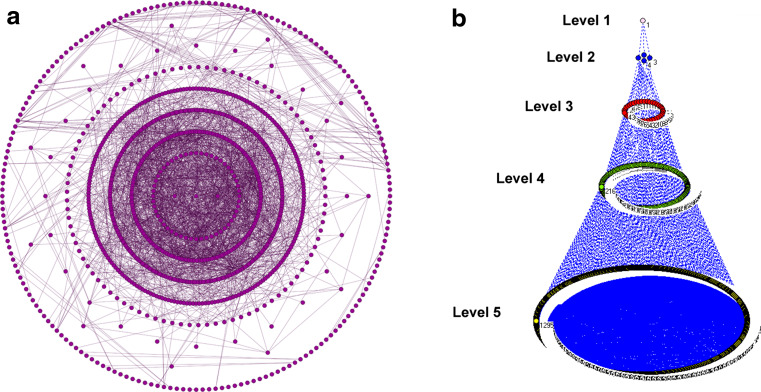
Additionally, it is widely accepted that hierarchical organization is a fundamental characteristic of many complex networks, implying that small groups of nodes organize in a hierarchical manner into increasingly large groups [4, 96]. Metabolic networks exhibit hierarchical modularity in the form of modularized bow-tie units, which are hierarchically nested and reoccur at different scales and levels, and then coupled level-by-level into a larger network [4, 97]. A structural module at a higher level should contain multiple structural modules at lower levels [80]. Some algorithms, like hierarchical clustering, can destruct this kind of organization by tuning a cutoff. The ModuLand method mentioned above can also identify several hierarchical layers of modules, where meta-nodes of the higher hierarchical level represent modules of the lower level [98]. As shown in Fig. 3, we constructed the hierarchy of the OMIM stroke-associated genes network, generating a total of seven hierarchical levels (Fig. 3a). In the stroke-associated genes network treated with cholic acid (CA), which has obvious therapeutic effects in the treatment of cerebral ischemia–reperfusion injury, a hierarchy of five levels was discovered using Pyramabs [99], a complex network analysis tool. Level 1 comprised one module, and the module was further divided into four modules at level 2, and so on. The original network was at the bottom (level 5) (Fig. 3b). In addition, a recent study also suggested the existence of spoke-like modules as opposed to the “deterministic hierarchical model” [100].

Fig. 3.

Different modular structures. a Hierarchical organization of the OMIM stroke-associated genes network. The hierarchy of the OMIM stroke-associated genes network mentioned in section Classification of module identification methods was constructed, generating a total of seven hierarchical levels. b Hierarchical organization of the stroke-associated genes network treated with cholic acid (CA), which has obvious therapeutic effects in the treatment of cerebral ischemia–reperfusion injury. The hierarchical levels were constructed using Pyramabs [99], a complex network analysis tool. There are five levels in the hierarchy. From level 1 to level 4, each circle represents a module. The original network is at the bottom (level 5). Higher-level networks are an abstraction of the next lowest network. Vertical relationships are denoted by blue dashed lines

Then, besides the structures mentioned above, are there any other structures? How to determine the key or core modules in a modular network mentioned above? And how to analyze the transformation between key modules and other modules? All of these questions remain to be answered. Therefore, functional module identification is just a start, and it is still necessary to develop corresponding methods to deconstruct different modular structures and conduct in-depth investigations into the inter-module relationships.